1. Introduction
Fiber grating can be used as narrow-band reflecting face to form a laser for sensing. The combination of light source and sensor improves signal–noise ratio as well as testing system performance, so that it is greatly applied in the domain of weak signal detection.
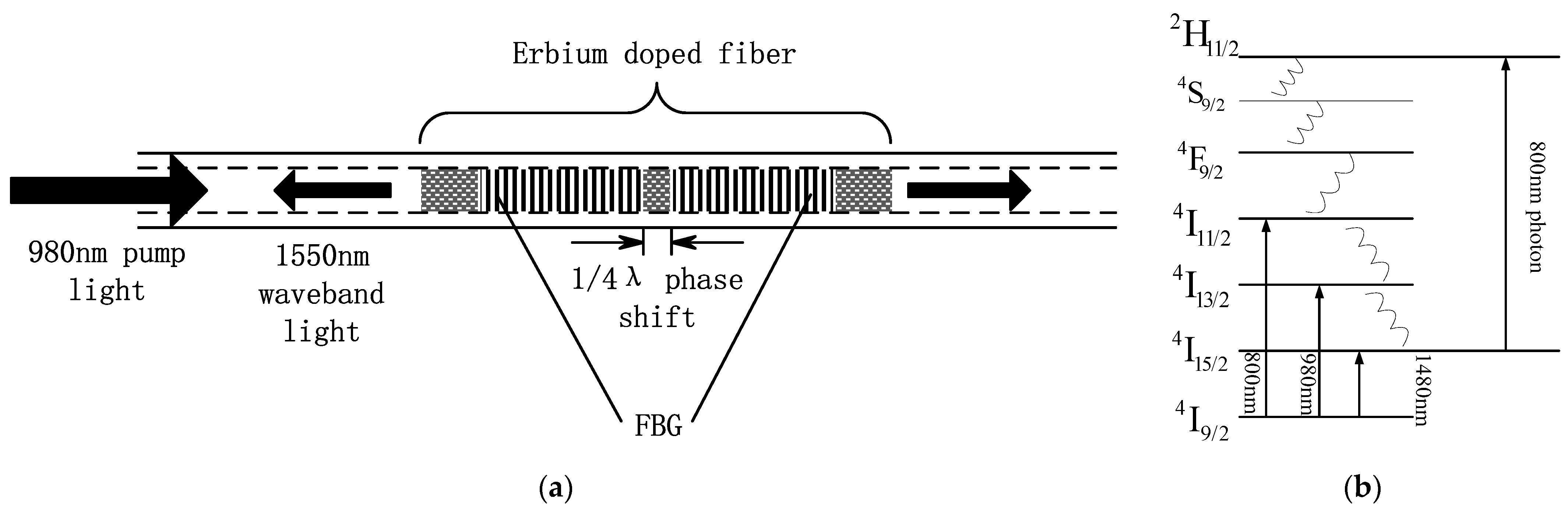
The structure of a distributed feedback (DFB) fiber laser is illustrated in
Figure 1a. A centimeter-level grating is carved on a section of fiber containing rare earth ions (e.g., Er
3+, Er
3+/Yb
3+) to form a linear resonator. The rare earth ions are taken as the medium for laser gain. For instance, in an erbium-doped optical fiber with Bragg grating, there are several pumping options, as given in
Figure 1b: Energy level of erbium ions. It is evident that excited state absorption (ESA) occurs at the wavelength of 800 nm, but not at 980 nm and 1480 m. The 980 nm light pumping of a three-energy-level system is highly efficient. Hence, a DFB light laser often uses 980 nm light pumping. After 980 nm pumping light enters the laser, erbium ions in the laser absorb a portion of light energy to excite Er
3+ transition from ground state energy level to extremely unstable high energy level. Without radiation, the quick transition to a higher energy level facilitates gradual energy accumulation to achieve the population conversion between higher and lower energy levels. The ions at the higher energy level transit to the ground state energy level through stimulated transition or spontaneous radiation. The generated energy amplifies the light of the 1550 nm waveband. When the energy of the radiation light exceeds the total loss in the resonator, the DFB fiber laser radiates the laser of the corresponding wavelength.
When the phase shift π is introduced, the resonant wavelength of the zero-order mode is the Bragg wavelength, which has the lowest gain threshold. Along with the increase in pumping light power, vibration happens first to the zero-order mode and massively consumes the gain particles at the excited state. Other modes are inhibited in this process, which is known as mode competition. The introduction of the phase shift π enables a DFB fiber laser to realize the stable output of a narrow line width and single longitudinal mode [
1,
2].
With such features as a higher sensitivity, lower line width and shorter cavity length, DFB fiber lasers can be packaged and used as fiber laser hydrophones (FLH) with a slender cylindrical structure. By virtue of optical multiplexing, FLHs can be formed into underwater acoustic detection systems such as flank arrays and thin-line towed arrays. Because of their compact structure and good applicability to small underwater mobile platforms, these FLHs can drive the significant improvement of underwater detection capability, which therefore attracts much research interest around the world [
3,
4]. As the sensing units of FLHs, DFB fiber lasers rely on the packaging technique for sensitivity enhancement and protection. Presently, packaging is often achieved in a bended beam [
5,
6,
7,
8], laterally compressed [
9,
10], or axially tensioned structure [
11,
12,
13,
14]. Among them, an axially tensioned packaging structure is favored and widely applied because of its simple structure and good consistency.
Huang from the Naval University of Engineering, China, borrowed the “axially tensioned” packaging structure to explore FLHs, and preliminarily devised two symmetric hydrophone structures, that is, polyurethane tensioned and metallic diaphragm tensioned. A polyurethane tensioned hydrophone responded flatly to the low frequency below 1 kHz in towed arrays, while a metallic diaphragm tensioned hydrophone clearly experienced a resonant peak in the response to 400 Hz [
15,
16].
In the low frequency range, a fiber laser of “string structure” is prone to flexural interference under the effect of sound waves, which becomes a major origin of oscillation in the frequency response of hydrophones.
As early as in 2003, Tikhomirov from Australia’s Defense Science and Technology pointed out the fiber flexure caused by sound waves as the principal interference with the response of fiber lasers for the first time. He also preliminarily tested and verified this theoretical finding in air [
17]. Song analyzed a metallic diaphragm tensioned hydrophone when a fiber laser was rigidly attached at both ends. The hydrophone experienced a dramatic fluctuation of frequency response near the first-order natural frequency of the fiber laser [
18]. Chandrika from the National University of Singapore adopted the method of controlling pre-stress to make the natural frequency of the fiber laser in axial tensile package far away from the working frequency band and reduce its vibration sensitivity [
12].
Therefore, theories, simulation and experiments for the flexural vibration of a fiber laser is established in this paper, using the polyurethane tensioned structure of a hydrophone. Considering the flexural interference with a fiber laser at low frequencies, this paper is used to further explore the frequency response anti-interference mechanism of an axially tensioned FLH at low frequencies.
2. Materials and Methods
The research group designed a polyurethane tensioned fiber laser hydrophone (FLH) for towed arrays as shown in
Figure 2. A fiber laser was located on the central axis of a sleeve with holes at all sides. Polyurethane was filled on both sides to attach the laser as an element for enhancing sensitivity by virtue of tension. End caps were mounted outside the polyurethane for further structural protection.
In the characteristic analysis of flexural vibration, a fiber laser is fixed at both ends, and relies mainly on own stiffness for elastic recovery. In this case, it functions like a beam, and can therefore be analogically analyzed with a beam model. Based on its operating principles, as given in
Figure 3, an FLH can be simplified into a beam with both axial and radial springs at both ends. Under the effect of the axial sound pressure
, a sensitivity enhancement element serves like an axial spring and stretches to enhance sensitivity, causing an effectively amplified variation of a grating center wavelength. Differently, lateral sound pressure
results in the lateral interference with a fiber laser. It is believed that the lateral spring has lower stiffness in flexible attachment, but higher stiffness in rigid attachment. At this time, the triggering of lateral interference with the fiber laser is decisive to the flatness of the hydrophone’s frequency response. In the detection of weak underwater signals, a fiber laser has small elastic deformation. Affected by axial unit sound pressure, a fiber laser is displaced by only 10
−17~10
−18 m. For this reason, axial displacement is negligible while analyzing the lateral vibration of a fiber beam model. Subsequently, a lateral vibration model for a bended beam under an elastic boundary is utilized to further analyze the low frequency flexural vibration of a fiber laser.
At low frequencies below 1 kHz, the Rayleigh–Ritz method is used in modeling and computation of the fiber laser’s first-order and second-order natural frequencies. It is assumed that the main vibration mode of the fiber laser satisfying elastic boundary conditions is subject to a second-order function . At this time, there is and , where the vibration mode of is set to ensure the computational accuracy of the fiber laser’s first-order natural frequency. At this time, the displacement function for the fiber laser’s lateral vibration is . If the load curve is , the displacement function is rewritten into .
Meanwhile, the lumped mass of the fiber laser can be ignored. Thus the maximum kinetic energy
of the system can be expressed by (1):
where the fiber density is
;
is the cross sectional area of the fiber;
and
represent the first-order and second-order amplitude coefficient of the load curve in the displacement function, respectively; the diameter of the uncoated fiber is
;
is the fiber length;
is the derivative of the displacement function, i.e., velocity; and
is the natural frequency of the system.
Considering the strain energy of the spring, the maximum potential energy of the system is expressed by (2):
where the stiffness of the spring subject to lateral vibration is
;
stands for the second-order derivative of the displacement function, i.e., acceleration. According to the law of energy conservation, the maximum kinetic energy of the system can be equal to its maximum potential energy. The natural frequency of the model is solved by (3):
Equation (3) is substituted into
to obtain (4):
Equation (3) is substituted into
to obtain (5):
Equations (4) and (5) are placed simultaneously to obtain a matrix (6). Since
and
are untrivial solutions, the determinant coefficient matrix of the matrix (6) is zero. The natural frequency
can be solved by (7):
In (7), the first-order and second-order natural frequencies of the lateral vibration model are obtained under the elastic boundary of the fiber laser. Based on the designed structure of the FLH, the variation of such natural frequencies with stiffness
and fiber length
is analyzed with the fiber length ranging from 50 mm to 70 mm. The analysis results are given in
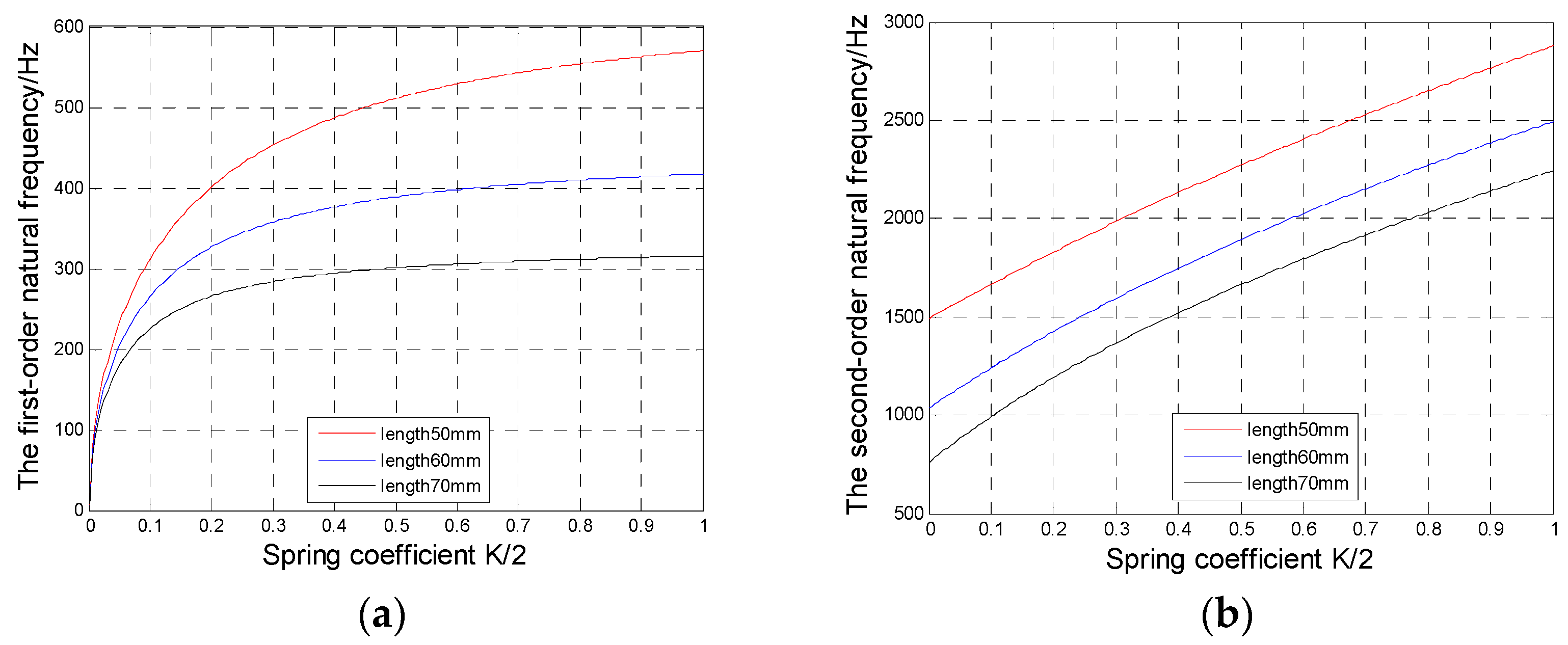
Figure 4a,b:
As shown in
Figure 4a, spring stiffness can reflect how the fiber laser’s natural frequency is affected by its attachment at both ends. The greater the spring stiffness, the higher the first-order natural frequency, so that the attachment at both ends of the fiber laser is tending to be more to be rigid. When the variation of spring stiffness becomes stable, and reaches 1, it is believed that the attachment at both ends of the fiber laser tends to be completely rigid. This is the attachment of a fiber laser by virtue of metallic diaphragms as given in reference [
18]. In this case, the first-order natural frequency of the fiber tends to be stable. Lower spring stiffness leads to lower first-order natural frequency, and makes the attachment at both ends of the fiber laser closer to flexible attachment until it becomes zero. In other words, it can be regarded as a fiber beam model with free ends, which matches with the actual situation. As for fiber material, the increase in fiber length results in the decrease in first-order natural frequency if spring stiffness remains unchanged. However, the variation of fiber length exerts no effect on the variation of first-order natural frequency with spring stiffness.
As revealed in
Figure 4b, the second-order natural frequency of the fiber laser increases with spring stiffness, but decreases with fiber length. This matches with the variation of its first-order natural frequency with spring stiffness and fiber length. Nevertheless, the increase in spring stiffness does not make the second-order natural frequency sufficiently stable, which must be attributed to the insufficient computational accuracy of the second-order natural frequency using the second-order Rayleigh–Ritz method. As for the low frequency range, in which towed arrays operate, the low frequency resonance resulting from the first-order natural frequency of the fiber laser is particularly addressed, but the medium and high frequency resonance of the fiber laser’s second-order and higher-order natural frequencies is negligible. Hence, the simplified analysis with the model is believed to be reasonable.
The first-order natural frequency in natural frequencies
is substituted into the matrix (6). The rank of the matrix is 1, so that the ratio of
A1 and
A2 can be obtained. The vibration mode function reflects the relative amplitude of vibration. We therefore let
A1 = 1, so that
A2 can be expressed by (8):
Thus the first-order vibration mode function of the fiber laser under elastic boundary can be expressed by (9):
With the finite element method, the first-order natural frequency of the fiber laser can be calculated more accurately based on the specific hydrophone structure. The spring stiffness in the theoretical model can be therefore inferred, and then used with (9) to further analyze its influence on the first-order vibration mode function of the fiber. For this reason, the finite element calculation is therefore conducted for the FLH in the next section.
Based on the designed structure given in
Figure 1, a finite element analysis is conducted for a polyurethane-packaged hydrophone. The designed hydrophone has a length of 95 mm and an outside diameter of 13 mm. Its probe is made of invar, and has the elastic modulus
, the Poisson’s ratio
, and the density
. Polyurethane is filled to the height of 8 mm with the elastic modulus
, the Poisson’s ratio
, and the density
[
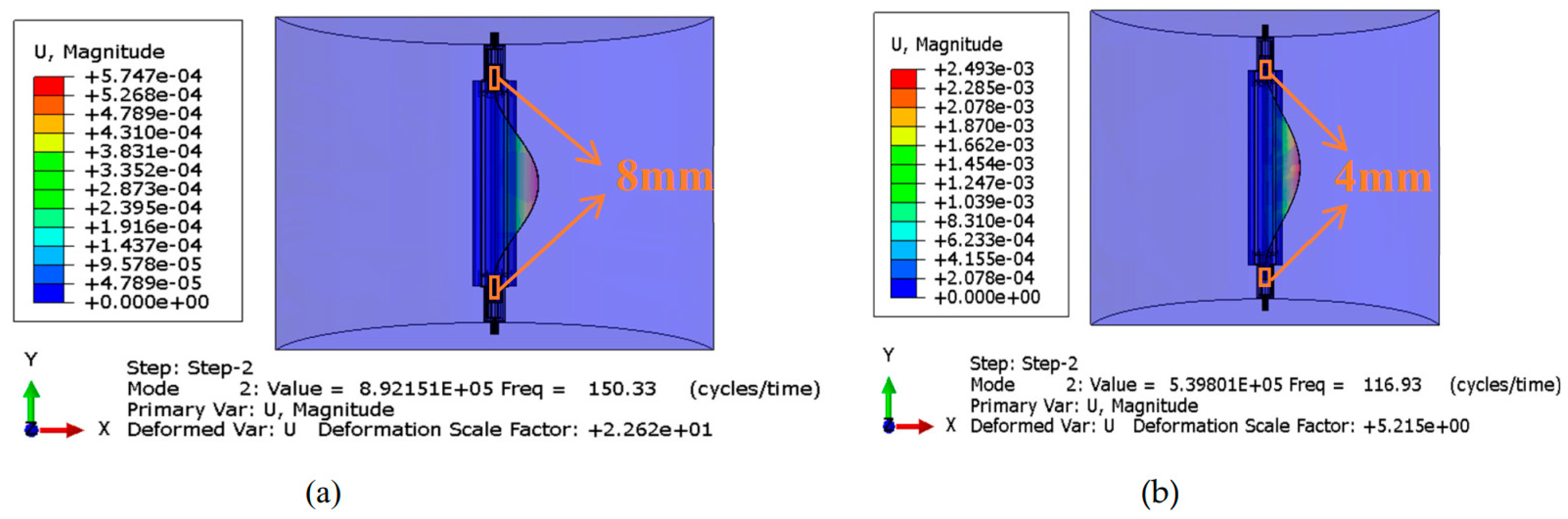
15]. To simplify the computation, a 1/2 symmetric model is constructed with symmetric constraint on the section. When an FLH operates in water, its natural frequency of local mode may be lowered under fluid–structure coupling effect. Hence, a finite element model for FLH fluid–structure coupling is built. At this time, the first-order natural frequency of the fiber laser is around 150 Hz as given in
Figure 5a. With (7), it is obtained that the spring stiffness of the fiber beam model is approximately 0.025, much lower than that of the metallic diaphragm packaged hydrophone in
Figure 4a. This must be attributed to the flexible attachment at both ends of the fiber laser in the polyurethane packaging.
In a polyurethane-packaged hydrophone, polyurethane filled at both ends forms a cylinder, and its hardness and height vary, which affects the attachment at both ends. Polyurethane hardness is influenced by elastic modulus, so that finite element simulation is conducted to calculate the first-order natural frequency of a fiber laser and the corresponding hydrophone sensitivity at different elastic moduli and heights of polyurethane. When polyurethane filled at both ends reaches the height of 4 mm as shown in
Figure 5b, the first-order natural frequency of the fiber laser is approximately 117 Hz, significantly lower than that in
Figure 5a. With (7), it is determined that spring stiffness is around 0.017.
Table 1 presents the first-order natural frequency of a fiber laser and the corresponding hydrophone sensitivity at different elastic moduli and heights of polyurethane from the finite element computation. In this case, the axial strain of grating is calculated with the finite element method, and then demodulated by Michelson interference combined with 50 m non-equilibrium path to obtain hydrophone sensitivity, with dB re rad/upa as the unit [
18].
Based on the data given in
Table 1, it is found that, if polyurethane height remains unchanged, the elasticity of polyurethane decreases with the increasing elastic modulus of polyurethane, and the fiber laser’s axial strain under unit sound pressure is lowered with the decreasing sensitivity of the hydrophone. At this time, the first-order natural frequency of the fiber laser goes up slightly, but is nearly unchanged. In other words, the spring stiffness in the fiber beam model is approximately invariant. Along with the reduced polyurethane height, the fiber laser’s axial strain under unit sound pressure increases with the improving hydrophone sensitivity. Meanwhile, the first-order natural frequency of the fiber laser goes down, and the spring stiffness in the fiber beam model decreases.
The amplitude of the first-order fiber vibration mode function is analyzed with (9). To sum up, the spring stiffness in the model is very low for polyurethane packaging. When polyurethane height is 8 mm, as shown in
Figure 5a, the actual length in the fiber beam model is 59 mm. The analysis with spring stiffness set to 0.017, 0.025, and 0.035, can reflect the variation of amplitude when the elastic modulus of polyurethane changes. As revealed in
Figure 5b, when polyurethane height is 4 mm, the actual length in the fiber beam model increases to 67 mm, and the corresponding spring stiffness is 0.017. It is comparatively analyzed to find out the variation of amplitude when polyurethane height decreases.
In
Figure 6a, it is revealed that, if fiber length is unchanged, the relative amplitude of the fiber decreases very slightly with the decrease in spring stiffness. The decrease in polyurethane height results in a gentle decrease in spring stiffness, resulting in a lower relative amplitude of the fiber. However, a gentle increase in fiber length exerts an insignificant effect on spring stiffness.
When the actual length in the fiber beam model is 59 mm, the comparative analysis with spring stiffness being 0.025 and 1, which can reflect the influence of flexible and rigid attachments on the amplitude of the fiber, as shown in
Figure 6b. Evidently, the amplitude of the fiber with rigid attachment is much higher than that with flexible attachment. At this time, interference is negligible for the amplitude of a fiber with flexible attachment. Generally, an axially tensioned FLH has an axial grating strain considerably higher than the radial grating strain. In the computation of its sensitivity, the radial grating strain can be ignored. However, rigid attachment at both ends of a fiber laser dramatically increases its first-order natural frequency. In this case, the total grating strain must be the sum of the lateral strain and radial strain, which are therefore taken into account in the computation of sensitivity.
In general, it is believed that the spring stiffness in the theoretical model reflects how different types of attachment can attenuate the vibration in the fiber beam model. Based on the data given in
Table 1, the varying elastic modulus and height of the polyurethane can affect the axial micro-strain of the fiber laser because of the unit sound pressure in the axial direction. This further exerts an effect on the sensitivity of hydrophone. Nevertheless, spring stiffness in the fiber beam model varies very slightly, and keeps the feature of flexible attachment, so that it has little influence on the fluctuation of hydrophone frequency response. Based on the above comparative analysis, we further analyze the influence of attachment at both ends of a fiber laser on the frequency response of hydrophone in the FLH packaging technique. The theoretical analysis is verified in an experiment as detailed in next section.
3. Results
To further verify the theoretical analysis, an experiment was performed to explore how the features of sensitivity enhancement element affect the frequency response of a fiber laser hydrophone (FLH). The hydrophone was packaged with different polyurethane heights including 8 mm (sleeve hole fully filled) and 4 mm (sleeve hole half filled) for comparison. Meanwhile, they were compared with an existing metallic diaphragm axially tensioned FLH [
18] in terms of frequency response with rigid attachment and flexible attachment at both ends of the fiber laser. Frequency response test was carried out for such three FLHs with vibrating column of fluid.
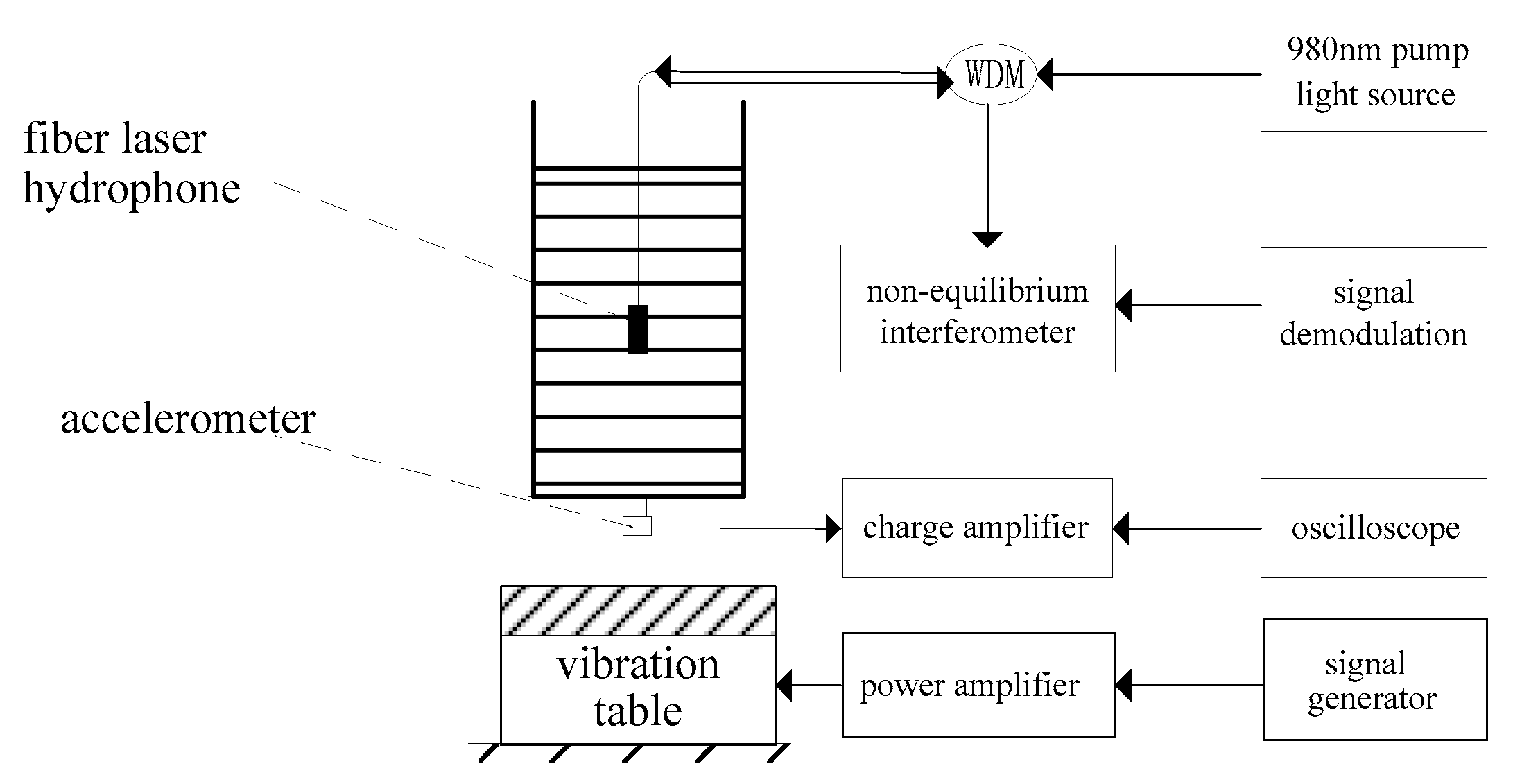
The principles of the calibration system for vibrating column of fluid are illustrated in
Figure 7. A signal generator transmitted single frequency signals, which were applied onto the excitation surface of a vibration test bed after power amplifier to form a stable standing wave field inside a metal tank. An accelerometer was attached to the lower surface of the metal tank, and its acceleration signals were matched by a charge amplifier, and then read in an oscilloscope. Meanwhile, an FLH was rigidly attached by clamps and placed at the center of the metal tank. With vibrating column of fluid, the sound pressure at the FLH inside the metal tank can be calculated by (10):
where
ρ is the water density;
c is the acoustic velocity in water;
α is the vibration acceleration;
k = ω·c stands for the wave number; h is the distance from the acoustic center of a hydrophone to the fluid surface; and
L is the depth of fluid column. Together with the phase change demodulated by an unbalanced interferometer in the optical path, we can calculate the sensitivity of the hydrophone.
The frequency response curves of three FLHs within the frequency range 10~1000 Hz in the experiment are presented in
Figure 8. They are analyzed as follows: the average frequency response of the FLH with a polyurethane height of 8 mm is around −142.5 dB, and the frequency response fluctuates at ±1.9 dB. The average frequency response of the FLH with a polyurethane height of 4 mm is approximately −137.4 dB, and the frequency response fluctuates at ±1.6 dB, which matches with the variation of hydrophone frequency response in the sensitivity calculation and analysis of the theoretical model.
Between two sensitivity curves, the frequency response fluctuation of the FLH with a polyurethane height of 4 mm is slightly lower than that of the FLH with a polyurethane height of 8 mm, which matches with the slight difference of spring stiffness between different polyurethane heights. Moreover, these two frequency response curves show fluctuate with a generally similar trend. In order to better compare the rigid attachment and flexible attachment of a fiber laser, a metallic diaphragm axially tensioned FLH was taken as a control group. Obviously, the rigid attachment in metallic diaphragm packaging is prone to flexural vibration at the fiber laser’s first-order natural frequency near 400 Hz, which causes the dramatic fluctuation of the FLH’s frequency response [
18]. Comparatively, the flexible attachment in polyurethane packaging serves like a supporting spring at both ends of the fiber beam model. Therefore, it can effectively attenuate the flexural vibration resulting from the fiber laser’s first-order natural frequency, resulting in a flatter frequency response of the FLH.