Simulation and Testing of the Radiation Performance of SiC Particles with Different Distribution Morphologies
Abstract
:1. Introduction
2. Materials and Methods
2.1. Mie Scattering Theory
2.2. GMM Theory
2.3. Fractal Theory and the Diffusion-Limited Aggregation (DLA) Model
3. Results
3.1. Simulation Result
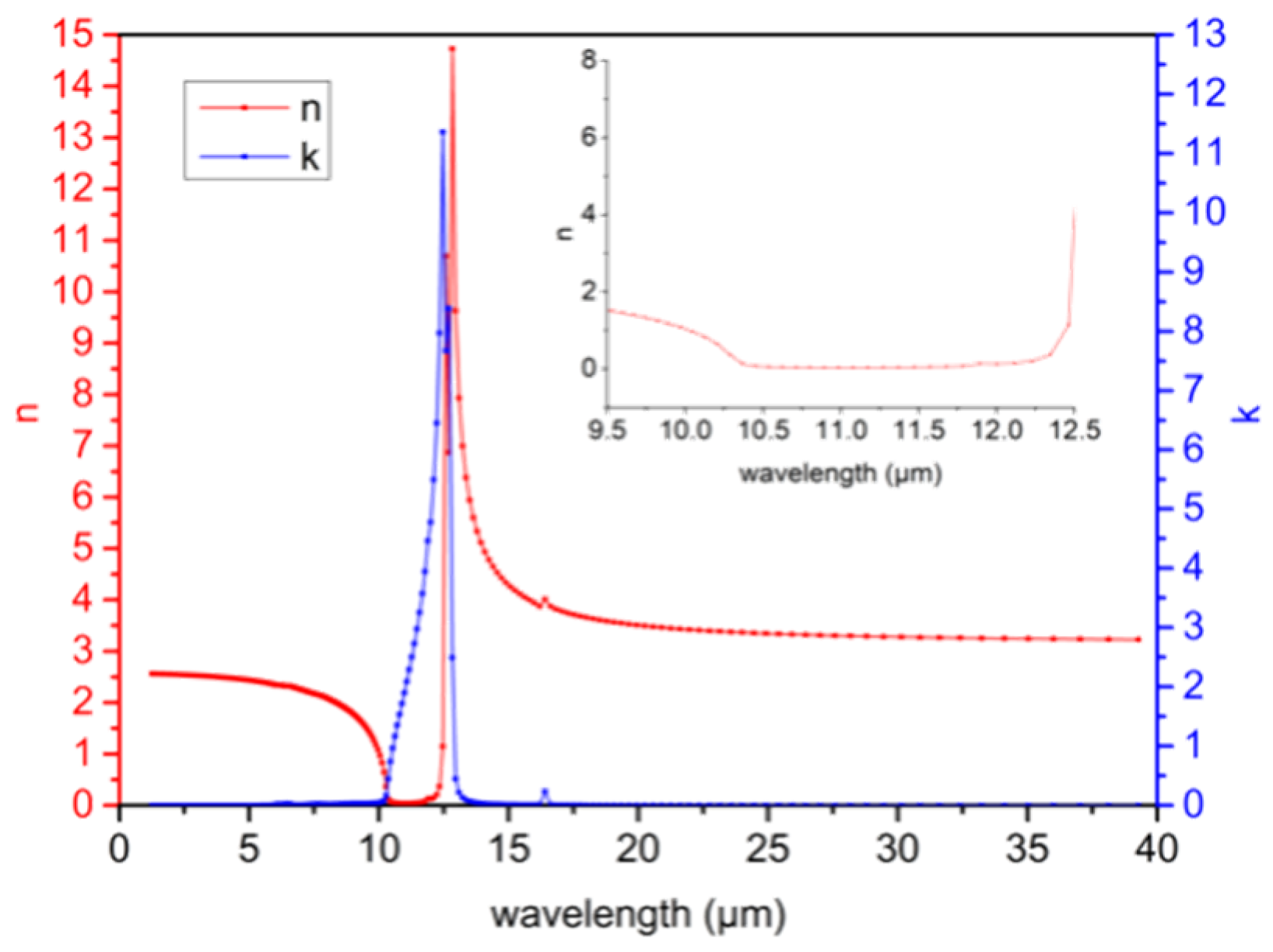
3.1.1. Radiation Characteristics of SiC Elementary Particles
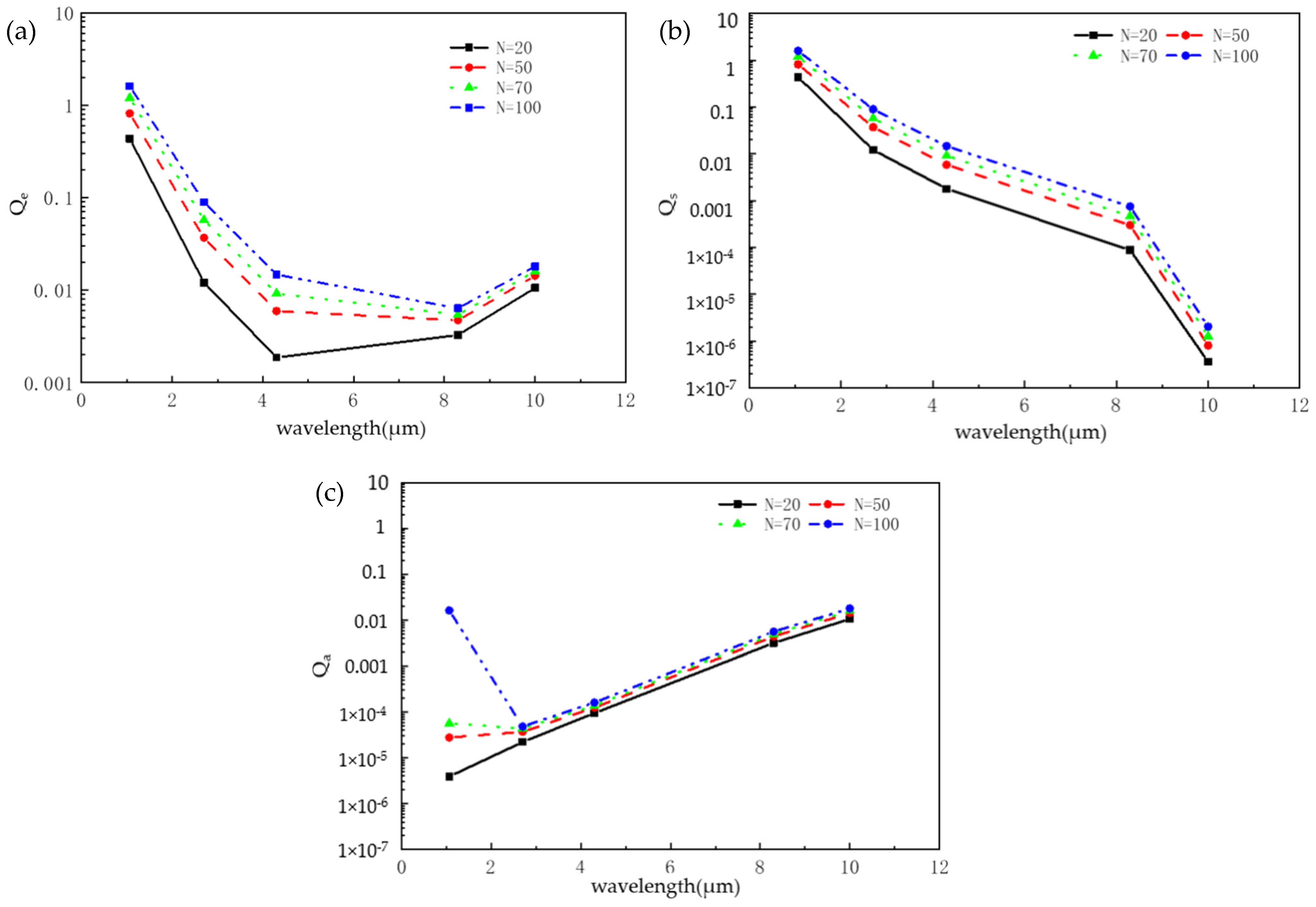
3.1.2. Radiation Characteristics of SiC Cluster Particles
3.2. Experimental Results
3.2.1. Morphology and Structure Analysis
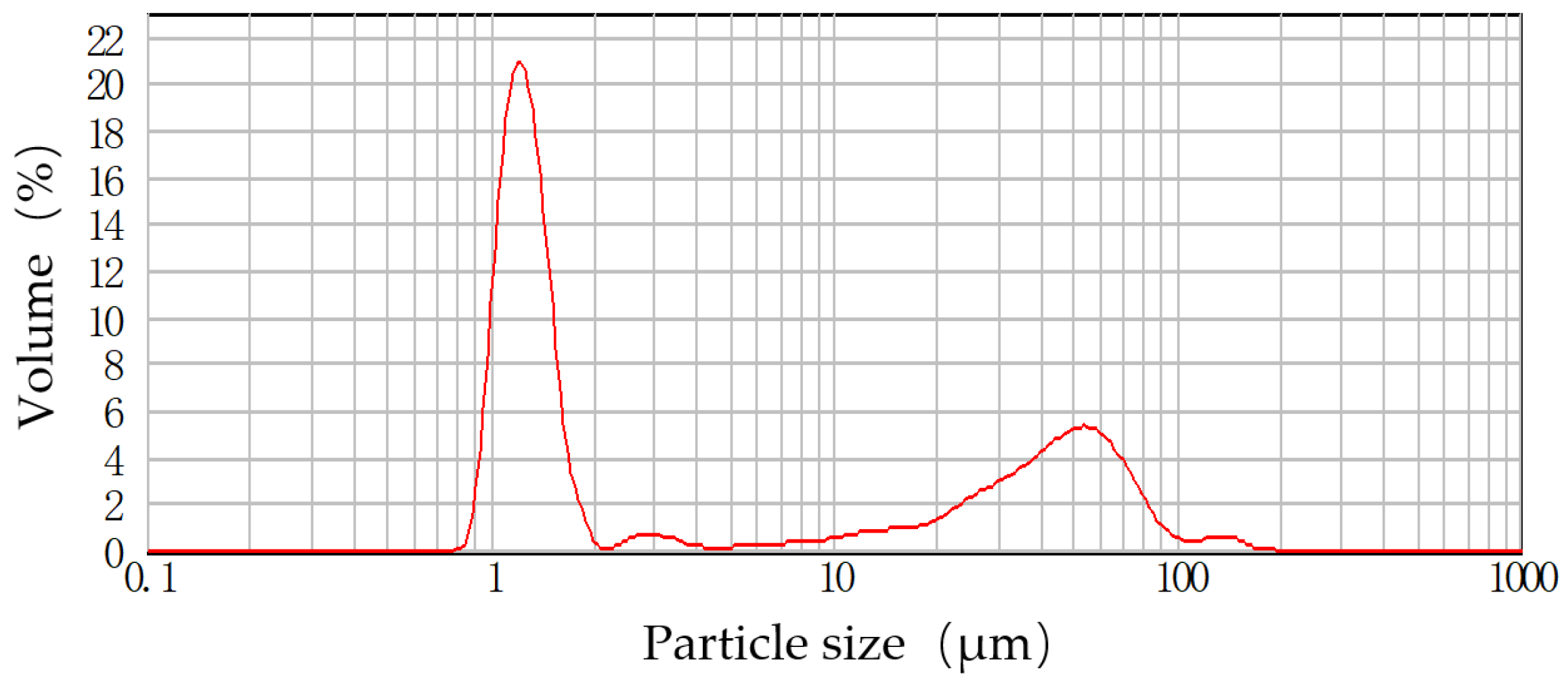
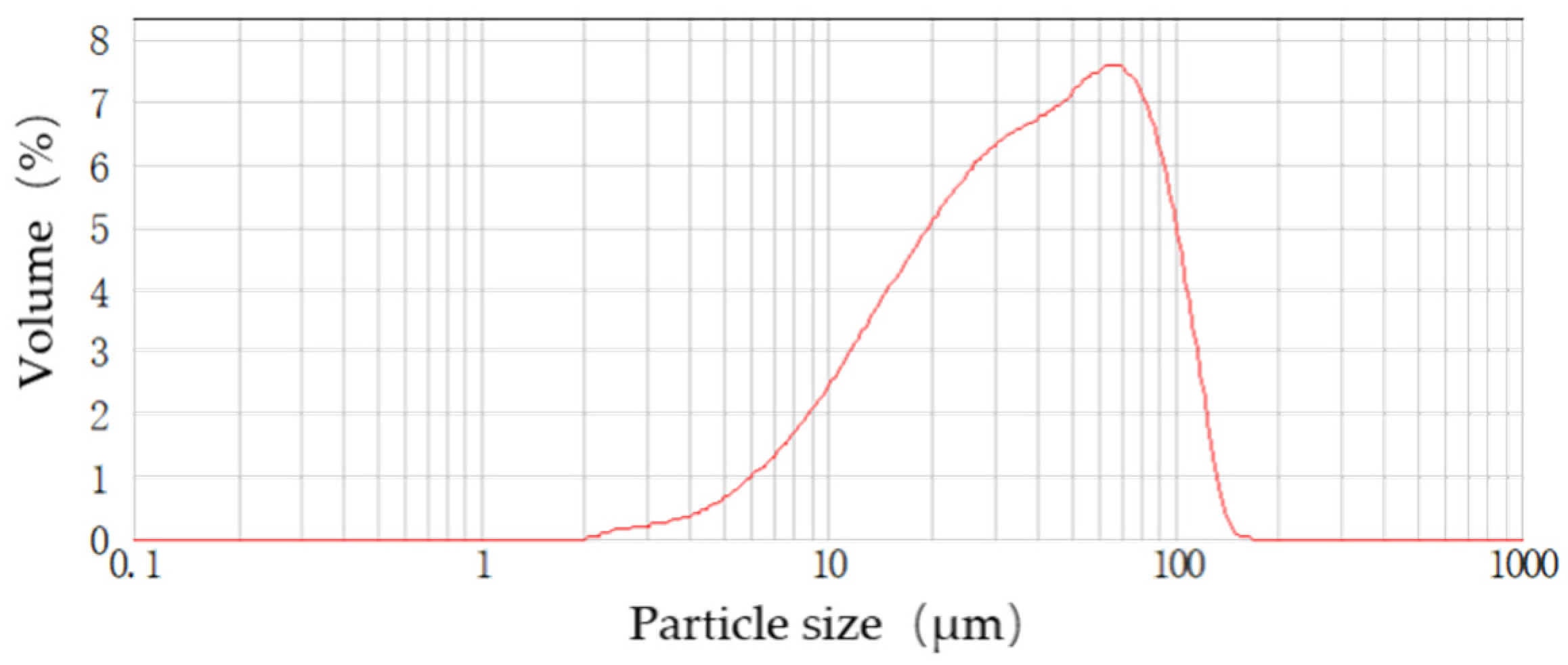
3.2.2. Particle Size Analysis
3.2.3. ATR-FTIR Infrared Spectrum Analysis
4. Discussion
4.1. Different Particle Distribution States Led to Different Scattering Directionalities of the SiC Particles
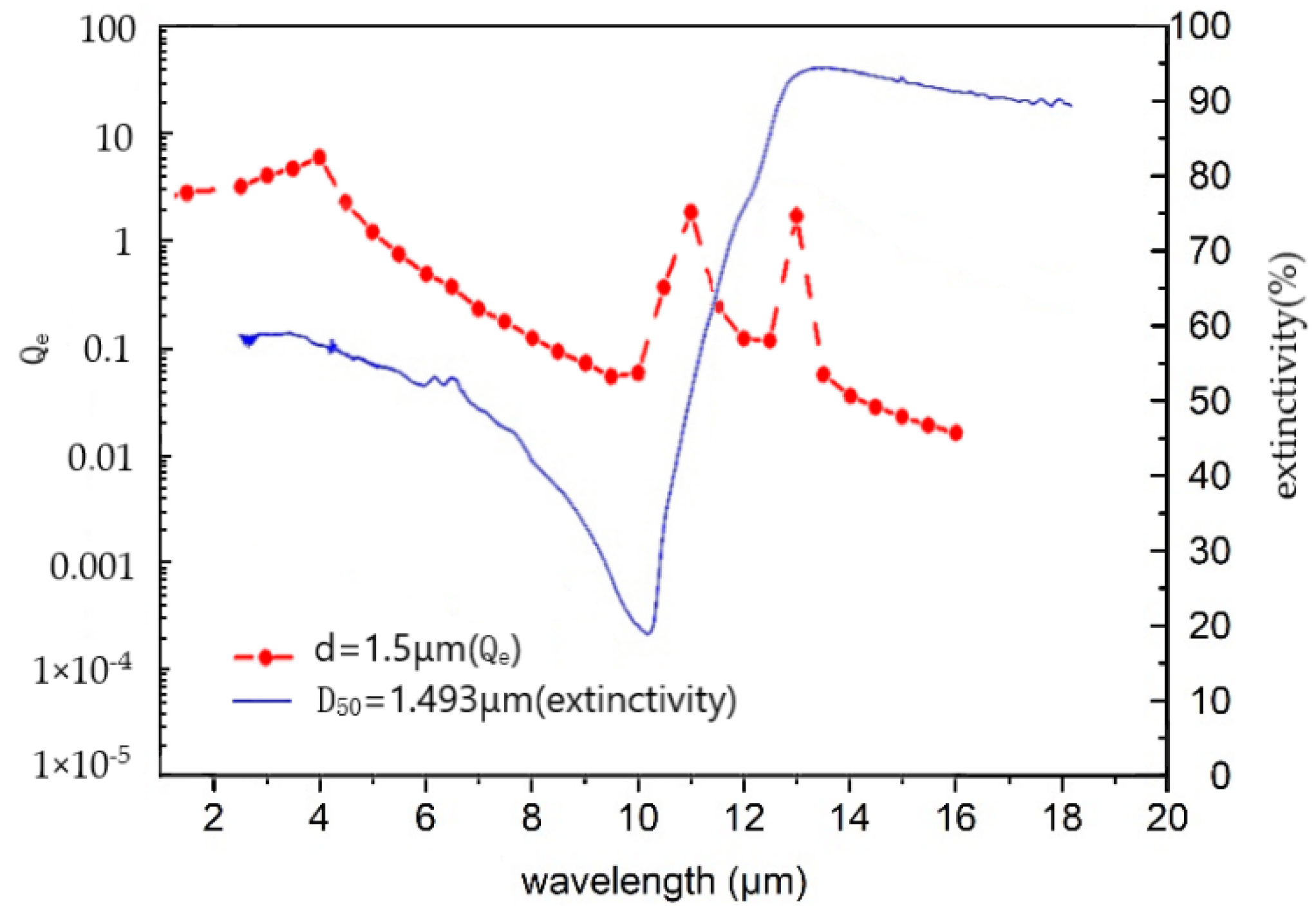
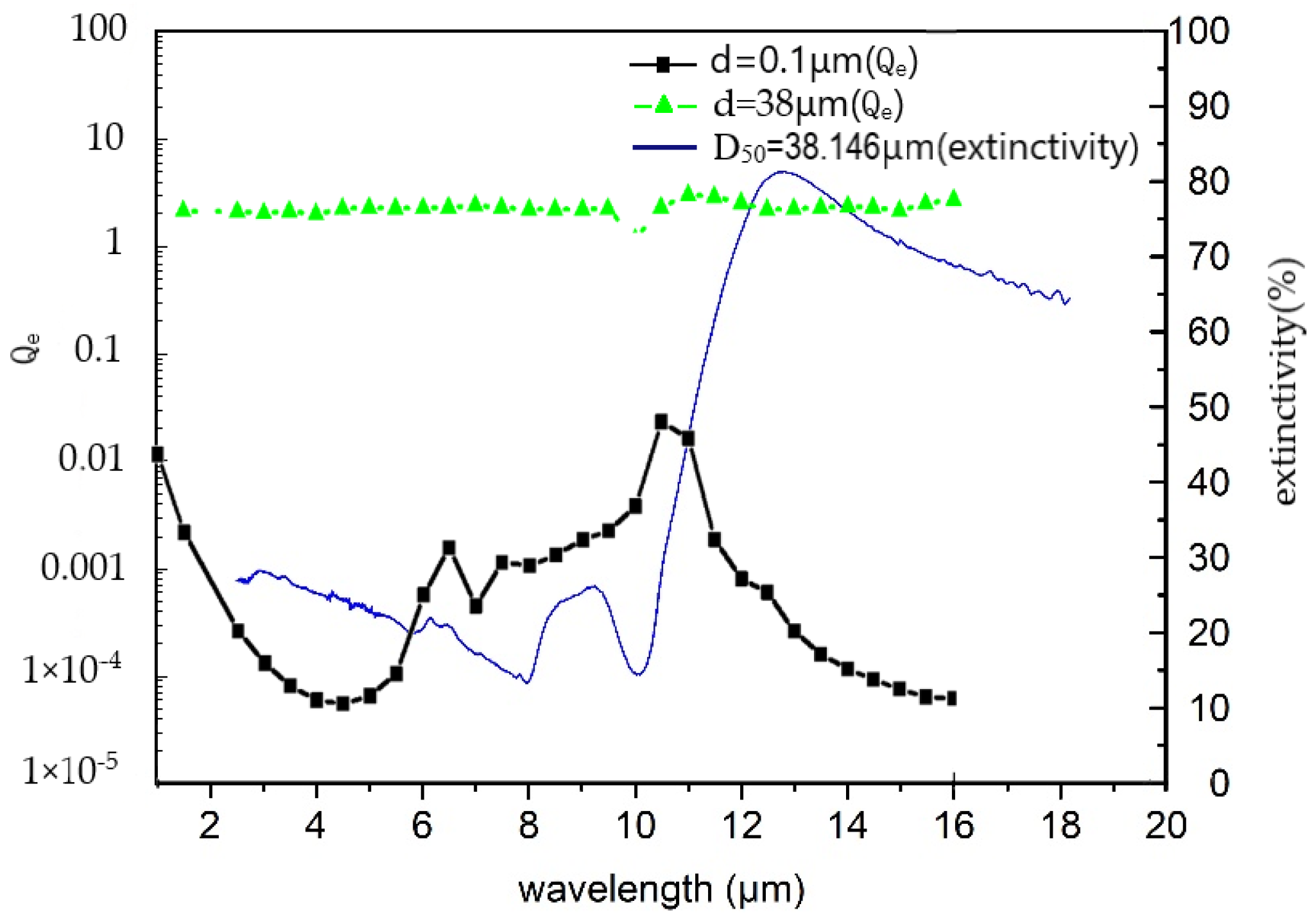
4.2. SiC Particle Size Distribution Had a Significant Effect on Its Radiation Performance
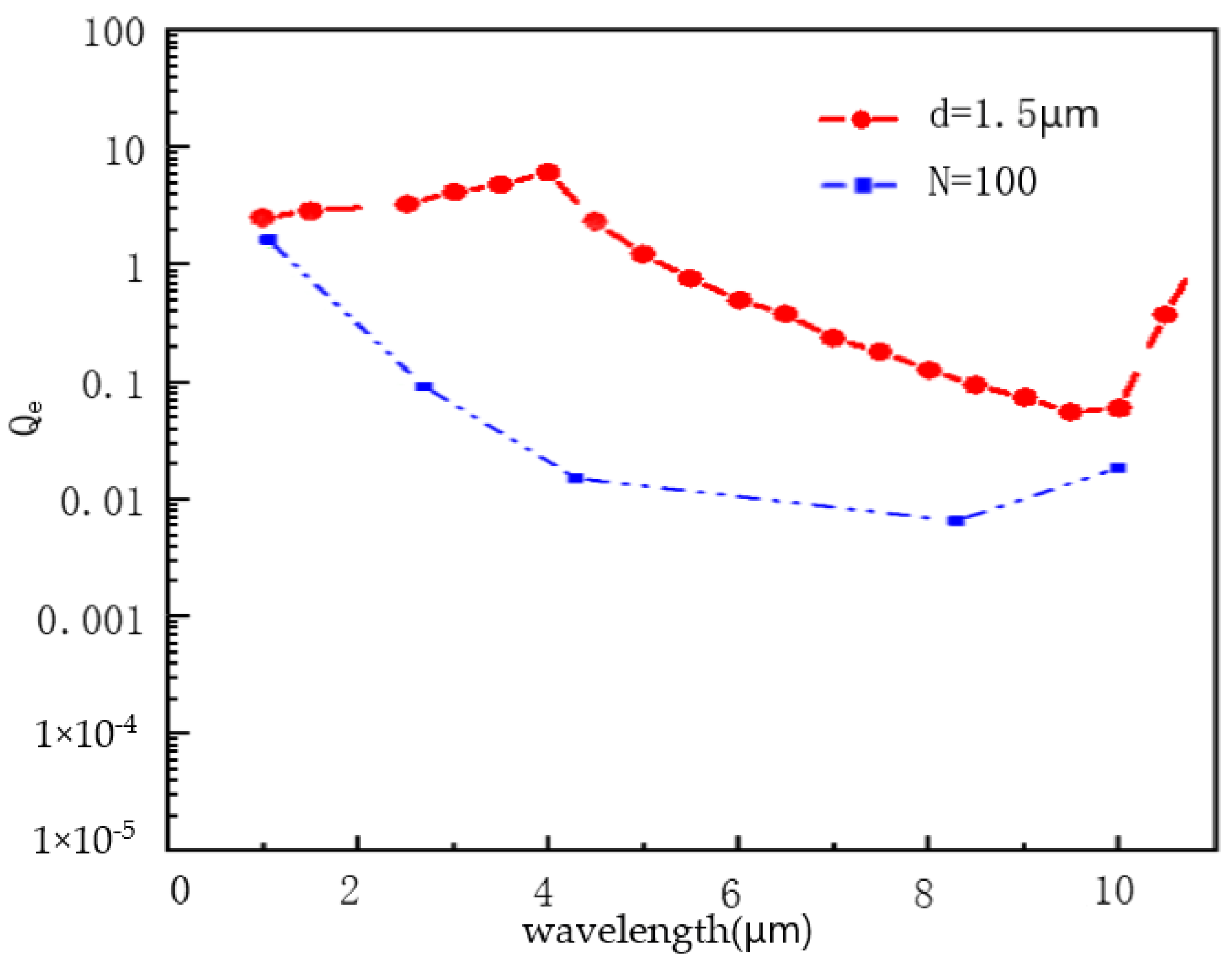
4.3. The Influence of SiC Particle Clusters on Their Radiation Performance Was Related to the Cluster Size
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shor, J.; Zhang, X.; Osgood, R. Laser-Assisted Photoelectrochemical Etching of n-type Beta-SiC. J. Electrochem. Soc. 1992, 139, 1213–1216. [Google Scholar] [CrossRef]
- Casady, J.; Johnson, R.W. Status of silicon carbide (SiC) as a wide-band gap semiconductor for high-temperature applications. Solid-State Electron. 1996, 39, 1409–1422. [Google Scholar] [CrossRef]
- Greffet, J.-J.; Carminati, R.; Joulain, K.; Mulet, J.-P.; Mainguy, S.; Cheng, Y. Coherent emission of light by thermal sources. Nature 2002, 416, 61–64. [Google Scholar] [CrossRef] [PubMed]
- Hillenbrand, R.; Taubner, T.; Keilmann, F. Phonon-enhanced light-matter interaction at the nanometre scale. Nature 2002, 418, 159. [Google Scholar] [CrossRef] [PubMed]
- Xiang, Z.N.; He, Q.C.; Wang, Y.Q.; Ren, L.G. Synthesis and wave absorption properties of hollow SiC spherical nanoparticles. Nonferrous Met. Sci. Eng. 2022, 13, 83–92. [Google Scholar]
- Liu, X.; Cao, L.Z.; Jiang, H.; Song, H. Preparation and photoluminescence of SiC nanoparticles. J. Funct. Mater. 2019, 50, 9093–9096+9101. [Google Scholar]
- Guo, X.X. Preparation, photoluminescence properties and phase transformation of SiC nanoparticles. Ph.D. Thesis, Southeast University, Nanjing, China, 2017. [Google Scholar]
- Guan, Z.; Fang, N.; Li, C.Y.; Ma, S.G.; Liu, H.L.; Mao, L.Q. Gaussian equation is used to analyze the particle size distribution of CoFe2O4 nanocomposite particles. Chem. Res. 2016, 27, 760–762+778. [Google Scholar]
- Huang, H.J.; Zhou, M.B.; Wu, X.; Zang, X.P. Low temperature pressure-less sintering of nano copper paste with bimodal particle size distribution for chip interconnection, nano connection mechanism and joint reliability. J. Mech. Eng. 2022, 58, 58–65. [Google Scholar]
- Tian, Y.P. Strategic thinking on the overall development of urban and rural mass sports in the construction of a harmonious society. China Sports Sci. Technol. 2009, 6, 90–96. [Google Scholar]
- Sun, J. Urban and rural overall planning is an innovation of comprehensive factor overall planning. China Dev. 2008, 12, 59–61. [Google Scholar]
- Wang, H.X.; Sun, H.H.; Song, Z.B.; Liu, D.Z.; Tian, T. Calculation and analysis of particle transmittance based on Monte Carlo method. Infrared Laser Eng. 2012, 41, 1200–1205. [Google Scholar]
- Li, Y.N.; Li, Y.Q.; Wang, Q.; Dong, S.K.; Mu, L.; Liu, J.Q. The optical properties and stability of submicron hollow particles. In Proceedings of the AOPC 2017: Optoelectronics and Micro/Nano-Optics, Beijing, China, 24 October 2017; SPIE: Bellingham, WA, USA, 2017; Volume 10460, p. 1046019. [Google Scholar]
- Li, Y.N.; Mu, L.; Cai, W.L.; Wang, Q.; Liu, X. Research on the extinction performance of particle clouds in space. In Proceedings of the Second Target Recognition and Artificial Intelligence Summit Forum, Beijing, China, 31 January 2020; SPIE: Bellingham, WA, USA, 2020; Volume 11427, p. 1142717. [Google Scholar]
- Tang, J.L. Study and analysis of morphology controlled ZnO nano materials by infrared spectroscopy. Master’s Thesis, Changchun University of Technology, Changchun, China, 2006. [Google Scholar]
- Zhang, Y.H.; Li, Y.L.; Tu, H.Q.; Meng, X.Q. Preparation and infrared absorption properties of Ag/Zn/Ag Nanocomposite particle films. In Proceedings of the National Annual Conference on Functional Materials, Dunhuang, China, 1 July 2006. [Google Scholar]
- Brewster, M.Q. Thermal Radiative Transfer and Properties; John Wiley & Sons: New York, NY, USA, 1992; pp. 315–316. [Google Scholar]
- Xu, Y.L. Electromagnetic Scattering by an Aggregate of Spheres. Appl. Opt. 1995, 34, 4573–4588. [Google Scholar] [CrossRef] [PubMed]
- Yu, Q.Z. Radiation Heat Transfer Principle, 1st ed.; Harbin Institute of Technology Press: Harbin, China, 2000; pp. 170–171. [Google Scholar]









| Particle Size (μm) | Wavelength (μm) | Scale Parameter |
|---|---|---|
| 0.1 | 1 | 0.3142 |
| 3.0197 | 0.1040 | |
| 4.9999 | 0.0628 | |
| 6.9972 | 0.0449 | |
| 9.0172 | 0.0348 | |
| 11.008 | 0.0285 | |
| 12.995 | 0.0242 | |
| 14.985 | 0.0210 | |
| 1.5 | 1 | 4.7124 |
| 3.0197 | 1.5605 | |
| 4.9999 | 0.9425 | |
| 6.9972 | 0.6735 | |
| 9.0172 | 0.5226 | |
| 11.008 | 0.4281 | |
| 12.995 | 0.3626 | |
| 14.985 | 0.3145 | |
| 38 | 1 | 119.3805 |
| 3.0197 | 39.5339 | |
| 4.9999 | 23.8766 | |
| 6.9972 | 17.0612 | |
| 9.0172 | 13.2392 | |
| 11.008 | 10.8449 | |
| 12.995 | 9.1867 | |
| 14.985 | 7.9667 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Wang, Q.; Wang, X.; Dong, S. Simulation and Testing of the Radiation Performance of SiC Particles with Different Distribution Morphologies. Photonics 2022, 9, 317. https://doi.org/10.3390/photonics9050317
Li Y, Wang Q, Wang X, Dong S. Simulation and Testing of the Radiation Performance of SiC Particles with Different Distribution Morphologies. Photonics. 2022; 9(5):317. https://doi.org/10.3390/photonics9050317
Chicago/Turabian StyleLi, Yanan, Qun Wang, Xiaoli Wang, and Shikui Dong. 2022. "Simulation and Testing of the Radiation Performance of SiC Particles with Different Distribution Morphologies" Photonics 9, no. 5: 317. https://doi.org/10.3390/photonics9050317
APA StyleLi, Y., Wang, Q., Wang, X., & Dong, S. (2022). Simulation and Testing of the Radiation Performance of SiC Particles with Different Distribution Morphologies. Photonics, 9(5), 317. https://doi.org/10.3390/photonics9050317






