Novel Measurement-Based Efficient Computational Approach to Modeling Optical Power Transmission in Step-Index Polymer Optical Fiber
Abstract
:1. Introduction
2. Materials and Methods
2.1. Fiber Types and Experimental Setup
2.2. Experimental Methodology
3. Computational Model and Fitting Algorithm
3.1. Computational Model
3.2. Fitting Algorithm
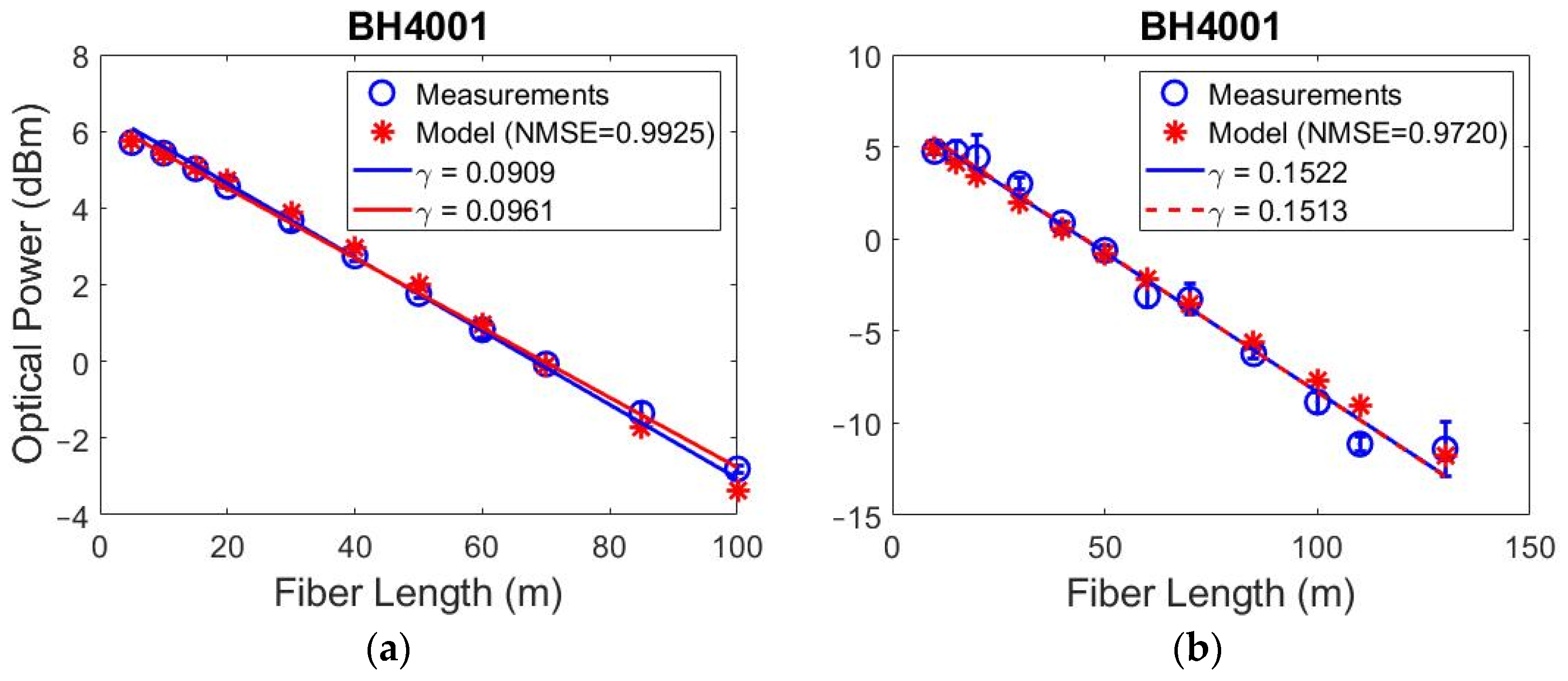
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ziemann, O.; Krauser, J.; Zamzowr, P.E.; Daum, W. Application of Polymer Optical and Glass Fibers. In POF Handbook: Optical Short Range Transmission Systems, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Mateo, J.; Losada, M.A.; López, A. POF misalignment model based on the calculation of the radiation pattern using the Hankel transform. Opt. Express 2015, 23, 8061. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Losada, M.A.; López, A.; Mateo, J. Attenuation and diffusion produced by small-radius curvatures in POFs. Opt. Express 2016, 24, 15710. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Tangdiongga, E.; Koonen, A.M.J.; Bluschke, A.; Rietzsch, P.; Montalvo, J.; De Laat, M.M.; Hoven, G.N.V.D.; Huiszoon, B. Plastic-optical-fiber-based in-home optical networks. IEEE Commun. Mag. 2014, 52, 186–193. [Google Scholar] [CrossRef]
- Mittal, N.; Shah, M.; John, J. A low cost short haul plastic optical fiber link for home networking applications. In Proceedings of the 2016 IEEE International Conference on Recent Trends in Electronics, Information & Communication Technology (RTEICT), Bengaluru, India, 20–21 May 2016; pp. 2112–2116. [Google Scholar] [CrossRef]
- Nazaretian, R.; Molen, G.M. Reducing Vehicle Weight and Improving Security by Using Plastic Optical Fiber. In Proceedings of the 2015 IEEE Vehicle Power and Propulsion Conference (VPPC), Montreal, QC, Canada, 19–22 October 2015; pp. 1–6. [Google Scholar] [CrossRef]
- López, A.; Losada, M.Á.; Mateo, J.; Jiang, X.; Richards, D.H.; Antoniades, N. Transmission Performance of Plastic Optical Fibers Designed for Avionics Platforms. J. Lightwave Technol. 2018, 36, 5082–5088. [Google Scholar] [CrossRef] [Green Version]
- Sercos Technology. Available online: https://www.sercos.org/technology/ (accessed on 24 January 2022).
- Theodosiou, A.; Kalli, K. Recent trends and advances of fibre Bragg grating sensors in CYTOP polymer optical fibres. Opt. Fiber Technol. 2020, 54, 102079. [Google Scholar] [CrossRef]
- Marques, C.A.F.; Min, R.; Junior, A.L.; Antunes, P.; Fasano, A.; Woyessa, G.; Nielsen, K.; Rasmussen, H.K.; Ortega, B.; Bang, O. Fast and stable gratings inscription in POFs made of different materials with pulsed 248 nm KrF laser. Opt. Express 2018, 26, 2013–2022. [Google Scholar] [CrossRef] [Green Version]
- Hu, X.; Chen, Y.; Gao, S.; Min, R.; Woyessa, G.; Bang, O.; Qu, H.; Wang, H.; Caucheteur, C. Direct Bragg Grating Inscription in Single Mode Step-Index TOPAS/ZEONEX Polymer Optical Fiber Using 520 nm Femtosecond Pulses. Polymers 2022, 14, 1350. [Google Scholar] [CrossRef]
- Junior, A.L.; Frizera, A.; Marques, C.; Sanchez, M.R.A.; Dos Santos, W.M.; Siqueira, A.A.G.; Segatto, M.V.; Pontes, M. Polymer Optical Fiber for Angle and Torque Measurements of a Series Elastic Actuator’s Spring. J. Lightwave Technol. 2018, 36, 1698–1705. [Google Scholar] [CrossRef]
- Koyama, S.; Haseda, Y.; Ishizawa, H.; Okazaki, F.; Bonefacino, J.; Tam, H.-Y. Measurement of Pulsation Strain at the Fingertip Using a Plastic FBG Sensor. IEEE Sens. J. 2021, 21, 21537–21545. [Google Scholar] [CrossRef]
- Leal-Junior, A.G.; Díaz, C.R.; Marques, C.; Pontes, M.J.; Frizera, A. Multiplexing technique for quasi-distributed sensors arrays in polymer optical fiber intensity variation-based sensors. Opt. Laser Technol. 2018, 111, 81–88. [Google Scholar] [CrossRef]
- Graded-Index Polymer Optical Fiber (GI-POF). Available online: https://www.thorlabs.com/catalogpages/v20/892.pdf (accessed on 1 December 2021).
- Loquai, S.; Kruglov, R.; Schmauss, B.; Bunge, C.-A.; Winkler, F.; Ziemann, O.; Hartl, E.; Kupfer, T. Comparison of Modulation Schemes for 10.7 Gb/s Transmission Over Large-Core 1 mm PMMA Polymer Optical Fiber. J. Light. Technol. 2013, 31, 2170–2176. [Google Scholar] [CrossRef]
- Gimeno, C.; Guerrero, E.; Sánchez-Azqueta, C.; Royo, G.; Aldea, C.; Celma, S. Continuous-Time Linear Equalizer for Multigigabit Transmission Through SI-POF in Factory Area Networks. IEEE Trans. Ind. Electron. 2015, 62, 6530–6532. [Google Scholar] [CrossRef]
- Koike, K.; Koike, Y. Design of Low-Loss Graded-Index Plastic Optical Fiber Based on Partially Fluorinated Methacrylate Polymer. J. Light. Technol. 2009, 27, 41–46. [Google Scholar] [CrossRef]
- Gloge, D. Optical Power Flow in Multimode Fibers. Bell Syst. Tech. J. 1972, 51, 1767–1783. [Google Scholar] [CrossRef]
- Drljača, B.; Djordjevich, A.; Savović, S. Frequency response in step-index plastic optical fibers obtained by numerical solution of the time-dependent power flow equation. Opt. Laser Technol. 2012, 44, 1808–1812. [Google Scholar] [CrossRef]
- Djordjevich, A.; Savovic, S. Investigation of mode coupling in step index plastic optical fibers using the power flow equation. IEEE Photonics Technol. Lett. 2000, 12, 1489–1491. [Google Scholar] [CrossRef]
- Mateo, J.; Losada, M.A.; Garcés, I.; Zubia, J. Global characterization of optical power propagation in step-index plastic optical 484 fibers. Opt. Express 2006, 14, 9028–9035. [Google Scholar] [CrossRef]
- Richards, D.H.; Losada, M.A.; Antoniades, N.; Lopez, A.; Mateo, J.; Jiang, X.; Madamopoulos, N. Modeling Methodology for Engineering SI-POF and Connectors in an Avionics System. J. Light. Technol. 2013, 31, 468–475. [Google Scholar] [CrossRef]
- Stepniak, G.; Siuzdak, J. Modeling of transmission characteristics in step-index polymer optical fiber using the matrix exponential method. Appl. Opt. 2018, 57, 9203–9207. [Google Scholar] [CrossRef]
- Mundus, M.; Hohl-Ebinger, J.; Warta, W. Estimation of angle-dependent mode coupling and attenuation in step-index plastic optical fibers from impulse responses. Opt. Express 2013, 21, 17077–17088. [Google Scholar] [CrossRef]
- International Electrotechnical Commission. Optical Fibres: Part 1–40: Measurement Methods and Test Procedures: Attenuation; IEC 60793-1-40; ICE: Geneva, Switzerland, 2001. [Google Scholar]
- Losada, M.A.; Mazo, M.; Lopez, A.; Muzas, C.; Mateo, J. Experimental assessment of the transmission performance of step index polymer optical fibers using a green laser diode. Polymers 2021, 13, 3397. [Google Scholar] [CrossRef]
- Mitsubishi Chemical Corporation. Basic Requirements for the Structure and Optical Performances of BH-4001; BH-4001 Datasheet: Tokyo, Japan, April 2019. [Google Scholar]
- Mitsubishi Chemical Corporation. Basic Requirements for the Structure and Optical Performances of MH-4001; MH-4001 Datasheet: Tokyo, Japan, April 2019. [Google Scholar]
- Mateo, J.; Losada, M.A.; Zubia, J. Frequency response in step index plastic optical fibers obtained from the generalized power flow equation. Opt. Express 2009, 17, 2850–2860. [Google Scholar] [CrossRef] [PubMed]
- Gloge, D. Impulse Response of Clad Optical Multimode Fibers. Bell Syst. Tech. J. 1973, 52, 801–816. [Google Scholar] [CrossRef]
- Gambling, W.; Payne, D.; Matsumura, H. Mode conversion coefficients in optical fibers. Appl. Opt. 1975, 14, 1538–1542. [Google Scholar] [CrossRef] [PubMed]
- Djordjevich, A.; Savovic, S. Numerical Solution of the Power Flow Equation in Step-Index Plastic Optical Fibers. J. Opt. Soc. Am. B USA 2004, 21, 1437–1442. [Google Scholar] [CrossRef]
- Breyer, F.; Hanik, N.; Lee, S.; Randel, S. POF Modelling: Theory, Measurement and Application. In Getting the Impulse Response of SI-POF by Solving the Time-Dependent Power-Flow Equation Using the Crank-Nicholson Scheme; Bunge, C.A., Poisel, H., Eds.; Verlag Books on Demand GmbH: Norderstedt, Germany, 2007. [Google Scholar]
- Djordjevich, A.; Savovic, S. Coupling length as an algebraic function of the coupling coefficient in step-index plastic optical fibers. Opt. Eng. 2008, 47, 125001. [Google Scholar] [CrossRef]
- López, A.; Losada, A.; Mateo, J.; Zubia, J. On the Variability of Launching and Detection in POF Transmission Systems. In Proceedings of the 20th International Conference on Transparent Optical Networks (ICTON), Bucharest, Romania, 1–5 July 2018. [Google Scholar] [CrossRef]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence Properties of the Nelder-Mead Simplex Method in Low Dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef] [Green Version]

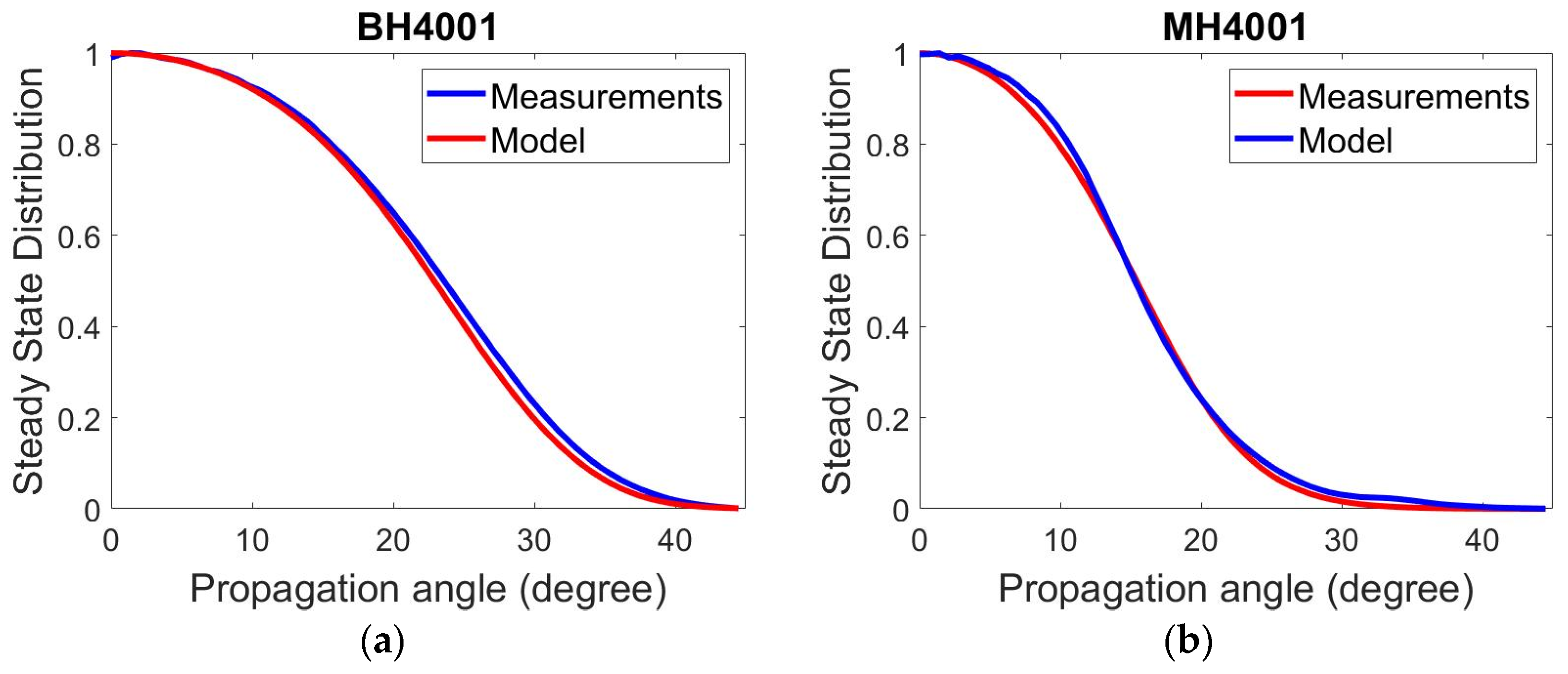
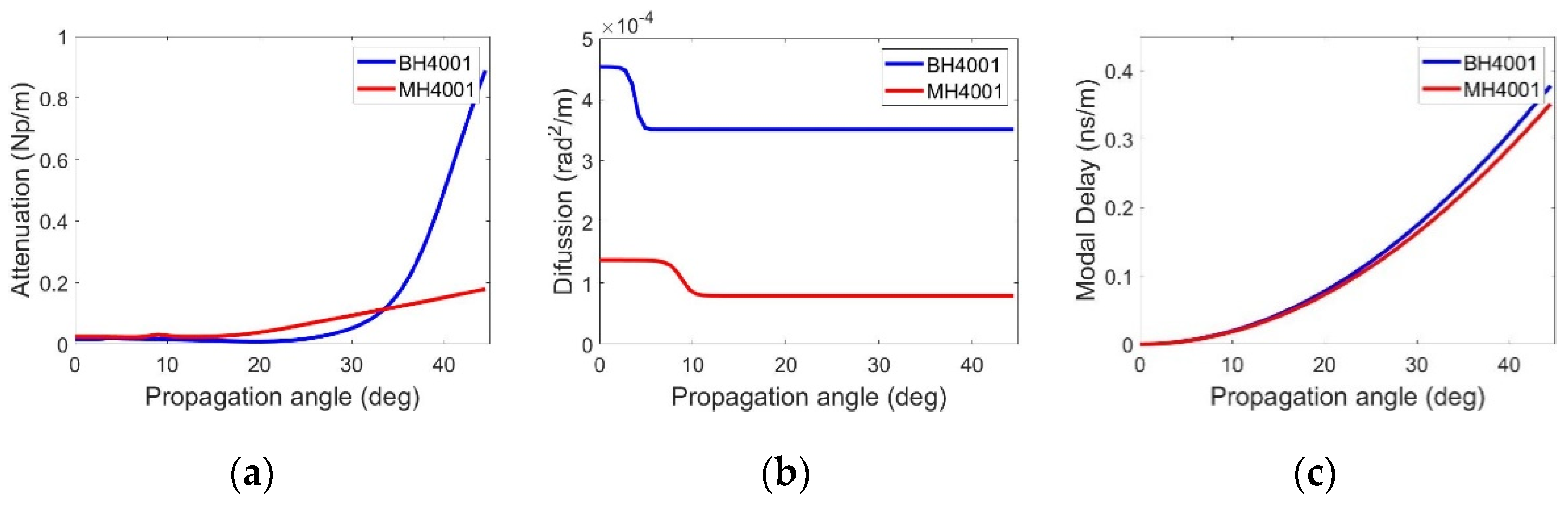
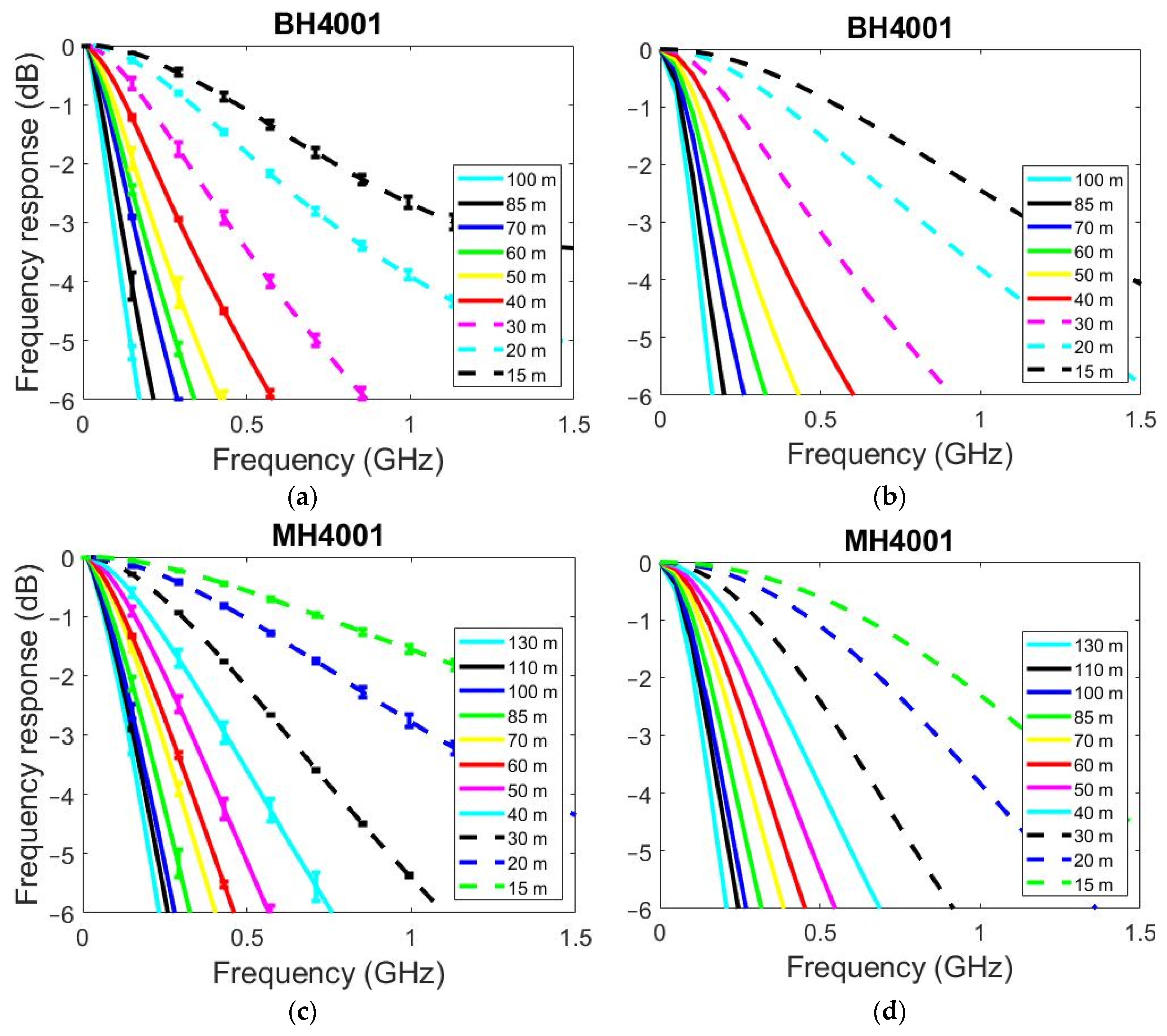
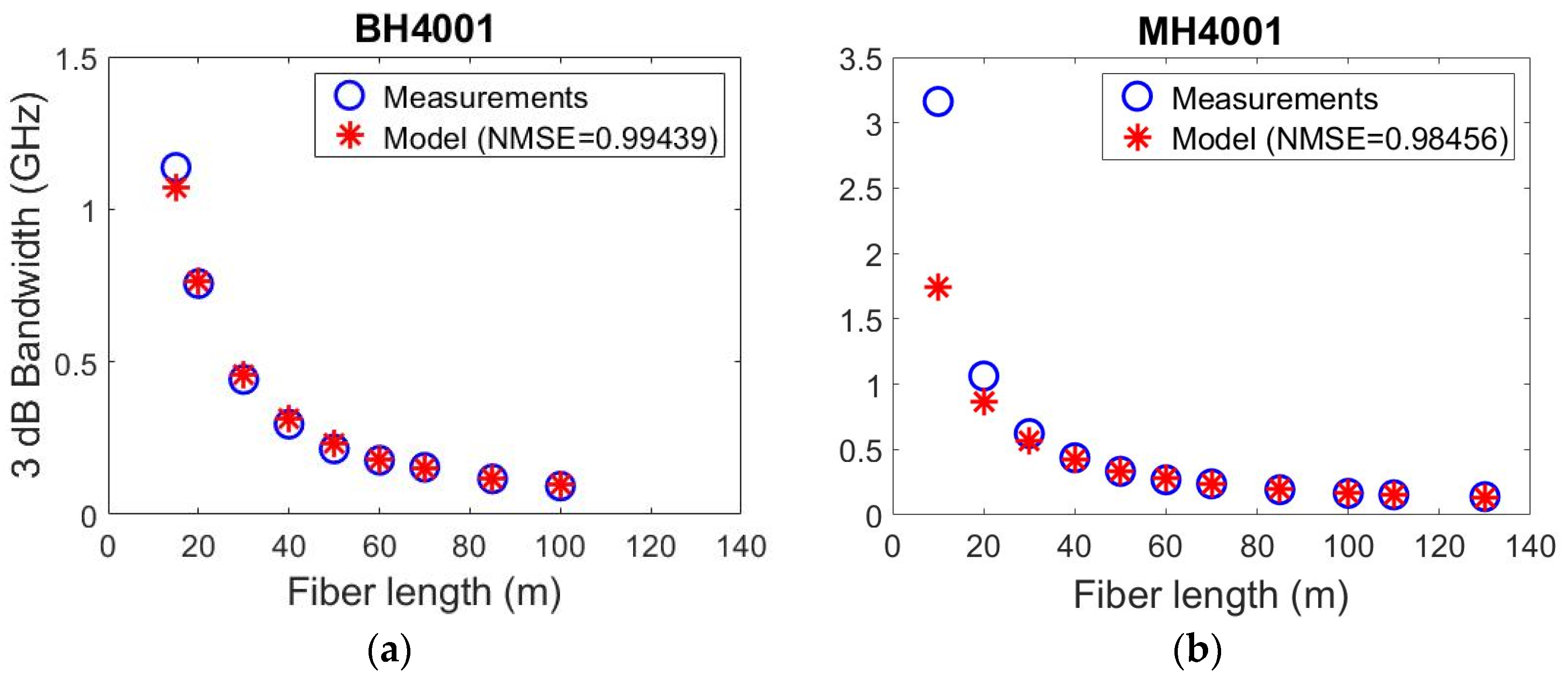
| Fiber | RMSE | ||||
|---|---|---|---|---|---|
| BH4001 | 22.9036 | 0.0566 | 32.4676 | 0.1276 | 1.668 × 10−3 |
| MH4001 | 45.3986 | 0.0185 | 72.9936 | 0.6564 | 7.0874 × 10−3 |
| Fiber | ||||
|---|---|---|---|---|
| BH4001 | 3.5114 × 10−4 | 1.0250 × 10−4 | 3 × 10−3 | 52.8281 |
| MH4001 | 7.8954 × 10−5 | 5.8804 × 10−5 | 8.2867 × 10−4 | 26.0533 |
| Fiber | (Np/m) | (dB/m) | |
|---|---|---|---|
| BH4001 | 0.0258 | 0.0961 | 0.5496 |
| MH4001 | 0.0307 | 0.1513 | 0.5310 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guerrero, J.; Losada, M.A.; Lopez, A.; Mateo, J.; Richards, D.; Antoniades, N.; Jiang, X.; Madamopoulos, N. Novel Measurement-Based Efficient Computational Approach to Modeling Optical Power Transmission in Step-Index Polymer Optical Fiber. Photonics 2022, 9, 260. https://doi.org/10.3390/photonics9040260
Guerrero J, Losada MA, Lopez A, Mateo J, Richards D, Antoniades N, Jiang X, Madamopoulos N. Novel Measurement-Based Efficient Computational Approach to Modeling Optical Power Transmission in Step-Index Polymer Optical Fiber. Photonics. 2022; 9(4):260. https://doi.org/10.3390/photonics9040260
Chicago/Turabian StyleGuerrero, Jorge, M. Angeles Losada, Alicia Lopez, Javier Mateo, Dwight Richards, N. Antoniades, Xin Jiang, and Nicholas Madamopoulos. 2022. "Novel Measurement-Based Efficient Computational Approach to Modeling Optical Power Transmission in Step-Index Polymer Optical Fiber" Photonics 9, no. 4: 260. https://doi.org/10.3390/photonics9040260
APA StyleGuerrero, J., Losada, M. A., Lopez, A., Mateo, J., Richards, D., Antoniades, N., Jiang, X., & Madamopoulos, N. (2022). Novel Measurement-Based Efficient Computational Approach to Modeling Optical Power Transmission in Step-Index Polymer Optical Fiber. Photonics, 9(4), 260. https://doi.org/10.3390/photonics9040260





