Physical Significance of the Determinant of a Mueller Matrix

Abstract

The determinant of a Mueller matrix M plays an important role in both polarization algebra and the interpretation of polarimetric measurements. While certain physical quantities encoded in M admit a direct interpretation, the understanding of the physical and geometric significance of the determinant of M ($\det M$) requires a specific analysis, performed in this work by using the normal form of M, as well as the indices of polarimetric purity (IPP) of the canonical depolarizer associated with M. We derive an expression for $\det M$ in terms of the diattenuation, polarizance and a parameter proportional to the volume of the intrinsic ellipsoid of M. We likewise establish a relation existing between the determinant of M and the rank of the covariance matrix H associated with M, and determine the lower and upper bounds of $\det M$ for the two types of Mueller matrices by taking advantage of their geometric representation in the IPP space.

1. Introduction

Mueller polarimetry is nowadays a well-known and useful optical characterization technique providing substantial information on a huge variety of materials and structures from many areas of science and engineering. Consequently, the physical interpretation of the information encoded in a measured Mueller matrix is a particularly relevant objective.

Despite the recognized importance of the role the matrix determinant plays in the algebraic structure of Mueller matrices [1,2], its physical interpretation is incomplete so far, and a specific analysis in the general case of depolarizing Mueller matrices is still missing.

As shown in Section 3, the interpretation problem can be tackled effectively by combining the concepts of the normal form of a Mueller matrix M and the indices of polarimetric purity (IPP) of its canonical depolarizer. As a result, the specific properties of the determinant of M $(\det M)$ follow directly from those of certain fundamental quantities that are intrinsic to the polarimetric behavior of the interaction represented by M. This approach likewise makes it possible to determine the lower and upper limits of $\det M$, as well as to identify its feasible regions in the purity space for type-I and type-II canonical depolarizers, thus providing a deeper insight in the understanding of the nature and properties of $\det M$.

Prior to addressing the problem, the necessary concepts and conventions are reported in Section 2.

2. Theoretical Background

The concept of Mueller matrix is based on that of the Jones matrix. In fact, any linear polarimetric interaction where the Stokes vector s of the incident electromagnetic wave is transformed into another Stokes vector $s^{\prime }=Ms$, M being the Mueller matrix, can be considered as an ensemble average of basic interactions that can be represented by respective Jones matrices. As a result, M can be expressed as [1,3,4].

$$M=ℒ \langle T\otimes T^{*}\rangle {ℒ}^{ †}, ℒ\equiv \frac{1}{\sqrt{2}}\left(\begin{array}{cccc}1& 0& 0& 1\\ 1& 0& 0& -1\\ 0& 1& 1& 0\\ 0& i& -i& 0\end{array}\right),$$

(1)

where superscripts * and $†$ stand for complex conjugate and conjugate transpose, respectively; the brackets indicate ensemble average; and the 2 × 2 complex matrix T is the Jones generator [4] of M. In general, T fluctuates as a consequence of the generally partial spatial, spectral or temporal coherence of the light-matter interaction phenomenon taking place during the polarimetric measurement process [5,6]. That is, even though the interaction of a photon with a single atom or molecule is necessarily nondepolarizing and therefore can be represented through the Jones formalism alone, the overall macroscopic interaction during measurement (typically involving a measurement time much larger than the polarization time [7,8] of the emerging polarization state) results in the averaging expressed by Equation (1).

The statistical nature of M becomes evident if its elements $m_{ij}$ $(i,j=0,1,2,3)$ are expressed as linear combinations of the second-order moments of the fluctuating elements $t_{kl}$ $(k,l=1,2)$ of T through the expansion of Equation (1). The second-order moments of the elements $t_{kl}$ can be rearranged into a Hermitian matrix H that has the mathematical structure of a covariance matrix [9,10,11], i.e., it is positive semidefinite.

The expressions that relate the elements $m_{ij}$ of M and its associated covariance matrix H are

$$\begin{array}{c}H=\frac{1}{4} {\displaystyle \sum _{k,l=0}^3{m}_{kl} \left({\sigma }_k\otimes {\sigma }_l^{*}\right)}, m_{kl}=\mathrm{tr}\left[\left({\sigma }_k\otimes {\sigma }_l^{*}\right) H\right],\\ {\sigma }_0=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right), {\sigma }_1=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right), {\sigma }_2=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right), {\sigma }_3=\left(\begin{array}{cc}0& -i\\ i& 0\end{array}\right),\end{array}$$

(2)

where ⊗ stands for the Kronecker product and ${\sigma }_i$ $(i=0,1,2,3)$ constitutes a set composed of the 2 × 2 identity matrix and the Pauli matrices.

Any Mueller matrix M can be written as [12,13,14]

$$M\equiv m_{00}\widehat{M}, \widehat{M}\equiv \left(\begin{array}{cc}1& D^T\\ P& m\end{array}\right),$$

(3)

where $m_{00}$ is the mean intensity coefficient (MIC), i.e., the transmittance or reflectance for incident unpolarized light; D and P are the diattenuation and polarizance vectors, with absolute values D (diattenuation) and P (polarizance); and m is a 3×3 submatrix.

The positive semidefiniteness of the covariance matrix H associated with (the generally depolarizing) M leads to a general characterization of Mueller matrices through the non-negativity property of the four eigenvalues $({\lambda }_0,{\lambda }_1,{\lambda }_2,{\lambda }_3)$ of H (expressed through four covariance conditions) or through other formulations equivalent to it [9,10,11,15,16,17,18,19,20,21,22]. In addition, the fact that passive polarimetric interactions do not amplify the intensity of incident light leads to the additional passivity condition $m_{00}(1+Q)\le 1$ where $Q\equiv \max (D,P)$ [11,23]. Thus, a given 4 × 4 real matrix is formally a Mueller matrix if and only if it satisfies the four covariance conditions together with the passivity condition.

In analogy to the degree of polarization of a two-dimensional polarization state, a complete quantitative characterization of the structure of polarimetric purity of the interaction represented by M is provided by the indices of polarimetric purity (IPP) [24,25].

$$\begin{array}{c}{P}_1={\widehat{\lambda }}_0-{\widehat{\lambda }}_1, P_2={\widehat{\lambda }}_0+{\widehat{\lambda }}_1-2{\widehat{\lambda }}_2, P_3={\widehat{\lambda }}_0+{\widehat{\lambda }}_1+{\widehat{\lambda }}_2-3{\widehat{\lambda }}_3,\\ \left[{\widehat{\lambda }}_i={\lambda }_i/\mathrm{tr}H={\lambda }_i/m_{00}, i=0,1,2,3\right],\end{array}$$

(4)

where the eigenvalues of H have been taken in decreasing order $({\lambda }_0\ge {\lambda }_1\ge {\lambda }_2\ge {\lambda }_3)$ so that the IPP satisfy the property $0\le P_1\le P_2\le P_3\le 1$ [24].

Mueller matrices that do not decrease the degree of polarization of any totally polarized incident electromagnetic wave are called pure (or nondepolarizing), and depolarizing otherwise. An overall measure of the closeness of a given M to a pure Mueller matrix is provided by the depolarization index [26] (or the degree of polarimetric purity) $P_{\Delta }=\sqrt{2P_1^2+2P_2^2/3+P_3^2/3}/\sqrt{3}$ [24]. Pure Mueller matrices have the genuine property $P_{\Delta }=1$, while $P_{\Delta }<1$ for depolarizing Mueller matrices. Wherever appropriate, pure Mueller matrices are denoted generically as $M_J$ in order to distinguish them from generally depolarizing Mueller matrices.

Given a Mueller matrix M, there are many ways to express it as the product of simpler Mueller matrices, $M=M_n\dots M_2{M}_1$, so that the interaction represented by M is polarimetrically indistinguishable from that of the sequential action of the serial components $M_1$, $M_2$…$M_n$.In particular, serial decompositions of the form $M^{\prime }=M_{R2}M M_{R1}$, where $M_{R1}$ and $M_{R2}$ are retarder Mueller matrices, are called dual retarder transformations [27]. They have the peculiarity of preserving the determinant (i.e., $\det M^{\prime }=\det M$), as well other physically meaningful algebraic quantities of M such as the MIC $m_{00}$, the diattenuation $D\equiv \left|D\right|$, the polarizance $P\equiv \left|P\right|$, the degree of spherical purity $P_S\equiv {\Vert m\Vert }_F/\sqrt{3}$ (where ${\Vert m\Vert }_F$ stands for the Frobenius norm of m) [28,29], the indices of polarimetric purity $P_1,P_2,P_3$, and the degree of polarimetric purity $P_{\Delta }$.

Another kind of serial decomposition of M that is useful for the physical interpretation of $\det M$ is the so-called normal form decomposition of M [13,30,31,32].

$$M=M_{J2}{M}_{\Delta }{M}_{J1},$$

(5)

where $M_{J1}$ and $M_{J2}$ are pure Mueller matrices, while the canonical depolarizer $M_{\Delta }$ adopts one of the following two type-I and type-II canonical forms $M_{\Delta d}$ and $M_{\Delta nd}$ depending on whether the auxiliary matrix $N\equiv G M^{T}G M$, with $G=\mathrm{diag} (1,-1,-1,-1)$, is diagonalizable or not [31,32].

$$\begin{array}{c}{M}_{\Delta d}=d_0 \mathrm{diag}\left(1,{\widehat{d}}_1,{\widehat{d}}_2,\epsilon {\widehat{d}}_3\right),\\ M_{\Delta nd}=m_{00}\left(\begin{array}{cccc}1& -1/2& 0& 0\\ 1/2& 0& 0& 0\\ 0& 0& {\widehat{a}}_2/2& 0\\ 0& 0& 0& {\widehat{a}}_2/2\end{array}\right),\\ \left[0\le {\widehat{d}}_3\le {\widehat{d}}_2\le {\widehat{d}}_1\le 1, \epsilon \equiv \det M/\left|\det M\right|, 0\le {\widehat{a}}_2\le 1\right].\end{array}$$

(6)

Decomposition (5) can be interpreted as stating the polarimetric equivalence of the action of M and that of the consecutive actions of a nondepolarizing system $M_{J1}$, a canonical depolarizer $M_{\Delta }$ and another nondepolarizing system $M_{J2}$.

As shown in [33], the Poincaré sphere mapping by ${\widehat{M}}_{\Delta d}=M_{\Delta d}/d_0$ and ${\widehat{M}}_{\Delta nd}=M_{\Delta nd}/m_{00}$ determines the respective canonical ellipsoids $E_{\Delta d}$ and $E_{\Delta nd}$ with respective semiaxes $({\widehat{d}}_1,{\widehat{d}}_2,{\widehat{d}}_3)$ and $(1/3,{\widehat{a}}_2/\sqrt{3},{\widehat{a}}_2/\sqrt{3})$ Note that, in the case of nonsingular pure Mueller matrices, which necessarily are of type-I, $E_{\Delta d}$ is the entire unit sphere itself and an alternative geometric representation has been introduced by Tudor and Manea [34].

To complete this summary of concepts, which are necessary to interpret the determinant of a Mueller matrix, let us recall that any depolarizing Mueller matrix M can be expressed through its arbitrary decomposition as a linear combination of pure parallel components

$$\begin{array}{c}M={\displaystyle \sum _{i=1}^r{k}_i}\left(m_{00i} {\widehat{M}}_{Ji}\right), {\left({\widehat{M}}_{Ji}\right)}_{ts}=\mathrm{tr}\left[({\sigma }_t\otimes {\sigma }_s^{*})\left({\widehat{w}}_i\otimes {\widehat{w}}_i^{†}\right)\right],\\ k_i=\frac{1}{m_{00i}\left({\widehat{w}}_i^{†}{H}^{-}{\widehat{w}}_i\right)}, r=\mathrm{rank}H, \left({\displaystyle \sum _{i=1}^r{k}_i}=1\right).\end{array}$$

(7)

where the subscripts t,s are those of the elements of the pure parallel components $M_{Ji}$, ${\widehat{w}}_i$ $(i=1,\dots ,r)$ is a set of r linearly independent unit vectors belonging to the image subspace of the covariance matrix H associated with M, and $H^{-}$ denotes the pseudoinverse of H defined as $H^{-}=U{D}^{-}{U}^{†}$. U is the unitary matrix that diagonalizes H, whereas $D^{-}$$D^{-}$ is the diagonal matrix whose r first diagonal elements are $1/{\lambda }_{ 1},1/{\lambda }_{ 2},\dots ,1/{\lambda }_{ r}$ and whose last $4-r$ elements are zero [35,36]. Consequently, M admits infinite possible parallel decompositions in terms of sets of r pure components, including the well-known Cloude (or spectral) decomposition [9], for which ${\widehat{w}}_i$ is precisely the eigenvector of H.

The physical interpretation of parallel decompositions is that of the sample representing M being decomposed into a number r of elements, spatially distributed over the area illuminated by the probing light [1].

The above most general formulation of the arbitrary decomposition shows that the minimum number of pure parallel components of M is given by the integer parameter $r=\mathrm{rank}H$ [35,36].

3. Physical Interpretation of the Determinant of a Mueller Matrix

From the normal form (5) of a given Mueller matrix, it follows that

$$\det M=m_{00}^4\det {\widehat{M}}_{J2}\det {\widehat{M}}_{\Delta }\det {\widehat{M}}_{J1}=m_{00}^4 {\left(1-D_1^2\right)}^2{\left(1-D_2^2\right)}^2\det {\widehat{M}}_{\Delta },$$

(8)

where $m_{00}$ is the MIC of M, and $D_1$ and $D_2$ are the respective polarizance-diattenuations of the pure components $M_{J1}$ and $M_{J2}$ (recall that $P=D$ for a pure component).

Therefore, apart from the dependence on $D_1$ and $D_2$, the value of $\det M$ is governed by that of $\det {\widehat{M}}_{\Delta }$ which takes the following expressions for the type-I and type-II canonical depolarizers

$$\det {\widehat{M}}_{\Delta d}=\epsilon {\widehat{d}}_1{\widehat{d}}_2{\widehat{d}}_3 \left(0\le {\widehat{d}}_3\le {\widehat{d}}_2\le {\widehat{d}}_1\right), \det {\widehat{M}}_{\Delta nd}= {\widehat{a}}_2^2/16 \left(0\le {\widehat{a}}_2\le 1\right).$$

(9)

These expressions show that $\det \widehat{M}$, whose sign coincides with that of $\det {\widehat{M}}_{\Delta }$(see Equation (8)), is always nonnegative for type-II matrices and can be either positive, negative or zero for type-I Mueller matrices.

Leaving aside its sign, $\det {\widehat{M}}_{\Delta }$ provides a scaled measure of the volume, $4\pi {\widehat{d}}_1{\widehat{d}}_2{\widehat{d}}_3 /3$, or $4\pi {\widehat{a}}_2^2 /27$, of the canonical ellipsoid associated with the corresponding normalized canonical depolarizer ${\widehat{M}}_{\Delta }$. Accordingly, we will write $\det {\widehat{M}}_{\Delta }\equiv V$ (with $\det {\widehat{M}}_{\Delta d}\equiv V_d$ and $\det {\widehat{M}}_{\Delta nd}\equiv V_{nd}$) and will call V the volume coefficient of ${\widehat{M}}_{\Delta }$.

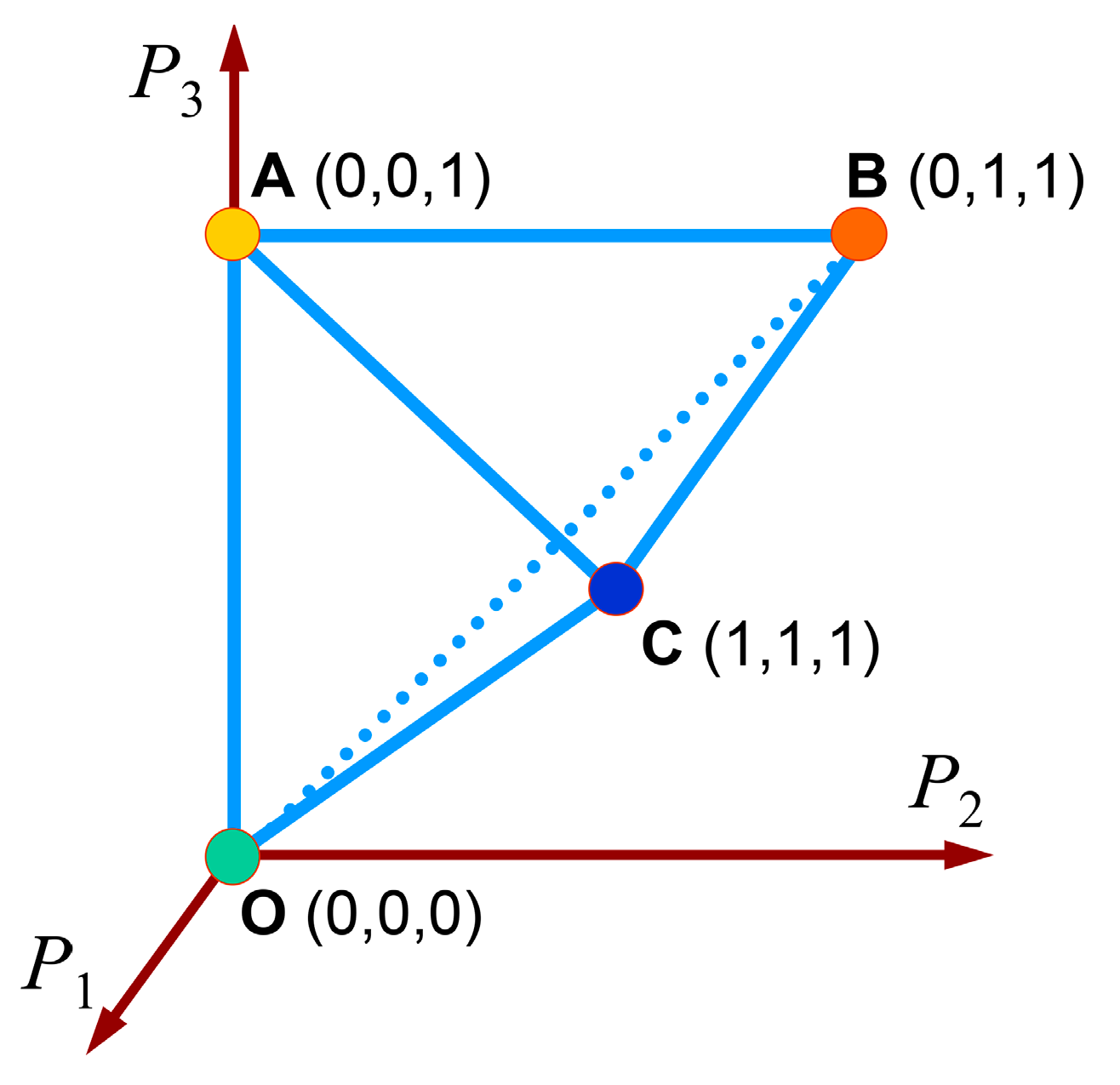
To go deeper into the exploration of the achievable values of $\det {\widehat{M}}_{\Delta }$ in terms of the three IPP $(P_1,P_2,P_3)$, it is worth considering the canonical purity space ${\Sigma }_{\Delta }$ defined as the tetrahedron determining the feasible region for the IPP [24,25] and shown in Figure 1,

Recall that the IPP of a Mueller matrix M provides complete quantitative information on the structure of polarimetric purity of M and, therefore, determines the minimum number r of parallel components of M (with $r=\mathrm{rank}H=\mathrm{rank}{H}_{\Delta }$, $H_{\Delta }$ being the covariance matrix associated with $M_{\Delta }$). In particular, $r=1\iff P_1=P_2=P_3=1$ (point C); $r=2\iff 1=P_2>P_1$ (segment BC, vertex C excluded); $r=3\iff 1=P_3>P_2$ (face ABC, segment BC excluded); and $r=4\iff 1>P_3$ (solid tetrahedron OABC, face ABC excluded). Comprehensive analyses of the different regions of ${\Sigma }_{\Delta }$ in terms of the minimum number r of parallel components of M can be found in Refs. [1,24].

The specific features of V are next analyzed separately for type-I and type-II Mueller matrices.

3.1. Determinant of the Type-I Canonical Depolarizer

In the case of type-I Mueller matrices, it turns out that there is a peculiar relation between $V_d$ and the polarimetric purity of $M_{\Delta d}$. In fact, the value $V_d=1$ (i.e., the canonical ellipsoid coincides with the entire Poincaré sphere) is characteristic of pure Mueller matrices. Conversely, the minimal value $V_d=0$ is achieved for different physical situations associated with the different possible types of type-I singular depolarizers described in Ref. [37]. These are associated with degenerate canonical ellipsoids with one, two or three zero semiaxes, with the latter being the only one corresponding to the particular case of the perfect depolarizer $(P_{\Delta }=0)$, whose Mueller matrix has the form $M_{\Delta d}=d_0\mathrm{diag} (1,0,0,0)$.

The expressions for the diagonal elements of ${\widehat{M}}_{\Delta d}$ in terms of its associated IPP can be found in [38].

$${\widehat{d}}_1=\left(2P_2+P_3\right)/3, {\widehat{d}}_2=P_1+\left(P_3-P_2\right)/3, \epsilon {\widehat{d}}_3=P_1-\left(P_3-P_2\right)/3.$$

(10)

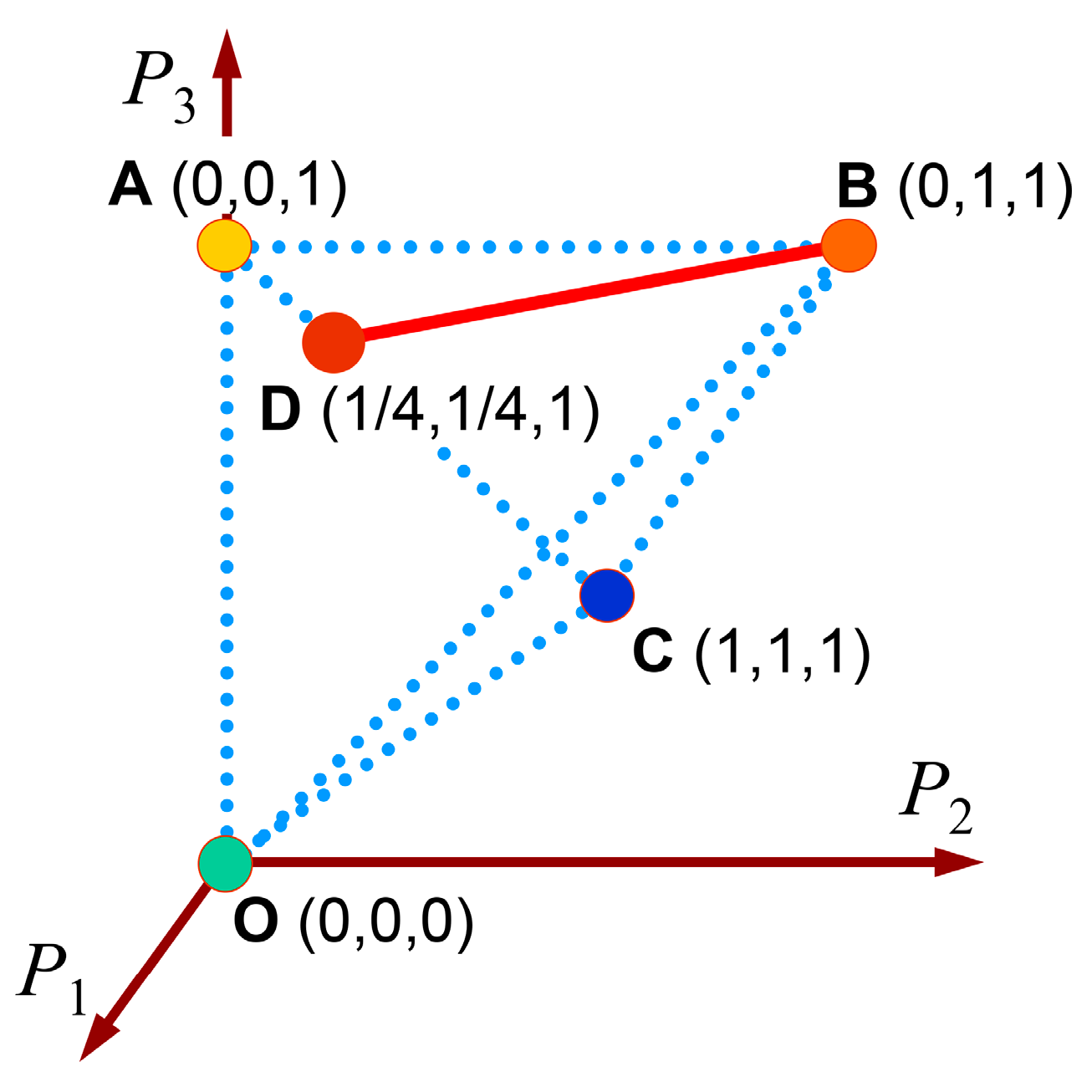
Therefore, the sign of $\det {\widehat{M}}_{\Delta d}$, determined by $\epsilon$, is positive if and only if the inequality $P_3<3P_1+P_2$ holds. This inequality may be satisfied by Mueller matrices with $r=1,2,3,4$. In particular, all pure Mueller matrices ($r=1$) correspond to the unique case where ${\widehat{M}}_{\Delta d}$ is simply the identity matrix and, consequently, they have nonnegative determinants.

By considering the intersection of the plane $P_3=3P_1+P_2$ with the purity space, the feasible region for type-I canonical depolarizers with positive determinant $(P_3<3P_1+P_2)$ is determined by the irregular tetrahedron OBCD (face OBD excluded), hereafter denoted as ${\Sigma }_{\Delta d+}$, see Figure 2a. Regarding the case $\det {\widehat{M}}_{\Delta d}=0$, the combination of Equations (9) and (10) shows that it corresponds to $P_3=3P_1+P_2$ (i.e., ${\widehat{d}}_3=0$; recall that $0\le {\widehat{d}}_3\le {\widehat{d}}_2\le {\widehat{d}}_1$) whose feasible region, ${\Sigma }_{\Delta d0}$, in the purity space is given by the triangular area OBD (edges included). Finally, $\det {\widehat{M}}_{\Delta d}$ is negative if and only if $P_3>3P_1+P_2$, which corresponds to the irregular tetrahedron OABD (face OBD excluded), hereafter called ${\Sigma }_{\Delta d-}$, see Figure 2b.

Since the IPP determine the value of r, negative values of $\det {\widehat{M}}_{\Delta d}$ correspond to $r=3$ or $r=4$, that is, when $\det M<0$ the arbitrary decomposition of M [36] has three or four pure components. Conversely, Mueller matrices with $r=1$ or $r=2$ (i.e., having one or two arbitrary components) feature $\det M\ge 0$. As a consequence, the tetrahedron ${\Sigma }_{\Delta d-}$ (face OBD excluded) of the type-I canonical depolarizers corresponds uniquely to Mueller matrices with $r=3$ or $r=4$ whose determinant is negative.

From Equations (9) and (10), $\det {\widehat{M}}_{\Delta d}$ can be expressed as follows in terms of the IPP of $M_{\Delta d}$

$$\det {\widehat{M}}_{\Delta d}=\frac{1}{27}\left[9P_1^2\left(P_3+2P_2\right)+P_2^2\left(3P_3-2P_2\right)-P_3^3\right].$$

(11)

The nested structure of the IPP $(0\le P_1\le P_2\le P_3\le 1)$ implies that the two first addends of the right member are nonnegative, while the last one $(-P_3^3/27)$ is intrinsically negative. Therefore,

$$-P_3^3/27\le \det {\widehat{M}}_{\Delta d}\le 1 ,$$

(12)

so that the minimum achievable value, $\det {\widehat{M}}_{\Delta d}=-1/27$, is necessarily realized for the combined values $P_1=P_2=0$ and $P_3=1$ (point A of ${\Sigma }_{\Delta d}$). The maximum $\det {\widehat{M}}_{\Delta d}=1$ is genuine of pure Mueller matrices ($P_1=P_2=P_3=1$,$r=1$, point C of ${\Sigma }_{\Delta d}$).

Since $P_3=1\Rightarrow r<4$ and $\det {\widehat{M}}_{\Delta d}<0\Rightarrow r=3,4$, we conclude that the above indicated minimum value can only be achieved when $r=3$, while $-1/27<\det {\widehat{M}}_{\Delta d}<1$ for Mueller matrices with $r=4$.

It should be noted that the values of $m_{00}$, $D_1$ and $D_2$ are independent of $\det {\widehat{M}}_{\Delta d}$ [31] and, consequently, they affect neither the sign of $\det M$ nor the value of r.

3.2. Determinant of the Type-II Canonical Depolarizer

Both the volume coefficient $V_{nd}= {\widehat{a}}_2^2/16$ and the degree of polarimetric purity

$$P_{\Delta nd}=\sqrt{\frac{1+{\widehat{a}}_2^2}{6}}=\sqrt{\frac{1+16 V_{nd}}{6}} ,$$

(13)

of the type-II canonical depolarizer $M_{\Delta nd}$ are uniquely determined by the parameter ${\widehat{a}}_2$, see Equation (6). Consequently, $V_{nd}$ and $P_{\Delta nd}$ reach their respective maximum values $V_{nd}=1/16$ and $P_{\Delta nd}=1/\sqrt{3}$ for ${\widehat{a}}_2=1$, which in turn corresponds to two-component type-II matrices $(r=2)$. Values $V_{nd}<1/16$ and $P_{\Delta nd}<1/\sqrt{3}$ below the maximum ones correspond to three-component type-II matrices $(r=3)$. The lower $V_{nd}$, the lower the degree of polarimetric purity, down to $V_{nd}=0$ and $P_{\Delta nd}=1/\sqrt{6}$, with the latter corresponding to the case where the canonical ellipsoid $E_{\Delta nd}$ degenerates into a segment (type-II singular depolarizer, see [37]). Note that $P_{\Delta nd}$ has the non-zero lower limit $P_{\Delta nd \min }=1/\sqrt{6}$ because of the contribution to polarimetric purity of the residual polarizance and diattenuation exhibited by $M_{\Delta nd}$.

Let us now recall that $P_3({\widehat{M}}_{\Delta nd})=1$ and $P_1({\widehat{M}}_{\Delta nd})<1$ (which express the fact that $r=1$ and $r=4$ are not achievable for ${\widehat{M}}_{\Delta nd}$). Consequently, since the right- or left- product of a Mueller matrix by a diattenuator preserves the value of r, type-II Mueller matrices contain two or three arbitrary components, while pure systems $(r=1)$ and systems with $r=4$ are necessarily of type-I.

The expressions for the IPP of ${\widehat{M}}_{\Delta nd}$ in terms of the single parameter ${\widehat{a}}_2$ are

$$P_1=\frac{1-{\widehat{a}}_2}{4}, P_2=\frac{1+3{\widehat{a}}_2}{4}=1-3P_1,$$

(14)

As shown in Figure 3, the feasible region for type-II canonical depolarizers in the purity space is determined by the straight segment BD, given by the intersection of planes $P_3=1$ and $3P_1+P_2=1$ (with the restriction $0\le P_1\le P_2$). Note in passing that Equations (9) and (14) lead to the following expressions for $\det {\widehat{M}}_{\Delta nd}$ in terms of its IPP

$$\begin{array}{c}\det {\widehat{M}}_{\Delta nd}=\frac{1}{16}\left[1+16P_1\left(P_1-\frac{1}{2}\right)\right]=\left(\frac{1}{9}\right)\frac{1}{16}\left[1+16P_2\left(P_2-\frac{1}{2}\right)\right],\\ \left(3P_1+P_2=1, 0\le P_1\le P_2\right).\end{array}$$

(15)

They are consistent with the fact that, by its definition, the parameter ${\widehat{a}}_2$ satisfies the inequalities $0\le {\widehat{a}}_2\le 1$. Therefore,

$$0\le \det {\widehat{M}}_{\Delta nd}\le 1/16.$$

(16)

The minimum, $\det {\widehat{M}}_{\Delta nd}=0$, corresponds to point D $(P_1=P_2=1/4,P_3=1\Rightarrow r=3)$. The maximum, $\det {\widehat{M}}_{\Delta nd}=1/16$, corresponds to point B $(P_1=0,P_2=1,P_3=1\Rightarrow r=2)$.

It is remarkable that, while the segment BD of the purity space ${\Sigma }_{\Delta d}$ corresponds to type-I canonical depolarizers with a zero determinant, only point D is associated with type-II canonical depolarizers with a zero determinant.

As with type-I matrices, the values of $m_{00}$, $D_1$ and $D_2$ are independent of $\det {\widehat{M}}_{\Delta nd}$ [1,31], and, therefore, they affect neither the sign of $\det M$ nor the value of r.

4. Discussion

Equation (8) shows that the determinant of a Mueller matrix M can be interpreted in terms of four physical quantities that are invariant under dual retarder transformations, namely, the MIC $m_{00}$; the diattenuations, $D_1$ and $D_2$, of the pure serial components $M_{J1}$ and $M_{J2}$ of the normal form $M=M_{J1} M_{\Delta } M_{J2}$; and the volume coefficient V of the canonical depolarizer $M_{\Delta }$ of M. The smaller the values of $m_{00}$ and V, the smaller $\left|\det M\right|$, while the smaller $D_1$ and $D_2$, the larger $\left|\det M\right|$ is.

One-component systems ($r=1$) correspond to pure Mueller matrices and are represented by point C of the purity space $\Sigma$, see Figure 1. The determinant of any pure Mueller matrix $M_J$ can be expressed as $\det M_J=m_{00}^4 {(1-D^2)}^2$, where D is the polarizance-diattenuation of $M_J$ and takes values in the interval $0\le \det M_J\le 1$ [1]. Regarding the determinant of the normalized version ${\widehat{M}}_J$ of $M_J$, it is exclusively determined by D, so that $\det {\widehat{M}}_J=1$ corresponds to retarders, regardless of whether the retardation effect is accompanied by an isotropic attenuation $(m_{00}< 1)$. Thus, $\det M_J=0$ corresponds to perfect polarizers $(D=1)$, while $\det M_J=1$ is exclusively satisfied by transparent retarders $(D=0, m_{00}=1)$. Note that the property $\det M=1$ implies that the canonical ellipsoid coincides with the entire surface of the Poincaré sphere (with homogeneous topological distribution of the transformed states) and is genuine of retarders (either transparent or affected by isotropic attenuation), so that there are no enpolarizing or depolarizing media satisfying $\det M=1$ (the term enpolarizing refers to media whose diattenuation or polarizance is nonzero).

Two-component systems (i.e., $r=2$, described by segment BC of ${\Sigma }_{\Delta d}$, vertex C excluded, see Figure 1) can correspond to either type-I or type-II Mueller matrices. In the first case, $0\le \det {\widehat{M}}_{\Delta d}<1$ and, therefore, $0\le \det M<1$, as follows from Equations (8) and (12) (because $0<m_{00}\le 1$, $0\le D_1\le 1$ and $0\le D_2\le 1$ [37]). In the second case of type-II matrices (for which only the point B of the segment BC is compatible with $r=2$, see Figure 3), $\det {\widehat{M}}_{\Delta nd}=1/16$ and the volume of the type-II canonical ellipsoid takes its maximum achievable value $4\pi /27$. Therefore, $0<\det M\le 1/16$, as follows from Equations (8) and (16). Note that, since, necessarily, in type-II Mueller matrices $D_1<1$ and $D_1<1$, $\det M>0$.

In the case of type-I three-component ($r=3$) Mueller matrices $-1/27\le \det {\widehat{M}}_{\Delta d}<1$ and, therefore, $-1/27\le \det M<1$. The minimum (corresponding to point A of ${\Sigma }_{\Delta d}$, see Figure 2) is achieved by depolarizing Mueller matrices of the form $M_{R2}{M}_{\Delta dr3}{M}_{R1}$, where $M_{R1}$ and $M_{R2}$ represent retarders and the canonical type-I depolarizer $M_{\Delta dr3}=\mathrm{diag} (1,1/3,1/3,-1/3)$ is expressible as an equiprobable incoherent mixture of its first three spectral components,

$$M_{\Delta dr3}=\frac{1}{3}\mathrm{diag}\left(1,1,1,1\right)+\frac{1}{3}\mathrm{diag}\left(1,-1,1,-1\right)+\frac{1}{3}\mathrm{diag}\left(1,1,-1,-1\right).$$

(17)

The value $\det M=1$ is excluded for depolarizing Mueller matrices (with two, three or four components) but plays the role of a limit to which $\det M$ can tend asymptotically.

Three-component type-II Mueller matrices feature $0\le \det {\widehat{M}}_{\Delta nd}<1/16$ (occupying the segment BD, vertex B excluded, see Figure 3) and, therefore, $0\le \det M<1/16$.

Finally, four-component systems (occupying the tetrahedron OABC, face ABC excluded) correspond exclusively to type-I matrices for which $-1/27<\det {\widehat{M}}_{\Delta nd}<1$ and, therefore, $-1/27<\det M<1$.

Regarding type-I and type-II singular Mueller matrices, a comprehensive analysis and classification can be found in [37], while certain peculiar features of Mueller matrices with negative determinants have been studied in [39,40].

The detailed analysis of the achievable values of $\det M$ depending on the value of r for type-I and type-II Mueller matrices is summarized in

Table 1. Classification of 2D states $(P_d=1)$.

	$r=1$	$r=2$	$r=3$	$r=4$
	$\left(P_1=P_2=P_3=1\right)$	$\left(P_3=P_2=1, P_1<1\right)$	$\left(P_3=1, P_2<1\right)$	$\left(P_2<1\right)$
Type-I	$0\le \det M\le 1$	$0\le \det M<1$	$-1/27\le \det M<1$	$-1/27<\det M<1$
Type-II	Not achievable	$0<\det M\le 1/16$	$0\le \det M<1/16$	Not achievable

.

5. Conclusions

We have analyzed the physical significance of the determinant of a Mueller matrix M in terms of intrinsic fundamental properties of M. These are the mean intensity coefficient $m_{00}$, and the diattenuations $D_1$ and $D_2$ of the pure components of the normal form of M, together with its volume coefficient defined as a scaled measure of the volume of the canonical ellipsoid associated with M. The canonical depolarizer $M_{\Delta }$ of M (either in its type-I or type-II forms) is crucial for the interpretation of $\det M$ and allows for meaningful geometric representations in the purity space determined by the indices of polarimetric purity of $M_{\Delta }$. We have established the lower and the upper limits of $\det M$, as well as the various achievable regions in the purity space, and have physically interpreted these in terms of the number of pure parallel components of M.