Abstract
Quantum key distribution (QKD) can protect the exchange process of confidential information between communicating parties. By using the basic principles of quantum mechanics and combined with “one-time pad” cipher encryption, information can be unconditionally secure. The BB84 protocol first describes the method of transmitting information by photon polarization state, and it expounds the transmission process of services between trusted relays. However, due to the defects of real experimental devices, there are security vulnerabilities in QKD in a real system. The birth of measurement-device-independent quantum key distribution (MDI-QKD) protocol solves the problem, providing immunity to hacker attacks at the end of the detector. It can enable both sides of the transmission service to establish a connection and generate secret keys through an untrusted relay node to ensure information security. However, the types and properties of link nodes in quantum key distribution network (QKDN) based on partially trusted relay are more complex, which can easily result in network fault. Therefore, how to prevent the impact of failure on QKDN has become an urgent problem. In this paper, we propose a protection scheme for QKDN with partially trusted relays. The method deals with trusted and untrusted relays differently and constructs the working and protection paths of the secret key for each service. It reduces resource conflict between the protection and working paths by establishing a key protection threshold, which realizes the resource trade-off between the two factors. Simulation results show that the scheme provides effective protection to the services, and it improves the stability and reliability of QKDN based on partially trusted relay.
1. Introduction
With the diversified development of information transmission methods since the third revolution in science and technology, optical networks carry a large amount of important information in many application fields such as military and finance. In 2014, an attack on an online trading platform caused huge economic loss [1]. In 2015, there were 16 known optical cable attacks in San Francisco [2]. Preventing the information in optical network from being intercepted and improving the security of data information transmission has become an increasingly urgent demand. The key distribution based on traditional cryptography has the risk of being cracked by more advanced attack algorithms, which cannot easily meet the needs of security.
Different from the traditional encryption methods based on mathematical computational complexity and the symmetric encryption algorithm, quantum key distribution (QKD) technology has more advantages. The BB84 protocol first describes the method of transmitting information by using photon polarization state coding [3]. It uses the characteristics and laws of quantum mechanics to maintain communication security, transmitting coded states through quantum channels. The protocol also enables both sides of communication to share random secure symmetric keys in the process of information transmission. The key is a secret bit string used for secure communication and authentication [4]. These pairwise keys allow terminal nodes to generate their own keys, provided that all intermediate nodes are trusted [5]. This process is based on the Heisenberg uncertainty principle, so the eavesdroppers can neither successfully measure and obtain quantum state information nor affect the key transmission. QKD also uses the quantum state no-cloning theorem, which improves the security of the communication process by making the eavesdropper unable to copy the quantum state. In the BB84 protocol, the linear polarization and circular polarization of photons are in conjugate states, which conforms the uncertainty principle. Therefore, whenever there is a third-party measurement made by eavesdroppers, the original quantum state will inevitably change [6]. According to the quantum bit error rate of the selected measurement base, we can judge whether the channel transmission data have been eavesdropped or tampered. Combined with the “one-time pad” encryption technology, the BB84 protocol can achieve unconditional security in theory.
The DARPA QKD network, the world’s first quantum key distribution network (QKDN), was proposed in December 2002, laying a foundation for the development of a QKDN based on trusted relay [7], which was developed in SECOQC [8]. In 2017, the backbone QKDN in Beijing and Shanghai began to operate. It was the longest QKDN in the world at that time, realizing the decoy state BB84 protocol based on optical polarization coding [9]. QKD has developed to the degree of networking communication and has become the key technology of quantum communication. In optical networks, the key generated in the process of QKD can occupy the resources of the communication channel. If the network fails, the key service will be interrupted. Therefore, it is necessary to study survivability technology based on a QKDN. In previous studies, protection schemes and recovery measures proposed for QKDNs have been proposed, such as an adaptive protection scheme of key capacity [10] and key recovery strategies [11,12].
Although the BB84 protocol has theoretical security, due to the gap between reality and theory, the devices in the actual QKD system are not perfect. Therefore, there are still some hidden dangers regarding security in the information key transmission. It may lead to the operation mode state of the real equipment being different from the mathematical model established in the previous ideal state, which can easily cause eavesdroppers to attack. Eavesdroppers can carry out time-shift attacks by learning distributed keys [13]. By changing the arrival time of each signal, the eavesdropper can not only not introduce any errors but also obtain the information of some final keys [14]. Quantum hackers can also use detector blinding attacks to steal information [15]. The measurement-device-independent quantum key distribution (MDI-QKD) protocol [16] can remove all side-channels of the measurement devices [15], which effectively solves the security vulnerability. The MDI-QKD protocol allows the communicating parties to connect through untrusted relay nodes. In MDI-QKD, the equipment used by untrusted relay is more expensive and complex, but it can expand the transmission distance and double the coverage distance of the traditional QKD scheme when the key rate is equivalent to QKD [16].
In MDI-QKD with discrete variables, different implementations are proposed. This approach can achieve a long-distance quantum cryptography system [17]. The protocol is suitable for asymmetric channels [18]. QKD based on two fields was proposed as a measurement-device-independent scheme [19,20]. A phase-matching QKD protocol is proposed, which is immune to all possible detection attacks [21]. It is related to the two field QKD protocol [22]. Continuous-variable MDI-QKD systems have also been studied. In order to generate secret correlations, they transmit the coherent state to the relay, where continuous-variable Bell detection and output broadcast are performed [23]. Strict security analysis of continuous-variable MDI-QKD is proposed, which shows its feasibility [24]. A multimode continuous-variable QKD system with non-Gaussian operations is proposed [25]. In the chip-based MDI-QKD network, each user only needs a compact transmitter chip, and the relay holds an expensive and huge measurement system (and quantum memory [26]) shared by all users. It is suitable for constructing a star-type quantum access network, placing complex and expensive measurement equipment in the central untrusted relay. Each user only needs a low-cost transmitter, such as an integrated photonic chip. The measuring equipment is placed on the central relay, which performs Bell state measurement (BSM). In a 200 square kilometer metropolitan area, an MDI-QKD star-type network was built by Tang and others [27]. For the mixed situation of trusted and untrusted relay in the network, the routing algorithm is proposed [28].
Because the link structure and node types of the QKDN based on partially trusted relay are more complex, it is more likely that the key distribution in the process of service transmission fails. Therefore, the survivability problem in partially trusted relay scenario is of great significance. In view of the situation that there is trusted and untrusted relay in the network, how to allocate the normal key resources of QKD and design an appropriate protection scheme became the core topic of this paper. To solve the problem, we first describe a conventional QKDN based on fully trusted relay and a QKDN based on partially trusted relay to show differences between them. Then, the partially trusted relay-based protection strategy is proposed, which considers the protection threshold to enhance the security. A simulation based on the scheme was carried out on two different topologies. The results show there is a trade-off between key service request blocking rate and protection path construction success rate.
The remainder of this paper is organized as follows. Section 2 describes the QKDN with fully trusted relay and partially trusted relay. Section 3 presents a problem statement to address the question. Section 4 proposes the protection strategy with partially trusted relay in detail. The simulation results and analysis are in Section 5. Finally, Section 6 outlines the summary and conclusions.
2. Quantum Key Distribution Network
2.1. QKDN Based on Fully Trusted Relays
A QKD link is a logical connection between two QKD nodes. In the component of a QKD optical network, the nodes of both sides of communication include a QKD module and a key server. Two QKD nodes are connected through optical links in optical network facilities. The links use optical elements and optical fiber transmission keys to reduce interference. In the QKDN, the channel between two nodes includes the classical channel and quantum channel. The classical channel is used for synchronization and data exchange between the QKD modules. Quantum channels are used to transmit encoded photons.
The network model based on QKD realizes the secure communication between end-to-end networking nodes by means of hop-by-hop manner or a key repeater, since the point-to-point QKD distance is limited by depolarization errors, dark counts and other factors [29]. The premise is that all nodes of the network are trusted. The QKD optical network can be divided into four layers: application layer, control layer, QKD layer and data layer [30]. In the network, the application layer is responsible for generating data service requests with security requirements. As shown in Figure 1, the control layer controls the functions of each layer through the internal controller, and it can manage the resources of the QKD layer and data layer. When the service request arrives, the controller allocates wavelength resources for the key in the QKD and data layer by notifying the corresponding node. The QKD layer provides key for data services.
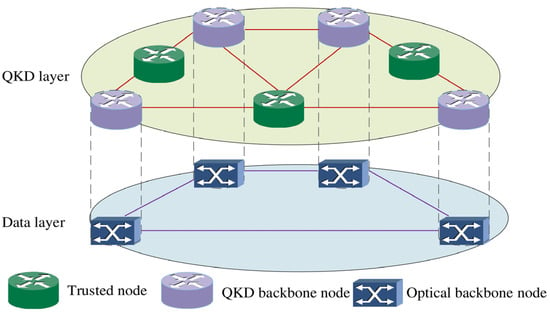
Figure 1.
QKD network based on trusted relays.
2.2. QKD Network Based on Partially Trusted Relays
The assumption of fully trusted repeaters can be relaxed in more than three ways. First, MDI-QKD can be used, and its security is higher than QKD network with trusted relay nodes. MDI-QKD extends the quantum channel, so the nodes of both sides of communication still need to be trusted. Second, quantum repeaters can be used as an alternative. Quantum entanglement of photons can be used to store and forward the information of quantum states, achieving the purpose of communication through different quantum links. The space distance that the technology can transmit is greatly affected by the fidelity of entanglement swapping, but practical deployment has not yet been realized [31]. Third, it depends on multipath transmission and threshold encryption to reduce the risk of eavesdropping. In this paper, we only consider the case of untrusted relays in the network following the MDI-QKD protocol.
As shown in Figure 2, the optical network model based on partially trusted relay includes four layers from top to bottom, namely the application layer, control layer, QKD layer and data layer. The data layer can also be named the optical layer. Similar to the ordinary QKDN, the application layer and control layer can also control and manage key services in practical application. In the QKD layer, a total of three types of QKD nodes are deployed, including QKD backbone nodes, trusted relays and untrusted relays. The optical layer is composed of the optical backbone network, and there are optical backbone nodes interconnected through optical links. Keys can be exchanged between the QKD layer and data layer.
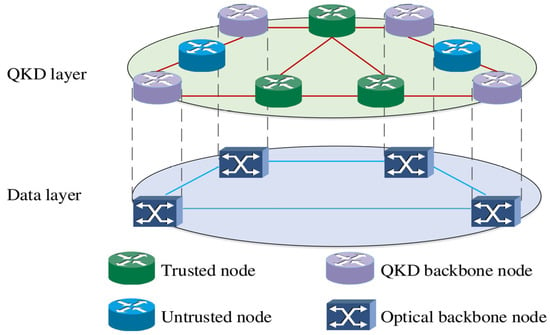
Figure 2.
QKD network based on partially trusted relays.
3. Problem Statement
In the existing study, there have been many attempts at a QKDN based on trusted relay [7,10,32]. In order to improve the security of QKD networking, network protection schemes are also proposed, including shared protection schemes and dedicated protection schemes [10]. For the QKD networking based on the partially trusted relay, there is a cost optimization method in the deployment stage [33]. In that research, it is concluded that using the partially trusted relay scheme can lead to lower cost and higher security level. A QKD method which can work in a partially trusted QKDN is proposed [28]. In 2022, a partially trusted relay-based QKD method and routing of keys in different kinds of typical network topologies were described [34]. Security is a crucial problem. A key management and data scheduling scheme has been proposed [35].
In large-scale or inter metropolitan quantum networks, the coexistence of multiple protocols is inevitable. The two users may communicate through trusted repeaters or exchange information through untrusted relays over a long distance. Nodes that follow the BB84 protocol and nodes that use the MDI-QKD protocol may appear in the same network topology. The QKDN link based on partially trusted relay is more complex, resulting in higher risk of failure. Since the channels used for QKD and data services are multiplexed in the common optical fiber, their protection against link failure can be considered separately. However, there is little research on the protection of QKD networking in a partially trusted relay situation. In order to reduce the impact of possible faults on QKD in a partially trusted relay scenario, the corresponding protection scheme is an important problem to be solved. For the sake of improving the security of QKD networking, we propose a protection scheme in a QKDN based on partially trusted relay. Protection refers to making a certain prediction before the fault occurs and reserving resources and paths for it. The proposed dedicated protection scheme transmits the key simultaneously on the working and protection paths to ensure security. The protection scheme mainly solves two sub-problems: (1) For the untrusted nodes that may appear in the network, different processing methods from the trusted nodes need to be considered. (2) A large number of protection paths can occupy the key resources in the link, resulting in a high blocking rate to the key distribution on working paths. Therefore, it is necessary to consider how to balance the resource allocation of secret keys on the working and protection paths.
In order to solve these two sub-problems, a topology-abstraction-based protection scheme in a QKDN with partially trusted relay is proposed. When designing the protection strategy, the processing method of untrusted nodes was considered, which is different from trusted nodes. In addition, a key protection threshold was proposed to adjust the distribution of key resources.
4. Topology-Abstraction-Based Protection Scheme in Quantum Key Distribution Networks with Partially Trusted Relay
4.1. Network Model
In this section, the network model of the topologies is described as follows. The network topology which runs the protection strategy is represented by a graph named G(V, L). V is the set of nodes, and L is the set of direct links. Every two nodes a and b are connected by one link la_b: thus, la_b ∈ L. The service arriving in the QKDN is denoted as rk(sr, dr, Mr, ta, tr). Rk is the set of all services. sr and dr respectively represent the source node and destination node of the service in the network topology. The number of secret keys required by the service in unit time is represented by Mr. ta represents the arrival time of service, and tr is the duration of the service. Pv_w represents the working path selected by the scheme, while Px_y is the selected protection path. The detailed parameter definitions are all shown in Table 1.

Table 1.
Notation and definitions.
4.2. Topology-Abstraction-Based Protection Scheme in Quantum Key Distribution Networks with Partially Trusted Relay
The overall steps of the topology-abstraction-based protection scheme in the QKDN with the partially trusted relay (TAPS-PTR) algorithm are as shown in Algorithm 1. First, the topology abstraction of the QKDN with partially trusted relay is introduced. Second, if the service arrives, the working path resources of the service are allocated. Lastly, protection path resources are allocated, and the key channel link resource status is updated. When the service leaves, the key resources are released. The specific process of the algorithm is as follows.
| Algorithm 1. Topology-abstraction-based protection scheme in QKDN with partially trusted relay. |
| Input: network topology G(V, L), service rk(sr, dr, Mr, ta, tr), Weights, Th, η Output: dedicated protection for each service |
| 1 Traverse and record the trusted and untrusted nodes u in the network topology |
| 2 for all la_b do |
| 3 if sa→sb = 1 and both sa, sb are untrusted nodes then |
| 4 remove the virtual link corresponding to link la_b |
| 5 end if |
| 6 if sa→sb = 2, sa→sc = 1, sc→sb = 1 and sa, sb are trusted nodes, sc is untrusted node |
| then |
| 7 forming virtual direct link la_b |
| 8 end if |
| 9 end for |
| 10 for all rk ∈ Rk do |
| 11 Calculate e paths P |
| 12 Obtain the lowest Weight path Pv_w from set P |
| 13 Delete Pv_w in P |
| 14 if Tv_w < Mr and P = Ø then |
| 15 The dedicated protection of rk failed |
| 16 else mark Pv_w as the working path |
| 17 Obtain the lowest Weight path Px_y from set P |
| 18 Delete Px_y in P |
| 19 if (Tx_y< Mr or Mr > Th*η) and P = Ø then |
| 20 The dedicated protection of rk failed |
| 21 else mark Px_y as the protection path |
| 22 end if |
| 23 end if |
| 24 end for |
In the process of network topology abstraction, there are four steps. Firstly, the strategy needs to traverse each node of the network topology for initialization and record the physical location of each trusted node and untrusted node in the topology. In particular, untrusted nodes need to be distinguished from trusted nodes. Secondly, the links that are untrusted nodes on both sides needs to be unconnected. The reason is that the service cannot be transmitted between two untrusted nodes. Thirdly, a virtual direct link is formed between two trusted nodes with an untrusted node in the middle. They are trusted node pairs that can transfer key services to each other. The untrusted node should also be abstracted. Finally, each untrusted node forms a corresponding virtual direct link group, and their resources are shared within the group. After that, network topology abstraction is completed.
Then there is the process of working path routing and secret key resource allocation. Firstly, when the service request arrives, the basic attributes of the service will be analyzed, such as the source node sr and destination node dr of the service, the start time ta and the duration tr of the service and the quantum key rate per unit time Mr required by the service. The data of the service are stored in the linked list. Secondly, according to the number of link hops between the source node and the destination node, the Dijkstra algorithm is used to calculate the shortest paths and put them into the path set P. The selected shortest path is temporarily marked as the working path, and the current remaining key resources of each hop route along the temporarily marked path are calculated. The key resources required by the service are compared to judge whether the link can provide the key quantity meeting the service requirements within the service duration. If the key resources on the selected link are sufficient, the secret key resources for the working path are allocated. Then, the protection path resource allocation stage is performed. However, if the key resources on the selected link are insufficient, the hop link with insufficient resources in the network topology should be abstracted, which means disconnecting it provisionally. After that, the process returns to the previous routing stage, and the new shortest path in the new topology is calculated, carrying out the process mentioned above. The process is repeated until the appropriate working path is found. The link abstraction interrupt flag will not be erased until the last path in the set of the possible paths set P cannot meet the key service requirements.
Lastly, there is the process of protection path and secret key resource allocation. The working paths in the path set P and the paths previously disconnected due to insufficient resources are removed, retaining the remaining optional paths in the network. Then, the Dijkstra algorithm is used to calculate the shortest path in the QKDN topology at this time, which is temporarily marked as the protection path. Then, it is judged whether the remaining key resources of the link are sufficient for each hop link along the temporarily marked protection path by comparison. If the key resources on the link are sufficient, the next judgment step can be entered. However, if the key resources on the link are insufficient, the hop link should be abstractly disconnected, and the protection path needs to be reselected. The process is repeated until the appropriate protection path is selected. After the protection path resource allocation is successful, the key resources in the network are updated. The whole topology is traversed to ensure that the key resources, link spectrum wavelength time slot resources and other status information on each link are updated. When the service leaves, all the resources allocated to it are retracted.
However, when the key resources on the network are limited, the unrestricted occupation of key resources by the protection path may lead to higher blocking rate of key service requests. To solve the problem, the key protection threshold Tp is proposed, the calculation method of which is as follows. The key protection threshold Tp is the product of the current remaining key resources Th of the link and η. η is a constant between 0 and 1 related to the key protection threshold, which can be adjusted as needed. The problem can be effectively solved by increasing the comparison between the number of keys required by the service and the key protection threshold.
QKD needs to take optical fiber resources as the transmission medium and provide users with secure keys through wavelength division multiplexing technology. The key resources mentioned above refer to the wavelength and time slot resources in the channel. The number of quantum signal channels (QSCh) in a fiber link can be multiple, and QSCh can be divided into several time slots (TS). The key resources of each service request need to occupy several time slots, which are measured by unit/s.
Figure 3 shows an example of the algorithm. The initial network topology is assumed as shown on the left. According to the method of network topology abstraction process, the abstract network topology is shown on the right in Figure 3. Dashed lines between node pairs represent virtual direct links, while solid lines between node pairs represent physical direct links. The link generation key resource rate is set to 50 unit/s. η is set to 0.8. Supposing service request 1 and service request 2 arrive at the same time, their routing and transmission in the link are shown in Table 2.
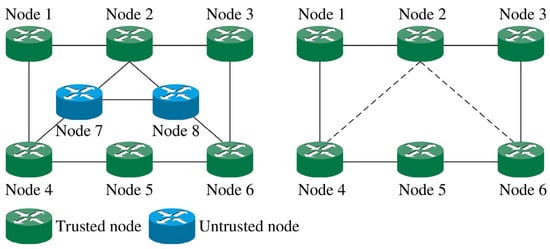
Figure 3.
Process of network topology abstraction.

Table 2.
The operation of the services in the TAPS-PTR.
4.3. Complexity of the Algorithm
The complexity of the protection scheme is evaluated as follows. Within one loop, the conditional expression is set to run at most |N| times. The time complexity of the Dijkstra algorithm in the algorithm is O(|N|2). There are two separate “for” loops in the algorithm. One loop is the process of topology abstraction, the other is selection of the working and protection paths, the process of which contains the Dijkstra algorithm. Therefore, the total time complexity of the protection algorithm is approximately O(K|N|3 + K|N|).
5. Simulation Results
In the QKD network topology, when the service arrives, the key service is numbered to distinguish it from other services. The start time and duration of the services obey Poisson distribution. The source node sr and destination node dr of services are both randomly generated. The time slot required for the service expresses the demand of the service for the key. For the link of QKD network topology, the remaining time slot of the current link represents the number of keys that can be provided by the link at this time. η indicates the percentage of the limited key protection threshold. The blocking rate of key service requests of the working path and the successful construction rate of the protection path are the data measuring the effect of the protection strategy.
On the link of the QKDN, the channel can include multiple wavelengths which are set as n. Each wavelength channel can be divided into m time slots. According to the number of keys generated in each time slot, the remaining time slot of the current link can be calculated by detecting the wavelength time slot resources in each fiber and the time slot required for the key unit time.
In this study, the protection scheme designed in a QKDN with partially trusted relay was simulated and verified in IntelliJ IDEA using Java language. The algorithm was completed on NSFNET topology and USNET topology, which are shown in Figure 4. The NSFNET topology has 14 nodes and 21 links, with the longest link length being 1140 km, while the USNET topology has 24 nodes and 43 links. In the process of algorithm verification, a total of 105 randomly generated services run on the topologies. In the two topologies, we conducted the simulation in three cases. The independent variables are the generation rate of key resources on the link, the number of untrusted nodes in the topology and the correlation percentage of key protection threshold η. The dependent variables are blocking rate of key service requests and protection path construction success rate.
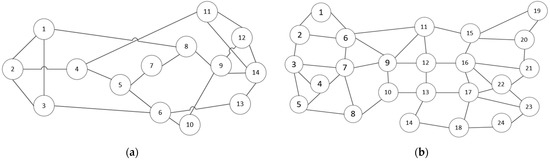
Figure 4.
(a) NSFNET topology; (b) USNET topology.
In order to observe the data more intuitively, the number of untrusted nodes in the NSFNET topology was set to 2. As shown in Figure 5a,b, the impact of the change of key resources and protection threshold on the blocking rate of key service requests was tested. It can be seen from the simulation results that with the increase in key resources provided by the link, the blocking rate of key service requests of each curve decreases. On the curve of η = 0.3, when the link generation key resource rate is the highest, the blocking rate of key service requests can be reduced to close to 0. However, when η is higher, the blocking rate of key service requests increases. The reason is that the key protection threshold rises with the increase in η. When the protection threshold rises, theoretically more protection paths are constructed, competing for the limited key resources with subsequent services.
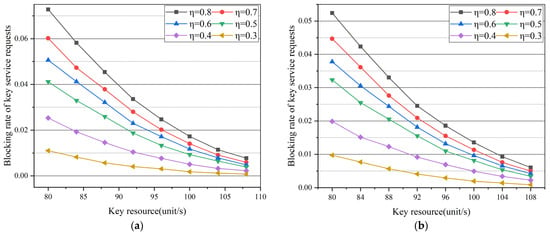
Figure 5.
Simulation results: (a) blocking rate of key service requests varies with link key resources in the case of different protection thresholds in NSFNET; (b) blocking rate of key service requests varies with link key resources in the case of different protection thresholds in USNET.
In USNET, the number of untrusted nodes was set to 3. The results show that the changes of curves are similar to those in NSFNET. The blocking rate of key service requests decreases significantly with the increase in key resources. When the key resource generation rate of the link is 80 unit/s, the blocking rate of key service requests can be reduced by at least 0.5% whenever η is reduced by 0.1.
In this case, the key generation rate of the link is set to 80unit/s in both NSFNET and USNET topologies. Figure 6a,b display that the blocking rate of key service requests is affected by the change of protection threshold in two different networks. As shown in Figure 6a, the blocking rate of key service requests rises with the increase in η. Because the protection threshold is the product of the remaining key resources of the link and variable quantity η, the protection threshold is related to η in direct proportion. Therefore, the blocking rate of key service requests in Figure 6 rises with protection threshold increasing. The results can be explained by the results of the success rate of protection path construction in the following result. The increase in the number of protection paths affects the number of key resources allocated to the working paths of other services. From the vertical comparison of different curves in Figure 6a,b, the blocking rate of key service requests increases with the increase in the number of untrusted nodes. The reason is that an untrusted node cannot act as a relay between more than two nodes like a trusted node. When the protection threshold and the number of untrusted nodes are the smallest in Figure 6, the blocking rate of key service requests can reach close to 0. The change trend of the curves in Figure 6a is similar to that in Figure 6b, indicating that the results are common in the network.
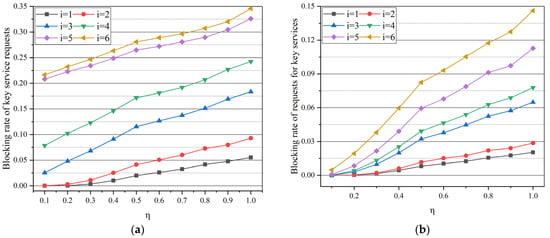
Figure 6.
Simulation results: (a) blocking rate of key service requests varies with η in the case of different untrusted node numbers in NSFNET; (b) blocking rate of key service requests varies with η in the case of different untrusted node numbers in USNET.
In this case, the percentage of key protection threshold η was set to 0.8 as shown in Figure 7. As shown in Figure 7a,b, the curves show the change of blocking rate of key service requests with link key resource increasing. Different from Figure 5a,b, the curves are distributed in the case of different untrusted node numbers. With the increase in key resources, the blocking rate of key service requests decreases in both figures.
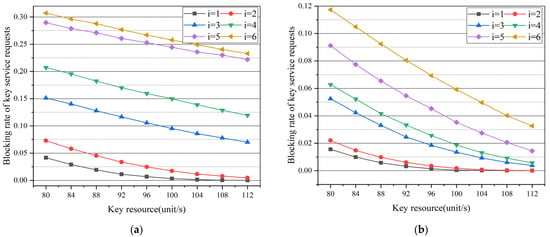
Figure 7.
Simulation results: (a) blocking rate of key service requests varies with key resource in the case of different untrusted node numbers in NSFNET; (b) blocking rate of key service requests varies with key resource in the case of different untrusted node numbers in USNET.
Comparing different curves vertically, it can be seen that the blocking rate of key service requests rises with the increase in the number of untrusted nodes. In Figure 7b, the key generation rate of the link, that is, the link key resource, is set to 80 unit/s. It can be seen from the curves that when the number of untrusted nodes changes from 3 to 2, the blocking rate of key service requests decreases by about 3%. With the increase in key resources, the gap of blocking rate of key service requests between different untrusted nodes gradually decreases. This is more obvious in the simulation results of USNET topology. When the number of untrusted nodes is the lowest and the key resource takes a higher value in the two figures, the blocking rate of key service requests can be close to 0.
In order to observe the results more conveniently, the number of untrusted nodes in NSFNET is set to 2, while that in USNET is 3. The protection threshold is proportional to η. Therefore, the change of η refers to the change of protection threshold. Figure 8a,b shows the change of protection path construction success rate with protection threshold with different untrusted node numbers. With the increase in key resources provided by the links, protection path construction success rate grows in both topologies. The reason is that more key resources can reduce the pressure of protection path construction.
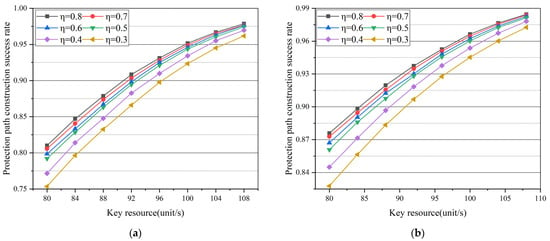
Figure 8.
Simulation results: (a) protection path construction success rate varies with link key resources in the case of different protection thresholds in NSFNET; (b) protection path construction success rate varies with link key resources in the case of different protection thresholds in USNET.
It can be seen from Figure 8 that the rise of protection threshold can also increase the probability of successful construction of protection path. With the increase in key protection threshold, the protection path construction success rate rises gradually. Comparing the curves in Figure 8a,b vertically, on the one hand, the success rate of protection path construction rises with the increase in protection threshold. On the other hand, as the protection threshold increases, the difference in the different curves of protection path construction success rate decreases with the same key resource.
As shown in Figure 9a,b, the key recourse is set to 80 unit/s. In this condition, the impact of the change of key protection threshold on the protection path construction success rate of different numbers of untrusted nodes was tested.
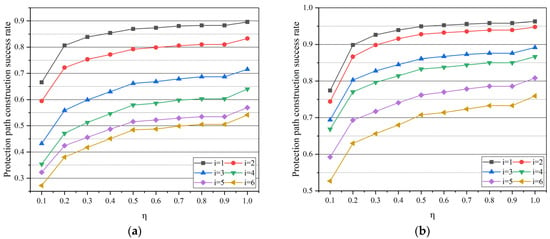
Figure 9.
Simulation results: (a) protection path construction success rate varies with η in the case of different untrusted node numbers in NSFNET; (b) protection path construction success rate varies with η in the case of different untrusted node numbers in USNET.
The trend of curve change is roughly similar in the two diagrams. With the increase in protection threshold, the protection path success rate goes up. When the protection threshold is the largest, the protection path construction success rate is also the maximum value. However, too many protection paths can have a negative impact on the smoothness of working paths to other services. Therefore, different protection thresholds are needed to adjust the conflict. When the number of untrusted nodes is different, the larger number of untrusted nodes can cause lower protection path construction rate in the case of the same η. The reason is that the requirements of untrusted nodes are more stringent than trusted nodes.
In this case, the percentage of key protection threshold η is set to 0.8. As shown in Figure 10a,b, the change of protection path construction success rate with different numbers of untrusted nodes is tested in the two different topologies. With the increase in key resources, the success rate of protection path construction rises. When the key resource reaches the maximum of the data shown in Figure 10a,b, the success rate of protection path construction can reach 100% in the case of the smallest untrusted node number.
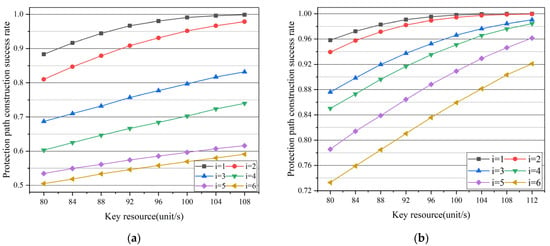
Figure 10.
Simulation results: (a) protection path construction success rate varies with key resource in the case of different untrusted node numbers in NSFNET; (b) protection path construction success rate varies with key resource in the case of different untrusted node numbers in USNET.
Comparing the curves in Figure 10a,b vertically, the success of protection path construction decreases with the increase in the number of untrusted nodes. In Figure 10b, when the key resource is set to 112 unit/s, assuming that the number of untrusted nodes is reduced from 6 to 5, the appreciation of protection path construction successful rate can rise about 4%. The number of untrusted nodes and key resource both have a significant impact on the success rate of protection path construction.
6. Conclusions
In this paper, we proposed a protection scheme in a QKDN with partially trusted relay. In the partially trusted relay-based QKDN, the topology abstraction method can handle the trusted and untrusted relay in different ways, which was conducive to the subsequent key resource allocation. In the newly formed abstract topology, the working and protection paths were found. Lastly, key resources were allocated to the services required for keys. In addition, the key protection threshold was proposed to ease up the conflict of working and protection paths on key resources. The protection scheme can improve the stability and reliability of transmission services in the QKDN with partially trusted relay. The simulation results show that there is a trade-off between the blocking rate of secret key requests and the success rate of protection path construction, which means a balance is needed to maintain the resource allocation between working paths and protection paths.
Author Contributions
Conceptualization, Q.Z. and X.Y.; methodology, X.Y. and Y.Z.; software, Q.Z. and Y.L.; validation, Q.Z. and Y.L.; writing—original draft preparation, Q.Z.; writing—review and editing, X.Y. and Y.Z.; supervision, J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the NSFC project (62150032, 61971068, 62021005), Fund of National Key Research and Development Program of China (2020YFE0200600), Fund of State Key Laboratory of Information Photonics and Optical Communications, BUPT (IPOC2020ZT04) and the Fundamental Research Funds for the Central Universities (2019XD-A05).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, H.; Zhao, Y.; Wang, D.; Wang, J.; Wang, Z. A Quantum Key Re-Transmission Mechanism for QKD-Based Optical Networks. ZTE Commun. 2018, 16, 52–58. [Google Scholar]
- Zhu, J.; Zhao, B.; Lu, W.; Zhu, Z. Attack-aware service provisioning to enhance physical-layer security in multi-domain EONs. J. Lightwave Technol. 2016, 34, 2645–2655. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G. Quantum Cryptography: Public-Key Distribution and Tossing. In Proceedings of the IEEE International Conference on Computers, Systems and Signal Processing, Bangalore, India, 9–12 December 1984; IEEE Press: Washington, DC, USA, 1984. [Google Scholar]
- Gisin, N.; Ribordy, G.; Tittel, W.; Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 2002, 74, 145. [Google Scholar] [CrossRef] [Green Version]
- Scarani, V.; Bechmann-Pasquinucci, H.; Cerf, N.J.; Dušek, M.; Lütkenhaus, N.; Peev, M. The security of practical quantum key distribution. Rev. Mod. Phys. 2009, 81, 1301. [Google Scholar] [CrossRef] [Green Version]
- Kartheek, D.N.; Kumar, M.A.; Kumar, M.P. Security using quantum key distribution protocols (QKDPs). Int. J. Sci. Eng. Res. 2012, 3, 21–25. [Google Scholar]
- Elliott, C.; Yeh, H. DARPA Quantum Network Testbed; BBN Technologies: Cambridge, MA, USA, 2007. [Google Scholar]
- Dianati, M.; Alléaume, R. Architecture of the Secoqc quantum key distribution network. In Proceedings of the 2007 First International Conference on Quantum, Nano, and Micro Technologies (ICQNM’07), Guadeloupe, France, 2–6 January 2007; p. 13. [Google Scholar]
- Zhang, Q.; Xu, F.; Chen, Y.A.; Peng, C.Z.; Pan, J.W. Large scale quantum key distribution: Challenges and solutions. Opt. Express 2018, 26, 24260–24273. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, H.; Zhao, Y.; Yu, X.; Ma, Z.; Wang, J.; Nag, A.; Yi, L.; Zhang, J. Protection schemes for key service in optical networks secured by quantum key distribution (QKD). J. Opt. Commun. Netw. 2019, 11, 67–78. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, Y.; Yu, X.; Nag, A.; Ma, Z.; Wang, J.; Zhang, J. Resilient quantum key distribution (QKD)-integrated optical networks with secret-key recovery strategy. IEEE Access 2019, 7, 60079–60090. [Google Scholar] [CrossRef]
- Li, X.; Zhao, Y.; Nag, A.; Yu, X.; Zhang, J. Key-Recycling Strategies in Quantum-Key-Distribution Networks. Appl. Sci. 2020, 10, 3734. [Google Scholar] [CrossRef]
- Zhao, Y.; Fung, C.H.F.; Qi, B.; Chen, C.; Lo, H.K. Quantum hacking: Experimental demonstration of time-shift attack against practical quantum-key-distribution systems. Phys. Rev. A 2008, 78, 042333. [Google Scholar] [CrossRef] [Green Version]
- Xu, F.; Curty, M.; Qi, B.; Qian, L.; Lo, H.K. Discrete and continuous variables for measurement-device-independent quantum cryptography. Nat. Photonics 2015, 9, 772–773. [Google Scholar] [CrossRef] [Green Version]
- Lydersen, L.; Wiechers, C.; Wittmann, C.; Elser, D.; Skaar, J.; Makarov, V. Hacking commercial quantum cryptography systems by tailored bright illumination. Nat. Photonics 2010, 4, 686–689. [Google Scholar] [CrossRef] [Green Version]
- Lo, H.K.; Curty, M.; Qi, B. Measurement-device-independent quantum key distribution. Phys. Rev. Lett. 2012, 108, 130503. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lim, C.C.W.; Wang, C. Long-distance quantum key distribution gets real. Nat. Photonics 2021, 15, 554–556. [Google Scholar] [CrossRef]
- Liu, H.; Wang, W.; Wei, K.; Fang, X.T.; Li, L.; Liu, N.L.; Liang, H.; Zhang, S.J.; Zhang, W.; Li, H.; et al. Experimental demonstration of high-rate measurement-device-independent quantum key distribution over asymmetric channels. Phys. Rev. Lett. 2019, 122, 160501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lucamarini, M.; Yuan, Z.L.; Dynes, J.F.; Shields, A.J. Overcoming the rate–distance limit of quantum key distribution without quantum repeaters. Nature 2018, 557, 400–403. [Google Scholar] [CrossRef] [PubMed]
- Yin, H.L.; Fu, Y. Measurement-device-independent twin-field quantum key distribution. Sci. Rep. 2019, 9, 3045. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ma, X.; Zeng, P.; Zhou, H. Phase-matching quantum key distribution. Phys. Rev. X 2018, 8, 031043. [Google Scholar] [CrossRef] [Green Version]
- Lin, J.; Lütkenhaus, N. Simple security analysis of phase-matching measurement-device-independent quantum key distribution. Phys. Rev. A 2018, 98, 042332. [Google Scholar] [CrossRef] [Green Version]
- Pirandola, S.; Ottaviani, C.; Spedalieri, G.; Weedbrook, C.; Braunstein, S.L.; Lloyd, S.; Gehring, T.; Jacobsen, C.S.; Andersen, U.L. High-rate quantum cryptography in untrusted networks. arXiv 2013, arXiv:1312.4104. [Google Scholar]
- Lupo, C.; Ottaviani, C.; Papanastasiou, P.; Pirandola, S. Composable Security of Measurement-Device-Independent Continuous-Variable Quantum Key Distribution against Coherent Attacks. arXiv 2017, arXiv:1704.07924. [Google Scholar] [CrossRef] [Green Version]
- He, M.; Malaney, R.; Green, J. Multimode CV-QKD with non-Gaussian operations. Quantum Eng. 2020, 2, e40. [Google Scholar] [CrossRef]
- Bhaskar, M.K.; Riedinger, R.; Machielse, B.; Levonian, D.S.; Nguyen, C.T.; Knall, E.; Park, H.; Englund, D.; Lončar, M.; Sukachev, D.D.; et al. Experimental Demonstration of Memory-Enhanced Quantum Communication. Nature 2020, 580, 60–64. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tang, Y.L.; Yin, H.L.; Zhao, Q.; Liu, H.; Sun, X.X.; Huang, M.Q.; Zhang, W.J.; Chen, S.J.; Zhang, L.; You, L.X.; et al. Measurement-device-independent quantum key distribution over untrustful metropolitan network. Phys. Rev. X 2016, 6, 011024. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Hou, G.; Lin, X.; Huang, J.; Yang, Q.; Chen, K.; Chen, R. A novel tree-topology based routing algorithm for partially-trusted QKD networks. In Proceedings of the 2020 IEEE International Conference on Advances in Electrical Engineering and Computer Applications(AEECA), Dalian, China, 25–27 August 2020; pp. 252–255. [Google Scholar]
- Muralidharan, S.; Li, L.; Kim, J.; Lütkenhaus, N.; Lukin, M.D.; Jiang, L. Optimal architectures for long distance quantum communication. Sci. Rep. 2016, 6, 20463. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Cao, Y.; Wang, W.; Wang, H.; Yu, X.; Zhang, J.; Tornatore, M.; Wu, Y.; Mukherjee, A.B. Resource allocation in optical networks secured by quantum key distribution. IEEE Commun. Mag. 2018, 56, 130–137. [Google Scholar] [CrossRef] [Green Version]
- Mehic, M.; Niemiec, M.; Rass, S.; Ma, J.; Peev, M.; Aguado, A.; Martin, V.; Schauer, S.; Poppe, A.; Pacher, C.; et al. Quantum key distribution: A networking perspective. ACM Comput. Surv. (CSUR) 2020, 53, 1–41. [Google Scholar] [CrossRef]
- Yu, X.; Liu, X.; Liu, Y.; Nag, A.; Zou, X.; Zhao, Y.; Zhang, J. Multi-path-based quasi-real-time key provisioning in quantum-key-distribution enabled optical networks (QKD-ON). Opt. Express 2021, 29, 21225–21239. [Google Scholar] [CrossRef]
- Cao, Y.; Zhao, Y.; Li, J.; Lin, R.; Zhang, J.; Chen, J. Hybrid Trusted/Untrusted Relay Based Quantum Key Distribution over Optical Backbone Networks. IEEE J. Sel. Areas Commun. 2021, 39, 2701–2718. [Google Scholar] [CrossRef]
- Yu, X.; Liu, Y.; Zou, X.; Cao, Y.; Zhao, Y.; Nag, A.; Zhang, J. Secret-Key Provisioning with Collaborative Routing in Partially-Trusted-Relay-based Quantum-Key-Distribution-Secured Optical Networks. J. Lightwave Technol. 2022. [Google Scholar] [CrossRef]
- Zhou, H.; Lv, K.; Huang, L.; Ma, X. Quantum Network: Security Assessment and Key Management. IEEE/ACM Trans. Netw. 2022. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).