Pulse Shape Estimation in a DSR Fiber Laser Using the Genetic Algorithm
Abstract
:1. Introduction
2. Ring Fiber Laser Numerical Model
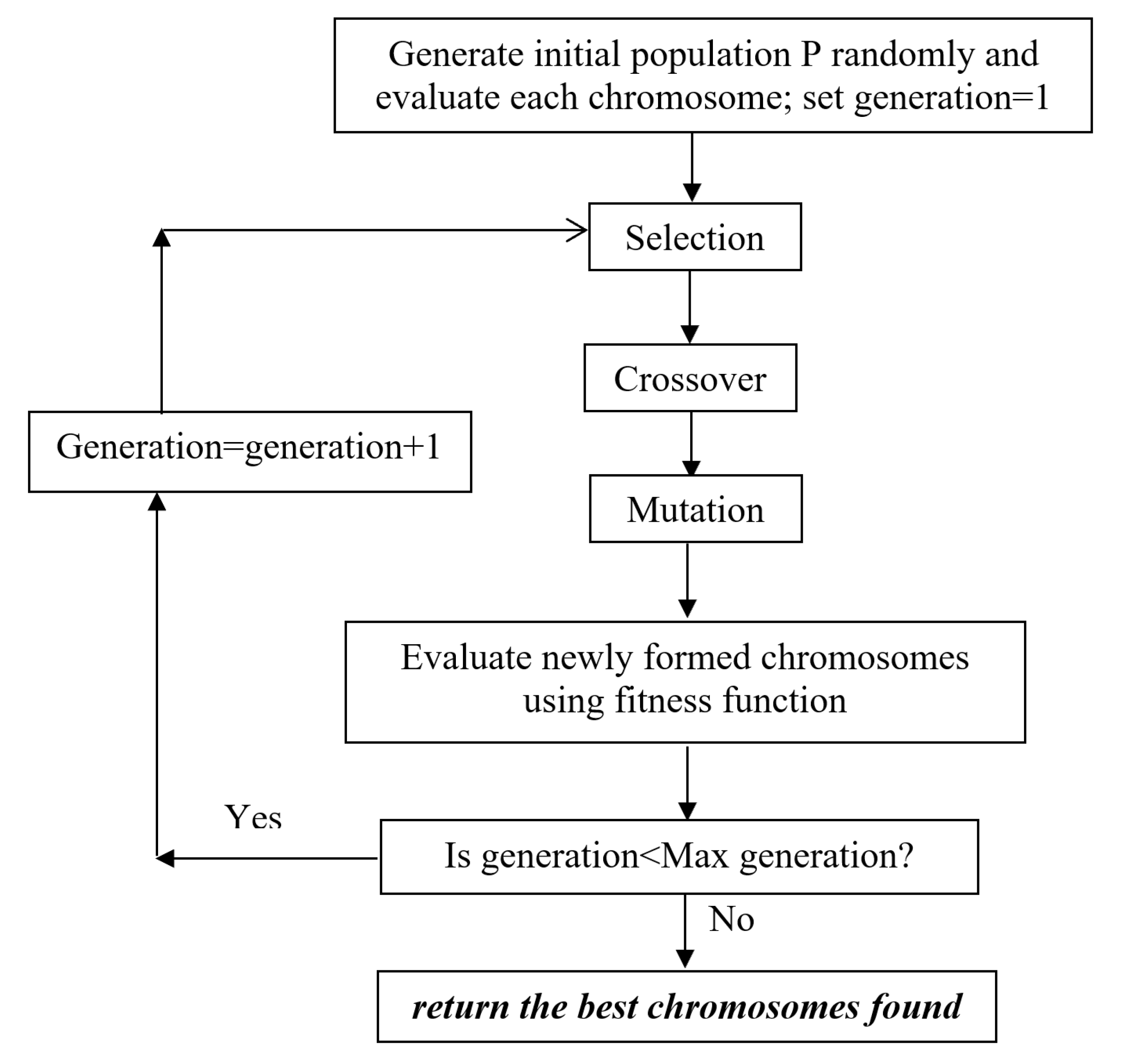
3. Genetic Algorithm Optimization
- Initial population: Each individual chromosome in the initial population is generated randomly. This is achieved through initializing each element in the individual chromosome using a uniform distribution from within the range restrictions outlined in Table 3.
- Selection operator: In this operation the GA selects the best two individual chromosomes from the generation at hand with the smallest objective function value. These individuals are deemed “fittest” and are denoted ( and ) and act as parents for generating offspring in the next combination operation. The applied selection rule is deterministic.
- Crossover operator: This operation is executed if a generated uniform random number is less than the assigned value for the crossover probability parameter. In such case, the elements of the two parents ( and ) are combined in a certain way to produce two new individual children. In multi-point crossover a binary mask with four values corresponding to each element in the individual chromosome is generated using a uniform random number generator. The elements of the two individual children ( and ) are selected from the elements of either parents () based on the if a “0” or “1” appears at the corresponding binary mask index, respectively [34].
- Mutation operator: This operation is executed if a generated uniform random number is less than the assigned value for the mutation probability parameter. In such case, a random element from within the individual chromosome is re-initialized with a random value using a uniform distribution from within the range restrictions outlined in Table 3.
- Elitism operator: This function reduces genetic drift by adopting the fittest individuals from previous and new populations after a predefined number of selection, crossover and mutation.
| Element | Description | Minimum Value | Maximum Value |
|---|---|---|---|
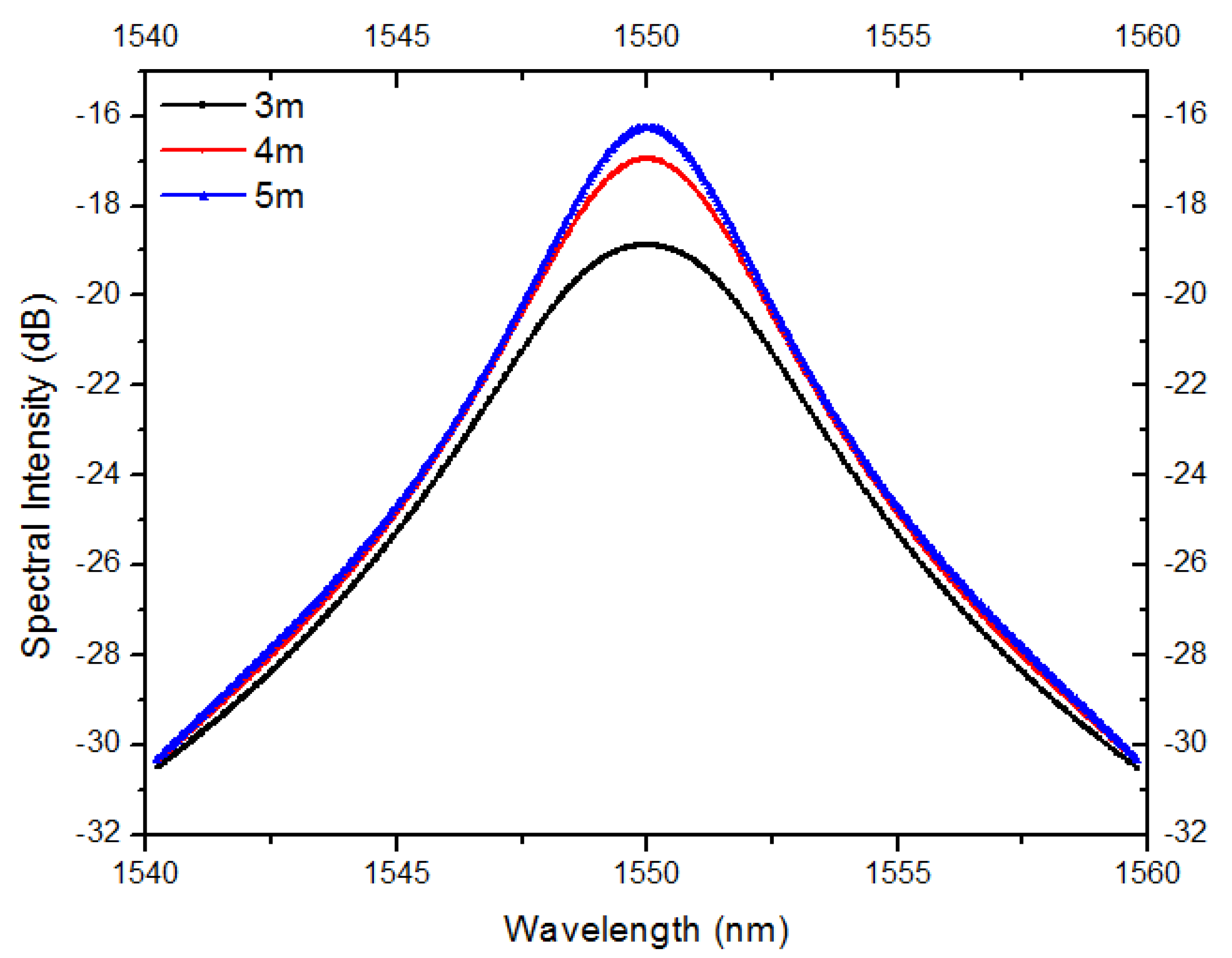
| Length of the PCF | 1 m | 10 m | |
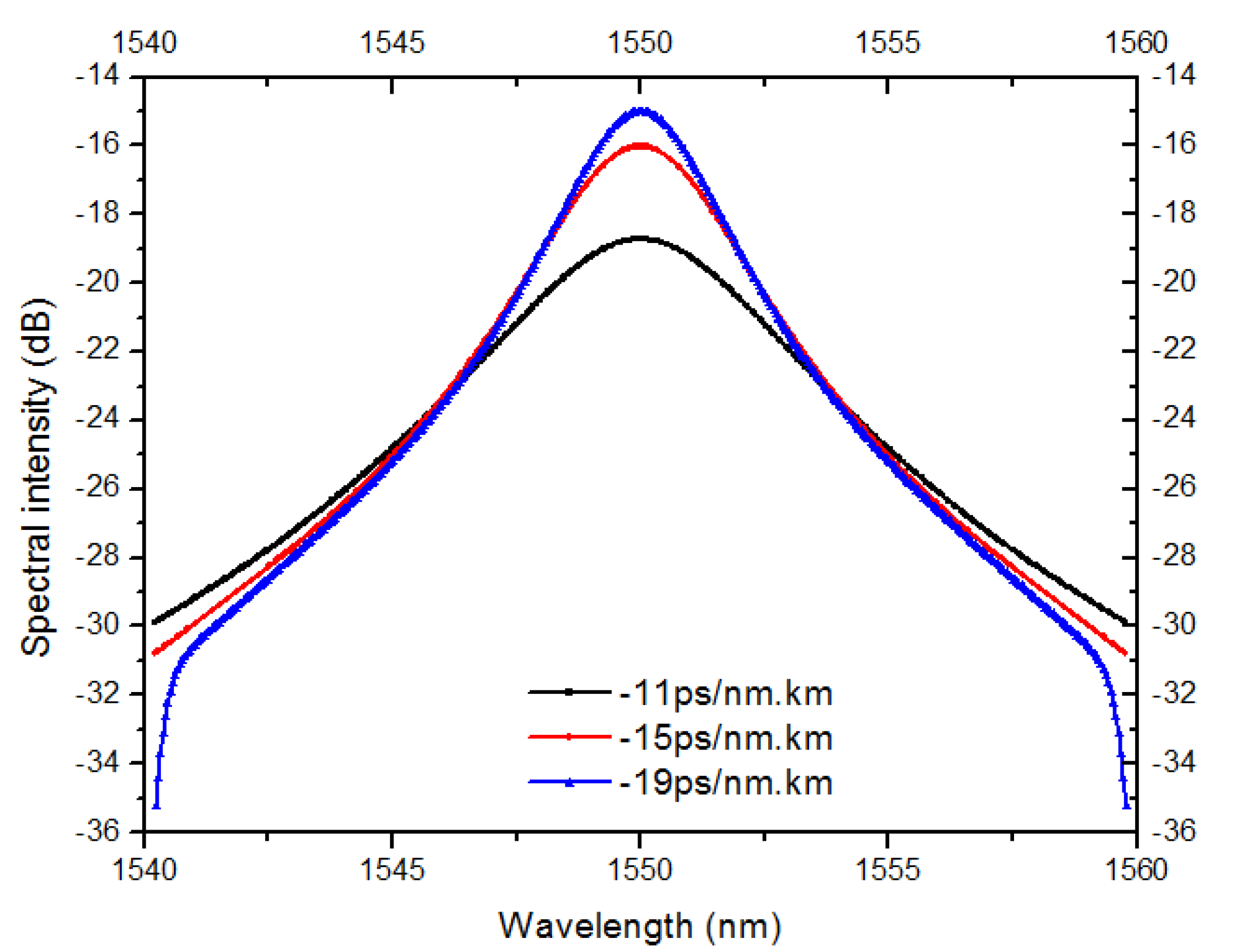
| Dispersion of the PCF | −30 ps/nm·km | 0 ps/nm·km | |
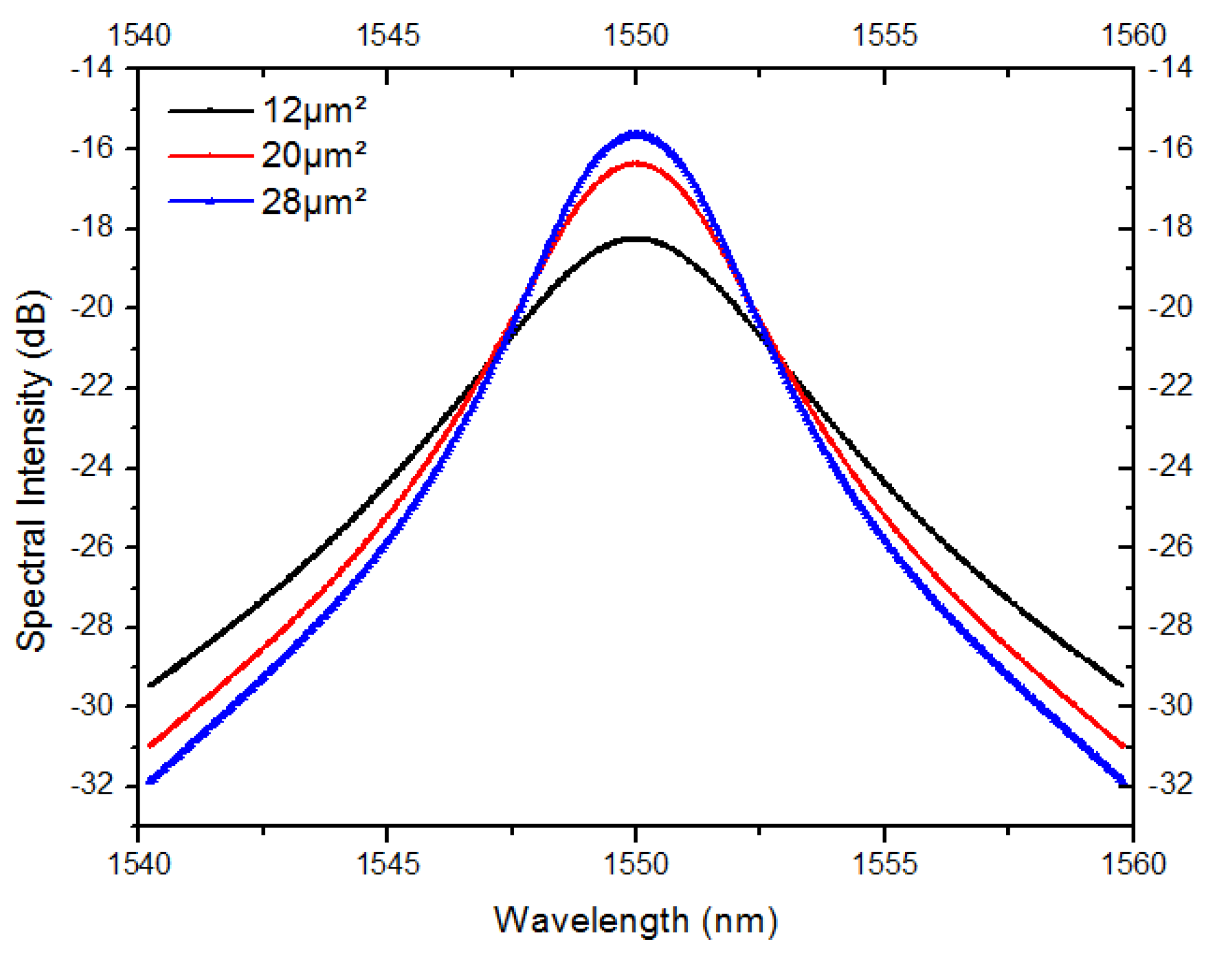
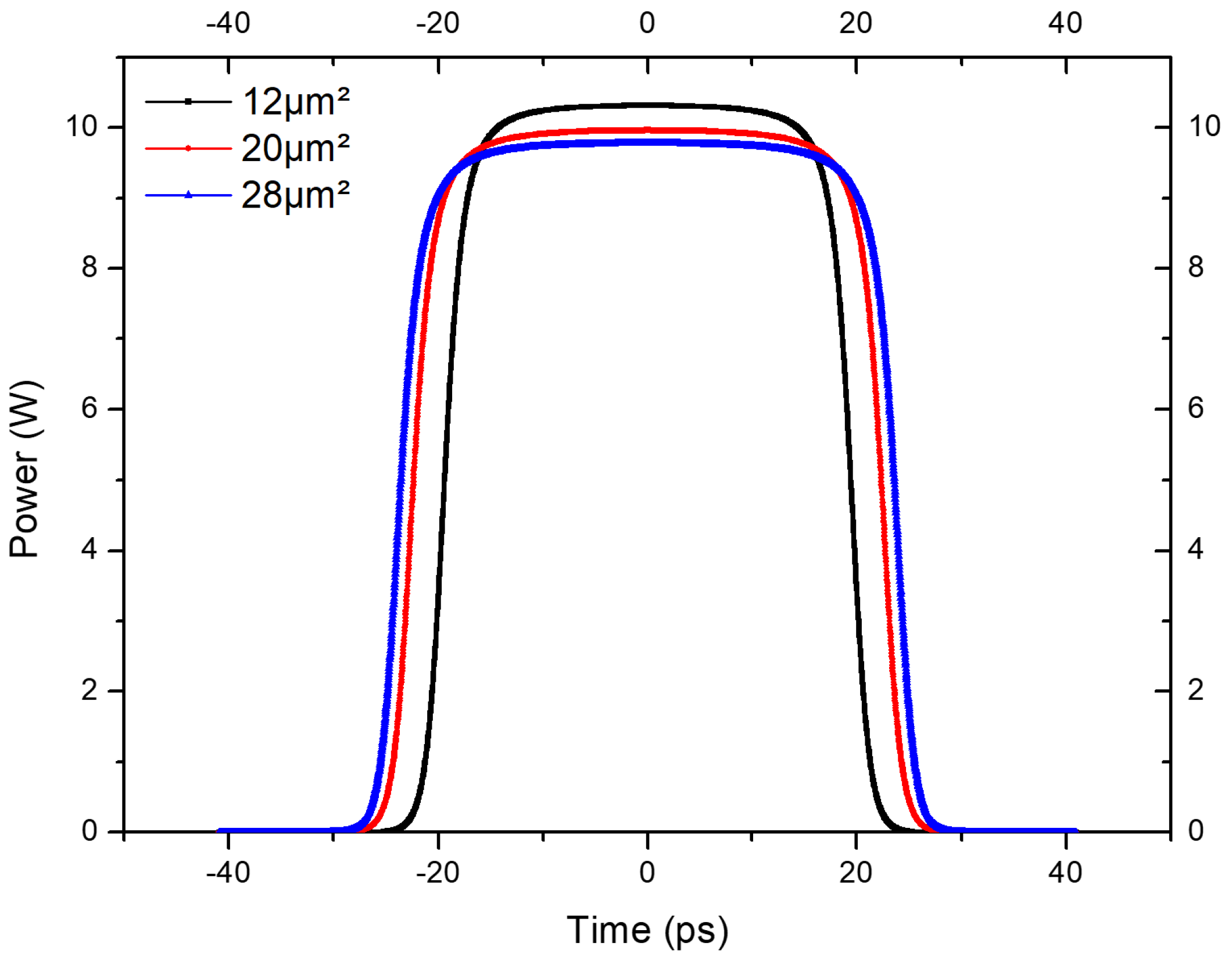
| Effective area of the PCF | 10 | 30 | |
| SA modulation depth | 0.1 | 0.4 |
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shi, W.; Fang, Q.; Zhu, X.; Norwood, R.A.; Peyghambarian, N. Fiber lasers and their applications. Appl. Opt. 2014, 53, 6554–6568. [Google Scholar] [CrossRef] [PubMed]
- Tamura, K.; Haus, H.A.; Ippen, E.P. Self-starting additive pulse mode-locked erbium fibre ring laser. Electron. Lett. 1992, 28, 2226–2228. [Google Scholar] [CrossRef]
- Hübner, P.; Kieleck, C.; Jackson, S.D.; Eichhorn, M. High-power actively mode-locked sub-nanosecond Tm3+-doped silica fiber laser. Opt. Lett. 2011, 36, 2483–2485. [Google Scholar] [CrossRef] [PubMed]
- Cautaerts, V.; Richardson, D.J.; Paschotta, R.; Hanna, D.C. Stretched pulse Yb3+:silica fiber laser. Opt. Lett. 1997, 22, 316–318. [Google Scholar] [CrossRef] [Green Version]
- Set, S.Y.; Yaguchi, H.; Tanaka, Y.; Jablonski, M. Laser mode locking using a saturable absorber incorporating carbon nanotubes. J. Light. Technol. 2004, 22, 51–56. [Google Scholar] [CrossRef]
- Chernysheva, M.A.; Krylov, A.A.; Kryukov, P.G.; Dianov, E.M. Nonlinear amplifying loop-mirror-based mode-locked thulium-doped fiber laser. IEEE Photonic Technol. Lett. 2012, 24, 1254–1256. [Google Scholar] [CrossRef]
- Komarov, A.; Komarov, K.; Leblond, H.; Sanchez, F. Spectral-selective management of dissipative solitons in passive mode-locked fibre lasers. J. Opt. A Pure Appl. Opt. 2007, 9, 1149. [Google Scholar] [CrossRef]
- Komarov, A.; Amrani, F.; Dmitriev, A.; Komarov, K.; Sanchez, F. Competition and coexistence of ultrashort pulses in passive mode-locked lasers under dissipative-soliton-resonance conditions. Phys. Rev. A 2013, 87, 023838. [Google Scholar] [CrossRef] [Green Version]
- Amrani, F.; Haboucha, A.; Salhi, M.; Leblond, H.; Komarov, A.; Grelu, P.; Sanchez, F. Passively mode-locked erbium-doped double-clad fiber laser operating at the 322nd harmonic. Opt. Lett. 2009, 34, 2120–2122. [Google Scholar] [CrossRef] [Green Version]
- Amrani, F.; Salhi, M.; Niang, A.; Komarov, A.; Sanchez, F. Soliton pattern formation in figure-of-eight laser. In Proceedings of the SPIE, Nonlinear Optics and Applications VI, Brussels, Belgium, 16 April 2012; Volume 8434, pp. 1–7. [Google Scholar]
- Luo, Z.; Liu, M.; Liu, H.; Zheng, X.; Luo, A.; Zhao, C.; Zhang, H.; Wen, S.; Xu, W. 2 GHz passively harmonic mode-locked fiber laser by a microfiber-based topological insulator saturable absorber. Opt. Lett. 2013, 38, 5212–5215. [Google Scholar] [CrossRef]
- Bao, C.; Xiao, X.; Yang, C. Soliton rains in a normal dispersion fiber laser with dual-filter. Opt. Lett. 2013, 38, 1875–1877. [Google Scholar] [CrossRef] [PubMed]
- Peng, J.; Boscolo, S.; Zhao, Z.; Zeng, H. Breathing dissipative solitons in mode-locked fiber lasers. Sci. Adv. 2019, 5, eaax1110. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kemel, M.; Nady, A.; Semaan, G.; Salhi, M.; Sanchez, F. Triple-lobe wavelength fiber laser with a composite-state soliton regime. Opt. Laser Technol. 2021, 133, 106519. [Google Scholar] [CrossRef]
- Soto-Crespo, J.M.; Grapinet, M.; Grelu, P.; Akhmediev, N. Bifurcation and multiple-period soliton pulsation in a passively mode-locked fiber laser. Phys. Rev. E 2004, 70, 066612. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tzelepis, V.; Markatos, S.; Kalpogiannis, S.; Sphicopoulos, T.H.; Caroubalos, C. Analysis of a passively mode-locked self-starting all-fiber soliton laser. J. Light. Technol. 1993, 11, 1729–1736. [Google Scholar] [CrossRef]
- Salhi, M.; Amrani, F.; Leblond, H.; Sanchez, F. Analytical investigation of a figure-eight single-pulse all-fiber laser based on a nonlinear amplifying loop mirror. Phys. Rev. A 2010, 82, 043834. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Pan, W.; Feng, Y. Period multiplication in mode-locked figure-of-9 fiber lasers. Opt. Express 2020, 28, 17424–17433. [Google Scholar] [CrossRef]
- Lecaplain, C.; Ortaç, B.; Machinet, G.; Boullet, J.; Baumgartl, M.; Schreiber, T.; Cormier, E.; Hideur, A. High-energy femtosecond photonic crystal fiber laser. Opt. Lett. 2010, 35, 3156–3158. [Google Scholar] [CrossRef]
- Chong, A.; Renninger, W.H.; Wise, F.W. All-normal-dispersion femtosecond fiber laser with pulse energy above 20 nJ. Opt. Lett. 2007, 32, 2408–2410. [Google Scholar] [CrossRef]
- Akhmediev, N.; Soto-Crespo, J.M.; Grelu, P. Roadmap to ultra-short record high-energy pulses out of laser oscillators. Phys. Lett. A 2008, 372, 3124–3128. [Google Scholar] [CrossRef]
- Wu, X.; Tang, D.Y.; Zhang, H.; Zhao, L.M. Dissipative soliton resonance in an all-normal-dispersion erbium-doped fber laser. Opt. Express 2009, 17, 5580–5584. [Google Scholar] [CrossRef] [PubMed]
- Krzempek, K.; Sotor, J.; Abramski, K. Compact all-fber fgure-9 dissipative soliton resonance mode-locked double-clad er:yb laser. Opt. Lett. 2016, 41, 4995–4998. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, H.; Aidit, S.N.; Ooi, S.I.; Samion, M.Z.; Wang, S.; Wang, Y.; Sahu, J.K.; Zamzuri, A.K. 1.3 µm dissipative soliton resonance generation in Bismuth doped fiber laser. Sci. Rep. 2021, 11, 6356. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef]
- Zayani, H.M.; Bahloul, F.M.; Saidani, T.S. Photonics components design optimization using genetic algorithm. Opt. Eng. 2020, 59, 056102. [Google Scholar] [CrossRef]
- Toyama, F.; Shoji, K.; Miyamichi, J.A. New Fitness Function for Shape Detection Using Genetic algorithm. Syst. Comput. Jpn. 2001, 32, 54–60. [Google Scholar] [CrossRef]
- Karar, A.S.; Ghandour, R.; Mahariq, I.; Alboon, S.A.; Maaz, I.; Neji, B.; Barakat, J.M.H. A Programmable Mode-Locked Fiber Laser Using Phase-Only Pulse Shaping and the Genetic Algorithm. Photonics 2020, 7, 69. [Google Scholar] [CrossRef]
- Arteaga-Sierra, F.R.; Milián, C.; Torres-Gómez, I.; Torres-Cisneros, M.; Moltó, G.; Ferrando, A. Supercontinuum optimization for dual-soliton based light sources using genetic algorithms in a grid platform. Opt. Express 2014, 22, 23686–23693. [Google Scholar] [CrossRef] [Green Version]
- Karar, A.S.; Ghandour, R.; Boulkaibet, I.; Collaku, D.; Barakat, J.M.H.; Neji, B.; Al Barakeh, Z. A Numerical Study of Optimization Methods for Phase-Only Optical Pulse-Shaping. Photonics 2021, 8, 490. [Google Scholar] [CrossRef]
- Bahloul, F.; Salhi, M.; Guesmi, K.; Sanchez, F.; Attia, R. Numerical demonstration of generation of bound solitons in figure of eight microstructured fiber laser in normal dispersion regime. Opt. Commun. 2013, 311, 282–287. [Google Scholar] [CrossRef] [Green Version]
- Paul, N.; Gupta, P.K.; Singh, C.P.; Mukhopadhyay, P.K.; Bindra, K.S. Effect of spectral filtering on pulse duration in dissipative soliton resonance (DSR) regime of modelocked fiber laser. Rev. Sci. Instrum. 2019, 90, 106102. [Google Scholar] [CrossRef]
- Boscolo, S.; Finot, C. Artificial neural networks for nonlinear pulse shaping in optical fibers. Opt. Laser Technol. 2020, 131, 106439. [Google Scholar] [CrossRef]
- Zeidler, D.; Frey, S.; Kompa, K.-L.; Motzkus, M. Evolutionary algorithms and their application to optimal control studies. Phys. Rev. A 2001, 64, 023420. [Google Scholar] [CrossRef] [Green Version]
- Cheng, Z.; Li, H.; Shi, H.; Ren, J.; Yang, Q.H.; Wang, P. Dissipative soliton resonance and reverse saturable absorption in graphene oxide modelocked all-normal-dispersion Yb-doped fiber laser. Opt. Express 2015, 23, 7000–7006. [Google Scholar] [CrossRef]
- Ben Braham, F.; Semaan, G.; Bahloul, F.; Salhi, M.; Sanchez, F. Experimental optimization of dissipative soliton resonance square pulses in all anomalous passively mode-locked fiber laser. J. Opt. 2017, 19, 105501. [Google Scholar] [CrossRef]





| Parameter | EDFA | ||
|---|---|---|---|
| L (m) | 2 | 5 | 5 |
| (dB/km) | 0.2 | 0.5 | 0.2 |
| () | 1.2 | 4.7 | 1.2 |
| (/km) | −21.6 | 25.5 | −21.6 |
| Parameter | Value/Method |
|---|---|
| Population size | 100 |
| Fitness function | minimize the misfit between the intensity profile of the output pulse and the target pulse |
| Selection technique | Select the best two individuals in the population |
| Crossover probability | 95% |
| Mutation probability | 10% |
| Number of generation | 20 |
| Parameter | Value |
|---|---|
| 4.2 m | |
| −13 ps/nm·km | |
| 20 | |
| 0.22 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bahloul, F.; Boussaidi, M.; Karar, A.S.; Salhi, M. Pulse Shape Estimation in a DSR Fiber Laser Using the Genetic Algorithm. Photonics 2022, 9, 212. https://doi.org/10.3390/photonics9040212
Bahloul F, Boussaidi M, Karar AS, Salhi M. Pulse Shape Estimation in a DSR Fiber Laser Using the Genetic Algorithm. Photonics. 2022; 9(4):212. https://doi.org/10.3390/photonics9040212
Chicago/Turabian StyleBahloul, Faouzi, Mariem Boussaidi, Abdullah S. Karar, and Mohamed Salhi. 2022. "Pulse Shape Estimation in a DSR Fiber Laser Using the Genetic Algorithm" Photonics 9, no. 4: 212. https://doi.org/10.3390/photonics9040212
APA StyleBahloul, F., Boussaidi, M., Karar, A. S., & Salhi, M. (2022). Pulse Shape Estimation in a DSR Fiber Laser Using the Genetic Algorithm. Photonics, 9(4), 212. https://doi.org/10.3390/photonics9040212







