The Optimization of a Convex Aspheric Lightweight SiC Mirror and Its Optical Metrology
Abstract
:1. Introduction
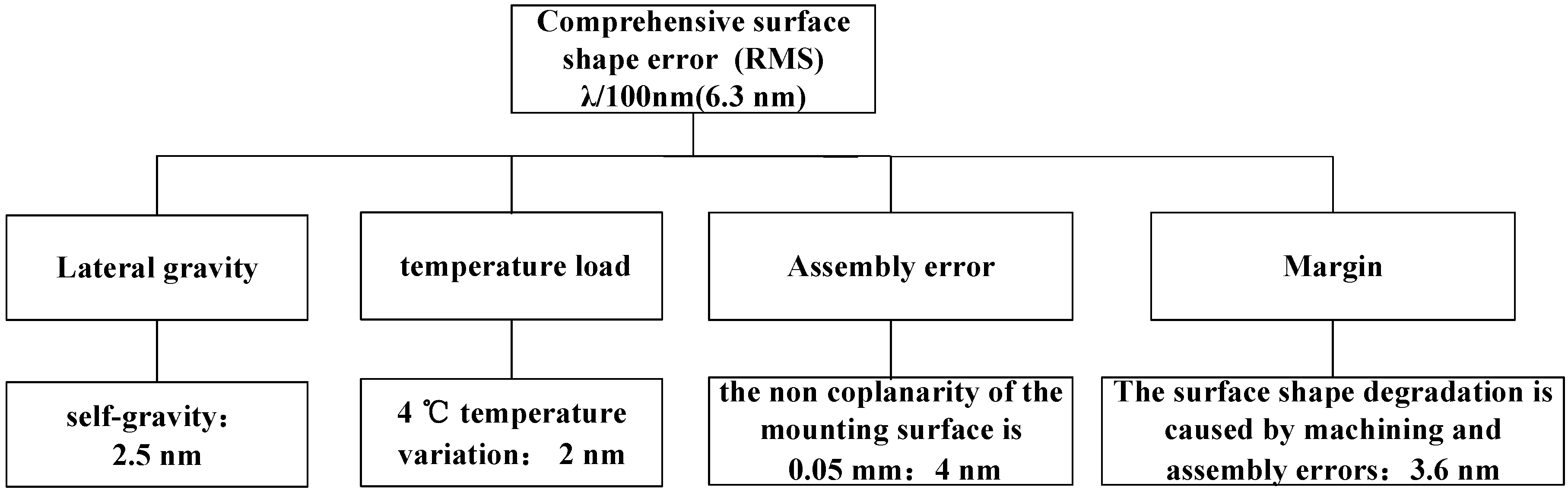
2. Performance Metrics
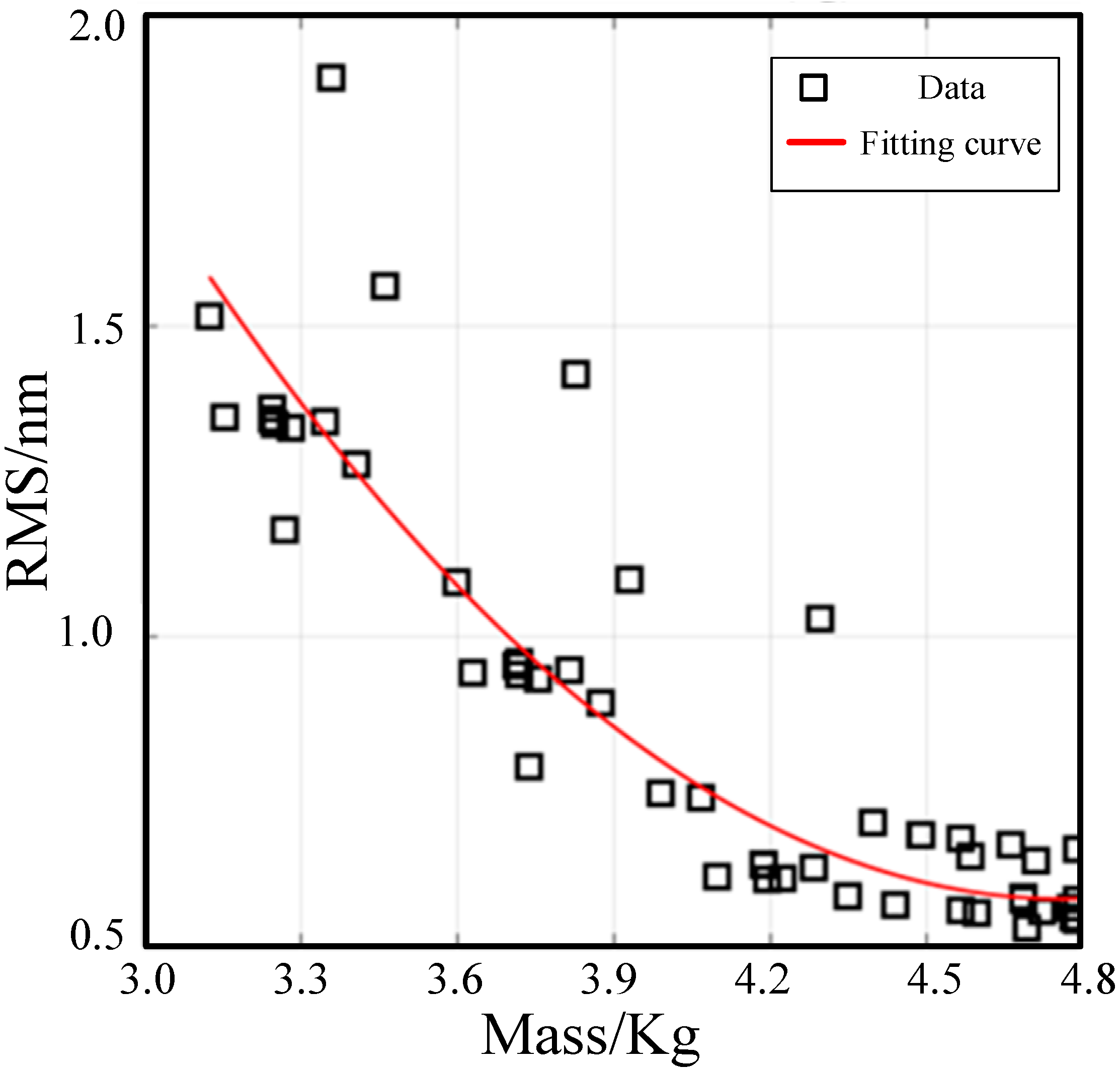
3. Lightweight Design of the Rectangular Mirror
4. Optimal Design of the S-Type Flexure
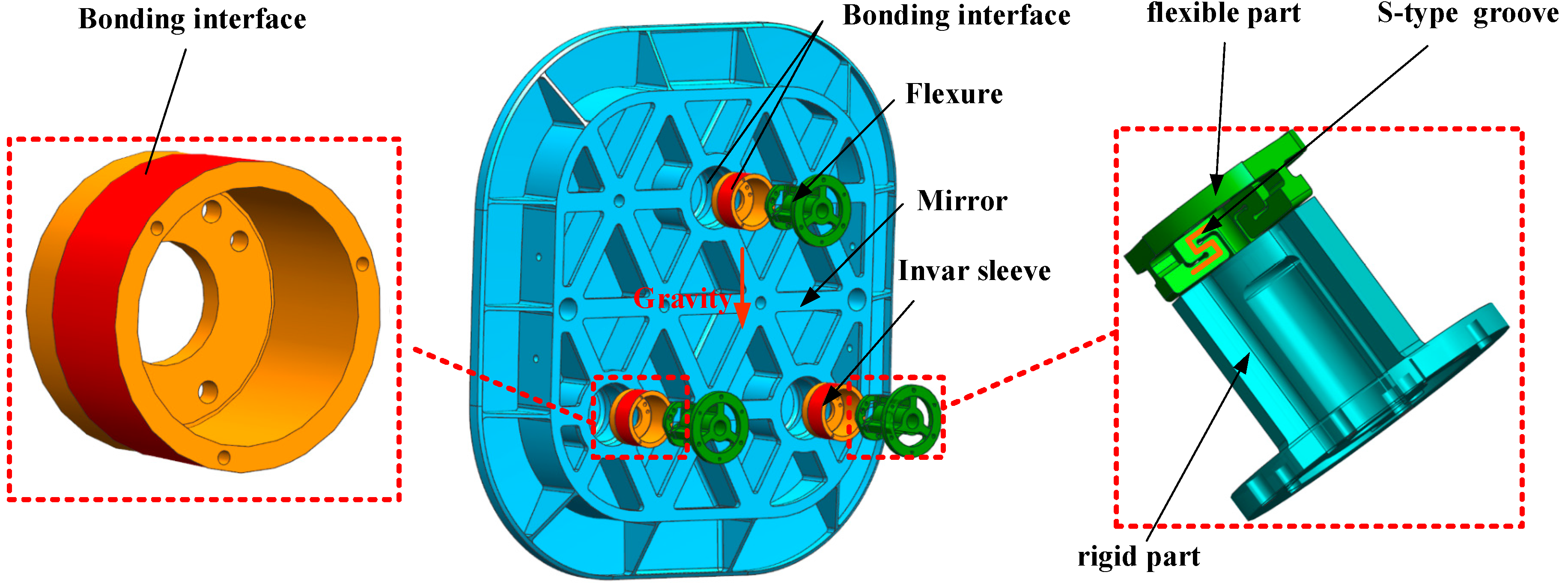
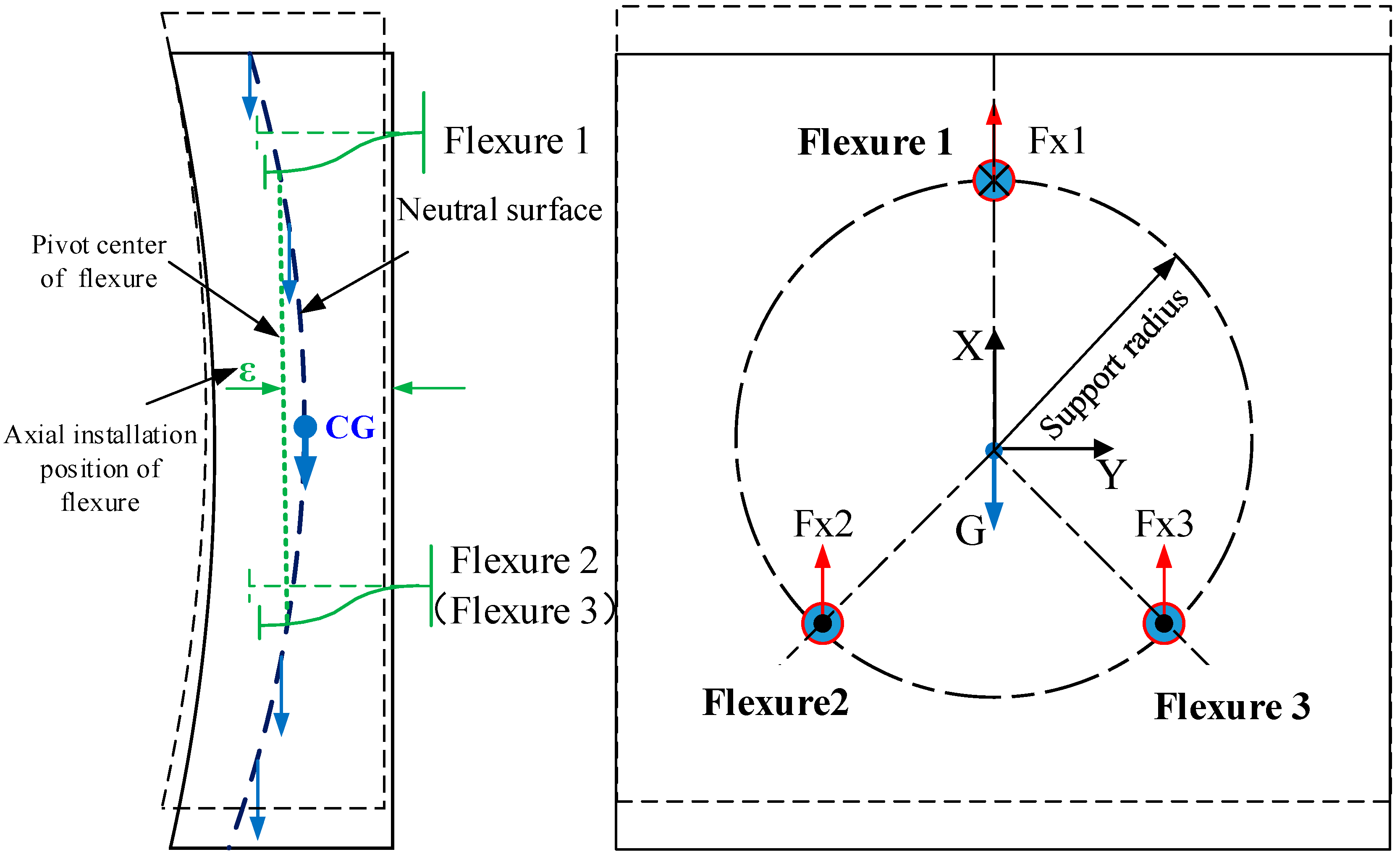
4.1. Design Principle of the Three-Point Support Flexure
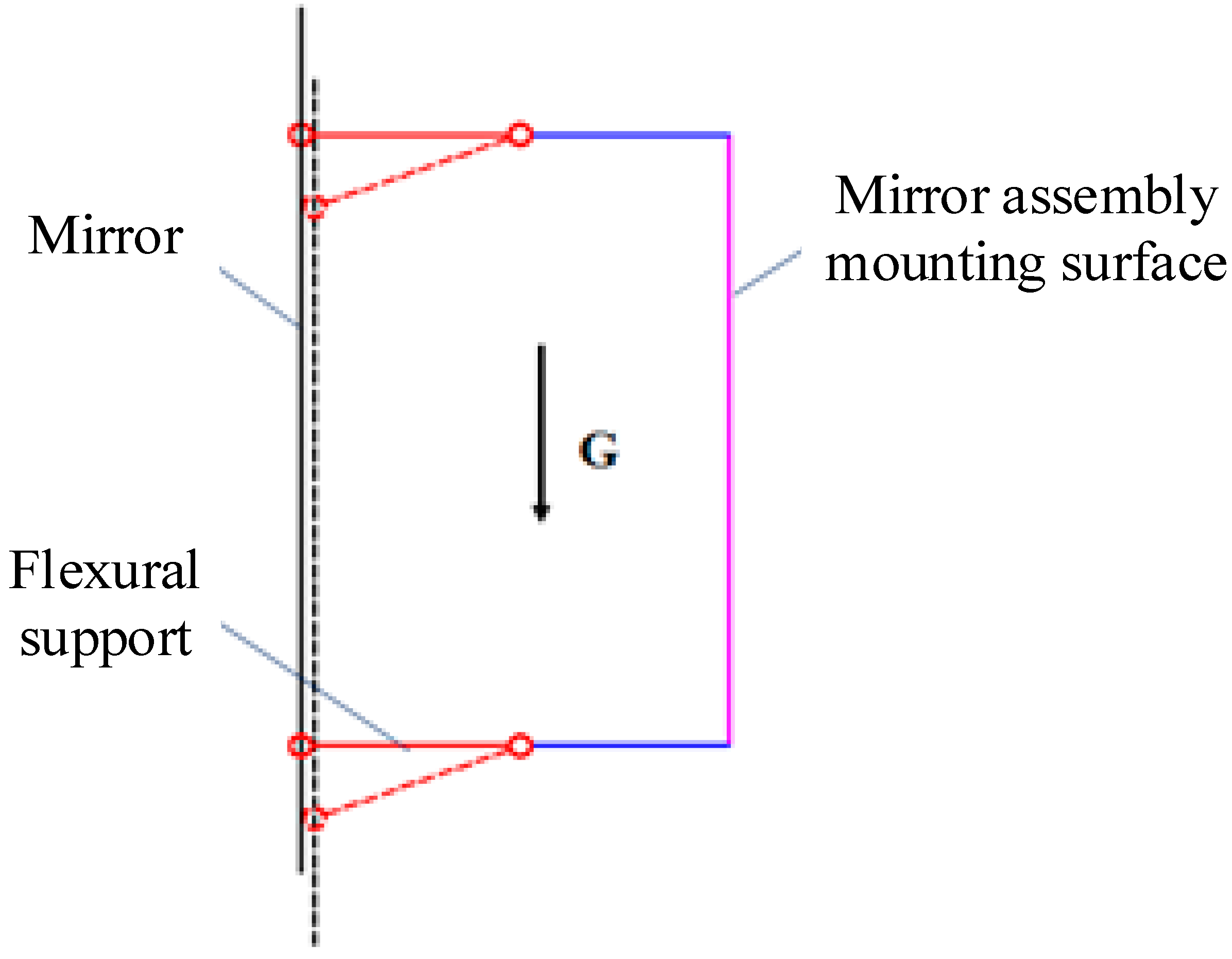
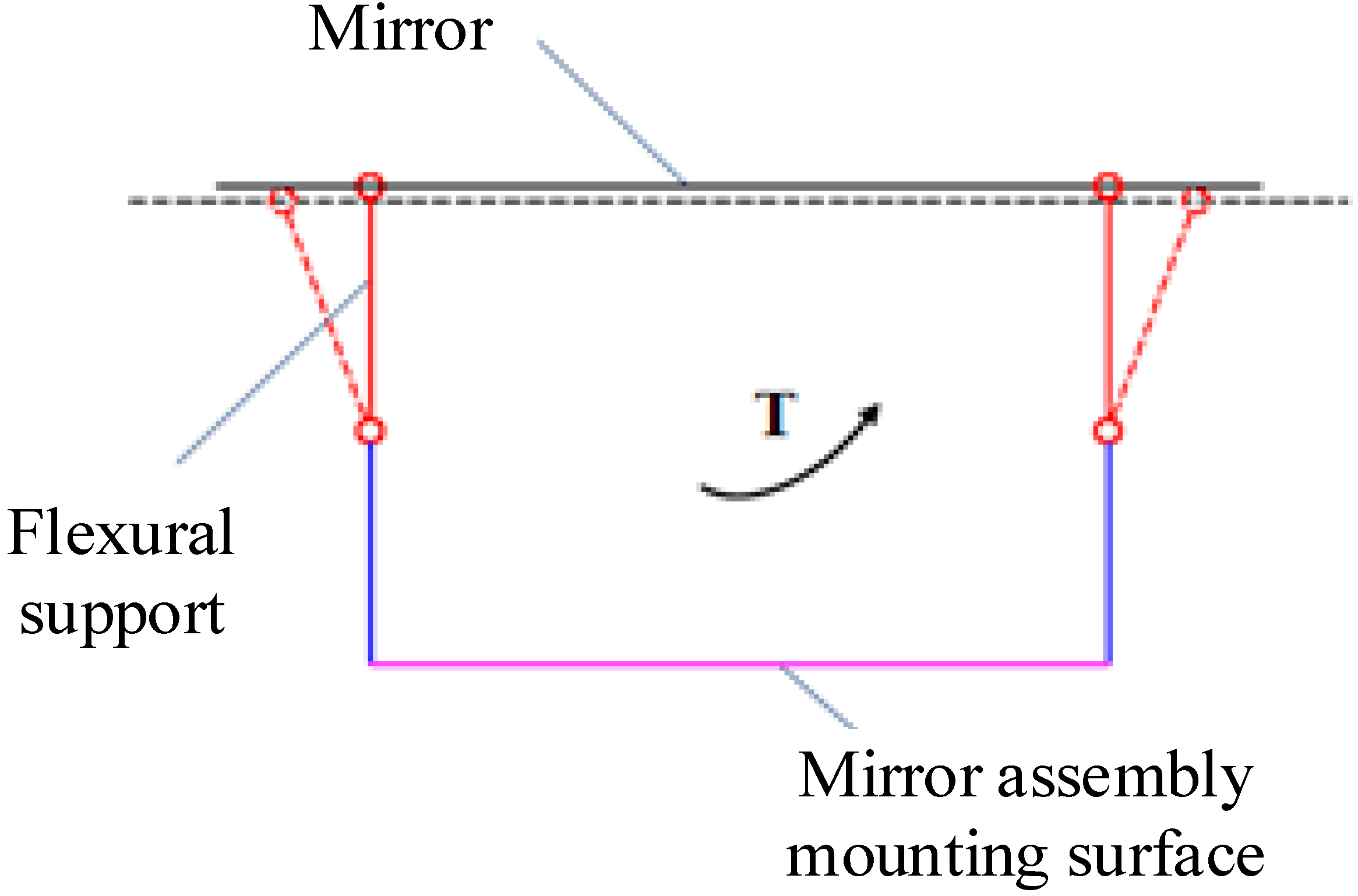
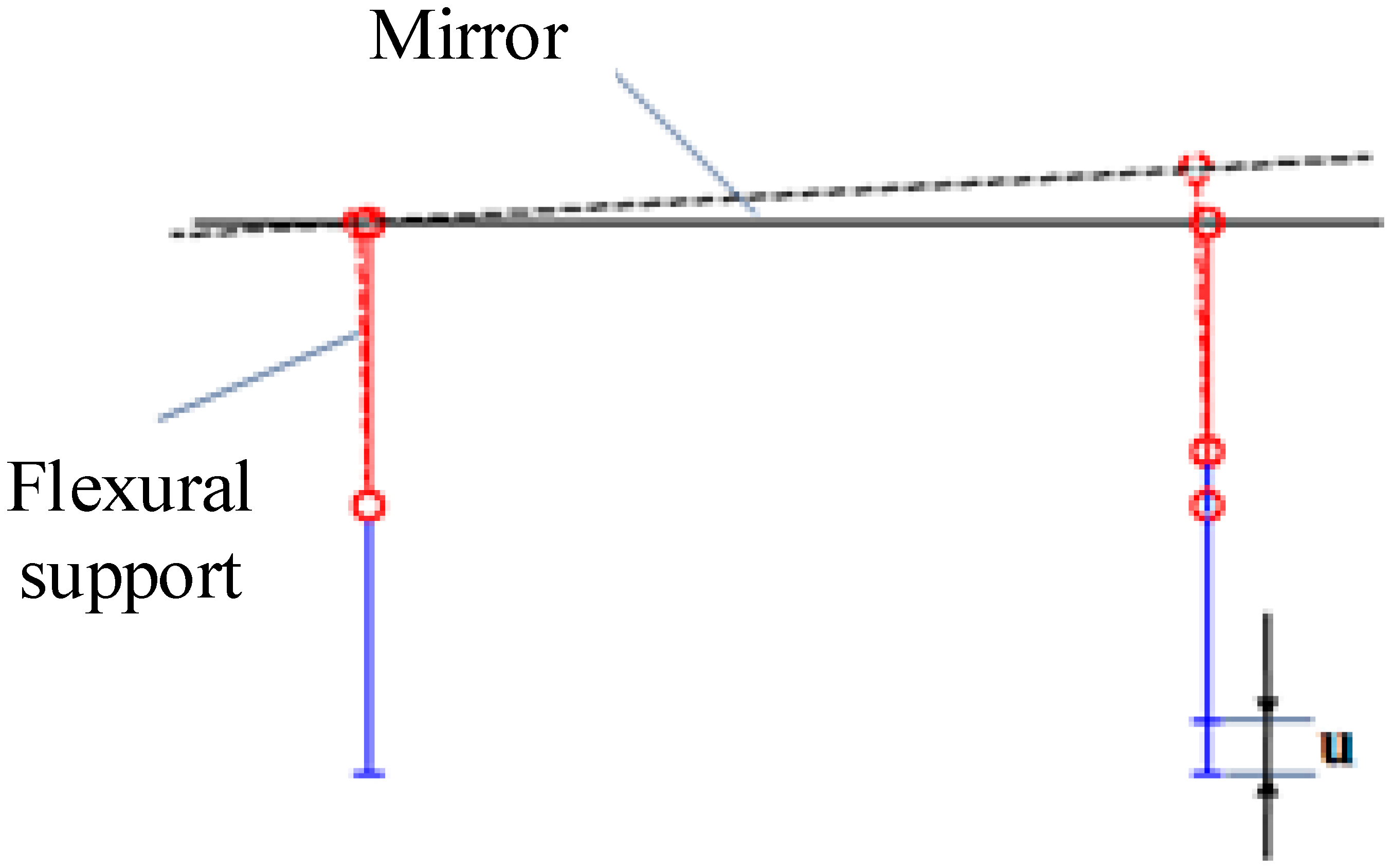
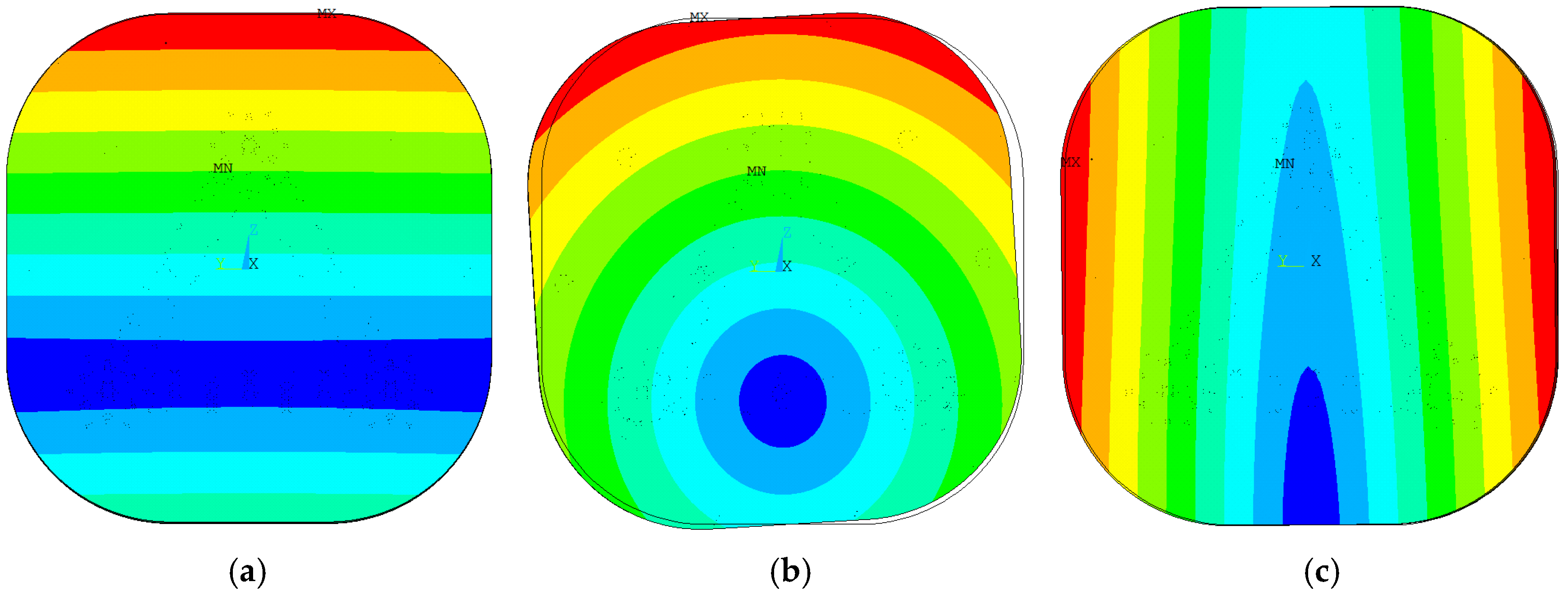
4.1.1. Unloading Gravity Load
4.1.2. Relieve Temperature Load
4.1.3. Improve the Adaptability to Assembly Errors
4.1.4. Improve Structural Stability and Frequency
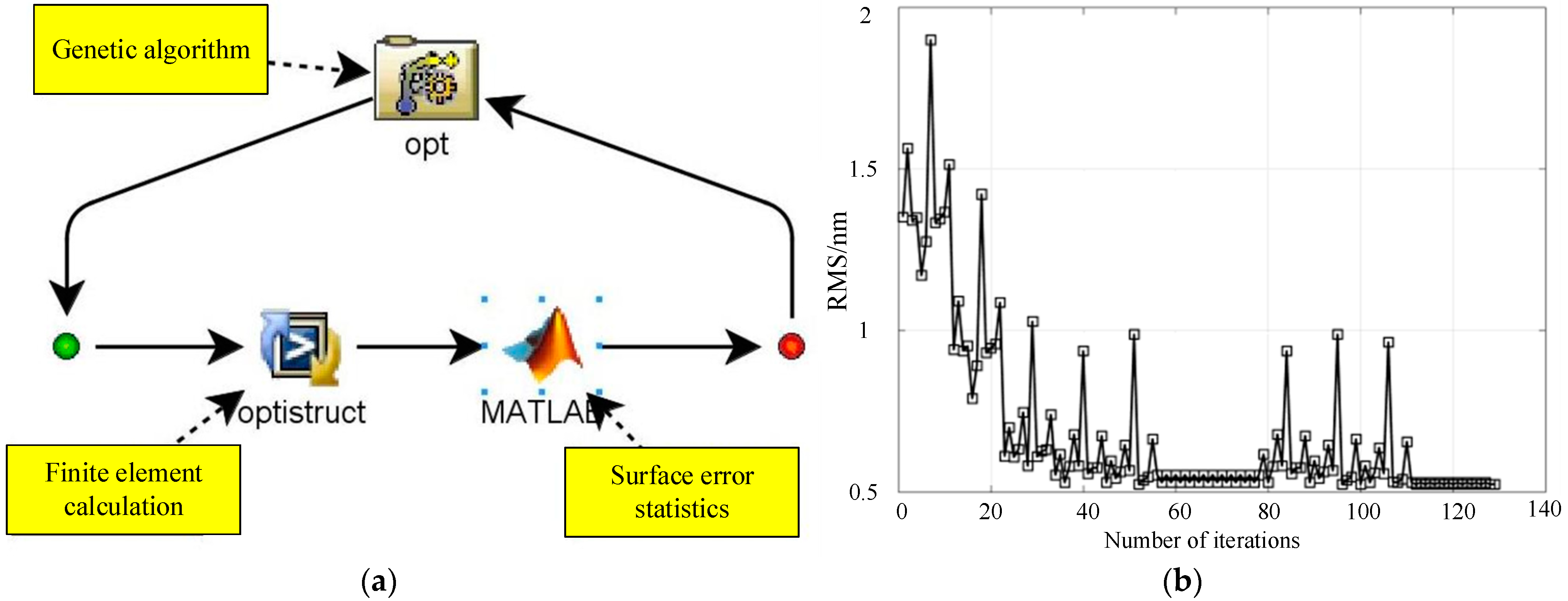
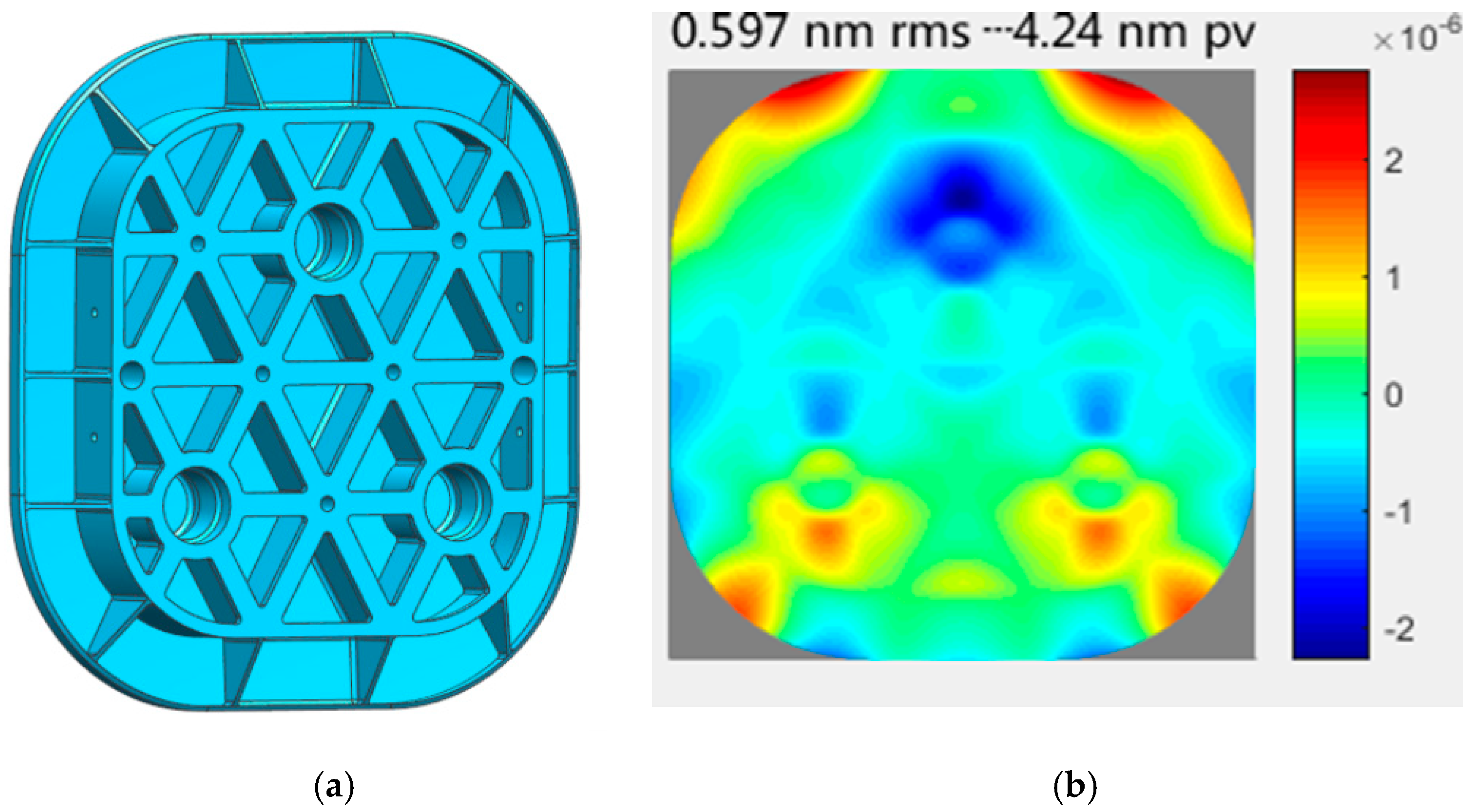
4.2. Structural Design of Flexure
5. Optical and Vibration Testing
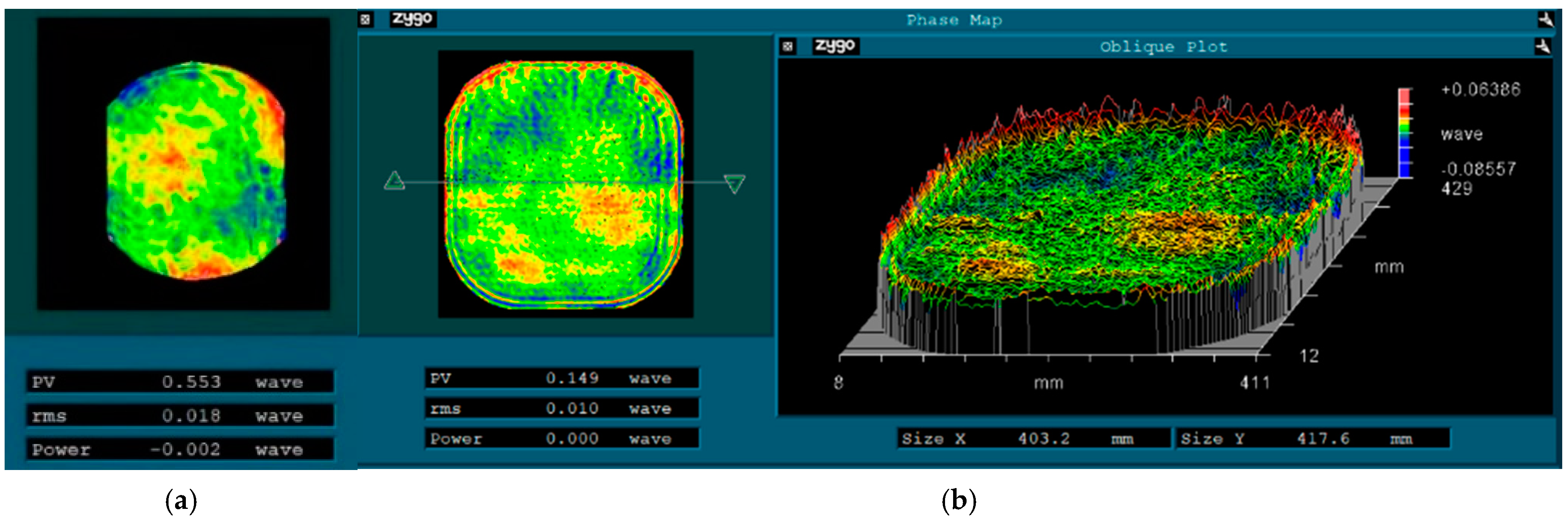
5.1. Optical Testing
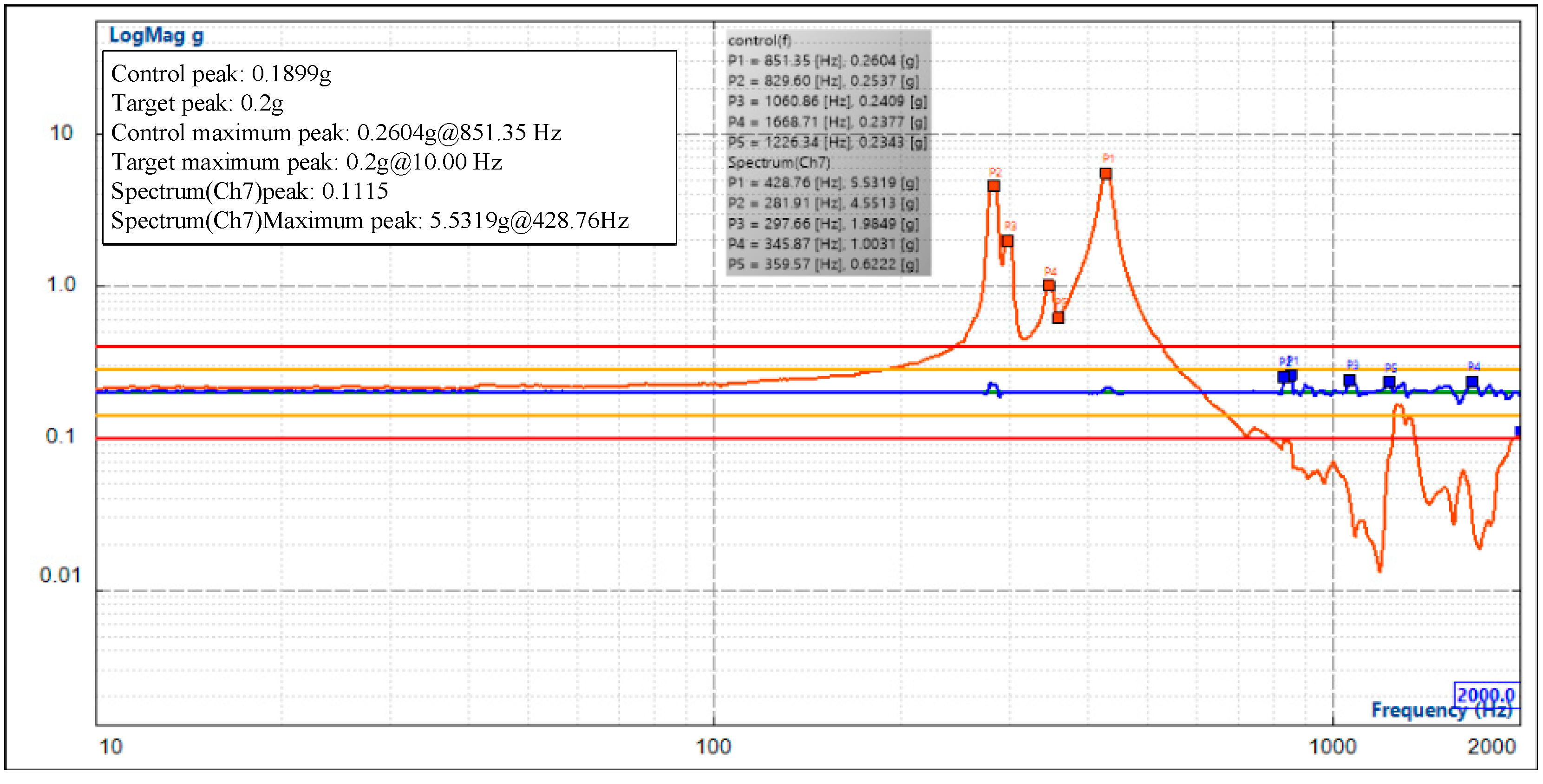
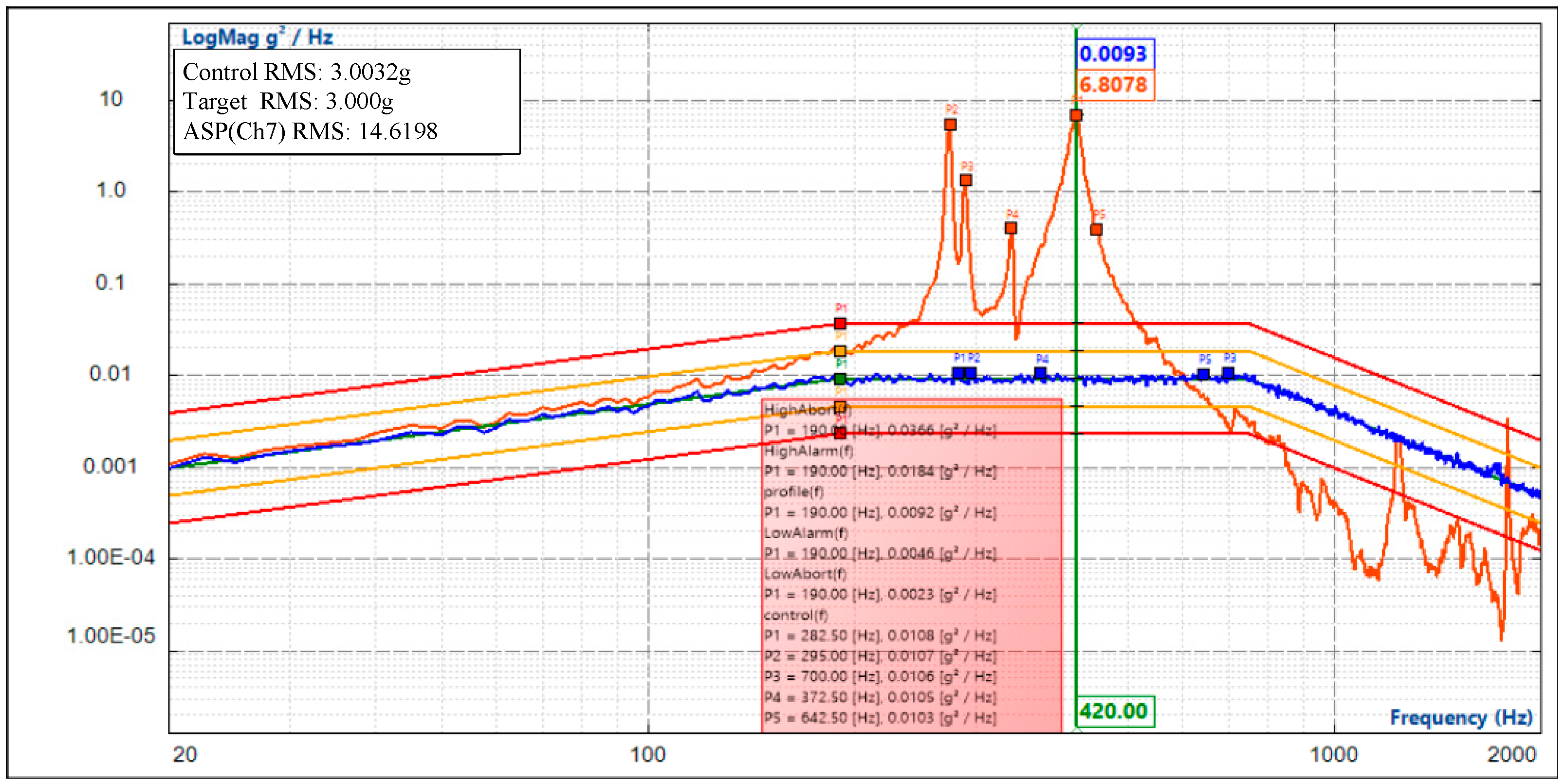
5.2. Vibration Testing
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Betensky, E. The role of asphere in zoom lens design. SPIE 1990, 1354, 656–662. [Google Scholar]
- Qu, Y.; Jian, Y.; Feng, L.; Li, X.; Liu, B. Lightweight design of multiobjective topology for a large-aperture space mirror. Appl. Sci. 2018, 8, 2259. [Google Scholar] [CrossRef] [Green Version]
- Bely, P. The Design and Construction of Large Optical Telescopes; Springer: New York, NY, USA, 2003; pp. 1–28. [Google Scholar]
- Pan, J.H. The Design Manufacture and Test of the Aspherical Optical Surfaces; Suzhou Soochow University Press: Suzhou, China, 2004; pp. 51–61. [Google Scholar]
- Hagyong, K.; Ho-Soon, Y.; Il Kweon, M.; Jeong-Heum, Y.; Seung-Hoon, L.; Yun-Woo, L. Adjustable bipod flexures for mounting mirrors in a space telescope. Appl. Opt. 2012, 51, 7776–7783. [Google Scholar]
- Xiong, G.H.; Liao, K.; Chang, X.Y.; Liu, J.A. Deformation Control by VSR Technique on Al alloy Thin-Walled Components. IOP Conf. Ser. Mater. Sci. Eng. 2017, 11, 269. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.J.; Dong, J.H.; Xuan, M. Compound support structure for large aperture mirror of space remote sensor. Opt. Precis. Eng. 2016, 27, 1719–1730. [Google Scholar] [CrossRef]
- Yoder, P.R. Opto-Mechanical System Design; Cooperate Marcel Dekker Inc.: New York, NY, USA, 1993. [Google Scholar]
- Xue, J.; Hu, H.B.; Song, H.Z. Research on the flexible supporting structure of the optical reflector. J. Chang Chun Univ. Technol. 2009, 30, 457–461. [Google Scholar]
- Liu, X.; Tian, X.; Zhang, W.; Cheng, L.F.; Zhang, B.; Wang, Z. Lightweight design of high volume SiC/Al composite mirror for remote camera. Optik 2019, 188, 64–70. [Google Scholar] [CrossRef]
- Yu, F.; Xu, S. Flexible support structure based on spring principle for a high precision reflecting mirror. Optik 2020, 207, 164341. [Google Scholar] [CrossRef]
- Li, Z.X.; Chen, S.; Jin, G. Optimal design of a Φ760 mm lightweight SiC mirror and the flexural mount for a space telescope. Rev. Sci. Instrum. 2017, 88, 125107. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Zhao, W.C.; Hu, M.Y.; Zhang, H.H.; Hao, P.M. Hindle testing of the off- axis convex ashpere surface. Opt. Precis. Eng. 2002, 10, 2. [Google Scholar]
- Wang, K.J.; Dong, J.H.; Zhao, Y.G.; Chi, C.Y.; Jiang, P.; Wang, X.Y. Research on high performance support technology of space-based large aperture mirror. Optik 2021, 226, 165929. [Google Scholar] [CrossRef]
- Zhou, P.W.; Xu, S.Y.; Yan, C.X.; Zhang, X.H. Research on neutral surface of lightweight, horizontally supported mirror. Opt. Eng. 2018, 57, 025107. [Google Scholar] [CrossRef]
- Valente, T.M.; Vukobratovich, D. A comparison of the merits of open-back, symmetric sandwich, and contoured back mirrors as light-weighted optics. Proc. SPIE 1989, 1167, 20–36. [Google Scholar]
- Abdulkadyrov, M.A.; Vladimirov, N.M.; Dobrikov, N.S.; Patrikeev, V.E.; Semenov, A.P. Optimizing design and manufacturability of reduced-weight mirrors for astronomy and space applications. J. Opt. Technol. 2016, 83, 168–172. [Google Scholar] [CrossRef]
- Li, Y.; Jiao, M.; Luo, C. Optimized design of lightweight flat mirror based on Isight. J. Appl. Opt. 2010, 31, 194–197. [Google Scholar]
- Hu, R.; Liu, S.; Li, Q. Topology-optimization-based design method of flexures for mounting the primary mirror of a large-aperture space telescope. Appl. Opt. 2017, 56, 4551–4560. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.J.; Xu, L.W.; Gao, R.Z. Multi-island genetic algorithm optimization of suspension system. Telkomnika 2012, 10, 1685–1691. [Google Scholar] [CrossRef]






| Design Indexes | Index Requirements |
|---|---|
| Mirror surface accuracy | λ/100 |
| Decenter | 0.017 mm |
| Tilt | 0.2″ |
| Mass (mirror assembly) | ≤10 kg |
| Frequency | ≥150 Hz |
| Dynamic stress | ≤800 Mpa (the microyield stress) |
| Parameter | Parameter Variation Range | Optimized Value |
|---|---|---|
| Diameter | 434 × 416 mm | |
| Main reinforcement thickness | 3–4 | 4 mm |
| Auxiliary reinforcement thickness | 3–4 | 3 mm |
| Radial reinforcement thickness | 3–4 | 3 mm |
| The front panel thickness | 4~5 | 4 mm |
| Mirror thickness | 45~60 | 50 mm |
| Backplane thickness | 4~6 | 5 mm |
| Support hole thickness | 4–7 | 6.5 mm |
| Total mass | 4.6 kg | |
| Lightweight ratio | 81.6% |
| Design Index | Result | Allowed Value |
|---|---|---|
| 1 g gravity | 1.61 nm | 2.0 nm |
| rigid body displacement | 0.00198 mm | 0.017 mm |
| inclination angle | 0.125″ | 0.2″ |
| 4 °C thermal change | 1.75 nm | 2.5 nm |
| forced displacement of 0.05 mm | 3.30 nm | 4.0 nm |
| comprehensive surface | 4.06 nm (λ/155) | 6.3 nm (λ/100) |
| fundamental frequency | 271.6 Hz | 150 Hz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, P.; Zhou, P. The Optimization of a Convex Aspheric Lightweight SiC Mirror and Its Optical Metrology. Photonics 2022, 9, 210. https://doi.org/10.3390/photonics9040210
Jiang P, Zhou P. The Optimization of a Convex Aspheric Lightweight SiC Mirror and Its Optical Metrology. Photonics. 2022; 9(4):210. https://doi.org/10.3390/photonics9040210
Chicago/Turabian StyleJiang, Ping, and Pingwei Zhou. 2022. "The Optimization of a Convex Aspheric Lightweight SiC Mirror and Its Optical Metrology" Photonics 9, no. 4: 210. https://doi.org/10.3390/photonics9040210
APA StyleJiang, P., & Zhou, P. (2022). The Optimization of a Convex Aspheric Lightweight SiC Mirror and Its Optical Metrology. Photonics, 9(4), 210. https://doi.org/10.3390/photonics9040210




