A Convolution Neural Network Implemented by Three 3 × 3 Photonic Integrated Reconfigurable Linear Processors
Abstract
:1. Introduction
2. Convolution Neural Network
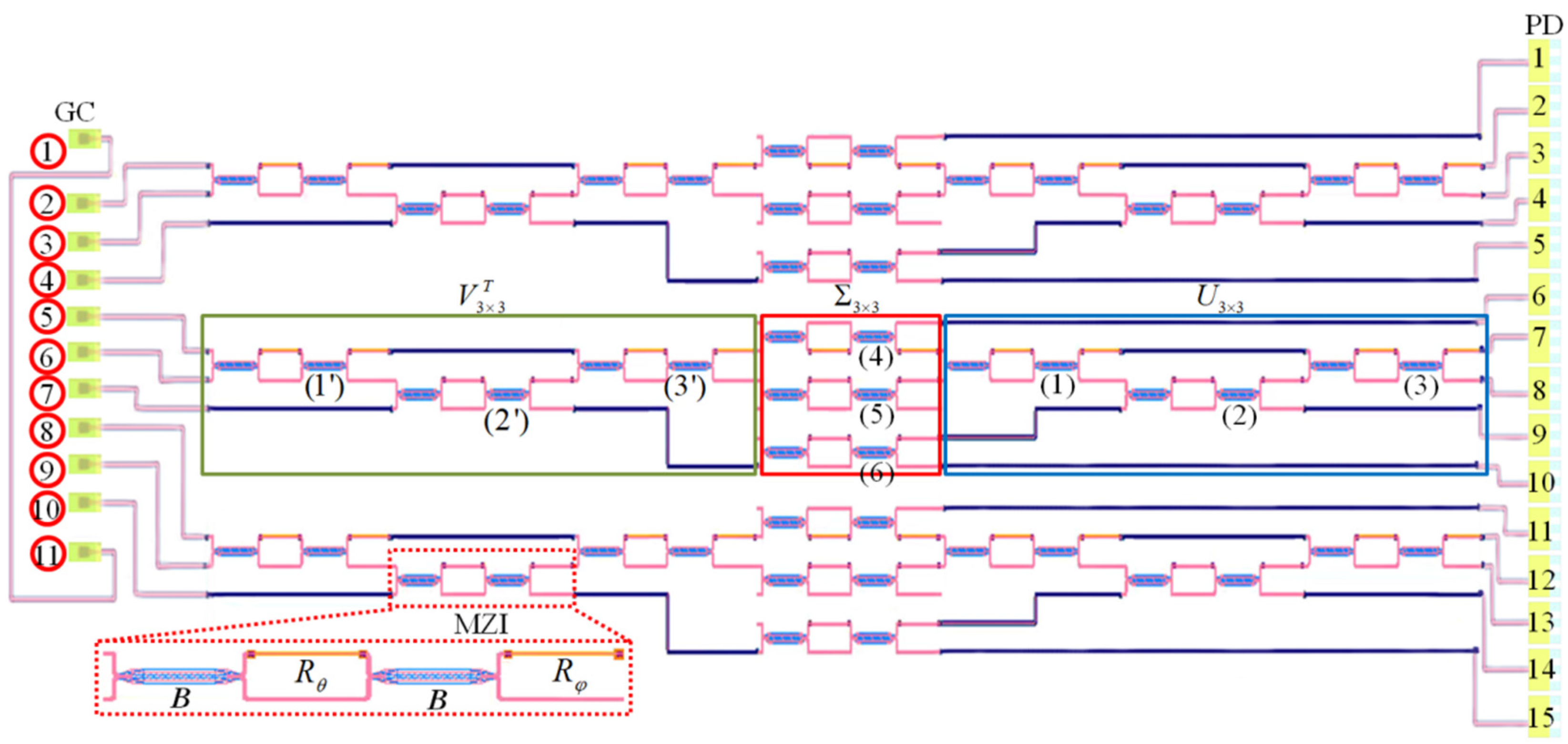
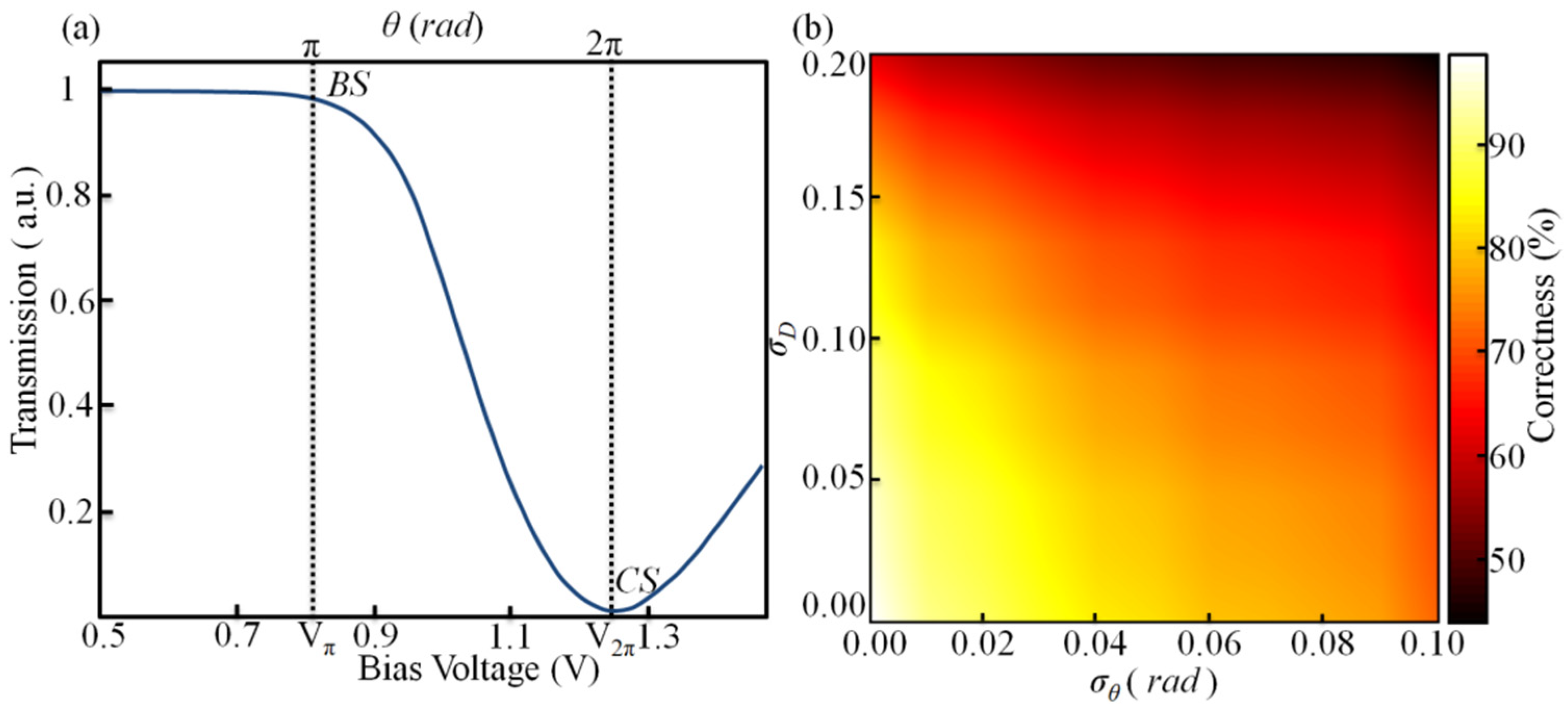
3. Reconfigurable Linear Optical Processors
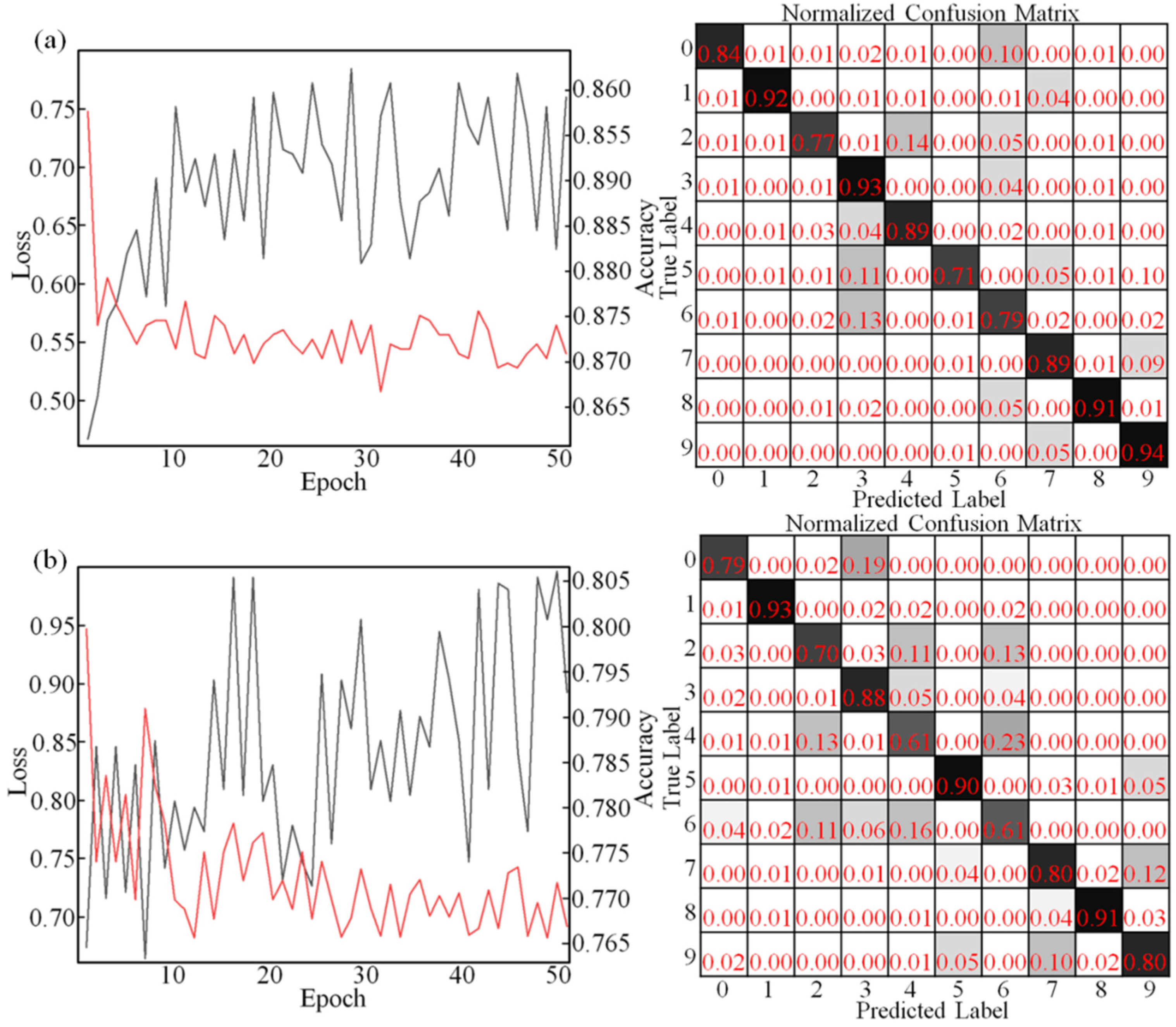
4. Training and Simulation
- optical source: wavelength = 1550 nm; power = 27 mW; half-height width = 20 pm;
- detector: response wavelength = 1550 nm; and the dark current = 20 nA.
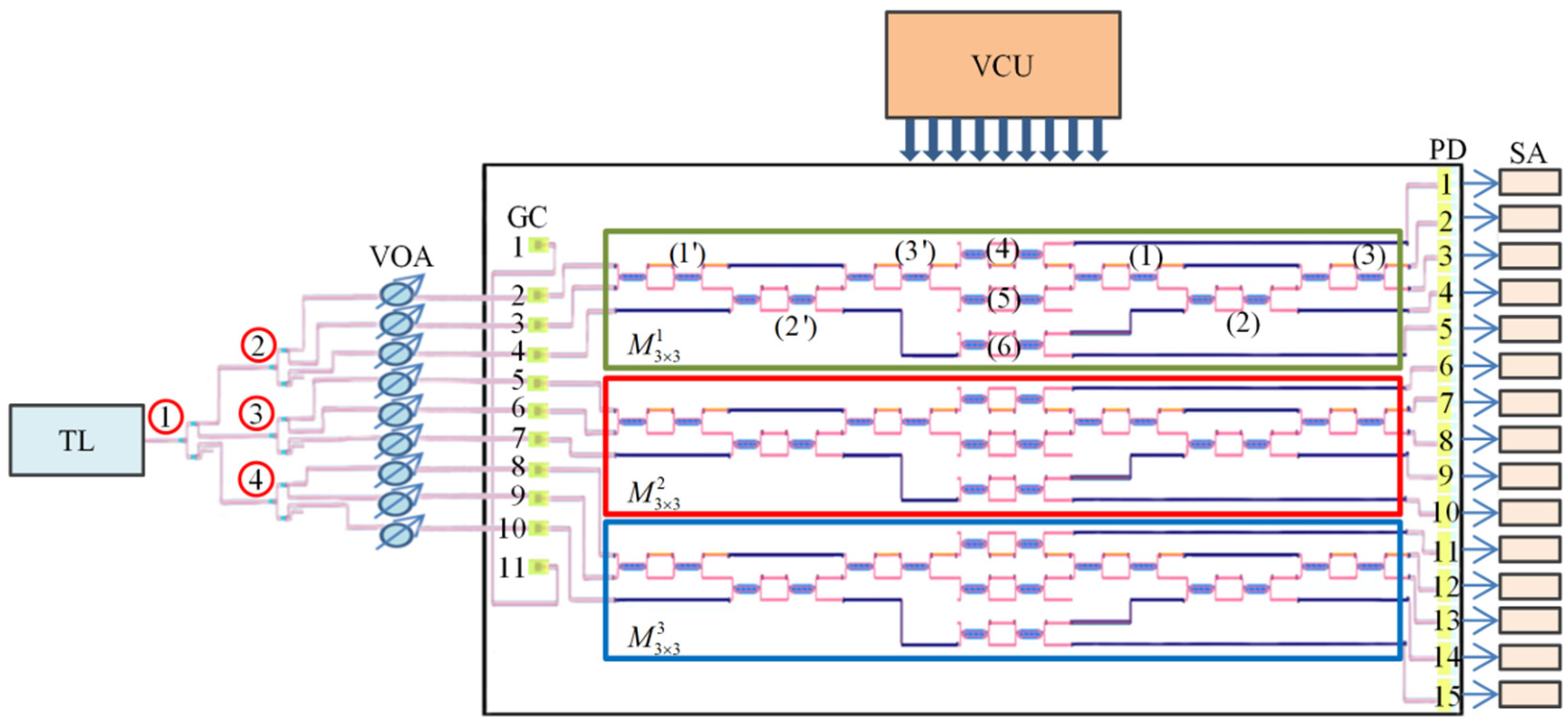
5. Experimental
6. Results and Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Athale, R.A.; Collins, W.C. Optical matrix–matrix multiplier based on outer product decomposition. Appl. Opt. 1982, 21, 2089–2090. [Google Scholar] [CrossRef] [PubMed]
- Farhat, N.H.; Psaltis, D.; Prata, A.; Paek, E. Optical implementation of the Hopfield model. Appl. Opt. 1985, 24, 1469–1475. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Harris, N.C.; Skirlo, S.; Prabhu, M.; Baehr-Jones, T.; Hochberg, M.; Sun, X.; Zhao, S.; LaRochelle, H.; Englund, D.; et al. Deep learning with coherent nanophotonic circuits. Nat. Photon. 2017, 11, 441–446. [Google Scholar] [CrossRef]
- Bagherian, H.; Skirlo, S.; Shen, Y.; Meng, H.; Ceperic, V.; Soljacic, M. On-Chip Optical Convolutional Neural Networks. arXiv 2018, arXiv:1808.03303. [Google Scholar]
- Shokraneh, F.; Geoffroy-Gagnon, S.; Nezami, M.S.; Liboiron-Ladouceur, O. A Single Layer Neural Network Implemented by a 4 × 4 MZI-Based Optical Processor. Phot. J. 2019, 11, 4501612. [Google Scholar] [CrossRef]
- Nahmias, M.A.; Lima, T.F.; Tait, A.N.; Peng, H.-T.; Shastri, B.J.; Prucnal, P.R. Photonic Multiply-Accumulate Operations for Neural Networks. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 7701518. [Google Scholar] [CrossRef]
- Marinis, L.D.; Cococcioni, M.; Liboiron-Ladouceur, O.; Contestabile, G. Photonic Integrated Reconfigurable Linear Processors as Neural Network Accelerators. Appl. Sci. 2021, 11, 6232. [Google Scholar] [CrossRef]
- Xu, X.; Zhu, L.; Zhuang, W.; Zhang, D.; Yuan, P.; Lu, L. Photoelectric hybrid convolution neural network with coherent nanophotonic circuits. Opt. Eng. 2021, 60, 117106. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Genz, A. Methods for generating random orthogonal matrices. In Monte Carlo and Quasi-Monte Carlo Methods; Springer: Berlin/Heidelberg, Germany, 1998; p. 199. [Google Scholar]
- Reck, M.; Zeilinger, A.; Bernstein, H.J.; Bertani, P. Experimental realization of any discrete unitary operator. Phys. Rev. Lett. 1994, 73, 58–61. [Google Scholar] [CrossRef] [PubMed]
- Clements, W.R.; Humphreys, P.C.; Metcalf, B.J.; Steven, K.W.; Walsmley, I.A. An Optimal Design for Universal Multiport Interferometers. Optica 2016, 3, 1460–1465. [Google Scholar] [CrossRef]
- Connelly, M.J. Semiconductor Optical Amplifiers; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Liu, S.; Tian, Y.; Lu, Y.; Feng, J. Comparison of thermo-optic phase-shifters implemented on CUMEC silicon photonics platform. Int. Soc. Opt. Photonics 2021, 11763, 1176374. [Google Scholar]
- Miller, D.A.B. Self-aligning universal beam coupler. Opt. Exp. 2013, 21, 6360–6370. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miller, D.A.B. Self-configuring universal linear optical component. Photon. Res. 2013, 1, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Jayatilleka, H.; Shoman, H.; Chrostowski, L.; Shekhar, S. Photoconductive heaters enable control of large-scale silicon photonic ring resonator circuits. Optica 2019, 6, 84–91. [Google Scholar] [CrossRef] [Green Version]


| Accuracy (%) | Kernel Number | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| Kernel size | 2 × 2 | 88.17 | 89.22 | 92.30 | 92.31 | 92.32 | 92.41 | 92.24 | 92.19 |
| 3 × 3 | 90.46 | 91.57 | 94.77 | 94.72 | 94.67 | 94.78 | 94.58 | 94.66 | |
| 4 × 4 | 89.90 | 91.01 | 94.10 | 94.08 | 94.10 | 94.19 | 93.93 | 94.02 | |
| 5 × 5 | 90.65 | 91.69 | 94.77 | 94.76 | 94.88 | 94.76 | 94.73 | 94.79 | |
| Accuracy (%) | Kernel Number | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| Kernel size | 2 × 2 | 83.08 | 84.29 | 87.43 | 87.36 | 87.02 | 84.68 | 86.73 | 87.17 |
| 3 × 3 | 85.48 | 86.21 | 89.67 | 89.05 | 89.58 | 89.68 | 89.00 | 89.56 | |
| 4 × 4 | 84.67 | 85.38 | 88.92 | 88.48 | 88.62 | 86.20 | 88.48 | 88.72 | |
| 5 × 5 | 85.62 | 86.55 | 89.66 | 89.39 | 89.39 | 87.26 | 89.13 | 89.45 | |
| MZI | (1′) | (2′) | (3′) | (4) | (5) | (6) | (1) | (2) | (3) |
|---|---|---|---|---|---|---|---|---|---|
| VCS,i | 2.21 | 2.51 | 2.17 | 2.55 | 1.94 | 1.34 | 2.84 | 1.82 | 2.87 |
| PCS,i (dBm) | −22.52 | −12.21 | −26.13 | −28.89 | −44.65 | −27.14 | −45.91 | −29.5 | −36.71 |
| VBS,i | 3.09 | 3.54 | 3.99 | 3.58 | 3.39 | 2.61 | 3.86 | 3.03 | 4.36 |
| PBS,i (dBm) | −11.97 | −1.91 | −12.18 | −18.1 | −23.03 | −17.71 | −20.12 | −22.2 | −20.71 |
| VHalf,i | 0.88 | 1.03 | 1.82 | 1.03 | 1.45 | 1.27 | 1.02 | 1.21 | 1.49 |
| ERi | 10.54 | 10.29 | 13.94 | 10.79 | 21.62 | 9.43 | 25.79 | 7.3 | 16 |
| Pπ,i (mW) | 8.43 | 11.15 | 19.88 | 11.34 | 13.75 | 9.06 | 12.10 | 10.57 | 18.97 |
| MZI | (1′) | (2′) | (3′) | (4) | (5) | (6) | (1) | (2) | (3) |
|---|---|---|---|---|---|---|---|---|---|
| VCS,i | 2.76 | 1.62 | 2.64 | 2.61 | 2.33 | 1.63 | 3.17 | 0.93 | 2.84 |
| PCS,i (dBm) | −22.47 | −12.24 | −25.9 | −28.81 | −44.21 | −26.88 | −45.73 | −29.83 | −37.45 |
| VBS,i | 4.15 | 2.87 | 4.61 | 4.21 | 4.17 | 3.17 | 4.64 | 1.84 | 4.36 |
| PBS,i (dBm) | −11.46 | −2.12 | −12.61 | −17.45 | −22.32 | −16.21 | −23.83 | −22.73 | −16.69 |
| VHalf,i | 1.39 | 1.25 | 1.97 | 1.6 | 1.84 | 1.54 | 1.47 | 0.91 | 1.52 |
| ERi | 11.01 | 10.12 | 13.29 | 11.36 | 21.89 | 10.67 | 21.9 | 7.1 | 20.76 |
| Pπ,i (mW) | 17.31 | 9.93 | 25.46 | 19.63 | 21.67 | 13.15 | 20.36 | 4.57 | 19.58 |
| MZI | (1′) | (2′) | (3′) | (4) | (5) | (6) | (1) | (2) | (3) |
|---|---|---|---|---|---|---|---|---|---|
| VCS,i | 1.31 | 2.92 | 2.03 | 2.17 | 1.04 | 1.28 | 2.03 | 2.06 | 3.36 |
| PCS,i (dBm) | −23.23 | −12.1 | −26.85 | −29.46 | −45.26 | −27.82 | −46.49 | −29.67 | −36.7 |
| VBS,i | 2.24 | 4.26 | 3.74 | 3.52 | 1.87 | 2.51 | 2.87 | 3.37 | 4.35 |
| PBS,i (dBm) | −13.16 | −2.49 | −12.67 | −21.95 | −29.74 | −18.46 | −22.94 | −19.78 | −20.6 |
| VHalf,i | 0.93 | 1.34 | 1.71 | 1.35 | 0.83 | 1.23 | 0.84 | 1.31 | 0.99 |
| ERi | 10.07 | 9.61 | 14.18 | 7.51 | 15.52 | 9.36 | 23.55 | 9.89 | 16.1 |
| Pπ,i (mW) | 5.97 | 17.09 | 17.49 | 13.64 | 4.37 | 8.41 | 7.46 | 12.82 | 13.61 |
| MZI | This Work | [3] | [4] | [5] | [7] | ||
|---|---|---|---|---|---|---|---|
| Network | CNN | DNN | CNN | DNN | DNN | ||
| Platforms | SOI | SOI | \ | SOI | SOI | SiN | |
| Footprint (mm2) | 5 × 1 | \ | \ | \ | 5 × 1.5 | 16 × 8 | |
| Datasets | MNIST | Fashion-MNIST | Vowel | MNIST | \ | \ | |
| Method | Experiment | Experiment | Simulation | Experiment | Experiment | ||
| Classification Accuracy | 86.9% | 79.3% | 76.7% | 97% | 72% | \ | |
| Central Wavelength | 1550 nm | \ | \ | 1310 nm | 1550 nm | ||
| Pπ (mW) | ~14 | \ | \ | ~22 | 55 | 296 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Zhu, L.; Zhuang, W.; Lu, L.; Yuan, P. A Convolution Neural Network Implemented by Three 3 × 3 Photonic Integrated Reconfigurable Linear Processors. Photonics 2022, 9, 80. https://doi.org/10.3390/photonics9020080
Xu X, Zhu L, Zhuang W, Lu L, Yuan P. A Convolution Neural Network Implemented by Three 3 × 3 Photonic Integrated Reconfigurable Linear Processors. Photonics. 2022; 9(2):80. https://doi.org/10.3390/photonics9020080
Chicago/Turabian StyleXu, Xiaofeng, Lianqing Zhu, Wei Zhuang, Lidan Lu, and Pei Yuan. 2022. "A Convolution Neural Network Implemented by Three 3 × 3 Photonic Integrated Reconfigurable Linear Processors" Photonics 9, no. 2: 80. https://doi.org/10.3390/photonics9020080
APA StyleXu, X., Zhu, L., Zhuang, W., Lu, L., & Yuan, P. (2022). A Convolution Neural Network Implemented by Three 3 × 3 Photonic Integrated Reconfigurable Linear Processors. Photonics, 9(2), 80. https://doi.org/10.3390/photonics9020080





