Mode Coupling Analysis for a Mode Selective Coupler Using the Supermode Theory
Abstract
:1. Introduction
2. Theory
2.1. Coupled Mode Theory for the MSC
2.2. Supermode Theory for the MSC
3. Simulation and Discussion
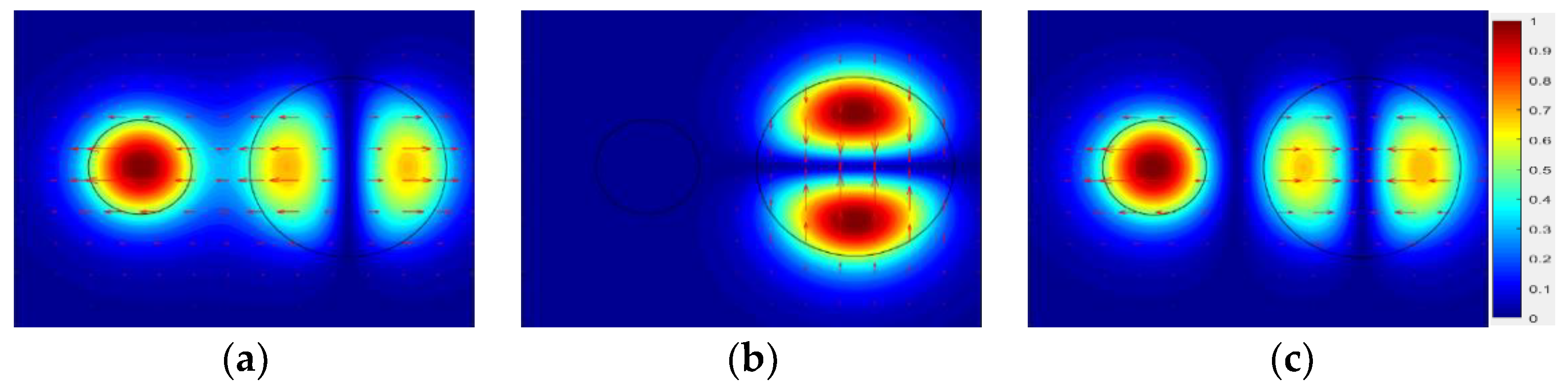
3.1. Supermodes for the MSC Structure
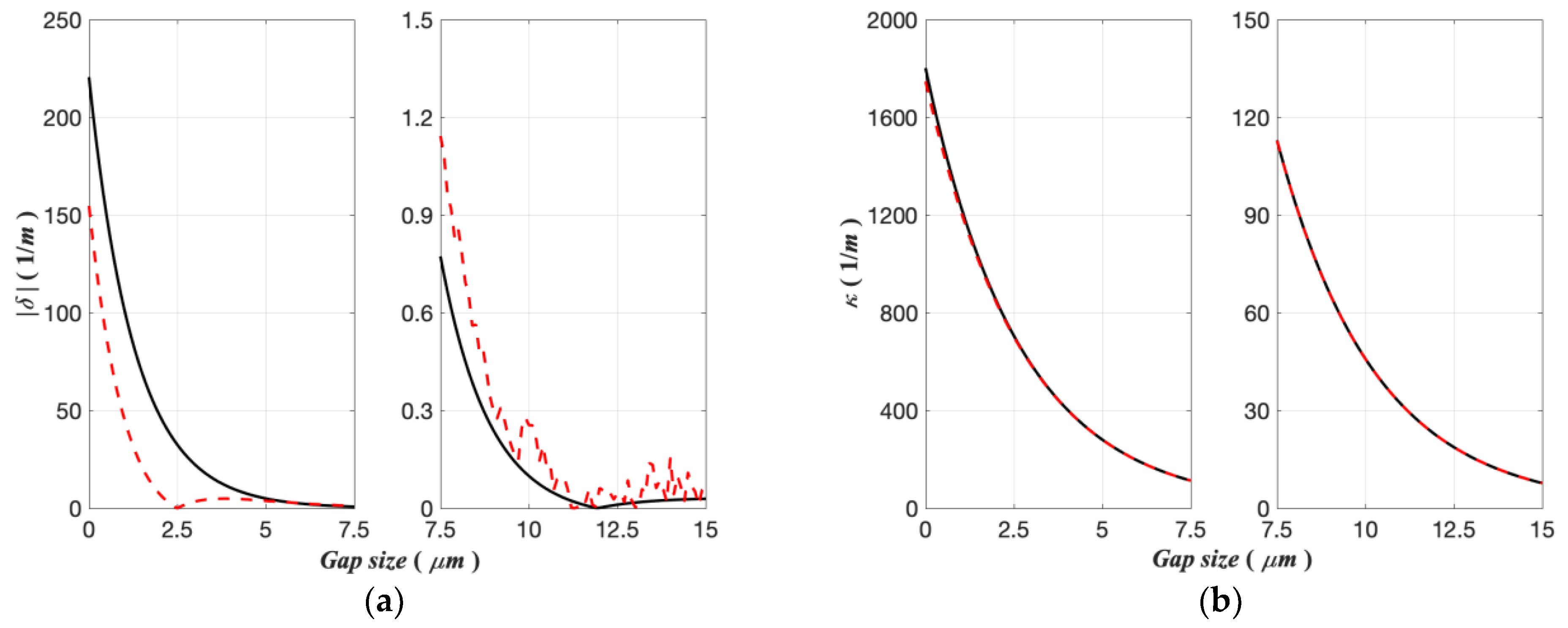
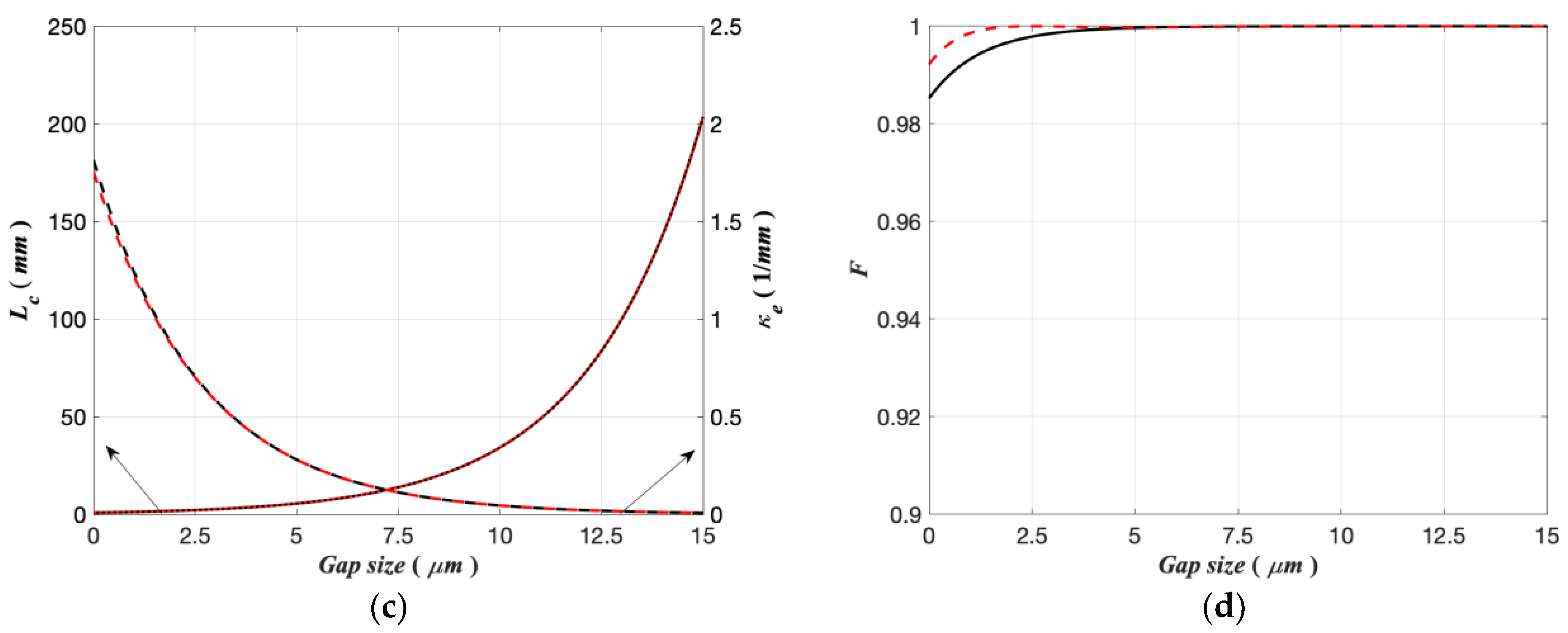
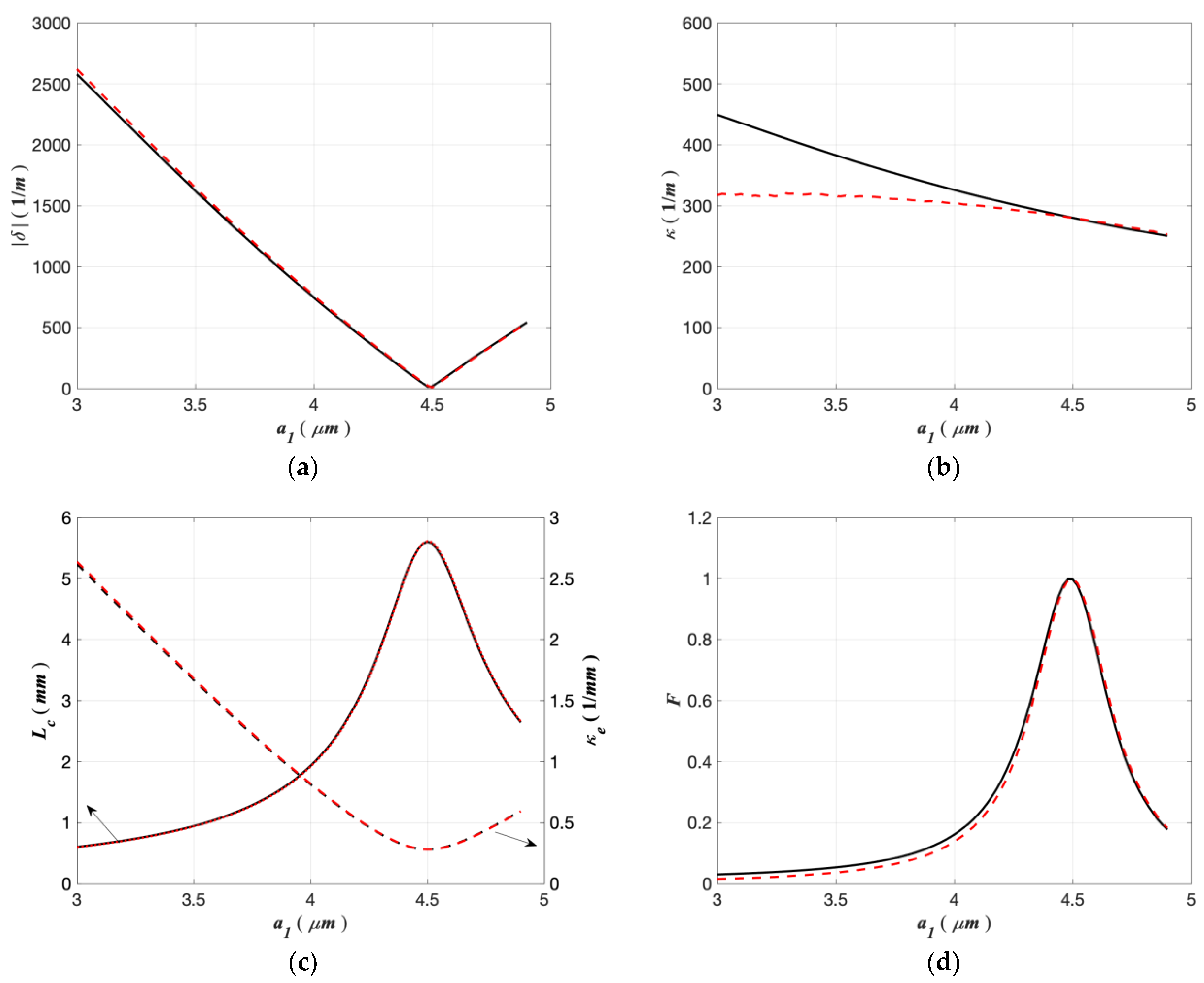
3.2. Calculation of the Characteristic Parameters of the MSC
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Richardson, D.J.; Fini, J.M.; Nelson, L.E. Space-division multiplexing in optical fibres. Nat. Photonics 2013, 7, 354–362. [Google Scholar] [CrossRef] [Green Version]
- Li, G.; Bai, N.; Zhao, N.; Xia, C. Space-division multiplexing: The next frontier in optical communication. Adv. Opt. Photonics 2014, 6, 413–487. [Google Scholar] [CrossRef] [Green Version]
- Ismaeel, R.; Lee, T.; Oduro, B.; Jung, Y.; Brambilla, G. All-fiber fused directional coupler for highly efficient spatial mode conversion. Opt. Express 2014, 22, 11610–11619. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chang, S.H.; Chung, H.S.; Ryf, R.; Fontaine, N.K.; Han, C.; Park, K.J.; Kim, K.; Lee, J.C.; Lee, J.H.; Kim, B.Y.; et al. Mode- and wavelength-division multiplexed transmission using all-fiber mode multiplexer based on mode selective couplers. Opt. Express 2015, 23, 7164–7172. [Google Scholar] [CrossRef] [Green Version]
- Chang, S.H.; Moon, S.-R.; Chen, H.; Ryf, R.; Fontaine, N.K.; Park, K.J.; Kim, K.; Lee, J.K. All-fiber 6-mode multiplexers based on fiber mode selective couplers. Opt. Express 2017, 25, 5734–5741. [Google Scholar] [CrossRef]
- Igarashi, K.; Wakayama, Y.; Soma, D.; Tsuritani, T.; Morita, I.; Park, K.J.; Ko, J.; Kim, B.Y. Low-loss and low-crosstalk all-fiber-based six-mode multiplexer and demultiplexer for mode-multiplexed QAM signals in C-band. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 13–15 March 2018. paper Th1K. 3. [Google Scholar]
- Luo, Y.; Zhou, W.; Wang, L.; Wang, A.; Wang, J. 16-QAM-carrying orbital angular momentum (OAM) mode-division multiplexing transmission using all-fiber fused mode selective coupler. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 13–15 March 2018. paper M4D. 2. [Google Scholar]
- Wang, T.; Wang, F.; Shi, F.; Pang, F.; Huang, S.; Wang, T.; Zeng, X. Generation of femtosecond optical vortex beams in all-fiber mode-locked fiber laser using mode selective coupler. J. Lightwave Technol. 2017, 35, 2161–2166. [Google Scholar] [CrossRef] [Green Version]
- Wang, T.; Shi, F.; Huang, Y.; Wen, J.; Luo, Z.; Pang, F.; Wang, T.; Zeng, X. High-order mode direct oscillation of few-mode fiber laser for high-quality cylindrical vector beams. Opt. Express 2018, 26, 11850–11858. [Google Scholar] [CrossRef]
- Huang, Y.; Shi, F.; Wang, T.; Liu, X.; Zeng, X.; Pang, F.; Wang, T.; Zhou, P. High-order mode Yb-doped fiber lasers based on mode-selective couplers. Opt. Express 2018, 26, 19171–19181. [Google Scholar] [CrossRef]
- Wan, H.; Wang, J.; Zhang, Z.; Cai, Y.; Sun, B.; Zhang, L. High efficiency mode-locked, cylindrical vector beam fiber laser based on a mode selective coupler. Opt. Express 2017, 25, 11444–11451. [Google Scholar] [CrossRef]
- Shen, Y.; Ren, G.; Yang, Y.; Yao, S.; Xiao, S.; Jiang, Y.; Xu, Y.; Wu, Y.; Jin, W.; Jian, S. Generation of the tunable second-order optical vortex beams in narrow linewidth fiber laser. IEEE Photonics Technol. Lett. 2017, 29, 1659–1662. [Google Scholar] [CrossRef]
- Zhang, Z.; Cai, Y.; Wang, J.; Wan, H.; Zhang, L. Switchable dual-wavelength cylindrical vector beam generation from a passively mode-locked fiber laser based on carbon nanotubes. IEEE J. Sel. Top. Quant. 2018, 24, 1100906. [Google Scholar] [CrossRef]
- Wan, H.; Wang, J.; Zhang, Z.; Wang, J.; Ruan, S.; Zhang, L. Passively mode-locked Ytterbium-doped fiber laser with cylindrical vector beam generation based on mode selective coupler. J. Lightwave Technol. 2018, 36, 3403–3407. [Google Scholar] [CrossRef] [Green Version]
- Cai, Y.; Wang, J.; Zhang, J.; Wan, H.; Zhang, Z.; Zhang, L. Generation of cylindrical vector beams in a mode-locked fiber laser using a mode-selective coupler. Chin. Opt. Lett. 2018, 16, 010602. [Google Scholar] [CrossRef]
- Wang, J.; Wan, H.; Cao, H.; Cai, Y.; Sun, B.; Zhang, Z.; Zhang, L. A 1μm cylindrical vector beam fiber ring laser based on a mode selective coupler. IEEE Photonics Tech. L. 2018, 30, 765–768. [Google Scholar] [CrossRef] [Green Version]
- Snyder, A.W. Coupled-Mode theory for optical fibers. J. Opt. Soc. Am. 1972, 62, 1267–1277. [Google Scholar] [CrossRef]
- Okamoto, K. Fundamentals of Optical Waveguides; Academic: San Diego, CA, USA, 2005. [Google Scholar]
- Agrawal, G.P. Applications of Nonlinear Fiber Optics; Academic: San Diego, CA, USA, 2001. [Google Scholar]
- Zheng, Y.; Yao, J.; Zhang, L.; Wang, Y.; Wen, W.; Zhou, R.; Di, Z.; Jing, L. Supermode analysis in multi-core photonic crystal fiber laser. Proc. SPIE 2010, 7843, 784316. [Google Scholar]
- Xia, C.; Bai, N.; Ozdur, I.; Zhou, X.; Li, G. Supermodes for optical transmission. Opt. Express 2011, 19, 16653–16664. [Google Scholar] [CrossRef]
- Chan, F.Y.M.; Lau, A.P.T.; Tam, H.Y. Mode coupling dynamics and communication strategies for multi-core fiber systems. Opt. Express 2012, 20, 4548–4563. [Google Scholar] [CrossRef]
- Ren, W.; Tan, Z. A study on the coupling coefficients for multi-core fibers. Optik 2016, 127, 3248–3252. [Google Scholar] [CrossRef]
- Zhou, J. Analytical formulation of super-modes inside multi-core fibers with circularly distributed cores. Opt. Express 2014, 22, 673–688. [Google Scholar] [CrossRef]
- Zhou, J. A non-orthogonal coupled mode theory for super-modes inside multi-core fibers. Opt. Express 2014, 22, 10815–10824. [Google Scholar] [CrossRef] [PubMed]
- Szostkiewicz, L.; Napierala, M.; Ziolowicz, A.; Pytel, A.; Tenderenda, T.; Nasilowski, T. Cross talk analysis in multicore optical fibers by supermode theory. Opt. Lett. 2016, 41, 3759–3762. [Google Scholar] [CrossRef] [PubMed]
- Bellanca, G.; Orlandi, P.; Bassi, P. Assessment of the orthogonal and non-orthogonal coupled-mode theory for parallel optical waveguide couplers. J. Opt. Soc. Am. A 2018, 35, 577–585. [Google Scholar] [CrossRef] [PubMed]
- COMSOL Multiphysics Software. Available online: https://cn.comsol.com/ (accessed on 9 November 2021).
- Lu, Y.; Huang, W.; Jian, S. Full vector complex coupled mode theory for tilted fiber gratings. Opt. Express 2010, 18, 713–726. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Chen, S.; Wang, Z.; Sun, B.; Wan, H.; Zhang, Z. Cylindrical vector beam fiber laser with a symmetric two-mode fiber coupler. Photonics Res. 2019, 7, 1479–1484. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, W.; Wang, F.; Ren, G. Mode Coupling Analysis for a Mode Selective Coupler Using the Supermode Theory. Photonics 2022, 9, 63. https://doi.org/10.3390/photonics9020063
Ren W, Wang F, Ren G. Mode Coupling Analysis for a Mode Selective Coupler Using the Supermode Theory. Photonics. 2022; 9(2):63. https://doi.org/10.3390/photonics9020063
Chicago/Turabian StyleRen, Wenhua, Fan Wang, and Guobin Ren. 2022. "Mode Coupling Analysis for a Mode Selective Coupler Using the Supermode Theory" Photonics 9, no. 2: 63. https://doi.org/10.3390/photonics9020063
APA StyleRen, W., Wang, F., & Ren, G. (2022). Mode Coupling Analysis for a Mode Selective Coupler Using the Supermode Theory. Photonics, 9(2), 63. https://doi.org/10.3390/photonics9020063



