Scanning Angle Magnification with Compact Reflective Optics for Light Detection and Ranging
Abstract
:1. Introduction
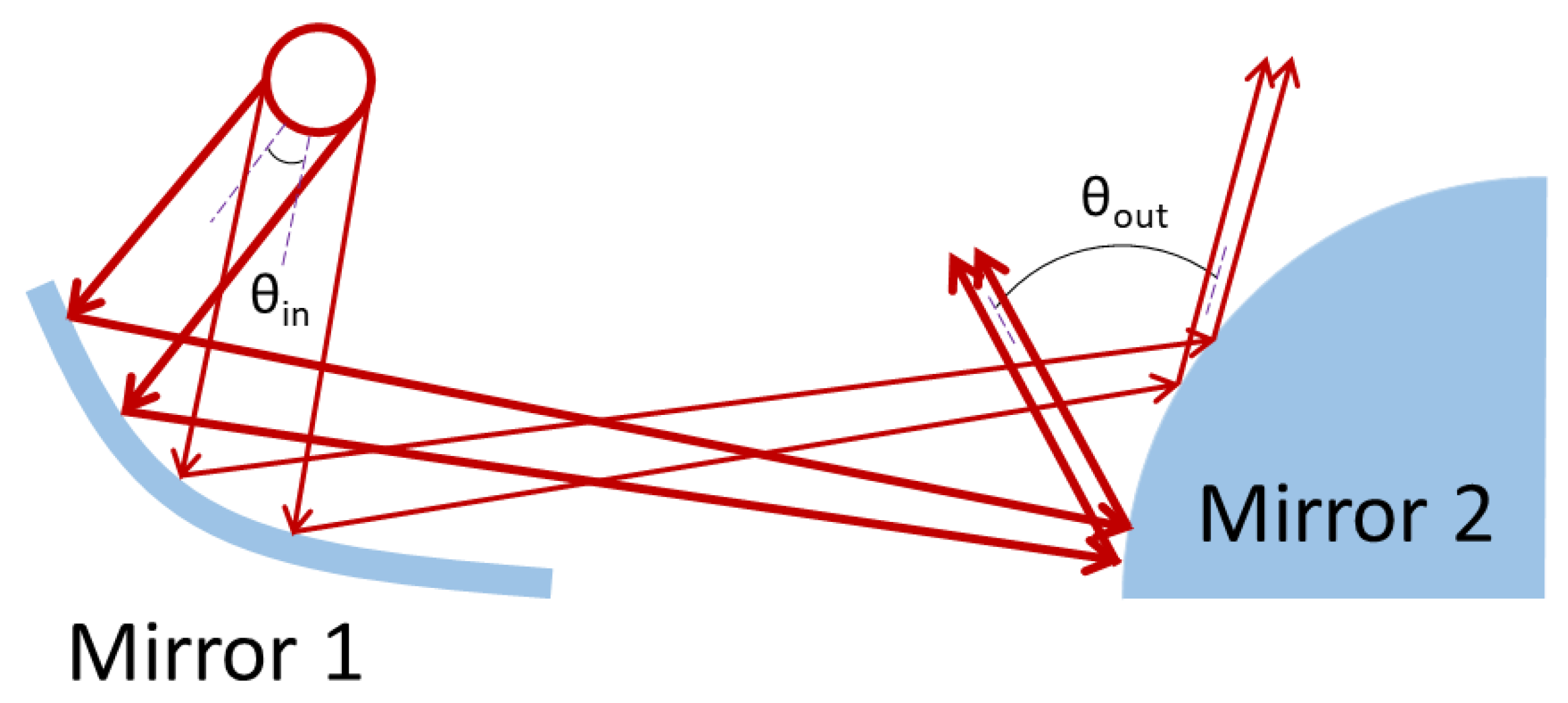
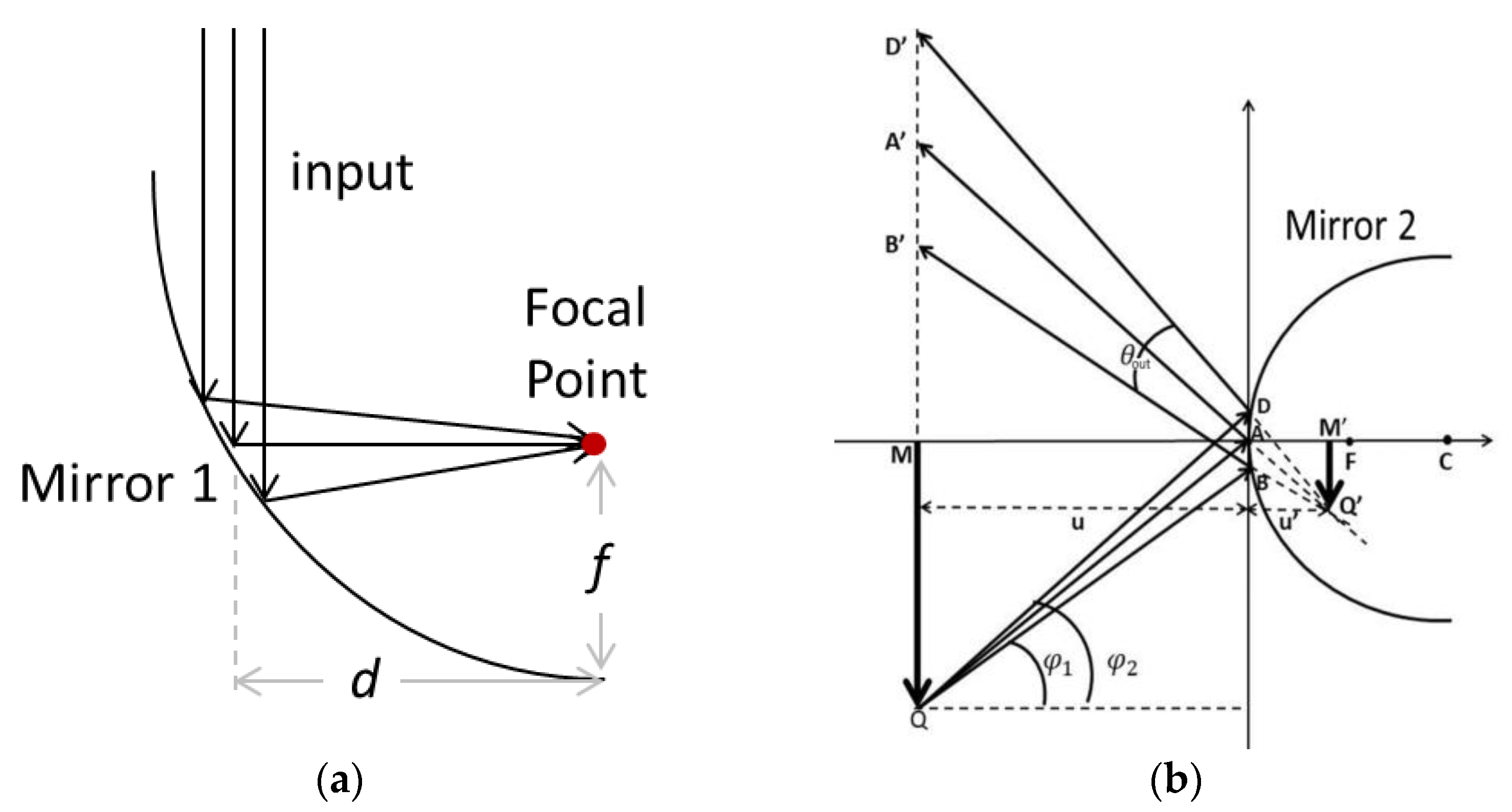
2. Conceptual Design of Scanning Angle Magnification with Reflective Optics
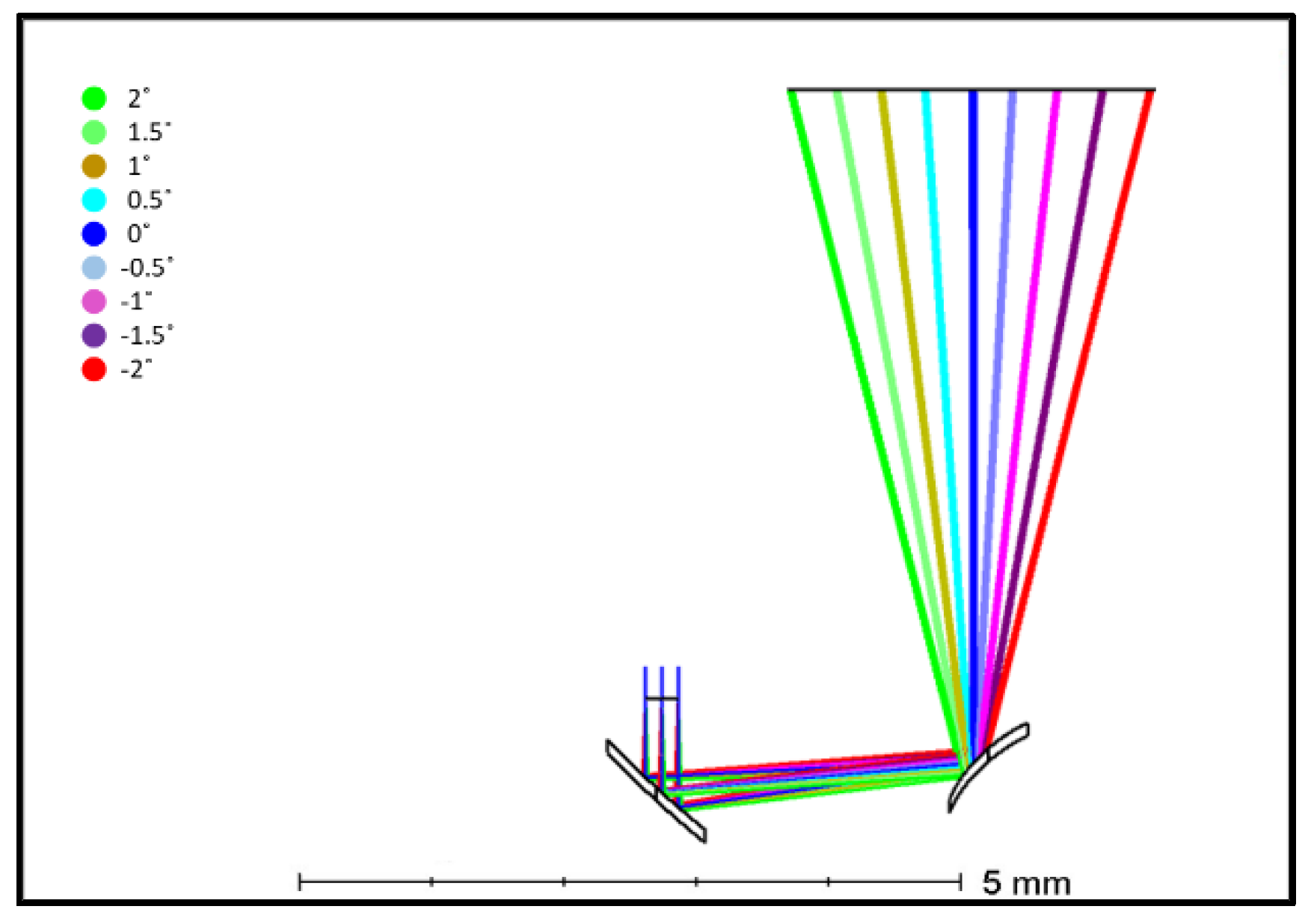
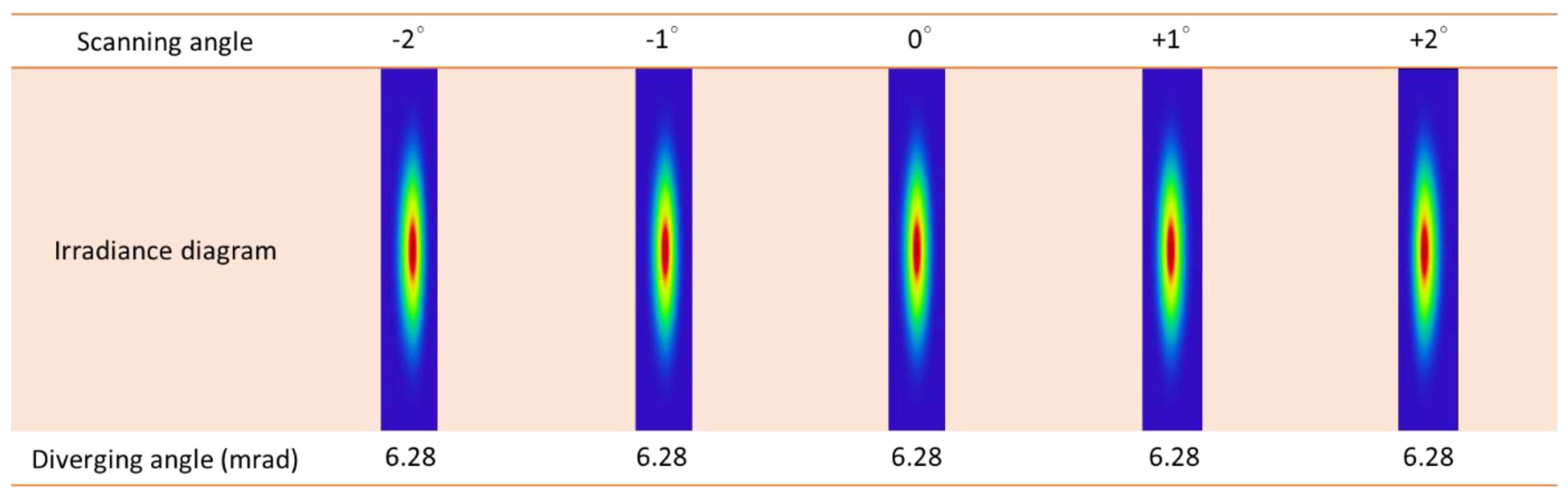
3. Optical Simulation and Optimization
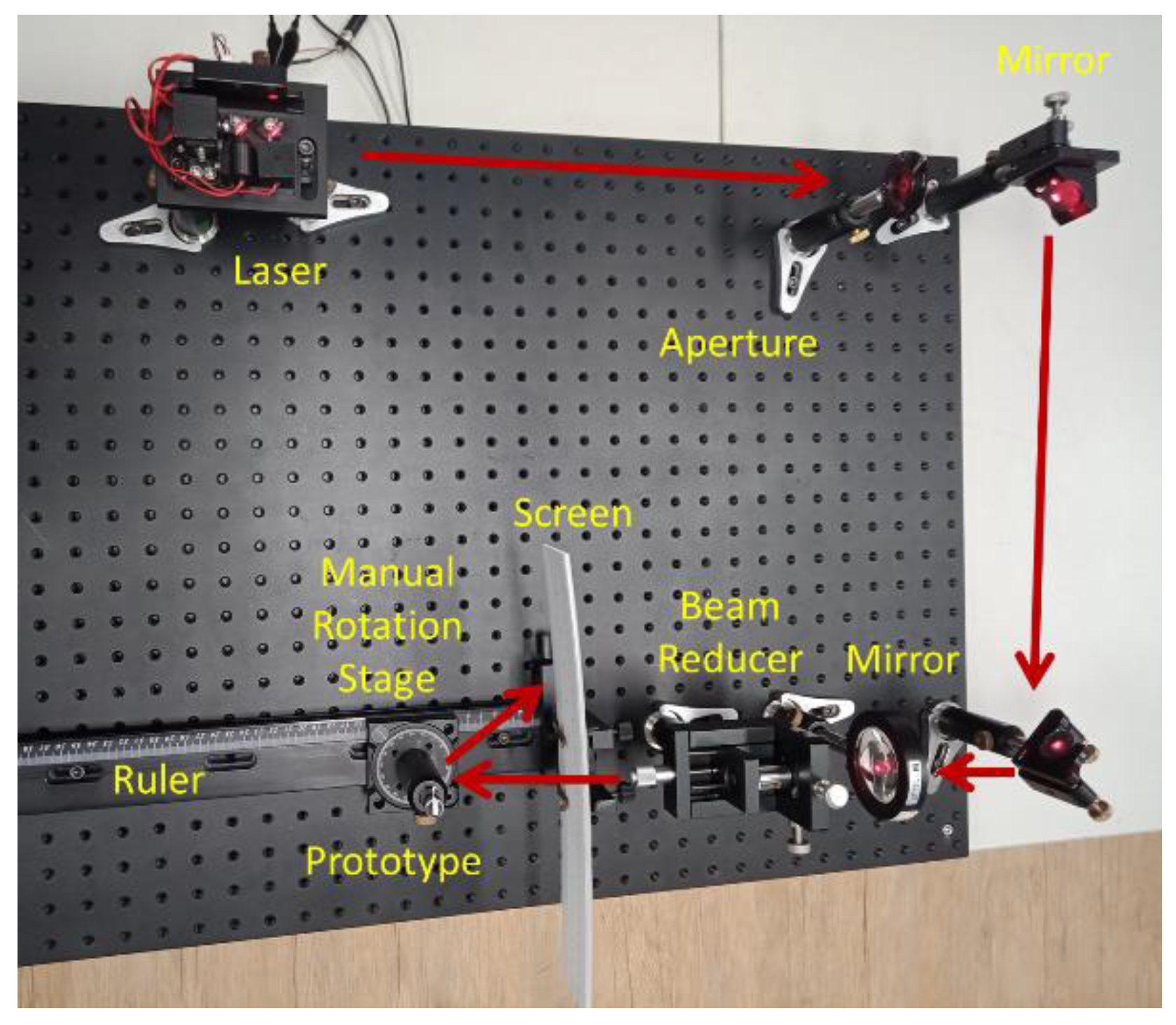
4. Prototype and Evaluation
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McManamon, P.F. LiDAR Technologies and Systems; SPIE Digital Library: Bellingham, WA, USA, 2019. [Google Scholar]
- Mehendale, N.; Neoge, S. Review on Lidar Technology. SSRN 2020. [Google Scholar] [CrossRef]
- Comerón, A.; Muñoz-Porcar, C.; Rocadenbosch, F.; Rodríguez-Gómez, A.; Sicard, M. Current Research in Lidar Technology Used for the Remote Sensing of Atmospheric Aerosols. Sensors 2017, 17, 1450. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Paul, A.; Chauhan, R.; Srivastava, R.; Baruah, M. Advanced Driver Assistance Systems. SAE Tech. Pap. 2016, 28, 0223. [Google Scholar]
- Jiménez, F.; Naranjo, J.E.; Anaya, J.J.; García, F.; Ponz, A.; Armingol, J.M. Advanced Driver Assistance System for Road Environments to Improve Safety and Efficiency. Transp. Res. Procedia 2016, 14, 2245–2254. [Google Scholar] [CrossRef] [Green Version]
- Lu, M.; Wevers, K.; van der Heijden, R. Technical feasibility of advanced driver assistance systems (ADAS) for road traffic safety. Transp. Plan. Technol. 2005, 28, 167–187. [Google Scholar] [CrossRef] [Green Version]
- Kumar, A.M.; Simon, P. Review of lane detection and tracking algorithms in advanced driver assistance system. Int. J. Comput. Sci. Inf. Technol. 2015, 7, 65–78. [Google Scholar] [CrossRef]
- Royo, S.; Ballesta-Garcia, M. An Overview of Lidar Imaging Systems for Autonomous Vehicles. Appl. Sci. 2019, 9, 4093. [Google Scholar] [CrossRef] [Green Version]
- Woodside Capital Partners & Yole Développement. Automotive LiDAR Market Report; OIDA Publications & Reports; Optical Society of America: Washington, DC, USA, 2018. [Google Scholar]
- Schoonover, D. The Driverless Car Is Closer Than You Think—And I Can’t Wait; Forbes: Randall Lane, NJ, USA, 2019. [Google Scholar]
- Schwarz, B. Mapping the world in 3D. Nat. Photon 2010, 4, 429–430. [Google Scholar] [CrossRef]
- Raj, T.; Hashim, F.H.; Huddin, A.B.; Ibrahim, M.F.; Hussain, A. A Survey on LiDAR Scanning Mechanisms. Electronics 2020, 9, 741. [Google Scholar] [CrossRef]
- Heck, M.J.R. Highly integrated optical phased arrays: Photonic integrated circuits for optical beam shaping and beam steering. Nanophotonics 2017, 6, 93–107. [Google Scholar] [CrossRef]
- Abediasl, H.; Hashemi, H. Monolithic optical phased-array transceiver in a standard SOI CMOS process. Opt. Express 2015, 23, 6509–6519. [Google Scholar] [CrossRef] [PubMed]
- Poulton, C.V.; Yaacobi, A.; Cole, D.B.; Byrd, M.J.; Raval, M.; Vermeulen, D.; Watts, M.R. Coherent solid-state LIDAR with silicon photonic optical phased arrays. Opt. Lett. 2017, 42, 4091–4094. [Google Scholar] [CrossRef] [PubMed]
- Hsu, C.-P.; Li, B.; Solano-Rivas, B.; Gohil, A.R.; Chan, P.H.; Moore, A.D.; Donzella, V. A Review and Perspective on Optical Phased Array for Automotive LiDAR. IEEE J. Sel. Top. Quantum Electron. 2021, 27, 1–16. [Google Scholar] [CrossRef]
- Sun, J.; Timurdogan, E.; Yaacobi, A.; Hosseini, E.S.; Watts, M.R. Large-scale nanophotonic phased array. Nature 2013, 493, 195–199. [Google Scholar] [CrossRef]
- Guo, W.; Binetti, P.R.; Althouse, C.; Mašanović, M.L.; Ambrosius, H.P.; Johansson, L.A.; Coldren, L.A. Two-Dimensional Optical Beam Steering with InP-Based Photonic Integrated Circuits. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 6100212. [Google Scholar]
- Hulme, J.C.; Doylend, J.K.; Heck, M.J.R.; Peters, J.D.; Davenport, M.L.; Bovington, J.T.; Coldren, L.A.; Bowers, J.E. Fully integrated hybrid silicon free-space beam steering source with 32-channel phased array. SPIE Proc. 2014, 8989, 898907–898921. [Google Scholar]
- Demersseman, B.; Hansson, P.; Hällstig, E. Detection system with reflection member and offset detection array. US20190101645A1, 4 April 2019. [Google Scholar]
- Lee, X.; Wang, C. Optical design for uniform scanning in MEMS-based 3D imaging lidar. Appl. Opt. 2015, 54, 2219–2223. [Google Scholar] [CrossRef] [PubMed]
- Lee, X.; Wang, C.; Luo, Z.; Li, S. Optical design of a new folding scanning system in MEMS-based lidar. Opt. Laser Technol. 2020, 125, 106013–106020. [Google Scholar] [CrossRef]





| d | θin | u |
|---|---|---|
| 3.5 mm | 4 | 1 mm |
| Configuration No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Input angle (°) | −2 | −1.5 | −1 | −0.5 | 0 | 0.5 | 1 | 1.5 | 2 |
| Scanning angle (°) | −14 | −10.5 | −7 | −3.5 | 0 | 3.5 | 7 | 10.5 | 14 |
| Mirror No. | Surface Type | Radius | Conic | X Radius | X Conic |
|---|---|---|---|---|---|
| 1 | Biconic Zernike | −4.781 | −1 | −55 | −1 |
| 2 | Biconic Zernike | −0.633 | −0.357 | −104.397 | −264.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mu, C.-T.; Chang, P.-C.; Chen, C.-H. Scanning Angle Magnification with Compact Reflective Optics for Light Detection and Ranging. Photonics 2022, 9, 59. https://doi.org/10.3390/photonics9020059
Mu C-T, Chang P-C, Chen C-H. Scanning Angle Magnification with Compact Reflective Optics for Light Detection and Ranging. Photonics. 2022; 9(2):59. https://doi.org/10.3390/photonics9020059
Chicago/Turabian StyleMu, Cheng-Ta, Po-Cheng Chang, and Cheng-Huan Chen. 2022. "Scanning Angle Magnification with Compact Reflective Optics for Light Detection and Ranging" Photonics 9, no. 2: 59. https://doi.org/10.3390/photonics9020059
APA StyleMu, C.-T., Chang, P.-C., & Chen, C.-H. (2022). Scanning Angle Magnification with Compact Reflective Optics for Light Detection and Ranging. Photonics, 9(2), 59. https://doi.org/10.3390/photonics9020059





