Unveiling the Role of the Beam Shape in Photothermal Beam Deflection Measurements: A 1D and 2D Complex Geometrical Optics Model Approach
Abstract
1. Introduction
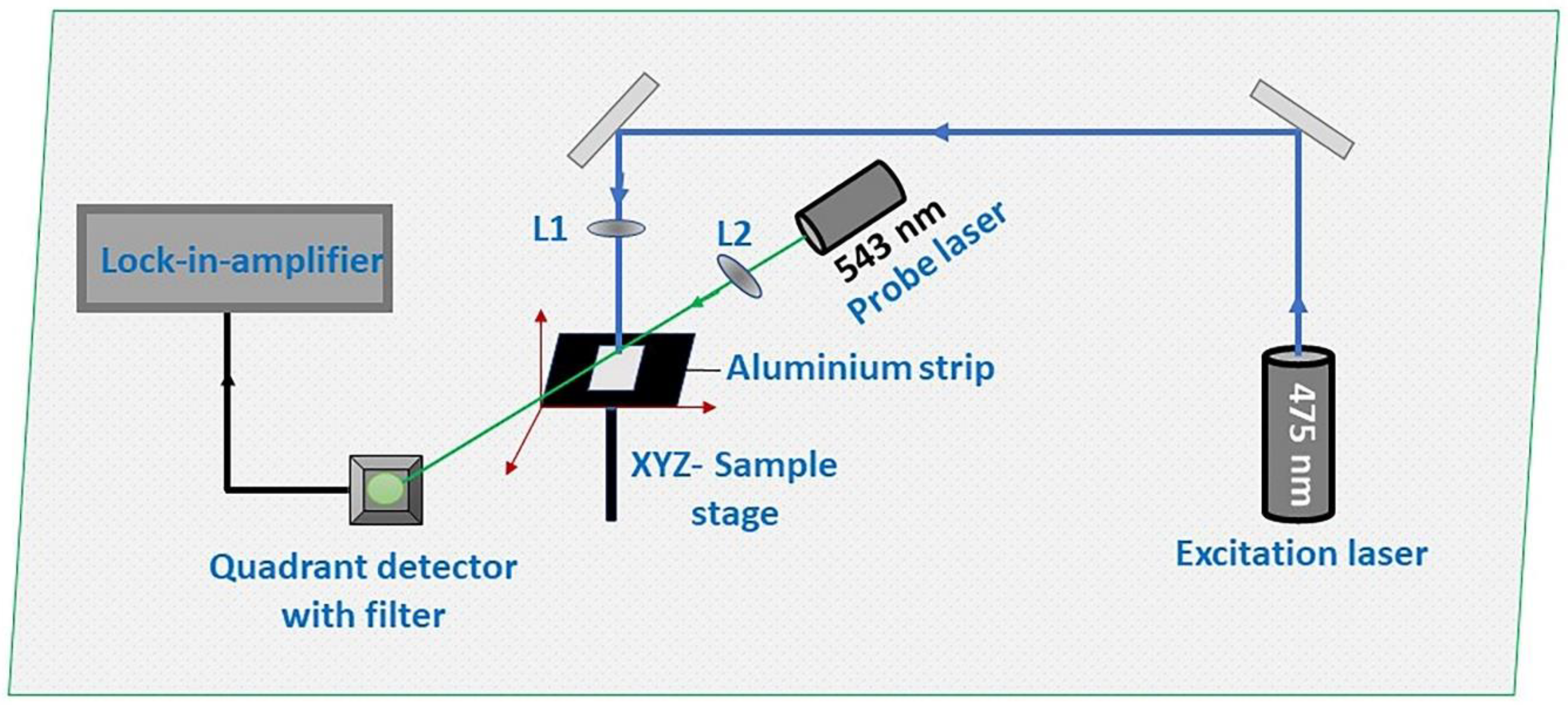
2. Experimental Section
3. Theory
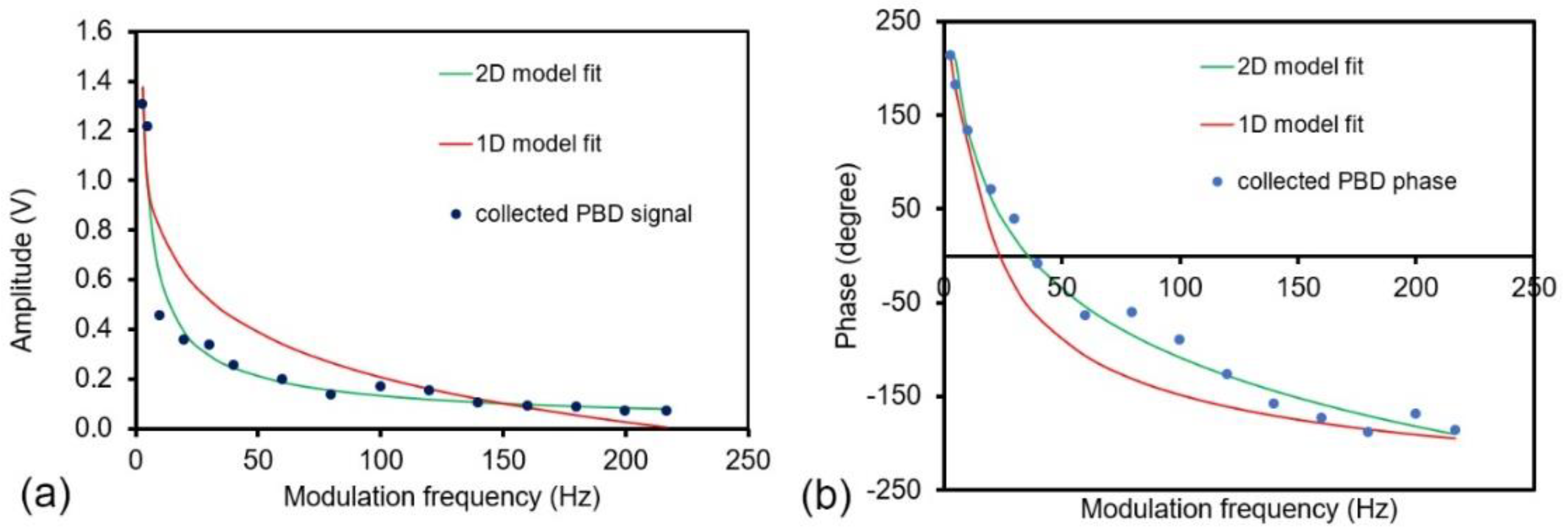
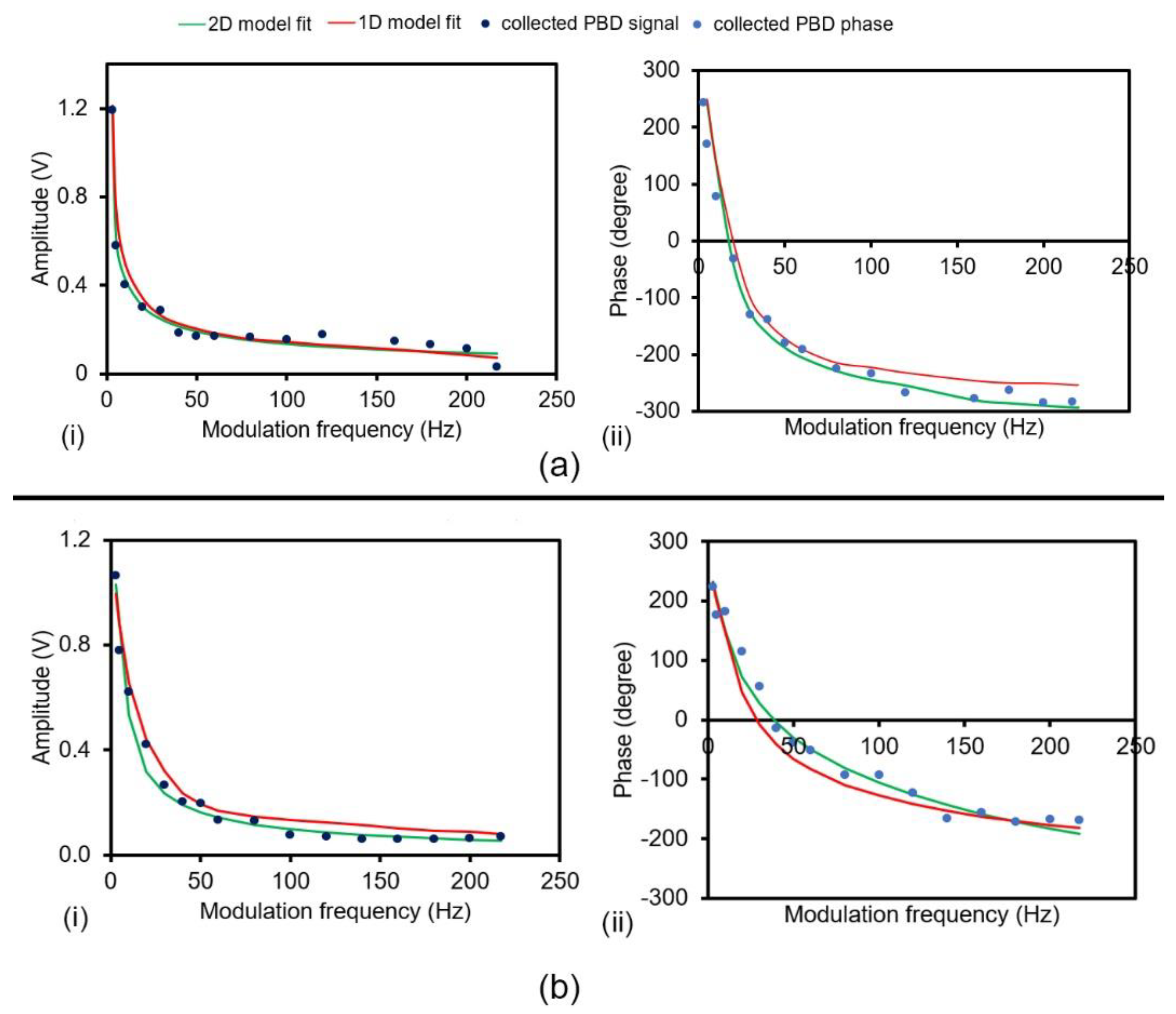
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Fourmaux, S.; Payeur, S.; Alexandrov, A.; Serbanescu, C.; Martin, F.; Ozaki, T.; Kudryashov, A.; Kieffer, J.C. Laser Beam Wavefront Correction for Ultra High Intensities with the 200 TW Laser System at the Advanced Laser Light Source. Opt. Express 2008, 16, 11987. [Google Scholar] [CrossRef] [PubMed]
- Samelsohn, G.; Mazar, R. Adaptive Wavefront Tilt Correction for Imaging and Laser Beam Formation in a Turbulent Atmosphere. In Proceedings of the 1995 International Geoscience and Remote Sensing Symposium, IGARSS ’95. Quantitative Remote Sensing for Science and Applications, Firenze, Italy, 10–14 July 1995; Volume 3, pp. 1941–1943. [Google Scholar]
- Huot, N.; Jonathan, J.-M.C.; Roosen, G. Dynamic Wavefront Correction of Nd:YAG Lasers by Self-Pumped Phase Conjugation in Photorefractive BaTiO/Sub 3/:Rh. Proc. IEEE 1999, 87, 2059–2073. [Google Scholar] [CrossRef]
- Salter, P.S.; Booth, M.J. Adaptive Optics in Laser Processing. Light Sci. Appl. 2019, 8, 110. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Zhong, L.; Min, L.; Wang, J.; Wu, Y.; Chen, K.; Wei, K.; Rao, C. Adaptive Optics Based on Machine Learning: A Review. Opto-Electron. Adv. 2022, 5, 200082. [Google Scholar] [CrossRef]
- Rukosuev, A.L.; Kudryashov, A.V.; Lylova, A.N.; Samarkin, V.V.; Sheldakova, Y.V. Adaptive Optics System for Real-Time Wavefront Correction. Atmos. Ocean. Opt. 2015, 28, 381–386. [Google Scholar] [CrossRef]
- Ribak, E. Atmospheric Turbulence, Speckle, and Adaptive Optics. Ann. N. Y. Acad. Sci. 1997, 808, 193–204. [Google Scholar] [CrossRef]
- Qin, Z.; She, Z.; Chen, C.; Wu, W.; Lau, J.K.Y.; Ip, N.Y.; Qu, J.Y. Deep Tissue Multi-Photon Imaging Using Adaptive Optics with Direct Focus Sensing and Shaping. Nat. Biotechnol. 2022, 40, 1663–1671. [Google Scholar] [CrossRef]
- Hampson, K.M.; Turcotte, R.; Miller, D.T.; Kurokawa, K.; Males, J.R.; Ji, N.; Booth, M.J. Adaptive Optics for High-Resolution Imaging. Nat. Rev. Methods Prim. 2021, 1, 68. [Google Scholar] [CrossRef]
- Shealy, D.L. Historical Perspective of Laser Beam Shaping. In Proceedings of the Laser Beam Shaping III, Seattle, WA, USA, 28 October 2002; Volume 4770, pp. 28–47. [Google Scholar]
- Paschotta, R. Field Guide to Lasers; SPIE press: Bellingham, WA, USA, 2008; Volume 12, p. 9610. ISBN 081946. [Google Scholar]
- Mielec, N.; Altorio, M.; Sapam, R.; Horville, D.; Holleville, D.; Sidorenkov, L.A.; Landragin, A.; Geiger, R. Atom Interferometry with Top-Hat Laser Beams. Appl. Phys. Lett. 2018, 113, 161108. [Google Scholar] [CrossRef]
- Hou, Z.; Afgan, M.S.; Sheta, S.; Liu, J.; Wang, Z. Plasma Modulation Using Beam Shaping to Improve Signal Quality for Laser Induced Breakdown Spectroscopy. J. Anal. At. Spectrom. 2020, 35, 1671–1677. [Google Scholar] [CrossRef]
- Shen, S.; Yang, Z.-J.; Pang, Z.-G.; Ge, Y.-R. The Complex-Valued Astigmatic Cosine-Gaussian Soliton Solution of the Nonlocal Nonlinear Schrödinger Equation and Its Transmission Characteristics. Appl. Math. Lett. 2022, 125, 107755. [Google Scholar] [CrossRef]
- Shen, S.; Yang, Z.; Li, X.; Zhang, S. Periodic Propagation of Complex-Valued Hyperbolic-Cosine-Gaussian Solitons and Breathers with Complicated Light Field Structure in Strongly Nonlocal Nonlinear Media. Commun. Nonlinear Sci. Numer. Simul. 2021, 103, 106005. [Google Scholar] [CrossRef]
- Li, B.; Blaschke, H.; Ristau, D. Pulsed Photothermal Deflection with a Top-Hat Beam Excitation. J. Appl. Phys. 2006, 100, 053509. [Google Scholar] [CrossRef]
- Astrath, F.B.; Astrath, N.G.; Shen, J.; Zhou, J.; Malacarne, L.C.; Pedreira, P.R.B.; Baesso, M.L. Time-Resolved Thermal Mirror Technique with Top-Hat Cw Laser Excitation. Opt. Express 2008, 16, 12214. [Google Scholar] [CrossRef] [PubMed]
- Astrath, N.G.C.; Astrath, F.B.G.; Shen, J.; Zhou, J.; Gu, C.E.; Malacarne, L.C.; Pedreira, P.R.B.; Bento, A.C.; Baesso, M.L. Top-Hat Cw Laser Induced Thermal Mirror: A Complete Model for Material Characterization. Appl. Phys. B 2009, 94, 473–481. [Google Scholar] [CrossRef][Green Version]
- Liu, M.; Li, B.; Hao, H. Comparison of Signals under Top-Hat and Gaussian Beam Excitations in Surface Thermal Lens Technique. In Proceedings of the Optical Design and Testing III, Beijing, China, 28 November 2007; p. 68342D. [Google Scholar]
- Li, B.; Xiong, S.; Zhang, Y. Fresnel Diffraction Model for Mode-Mismatched Thermal Lens with Top-Hat Beam Excitation. Appl. Phys. B 2005, 80, 527–534. [Google Scholar] [CrossRef]
- Pawlak, M.; Kruck, T.; Spitzer, N.; Dziczek, D.; Ludwig, A.; Wieck, A.D. Experimental Validation of Formula for Calculation Thermal Diffusivity in Superlattices Performed Using a Combination of Two Frequency-Domain Methods: Photothermal Infrared Radiometry and Thermoreflectance. Appl. Sci. 2021, 11, 6125. [Google Scholar] [CrossRef]
- Boccara, A.C.; Jackson, W.; Amer, N.M.; Fournier, D. Sensitive Photothermal Deflection Technique for Measuring Absorption in Optically Thin Media. Opt. Lett. 1980, 5, 377. [Google Scholar] [CrossRef]
- Yun, S.I.; Seo, H.J. Photothermal Beam Deflection Technique for the Study of Solids? Chin. J. Phys. 1992, 30, 753–767. [Google Scholar]
- Cabrera, H.; Korte, D.; Budasheva, H.; Asbaghi, B.A.N.; Bellucci, S. Through-Plane and in-Plane Thermal Diffusivity Determination of Graphene Nanoplatelets by Photothermal Beam Deflection Spectrometry. Materials 2021, 14, 7273. [Google Scholar] [CrossRef]
- Vodišek, N.; Šuligoj, A.; Korte, D.; Štangar, U.L. Transparent Photocatalytic Thin Films on Flexible Polymer Substrates. Materials 2018, 11, 1945. [Google Scholar] [CrossRef] [PubMed]
- Soumya, S.; Arun Kumar, R.; Raj, V.; Swapna, M.S.; Sankararaman, S. Thermal Diffusivity of Molybdenum Oxide Nanowire Film: A Photothermal Beam Deflection Study. Opt. Laser Technol. 2021, 139, 106993. [Google Scholar] [CrossRef]
- Sell, J. Photothermal Investigations of Solids and Fluids, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2012; ISBN 0323154220. [Google Scholar]
- Korte, D.; Franko, M. Photothermal Deflection Experiments: Comparison of Existing Theoretical Models and Their Applications to Characterization of TiO2-Based Thin Films. Int. J. Thermophys. 2014, 35, 2352–2362. [Google Scholar] [CrossRef]
- Soumya, S.; Raj, V.; Swapna, M.S.; Sankararaman, S. Thermal Diffusivity Downscaling of Molybdenum Oxide Thin Film through Annealing Temperature-Induced Nano-Lamelle Formation: A Photothermal Beam Deflection Study. Eur. Phys. J. Plus 2021, 136, 187. [Google Scholar] [CrossRef]
- Budasheva, H.; Kravos, A.; Korte, D.; Bratkič, A.; Gao, Y.; Franko, M. Determination of Dissolved Iron Redox Species in Freshwater Sediment Using DGT Technique Coupled to BDS. Acta Chim. Slov. 2019, 66, 239–246. [Google Scholar] [CrossRef]
- Proskurnin, M.A.; Korte, D.; Rogova, O.B.; Volkov, D.S.; Franko, M. Photothermal Beam Deflection Spectroscopy for the Determination of Thermal Diffusivity of Soils and Soil Aggregates. Int. J. Thermophys. 2018, 39, 81. [Google Scholar] [CrossRef]
- Li, B.; Welsch, E. Probe-Beam Diffraction in a Pulsed Top-Hat Beam Thermal Lens with a Mode-Mismatched Configuration. Appl. Opt. 1999, 38, 5241. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Chen, X.; Gong, Y. Analysis of Surface Thermal Lens Signal in Optical Coatings with Top-Hat Beam Excitation. J. Appl. Phys. 2008, 103, 033518. [Google Scholar] [CrossRef]
- Touloukian, Y.S.; Powell, R.W.; Ho, C.Y.; Klemens, P.G. Thermophysical Properties of Matter-the TPRC Data Series. In Thermal Conductivity-Metallic Elements and Alloys (Reannouncement); Data Book; Purdue University, Thermophysical and Electronic Properties Information Center: Lafayette, IN, USA, 1970; Volume 1. [Google Scholar]
- Omini, M.; Sparavigna, A.; Strigazzi, A. Dilatometric Determination of Thermal Diffusivity in Low Conducting Materials. Meas. Sci. Technol. 1990, 1, 166–171. [Google Scholar] [CrossRef]
- Instruments, T.T. Materials Thermal Properties Database. Available online: https://thermtest.com/thermal-resources/materials-database (accessed on 25 November 2022).
- Aamodt, L.C.; Murphy, J.C. Photothermal Measurements Using a Localized Excitation Source. J. Appl. Phys. 1981, 52, 4903–4914. [Google Scholar] [CrossRef]
- Aamodt, L.C.; Murphy, J.C. Thermal Effects in Photothermal Spectroscopy and Photothermal Imaging. J. Appl. Phys. 1983, 54, 581–591. [Google Scholar] [CrossRef]
- Glazov, A.L.; Muratikov, K.L. Calculation of the Photodeflection Signal in the Framework of Wave Optics. Technol. Phys. 1993, 38, 344–347. [Google Scholar]
- Glazov, A.L.; Muratikov, K.L. Photodeflection and Interferometric Thermal Wave Microscopy of Solids. Int. J. Optoelectron. 1989, 4, 589–597. [Google Scholar]
- Kobylinska, D.K.; Bukowski, R.J.; Burak, B.; Bodzenta, J.; Kochowski, S. The Complex Ray Theory of Photodeflection Signal Formation: Comparison with the Ray Theory and the Experimental Results. J. Appl. Phys. 2006, 100, 063501. [Google Scholar] [CrossRef]
- Bukowski, R.J.; Korte, D. Perturbation Calculus for Eikonal Application to Analysis of the Deflectional Signal in Photothermal Measurements. Opt. Appl. 2002, 32, 817–828. [Google Scholar]
- Kobylińska, D.K.; Bukowski, R.J.; Bodzenta, J.; Kochowski, S. Thermal Parameters of Solids Determination by the Photodeflection Method—Theories and Experiment Comparison. Opt. Appl. 2008, 38, 445–458. [Google Scholar]
- Kobylińska, D.K.; Bukowski, R.J.; Burak, B.; Bodzenta, J.; Kochowski, S. Photodeflection Signal Formation in Photothermal Measurements: Comparison of the Complex Ray Theory, the Ray Theory, the Wave Theory, and Experimental Results. Appl. Opt. 2007, 46, 5216–5227. [Google Scholar] [CrossRef]
- Lobemeier, M.L. Linearization Plots: Time for Progress in Regression. HMS Beagle 2000, 3, 73. Available online: https://nanopdf.com/download/linearization-plots_pdf (accessed on 25 November 2022).
- Strak, K.; Piasecka, M.; Maciejewska, B. Comparison of the 1D and 2D Calculation Models Used for Determination of the Heat Transfer Coefficient during Flow Boiling Heat Transfer in a Minichannel. E3S Web Conf. 2019, 128, 01017. [Google Scholar] [CrossRef]
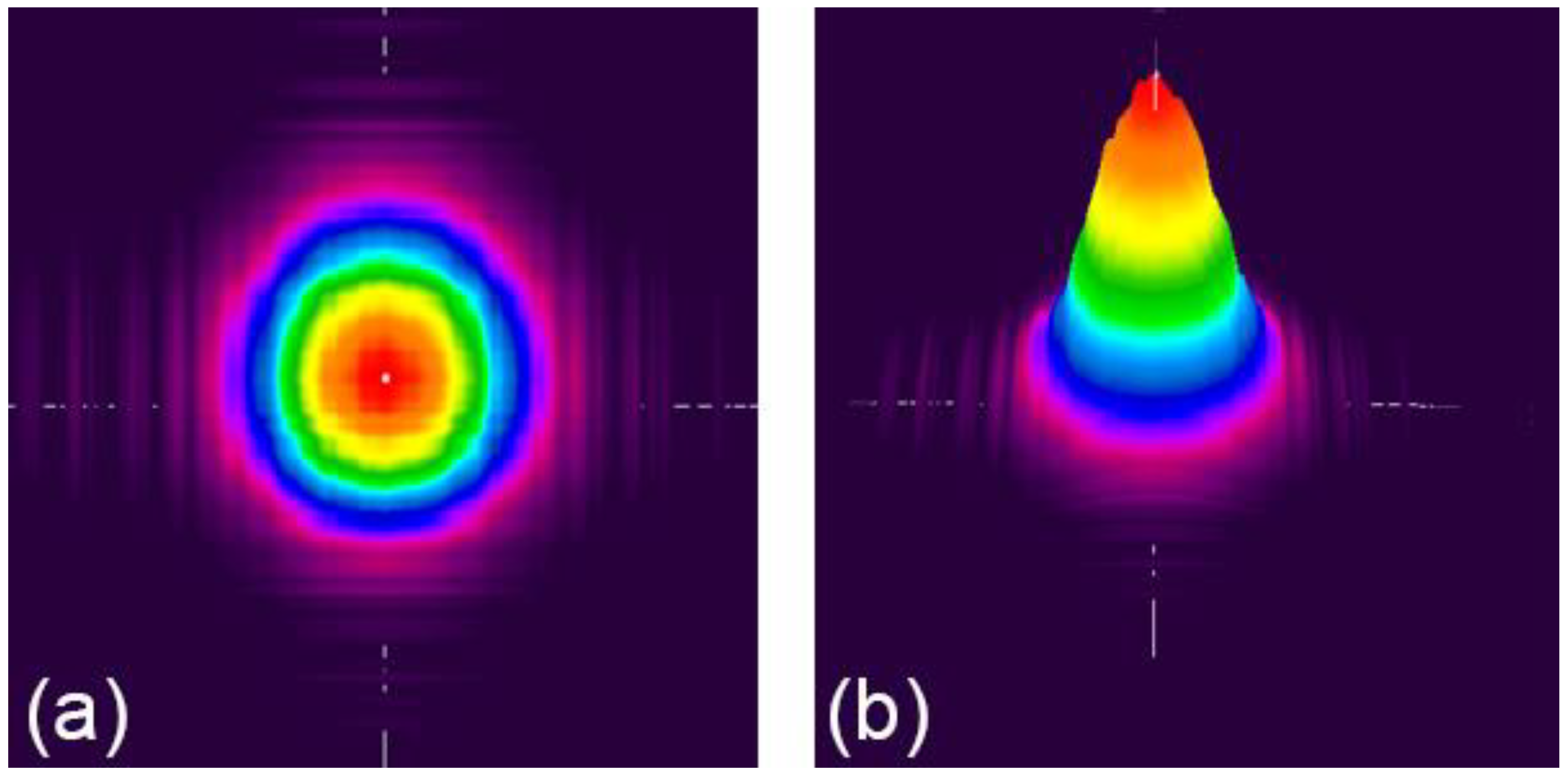
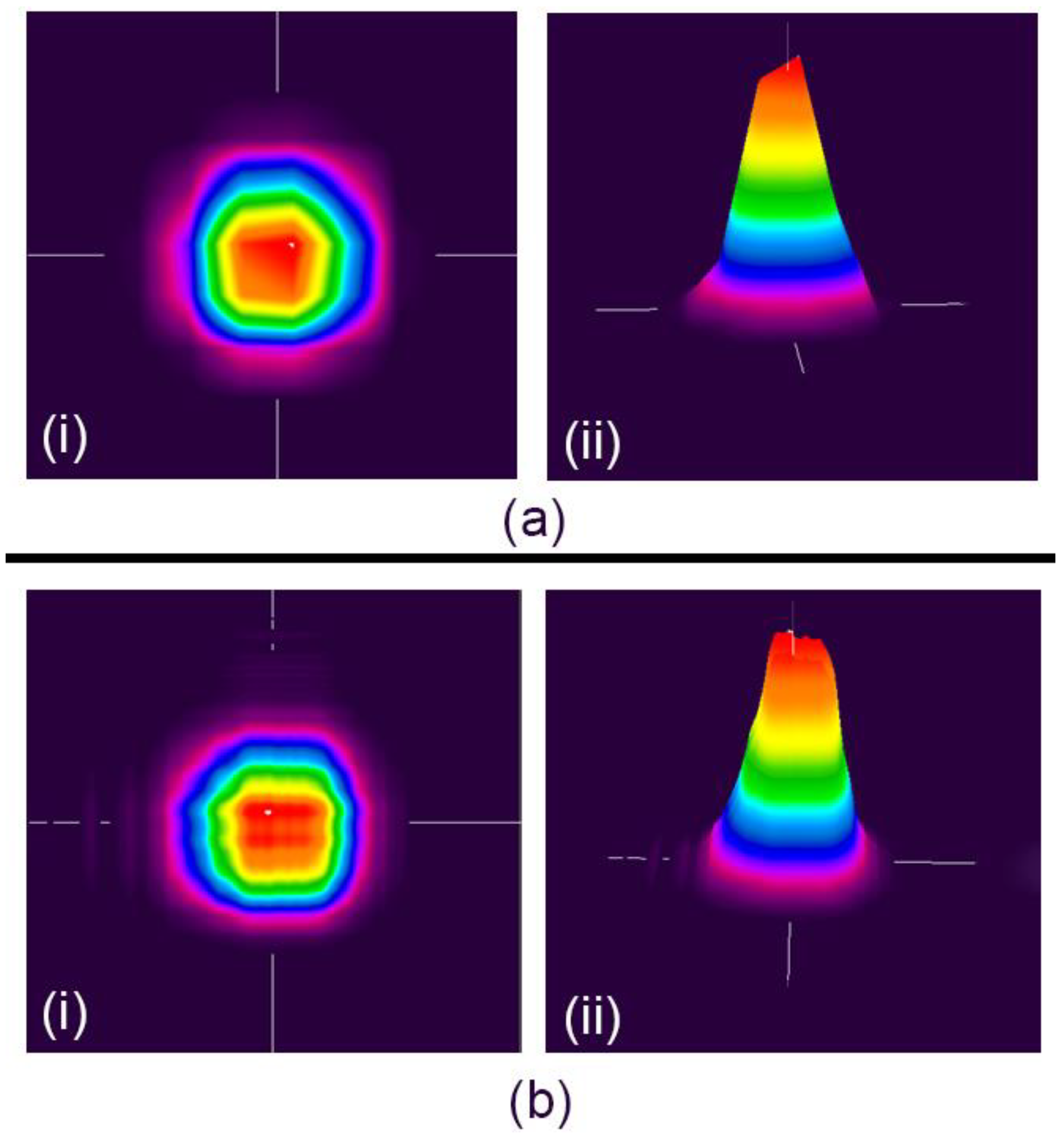

| Lens Position, cm | PuB Radius, μm | PuB/PrB Ratio |
|---|---|---|
| 4.7 | 259 | 9.6 |
| 4.8 | 173 | 6.4 |
| 4.9 | 86 | 3.2 |
| 5.0 | 36 | 1.4 |
| 5.1 | 86 | 3.2 |
| 5.2 | 173 | 6.4 |
| 5.3 | 259 | 9.6 |
| 1D Theoretical Model | 2D Theoretical Model | |||
|---|---|---|---|---|
| Lens Position (cm) | DT (×10−2 cm2 s−1) | kT (W m−1 K−1) | DT (×10−2 cm2 s−1) | kT (W m−1 K−1) |
| 4.7 | 94 ± 5 | 243 ± 12 | 92 ± 3 | 238 ± 7 |
| 4.8 | 89 ± 7 | 228 ± 15 | 93 ± 3 | 239 ± 8 |
| 4.9 | 112 ± 9 | 278 ± 22 | 97 ± 4 | 249 ± 8 |
| 5.0 | 125 ± 9 | 312 ± 25 | 95 ± 4 | 241 ± 7 |
| 5.1 | 108 ± 8 | 271 ± 21 | 92 ± 3 | 237 ± 6 |
| 5.2 | 87 ± 7 | 226 ± 16 | 92 ± 2 | 234 ± 6 |
| 5.3 | 95 ± 5 | 244 ± 12 | 93 ± 3 | 240 ± 5 |
| Lens Position, cm | σDT, % | σkT, % |
|---|---|---|
| 4.7 | 2 | 2 |
| 4.8 | 5 | 4 |
| 4.9 | 18 | 16 |
| 5.0 | 32 | 30 |
| 5.1 | 16 | 17 |
| 5.2 | 4 | 4 |
| 5.3 | 2 | 2 |
| 1D Theoretical Model | ||||
|---|---|---|---|---|
| Lens Position, (cm) | RSDDT (%) | RSDkT (%) | Sum of Amplitude Residues (V) | Sum of Phase Residues (Degree) |
| 4.7 | 5.3 | 4.9 | 0.585 | 193 |
| 4.8 | 7.9 | 6.6 | 0.783 | 234 |
| 4.9 | 8.1 | 7.9 | 1.277 | 289 |
| 5.0 | 7.2 | 8.0 | 1.992 | 304 |
| 5.1 | 7.4 | 7.8 | 1.432 | 295 |
| 5.2 | 8.0 | 7.1 | 0.806 | 262 |
| 5.3 | 5.6 | 5.4 | 0.531 | 241 |
| 2D Theoretical Model | ||||
| Lens Position, (cm) | RSDDT (%) | RSDkT (%) | Sum of Amplitude Residues (V) | Sum of Phase Residues (Degree) |
| 4.7 | 3.3 | 2.9 | 0.443 | 158 |
| 4.8 | 3.2 | 3.3 | 0.285 | 112 |
| 4.9 | 4.1 | 3.2 | 0.322 | 118 |
| 5.0 | 4.2 | 2.9 | 0.413 | 151 |
| 5.1 | 3.3 | 2.6 | 0.387 | 124 |
| 5.2 | 2.2 | 2.6 | 0.436 | 153 |
| 5.3 | 3.2 | 2.1 | 0.279 | 103 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Swapna, M.N.S.; Korte, D.; Sankararaman, S.I. Unveiling the Role of the Beam Shape in Photothermal Beam Deflection Measurements: A 1D and 2D Complex Geometrical Optics Model Approach. Photonics 2022, 9, 991. https://doi.org/10.3390/photonics9120991
Swapna MNS, Korte D, Sankararaman SI. Unveiling the Role of the Beam Shape in Photothermal Beam Deflection Measurements: A 1D and 2D Complex Geometrical Optics Model Approach. Photonics. 2022; 9(12):991. https://doi.org/10.3390/photonics9120991
Chicago/Turabian StyleSwapna, Mohanachandran Nair Sindhu, Dorota Korte, and Sankaranarayana Iyer Sankararaman. 2022. "Unveiling the Role of the Beam Shape in Photothermal Beam Deflection Measurements: A 1D and 2D Complex Geometrical Optics Model Approach" Photonics 9, no. 12: 991. https://doi.org/10.3390/photonics9120991
APA StyleSwapna, M. N. S., Korte, D., & Sankararaman, S. I. (2022). Unveiling the Role of the Beam Shape in Photothermal Beam Deflection Measurements: A 1D and 2D Complex Geometrical Optics Model Approach. Photonics, 9(12), 991. https://doi.org/10.3390/photonics9120991







