Laser Driven Electron Acceleration from Near-Critical Density Targets towards the Generation of High Energy γ-Photons
Abstract
1. Introduction
| Author | Target | Target Density | Laser Intensity [ W/cm] | Conversion to -Photons Coefficient |
|---|---|---|---|---|
| Zhang et al. 2022 [4] | cone | exponential from to | ||
| Wang et al. 2020 [9] | cylindrical channel | channel: bulk: | ||
| Martinez et al. 2020 [15] | plasma | |||
| Brady et al. 2012 [16] | plastic | |||
| Stark et al. 2016 [17] | cylindrical channel | channel: bulk: | ||
| Hadjisolomou et al. 2022 [18] | Lithium foil | |||
| Ridgers et al. 2012 [7] | Aluminium foil | |||
| Lobet et al. 2015 [19] | Aluminium foil | |||
| Ji et al. 2014 [5] | Hydrogen plasma |
2. High Energy Radiation Emitted by the Energetic Electrons
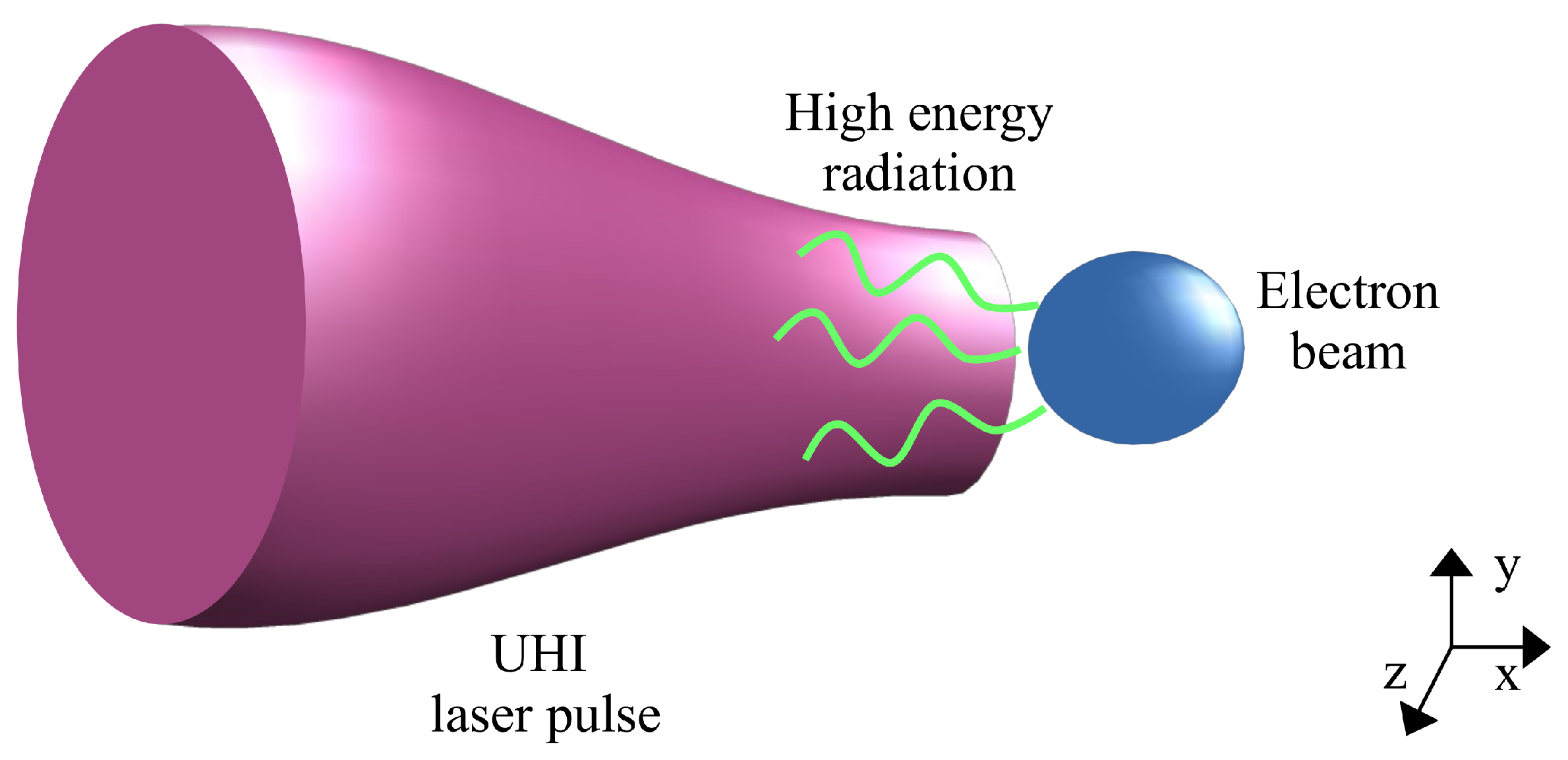
2.1. Laser-Electron Beam Interaction
2.2. Laser–Plasma Interaction
3. Results and Discussion
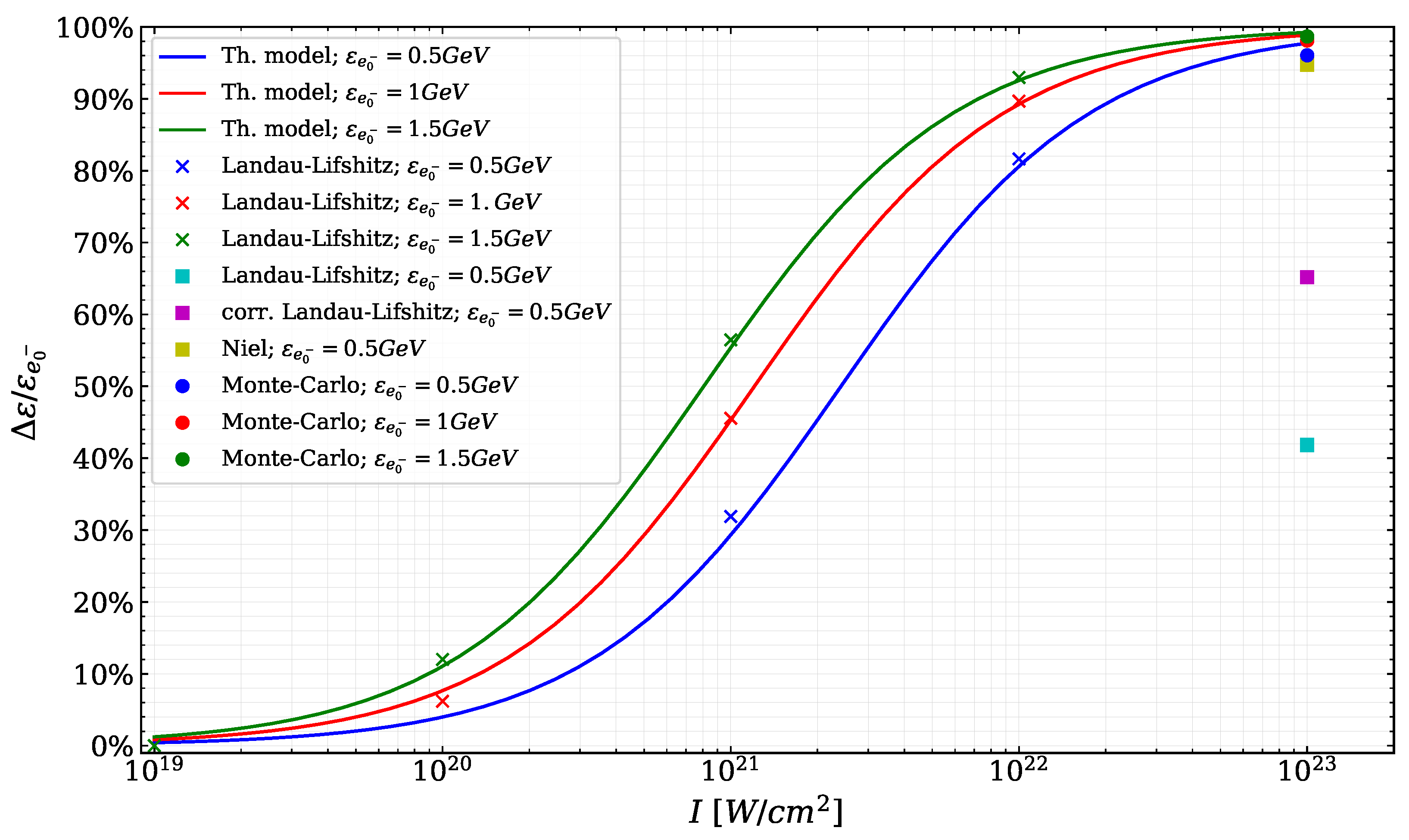
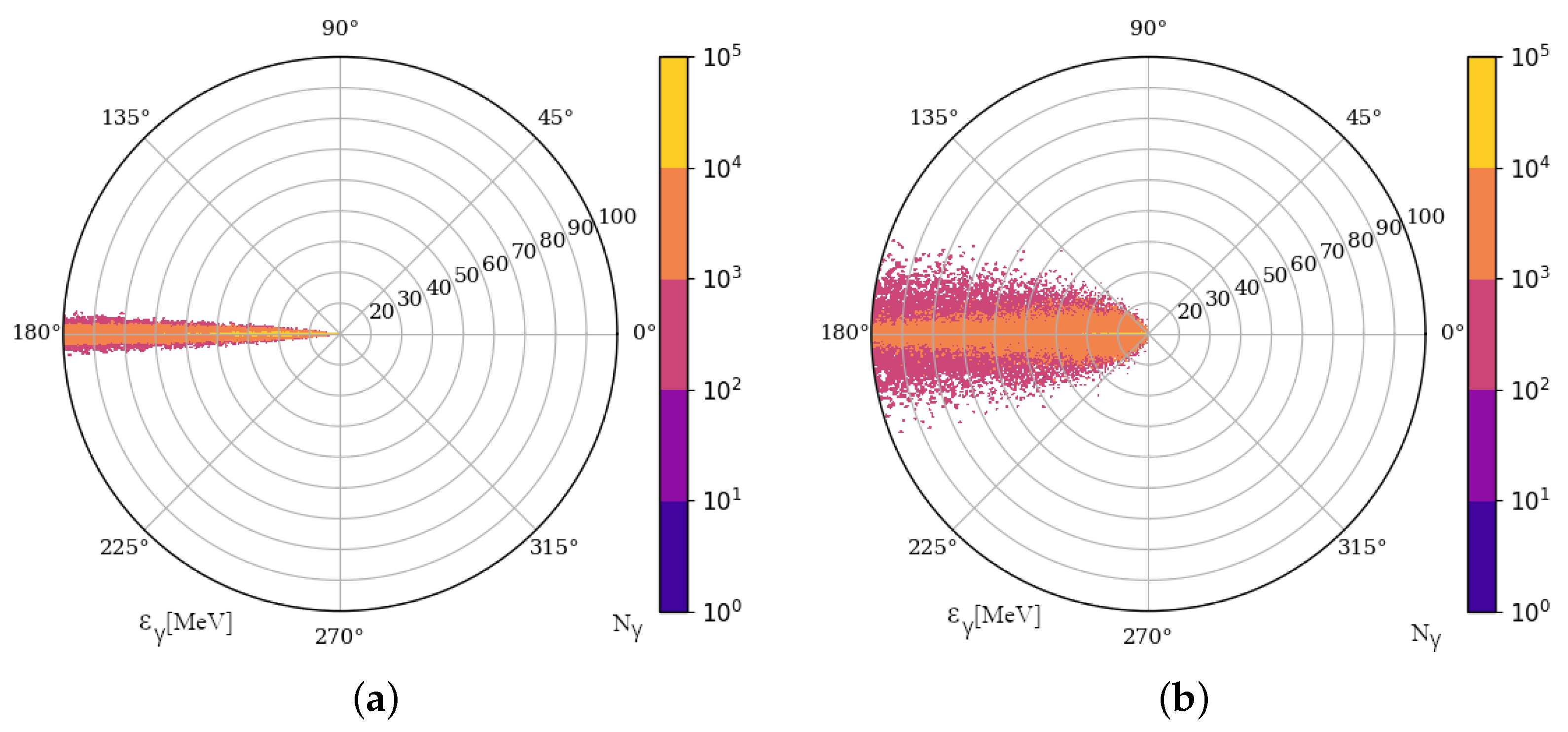
3.1. High Energy Radiation in Laser-Electron Beam Interaction
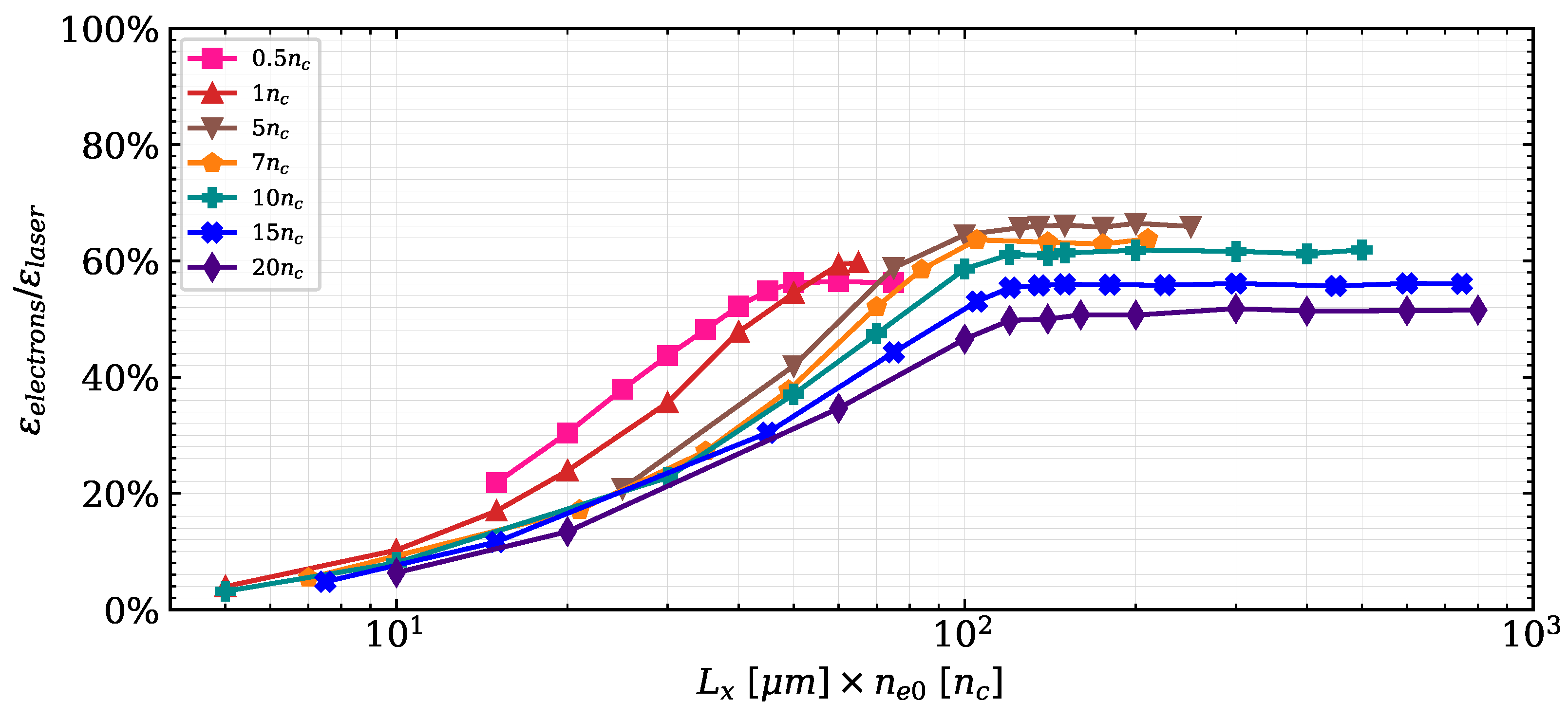
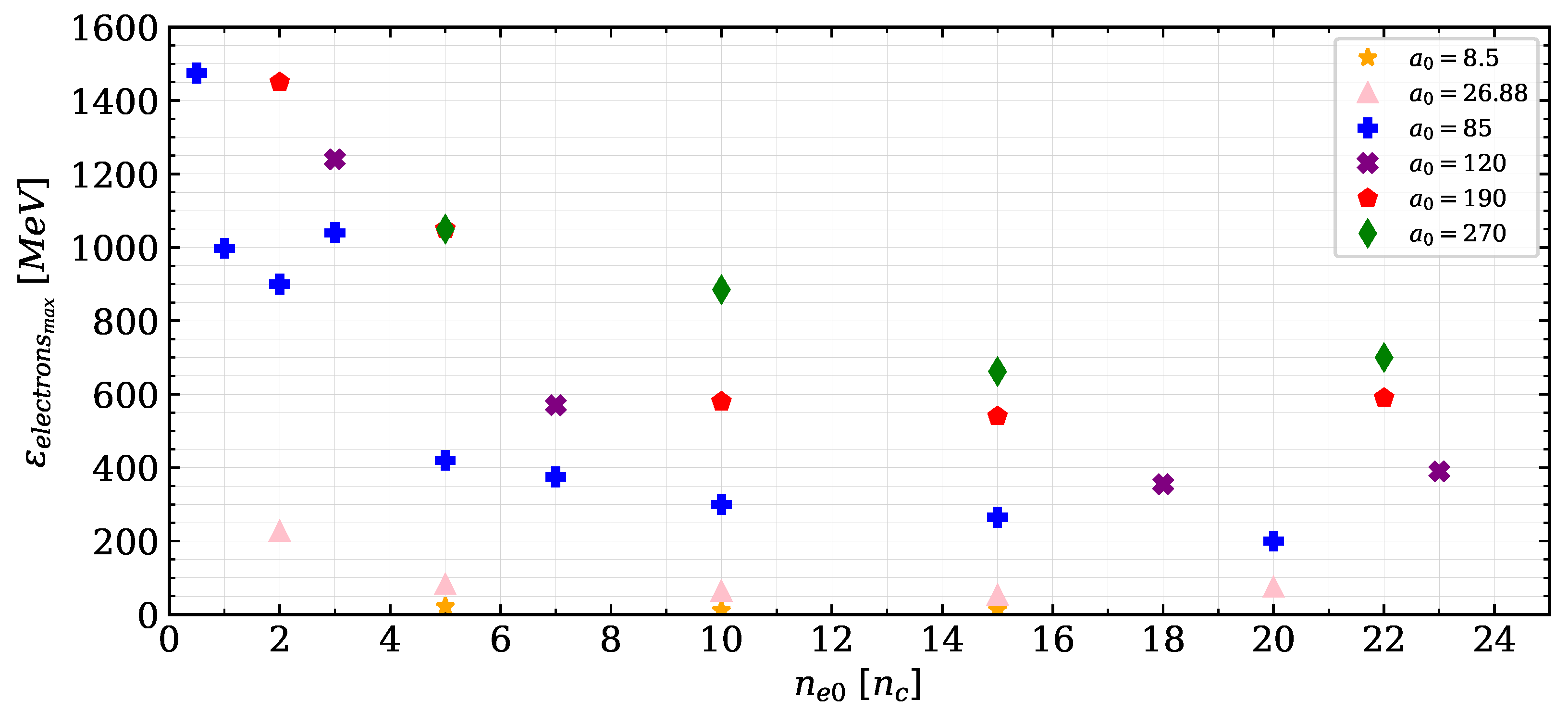
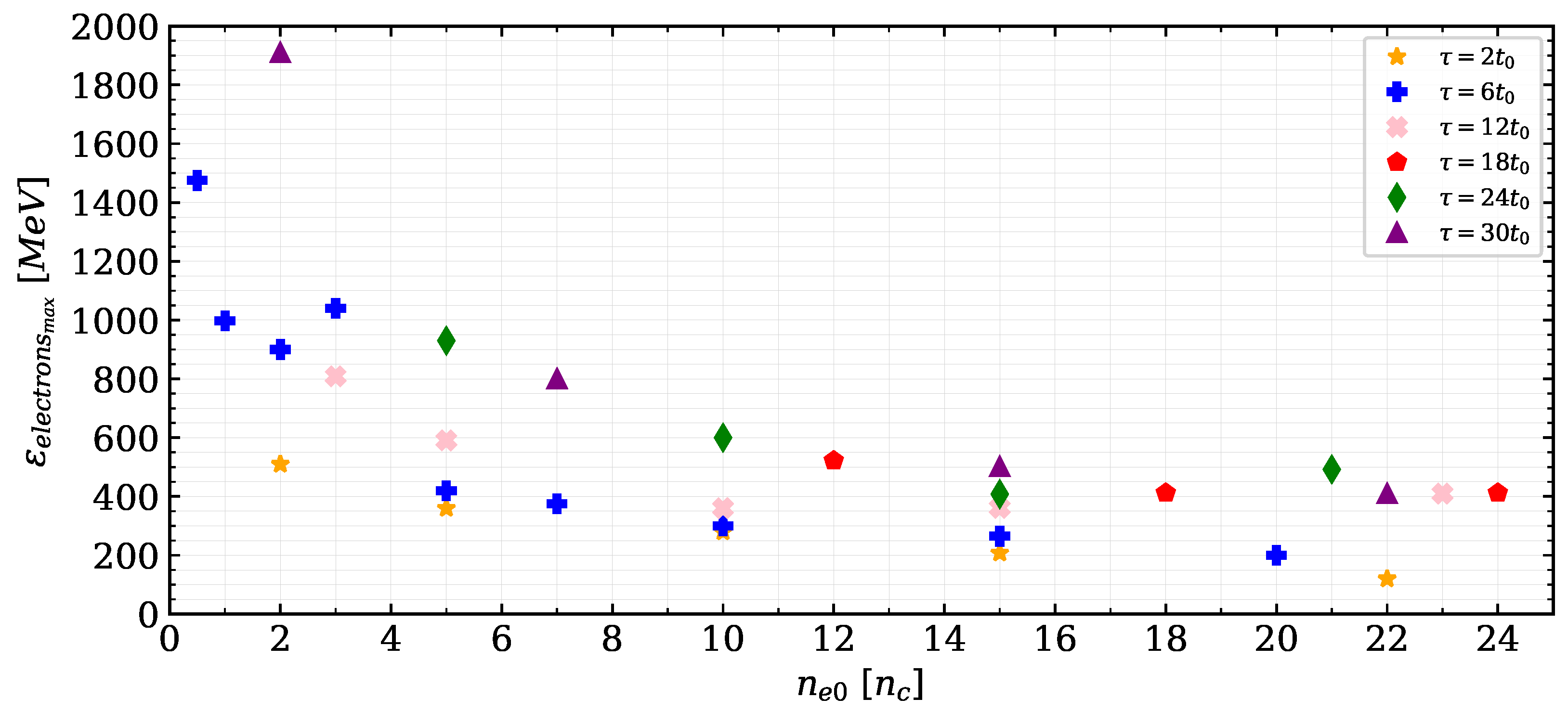
3.2. Laser-Driven Electron Acceleration in the Laser–Plasma Interaction Case
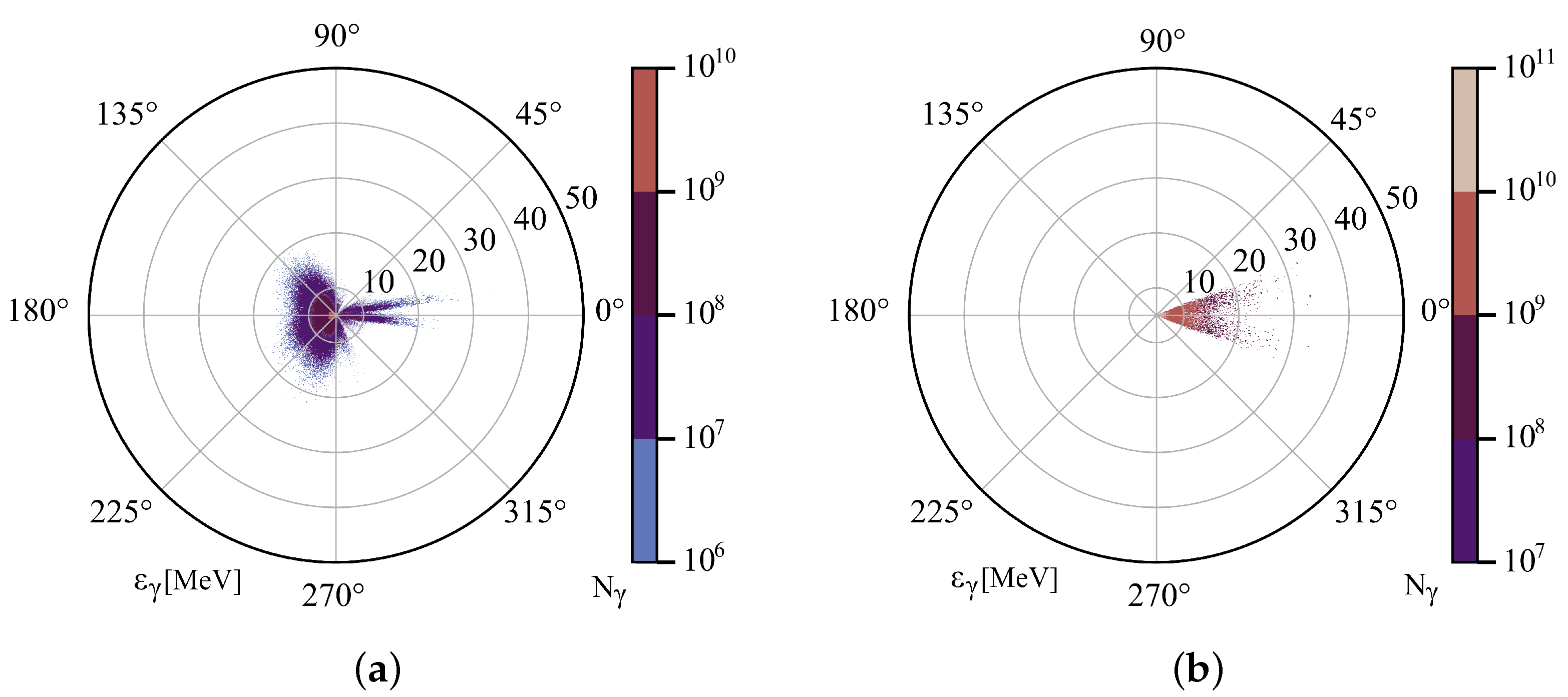
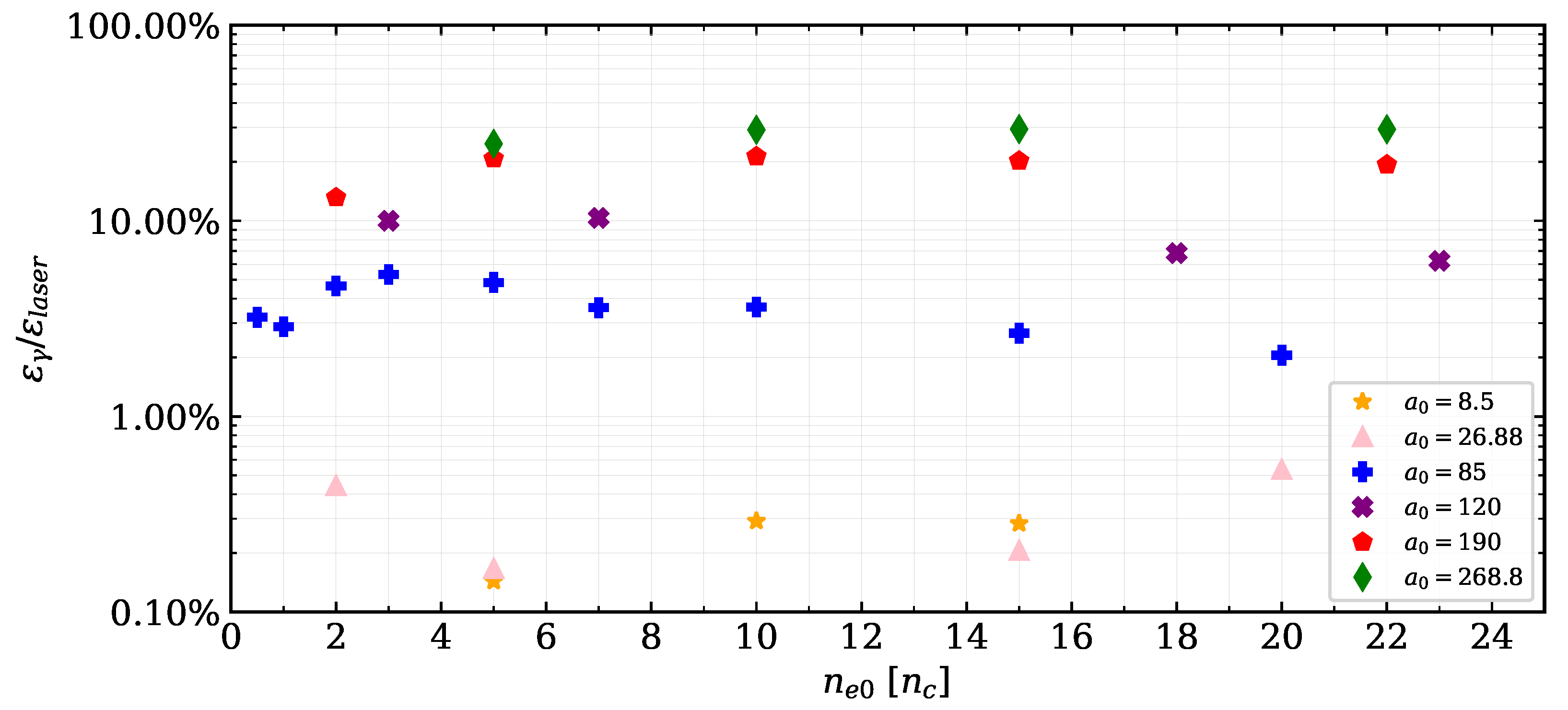
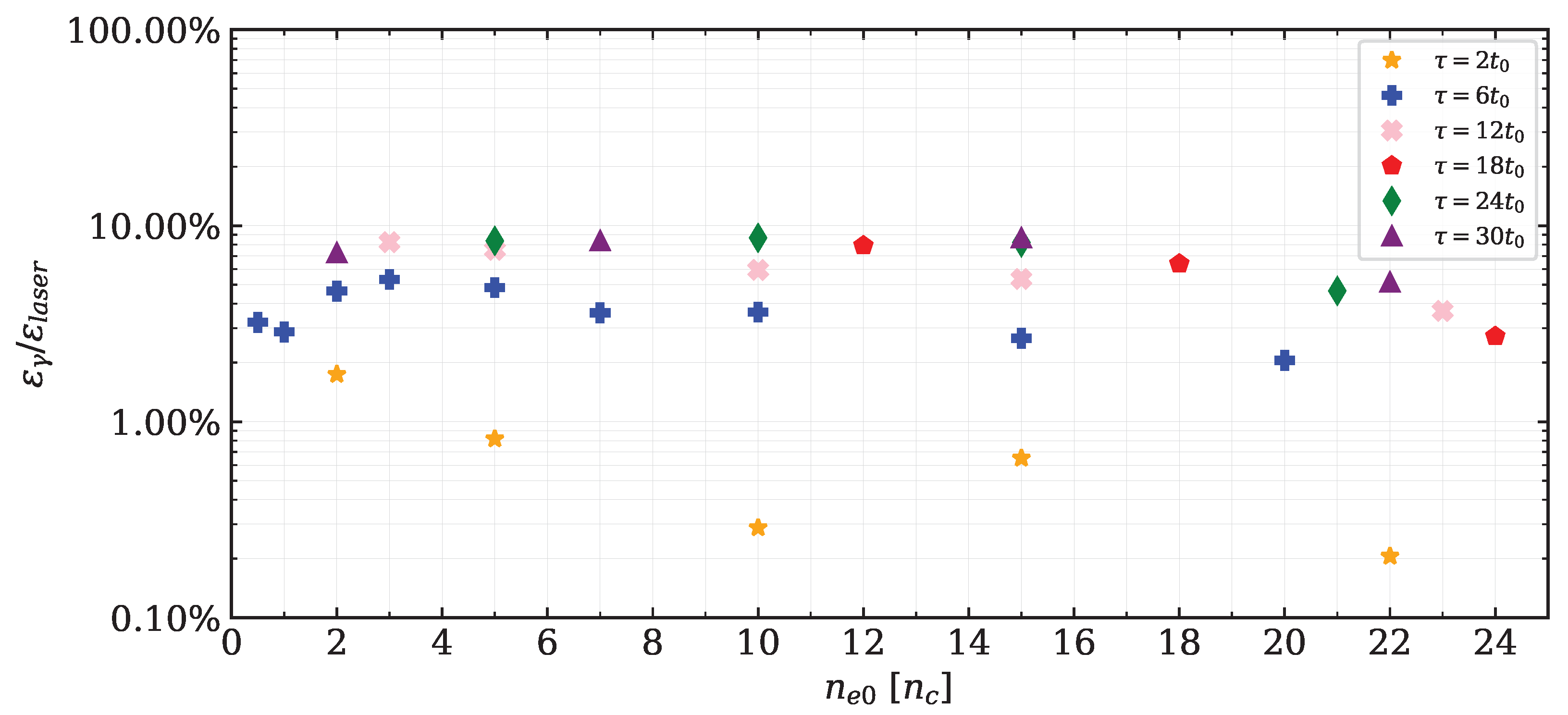
3.3. Emission of High Energy Radiation in Laser–Plasma Interaction
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, H.Y.; Yan, X.Q.; Zepf, M. Signatures of quantum radiation reaction in laser-electron-beam collisions. Phys. Plasmas 2015, 22, 093103. [Google Scholar] [CrossRef]
- Vranic, M.; Grismayer, T.; Fonseca, R.A.; Silva, L.O. Quantum radiation reaction in head-on laser-electron beam interaction. New J. Phys. 2016, 18, 073035. [Google Scholar] [CrossRef]
- Bulanov, S.V.; Esirkepov, T.Z.; Hayashi, Y.; Kando, M.; Kiriyama, H.; Koga, J.K.; Kondo, K.; Kotaki, H.; Pirozhkov, A.S.; Bulanov, S.S.; et al. On the design of experiments for the study of extreme field limits in the interaction of laser with ultrarelativistic electron beam. Nucl. Instruments Methods Phys. Res. A 2011, 660, 31–42. [Google Scholar] [CrossRef]
- Zhang, C.-W.; Zhu, Y.-X.; Lv, J.-F.; Xie, B.-S. Simulation Study of a Bright Attosecond γ-ray Source Generation by Irradiating an Intense Laser on a Cone Target. Appl. Sci. 2022, 12, 4361. [Google Scholar] [CrossRef]
- Ji, L.L.; Pukhov, A.; Nerush, E.N.; Kostyukov, I.Y.; Shen, B.F.; Akli, K.U. Energy partition, γ-ray emission, and radiation reaction in the near-quantum electrodynamical regime of laser-plasma interaction. Phys. Plasmas 2014, 21, 023109. [Google Scholar] [CrossRef]
- Breit, G.; Wheeler, J.A. Collision of Two Light Quanta. Phys. Rev. 1934, 46, 1087–1091. [Google Scholar] [CrossRef]
- Ridgers, C.P.; Brady, C.S.; Duclous, R.; Kirk, J.G.; Bennett, K.; Arber, T.D.; Robinson, A.P.L.; Bell, A.R. Dense Electron-Positron Plasmas and Ultraintense γ rays from Laser-Irradiated Solids. Phys. Rev. Lett. 2012, 108, 165006. [Google Scholar] [CrossRef] [PubMed]
- Ribeyre, X.; d’Humières, E.; Jansen, O.; Jequier, S.; Tikhonchuk, V.T.; Lobet, M. Pair creation in collision of γ-ray beams produced with high-intensity lasers. Phys. Rev. E 2016, 93, 013201. [Google Scholar] [CrossRef]
- Wang, T.; Ribeyre, X.; Gong, Z.; Jansen, O.; d’Humières, E.; Stutman, D.; Toncian, T.; Arefiev, A. Power Scaling for Collimated γ-Ray Beams Generated by Structured Laser-Irradiated Targets and Its Application to Two-Photon Pair Production. Phys. Rev. Appl. 2020, 13, 054024. [Google Scholar] [CrossRef]
- Chen, H.; Wilks, S.C.; Bonlie, J.D.; Liang, E.P.; Myatt, J.; Price, D.F.; Meyerhofer, D.D.; Beiersdorfer, P. Relativistic Positron Creation Using Ultraintense Short Pulse Lasers. Phys. Rev. Lett. 2009, 102, 105001. [Google Scholar] [CrossRef]
- Derouillat, J.; Beck, A.; Pérez, F.; Vinci, T.; Chiaramello, M.; Grassi, A.; Flé, M.; Bouchard, G.; Plotnikov, I.; Aunai, N.; et al. SMILEI: A collaborative, open-source, multi-purpose particle-in-cell code for plasma simulation. Comput. Phys. Commun. 2018, 222, 351–373. [Google Scholar] [CrossRef]
- Vranic, M.; Martins, J.L.; Vieira, J.; Fonseca, R.A.; Silva, L.O. All-Optical Radiation Reaction at 1021 W/cm2. Phys. Rev. Lett. 2014, 113, 134801. [Google Scholar] [CrossRef] [PubMed]
- Vladisavlevici, I.M.; Vizman, D.; Humières, E.D. Theoretical investigation of the interaction of ultra-high intensity laser pulses with near critical density plasmas. In preparation.
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields, 3rd ed.; Pergamon Press: Oxford, UK, 1971. [Google Scholar]
- Martinez, B.; d’Humières, E.; Gremillet, L. Synchrotron radiation from ultrahigh-intensity laser-plasma interactions and competition with Bremsstrahlung in thin foil targets. Phys. Rev. Res. 2020, 2, 043341. [Google Scholar] [CrossRef]
- Brady, C.S.; Ridgers, C.P.; Arber, T.D.; Bell, A.R.; Kirk, J.G. Laser Absorption in Relativistically Underdense Plasmas by Synchrotron Radiation. Phys. Rev. Lett. 2012, 109, 245006. [Google Scholar] [CrossRef]
- Stark, D.J.; Toncian, T.; Arefiev, A.V. Enhanced Multi-MeV Photon Emission by a Laser-Driven Electron Beam in a Self-Generated Magnetic Field. Phys. Rev. Lett. 2016, 116, 185003. [Google Scholar] [CrossRef]
- Hadjisolomou, P.; Jeong, T.M.; Bulanov, S.V. Towards bright gamma-ray flash generation from tailored target irradiated by multi-petawatt laser. Sci. Rep. 2022, 12, 17143. [Google Scholar] [CrossRef]
- Lobet, M.; Ruyer, C.; Debayle, A.; d’Humières, E.; Grech, M.; Lemoine, M.; Gremillet, L. Ultrafast Synchrotron-Enhanced Thermalization of Laser-Driven Colliding Pair Plasmas. Phys. Rev. Lett. 2015, 115, 215003. [Google Scholar] [CrossRef]
- Lobet, M.; d’Humières, E.; Grech, M.; Ruyer, C.; Davoine, X.; Gremillet, L. Modeling of radiative and quantum electrodynamics effects in PIC simulations of ultra-relativistic laser-plasma interaction. J. Phys. Conf. Ser. 2016, 688, 012058. [Google Scholar] [CrossRef]
- Di Piazza, A.; Hatsagortsyan, K.Z.; Keitel, C.H. Quantum Radiation Reaction Effects in Multiphoton Compton Scattering. Phys. Rev. Lett. 2010, 105, 220403. [Google Scholar] [CrossRef]
- Centre Interdisciplinaire Lumière Extrême. Available online: https://cilexsaclay.fr (accessed on 8 December 2022).
- Extreme Light Infrastructure. Available online: https://eli-laser.eu/ (accessed on 8 December 2022).
- Niel, F.; Riconda, C.; Amiranoff, F.; Duclous, R.; Grech, M. From quantum to classical modelling of radiation reaction: A focus on stochasticity effects. Phys. Rev. E 2018, 97, 043209. [Google Scholar] [CrossRef] [PubMed]
- Mésocentre de Calcul Intensif Aquitain. Available online: https://redmine.mcia.fr/projects/cluster-curta/ (accessed on 2 September 2022).
- Snavely, R.A.; Key, M.H.; Hatchett, S.P.; Cowan, T.E.; Roth, M.; Phillips, T.W.; Stoyer, M.A.; Henry, E.A.; Sangster, T.C.; Singh, M.S.; et al. Intense High-Energy Proton Beams from Petawatt-Laser Irradiation of Solids. Phys. Rev. Lett. 2000, 85, 2945. [Google Scholar] [CrossRef] [PubMed]
- Wilks, S.C.; Langdon, A.B.; Cowan, T.E.; Roth, M.; Singh, M.; Hatchett, S.; Key, M.H.; Pennington, D.; MacKinnon, A.; Snavely, R.A. Energetic proton generation in ultra-intense laser–solid interactions. Phys. Plasma 2001, 8, 542–549. [Google Scholar] [CrossRef]
- Burke, D.L.; Field, R.C.; Horton-Smith, G.; Spencer, J.E.; Walz, D.; Berridge, S.C.; Bugg, W.M.; Shmakov, K.; Weidemann, A.W.; Bula, C.; et al. Positron Production in Multiphoton Light-by-Light Scattering. Phys. Rev. Lett. 1997, 79, 1626–1629. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vladisavlevici, I.-M.; Vizman, D.; d’Humières, E. Laser Driven Electron Acceleration from Near-Critical Density Targets towards the Generation of High Energy γ-Photons. Photonics 2022, 9, 953. https://doi.org/10.3390/photonics9120953
Vladisavlevici I-M, Vizman D, d’Humières E. Laser Driven Electron Acceleration from Near-Critical Density Targets towards the Generation of High Energy γ-Photons. Photonics. 2022; 9(12):953. https://doi.org/10.3390/photonics9120953
Chicago/Turabian StyleVladisavlevici, Iuliana-Mariana, Daniel Vizman, and Emmanuel d’Humières. 2022. "Laser Driven Electron Acceleration from Near-Critical Density Targets towards the Generation of High Energy γ-Photons" Photonics 9, no. 12: 953. https://doi.org/10.3390/photonics9120953
APA StyleVladisavlevici, I.-M., Vizman, D., & d’Humières, E. (2022). Laser Driven Electron Acceleration from Near-Critical Density Targets towards the Generation of High Energy γ-Photons. Photonics, 9(12), 953. https://doi.org/10.3390/photonics9120953






