Dual Optical and Acoustic Negative Refraction in Phoxonic Crystals
Abstract
1. Introduction
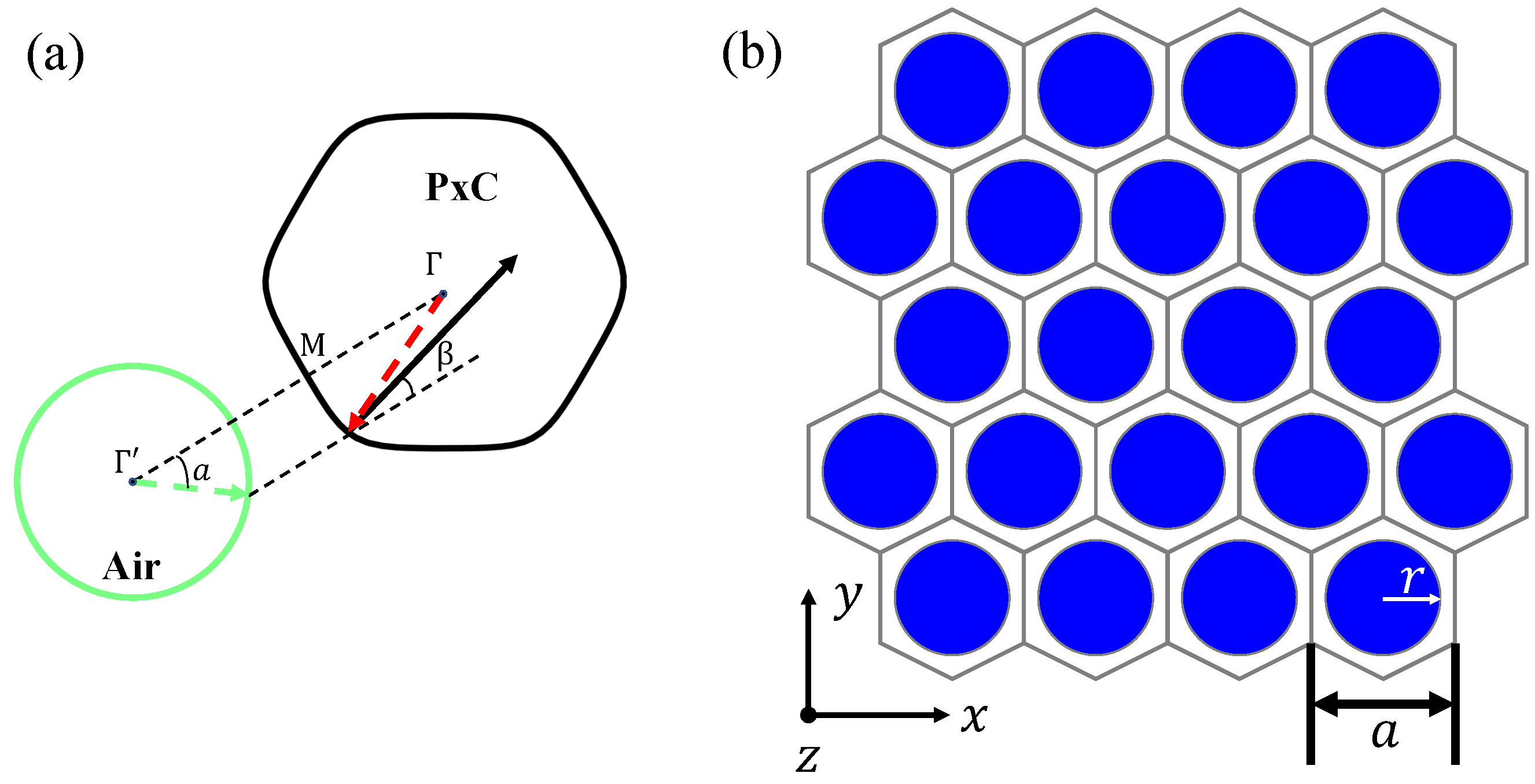
2. Principle and Structure Design
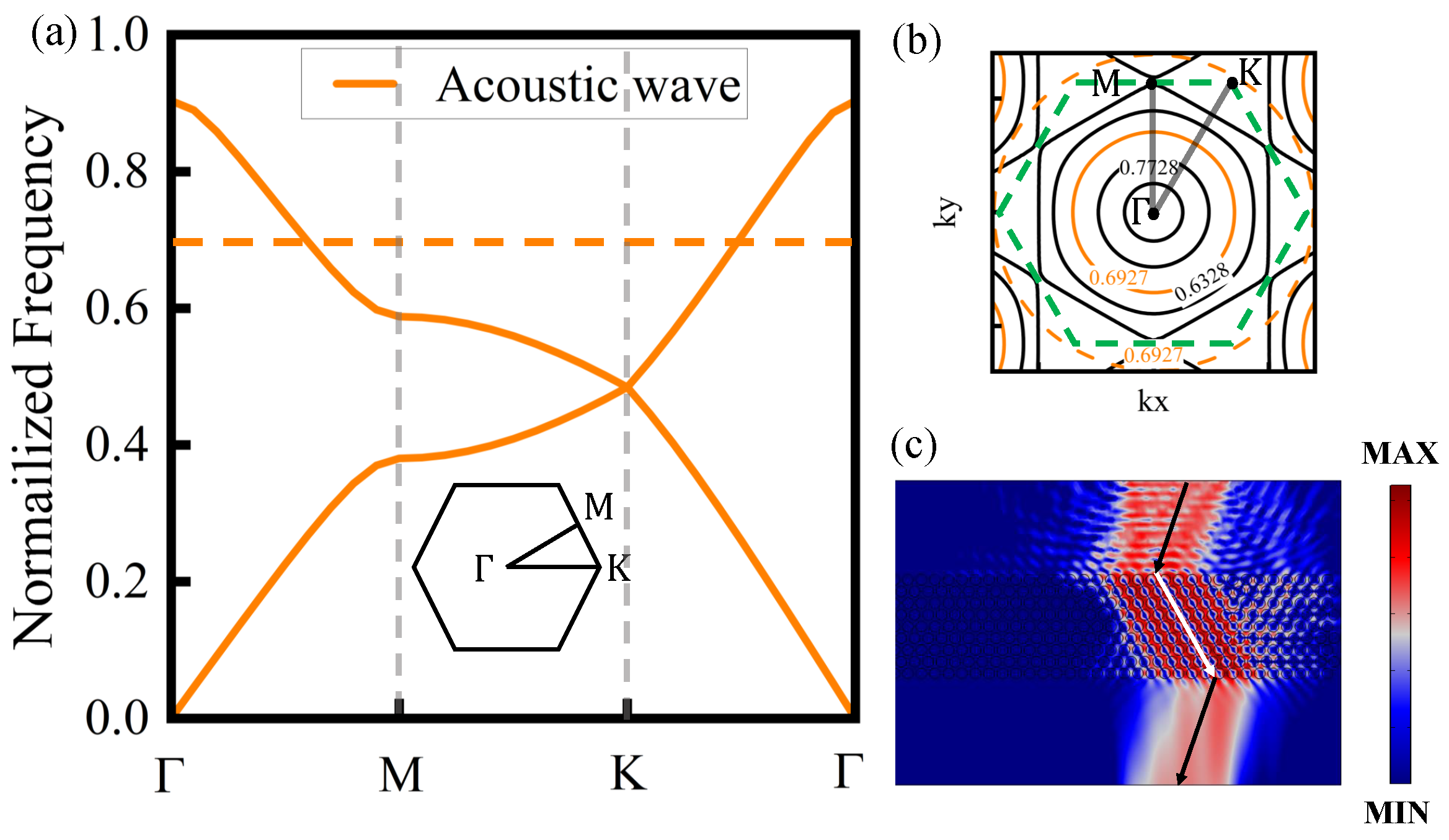
3. Dual Optical and Acoustic Negative Refraction Based on 2D PxC
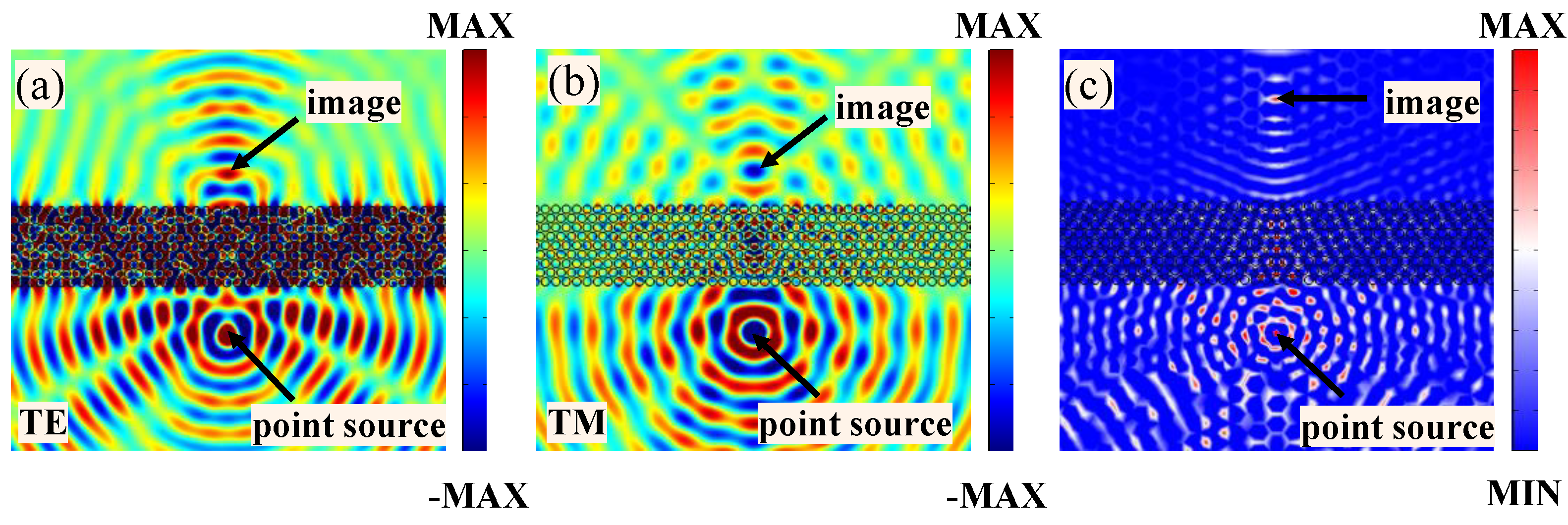
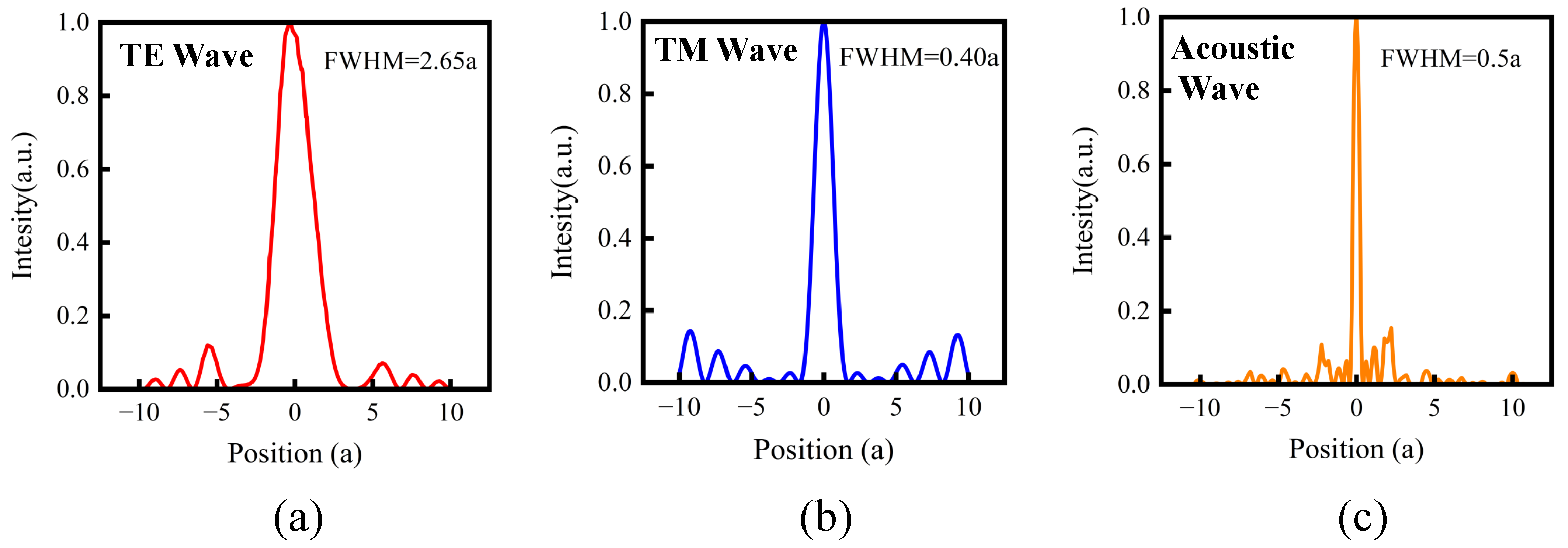
4. Dual Optical and Acoustic Imaging
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Schneider, D.; Liaqat, F.; Boudouti, E.H.E.; Abouti, O.E.; Tremel, W.; Butt, H.J.; Djafari-Rouhani, B.; Fytas, G. Defect-Controlled Hypersound Propagation in Hybrid Superlattices. Phys. Rev. Lett. 2013, 111, 164301. [Google Scholar] [CrossRef] [PubMed]
- Alonso-Redondo, E.; Huesmann, H.; El Boudouti, E.H.; Tremel, W.; Djafari-Rouhani, B.; Butt, H.J.; Fytas, G. Phoxonic Hybrid Superlattice. ACS Appl. Mater. Interfaces 2015, 7, 12488–12495. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Liu, W.; Yu, T.; Wang, T.; Liao, Q. Simultaneous unidirectional reciprocal filters of electromagnetic and elastic waves based on the modal symmetry of phoxonic crystal waveguides and cavity. Phys. Lett. A 2020, 384, 126499. [Google Scholar] [CrossRef]
- Alagoz, S.; Alagoz, B.B.; Sahin, A.; Nur, S. Negative refractions by triangular lattice sonic crystals in partial band gaps. Chin. Phys. B 2015, 24, 046201. [Google Scholar] [CrossRef]
- El-Jallal, S.; Oudich, M.; Pennec, Y.; Djafari-Rouhani, B.; Makhoute, A.; Gomis-Bresco, J.; Navarro-Urrios, D.; Martínez, A.; Torres, C.M.S. Cavity modes and optomechanic interactions in strip waveguide. IOP Conf. Ser. Mater. Sci. Eng. 2014, 68, 012003. [Google Scholar] [CrossRef]
- Ma, X.; Xiang, H.; Yang, X.; Xiang, J. Dual band gaps optimization for a two-dimensional phoxonic crystal. Phys. Lett. A 2021, 391, 127137. [Google Scholar] [CrossRef]
- Eichenfield, M.; Chan, J.; Camacho, R.M.; Vahala, K.J.; Painter, O. Optomechanical crystals. Nature 2009, 462, 78–82. [Google Scholar] [CrossRef]
- Liu, S.; Tong, H.; Fang, K. Optomechanical crystal with bound states in the continuum. Nat. Commun. 2022, 13, 3187. [Google Scholar] [CrossRef] [PubMed]
- Burek, M.J.; Cohen, J.D.; Meenehan, S.M.; El-Sawah, N.; Chia, C.; Ruelle, T.; Meesala, S.; Rochman, J.; Atikian, H.A.; Markham, M.; et al. Diamond optomechanical crystals. Optica 2016, 3, 1404. [Google Scholar] [CrossRef]
- Sharma, G.; Kumar, S.; Singh, V. Design of Si–SiO2 phoxonic crystal having defect layer for simultaneous sensing of biodiesel in a binary mixture of diesel through optical and acoustic waves. Acoust. Phys. 2017, 63, 159–167. [Google Scholar] [CrossRef]
- Li, K.Y.; Sun, X.W.; Song, T.; Wen, X.D.; Wang, Y.W.; Liu, X.X.; Liu, Z.J. A high-sensitivity liquid concentration-sensing structure based on a phoxonic crystal slot nanobeam. J. Appl. Phys. 2022, 131, 024501. [Google Scholar] [CrossRef]
- Ma, T.X.; Wang, Y.S.; Zhang, C.; Su, X.X. Simultaneous guiding of slow elastic and light waves in three-dimensional topology-type phoxonic crystals with a line defect. J. Opt. 2014, 16, 085002. [Google Scholar] [CrossRef]
- Schmidt, M.; Kessler, S.; Peano, V.; Painter, O.; Marquardt, F. Optomechanical creation of magnetic fields for photons on a lattice. Optica 2015, 2, 635. [Google Scholar] [CrossRef]
- Aram, M.H.; Khorasani, S. Optomechanical coupling strength in various triangular phoxonic crystal slab cavities. J. Opt. Soc. Am. B 2018, 35, 1390. [Google Scholar] [CrossRef]
- Wang, D.H.; Lee, K.M.; Lee, D.H.; Baczkowski, M.; Lee, J.G.; Wie, J.J.; Tan, L.S. Intermolecular Interactions and Intramolecular Motions in Photomechanical Effect: Nonlinear Thermo- and Photomechanical Behaviors of Azobenzene-Functionalized Amide–Imide Block Copolymers. ACS Appl. Mater. Interfaces 2021, 13, 48127–48140. [Google Scholar] [CrossRef]
- Pendry, J.B. Negative Refraction Makes a Perfect Lens. Phys. Rev. Lett. 2000, 85, 3966–3969. [Google Scholar] [CrossRef] [PubMed]
- Feng, S.; Li, Z.Y.; Feng, Z.F.; Cheng, B.Y.; Zhang, D.Z. Engineering the imaging properties of a metallic photonic-crystal slab lens. Appl. Phys. Lett. 2006, 88, 031104. [Google Scholar] [CrossRef]
- Cai, Z.; Zhao, S.; Huang, Z.; Li, Z.; Su, M.; Zhang, Z.; Zhao, Z.; Song, Y. Negative Refraction Acoustic Lens Based on Elastic Shell Encapsulated Bubbles. Adv. Mater. Technol. 2022, 7, 2101186. [Google Scholar] [CrossRef]
- Kosaka, H.; Kawashima, T.; Tomita, A.; Notomi, M.; Tamamura, T.; Sato, T.; Kawakami, S. Superprism phenomena in photonic crystals: Toward microscale lightwave circuits. J. Light. Technol. 1999, 17, 2032–2038. [Google Scholar] [CrossRef]
- Ma, T.X.; Zhang, C.; Wang, Y.S. Topological electromagnetic and elastic states in phoxonic crystal cavity arrays. PAMM 2021, 20. [Google Scholar] [CrossRef]
- Xia, B.; Fan, H.; Liu, T. Topologically protected edge states of phoxonic crystals. Int. J. Mech. Sci. 2019, 155, 197–205. [Google Scholar] [CrossRef]
- Hu, Z.; Lei, L.; He, L.; Liu, W.; Yu, T.; Wang, T.; Liao, Q. Simultaneous photonic and phononic topological pseudospin-dependent edge states in phoxonic crystals. Europhys. Lett. 2022, 138, 15001. [Google Scholar] [CrossRef]
- Wu, F.; Lyu, K.; Hu, S.; Yao, M.; Xiao, S. Ultra-large omnidirectional photonic band gaps in one-dimensional ternary photonic crystals composed of plasma, dielectric and hyperbolic metamaterial. Opt. Mater. 2021, 111, 110680. [Google Scholar] [CrossRef]
- Tan, Y.; Yu, T.; Yu, M.; Liu, W.; Wang, T.; Liu, N.; Liao, Q. Simultaneous beam guides of electromagnetic and acoustic waves in defect-free phoxonic crystals using self-collimation effect. Appl. Phys. Express 2019, 12, 062015. [Google Scholar] [CrossRef]
- Xiao, S.; Liu, T.; Wang, X.; Liu, X.; Zhou, C. Tailoring the absorption bandwidth of graphene at critical coupling. Phys. Rev. B 2020, 102, 085410. [Google Scholar] [CrossRef]
- Morvan, B.; Tinel, A.; Hladky-Hennion, A.C.; Vasseur, J.; Dubus, B. Experimental demonstration of the negative refraction of a transverse elastic wave in a two-dimensional solid phononic crystal. Appl. Phys. Lett. 2010, 96, 101905. [Google Scholar] [CrossRef]
- Nemat-Nasser, S. Unified homogenization of photonic/phononic crystals with first-band negative refraction. Mech. Mater. 2017, 105, 29–41. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, H.T.; Liu, W.W.; Ran, J.; Lai, Y.; Chen, H. Experimental realization of subwavelength flux manipulation in anisotropic near-zero index metamaterials. EPL Europhys. Lett. 2016, 113, 57006. [Google Scholar] [CrossRef]
- Lei, L.; Yu, T.; Liu, W.; Wang, T.; Liao, Q. Dirac cones with zero refractive indices in phoxonic crystals. Opt. Express 2021, 30, 308. [Google Scholar] [CrossRef]
- Kong, J. Electromagnetic Wave Interaction With Stratified Negative Isotropic Media—Abstract. J. Electromagn. Waves Appl. 2001, 15, 1319–1320. [Google Scholar] [CrossRef][Green Version]
- Hannan, S.; Islam, M.T.; Soliman, M.S.; Sahar, N.B.M.; Singh, M.S.J.; Faruque, M.R.I.; Alzamil, A. A filling-factor engineered, perfect metamaterial absorber for multiple applications at frequencies set by IEEE in C and X bands. J. Mater. Res. Technol. 2022, 19, 934–946. [Google Scholar] [CrossRef]
- Veselago, V.G. The electrodynamics of substances with simultaneously negative values of ε and μ. Sov. Phys. Uspekhi 1968, 10, 509–514. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, G.P.; Pendry, J.B.; Zhang, S. All-angle reflectionless negative refraction with ideal photonic Weyl metamaterials. Light. Sci. Appl. 2022, 11, 276. [Google Scholar] [CrossRef] [PubMed]
- Nemat-Nasser, S. Inherent negative refraction on acoustic branch of two dimensional phononic crystals. Mech. Mater. 2019, 132, 1–8. [Google Scholar] [CrossRef]
- Lu, M.H.; Zhang, C.; Feng, L.; Zhao, J.; Chen, Y.F.; Mao, Y.W.; Zi, J.; Zhu, Y.Y.; Zhu, S.N.; Ming, N.B. Negative birefraction of acoustic waves in a sonic crystal. Nat. Mater. 2007, 6, 744–748. [Google Scholar] [CrossRef]
- Ummer, K.V.; Vijaya, R. All-angle negative refraction effects and subwavelength imaging in photonic crystals with honeycomb lattice. J. Nanophotonics 2017, 11, 036005. [Google Scholar] [CrossRef]
- Jiang, L.; Wu, H.; Li, X. Dual-negative-refraction and imaging effects in normal two-dimensional photonic crystals with hexagonal lattices. Opt. Lett. 2012, 37, 1829. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Qin, F.; Xu, Y.; Fu, S.; Wang, Y.; Qin, Y. Negative refraction mediated by bound states in the continuum. Photonics Res. 2021, 9, 1592. [Google Scholar] [CrossRef]
- Huang, H.; Huo, S.; Chen, J. Subwavelength elastic topological negative refraction in ternary locally resonant phononic crystals. Int. J. Mech. Sci. 2021, 198, 106391. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, S.; Lei, L.; Tang, Q.; Xin, F.; Yu, T. Dual Optical and Acoustic Negative Refraction in Phoxonic Crystals. Photonics 2022, 9, 908. https://doi.org/10.3390/photonics9120908
Zhao S, Lei L, Tang Q, Xin F, Yu T. Dual Optical and Acoustic Negative Refraction in Phoxonic Crystals. Photonics. 2022; 9(12):908. https://doi.org/10.3390/photonics9120908
Chicago/Turabian StyleZhao, Shuyi, Linlin Lei, Qin Tang, Feng Xin, and Tianbao Yu. 2022. "Dual Optical and Acoustic Negative Refraction in Phoxonic Crystals" Photonics 9, no. 12: 908. https://doi.org/10.3390/photonics9120908
APA StyleZhao, S., Lei, L., Tang, Q., Xin, F., & Yu, T. (2022). Dual Optical and Acoustic Negative Refraction in Phoxonic Crystals. Photonics, 9(12), 908. https://doi.org/10.3390/photonics9120908



