Phase-Controlled Entanglement in a Four-Mode Optomechanical System
Abstract
1. Introduction
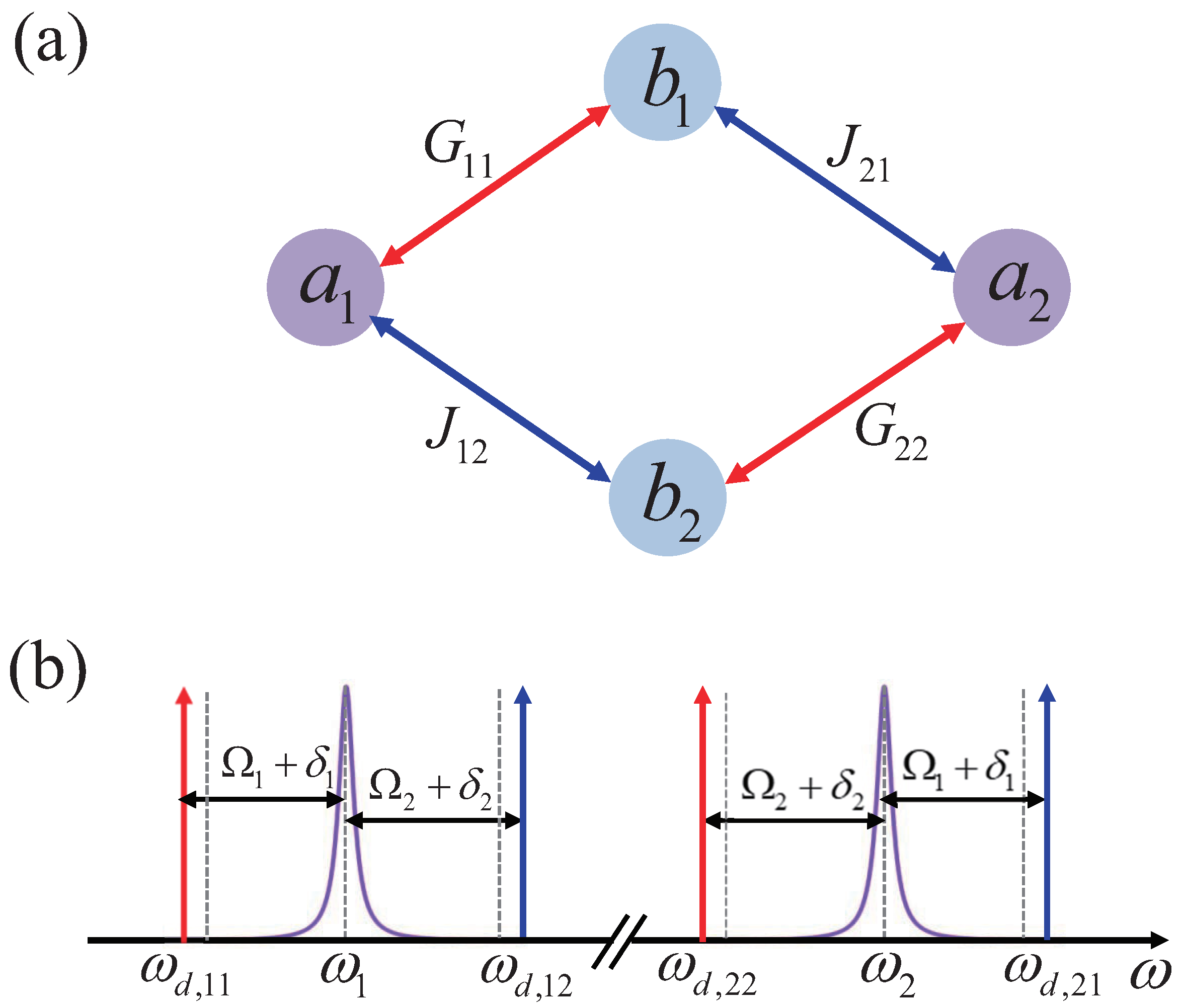
2. Model and Theory
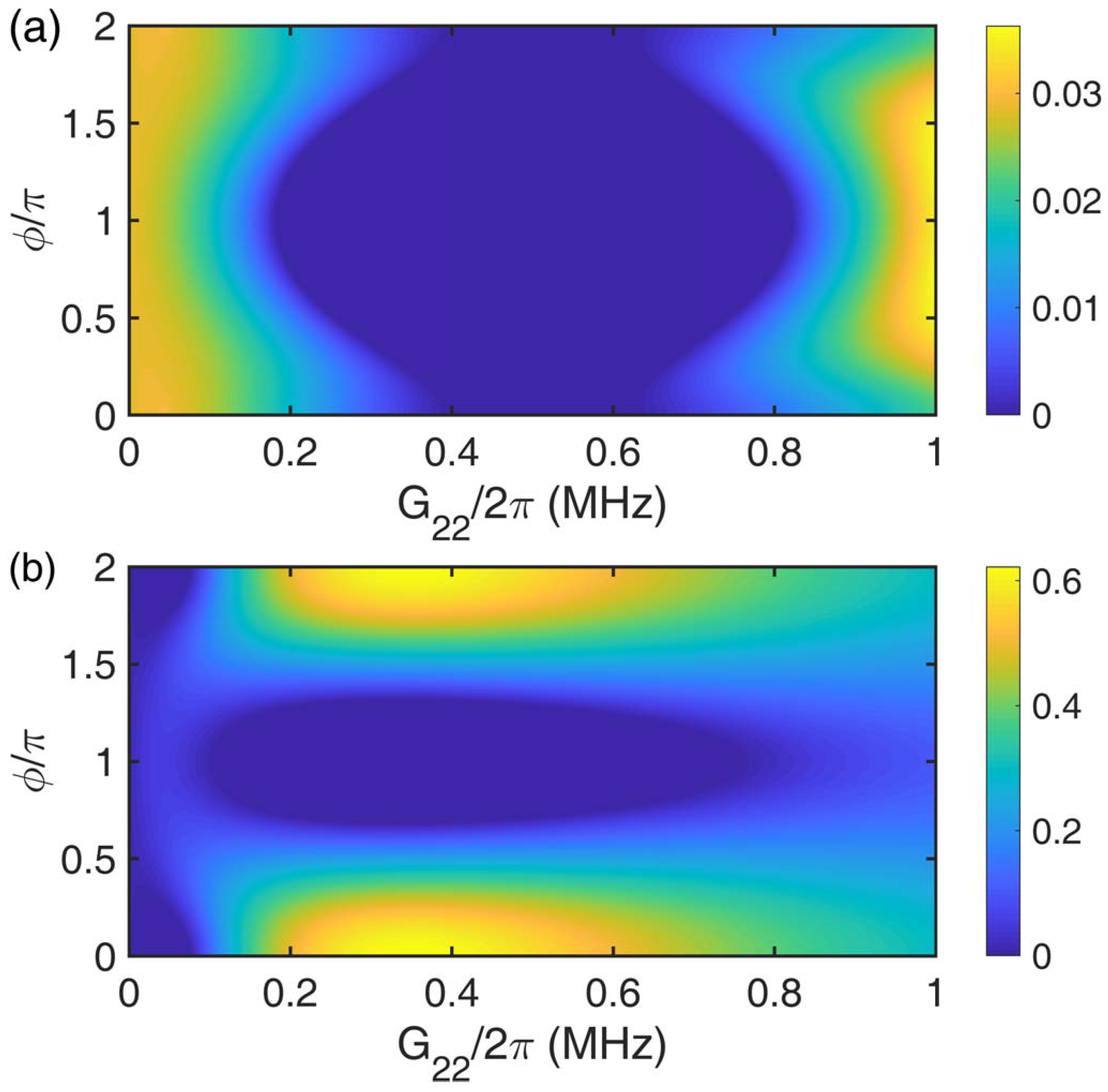
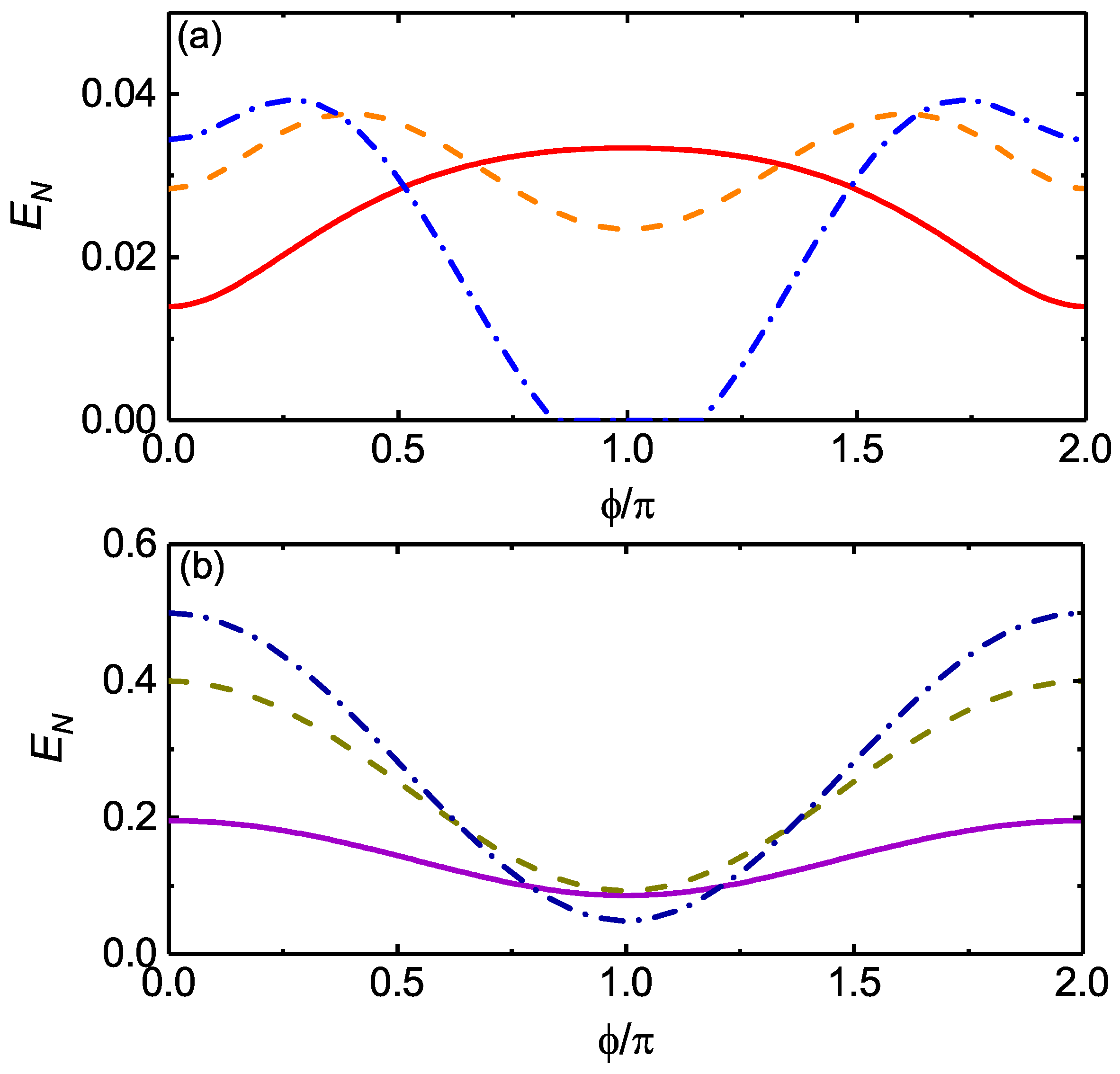
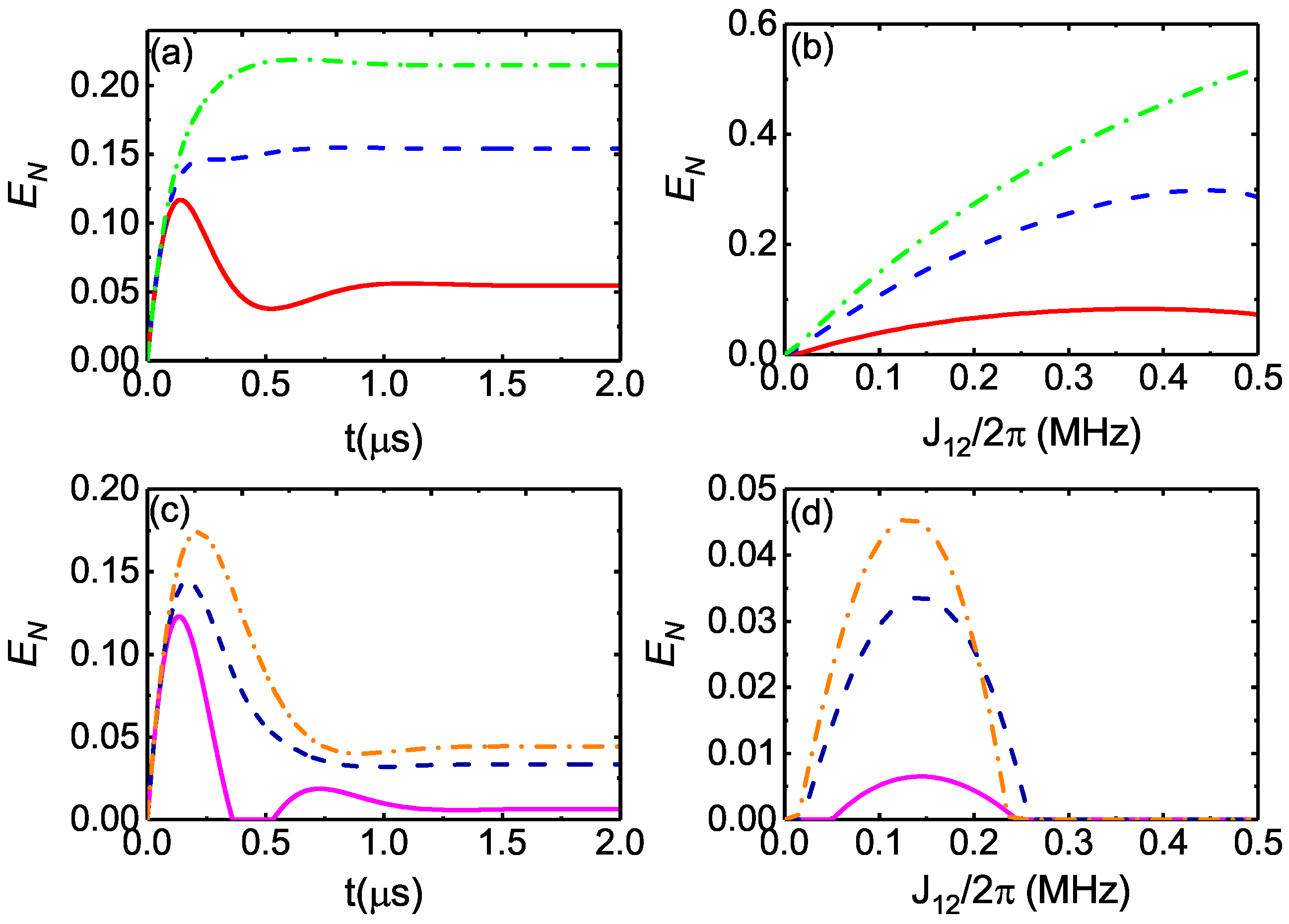
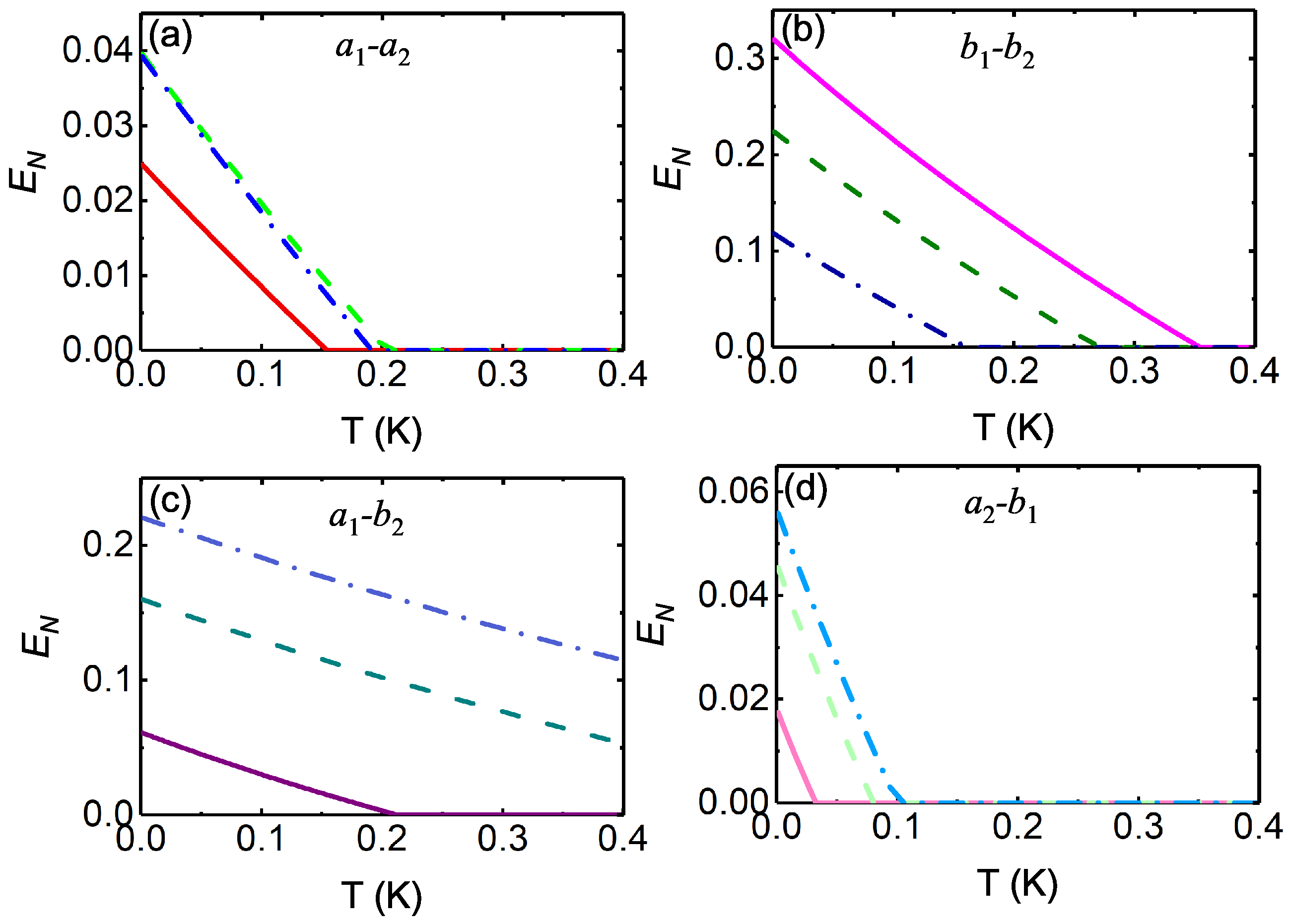
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Derivation of the Linearized Hamiltonian
References
- Berkley, A.J.; Xu, H.; Ramos, R.C.; Gubrud, M.A.; Strauch, F.W.; Johnson, P.R.; Anderson, J.R.; Dragt, A.J.; Lobb, C.J.; Wellstood, F.C. Entangled macroscopic quantum states in two superconducting qubits. Science 2003, 300, 1548–1550. [Google Scholar] [CrossRef] [PubMed]
- Julsgaard, B.; Kozhekin, A.; Polzik, E.S. Experimental long-lived entanglement of two macroscopic objects. Nature 2001, 413, 400–403. [Google Scholar] [CrossRef] [PubMed]
- Chou, C.W.; Riedmatten, H.; Felinto, D.; Polyakov, S.V.; van Enk, S.J.; Kimble, H.J. Measurement-induced entanglement for excitation stored in remote atomic ensembles. Nature 2005, 438, 828–832. [Google Scholar] [CrossRef]
- Ritter, S.; Nölleke, C.; Hahn, C.; Reiserer, A.; Neuzner, A.; Uphoff, M.; Mücke, M.; Figueroa, E.; Bochmann, J.; Rempe, G. An elementary quantum network of single atoms in optical cavities. Nature 2012, 484, 195–200. [Google Scholar] [CrossRef]
- Moehring, D.L.; Maunz, P.; Olmschenk, S.; Younge, K.C.; Matsukevich, D.N.; Duan, L.-M.; Monroe, C. Entanglement of single-atom quantum bits at a distance. Nature 2007, 449, 68–71. [Google Scholar] [CrossRef]
- Hensen, B.; Bernien, H.; Dréau, A.E.; Reiserer, A.; Kalb, N.; Blok, M.S.; Ruitenberg, J.; Vermeulen, R.F.L.; Schouten, R.N.; Abellán, C.; et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature 2015, 526, 682–686. [Google Scholar] [CrossRef]
- O’Connell, A.D.; Hofheinz, M.; Ansmann, M.; Bialczak, R.C.; Lenander, M.; Lucero, E.; Neeley, M.; Sank, D.; Wang, H.; Weides, M.; et al. Quantum ground state and single-phonon control of a mechanical resonator. Nature 2010, 464, 697–703. [Google Scholar] [CrossRef]
- Yeo, I.; Assis, P.L.; Gloppe, A.; Dupont-Ferrier, E.; Verlot, P.; Malik, N.S.; Dupuy, E.; Claudon, J.; Gérard, J.-M.; Auffêves, A.; et al. Strain-mediated coupling in a quantum dot-mechanical oscillator system. Nat. Nanotechnol. 2014, 9, 106–110. [Google Scholar] [CrossRef]
- Kolkowitz, S.; Jayich, A.C.B.; Unterreithmeier, Q.P.; Bennett, S.D.; Rabl, P.; Harris, J.G.E.; Lukin, M.D. Coherent sensing of a mechanical resonator with a single-spin qubit. Science 2012, 335, 1603–1606. [Google Scholar] [CrossRef]
- Hunger, D.; Camerer, S.; Hänsch, T.W.; König, D.; Kotthaus, J.P.; Reichel, J.; Treutlein, P. Resonant coupling of a Bose-Einstein Condensate to a micromechanical oscillator. Phys. Rev. Lett. 2010, 104, 143002. [Google Scholar] [CrossRef]
- Thomas, R.A.; Parniak, M.; Østfeldt, C.; Møller, C.B.; Bærentsen, C.; Tsaturyan, Y.; Schliesser, A.; Appel, J.; Zeuthen, E.; Polzik, E.S. Entanglement between distant macroscopic mechanical and spin systems. Nat. Phys. 2021, 17, 228–233. [Google Scholar] [CrossRef]
- Bienfait, A.; Satzinger, K.J.; Zhong, Y.P.; Chang, H.S.; Chou, M.H.; Conner, C.R.; Dumur, E.; Grebel, J.; Peairs, G.A.; Povey, R.G.; et al. Phonon-mediated quantum state transfer and remote qubit entanglement. Science 2019, 364, 368–371. [Google Scholar] [CrossRef] [PubMed]
- Kimble, H.J. The quantum internet. Nature 2008, 453, 1023–1030. [Google Scholar] [CrossRef] [PubMed]
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 2014, 86, 1391–1452. [Google Scholar] [CrossRef]
- Stannigel, K.; Rabl, P.; Sørensen, A.S.; Zoller, P.; Lukin, M.D. Optomechanical transducers for long-distance quantum communication. Phys. Rev. Lett. 2010, 105, 220501. [Google Scholar] [CrossRef]
- Wang, Y.D.; Clerk, A.A. Using interference for high fidelity quantum state transfer in optomechanics. Phys. Rev. Lett. 2012, 108, 153603. [Google Scholar] [CrossRef]
- Tian, L. Adiabatic state conversion and pulse transmission in optomechanical systems. Phys. Rev. Lett. 2012, 108, 153604. [Google Scholar] [CrossRef]
- Barzanjeh, S.; Abdi, M.; Milburn, G.J.; Tombesi, P.; Vitali, D. Reversible optical-to-microwave quantum interface. Phys. Rev. Lett. 2012, 109, 130503. [Google Scholar] [CrossRef]
- Andrews, R.W.; Peterson, R.W.; Purdy, T.P.; Cicak, K.; Simmonds, R.W.; Regal, C.A.; Lehnert, K.W. Bidirectional and efficient conversion between microwave and optical light. Nat. Phys. 2014, 10, 321–326. [Google Scholar] [CrossRef]
- Dong, C.H.; Wang, Y.D.; Wang, H.L. Optomechanical interfaces for hybrid quantum networks. Natl. Sci. Rev. 2015, 2, 510–519. [Google Scholar] [CrossRef]
- Forsch, M.; Stockill, R.; Wallucks, A.; Marinković, I.; Gärtner, C.; Norte, R.A.; van Otten, F.; Fiore, A.; Srinivasan, K.; Gröblacher, S. Microwave-to-Optics conversion using a mechanical oscillator in its quantum ground state. Nat. Phys. 2020, 16, 69–74. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.T.; Sarabalis, C.J.; Dahmani, Y.D.; Patel, R.N.; Mayor, F.M.; McKenna, T.P.; Laer, R.V.; Safavi-Naeini, A.H. Efficient bidirectional piezo-optomechanical transduction between microwave and optical frequency. Nat. Commun. 2020, 11, 1166. [Google Scholar] [CrossRef] [PubMed]
- Teufel, J.D.; Donner, T.; Li, D.; Harlow, J.W.; Allman, M.S.; Cicak, K.; Sirois, A.J.; Whittaker, J.D.; Lehnert, K.W.; Simmonds, R.W. Sideband cooling of micromechanical motion to the quantum ground state. Nature 2011, 475, 359–363. [Google Scholar] [CrossRef] [PubMed]
- Chan, J.; Alegre, T.P.M.; Safavi-Naeini, A.H.; Hill, J.T.; Krause, A.; Gröblacher, S.; Aspelmeyer, M.; Painter, O. Laser cooling of a nanomechanical oscillator into its quantum ground state. Nature 2011, 478, 89–92. [Google Scholar] [CrossRef] [PubMed]
- Delić, U.; Reisenbauer, M.; Dare, K.; Grass, D.; Vuletic, V.; Kiesel, N.; Aspelmeyer, M. Cooling of a levitated nanoparticle to the motional quantum ground state. Science 2020, 367, 892–895. [Google Scholar] [CrossRef]
- Safavi-Naeini, A.H.; Gröblacher, S.; Hill, J.T.; Chan, J.; Aspelmeyer, M.; Painter, O. Squeezed light from a silicon micromechanical resonator. Nature 2013, 500, 185–189. [Google Scholar] [CrossRef]
- Purdy, T.P.; Yu, P.L.; Peterson, R.W.; Kampel, N.S.; Regal, C.A. Strong optomechanical squeezing of light. Phys. Rev. X 2013, 3, 031012. [Google Scholar] [CrossRef]
- Wollman, E.E.; Lei, C.U.; Weinstein, A.J.; Suh, J.; Kronwald, A.; Marquardt, F.; Clerk, A.A.; Schwab, K.C. Quantum squeezing of motion in a mechanical resonator. Science 2015, 349, 952–955. [Google Scholar] [CrossRef]
- Pirkkalainen, J.M.; Damskägg, E.; Brandt, M.; Massel, F.; Sillanpää, M.A. Squeezing of quantum noise of motion in a micromechanical resonator. Phys. Rev. Lett. 2015, 115, 243601. [Google Scholar] [CrossRef]
- Vitali, D.; Gigan, S.; Ferreira, A.; Böhm, H.R.; Tombesi, P.; Guerreiro, A.; Vedral, V.; Zeilinger, A.; Aspelmeyer, M. Optomechanical entanglement between a movable mirror and a cavity field. Phys. Rev. Lett. 2007, 98, 030405. [Google Scholar] [CrossRef]
- Genes, C.; Mari, A.; Tombesi, P.; Vitali, D. Robust entanglement of a micromechanical resonator with output optical fields. Phys. Rev. A 2008, 78, 032316. [Google Scholar] [CrossRef]
- Barzanjeh, S.; Vitali, D.; Tombesi, P.; Milburn, G.J. Entangling optical and microwave cavity modes by means of a nanomechanical resonator. Phys. Rev. A 2011, 84, 042342. [Google Scholar] [CrossRef]
- Kuzyk, M.C.; Enk, S.J.; Wang, H.L. Generating robust optical entanglement in weak-coupling optomechanical systems. Phys. Rev. A 2013, 88, 062341. [Google Scholar] [CrossRef]
- Tian, L. Robust photon entanglement via quantum interference in optomechanical interfaces. Phys. Rev. Lett. 2013, 110, 233602. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.D.; Clerk, A.A. Reservoir-engineered entanglement in optomechanical systems. Phys. Rev. Lett. 2013, 110, 253601. [Google Scholar] [CrossRef]
- Wang, G.L.; Huang, L.; Lai, Y.C.; Grebogi, C. Nonlinear dynamics and quantum entanglement in optomechanical systems. Phys. Rev. Lett. 2014, 112, 110406. [Google Scholar] [CrossRef]
- Liao, J.Q.; Wu, Q.Q.; Nori, F. Entangling two macroscopic mechanical mirrors in a two-cavity optomechanical system. Phys. Rev. A 2014, 89, 014302. [Google Scholar] [CrossRef]
- Wang, M.; Lu, X.Y.; Wang, Y.D.; You, J.Q.; Wu, Y. Macroscopic quantum entanglement in modulated optomechanics. Phys. Rev. A 2016, 94, 053807. [Google Scholar] [CrossRef]
- Sun, F.X.; Mao, D.; Dai, Y.T.; Ficek, Z.; He, Q.Y.; Gong, Q.H. Phase control of entanglement and quantum steering in a three-mode optomechanical system. New J. Phys. 2017, 19, 123039. [Google Scholar] [CrossRef]
- Li, J.; Li, G.; Zippilli, S.; Vitali, D.; Zhang, T. Enhanced entanglement of two different mechanical resonators via coherent feedback. Phys. Rev. A 2017, 95, 043819. [Google Scholar] [CrossRef]
- Qin, L.G.; Wang, Z.Y.; Ma, H.Y.; Zhang, C.M.; Ren, L.; Wang, L.L.; Gong, S.Q. Optomechanical entanglement switch in the hybrid opto-electromechanical device. JOSA B 2019, 36, 1544–1550. [Google Scholar] [CrossRef]
- Hu, C.S.; Liu, Z.Q.; Liu, Y.; Shen, L.T.; Wu, H.; Zheng, S.B. Entanglement beating in a cavity optomechanical system under two-field driving. Phys. Rev. A 2020, 101, 033810. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Yang, C.S.; Shen, Z.; Dong, C.H.; Guo, G.C.; Zou, C.L.; Zou, X.B. Enhanced optomechanical entanglement and cooling via dissipation engineering. Phys. Rev. A 2020, 101, 063836. [Google Scholar] [CrossRef]
- Zhong, C.C.; Han, X.; Tang, H.X.; Jiang, L. Entanglement of microwave-optical modes in a strongly coupled electro-optomechanical system. Phys. Rev. A 2020, 101, 032345. [Google Scholar] [CrossRef]
- Li, G.Y.; Nie, W.J.; Wu, Y.; Liao, Q.; Chen, A.; Lan, Y. Manipulating the steady-state entanglement via three-level atoms in a hybrid levitated optomechanical system. Phys. Rev. A 2020, 102, 063501. [Google Scholar] [CrossRef]
- Jiao, Y.F.; Zhang, S.D.; Zhang, Y.L.; Miranowicz, A.; Kuang, L.M.; Jing, H. Nonreciprocal optomechanical entanglement against backscattering losses. Phys. Rev. Lett. 2020, 125, 143605. [Google Scholar] [CrossRef]
- Lin, Q.; He, B.; Xiao, M. Entangling two macroscopic mechanical resonators at high temperature. Phys. Rev. Appl. 2020, 13, 034030. [Google Scholar] [CrossRef]
- Jiang, C.; Tserkis, S.; Collins, K.; Onoe, S.; Li, Y.; Tian, L. Switchable bipartite and genuine tripartite entanglement via an optoelectromechanical interface. Phys. Rev. A 2020, 101, 042320. [Google Scholar] [CrossRef]
- Palomaki, T.A.; Teufel, J.D.; Simmonds, R.W.; Lehnert, K.W. Entangling mechanical motion with microwave fields. Science 2013, 342, 710–713. [Google Scholar] [CrossRef]
- Ockeloen-Korppi, C.F.; Damskägg, E.; Pirkkalainen, J.M.; Asjad, M.; Clerk, A.A.; Massel, F.; Woolley, M.J.; Sillanpää, M.A. Stabilized entanglement of massive mechanical oscillators. Nature 2018, 556, 478–482. [Google Scholar] [CrossRef]
- Riedinger, R.; Wallucks, A.; Marinković, I.; Löschnauzer, C.; Aspelmeyer, M.; Hong, S.; Gröblacher, S. Remote quantum entanglement between two micromechanical oscillators. Nature 2018, 556, 473–477. [Google Scholar] [CrossRef] [PubMed]
- de Lépinay, L.M.; Ockeloen-Korppi, C.F.; Woolley, M.J.; Sillanpää, M.A. Quantum mechanics–free subsystem with mechanical oscillators. Science 2021, 372, 625. [Google Scholar] [CrossRef] [PubMed]
- Kotler, S.; Peterson, G.A.; Shojaee, E.; Lecocq, F.; Cicak, K.; Kwiatkowski, A.; Geller, S.; Glancy, S.; Knill, E.; Simmonds, R.W.; et al. Direct observation of deterministic macroscopic entanglement. Science 2021, 372, 622. [Google Scholar] [CrossRef]
- Chen, J.X.; Rossi, M.; Mason, D.; Schliesser, A. Entanglement of propagating optical modes via a mechanical interface. Nat. Commun. 2020, 11, 943. [Google Scholar] [CrossRef] [PubMed]
- Barzanjeh, S.; Redchenko, E.S.; Peruzzo, M.; Wulf, M.; Lewis, D.P.; Arnold, G.; Fink, J.M. Stationary entangled radiation from micromechanical motion. Nature 2019, 570, 480–483. [Google Scholar] [CrossRef]
- Xu, X.W.; Li, Y.; Chen, A.X.; Liu, Y. Nonreciprocal conversion between microwave and optical photons in electro-optomechanical systems. Phys. Rev. A 2016, 93, 023827. [Google Scholar] [CrossRef]
- Li, Y.; Huang, Y.Y.; Zhang, X.Z.; Tian, L. Optical directional amplification in a three-mode optomechanical system. Opt. Express 2017, 25, 18907. [Google Scholar] [CrossRef]
- Zhang, X.Z.; Tian, L.; Li, Y. Optomechanical transistor with mechanical gain. Phys. Rev. A 2018, 97, 043818. [Google Scholar] [CrossRef]
- Tian, L.; Li, Z. Nonreciprocal quantum-state conversion between microwave and optical photons. Phys. Rev. A 2017, 96, 013808. [Google Scholar] [CrossRef]
- Jiang, C.; Song, L.N.; Li, Y. Directional amplifier in an optomechanical system with optical gain. Phys. Rev. A 2018, 97, 053812. [Google Scholar] [CrossRef]
- Ruesink, F.; Miri, M.A.; Alù, A.; Verhagen, E. Nonreciprocity and magnetic-free isolation based on optomechanical interactions. Nat. Commun. 2016, 7, 13662. [Google Scholar] [CrossRef] [PubMed]
- Miri, M.A.; Ruesink, F.; Verhagen, E.; Alù, A. Optical nonreciprocity based on optomechanical coupling. Phys. Rev. Appl. 2017, 7, 064014. [Google Scholar] [CrossRef]
- Fang, K.J.; Luo, J.; Metelmann, A.; Matheny, M.H.; Marquardt, F.; Clerk, A.A.; Painter, O. Generalized non-reciprocity in an optomechanical circuit via synthetic magnetism and reservoir engineering. Nat. Phys. 2017, 13, 465. [Google Scholar] [CrossRef]
- Bernier, N.R.; Tóth, L.D.; Koottavida, A.; Ioannou, M.A.; Malz, D.; Nunnenkamp, A.; Feofanov, A.K.; Kippenberg, T.J. Nonreciprocal reconfigurable microwave optomechanical circuit. Nat. Commun. 2017, 8, 604. [Google Scholar] [CrossRef] [PubMed]
- Barzanjeh, S.; Wulf, M.; Peruzzo, M.; Kalaee, M.; Dieterle, P.B.; Painter, O.; Fink, J.M. Mechanical on-chip microwave circulator. Nat. Commun. 2017, 8, 953. [Google Scholar] [CrossRef]
- Peterson, G.A.; Lecocq, F.; Cicak, K.; Simmonds, R.W.; Aumentado, J.; Teufel, J.D. Demonstration of efficient nonreciprocity in a microwave optomechanical circuit. Phys. Rev. X 2017, 7, 031001. [Google Scholar] [CrossRef]
- de Lépinay, L.M.; Damskägg, E.; Ockeloen-Korppi, C.F.; Sillanpää, M.A. Realization of directional amplification in a microwave optomechanical device. Phys. Rev. Appl. 2019, 11, 034027. [Google Scholar] [CrossRef]
- Malz, D.; Tóth, L.D.; Bernier, N.R.; Feofanov, A.K.; Kippenberg, T.J.; Nunnenkamp, A. Quantum-limited directional amplifiers with optomechanics. Phys. Rev. Lett. 2018, 120, 023601. [Google Scholar] [CrossRef]
- Shen, Z.; Zhang, Y.L.; Chen, Y.; Sun, F.W.; Zou, X.B.; Guo, G.C.; Zou, C.L.; Dong, C.H. Reconfigurable optomechanical circulator and directional amplifier. Nat. Commun. 2018, 9, 1797. [Google Scholar] [CrossRef]
- Ruesink, F.; Mathew, J.P.; Miri, M.A.; Alù, A.; Verhagen, E. Optical circulation in a multimode optomechanical resonator. Nat. Commun. 2018, 9, 1798. [Google Scholar] [CrossRef]
- Lai, D.G.; Liao, J.Q.; Miranowicz, A.; Nori, F. Noise-tolerant optomechanical entanglement via synthetic magnetism. Phys. Rev. Lett. 2022, 129, 063602. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.X.; Jiao, Y.F.; Li, Y.; Xu, X.W.; He, Q.Y.; Jing, H. Phase-controlled asymmetric optomechanical entanglement against defect losses. arXiv 2022, arXiv:2209.12508. [Google Scholar]
- DeJesus, E.X.; Kaufman, C. Routh-Hurwitz criterion in the examination of eigenvalues of a system of nonlinear ordinary differential equations. Phys. Rev. A 1987, 35, 5288. [Google Scholar] [CrossRef] [PubMed]
- Adesso, G.; Serafini, A.; Illuminati, F. Extremal entanglement and mixedness in continuous variable systems. Phys. Rev. A 2004, 70, 022318. [Google Scholar] [CrossRef]
- Shen, L.T.; Yang, J.W.; Zhong, Z.R.; Yang, Z.B.; Zheng, S.B. Quantum phase transition and quench dynamics in the two-mode Rabi model. Phys. Rev. A 2021, 104, 063703. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, C.; Lu, H.; Zhai, Z.; Chen, G. Phase-Controlled Entanglement in a Four-Mode Optomechanical System. Photonics 2022, 9, 818. https://doi.org/10.3390/photonics9110818
Jiang C, Lu H, Zhai Z, Chen G. Phase-Controlled Entanglement in a Four-Mode Optomechanical System. Photonics. 2022; 9(11):818. https://doi.org/10.3390/photonics9110818
Chicago/Turabian StyleJiang, Cheng, Hongxia Lu, Zhangyin Zhai, and Guibin Chen. 2022. "Phase-Controlled Entanglement in a Four-Mode Optomechanical System" Photonics 9, no. 11: 818. https://doi.org/10.3390/photonics9110818
APA StyleJiang, C., Lu, H., Zhai, Z., & Chen, G. (2022). Phase-Controlled Entanglement in a Four-Mode Optomechanical System. Photonics, 9(11), 818. https://doi.org/10.3390/photonics9110818



