Next Article in Journal
Broadband Polarization Rotator and Splitter Based on 70 nm-Etched Waveguides on SOI Platform
Previous Article in Journal
Tunable and Switchable Dual-Wavelength SLM Narrow-Linewidth Fiber Laser with a PMFBG-FP Filter Cascaded by Multi-Ring Cavity
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Photonics
Volume 9
Issue 10
10.3390/photonics9100757
photonics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Low- and High-Order Optical Nonlinearities of Quantum Dots

by
Rashid A. Ganeev
1,2,3
1
Laboratory of Nonlinear Optics, Institute of Astronomy, University of Latvia, Jelgavas iela 3, LV-1004 Riga, Latvia
2
Tashkent Institute of Irrigation and Agricultural Mechanization Engineers, National Research University, Kori Niyazov Street 39, Tashkent 100000, Uzbekistan
3
Department of Physics, Voronezh State University, 394006 Voronezh, Russia
Photonics 2022, 9(10), 757; https://doi.org/10.3390/photonics9100757
Submission received: 6 September 2022 / Revised: 6 October 2022 / Accepted: 8 October 2022 / Published: 12 October 2022
Browse Figures
Versions Notes

Abstract

:
Various potential applications of quantum dots (QDs) require knowledge of their optical nonlinearities. In this review, the third-order nonlinearities responsible for the saturable absorption, two-photon absorption, reverse saturable absorption, and nonlinear refraction in QDs, as well as the high-order harmonics generation in the laser-induced plasmas containing QDs, are analyzed. The methods of QD synthesis and preparation strongly affect their optical nonlinearities. Above-mentioned nonlinear optical studies in QDs are analyzed for various potential applications (sources of coherent extreme ultraviolet radiation, optical limiters, mode-lockers, etc.).

1. Why Quantum Dots?

There is a variety of small-sized aggregates. The choice of them for the analysis of different physical properties depends on the spatial characteristics of these species. Particularly, previous experiments regarding the frequency conversion of laser radiation using both gas clusters and plasma nanoparticles have shown the enhancement of harmonic yield with regard to the atomic/ionic species of the same elemental consistence. The qualitative explanation of this effect is a growth of the cross-section of recombination of the accelerated electron with the parent particle in the case of larger species. Another mechanism is a quantum confinement induced growth of the local field in such species, which effectively interacts with the laser field. In this connection, quantum dots (QDs), sizes of which (2–6 nm) belong to the intermediate range between clusters (0.2–1 nm) [1,2,3,4] and nanoparticles (12–100 nm) [5,6], can be considered as rather efficient emitters of harmonics among the three groups of small-sized aggregates. In the case of nanoparticles, only surface atoms actively participate in high-order harmonics generation (HHG), since inner atoms hardly can be considered as the efficient emitters of harmonics due to the absorption and screening effect. As for the clusters containing up to 1000 atoms, their number is notably smaller than the number of emitters from the QDs.
A similar conclusion can be applied to the lower-order optical nonlinearities of the small-sized aggregates [7,8,9,10,11]. The formation of Q-switchers and mode-lockers based on QDs is an important goal for the application of the low-order optical nonlinearities of these small-sized species. The conditions for the efficient application of nonlinear optical (NLO) properties of QDs in various fields of physics, chemistry, and biology require further studies of these species.
Below, I present the overview of the NLO properties of two groups of QDs. I provide some details of the preparation and characterization of QD samples and then discuss the experiments revealing their NLO properties. In Section 2, I analyze the saturated absorption, reverse saturated absorption, two-photon absorption, OL, and nonlinear refraction of Cd0.5Zn0.5S and Ag2S QD suspensions and films. In Section 3, I discuss the NLO properties of the QDs comprising of mercury sulfides, selenides, and tellurides. In Section 4, HHG in various QDs is analyzed.

2. Low-Order Nonlinearities of the QDs Containing Various Sulfides

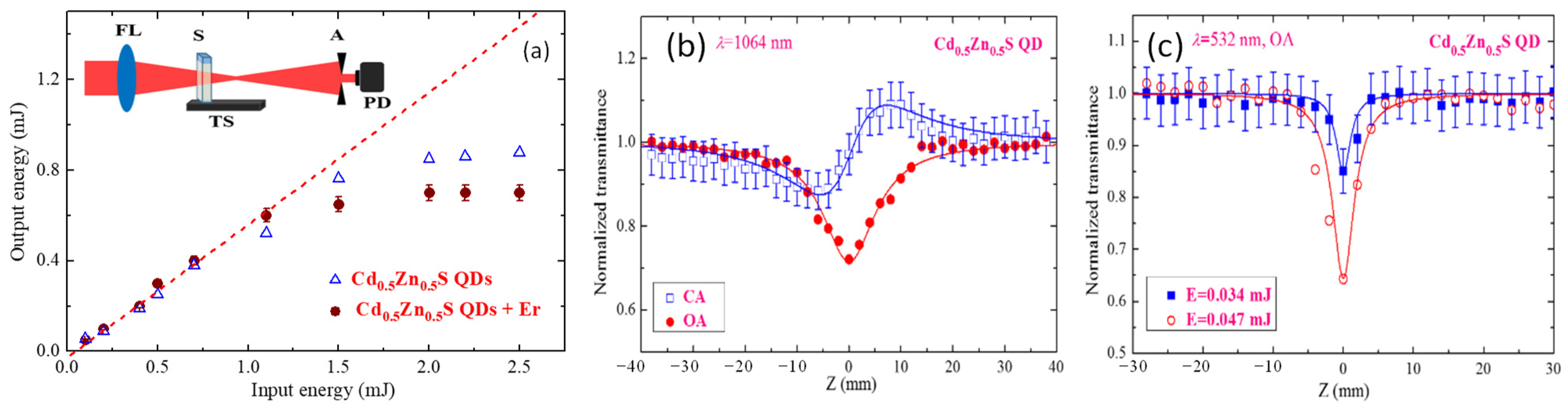
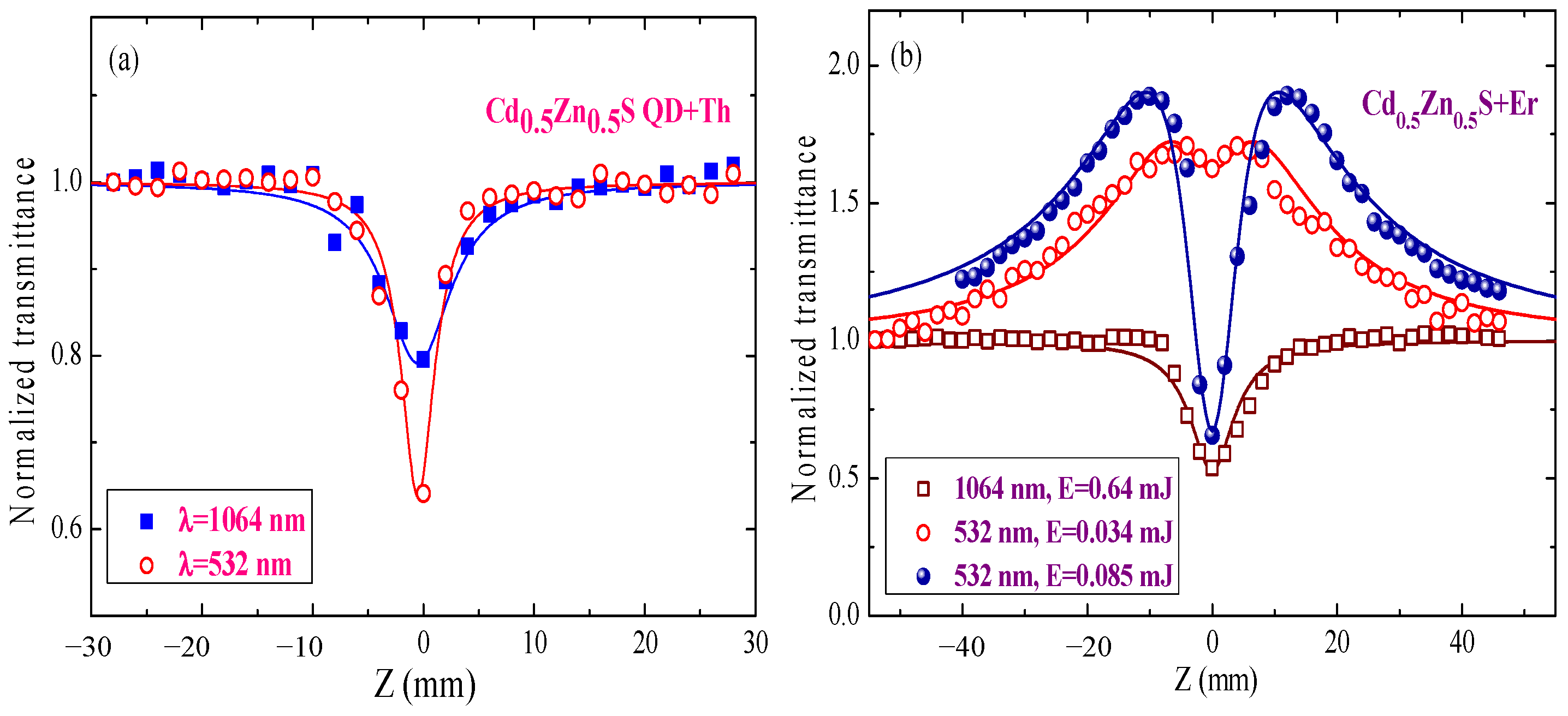
2.1. Cd0.5Zn0.5S Quantum Dots

Low-order nonlinearities of QDs attracted attention due to their strong nonlinear absorptive and refractive properties. Particularly, the nonlinear refraction in such QDs, e.g., CdSe0.8S0.2 [12,13] and CdSexS1−x [14], was three orders of magnitude larger than that of glasses containing CdSeS molecules. The same can be said about the two-photon absorption (TPA) in those species. Thus, the knowledge of nonlinear absorption coefficients (β) and nonlinear refractive indices (γ) allows to determine the role of various processes like TPA, saturable absorption (SA), optical limiting (OL), and reverse saturable absorption (RSA).
In [15], various nonlinear optical processes in the Cd0.5Zn0.5S QDs + dye associates synthesized by a method described in [16] are reported. The 1064 nm and 532 nm picosecond pulses were used during these studies. A 40 ps pulse was used during open-aperture (OA) and closed-aperture (CA) Z-scans (inset in Figure 1a). OL was analyzed using the 532 nm, 40 ps pulses propagating through the solution of Cd0.5Zn0.5S QDs and erythrosine associates in water. OL was observed at the pulse energies above 1 mJ (Figure 1a). The joint influence of TPA and RSA at high pulse energies became stronger than SA.
The OA and CA scans using the 1064 nm radiation propagating through the water solution of Cd0.5Zn0.5S QDs is shown in Figure 1b. The corresponding β and γ of solution were determined to be 3.2 × 10−11 cm W−1 and 5.5 × 10−16 cm2 W−1, which corresponded to 1.2 × 10−8 cm W−1 and 2 × 10−13 cm2 W−1 assuming the volume ratio (~3 × 10−3) of QDs in this suspension.
Two energies of 532 nm pulse (0.034 and 0.047 mJ) were used to determine β of solution (Figure 1c), which showed different values of nonlinear absorption (1 × 10−10 and 1.5 × 10−10 cm W−1). Probably, some additional process such as RSA plays a role in the variation of β alongside TPA.
The addition of thionine in the suspension of Cd0.5Zn0.5S QDs led to similar results (Figure 2a). The nonlinear absorption measured by 1064 nm pulses was significantly smaller compared with the case of 532 nm radiation (1.0 × 10−11 and 2.3 × 10−10 cm W−1, respectively).
The addition of erythrosine instead of thionine showed the notable variation of the nonlinear absorption (Figure 2b). Different types of nonlinear absorption, e.g., TPA, SA, and RSA, were presented in this solution. SA and RSA dominated at 532 nm, while in the case of 1064 nm pulses, TPA was a main nonlinear optical process. The RSA coefficient was determined to be 3 × 10−9 cm W−1.

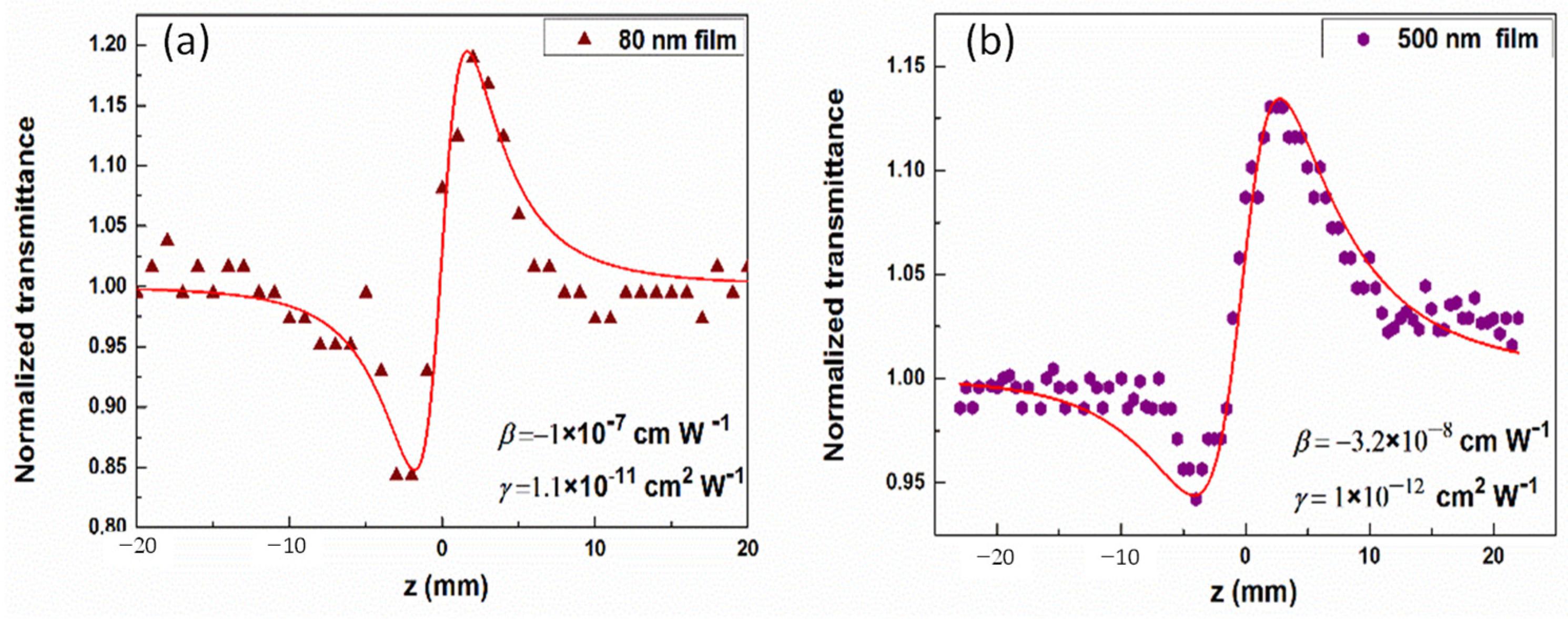
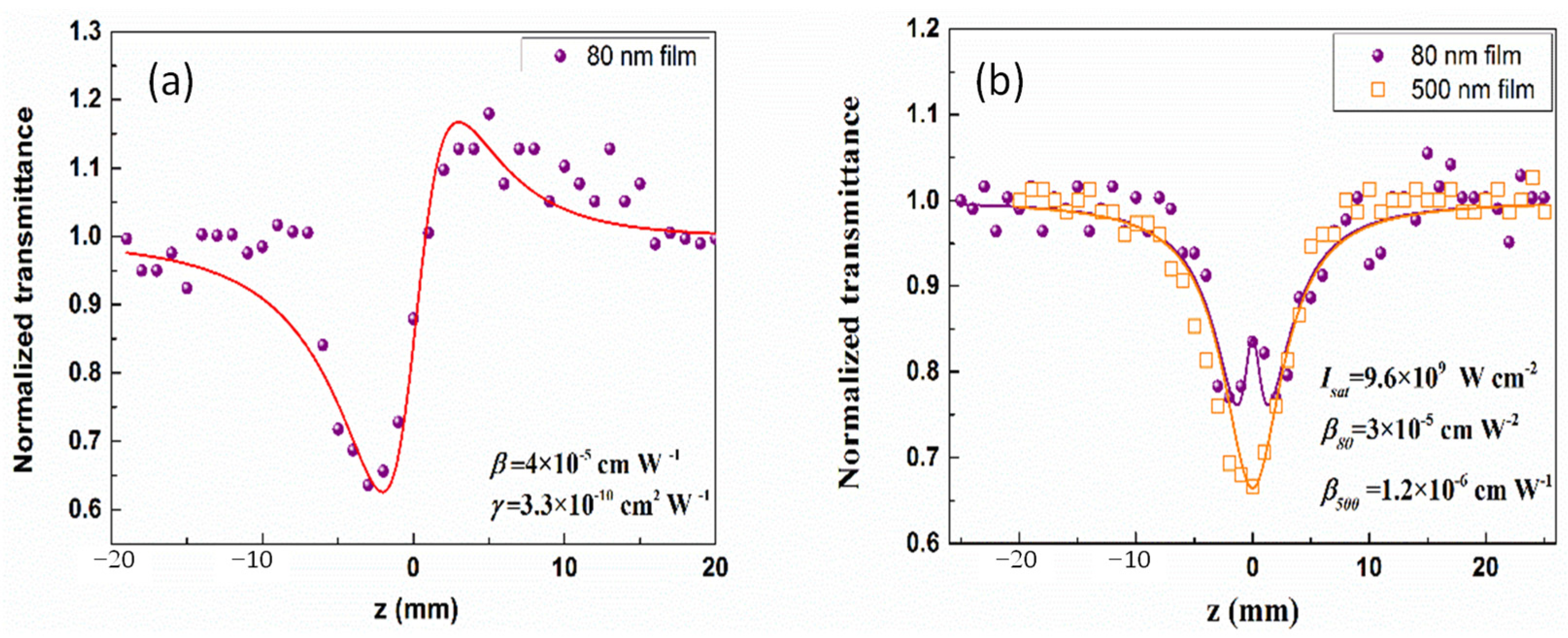
2.2. Thin Films Containing Ag2S Quantum Dots

The RSA and TPA are two most pronounced processes in Ag2S QDs liquid suspensions [17,18,19,20]. It is interesting to analyze the optical nonlinearities of these small-sized species prepared as thin films. Thin films can be used as the optical elements [21,22,23,24]. Here, I analyze the optical nonlinearities of Ag2S QD thin films [25].
The silver sulfide QD suspension was deposited on the thin glasses to produce the 80 and 500 nm thick films. The CA scans of Ag2S QD films are shown in Figure 3. The characteristics of probe pulses were as follow: pulse duration 30 fs, wavelength 800 nm, pulse energy 0.36 μJ. Those studies have shown that thinner film had larger nonlinear absorption attributed to the SA (−1 × 10−7 and −3.2 × 10−8 cm W−1 in the case of 80 and 500 nm films, respectively). The same can be said about the nonlinear refractive properties of the films of different thickness. The nonlinear refractive index of thinner film (1.1 × 10−11 cm2 W−1) was more than one order of magnitude larger than that of the thick film (γ = 1 × 10−12 cm2 W−1). Notice that previous studies of silver sulfide QDs were mostly limited by the the analysis of QD suspensions [26,27,28].
The same features were observed in the case of the measurements of the nonlinear refraction when γ in the case of 800 nm pulses was smaller than in the case of 400 nm pulses. The CA Z-scan of 80 nm film showed the positive nonlinear refraction (γ = 3.3 × 10−10 cm2 W−1,) and positive nonlinear absorption dominating in the CA scans of 80 nm film (Figure 4a). Meanwhile, the nonlinear refractive index of this thin film was calculated to be γ = 3.3 × 10−10 cm2 W−1, while the same parameter in the case of thicker film (500 nm) was 25 times smaller. In the case of 400 nm radiation (Figure 4b), the variation of the nonlinear absorption from SA to RSA was observed. Thus, the reviewed studies [25] have demonstrated the strong nonlinear optical response of films containing Ag2S QDs.

3. Low-Order NLO Properties of HgS, HgTe, and HgSe Quantum Dots

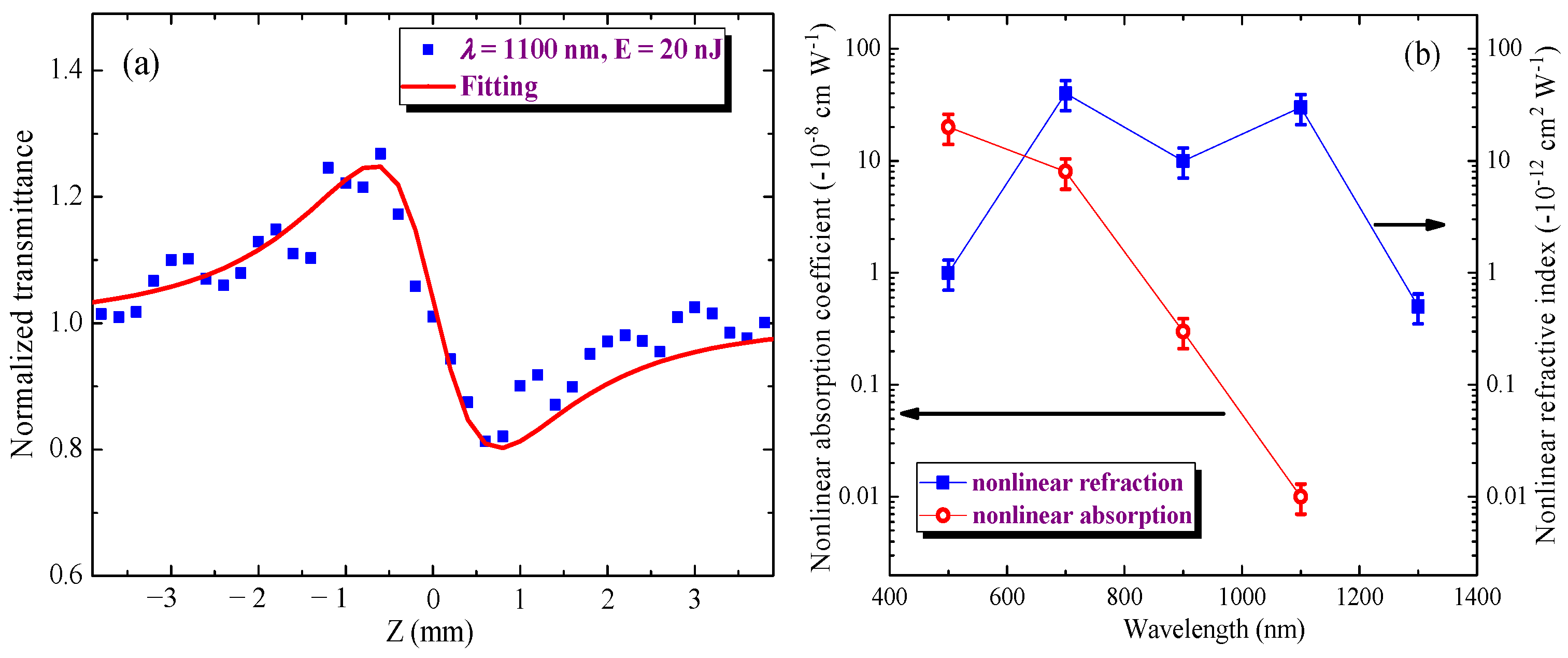
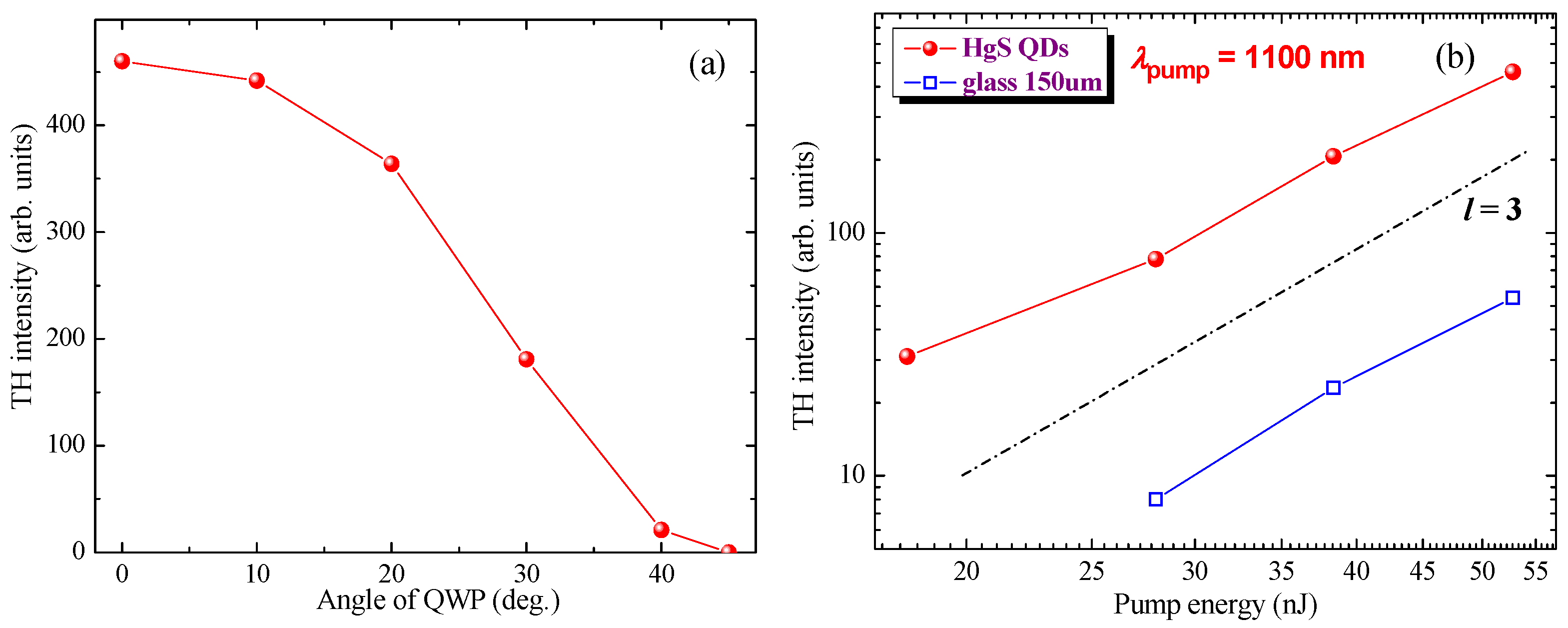
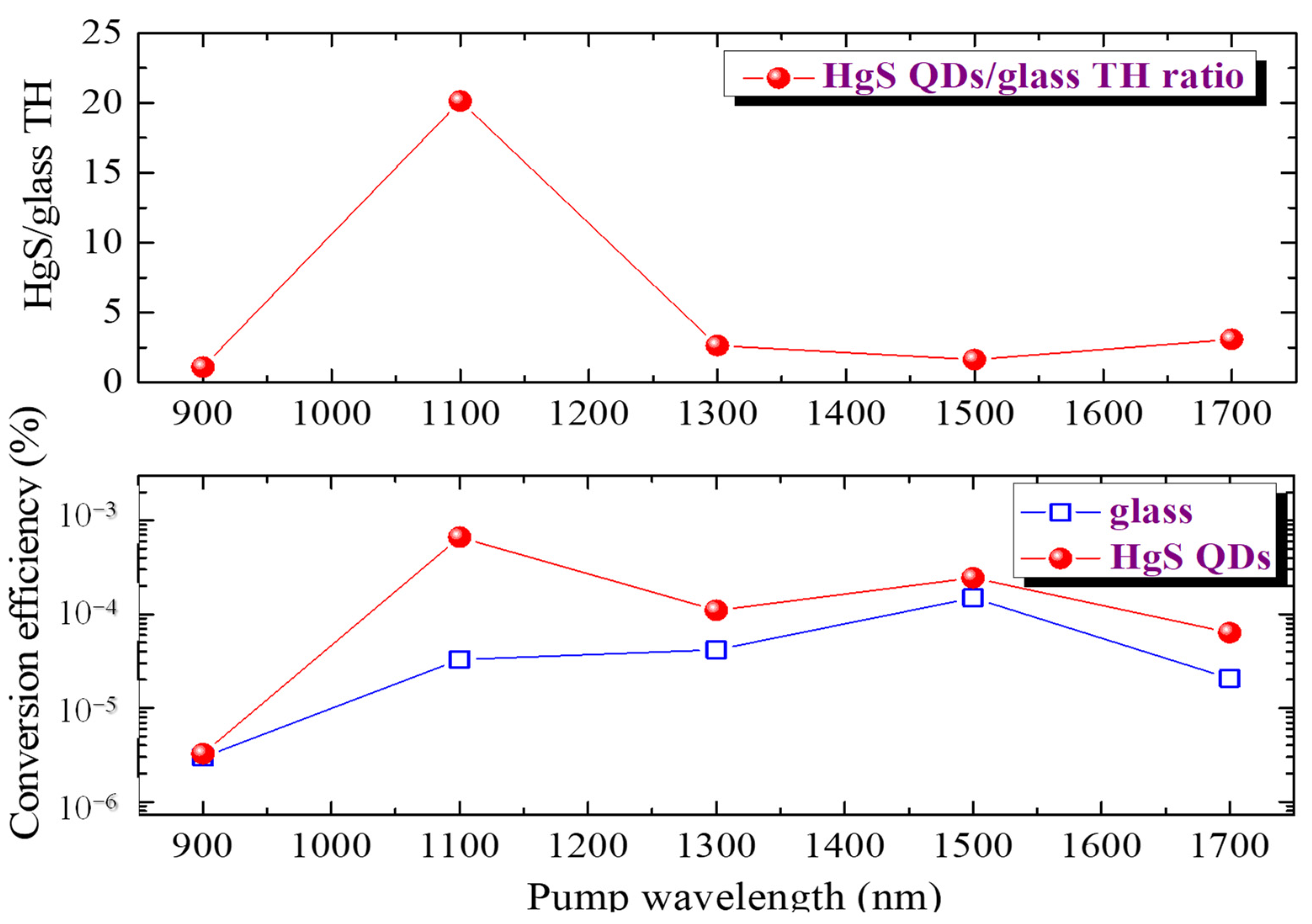
3.1. Mercury Sulfide Quantum Dots

Mercury sulfide (HgS) is a material useful in various areas of optoelectronics. Different modifications of this material like α-HgS (cinnabar, hexagonal) and β-HgS (meta cinnabar, zinc-blend type, cubic) have been extensively investigated. α-HgS is a wide bandgap semiconductor (Ebg = 2.0 eV), but it converts to the zinc-blende modification (β-HgS) at temperatures above 344 °C and becomes a narrow band gap semimetal (Ebg = 0.5 eV). It is a promising material for solar cells and sensors [29]. Bulk mercury sulfide is also suggested to be a topological insulator with potential applications in spintronics [30].
The nanostructures of HgS allow further applications of this material in different fields. Special attention attracts the cinnabar nanocrystals that crystallize in the trigonal system with a noncentrosymmetric structure. Meanwhile, HgS QDs remain much less studied species in comparison to other sulfides, e.g., PbS, ZnS, or CdS. The interest in their properties is related to the applications of HgS QDs as optical limiters, mode-lockers, and Q-switchers.
The third-harmonic generation (THG), nonlinear refraction, and nonlinear absorption in HgS QD suspensions and films were analyzed in [31] using the femtosecond and nanosecond pulses. The scheme and parameters of laser pulses were almost the same as in previously discussed cases. The 70-nm thick film of HgS QDs deposited on the 0.15-mm thick silica glass plate was used during those studies [32]. The mean size of the HgS QDs was 4 nm. The standard fitting procedure was applied to the measured Z-scans, when commonly used relations for the determination of the γ and nonlinear absorption coefficients attributed to the TPA (βTPA), SA (βsat), and RSA (βRSA), as well as saturated intensity (Isat), were applied to fit the experimental data.
The scheme for the measurements of TH yield was almost similar to the Z-scan scheme. The wavelength of laser allowed the tuning in the range of 190–2500 nm, while THG was analyzed in the 900–1700 nm range of laser radiation.
Figure 5a shows that the dominating nonlinear absorption process in HgS QD film is SA. The bleaching of the film steadily decreased for the longer-wavelength radiation. The spectral dependence of βsat was observed. The dependence of the βsat on the energy of the 500 nm PP is shown in Figure 5b.
The closed-aperture scan of studied film in the case of 1100 nm, 20 nJ, 150 fs pulses is shown in Figure 6a. This film was characterized by the negative sign of nonlinear refraction in a broad spectral range (500–1300 nm; γ = −2 × 10−11 cm2 W−1, Figure 6b, blue filled squares). Meanwhile, βsat was abruptly decreased in the case of the longer-wavelength PPs (Figure 6b, red empty circles).
Below, the nonlinear optical studies of the HgS QDs HgS QDs suspensions and films using nanosecond pulses are discussed. The longer PPs allowed observation of the replacement of the SA by the RSA in the extended (0.2 mm) medium (Figure 7a). The application of 532 nm pulses led to even stronger modification of the nonlinear absorption in this sample (Figure 7c). The scans shown in Figure 7c were fitted by standard procedure [33,34] to determine the corresponding SA and RSA processes (βsat = −6 × 10−8 cm W−1 and βRSA = 5 × 10−7 cm W−1). A similar parameter in the case of 1064 nm PP was derived using the same procedure (βsat = −4 × 10−9 cm W−1).
The application of relatively strong laser pulses (0.85 mJ) allowed observation of the negative nonlinear refraction of sample at λ = 1064 nm (Figure 7b, γ = −1 × 10−13 cm2 W−1). The self-defocusing at 532 nm was observed at the rather small energy of PP (0.005 mJ), thus determining the large value of the nonlinear refractive index (Figure 7d, γ = −6 × 10−13 cm2 W−1).
Below, I discuss the THG studies using the 1100 nm radiation. The intensity of the third harmonic (TH) from the 0.15 mm thick glass plate was more than one order of magnitude smaller than the thin (70 nm) film of HgS QDs deposited on the glass plate. The TH yield from thin film was calculated to be at least 4 × 107 times larger compared with TH yield from the pure glass substrate of similar thickness.
The polarization of PP strongly influenced the TH yield (Figure 8a). The experiments using the film + plate and pure plate samples followed the cubic dependence of the TH yield on the pulse energy along the whole range of the pulse energy variations (15–55 nJ, Figure 8b).
The spectral dependence of TH yield was analyzed by tuning the wavelength of PP in the 900–1700 nm range (Figure 9). The ratio of TH yields from the film + plate and pure plate are presented in the upper panel of this figure. The maximal ratio was achieved at the 1100 nm wavelength of PP.
In the case of thin film, the conversion efficiency towards third harmonic at λpump = 1100 nm was 7 × 10−4. The influence of the quantum confinement effect in the case of small-sized species (QDs) is a main factor increasing the harmonic yield.

3.2. Third-Order Nonlinearities of Mercury Telluride and Mercury Selenide QDs

The passive mode-lockers and optical switches can be based on the application of HgTe QDs. Mercury telluride QDs have the absorption range, which is useful for data transmission (1250 nm to 1630 nm) [35,36,37]. HgTe CQDs can also be used in various areas of photonics, e.g., quantum sensors, phototransistors, IR radiation detectors, and photovoltaic devices, as well as for photoconductive components of the optical schemes. Other properties of these QDs (multicolor detection and plasmon assisted photodetection) also attract the attention to these multi-particle species [38].
The 70-nm-thick films containing 4 nm HgTe QDs demonstrate large, saturated intensities, saturable absorption, and nonlinear refraction [39]. They also possess large values of saturable absorption and nonlinear refractive index in the case of probing by 150 fs and 28 ps pulses. The tunable laser source (400–1100 nm) allowed analyzing the spectral dependencies of above nonlinear optical parameters (γ = −3 × 10−9 cm2 W−1 at λ = 400 nm and β = −2.4 × 10−5 cm2 W−1 at 700 nm). In the case of 532 nm, 10 ns PP, the RSA was strongly manifested in those films, while in the case of short laser pulses this nonlinear optical process was not observed. Meanwhile, a significant growth of SA in the case of 28 ps pulses was demonstrated in the thin HgTe QD films. These films can thus be used as the low-Isat saturable absorbers, allowing the creation of low-threshold femtosecond lasers.
The saturated intensity in the case of 10 ns pulses (Isat = 5 × 108 W cm−2) was lower compared with the shorter probe pulses (7 × 109 and 4 × 1010 W cm−2 in the case of 28 ps and 150 fs pulses, respectively). The saturable absorbers possessing low Isat may allow formation of the low-threshold femtosecond laser sources. As for the measurements of nonlinear refraction, the variation of γ in the case of 28 ps and 10 ns PPs (−3 × 10−9 cm2 W−1 and −7 × 10−13 cm2 W−1, respectively) was attributed to the Kerr effect enhanced in the vicinity of the absorption band of QDs and the formation of the thermal lens.
One can expect the effectiveness in application of HgTe QDs for HHG due to the assumption about the connection between different types of optical nonlinearities. Numerous gas and plasma HHG studies have shown that small-sized species effectively generate stronger harmonics with regard to the atomic and molecular species. In this connection, HgTe QDs can generate stronger harmonics than HgTe nanoparticles and HgTe clusters.
The application of nanosecond pulses for the analysis of the low-order optical nonlinearities of mercury telluride QDs was reported in [40]. The characteristic features of those experiments using 532 nm pulses were the relatively large nonlinear refraction (γ = −6 × 10−13 cm2 W−1) and nonlinear absorption (βRSA = 1 × 10−8 cm W−1 and βSA = −4 × 10−9 cm W−1). These parameters were notably larger in comparison with the use of 1064 nm pulses (γ = −5 × 10−14 cm2 W−1, βTPA = 6 × 10−10 cm W−1).
In the case of mercury selenide QDs, the important parameter is the dependence of the position of intraband absorption peak in HgSe QDs on the ratio of Hg and Se components [41]. This species demonstrated the nonlinear absorption (β = 6 × 10−7 cm W−1) and negative nonlinear refraction (γ = −5 × 10−12 cm2 W−1) in the case of 10 ns, 532 nm PP. Meanwhile, for the twice longer wavelength, the only process was the negative nonlinear refraction.

4. Perspectives of Efficient High-Order Harmonics Generation of Ultrashort Laser Pulses Using Quantum Dots

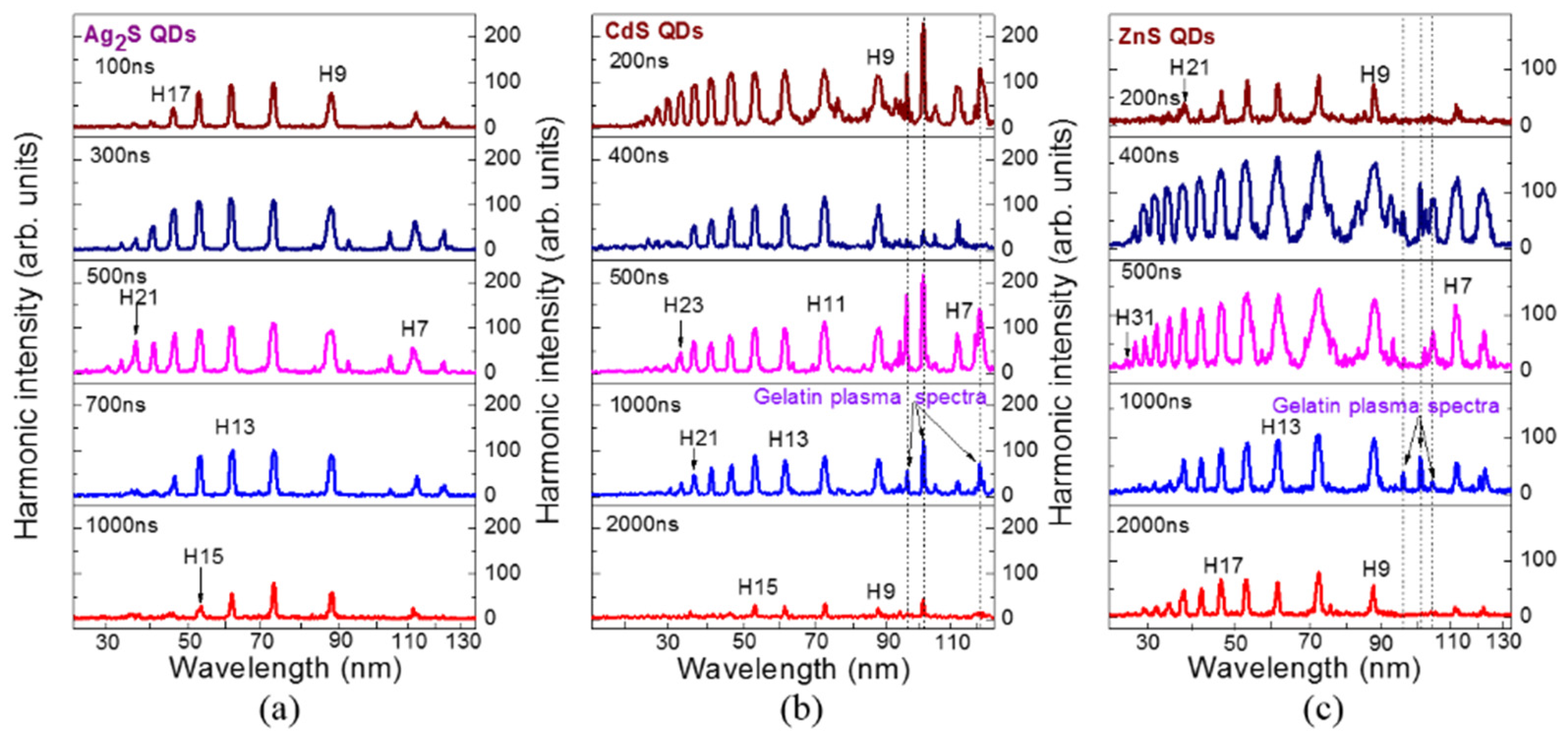
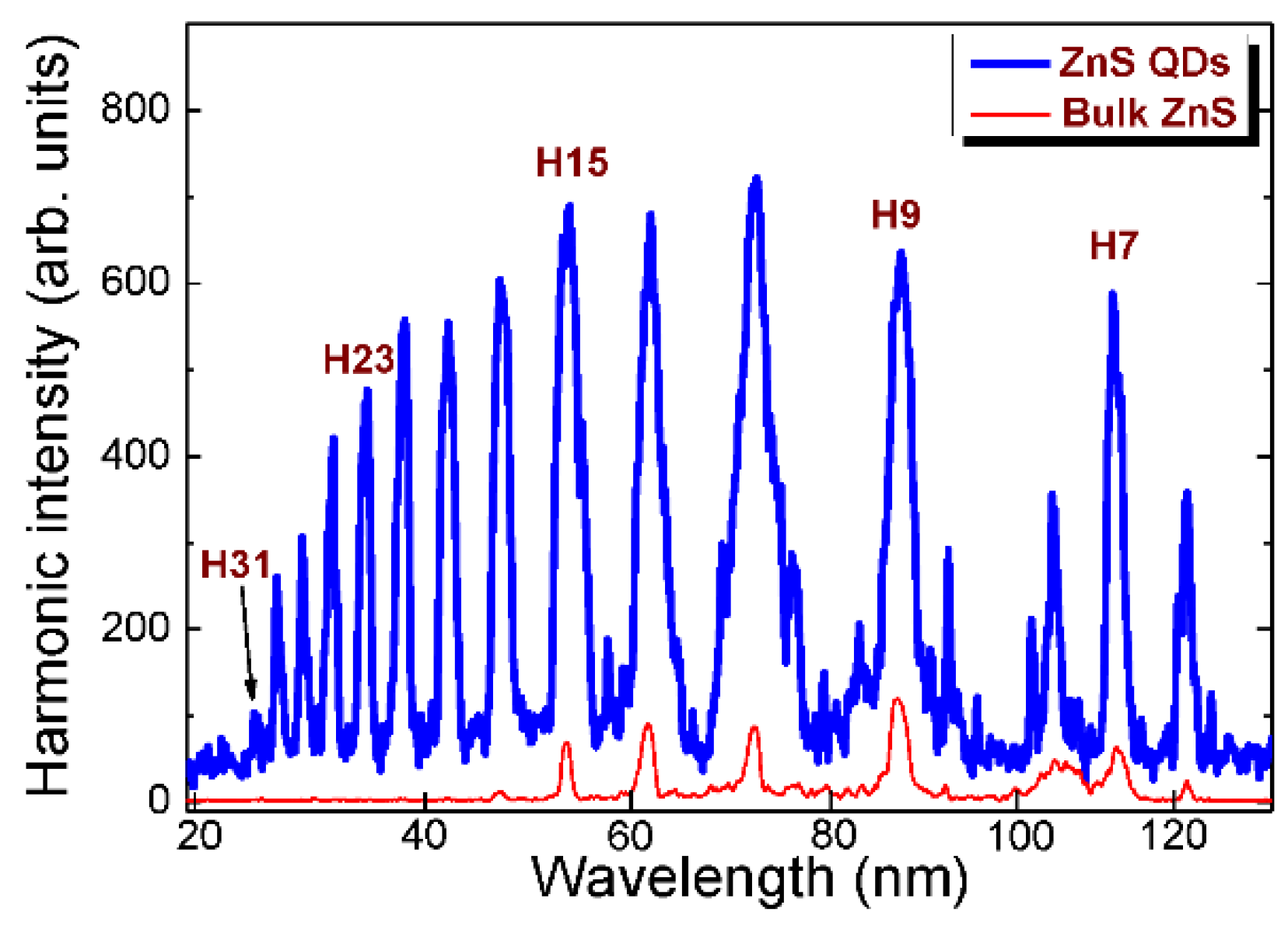
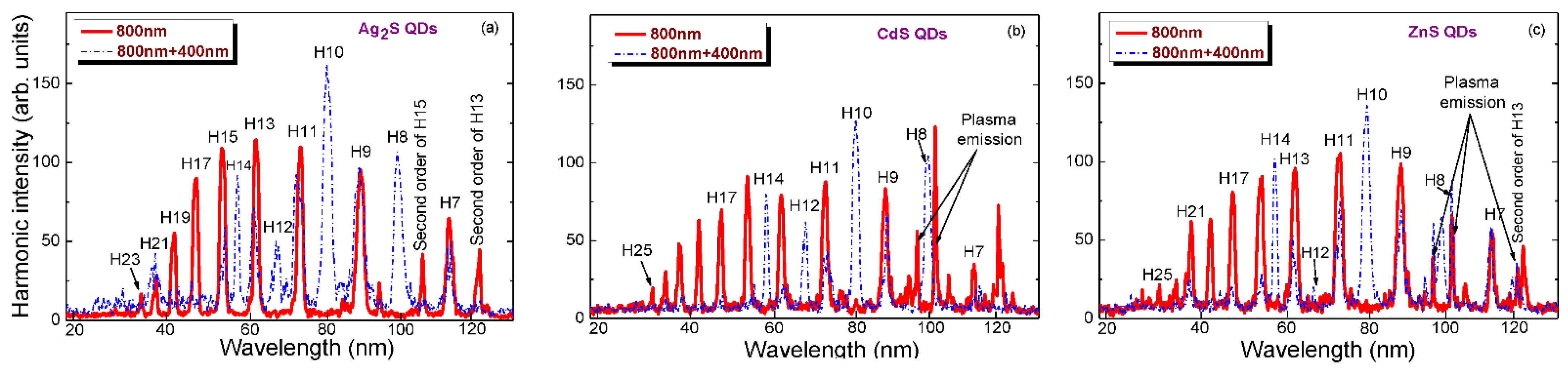
4.1. Application of Metal Sulfide QDs for HHG

In previous sections, it has been shown that large low-order optical nonlinearities of QDs make them attractive for various applications in photonics [42]. One of such applications is the generation of high-order harmonics of ultrashort laser pulses in the laser-induced plasmas (LIP) containing metal sulfide QDs [43]. A synthesis of such QDs followed by a formation of the QD-containing LIP make it possible to optimize the process of HHG during propagation of laser pulses through the plasma.
In the discussed studies [43], the synthesized colloidal silver, zinc, and cadmium sulfide QDs in stabilized polymers formed solid species, which being installed inside the vacuum chamber were then ablated to create the plasma cloud. The nanosecond heating pulses (HP) from a separate laser allowed the ignition of LIP at different delays varying between 0 and 106 ns with regard to the propagation of converting pulses using the digital delay generator. Then, after some delay from the beginning of ablation, the 30 fs, 800 nm driving pulses (DP) propagated at the distance of 0.2 mm from the target surface through the LIP to generate harmonics (Figure 10). The generated harmonics were analyzed by an extreme ultraviolet (XUV) spectrometer.
The two-color pump (TCP) of plasma was also used for harmonics generation. This technique has been successfully applied, alongside the single-color pump (SCP) of plasma or gas targets, to generated strong harmonics. The additional advantage of TCP is a generation of even and odd harmonics, contrary the case of SCP, when only odd harmonics generated [44,45,46,47]. Finally, this technique allowed achieving stronger harmonics compared with SCP of gases and plasmas. Second field (400 nm) was produced by installing the nonlinear crystal barium borate (BBO) on the path of the converting beam. In the discussed studies, the thin BBO installed inside the vacuum chamber allowed converting 4% of the driving field to the second harmonic. This amount of 400 nm radiation wave was sufficient for the efficient interaction of two waves in LIP.
The harmonic spectra generating in QDs are shown in Figure 11. HHG spectra at different delays between HP and DP allowed maximizing the yield of generating harmonics. Three studied QD plasmas showed different optimal delay between HP and DP (250, 300, and 400 ns for ZnS, CdS, and Ag2S QDs, respectively). The cutoffs in these experiments using Ag2S, CdS, and ZnS QD plasmas were H25, H29, and H31, respectively. These studies were carried out at the DP intensity 3 × 1014 W cm−2.
A comparison of the harmonic yields from the ablated bulk and QD-containing ZnS targets is shown in Figure 12. Similar conditions of experiment led to a significant difference in harmonic yields in these two cases. Stronger harmonics and extended cutoff (H31; ~50 eV (25 nm)) were obtained in the case of the QD plasma. Regarding the bandwidths of harmonics during the propagation of ultrashort pulses through the QD- and ions-containing plasmas, the former medium allowed a larger bandwidth. This effect can be induced by the growing bandwidth of the driving pulses propagating through the plasmas containing multi-particle species due to the self-phase modulation.
Figure 13 shows the three pairs of harmonics spectra in the case of SCP and TCP of Ag2S, CdS, and ZnS QD plasmas. One can see the appearance of even harmonics in the case of TCP of the studied LIPs. A very low energy of the 400 nm radiation with respect to the 800 nm one (~1:20) allowed to generate the even harmonics at similar efficiency as the odd ones. The reasons for the improvement of HHG efficiency in that case were suggested in [48]. A selection of the short quantum path component, which has a denser electron wave packet and higher ionization rate compared to SCP, the modification of the trajectory of accelerated electrons from being two-dimensional to three-dimensional, which may lead to a removal of the medium symmetry, and formation of a quasi-linear field in the case of the TCP of the generating medium were among the possible reasons for the growth of harmonic yield. The estimated conversion efficiency to the plateau harmonics was calculated to be ~3 × 10−5 in the case of ZnS QD LIP. Thus, the QDs having sizes of the order of a few nanometers efficiently generate harmonics. The simulations of harmonic yield from clusters predicted the increase of HHG efficiency.

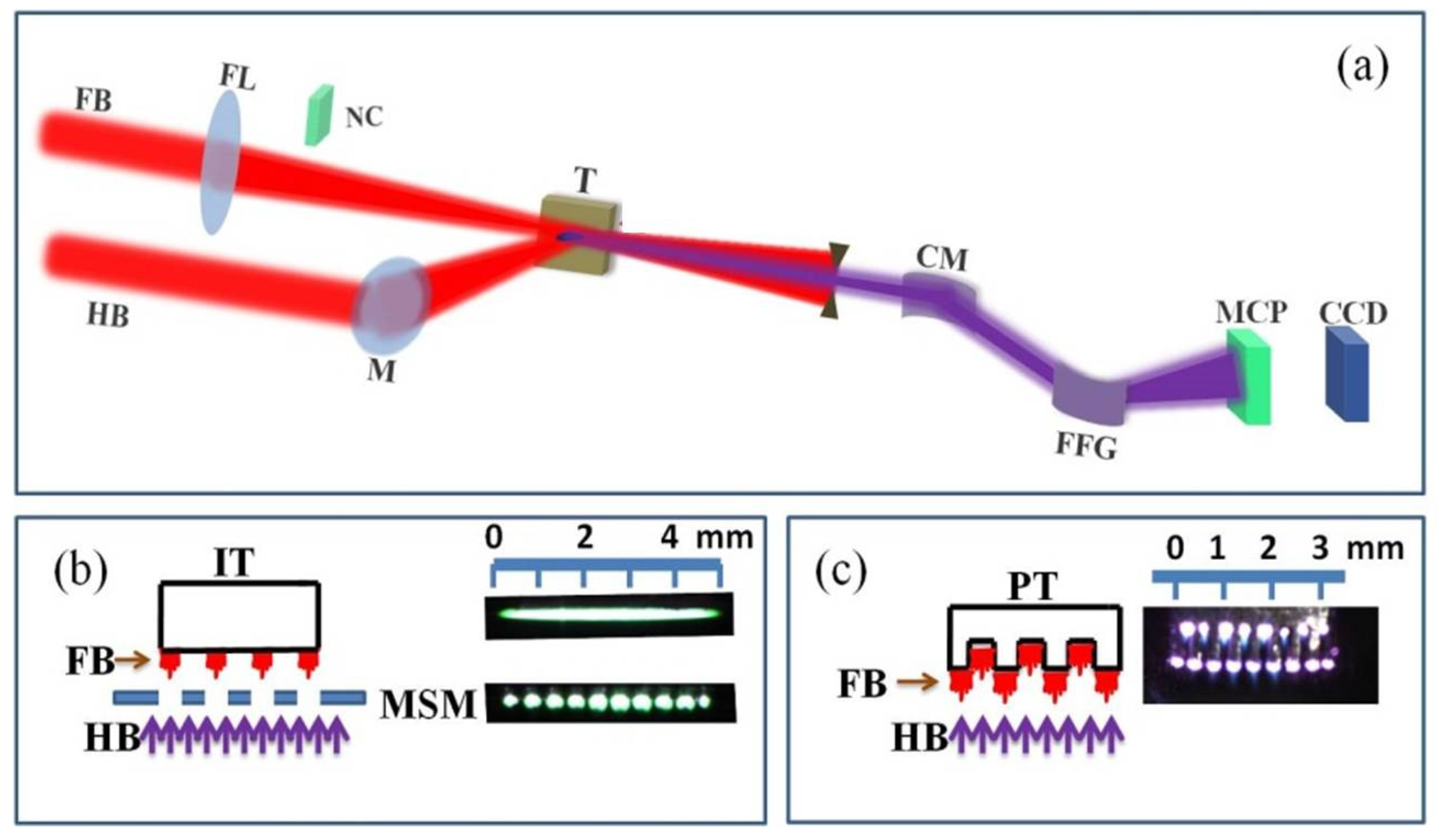
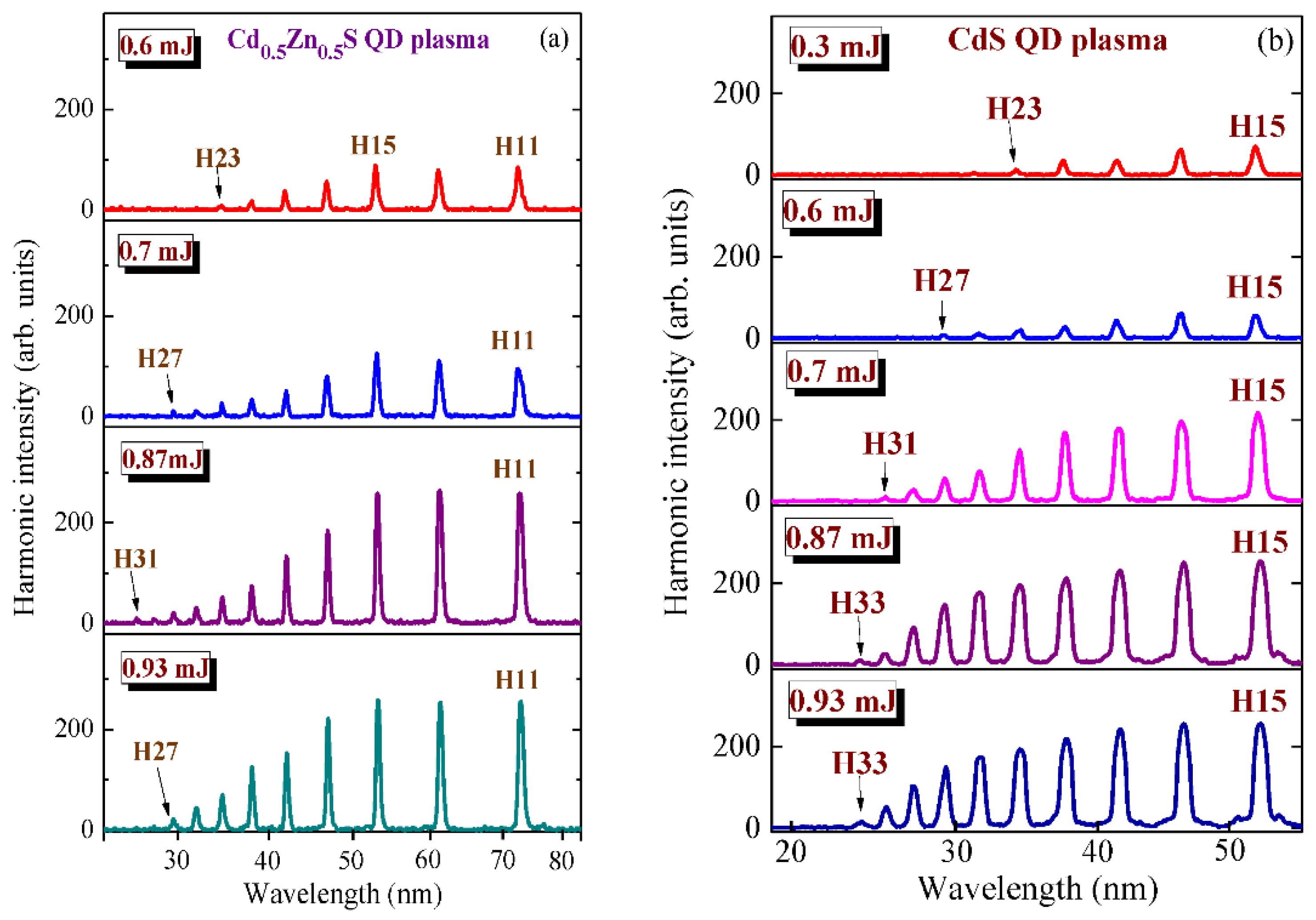
4.2. Quasi-Phase-Matching and Two-Color Pump of Extended QD Plasmas

The application of different approaches, such as quasi-phase-matching and TCP of QD LIPs, was reported in [49]. Various methods of optimization were applied to enhance the harmonic yield from QD emitters.
The mean sizes of Ag2S, CdS, and Cd0.5Zn0.5S QDs were 1.7, 3, and 2 nm, respectively. They were ablated in a vacuum chamber (Figure 14a). The cylindrical focusing optics allowed formation of the extended (5 mm) LIP contained QDs. The formation of extended plasmas allowed increasing the harmonic yield using both SCP and TCP schemes. The variation of extended QD-containing LIP using spatially structured heating beams allowed to achieve the quasi-phase-matching for driving and harmonic waves. The spatially structured beam of HPs was produced by insertion of the multi-slit mask on the path of this beam (Figure 14b). The application of another method when the target was initially perforated (Figure 14c) was less efficient compared with the structuring of the heating beam by multi-slit mask.
Two groups of harmonic spectra from extended LIPs containing Cd0.5Zn0.5S and CdS QDs at the DP energies varying from 0.3 to 0.93 mJ are shown in Figure 15. The spectral width of harmonics became a few times broader compared with the monomolecular plasmas. Similar behavior was observed in the case of bulk zinc sulfide and ZnS QD plasma (see Figure 12).
The formation of quasi-phase-matching conditions between the driving and harmonic waves in QD LIP is shown in Figure 16. Previously, gaseous [50,51] and atomic plasma [52] media were used for the demonstration of this phenomenon. A division of an extended medium into the groups of narrow media separated by a vacuum is a most useful method to realize this process in LIP.
The quasi-phase-matching in multi-jet LIP is determined by the presence of an optimal concentration of free electrons in a single jet. The formation of spatially structured plasma allows to achieve the difference in electron concentrations inside the plasma jet and the inter-jet space. The quasi-phase-matching conditions in the case of Ag2S bulk target are shown in Figure 16a in the form of a difference in the envelopes of harmonics distribution in the cases of extended homogeneous plasma and spatially structured plasma. The enhancement of higher orders of harmonics is clearly seen in the case of multi-jet plasmas compared with the extended imperforated plasma. Meanwhile, in the case of extended imperforated plasma, the harmonics above the 33rd order were barely seen. The 30× enhancement factor for H41 was achieved in the case of perforated LIP. The ablation of the mixture of Cd0.5Zn0.5S QDs and gelatin with and without the application of multi-slit mask led to a similar pattern (Figure 16b).
One can admit that all HHG studies were performed using the metal sulfide QDs. Why were only these species used in the first HHG experiments using QDs? Previous comparative studies have shown that metal sulfides possess larger nonlinear absorption and nonlinear refraction in the studied range of wavelengths and pulse durations compared with other QDs. They also demonstrated the relatively large conversion efficiency towards the third harmonic. There is an empirical assumption that the species possessing large value of the third-order nonlinear optical susceptibilities can demonstrate the enhanced yield of the high-order harmonics. Because of this, the metal sulfides were chosen for these experiments. Moreover, those QDs were synthesized and well characterized prior to the HHG experiments. The additional advantage of using those QDs is the narrow distribution of the sizes of metal sulfide QDs.
Another question is related with the QD size considered in those experiments. There is an assumption that the variations of QD sizes in the range of 2–7 nm should not significantly affect the nonlinear optical response of these species. For example, the mean size of Cd0.5Zn0.5S QDs was 2 nm. It was difficult to change the sizes of these synthesized QDs using chemical methods. In some particular cases, the sizes of some synthesized QD species were varied. However, for the discussed experimental studies, the most stable and homogeneous QDs were used. As it was pointed out, HHG in the studied cases can most probably be considered as a sum of harmonic emissions from different emitters. The size effect can be manifested once one compares the multi-particle species belonging to different categories of emitters (e.g., clusters, QDs, and NPs).

5. Summary

Different aspects of the nonlinear optical studies of QDs shown in this review underline the importance of the determination of the processes in these species manifested under the action of strong laser fields. Both low-order nonlinearities of QDs and HHG show the strong nonlinear optical response of these multi-particle species. The two-photon absorption, saturable absorption, reverse saturable absorption, as well as the nonlinear refraction in the solutions and films containing QDs were discussed. The generation of high-order harmonics at different regimes of laser–QD interaction was analyzed.

Funding

European Regional Development Fund (1.1.1.5/19/A/003).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

No new data were created or analyzed in this study. Data sharing is not applicable to this article.

Acknowledgments

I am grateful to V. V. Kim, I. A. Shuklov, G. S. Boltaev, A. I. Zvyagin, A. Bundulis, J. Grube, S. R. Konda, C. Guo, O. V. Ovchinnikov, A. Sarakovskis, and H. Zacharias for their collaboration during studies of the nonlinear optical properties of quantum dots.

Conflicts of Interest

The author declares no conflict of interest.

References

  1. Donnelly, T.D.; Ditmire, T.; Neuman, K.; Perry, M.D.; Falcone, R.W. High-order harmonic generation in atom clusters. Phys. Rev. Lett. 1996, 76, 2472. [Google Scholar] [CrossRef] [Green Version]
  2. Tisch, J.W.G.; Ditmire, T.; Fraser, D.J.; Hay, N.; Mason, M.B.; Springate, E.; Marangos, J.P.; Hutchinson, M.H.R. Investigation of high-harmonic generation from xenon atom clusters. J. Phys. B 1997, 30, L709. [Google Scholar] [CrossRef]
  3. Vozzi, C.; Nisoli, M.; Caumes, J.-P.; Sansone, G.; Stagira, S.; De Silvestri, S.; Vecchiocattivi, M.; Bassi, D.; Pascolini, M.; Poletto, L.; et al. Cluster effects in high-order harmonics generated by ultrashort light pulses. Appl. Phys. Lett. 2005, 86, 111121. [Google Scholar] [CrossRef]
  4. Ruf, H.; Handschin, C.; Cireasa, R.; Thiré, N.; Ferré, A.; Petit, S.; Descamps, D.; Mével, E.; Constant, E.; Blanchet, V.; et al. Inhomogeneous high harmonic generation in krypton clusters. Phys. Rev. Lett. 2013, 110, 083902. [Google Scholar] [CrossRef] [Green Version]
  5. Ganeev, R.A.; Suzuki, M.; Baba, M.; Ichihara, M.; Kuroda, H. High-order harmonic generation in Ag nanoparticle-contained plasma. J. Phys. B 2008, 41, 045603. [Google Scholar] [CrossRef]
  6. Singhal, H.; Naik, P.A.; Kumar, M.; Chakera, J.A.; Gupta, P.D. Enhanced coherent extreme ultraviolet emission through high order harmonic generation from plasma plumes containing nanoparticles. J. Appl. Phys. 2014, 115, 033104. [Google Scholar] [CrossRef]
  7. Chen, F.; Dai, S.; Xu, T.; Shen, X.; Lin, C.; Nie, Q.; Liu, C.; Heo, J. Surface-plasmon enhanced ultrafast third-order optical nonlinearities in ellipsoidal gold nanoparticles embedded bismuthate glasses. Chem. Phys. Lett. 2011, 514, 79–82. [Google Scholar] [CrossRef]
  8. Bailey, R.E.; Nie, S. Alloyed semiconductor quantum dots:  tuning the optical properties without changing the particle size. J. Am. Chem. Soc. 2003, 125, 7100–7106. [Google Scholar] [CrossRef]
  9. Tutt, L.W.; Kost, A. Optical limiting performance of C60 and C70 solutions. Nature 1992, 356, 225–226. [Google Scholar] [CrossRef]
  10. Venkatram, N.; Rao, D.N.; Akundi, M.A. Nonlinear absorption, scattering and optical limiting studies of CdS nanoparticles. Opt. Express 2005, 13, 867–872. [Google Scholar] [CrossRef]
  11. Karimzadeh, R.; Aleali, H.; Mansour, N. Thermal nonlinear refraction properties of Ag2S semiconductor nanocrystals with its application as a low power optical limiter. Opt. Commun. 2011, 284, 2370–2375. [Google Scholar] [CrossRef]
  12. Wu, F.; Zhang, G.; Tian, W.; Ma, L.; Chen, W.; Zhao, G.; Cao, S.; Xie, W. Nonlinear optical properties of CdSe0.8 S0.2 quantum dots. J. Opt. A 2008, 10, 075103. [Google Scholar] [CrossRef]
  13. Danilov, A.V.; Panfutova, A.S.; Khrebtov, A.I.; Titova, T.S. Specific features of resonant nonlinear absorption in colloidal solutions of CdSe/ZnS quantum dots. Opt. Spectrosc. 2015, 118, 94–98. [Google Scholar] [CrossRef]
  14. Yu, D.; Du, K.; Zhang, J.; Wang, F.; Chen, L.; Zhao, M.; Bian, J.; Feng, Y.; Jiao, Y. Composition-tunable nonlinear optical properties of ternary CdSexS1−x (x = 0–1) alloy quantum dots. New J. Chem. 2014, 38, 5081–5086. [Google Scholar] [CrossRef]
  15. Boltaev, G.S.; Fu, D.J.; Sobirov, B.R.; Smirnov, M.S.; Ovchinnikov, O.V.; Zvyagin, A.I.; Ganeev, R.A. Optical limiting, nonlinear refraction and nonlinear absorption of the associates of Cd0.5Zn0.5S quantum dots and dyes. Opt. Express 2018, 26, 13865. [Google Scholar] [CrossRef]
  16. Klyuev, V.G.; Volykhin, D.V.; Ovchinnikov, O.V.; Pokutnyi, S.I. Relationship between structural and optical properties of colloidal CdxZn1−xS quantum dots in gelatin. J. Nanophot. 2016, 10, 033507. [Google Scholar] [CrossRef]
  17. Sun, Y.P.; Riggs, J.E.; Henbest, K.B.; Martin, R.B. Nanomaterials as optical limiters. J. Nonlinear Opt. Phys. Mater. 2000, 9, 481–503. [Google Scholar] [CrossRef]
  18. Sheik-Bahae, M.; Said, A.A.; Wei, T.H.; Hagan, D.J.; Van Stryland, E.W. Sensitive measurement of optical nonlinearities using a single beam. IEEE J. Quantum Electron. 1990, 26, 760–769. [Google Scholar] [CrossRef] [Green Version]
  19. Liu, L.-W.; Hu, S.-Y.; Dou, Y.-P.; Liu, T.-H.; Lin, J.-Q.; Wang, Y. Nonlinear optical properties of near-infrared region Ag2S quantum dots pumped by nanosecond laser pulses. Beilstein J. Nanotech. 2015, 6, 1781–1787. [Google Scholar] [CrossRef] [Green Version]
  20. Fan, G.; Qu, S.; Wang, Q.; Zhao, C.; Zhang, L.; Li, Z. Pd nanoparticles formation by femtosecond laser irradiation and the nonlinear optical properties at 532 nm using nanosecond laser pulses. J. Appl. Phys. 2011, 109, 023102. [Google Scholar] [CrossRef]
  21. Disney, C.E.; Pillai, S.; Johnson, C.M.; Green, M.A. Self-assembled nanostructured rear reflector designs for thin-film solar cells. ACS Photonics 2015, 2, 1108–1116. [Google Scholar] [CrossRef]
  22. Kuang, P.; Eyderman, S.; Hsieh, M.L.; Post, A.; John, S.; Lin, S.-Y. Achieving an accurate surface profile of a photonic crystal for near-unity solar absorption in a super thin-film architecture. ACS Nano 2016, 10, 6116–6124. [Google Scholar] [CrossRef]
  23. Oskooi, A.; De Zoysa, M.; Ishizaki, K.; Noda, S. Experimental demonstration of quasi-resonant absorption in silicon thin films for enhanced solar light trapping. ACS Photonics 2014, 1, 304–309. [Google Scholar] [CrossRef] [Green Version]
  24. Aleali, H.; Mansour, N. Nanosecond high-order nonlinear optical effects in wide band gap silver sulfide nanoparticles colloids. Optik 2016, 127, 2485–2489. [Google Scholar] [CrossRef]
  25. Fu, Y.; Ganeev, R.A.; Boltaev, G.S.; Maurya, S.K.; Kim, V.V.; Zhao, C.; Rout, A.; Guo, C. Low- and high-order nonlinear optical properties of Ag2S quantum dot thin films. Nanophotonics 2019, 8, 849–858. [Google Scholar] [CrossRef]
  26. Fu, Y.; Ganeev, R.A.; Zhao, C.; Rao, K.S.; Maurya, S.k.; Yu, W.; Zhang, K.; Guo, C. Ag2S quantum dots in the fields of picosecond and femtosecond UV and IR pulses: Optical limiting, nonlinear absorption and refraction properties. Appl. Phys. B 2019, 125, 1. [Google Scholar] [CrossRef]
  27. Kondratenko, T.S.; Smirnov, M.S.; Ovchinnikov, O.V.; Zvyagin, A.I.; Ganeev, R.A.; Grevtseva, I.G. Nonlinear optical properties of hybrid associates of Ag2S quantum dots with erythrosine molecules. Optik 2020, 200, 163391. [Google Scholar] [CrossRef]
  28. Zvyagin, A.I.; Chevychelova, T.A.; Grevtseva, I.G.; Smirnov, M.S.; Selyukov, A.S.; Ovchinnikov, O.V.; Ganeev, R.A. Nonlinear refraction in colloidal silver sulfide quantum dots. J. Rus. Laser Res. 2020, 41, 670–680. [Google Scholar] [CrossRef]
  29. Wagh, R.A.; Kulkarni, A.N.; Baviskar, P.K.; Pathan, H.M.; Patil, R.S. Fabrication of titanium dioxide (TiO2) and mercury sulfide (HgS) heterojunction for photoelectrochemical study. Mater. Renew Sustain. Energy 2018, 7, 13. [Google Scholar] [CrossRef] [Green Version]
  30. Schooss, D.; Mews, A.; Eychmuller, A.; Weller, H. Quantum-dot quantum well CdS/HgS/CdS: Theory and experiment. Phys. Rev. B 1994, 49, 17072. [Google Scholar] [CrossRef]
  31. Kim, V.V.; Shuklov, I.A.; Mardini, A.A.; Bundulis, A.; Zvyagin, A.I.; Kholany, R.; Lizunova, A.A.; Grube, J.; Sarakovskis, A.; Ovchinnikov, O.V.; et al. Investigation of nonlinear optical processes in mercury sulfide quantum dots. Nanomaterials 2022, 12, 1264. [Google Scholar] [CrossRef] [PubMed]
  32. Goubet, N.; Jagtap, A.; Livache, C.; Martinez, B.; Portales, H.; Xu, X.Z.; Lobo, R.P.S.M.; Dubertret, B.; Lhuillier, E. Terahertz HgTe nanocrystals: Beyond confinement. J. Am. Chem. Soc. 2018, 140, 5033–5036. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  33. Yang, L.; Dorsinville, R.; Wang, Q.Z.; Ye, P.X.; Alfano, R.R.; Zamboni, T.; Taliani, C. Excited-state nonlinearity in polythiophene thin films investigated by the Z-scan technique. Opt. Lett. 1992, 17, 323–325. [Google Scholar] [CrossRef]
  34. Samoc, M.; Samoc, A.; Luther-Davies, B.; Reisch, H.; Scherf, U. Saturable absorption in poly(indenofluorene): A picket-fence polymer. Opt. Lett. 1998, 23, 1295–1297. [Google Scholar] [CrossRef] [PubMed]
  35. Gréboval, C.; Chu, A.; Goubet, N.; Livache, C.; Ithurria, S.; Lhuillier, E. Mercury chalcogenide quantum dots: Material perspective for device integration. Chem. Rev. 2021, 121, 3627–3700. [Google Scholar] [CrossRef]
  36. Rogalski, A. HgCdTe infrared detector material: History, status and outlook. Rep. Prog. Phys. 2005, 68, 2267. [Google Scholar] [CrossRef] [Green Version]
  37. Wang, P.; Xia, H.; Li, Q.; Wang, F.; Zhang, L.; Li, T.; Martyniuk, P.; Rogalski, A.; Hu, W. Sensing infrared photons at room temperature: From bulk materials to atomic layers. Small 2019, 15, 1904396. [Google Scholar] [CrossRef]
  38. Melnychuk, C.; Guyot-Sionnest, P. Thermodynamic limits to HgTe quantum dot infrared detector performance. J. Electron. Mater. 2022, 51, 1428–1435. [Google Scholar] [CrossRef]
  39. Bundulis, A.; Shuklov, I.A.; Kim, V.V.; Mardini, A.; Grube, J.; Alnis, J.; Lizunova, A.A.; Razumov, V.F.; Ganeev, R.A. Nonlinear absorption and refraction of picosecond and femtosecond pulses in HgTe quantum dot films. Nanomaterials 2021, 11, 3351. [Google Scholar] [CrossRef]
  40. Ganeev, R.A.; Shuklov, I.A.; Zvyagin, A.I.; Mardini, A.; Lizunova, A.A.; Boltaev, G.S.; Sapaev, I.B.; Kim, V.V.; Ovchinnikov, O.V.; Razumov, V.F. Optical nonlinearities of mercury telluride quantum dots measured by nanosecond pulses. Photon. Nanostruct. 2022, 50, 101025. [Google Scholar] [CrossRef]
  41. Ganeev, R.A.; Shuklov, I.A.; Zvyagin, A.I.; Dyomkin, D.V.; Smirnov, M.S.; Ovchinnikov, O.V.; Lizunova, A.A.; Perepukhov, A.M.; Popov, V.S.; Razumov, V.F. Synthesis and low-order optical nonlinearities of colloidal HgSe quantum dots in the visible and near infrared ranges. Opt. Express 2021, 29, 16710–16726. [Google Scholar] [CrossRef]
  42. Zeng, Z.; Garoufalis, C.S.; Terzis, A.F.; Baskoutas, S. Linear and nonlinear optical properties of ZnO/ZnS and ZnS/ZnO core shell quantum dots: Effects of shell thickness, impurity, and dielectric environment. J. Appl. Phys. 2013, 114, 023510. [Google Scholar] [CrossRef]
  43. Ganeev, R.A.; Boltaev, G.S.; Kim, V.V.; Zhang, K.; Zvyagin, A.I.; Smirnov, M.S.; Ovchinnikov, O.V.; Redkin, P.V.; Wöstmann, M.; Zacharias, H.; et al. Effective high-order harmonic generation from metal sulfide quantum dots. Opt. Express 2018, 26, 35013. [Google Scholar] [CrossRef] [PubMed]
  44. Kim, C.M.; Nam, C.H. Selection of an electron path of high-order harmonic generation in a two-colour femtosecond laser field. J. Phys. B 2006, 39, 3199. [Google Scholar] [CrossRef]
  45. Pfeifer, T.; Gallmann, L.; Abel, M.J.; Neumark, D.M.; Leone, S.R. Single attosecond pulse generation in the multicycle-driver regime by adding a weak second-harmonic field. Opt. Lett. 2006, 31, 975–977. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  46. Ganeev, R.A.; Singhal, H.; Naik, P.A.; Kulagin, I.A.; Redkin, P.V.; Chakera, J.A.; Tayyab, M.; Khan, R.A.; Gupta, P.D. Enhancement of high-order harmonic generation using two-color pump in plasma plumes. Phys. Rev. A 2009, 80, 033845. [Google Scholar] [CrossRef]
  47. Ganeev, R.A.; Strelkov, V.V.; Hutchison, C.; Zaïr, A.; Kilbane, D.; Khokhlova, M.A.; Marangos, J.P. Experimental and theoretical studies of two-color pump resonance-induced enhancement of odd and even harmonics from a tin plasma. Phys. Rev. A 2012, 85, 023832. [Google Scholar] [CrossRef]
  48. Kim, J.; Lee, G.H.; Park, S.B.; Lee, Y.S.; Kim, T.K.; Nam, C.H.; Mocek, T.; Jakubczak, K. Generation of submicrojoule high harmonics using a long gas jet in a two-color laser field. Appl. Phys. Lett. 2008, 92, 021125. [Google Scholar] [CrossRef] [Green Version]
  49. Ganeev, R.A.; Boltaev, G.S.; Kim, V.V.; Venkatesh, M.; Zvyagin, A.I.; Smirnov, M.S.; Ovchinnikov, O.V.; Wöstmann, M.; Zacharias, H.; Guo, C. High-order harmonic generation using quasi-phase matching and two-color pump of the plasmas containing molecular and alloyed metal sulfide quantum dots. J. Appl. Phys. 2019, 126, 193103. [Google Scholar] [CrossRef]
  50. Seres, J.; Yakovlev, V.S.; Seres, E.; Streli, C.H.; Wobrauschek, P.; Spielmann, C.H.; Krausz, F. Coherent superposition of laser-driven soft-X-ray harmonics from successive sources. Nat. Phys. 2007, 3, 878–883. [Google Scholar] [CrossRef]
  51. Pirri, A.; Corsi, C.; Bellini, M. Enhancing the yield of high-order harmonics with an array of gas jets. Phys. Rev. A 2008, 78, 011801. [Google Scholar] [CrossRef] [Green Version]
  52. Wöstmann, M.; Splitthoff, L.; Zacharias, H. Control of quasi-phase-matching of high-harmonics in a spatially structured plasma. Opt. Express 2018, 26, 14524–14537. [Google Scholar] [CrossRef] [PubMed]
Photonics 09 00757 g001 550
Figure 1. (a) OL in Cd0.5Zn0.5S QDs and Cd0.5Zn0.5S QDs+erythrosine. Z-scan scheme is presented in the inset. (b,c) OA and CA scans of Cd0.5Zn0.5S QDs using 1064 nm (b) and 532 nm (c) pulses. Adapted with permission from Ref. [15], 2018, Optica Publishing Group.
Figure 1. (a) OL in Cd0.5Zn0.5S QDs and Cd0.5Zn0.5S QDs+erythrosine. Z-scan scheme is presented in the inset. (b,c) OA and CA scans of Cd0.5Zn0.5S QDs using 1064 nm (b) and 532 nm (c) pulses. Adapted with permission from Ref. [15], 2018, Optica Publishing Group.
Photonics 09 00757 g001
Photonics 09 00757 g002 550
Figure 2. (a) Open-aperture scans of Cd0.5Zn0.5S QD+thionine suspension in the case of 1064 and 532 nm pulses. (b) Open-aperture scans of Cd0.5Zn0.5S QD+erythrosine suspension in the case of 1064 and 532 nm pulses. Reprinted with permission from Ref. [15], 2018, Optica Publishing Group.
Figure 2. (a) Open-aperture scans of Cd0.5Zn0.5S QD+thionine suspension in the case of 1064 and 532 nm pulses. (b) Open-aperture scans of Cd0.5Zn0.5S QD+erythrosine suspension in the case of 1064 and 532 nm pulses. Reprinted with permission from Ref. [15], 2018, Optica Publishing Group.
Photonics 09 00757 g002
Photonics 09 00757 g003 550
Figure 3. Z-scan measurements of Ag2S QD films at λ = 800 nm. CA Z-scans of (a) 80 nm and (b) 500 nm thick films. Solid curves show the fits of Z-scans. Reprinted with permission from Ref. [25], 2019, Walter de Gruyter GmbH & Science Wise Publishing.
Figure 3. Z-scan measurements of Ag2S QD films at λ = 800 nm. CA Z-scans of (a) 80 nm and (b) 500 nm thick films. Solid curves show the fits of Z-scans. Reprinted with permission from Ref. [25], 2019, Walter de Gruyter GmbH & Science Wise Publishing.
Photonics 09 00757 g003
Photonics 09 00757 g004 550
Figure 4. Normalized transmittances in the case of (a) CA Z-scan of 80 nm film and (b) OA Z-scans of 80 nm and 500 nm films measured using the 400 nm, 35 fs pulses. Theoretical curves are the fits using Z-scan theory. Reprinted with permission from Ref. [25], 2019, Walter de Gruyter GmbH & Science Wise Publishing.
Figure 4. Normalized transmittances in the case of (a) CA Z-scan of 80 nm film and (b) OA Z-scans of 80 nm and 500 nm films measured using the 400 nm, 35 fs pulses. Theoretical curves are the fits using Z-scan theory. Reprinted with permission from Ref. [25], 2019, Walter de Gruyter GmbH & Science Wise Publishing.
Photonics 09 00757 g004
Photonics 09 00757 g005 550
Figure 5. (a) Application of 500, 700, and 900 nm radiation for OA Z-scan studies of HgS QD film. (b) Variation of β at different energies of PP. Reprinted with permission from Ref. [31], 2022, MDPI.
Figure 5. (a) Application of 500, 700, and 900 nm radiation for OA Z-scan studies of HgS QD film. (b) Variation of β at different energies of PP. Reprinted with permission from Ref. [31], 2022, MDPI.
Photonics 09 00757 g005
Photonics 09 00757 g006 550
Figure 6. (a) Negative nonlinear refraction in the case of 1100 nm, 20 nJ, 150 fs PP. (b) Variations of βsat and γ along the studied spectral range. Reprinted with permission from Ref. [31], 2022, MDPI.
Figure 6. (a) Negative nonlinear refraction in the case of 1100 nm, 20 nJ, 150 fs PP. (b) Variations of βsat and γ along the studied spectral range. Reprinted with permission from Ref. [31], 2022, MDPI.
Photonics 09 00757 g006
Photonics 09 00757 g007 550
Figure 7. (a,c) Open-aperture scans and (b,d) closed-aperture of HgS QD suspension using 1064 nm pulses (a,b) and 532 nm pulses (c,d). Reprinted with permission from Ref. [31], 2022, MDPI.
Figure 7. (a,c) Open-aperture scans and (b,d) closed-aperture of HgS QD suspension using 1064 nm pulses (a,b) and 532 nm pulses (c,d). Reprinted with permission from Ref. [31], 2022, MDPI.
Photonics 09 00757 g007
Photonics 09 00757 g008 550
Figure 8. (a) The dependence of TH yield on the angle of quarter-wave plate (QWP). (b) Dependence of harmonic yield on the pulse energy. Reprinted with permission from Ref. [31], 2022, MDPI.
Figure 8. (a) The dependence of TH yield on the angle of quarter-wave plate (QWP). (b) Dependence of harmonic yield on the pulse energy. Reprinted with permission from Ref. [31], 2022, MDPI.
Photonics 09 00757 g008
Photonics 09 00757 g009 550
Figure 9. Upper panel shows the ratio of TH yields from the film + plate and pure plate. Bottom panel shows the absolute values of TH conversion efficiencies in the case of film + plate and plate. Reprinted with permission from Ref. [31], 2022, MDPI.
Figure 9. Upper panel shows the ratio of TH yields from the film + plate and pure plate. Bottom panel shows the absolute values of TH conversion efficiencies in the case of film + plate and plate. Reprinted with permission from Ref. [31], 2022, MDPI.
Photonics 09 00757 g009
Photonics 09 00757 g010 550
Figure 10. Experimental setup of harmonic generation in the LIP containing QDs. Reprinted with permission from Ref. [43], 2018, Optica Publishing Group.
Figure 10. Experimental setup of harmonic generation in the LIP containing QDs. Reprinted with permission from Ref. [43], 2018, Optica Publishing Group.
Photonics 09 00757 g010
Photonics 09 00757 g011 550
Figure 11. HHG in (a) silver sulfide QDs, (b) cadmium sulfide QDs, and (c) zinc sulfide QDs. Reprinted with permission from Ref. [43], 2018, Optica Publishing Group.
Figure 11. HHG in (a) silver sulfide QDs, (b) cadmium sulfide QDs, and (c) zinc sulfide QDs. Reprinted with permission from Ref. [43], 2018, Optica Publishing Group.
Photonics 09 00757 g011
Photonics 09 00757 g012 550
Figure 12. Harmonic distributions during propagation of DP through the plasmas produced on the bulk ZnS (red curve) and ZnS QD (blue curve) targets. Reprinted with permission from Ref. [43], 2018, Optica Publishing Group.
Figure 12. Harmonic distributions during propagation of DP through the plasmas produced on the bulk ZnS (red curve) and ZnS QD (blue curve) targets. Reprinted with permission from Ref. [43], 2018, Optica Publishing Group.
Photonics 09 00757 g012
Photonics 09 00757 g013 550
Figure 13. SCP and TCP of (a) Ag2S, (b) CdS, and (c) ZnS QDs. Reprinted with permission from Ref. [43], 2018, Optica Publishing Group.
Figure 13. SCP and TCP of (a) Ag2S, (b) CdS, and (c) ZnS QDs. Reprinted with permission from Ref. [43], 2018, Optica Publishing Group.
Photonics 09 00757 g013
Photonics 09 00757 g014 550
Figure 14. (a) HHG scheme. (b) Multi-jet plasma using multi-slit mask and flat surface. (c) Multi-jet plasma formed on the perforated target. Reprinted with permission from Ref. [49], 2019, American Institute of Physics.
Figure 14. (a) HHG scheme. (b) Multi-jet plasma using multi-slit mask and flat surface. (c) Multi-jet plasma formed on the perforated target. Reprinted with permission from Ref. [49], 2019, American Institute of Physics.
Photonics 09 00757 g014
Photonics 09 00757 g015 550
Figure 15. (a) HHG in Cd0.5Zn0.5S QD LIP. (b) HHG in CdS QD LIP. Reprinted with permission from Ref. [49], 2019, American Institute of Physics.
Figure 15. (a) HHG in Cd0.5Zn0.5S QD LIP. (b) HHG in CdS QD LIP. Reprinted with permission from Ref. [49], 2019, American Institute of Physics.
Photonics 09 00757 g015
Photonics 09 00757 g016 550
Figure 16. Quasi-phase-matching in (a) bulk (Ag2S) and (b) QD (Cd0.5Zn0.5S) plasmas. Reprinted with permission from Ref. [49], 2019, American Institute of Physics.
Figure 16. Quasi-phase-matching in (a) bulk (Ag2S) and (b) QD (Cd0.5Zn0.5S) plasmas. Reprinted with permission from Ref. [49], 2019, American Institute of Physics.
Photonics 09 00757 g016
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Ganeev, R.A. Low- and High-Order Optical Nonlinearities of Quantum Dots. Photonics 2022, 9, 757. https://doi.org/10.3390/photonics9100757

AMA Style

Ganeev RA. Low- and High-Order Optical Nonlinearities of Quantum Dots. Photonics. 2022; 9(10):757. https://doi.org/10.3390/photonics9100757

Chicago/Turabian Style

Ganeev, Rashid A. 2022. "Low- and High-Order Optical Nonlinearities of Quantum Dots" Photonics 9, no. 10: 757. https://doi.org/10.3390/photonics9100757

APA Style

Ganeev, R. A. (2022). Low- and High-Order Optical Nonlinearities of Quantum Dots. Photonics, 9(10), 757. https://doi.org/10.3390/photonics9100757

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop