Generation of Three-Mode Entanglement Based on Parametric Amplifiers Using Quantum Entanglement Swapping
Abstract
1. Introduction
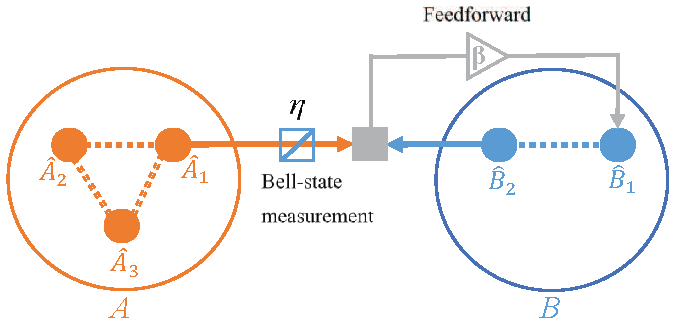
2. The Scheme for the Generation of Three-Mode Entanglement
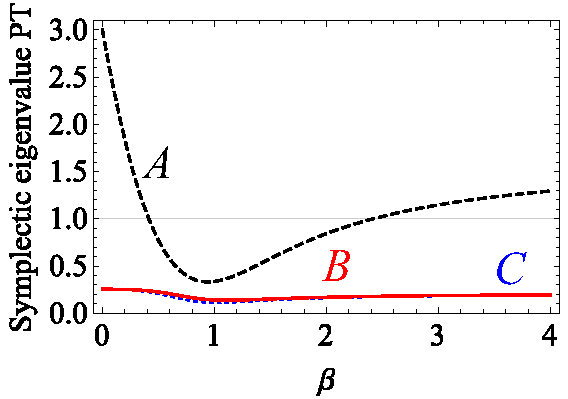
3. Three-Mode Entanglement
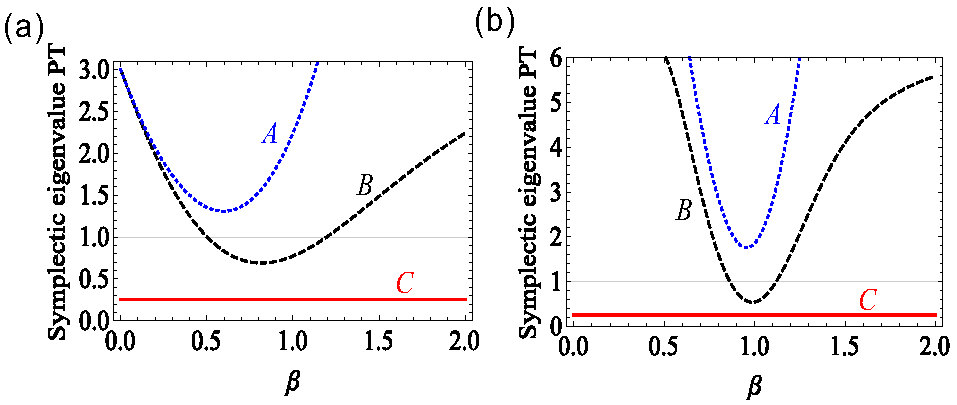
4. Two-Mode Entanglement
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zukowski, M.; Zeilinger, A.; Horne, M.A.; Ekert, A. “Event-ready-detectors” Bell experiment via entanglement swapping. Phys. Rev. Lett. 1993, 71, 4287–4290. [Google Scholar] [CrossRef] [PubMed]
- Pan, J.W.; Bouwmeester, D.; Weinfurter, H.; Zeilinger, A. Experimental Entanglement Swapping: Entangling Photons That Never Interacted. Phys. Rev. Lett. 1998, 80, 3891–3894. [Google Scholar] [CrossRef]
- Tan, S.M. Confirming entanglement in continuous variable quantum teleportation. Phys. Rev. A 1999, 60, 2752–2758. [Google Scholar] [CrossRef]
- Van Loock, P.; Braunstein, S.L. Unconditional teleportation of continuous-variable entanglement. Phys. Rev. A 1999, 61, 010302. [Google Scholar] [CrossRef]
- Sciarrino, F.; Lombardi, E.; Milani, G.; Martini, F. Delayed-choice entanglement swapping with vacuum-one-photon quantum states. Phys. Rev. A 2002, 66, 024309. [Google Scholar] [CrossRef]
- Jia, X.; Su, X.; Pan, Q.; Gao, J.; Xie, C.; Peng, K. Experimental Demonstration of Unconditional Entanglement Swapping for Continuous Variables. Phys. Rev. Lett. 2004, 93, 250503. [Google Scholar] [CrossRef] [PubMed]
- De Riedmatten, H.; Marcikic, I.; van Houwelingen, J.A.W.; Tittel, W.; Zbinden, H.; Gisin, N. Long-distance entanglement swapping with photons from separated sources. Phys. Rev. A 2005, 71, 050302. [Google Scholar] [CrossRef]
- Takei, N.; Yonezawa, H.; Aoki, T.; Furusawa, A. High-Fidelity Teleportation beyond the No-Cloning Limit and Entanglement Swapping for Continuous Variables. Phys. Rev. Lett. 2005, 94, 220502. [Google Scholar] [CrossRef] [PubMed]
- Bose, S.; Vedral, V.; Knight, P.L. Multiparticle generalization of entanglement swapping. Phys. Rev. A 1998, 57, 822. [Google Scholar] [CrossRef]
- Su, X.; Tian, C.; Deng, X.; Li, Q.; Xie, C.; Peng, K. Quantum Entanglement Swapping between Two Multipartite Entangled States. Phys. Rev. Lett. 2016, 117, 240503. [Google Scholar] [CrossRef]
- Lu, C.Y.; Yang, T.; Pan, J.W. Experimental Multiparticle Entanglement Swapping for Quantum Networking. Phys. Rev. Lett. 2009, 103, 020501. [Google Scholar] [CrossRef]
- Takeda, S.; Fuwa, M.; van Loock, P.; Furusawa, A. Entanglement Swapping between Discrete and Continuous Variables. Phys. Rev. Lett. 2015, 114, 10050. [Google Scholar] [CrossRef] [PubMed]
- Polkinghorne, R.E.S.; Ralph, T.C. Continuous Variable Entanglement Swapping. Phys. Rev. Lett. 1999, 83, 2095–2099. [Google Scholar] [CrossRef]
- Qin, Z.; Cao, L.; Wang, H.; Marino, A.M.; Zhang, W.; Jing, J. Experimental Generation of Multiple Quantum Correlated Beams from Hot Rubidium Vapor. Phys. Rev. Lett. 2014, 113, 023602. [Google Scholar] [CrossRef] [PubMed]
- Boyer, V.; Marino, A.M.; Pooser, R.C.; Lett, P.D. Entangled images from four-wave mixing. Science 2008, 321, 544–547. [Google Scholar] [CrossRef] [PubMed]
- Marino, A.M.; Pooser, R.C.; Boyer, V.; Lett, P.D. Tunable delay of Einstein-Podolsky-Rosen entanglement. Nature 2009, 457, 859–862. [Google Scholar] [CrossRef] [PubMed]
- Glorieux, Q.; Guidoni, L.; Guibal, S.; Likforman, J.P.; Coudreau, T. Quantum correlations by four-wave mixing in an atomic vapor in a nonamplifying regime: Quantum beam splitter for photons. Phys. Rev. A 2011, 84, 053826. [Google Scholar] [CrossRef]
- Jasperse, M.; Turner, L.D.; Scholten, R.E. Relative intensity squeezing by four-wave mixing with loss: An analytic model and experimental diagnostic. Opt. Express 2011, 19, 3765–3774. [Google Scholar] [CrossRef] [PubMed]
- Pooser, R.C.; Marino, A.M.; Boyer, V.; Jones, K.M.; Lett, P.D. Low-Noise Amplification of a Continuous-Variable Quantum State. Phys. Rev. Lett. 2009, 103, 010501. [Google Scholar] [CrossRef]
- Pooser, R.C.; Lawrie, B. Ultrasensitive measurement of microcantilever displacement below the shot-noise limit. Optica 2015, 2, 393–399. [Google Scholar] [CrossRef]
- Lawrie, B.J.; Evans, P.G.; Pooser, R.C. Extraordinary Optical Transmission of Multimode Quantum Correlations via Localized Surface Plasmons. Phys. Rev. Lett. 2013, 110, 156802. [Google Scholar] [CrossRef] [PubMed]
- Fan, W.; Lawrie, B.J.; Pooser, R.C. Quantum plasmonic sensing. Phys. Rev. A 2015, 92, 053812. [Google Scholar] [CrossRef]
- MacRae, A.; Brannan, T.; Achal, R.; Lvovsky, A.I. Tomography of a High-Purity Narrowband Photon from a Transient Atomic Collective Excitation. Phys. Rev. Lett. 2012, 109, 033601. [Google Scholar] [CrossRef] [PubMed]
- Hudelist, F.; Kong, J.; Liu, C.; Jing, J.; Ou, Z.; Zhang, W. Quantum metrology with parametric amplifier-based photon correlation interferometers. Nat. Commun. 2014, 5, 3049. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Zheng, Z.; Wang, Y.; Jing, J. Generation of tripartite entanglement from cascaded four-wave mixing processes. Opt. Express 2016, 24, 23459–23470. [Google Scholar] [CrossRef]
- Cao, L.; Qi, J.; Du, J.; Jing, J. Experimental generation of quadruple quantum-correlated beams from hot rubidium vapor by cascaded four-wave mixing using spatial multiplexing. Phys. Rev. A 2017, 95, 023803. [Google Scholar] [CrossRef]
- Simon, R. Peres-Horodecki Separability Criterion for Continuous Variable Systems. Phys. Rev. Lett. 2000, 84, 2726–2729. [Google Scholar] [CrossRef] [PubMed]
- Werner, R.F.; Wolf, M.M. Bound Entangled Gaussian States. Phys. Rev. Lett. 2001, 86, 3658–3661. [Google Scholar] [CrossRef] [PubMed]
- Cassemiro, K.N.; Villar, A.S. Scalable continuous-variable entanglement of light beams produced by optical parametric oscillators. Phys. Rev. A 2008, 77, 022311. [Google Scholar] [CrossRef]
- Barbosa, F.A.S.; de Faria, A.J.; Coelho, A.S.; Cassemiro, K.N.; Villar, A.S.; Nussenzveig, P.; Martinelli, M. Disentanglement in bipartite continuous-variable systems. Phys. Rev. A 2011, 84, 052330. [Google Scholar] [CrossRef]
- Barbosa, F.A.S.; Coelho, A.S.; de Faria, A.J.; Cassemiro, K.N.; Villar, A.S.; Nussenzveig, P.; Martinelli, M. Robustness of bipartite Gaussian entangled beams propagating in lossy channels. Nat. Photon. 2010, 4, 858–861. [Google Scholar] [CrossRef]
- Coelho, A.S.; Barbosa, F.A.S.; Cassemiro, K.N.; Villar, A.S.; Martinelli, M.; Nussenzveig, P. Three-Color Entanglement. Science 2009, 326, 823–826. [Google Scholar] [CrossRef] [PubMed]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Ru, N.; Lin, P. Generation of Three-Mode Entanglement Based on Parametric Amplifiers Using Quantum Entanglement Swapping. Photonics 2022, 9, 687. https://doi.org/10.3390/photonics9100687
Wang H, Ru N, Lin P. Generation of Three-Mode Entanglement Based on Parametric Amplifiers Using Quantum Entanglement Swapping. Photonics. 2022; 9(10):687. https://doi.org/10.3390/photonics9100687
Chicago/Turabian StyleWang, Hailong, Ning Ru, and Pingwei Lin. 2022. "Generation of Three-Mode Entanglement Based on Parametric Amplifiers Using Quantum Entanglement Swapping" Photonics 9, no. 10: 687. https://doi.org/10.3390/photonics9100687
APA StyleWang, H., Ru, N., & Lin, P. (2022). Generation of Three-Mode Entanglement Based on Parametric Amplifiers Using Quantum Entanglement Swapping. Photonics, 9(10), 687. https://doi.org/10.3390/photonics9100687



