Dynamics of Semiconductor Lasers under External Optical Feedback from Both Sides of the Laser Cavity
Abstract
:1. Introduction
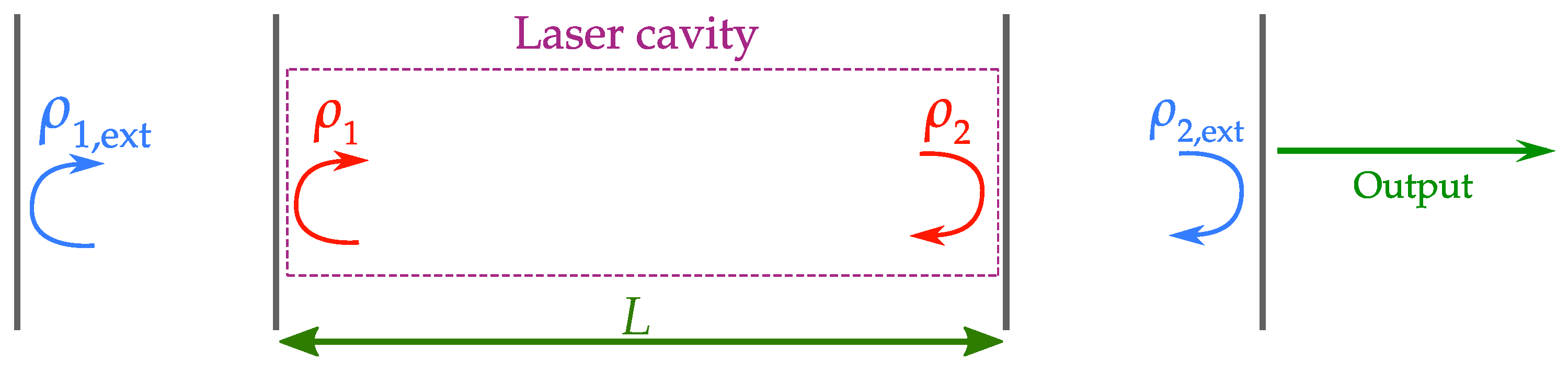
2. Rate Equations Model
2.1. Lasing Conditions
2.2. Rate Equations
2.3. Power Spectral Density and Laser Intrinsic Linewidth
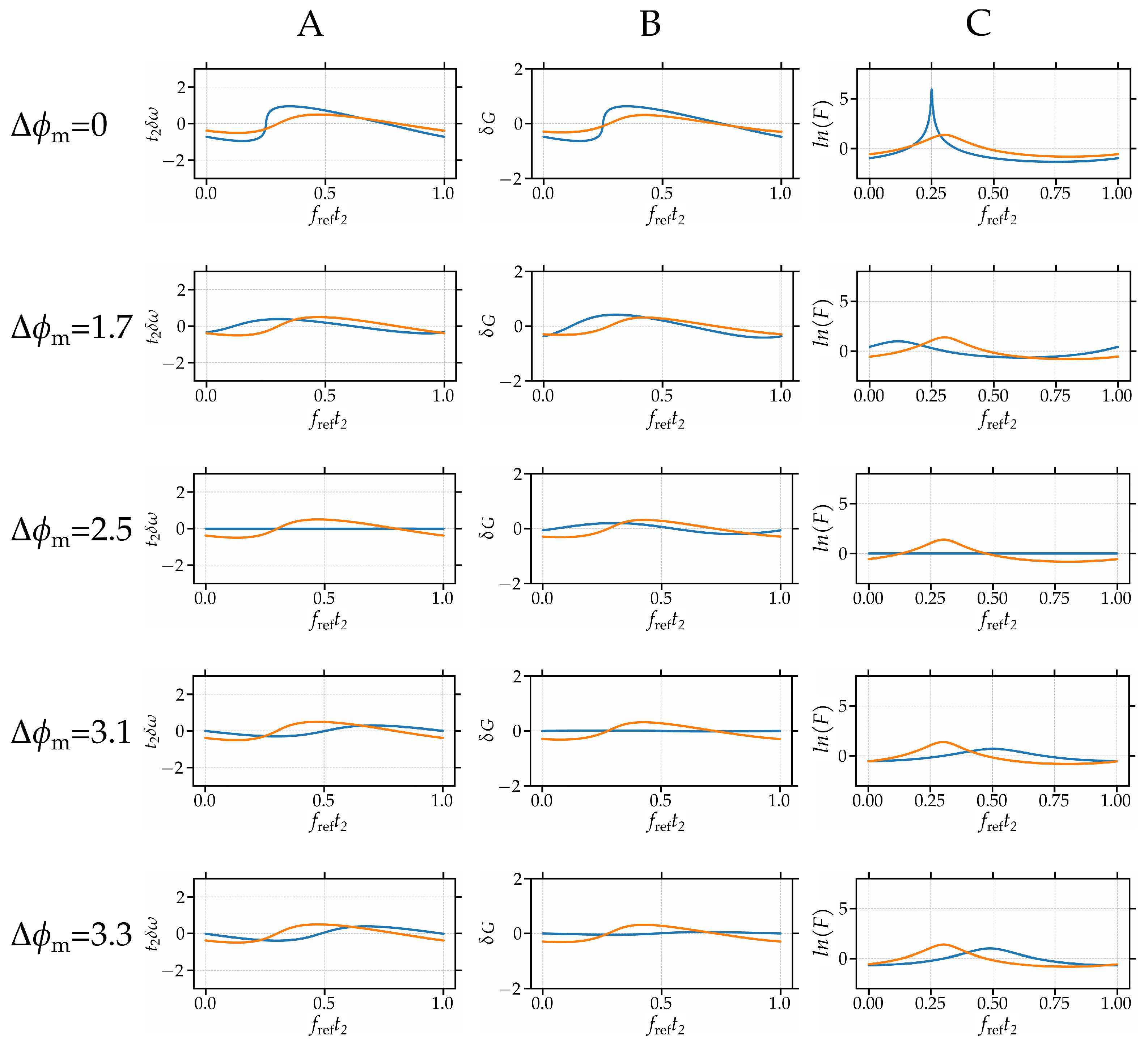
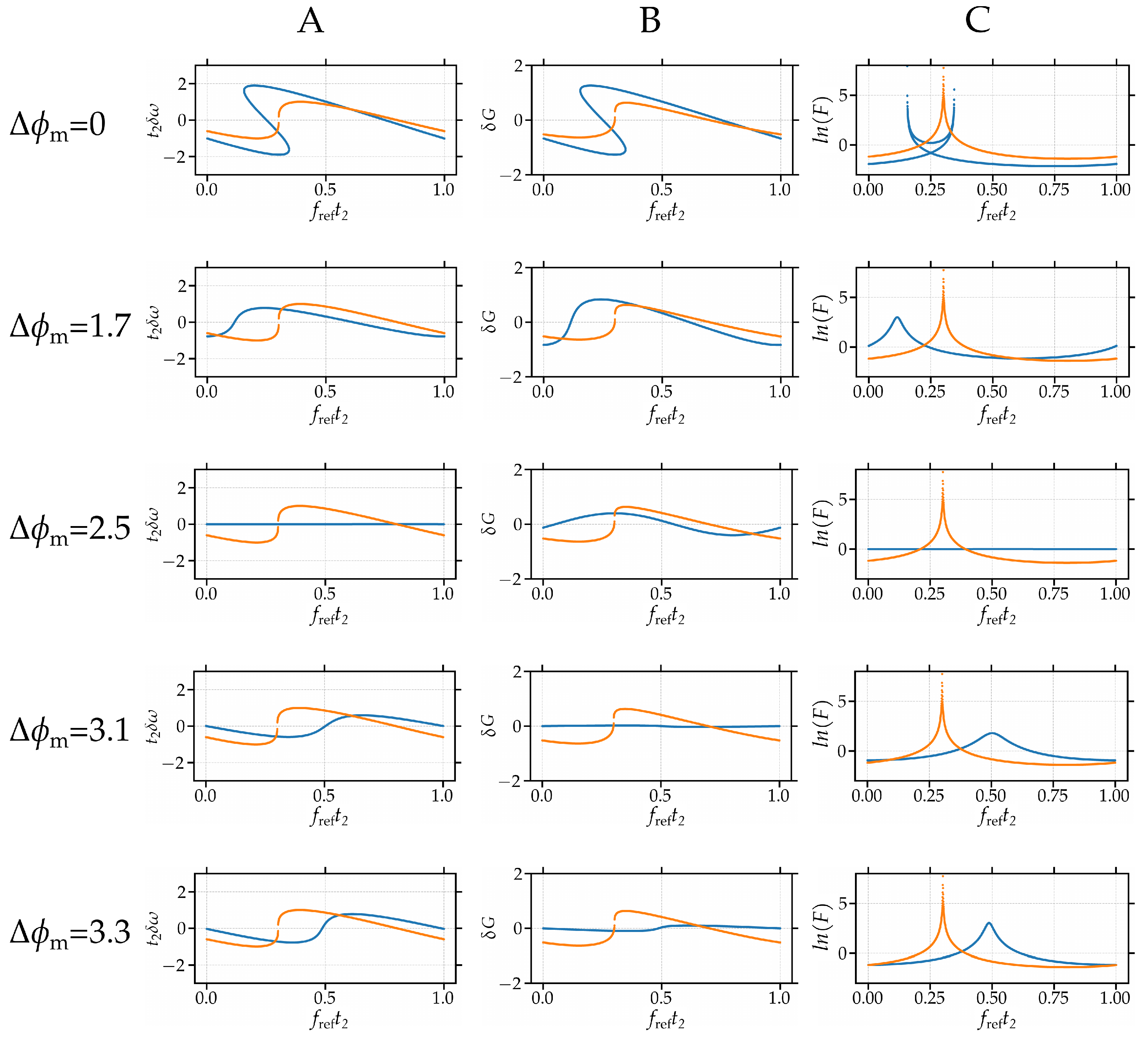
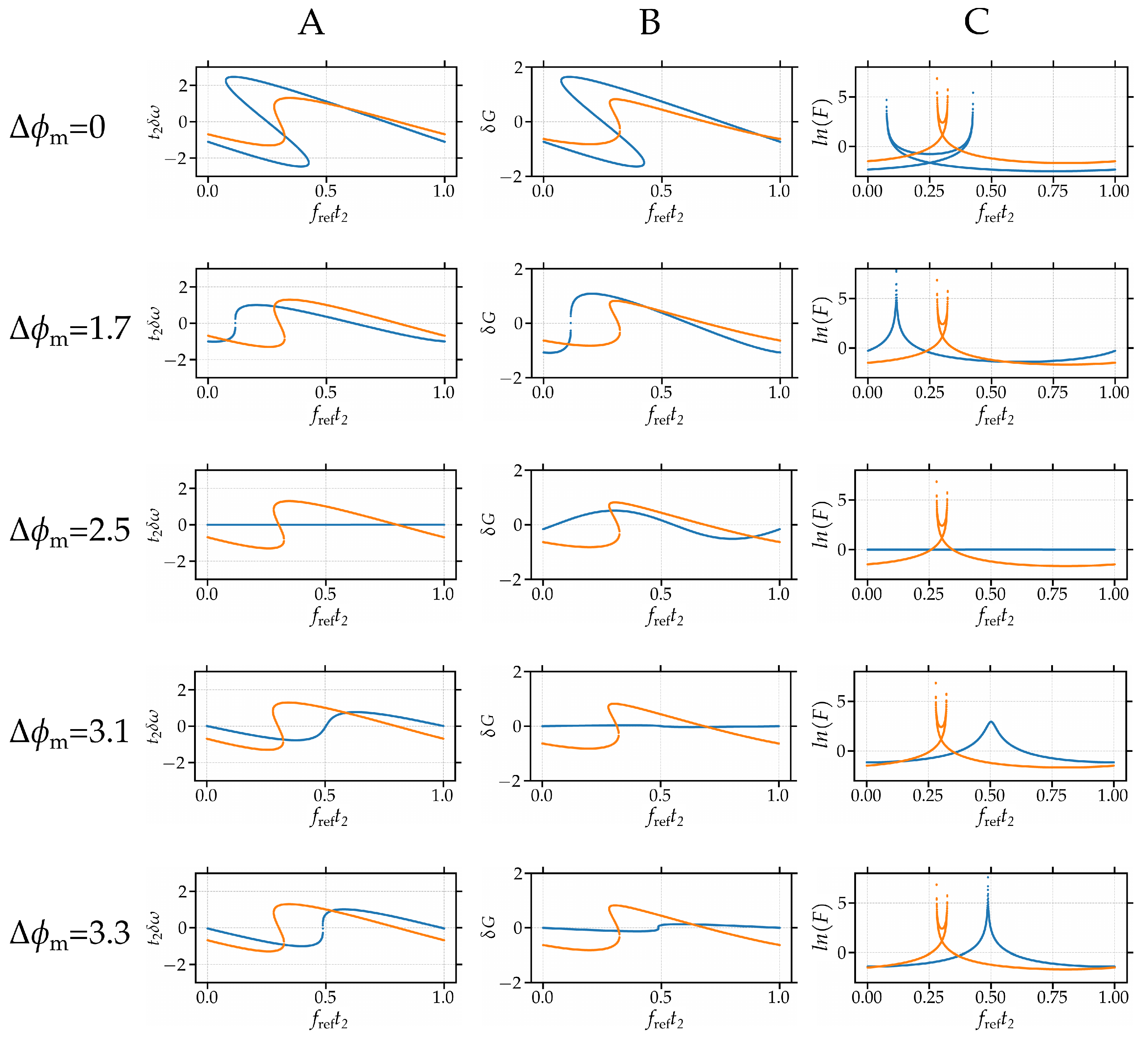
3. Numerical Study
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Amplitude and Phase Conditions
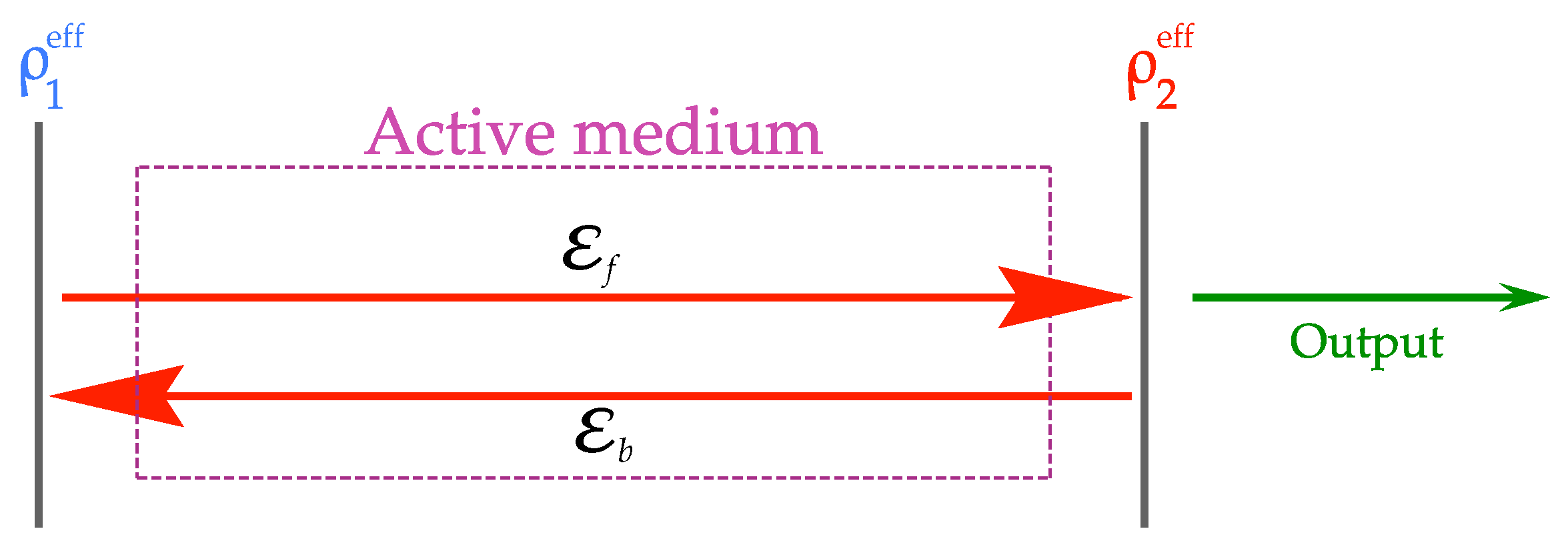
Appendix B. Threshold Gain Reduction and Lasing Frequency Shift
Appendix C. Deriving the Rate Equation for the Intensity and Phase
Appendix D. Small-Signal Analysis
Appendix E. Power Spectral Density
Appendix F. Expression for the Intrinsic Linewidth
Appendix G. Suplementary Images: Tolerances
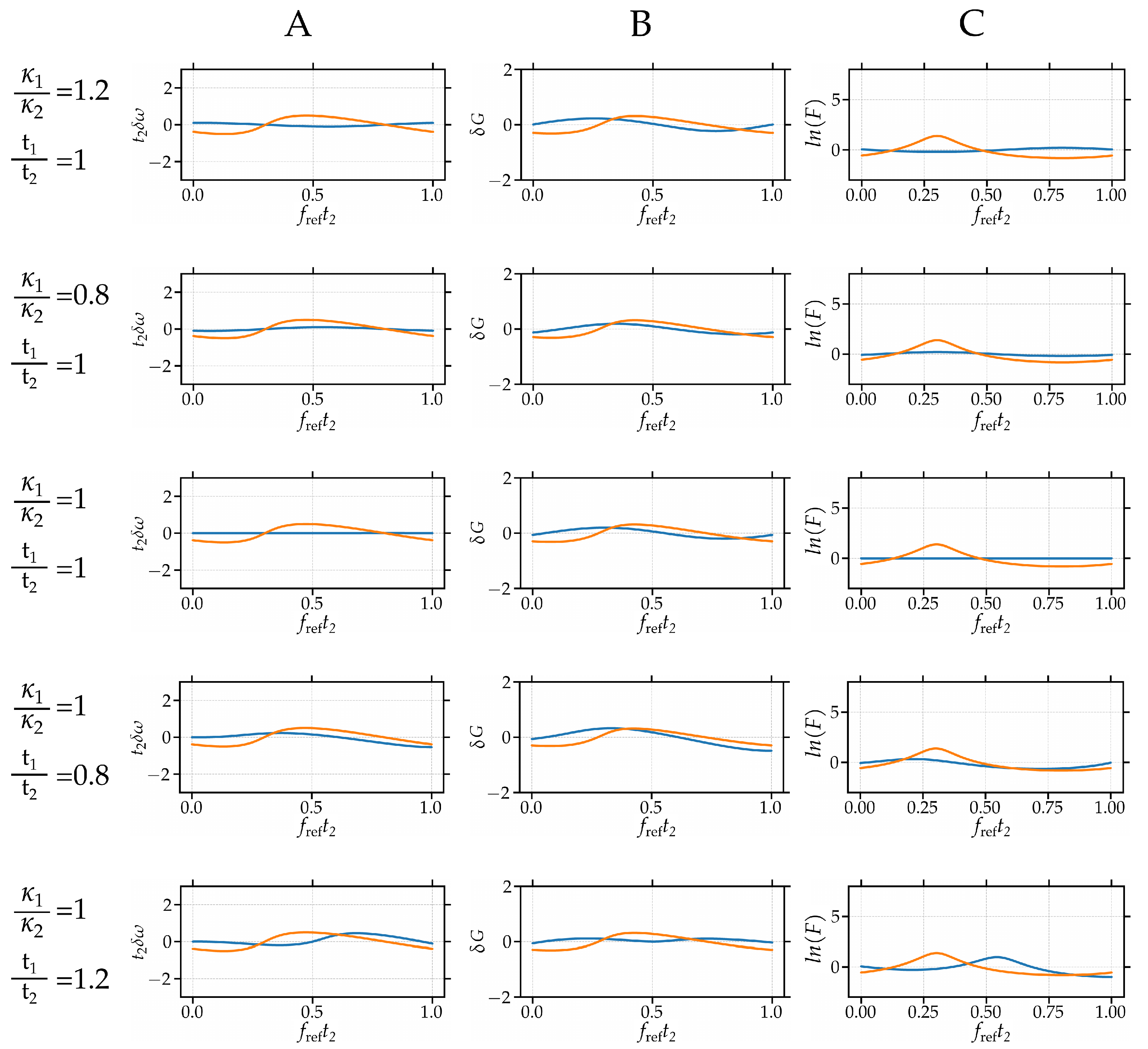
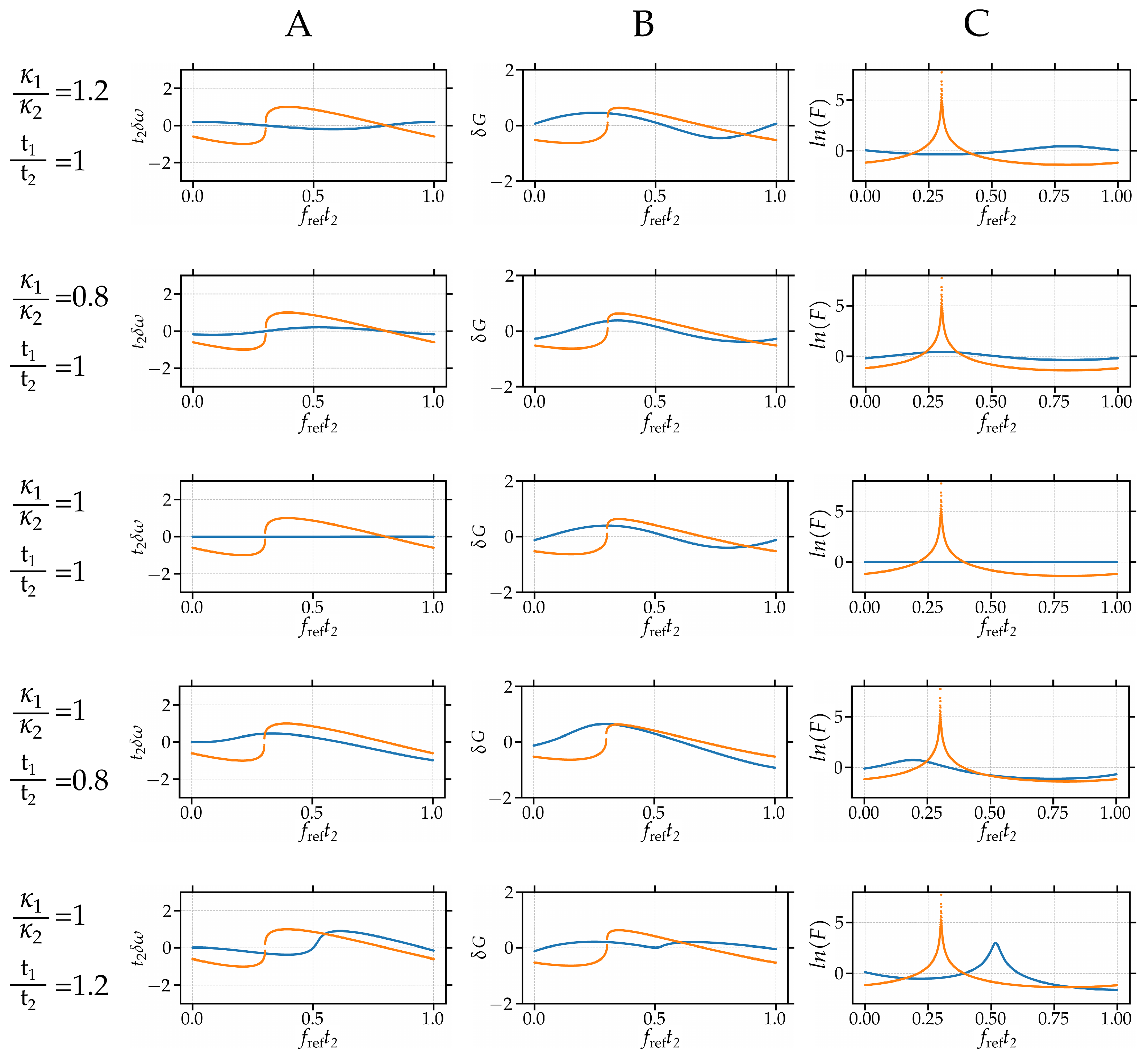
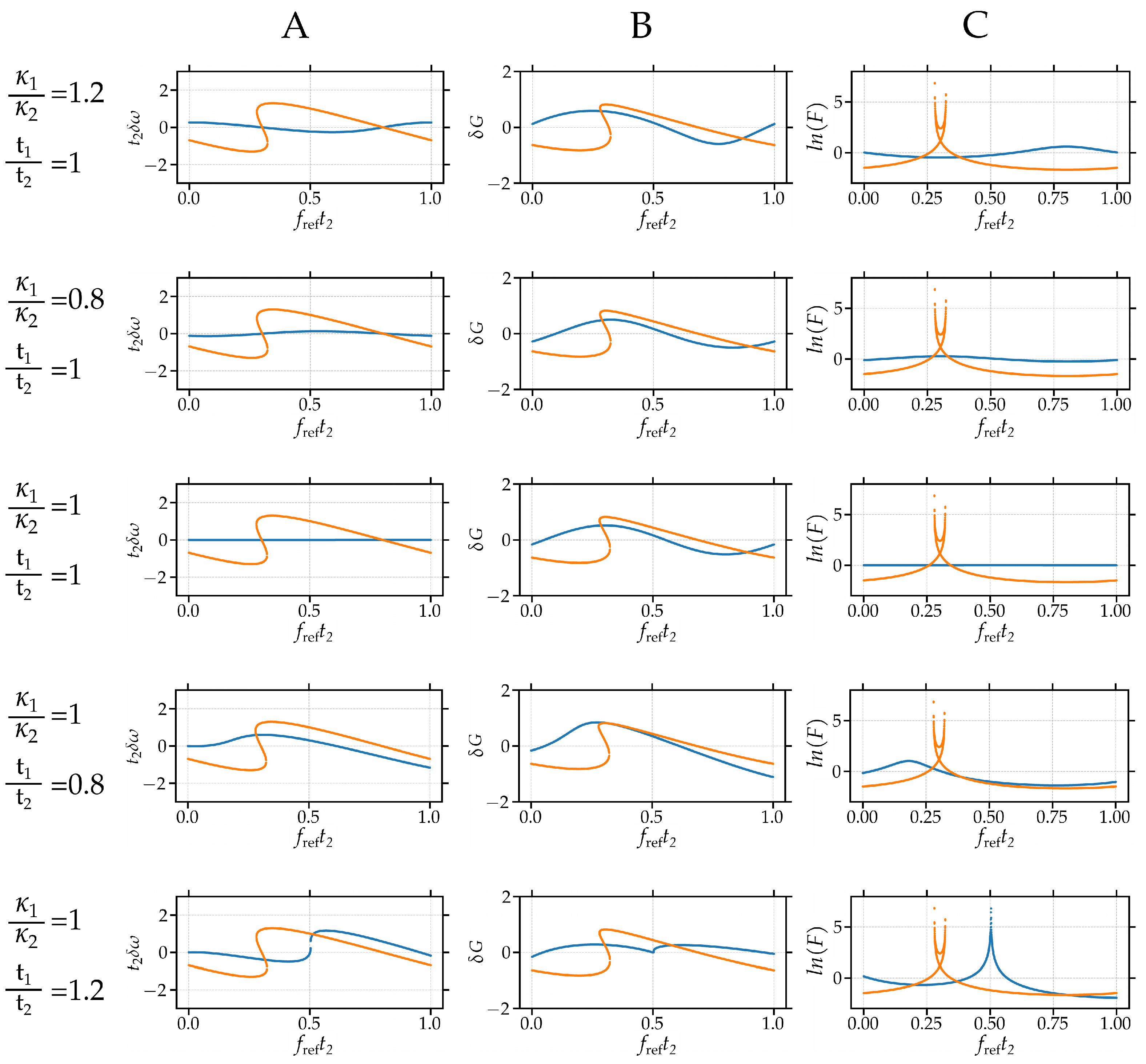
References
- Sciamanna, M.; Shore, K.A. Physics and applications of laser diode chaos. Nat. Photonics 2015, 9, 151–162. [Google Scholar] [CrossRef] [Green Version]
- Soriano, M.C.; García-Ojalvo, J.; Mirasso, C.R.; Fischer, I. Complex photonics: Dynamics and applications of delay-coupled semiconductors lasers. Rev. Modern Phys. 2013, 85, 421–470. [Google Scholar] [CrossRef] [Green Version]
- Agrawal, G.P. Line Narrowing in a Single-Mode Injection Laser Due to External Optical Feedback. IEEE J. Quantum Electron. 1984, 20, 468–471. [Google Scholar] [CrossRef]
- Olesen, H.; Osmundsen, J.H.; Tromborg, B. Nonlinear dynamics and spectral behaviour for an external cavity laser. IEEE J. Quantum Electron. 1986, 22, 762–773. [Google Scholar] [CrossRef]
- Petermann, K. External optical feedback phenomena in semiconductor lasers. IEEE J. Sel. Top. Quantum Electron. 1995, 1, 480–489. [Google Scholar] [CrossRef]
- Patzak, E.; Olesen, H.; Sugimura, A.; Saito, S.; Mukai, T. Spectral linewidth reduction in semiconductor lasers by an external cavity with weak optical feedback. Electron. Lett. 1983, 19, 938–940. [Google Scholar] [CrossRef]
- Tkach, R.W.; Chraplyvy, A.R. Regimes of Feedback Effects in 1.5-µm Distributed Feedback Lasers. J. Lightw. Technol. 1986, 4, 1655–1661. [Google Scholar] [CrossRef]
- Lenstra, D.; Verbeek, B.; Boef, A.D. Coherence collapse in single-mode semiconductor lasers due to optical feedback. IEEE J. Quantum Electron. 1985, 21, 674–679. [Google Scholar] [CrossRef]
- Henry, C.; Kazarinov, R. Instability of semiconductor lasers due to optical feedback from distant reflectors. IEEE J. Quantum Electron. 1986, 22, 294–301. [Google Scholar] [CrossRef]
- Ebisawa, S.; Komatsu, S. Orbital Instability of Chaotic Laser Diode with Optical Injection and Electronically Applied Chaotic Signal. Photonics 2020, 7, 25. [Google Scholar] [CrossRef] [Green Version]
- Locquet, A. Routes to Chaos of a Semiconductor Laser Subjected to External Optical Feedback: A Review. Photonics 2020, 7, 22. [Google Scholar] [CrossRef] [Green Version]
- Gomez, S.; Huang, H.; Duan, J.; Combrié, S.; Shen, A.; Baili, G.; de Rossi, A.; Grillot, F. High coherence collapse of a hybrid III–V/Si semiconductor laser with a large quality factor. J. Phys. Photonics 2020, 2, 025005. [Google Scholar] [CrossRef]
- Zhao, D.; Andreou, S.; Yao, W.; Lenstra, D.; Williams, K.; Leijtens, X. Monolithically Integrated Multiwavelength Laser With Optical Feedback: Damped Relaxation Oscillation Dynamics and Narrowed Linewidth. IEEE Photonics J. 2018, 10, 6602108. [Google Scholar] [CrossRef]
- Aoyama, K.; Yokota, N.; Yasaka, H. Strategy of optical negative feedback for narrow linewidth semiconductor lasers. Opt. Express 2018, 26, 21159–21169. [Google Scholar] [CrossRef]
- Doerr, C.R.; Dupuis, N.; Zhang, L. Optical isolator using two tandem phase modulators. Opt. Lett. 2011, 36, 4293–4295. [Google Scholar] [CrossRef]
- Van Schaijk, T.T.M.; Lenstra, D.; Williams, K.A.; Bente, E.A.J.M. Model and experimental validation of a unidirectional phase modulator. Opt. Express 2018, 26, 32388–32403. [Google Scholar] [CrossRef] [PubMed]
- Septon, T.; Becker, A.; Gosh, S.; Shtendel, G.; Sichkovskyi, V.; Schnabel, F.; Sengül, A.; Bjelica, M.; Witzigmann, B.; Reithmaier, J.P.; et al. Large linewidth reduction in semiconductor lasers based on atom-like gain material. Optica 2019, 6, 1071–1077. [Google Scholar] [CrossRef]
- Duan, J.; Huang, H.; Dong, B.; Jung, D.; Norman, J.C.; Bowers, J.E.; Grillot, F. 1.3-µ m Reflection Insensitive InAs/GaAs Quantum Dot Lasers Directly Grown on Silicon. IEEE Photonics Technol. Lett. 2019, 31, 345–348. [Google Scholar] [CrossRef]
- Yamasaki, K.; Kanno, K.; Matsumoto, A.; Akahane, K.; Yamamoto, N.; Naruse, M.; Uchida, A. Fast dynamics of low-frequency fluctuations in a quantum-dot laser with optical feedback. Opt. Express 2021, 29, 17962–17975. [Google Scholar] [CrossRef] [PubMed]
- Huang, D.; Pintus, P.; Bowers, J.E. Towards heterogeneous integration of optical isolators and circulators with lasers on silicon. Opt. Mat. Express 2018, 8, 2471–2483. [Google Scholar] [CrossRef] [Green Version]
- Yan, W.; Yang, Y.; Liu, S.; Zhang, Y.; Xia, S.; Kang, T.; Yang, W.; Qin, J.; Deng, L.; Bi, L. Waveguide-integrated high-performance magneto-optical isolators and circulators on silicon nitride platforms. Optica 2020, 7, 1555–1562. [Google Scholar] [CrossRef]
- Lenstra, D.; van Schaijk, T.T.M.; Williams, K.A. Toward a Feedback-Insensitive Semiconductor Laser. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 1–13. [Google Scholar] [CrossRef]
- Khoder, M.; der Sande, G.V.; Danckaert, J.; Verschaffelt, G. Effect of External Optical Feedback on Tunable Micro-Ring Lasers Using On-Chip Filtered Feedback. IEEE Photonics Technol. Lett. 2016, 28, 959–962. [Google Scholar] [CrossRef]
- Komljenovic, T.; Liang, L.; Chao, R.L.; Hulme, J.; Srinivasan, S.; Davenport, M.; Bowers, J.E. Widely-Tunable Ring-Resonator Semiconductor Lasers. Appl. Sci. 2017, 7, 732. [Google Scholar] [CrossRef]
- Kasai, K.; Nakazawa, M.; Ishikawa, M.; Ishii, H. 8 kHz linewidth, 50 mW output, full C-band wavelength tunable DFB LD array with self-optical feedback. Opt. Express 2018, 26, 5675–5685. [Google Scholar] [CrossRef]
- Morton, P.A.; Morton, M.J. High-Power, Ultra-Low Noise Hybrid Lasers for Microwave Photonics and Optical Sensing. J. Lightw. Technol. 2018, 36, 5048–5057. [Google Scholar] [CrossRef]
- Xiang, C.; Morton, P.A.; Bowers, J.E. Ultra-narrow linewidth laser based on a semiconductor gain chip and extended Si3N4 Bragg grating. Opt. Lett. 2019, 44, 3825–3828. [Google Scholar] [CrossRef]
- Liu, Y.; Ohtsubo, J. Dynamics and chaos stabilization of semiconductor lasers with optical feedback from an interferometer. IEEE J. Quantum. Elect. 1997, 33, 1163–1169. [Google Scholar] [CrossRef]
- Mezzapesa, F.P.; Columbo, L.L.; Dabbicco, M.; Brambilla, M.; Scamarcio, G. QCL-based nonlinear sensing of independent targets dynamics. Opt. Express 2014, 22, 5867. [Google Scholar] [CrossRef] [PubMed]
- Zhu, W.; Chen, Q.; Wang, Y.; Luo, H.; Wu, H.; Ma, B. Improvement on vibration measurement performance of laser self-mixing interference by using a pre-feedback mirror. Opt. Laser Eng. 2018, 105, 150–158. [Google Scholar] [CrossRef]
- Ruan, Y.; Liu, B.; Yu, Y.; Xi, J.; Guo, Q.; Tong, J. High sensitive sensing by a laser diode with dual optical feedback operating at period-one oscillation. Appl. Phys. Lett. 2019, 115, 011102. [Google Scholar] [CrossRef]
- Seimetz, M. Laser Linewidth Limitations for Optical Systems with High-Order Modulation Employing Feed Forward Digital Carrier Phase Estimation; Paper OTuM2; OFC: Auckland, New Zealand, 2008. [Google Scholar]
- Liang, W.; Ilchenko, V.S.; Eliyahu, D.; Dale, E.; Savchenkov, A.A.; Seidel, D.; Matsko, A.B.; Maleki, L. Compact stabilized semiconductor laser for frequency metrology. Appl. Opt. 2015, 54, 3353. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barton, J.S.; Skogen, E.J.; Mašanović, M.L.; Denbaars, S.P.; Coldren, L.A. A widely tunable high-speed transmitter using an integrated SGDBR laser-semiconductor optical amplifier and Mach–Zehnder modulator. IEEE J. Sel. Top. Quantum Electron. 2003, 9, 1113–1117. [Google Scholar] [CrossRef]
- Huang, D.; Tran, M.A.; Guo, J.; Peters, J.; Komljenovic, T.; Malik, A.; Morton, P.A.; Bowers, J.E. High-power sub-kHz linewidth lasers fully integrated on silicon. Optica 2019, 5, 745–752. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Kim, D.; Harfouche, M.; Santis, C.T.; Satyan, N.; Rakuljic, G.; Yariv, A. Narrow-Linewidth Oxide-Confined Heterogeneously Integrated Si III-V Semiconductor Lasers. IEEE Photonics Technol. Lett. 2017, 29, 2199–2202. [Google Scholar] [CrossRef]
- Lin, Y.; Browning, C.; Timens, R.B.; Geuzebroek, D.H.; Roeloffzen, C.G.H.; Hoekman, M.; Geskus, D.; Oldenbeuving, R.M.; Heideman, R.G.; Fan, Y.; et al. Characterization of Hybrid InP-TriPleX Photonic Integrated Tunable Lasers Based on Silicon Nitride (Si3N4/SiO2) Microring Resonators for Optical Coherent System. IEEE Photonics J. 2018, 10, 1400108. [Google Scholar] [CrossRef]
- Li, B.; Jin, W.; Wu, L.; Chang, L.; Wang, H.; Shen, B.; Yuan, Z.; Feshali, A.; Paniccia, M.; Vahala, K.J.; et al. Reaching fiber-laser coherence in integrated photonics. Opt. Lett. 2021, 46, 5201–5204. [Google Scholar] [CrossRef]
- Lang, R.; Kobayashi, K. External Optical Feedback Effects on Semiconductor Injection Laser Properties. IEEE J. Quantum Electron. 1980, 16, 347–355. [Google Scholar] [CrossRef]
- Smit, M.; Leijtens, X.; Ambrosius, H.; Bente, E.; van der Tol, J.; Smalbrugge, B.; de Vries, T.; Geluk, E.J.; Bolk, J.; van Veldhoven, R.; et al. An introduction to InP-based generic integration technology. Semicond. Sci. Technol. 2014, 29, 083001. [Google Scholar] [CrossRef]
- Augustin, L.M.; Santos, R.; den Haan, E.; Kleijn, S.; Thijs, P.J.A.; Latkowski, S.; Zhao, D.; Yao, W.; Bolk, J.; Ambrosius, H.; et al. InP-Based Generic Foundry Platform for Photonic Integrated Circuits. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 6100210. [Google Scholar] [CrossRef]
- Henry, C.H. Theory of the Linewidth of Semiconductor Lasers. IEEE J. Quantum Electron. 1982, 18, 259–264. [Google Scholar] [CrossRef]
- Osinski, M.; Buus, J. Linewidth broadening factor in semiconductor lasers–An overview. IEEE J. Quantum Electron. 1987, 23, 9–29. [Google Scholar] [CrossRef]
- Lax, M.; Noise, V.C. Noise in Self-Sustained Oscillators. Phys. Rev. 1967, 160, 290–307. [Google Scholar] [CrossRef]
- Rowe, H.E. Signals and Noise in Communication Systems, 1st ed.; D. Van Nostrand Company. Inc.: Princeton, NJ, USA, 1965. [Google Scholar]
- Spano, P.; Piazzolla, S.; Tamburrini, M. Theory of noise in semiconductor lasers in the presence of optical feedback. IEEE J. Quantum Electron. 1984, 20, 350–357. [Google Scholar] [CrossRef]
- Schawlow, A.L.; Townes, C.H. Infrared and Optical Masers. Phys. Rev. 1958, 112, 1940–1949. [Google Scholar] [CrossRef] [Green Version]
- Yu, Y.; Giuliani, G.; Donati, S. Measurement of the Linewidth Enhancement Factor of Semiconductor Lasers Based on the Optical Feedback Self-Mixing Effect. IEEE Photonics Technol. Lett. 2004, 16, 990–992. [Google Scholar] [CrossRef]
- Schunk, N.; Petermann, K. Numerical analysis of the feedback regimes for a single-mode semiconductor laser with external feedback. IEEE J. Quantum Electron. 1988, 24, 1242–1247. [Google Scholar] [CrossRef]
- Panozzo, M.; Quintero-Quiroz, C.; Tiana-Alsina, J.; Torrent, M.C.; Masoller, C. Experimental characterization of the transition to coherence collapse in a semiconductor laser with optical feedback. Chaos 2017, 27, 114315. [Google Scholar] [CrossRef] [Green Version]
- Happach, M.; Felipe, D.D.; Friedhoff, V.N.; Kresse, M.; Irmscher, G.; Kleinert, M.; Zawadzki, C.; Rehbein, W.; Brinker, W.; Mohrle, M.; et al. Influence of Integrated Optical Feedback on Tunable Lasers. IEEE J. Quantum Electron. 2020, 56. [Google Scholar] [CrossRef]
- Petermann, K. Laser Diode Modulation and Noise (Advances in Optoelectronics 3); Kluwer Academic Publishers: Dordrecht, The Netherlands, 1988; Chapter 2. [Google Scholar]
| Parameter | Value |
|---|---|
| (0,2) | |
| 3 | |
| 0.1581 (case 1) | |
| 0.3162 (case 2) | |
| 0.4111 (case 3) | |
| 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Far Brusatori, M.; Volet, N. Dynamics of Semiconductor Lasers under External Optical Feedback from Both Sides of the Laser Cavity. Photonics 2022, 9, 43. https://doi.org/10.3390/photonics9010043
Far Brusatori M, Volet N. Dynamics of Semiconductor Lasers under External Optical Feedback from Both Sides of the Laser Cavity. Photonics. 2022; 9(1):43. https://doi.org/10.3390/photonics9010043
Chicago/Turabian StyleFar Brusatori, Mónica, and Nicolas Volet. 2022. "Dynamics of Semiconductor Lasers under External Optical Feedback from Both Sides of the Laser Cavity" Photonics 9, no. 1: 43. https://doi.org/10.3390/photonics9010043
APA StyleFar Brusatori, M., & Volet, N. (2022). Dynamics of Semiconductor Lasers under External Optical Feedback from Both Sides of the Laser Cavity. Photonics, 9(1), 43. https://doi.org/10.3390/photonics9010043




