A Mixed FSO/RF Integrated Satellite-High Altitude Platform Relaying Networks for Multiple Terrestrial Users with Presence of Eavesdropper: A Secrecy Performance

Abstract

In this paper, the secrecy performance of a mixed free space optical (FSO)/radio frequency (RF) integrated satellite-high altitude platform (HAP) relaying networks for terrestrial multiusers with the existence of an eavesdropper is investigated. In this network, FSO is adopted to establish the link between the satellite and HAP for which it experiences Gamma-Gamma distributions under different detection schemes (i.e., heterodyne and intensity modulation direct detection). The transmission between the amplify-and-forward (AF) relaying HAP and terrestrial multiusers is through the RF and is modeled as shadowed-Rician fading distribution. Owning to broadcasting nature of RF link, it is assumed that an eavesdropper attempts to intercept the users’ confidential message, and the eavesdropper link is subjected to Rician distributions. Specifically, the closed-form expression for the system equivalent end-to-end cumulative distribution function is derived by exploiting the Meijer’s G and Fox’s H functions. Based on this expression, the exact closed-form expressions of the system connection outage probability, secrecy outage probability, and strictly positive secrecy capacity are obtained under the different detection schemes at HAP. Moreover, the asymptotic analyze of the system secrecy outage probability is provided to obtain more physical insights. Furthermore, the accuracy of all the derived analytical closed-form expressions is verified through the Monte-Carlo simulations. In addition, the impact of atmospheric turbulence, pointing errors, shadowing severity parameters, and Rician factor are thoroughly evaluated. Under the same system conditions, the results depict that heterodyne detection outperforms the intensity modulation direct detection.

1. Introduction

Recently, there is tremendous growth in the deployment of emergency wireless communication supporting services for large scale disasters in order to provide vital information for both rescue teams and survivors [1]. In this scenario, a fast and reliable communication is highly difficult to establish owing to geographical complexity of the disaster area where the communication infrastructures of such base stations and optical fibers have been destroyed [2]. As a result of this, satellite communication has been suggested as most promising solution due to its large coverage footprint and reliable wireless connectivity for various fixed and mobile users [3]. Conventionally, satellite communication systems are RF-based, in which different frequency bands are used for a particular application. However, this RF-based systems suffer from spectrum congested, licensed band, low security, and interference with other frequency bands [4]. To overcome this problems, FSO has been recently proposed for satellite communication link owing to its ability to offer extremely large bandwidth, high security, unlicensed spectrum, low interference, ease of deployment, etc., compared to its RF counterpart [5]. Despite these unique features, the FSO link usually suffers from atmospheric turbulence due to variation in refractive index as the result of inhomogeneity in atmospheric temperature and pressure that can degrade the system performance [6]. In addition, the link is highly prone to pointing error caused by building sways, leading to misalignment between the transmitter and receiver [7]. As a directional link, it requires line-of-sight (LOS) between the transmitter and receiver, which may be stochastically blocked by the moving, surrounding objects, such as birds, airplanes, etc. [8].

High altitude platforms (HAPs) have attracted immense attention in the research community due to their inherit advantages from both the terrestrial and satellite communication systems [9]. They have been suggested as a future candidate for communication system to offer efficient broadband wireless access at low cost [10]. As flying aerial platforms, such as airships, planes, and balloons; they are usually deployed in stratosphere at altitude between $17 \mathrm{to} 22 \mathrm{km}$ above the earth’s surface, where there is existence of strong LOS between the satellite and HAP for efficient wireless transmission [11]. According to International Telecommunication Union (ITU), a larger footprint of $100 \mathrm{km}$ radius has been suggested to act as HAPs, and this can replace various terrestrial base stations [12]. Regardless of the communication link, satellite communication system link usually experiences a masking effect due to unavailability of LOS between the satellite and user equipment. This occurs as a result of obstacles and shadowing, leading to poor quality of services and long delay propagation, especially in the case of geostationary satellites [13]. To overcome this effect, an integrated satellite-high altitude platform (ISHAP) mixed FSO/RF relaying scheme has been proposed in literature, where the RF communication can be used in conjunction with the FSO counterpart. This combined technology can significantly improve the performance of wireless communication networks by taking advantage of the complementary benefits of both connections [14] In this concept, therefore, HAPs can, thus, serve as intermediate relay node to enhance the transmission between the satellite and the ground users by using decode-and-forward (DF) and amplify-and-forward (AF) relaying protocols [13].

Today, security is the most critical challenge in wireless communication system due to the broadcasting nature of RF medium [15]. As a result of this, the ISHAP system is highly susceptible to any external eavesdroppers which have the capacity to intercept the confidential information of the legitimate users via the system RF link. In this view, physical layer security has been suggested to offer better security performance by exploiting the channel characteristics and imperfections without data encryption [16]. Scanning through the open literature, it was found that there have been intense studies on the performance of cooperative satellite-terrestrial relaying networks. A dual-hop satellite communication system with AF relay was presented in Reference [17], where maximum ratio transmission and maximum ratio combiner scheme were adopted at the system source and destination, respectively. In Reference [18], the performance of a hybrid satellite-terrestrial free space optical cooperative network was evaluated, where the system error rate was obtained. In addition, the performance of an AF hybrid satellite terrestrial system over generalized fading channels was investigated in Reference [19], and the authors obtained the analytical expression for the average symbol error rate of the network. In Reference [20], the impact of hardware impairment on the reliability performance of hybrid satellite-terrestrial system was evaluated, where the geosynchronous orbit satellite sends its information to the multiple terrestrial relay nodes. Furthermore, the performance of hybrid satellite-terrestrial network having multi-antennas terrestrial relays was investigated in Reference [21]. It was assumed that there was direct link between the satellite and the destination, and the effect of hardware impairments with the interference on both relay and destination were investigated. The outage performance of a partial relay selection-based hybrid satellite-terrestrial network was analyzed in Reference [22]. In Reference [23], the performance of an underlay hybrid cognitive satellite terrestrial network was evaluated, where the primary satellite coexists with the second terrestrial relay system. The performance of joint impact of CSI and hardware impairments on a cognitive satellite terrestrial relay network was presented in Reference [24]. However, all these aforementioned works only focused on the scenario of single terrestrial user. In this view, future satellite communication network is required to provide reliable and efficient services for a large number of users. As a result of this, many research studies are focusing on evaluating the performance of hybrid satellite-terrestrial multiuser networks. Thus, the performance of a multi-antenna multiusers hybrid satellite terrestrial relay network was studied in Reference [25]. The authors employed opportunistic user scheduling with outdated channel state information (CSI) and AF relaying with co-channel interference. The outage performance of a multi-antenna multiple users integrated in a satellite-unmanned aerial vehicle (UAV) cooperative network was presented in Reference [13]. However, all these works were RF-based multiusers hybrid satellite-terrestrial systems. In addition, the outage performance of a mixed FSO/RF satellite-aerial terrestrial network was evaluated in Reference [26], where the satellite sent messages to multiple users with the help of a multi-antenna aerial platform as a relay. In Reference [27], the performance analysis of a mixed FSO/RF satellite-UAV multiuser network was studied, where the UAV relay node adopts DF relaying protocol. Kong et al. [28] evaluated the outage probability performance of an asymmetric FSO/RF of multiusers satellite-UAV-terrestrial system, and the authors considered DF relay UAV node for transmission and RF link exploit transmit beamforming scheme. However, in all these previous research works on a mixed FSO/RF, multiusers integrated satellite-terrestrial systems are DF-based relay node and the secrecy performance of cooperative satellite terrestrial relaying networks was not considered.

Recently, some research studies have examined hybrid satellite-terrestrial systems in the context of physical layer security. The secrecy performance of a hybrid satellite relay network with multiple external eavesdroppers was studied [29] with the assumption that multiple eavesdroppers receive signals from the terrestrial networks. In Reference [30], the secrecy outage performance of a land mobile satellite system was evaluated, where both the legitimate user and eavesdropper utilize the diversity technique with multiple antennas. Moreover, the physical layer secrecy performance of a hybrid satellite and terrestrial free space optical cooperative network was presented in Reference [31], where the eavesdropper was assumed to intercept the satellite signal. In addition, the secrecy performance of RF eavesdropping for a HAP aided satellite system was investigated in Reference [32]. However, the security performance of all aforementioned studies was not based on multiple legitimate users, and DF relay was considered for the system. Motivated by this, the performance of the secrecy performance of a mixed FSO/RF integrated satellite-high altitude platform (HAP) relaying networks for terrestrial multiusers with the existence of an eavesdropper. The HAP relay node is considered to utilize AF relaying with different detection schemes for FSO signal detection. The closed-form expression for the system equivalent end-to-end cumulative distribution function is derived. Thus, to quantify the system performance, the exact closed-form expressions of the system connection outage probability, secrecy outage probability, and strictly positive secrecy capacity are obtained under the different HAP detection schemes. To gain better insight, the asymptotic expression for the system SOP is derived. The main contributions of this work are summarized as follows:

• The exact closed-form expression for the system equivalent end-to-end cumulative distribution function (CDF) is derived by exploiting the Meijer’s G and Fox’s H functions. To the best of authors’ knowledge, the derived CDF is novel as a mixed Gamma-Gamma and shadowed-Rician structure under AF relaying protocol is not found in the existing literature.
• The analytical closed-form expressions of the system performance in terms of connection outage probability (COP), secrecy outage probability (SOP), and strictly positive secrecy capacity (SPSC) are obtained.
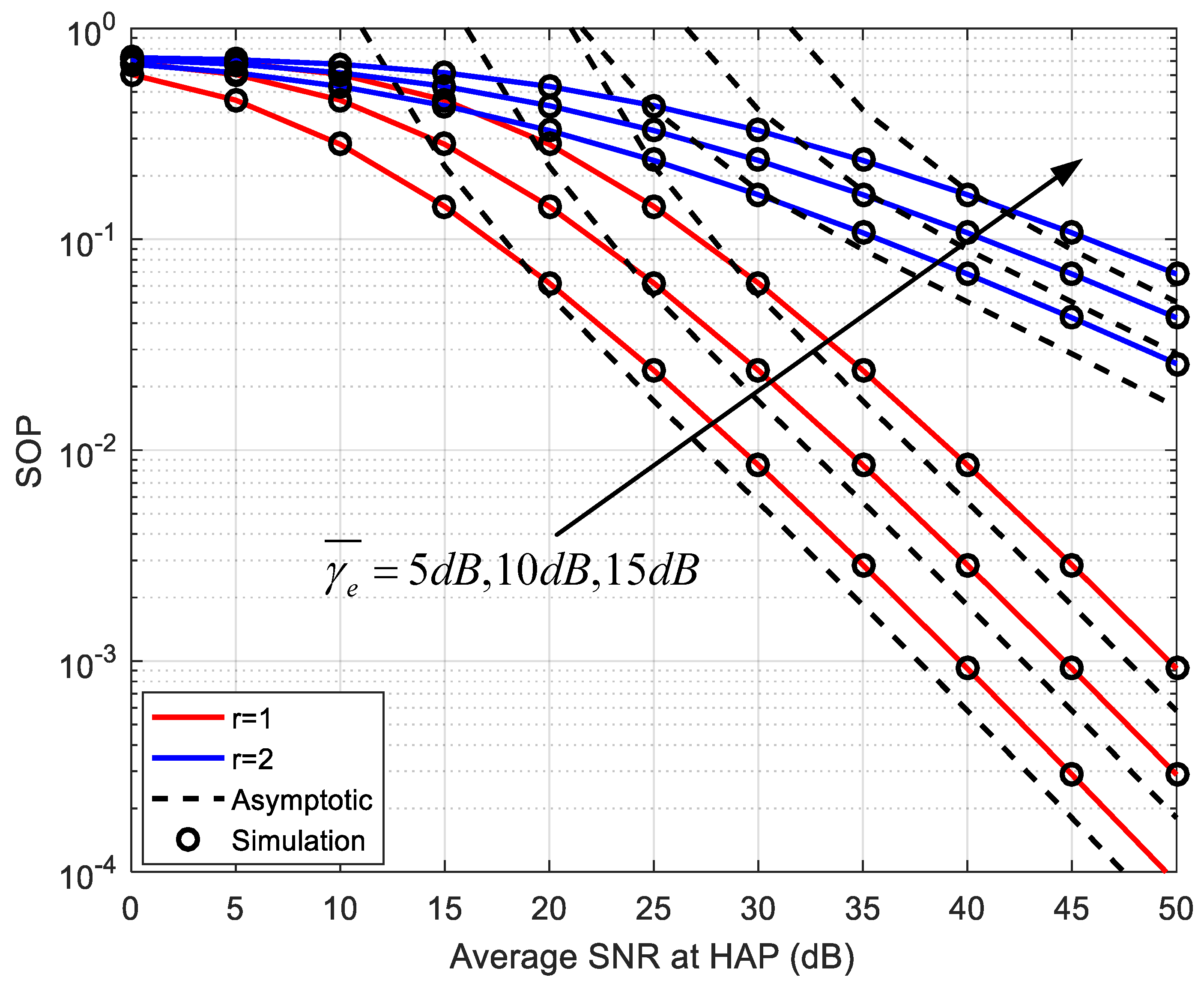
• The asymptotic expression for the system secrecy outage probability is derived to obtain physical insight.
• Relative to Reference [26], where multiple users are considered, the system performance was not based on physical layer secrecy. In addition, the RF link was subjected to Nakagami-m distributions. In this paper, the system performance is based on physical layer secrecy, and the RF links are subjected to Rician fading distributions.
• Relative to Reference [32], where the HAP relay aided node employed DF relaying protocol, and the system only considered a single terrestrial user. The HAP in this paper is an AF-based relaying protocol, and the multiple legitimate users are considered at the ground station.

The rest of the paper is organized as follows. The system and channel models are provided in Section 2. In Section 3, the exact closed-form expression for the system equivalent end-to-end cumulative distribution function is presented We derive the analytical expressions of the COP, SOP, and SPSC subject to different detection schemes in Section 4. Numerical results and discussions are depicted in Section 5. Finally, concluding remarks are detailed in Section 6.

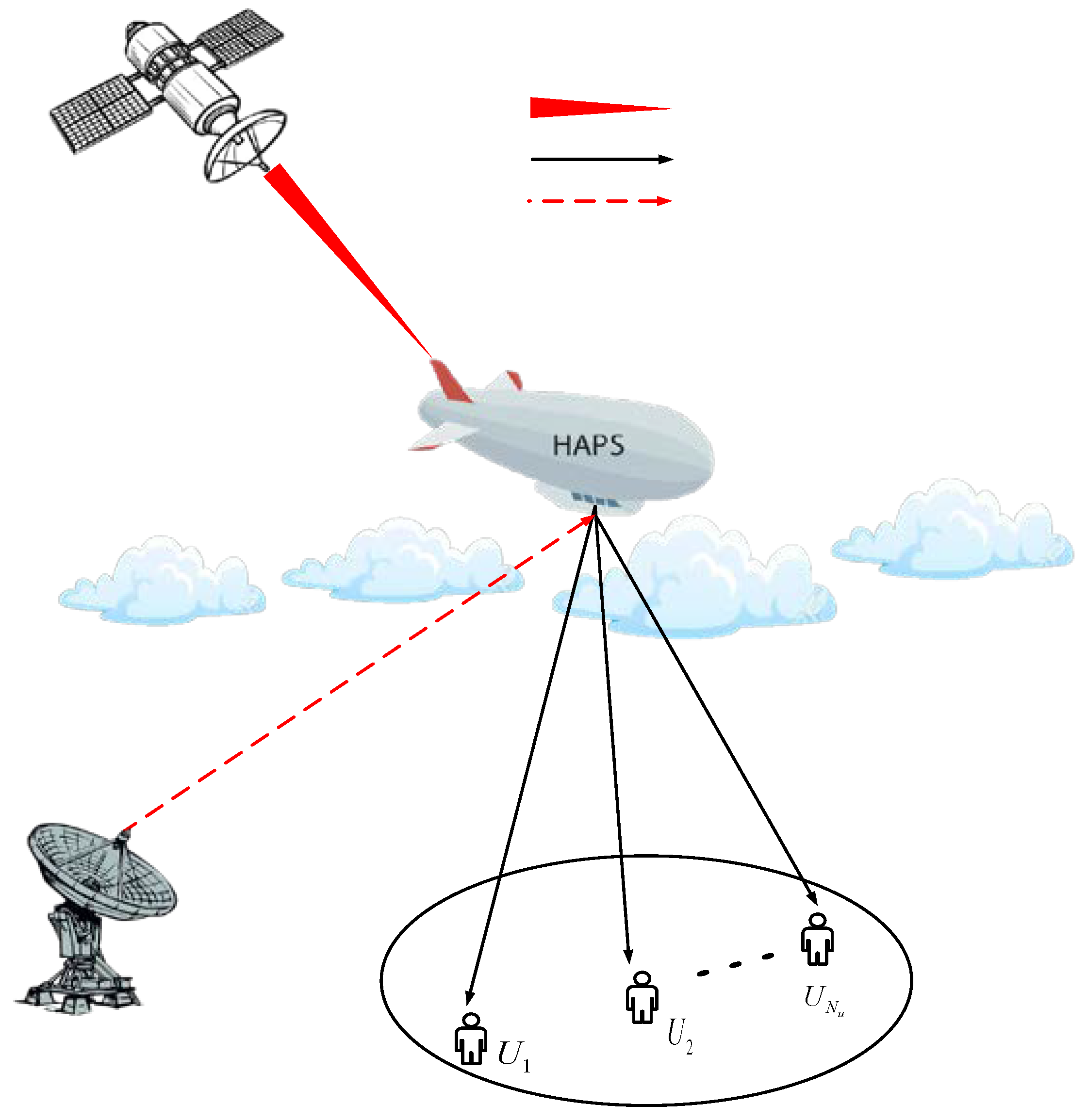
2. System and Channel Models

A mixed FSO/RF integrated satellite-HAP relaying network is illustrated in Figure 1, where the satellite (S) transmits confidential information to the legitimate terrestrial users (D) through an AF HAP relay (R) in the presence of an eavesdropper attempting to wiretap confidential information. It is assumed that there is no direct link between satellite and the terrestrial users due to masking effects as a result of weather, environmental obstacles, long distance, etc. It is assumed that the FSO link follows Gamma-Gamma fading distribution, while the RF link between the HAP relay and the terrestrial users follows Shadowed-Rician fading distribution. In addition, the eavesdroppers RF link between the E and R is considered to undergo Rician distribution. In addition, the HAP relay in the network employs AF relaying protocol, which will introduce a fixed gain into the receive signal irrespective of the fading amplitude on the FSO link. Thus, the network end-to-end signal-to-noise ratio (SNR) can be defined as [33]:

$${\gamma }_{eq}=\frac{{\gamma }_1{\gamma }_2}{{\gamma }_2+C},$$

(1)

where $C$ denotes the fixed relay gain parameter, ${\gamma }_1={\overline{\gamma }}_1{\left|h_1\right|}^2$ represents the instantaneous SNR at the HAP with ${\overline{\gamma }}_1$, and ${\left|h_1\right|}^2$, respectively, signifies the average SNR and channel power gain of satellite-to-HAP relay link, while the ${\gamma }_2={\overline{\gamma }}_2{h}_2$ indicates the instantaneous SNR at the destination, with ${\overline{\gamma }}_2$ and $h_2$ representing the average SNR and channel power gain of HAP-to-terrestrial users link, respectively.

2.1. FSO Link Statistical Distributions

Since the FSO link experiences Gamma-Gamma fading distribution, the probability density function (PDF) of the instantaneous SNR ${\gamma }_1$ under different detection techniques can be defined as [5]:

$$f_{{\gamma }_1}\left({\gamma }_1\right)=\omega {\gamma }^{-1}{G}_{1,3}^{3,0}\left(M{\left(\frac{{\gamma }_1}{{\mu }_r}\right)}^{1/r}|\begin{array}{c}{\xi }^2+1\\ {\xi }^2,\alpha ,\beta \end{array}\right),$$

(2)

where $\omega =\frac{{\xi }^2}{r\left(\mathsf{\Gamma }\left(\alpha \right)\mathsf{\Gamma }\left(\alpha \right)\right)}$, $M=\frac{{\xi }^2\alpha \beta }{\left(1+{\xi }^2\right)}$, $\mathsf{\Gamma }(.)$ signifies the Gamma function, $\xi$ signifies the pointing error, $\alpha$ and $\beta$ are the scintillation parameters which are specified in references [34,35], the $r$ parameter shows the type of detection at the HAP relay node (i.e., $r=1$ for heterodyne detection, and $r=2$ for IM/DD), ${\mu }_r$ indicates the average electrical SNR of the link. Specifically, for heterodyne detection, ${\mu }_1={\overline{\gamma }}_1$ with ${\overline{\gamma }}_1$ represents the average instantaneous SNR of the link, and, for IM/DD, ${\mu }_2={\overline{\gamma }}_1\frac{\alpha \beta {\xi }^2\left({\xi }^2+1\right)}{\left({\xi }^2+1\right)\left(\alpha +1\right)\left(\beta +1\right)}$.

By integrating (2) through the integral identity detailed in Reference [36] (Equation (26)), the cumulative density function (CDF) of the instantaneous SNR ${\gamma }_1$can be expressed as:

$$F_{{\gamma }_1}\left({\gamma }_1\right)=\frac{{\xi }^2{r}^{\alpha +\beta -2}}{2{\pi }^{r-1}\left(\mathsf{\Gamma }\left(\alpha \right)\mathsf{\Gamma }\left(\alpha \right)\right)}{G}_{r+1,3r+1}^{3r,1}\left(\frac{{\left(\alpha \beta \right)}^r}{r^{2r}{\mu }_r}{\gamma }_1|\begin{array}{c}1, {\psi }_1\\ {\psi }_2,0\end{array}\right),$$

(3)

where ${\psi }_1=\mathsf{\Delta }\left(r, {\xi }^2+1\right)$ and ${\psi }_2=\mathsf{\Delta }\left(r, {\xi }^2\right), \mathsf{\Delta }\left(r, \alpha \right), \mathsf{\Delta }\left(r,\beta \right)$ with $\mathsf{\Delta }\left(\psi ,a\right)=\frac{a}{\psi },\frac{a+1}{\psi },\dots , \frac{a+\psi -1}{\psi }$.

2.2. RF Link Statistical Distributions

It is assumed that the RF link between the HAP and terrestrial users link follows Shadowed-Rician fading distribution and the PDF of instantaneous SNR ${\gamma }_2$ can be expressed as [17,25,37]:

$$f_{\gamma 2}({\gamma }_2)=\mho exp{(-a{\gamma }_2)}_1{F}_1(m_h;1;\delta {\gamma }_2), {\gamma }_2>0$$

(4)

where $\mho =1/2{\left(\frac{2b{m}_h}{2b{m}_h+\mathsf{\Omega }}\right)}^{m_h}$, $a=1/2b$ and $\delta =\mathsf{\Omega }/2b\left(2b{m}_h+\mathsf{\Omega }\right)$, with $\mathsf{\Omega }$, $m_h$, and $2b$ being the average power of LOS, Nakagami fading severity parameter with $0<m_h<\infty$, and the multipath component, respectively, and ${ }_1{F}_1\left(x;y;z\right)$ denotes the confluent hypergeometric function. By using the identity detail in Reference [38], the confluent hypergeometric function in (4) can be expressed as:

$${ }_1{F}_1\left(m_h;1;\delta {\gamma }_2\right)=exp\left(\delta {\gamma }_2\right){{\displaystyle \sum }}_{q=0}^{m_h-1}\frac{{\left(1-m_h\right)}_q{\left(-\delta {\gamma }_{SR}\right)}^q}{{\left(q!\right)}^2},$$

(5)

where ${(.)}_q$ denotes the Pochhammer symbol.

By invoking (5) into (4), the Shadowed-Rician distribution of the RF link can be further simplified as:

$$f_{{\gamma }_2}\left({\gamma }_2\right)={{\displaystyle \sum }}_{q=0}^{m_h-1}\frac{\mho {\left(1-m_h\right)}_p{\left(-\delta \right)}^q}{{\left(p!\right)}^2{\left({\overline{\gamma }}_1\right)}^{q+1}}{\gamma }_2^q\exp \left(-{\mathsf{\Delta }}_H{\gamma }_{SR}\right),$$

(6)

where ${\mathsf{\Delta }}_H=\left(a-\delta \right)/{\overline{\gamma }}_2$.

Since the sum of SNR at the terrestrial users can be expressed as ${\gamma }_2={{\displaystyle \sum }}_{q=1}^{N_u}{\left|h_{2,q}\right|}^2$, then, by following the same approach detailed in Reference [17], the PDF of instantaneous SNR ${\gamma }_2$ Shadowed-Rician distribution can be expressed as:

$$f_{{\gamma }_2}\left({\gamma }_2\right)={{\displaystyle \sum }}_{q_1=0}^{m_h-1}\dots {{\displaystyle \sum }}_{q_{N_u}=0}^{m_h-1}\Xi \left(N_u\right){\gamma }_2{}^{\lambda -1}\exp \left(-{\Delta }_H{\gamma }_2\right),$$

(7)

where

$$\{\begin{array}{c}\Xi \left(N_u\right)={{\displaystyle \prod }}_{j=1}^{N_u}\rho \left(q_j\right){\mho }^{N_u}{{\displaystyle \prod }}_{t=1}^{N_u-1}B\left({{\displaystyle \sum }}_{k=1}^{\epsilon }{q}_k+\epsilon ,q_{\epsilon +1}+1\right)\\ \rho \left(q_j\right)=\frac{{\left(1-m_h\right)}_{q_j}{\left(-\delta \right)}^{q_j}}{{\left(q_j!\right)}^2{\left({\overline{\gamma }}_2\right)}^{q_j+1}}\\ \lambda ={{\displaystyle \sum }}_{i=1}^{N_u}{q}_j+N_u\end{array},$$

(8)

with $B\left(.,.\right)$ denoting Beta function.

By integration (7) using the integral identity detailed in Reference [38] (Equation (3.351(1), the CDF of the link can be obtained as:

$$F_{{\gamma }_2}\left({\gamma }_2\right)={{\displaystyle \sum }}_{q_1=0}^{m_h-1}\dots {{\displaystyle \sum }}_{q_{N_u}=0}^{m_h-1}\Xi \left(N_u\right){\mathsf{\Delta }}_H^{-\lambda }\gamma \left(\lambda ,{\Delta }_H{\gamma }_2\right),$$

(9)

where $\gamma \left(.,.\right)$ is the lower incomplete Gamma function.

By converting the incomplete Gamma function to Meijer-G function using the identity detailed in Reference [39] (Equation (8.4.16(1))), then, (9) can be further expressed as:

$$F_{{\gamma }_2}\left({\gamma }_2\right)={{\displaystyle \sum }}_{q_1=0}^{m_h-1}\dots {{\displaystyle \sum }}_{q_{N_u}=0}^{m_h-1}\Xi \left(N_u\right){\mathsf{\Delta }}_H^{-\lambda }{G}_{1,2}^{1,1}\left({\Delta }_H{\gamma }_2|\begin{array}{c}1\\ \lambda , 0\end{array}\right).$$

(10)

Owing to broadcast nature of RF link, the eavesdropper attempts to intercept the secret information of the ground users from the HAP relay node. As a result of this, the eavesdropper link is assumed to follow Rican distribution with the PDF of instantaneous SNR ${\gamma }_e$ defined as [40,41]:

$$f_e\left({\gamma }_e\right)=\frac{\left(K+1\right)\exp \left(-K\right)}{{\overline{\gamma }}_e}exp\left(-\frac{K+1}{{\overline{\gamma }}_e}\right)I_o\left(2\sqrt{\frac{K\left(K+1\right)}{{\overline{\gamma }}_e}}{\gamma }_e\right),$$

(11)

where $K$ is the Rician fading factor which is defined as the ratio of the power of the line-of-sight component to the scattered components, and $I_o(.)$denotes the zero-order modified Bessel function of the first kind. By using the identity detailed in Reference [38], $I_o={{\displaystyle \sum }}_{l=0}^{\infty }{x}^l/2^{2l}{\left(l!\right)}^2$,

$$f_e\left({\gamma }_e\right)=\eta exp\left(-K\right){{\displaystyle \sum }}_{l=0}^{\infty }\frac{{\left(K\eta \right)}^l}{{\left(l!\right)}^2}{\gamma }_e{}^l\exp \left(-\eta {\gamma }_e\right),$$

(12)

where $\eta =\frac{K+1}{{\overline{\gamma }}_e}$.

3. Statistics of End-to-End SNR

Since the HAP relay node employs AF relaying protocol, the equivalent end-to-end CDF of the concerned system can expressed as [33,42]:

$$F_{eq}\left(\gamma \right)={{\displaystyle \int }}_0^{\infty }P\left[{\gamma }_{eq}=\frac{{\gamma }_1{\gamma }_2}{{\gamma }_2+C}<\gamma |{\gamma }_1\right]f_{{\gamma }_1}\left({\gamma }_1\right)d{\gamma }_1.$$

(13)

By variable transformation of $y={\gamma }_1-\gamma$, (13) can be further expressed as [33,43]:

$$F_{eq}\left(\gamma \right)=F_{{\gamma }_1}\left({\gamma }_1\right)+\underset{\mathsf{{\rm Y}}}{\underbrace{{{\displaystyle \int }}_0^{\infty }{F}_{{\gamma }_2}\left(\frac{C\gamma }{y}\right)f_{{\gamma }_1}\left(y+\gamma \right)dy}}.$$

(14)

By putting (2), (3), and (10) into (13), the integral term of (14) can be expressed as:

$$\mathsf{{\rm Y}}=\omega {{\displaystyle \sum }}_{q_1=0}^{m_h-1}\dots {{\displaystyle \sum }}_{q_{N_u}=0}^{m_h-1}\Xi \left(N_u\right){\mathsf{\Delta }}_H^{-\lambda }{{\displaystyle \int }}_0^{\infty }{G}_{1,2}^{1,1}\left(\frac{{\Delta }_{H}C\gamma }{y}|\begin{array}{c}1\\ \lambda , 0\end{array}\right){\left(y+\gamma \right)}^{-1}{G}_{1,3}^{3,0}\left(M{\left(\frac{\left(y+\gamma \right)}{{\mu }_r}\right)}^{1/r}|\begin{array}{c}{\xi }^2+1\\ {\xi }^2,\alpha ,\beta \end{array}\right)dy.$$

(15)

By applying the identity defined in Reference [44] (Equation (1.112)), the Meijer-G functions in (15) can be expressed as follows:

$$\begin{gathered} \mathsf{{\rm Y}}=\frac{\omega }{{\left(2\pi i\right)}^2}{{\displaystyle \sum }}_{q_1=0}^{m_h-1}\dots {{\displaystyle \sum }}_{q_{N_u}=0}^{m_h-1}\Xi \left(N_u\right){\mathsf{\Delta }}_H^{-\lambda }{{\displaystyle \int }}_{L_1}{{\displaystyle \int }}_{L_2}\frac{\mathsf{\Gamma }\left(\lambda +s_1\right)\mathsf{\Gamma }\left(-s_1\right)}{\mathsf{\Gamma }\left(1-s_1\right)}\frac{\mathsf{\Gamma }\left({\xi }^2+s_2\right)\mathsf{\Gamma }\left(\alpha +s_2\right)\mathsf{\Gamma }\left(\beta +s_2\right)}{\mathsf{\Gamma }\left({\xi }^2+1+s_2\right)} \times \\ {\left({\Delta }_{H}C\gamma \right)}^{-s_1}{\left(\frac{M}{{\mu }_r^{1/r}}\right)}^{-s_2}{{\displaystyle \int }}_0^{\infty }{y}^{s_1}{\left(y+\gamma \right)}^{-\frac{s_2}{r}-1}dyd{s}_{1}d{s}_2. \end{gathered}$$

(16)

By applying the identity in Reference [38] (Equations (3.193(3)) and (8.384(1))), (16) can be solved as:

$$\begin{gathered} \mathsf{{\rm Y}}=\frac{\omega }{{\left(2\pi i\right)}^2}{{\displaystyle \sum }}_{q_1=0}^{m_h-1}\dots {{\displaystyle \sum }}_{q_{N_u}=0}^{m_h-1}\Xi \left(N_u\right){\mathsf{\Delta }}_H^{-\lambda }{{\displaystyle \int }}_{L_1}{{\displaystyle \int }}_{L_2}\frac{\mathsf{\Gamma }\left(\lambda +s_1\right)\mathsf{\Gamma }\left(-s_1\right)}{\mathsf{\Gamma }\left(1-s_1\right)}\frac{\mathsf{\Gamma }\left({\xi }^2+s_2\right)\mathsf{\Gamma }\left(\alpha +s_2\right)\mathsf{\Gamma }\left(\beta +s_2\right)}{\mathsf{\Gamma }\left({\xi }^2+1+s_2\right)} \times \\ \frac{\mathsf{\Gamma }\left(s_1+1\right)\mathsf{\Gamma }\left(\frac{s_2}{r}-s_1\right)}{\mathsf{\Gamma }\left(\frac{s_2}{r}+1\right)}{\left({\Delta }_{H}C\right)}^{-s_1}{\left(\frac{{\gamma }^{1/r}M}{{\mu }_r^{1/r}}\right)}^{-s_2}d{s}_{1}d{s}_2. \end{gathered}$$

(17)

By letting $s=s_1$ and $t=s_2$, then, (17) can be rewritten as:

$$\begin{gathered} \mathsf{{\rm Y}}=\frac{\omega }{{\left(2\pi i\right)}^2}{{\displaystyle \sum }}_{q_1=0}^{m_h-1}\dots {{\displaystyle \sum }}_{q_{N_u}=0}^{m_h-1}\Xi \left(N_u\right){\mathsf{\Delta }}_H^{-\lambda }{{\displaystyle \int }}_{L_1}{{\displaystyle \int }}_{L_2}\mathsf{\Gamma }\left(\frac{t}{r}-s\right)\frac{\mathsf{\Gamma }\left(\lambda +s\right)\mathsf{\Gamma }\left(-s\right)\mathsf{\Gamma }\left(s+1\right)}{\mathsf{\Gamma }\left(1-s\right)}\times \\ \frac{\mathsf{\Gamma }\left({\xi }^2+t\right)\mathsf{\Gamma }\left(\alpha +t\right)\mathsf{\Gamma }\left(\beta +t\right)}{\mathsf{\Gamma }\left({\xi }^2+1+t\right)\mathsf{\Gamma }\left(\frac{t}{r}+1\right)}{\left({\Delta }_{H}C\right)}^{-s}{\left(\frac{{\gamma }^{1/r}M}{{\mu }_r^{1/r}}\right)}^{-t}dsdt. \end{gathered}$$

(18)

By applying the identity detailed in Reference [45], (18) can be obtained as:

$$\begin{gathered} \mathsf{{\rm Y}}=\omega {\displaystyle \sum }_{q_1=0}^{m_h-1}\dots {\displaystyle \sum }_{q_{N_u}=0}^{m_h-1}\Xi \left(N_u\right){\mathsf{\Delta }}_H^{-\lambda } \\ \times H_{1,0:3,1:3,2}^{0,1:1,2:0,3}\left(\begin{array}{c}\left(1,-1,\frac{1}{r}\right)\\ -\end{array}|\begin{array}{c}\left(1-\lambda ,1\right)\left(0,1\right)\left(1,1\right)\\ \left(0,1\right)\end{array}|\begin{array}{c}\left(1-{\xi }^2,1\right)\left(1-\alpha , 1\right)\left(1-\beta ,1\right)\\ \left(-{\xi }^2,1\right)\left(0, \frac{1}{r}\right)\end{array}| \frac{1}{{\Delta }_{H}C},\frac{{\mu }_r^{1/r}}{{\gamma }^{1/r}M}\right), \end{gathered}$$

(19)

where $H_{p_1, q_1: p_2, q_2: p_3, q_3}^{m_1,n_1:m_2,n_2:m_3,n_3}$ [.] is the Extended Generalized Bivariate Fox’s H-function (EGBFHF).

By substituting (3) and (19) into (13), the concerned system equivalent end-to-end CDF can be obtained as:

$$\begin{gathered} F_{eq}\left(\gamma \right)=\frac{{\xi }^2{r}^{\alpha +\beta -2}}{2{\pi }^{r-1}\left(\mathsf{\Gamma }\left(\alpha \right)\mathsf{\Gamma }\left(\alpha \right)\right)}{G}_{r+1,3r+1}^{3r,1}\left(\frac{{\left(\alpha \beta \right)}^r}{r^{2r}{\mu }_r}\gamma |\begin{array}{c}1, {\psi }_1\\ {\psi }_2,0\end{array}\right)+\omega {{\displaystyle \sum }}_{q_1=0}^{m_h-1}\dots {{\displaystyle \sum }}_{q_{N_u}=0}^{m_h-1}\Xi \left(N_u\right){\mathsf{\Delta }}_H^{-\lambda }\times \\ {H}_{1,0:3,1:3,2}^{0,1:1,2:0,3}\left(\begin{array}{c}\left(1,-1,\frac{1}{r}\right)\\ -\end{array}|\begin{array}{c}\left(1-\lambda ,1\right)\left(0,1\right)\left(1,1\right)\\ \left(0,1\right)\end{array}|\begin{array}{c}\left(1-{\xi }^2,1\right)\left(1-\alpha , 1\right)\left(1-\beta ,1\right)\\ \left(-{\xi }^2,1\right)\left(0, \frac{1}{r}\right)\end{array}| \frac{1}{{\Delta }_{H}C},\frac{{\mu }_r^{1/r}}{{\gamma }^{1/r}M}\right)). \end{gathered}$$

(20)

4. Performance Analysis

In this section, the exact closed-form expression of the system connection outage probability (COP), secrecy outage probability, and strictly positive secrecy capacity (SPSC) are derived. In addition, to gain more insight about the derived expression, the asymptotic expression of the concerned system is obtained.

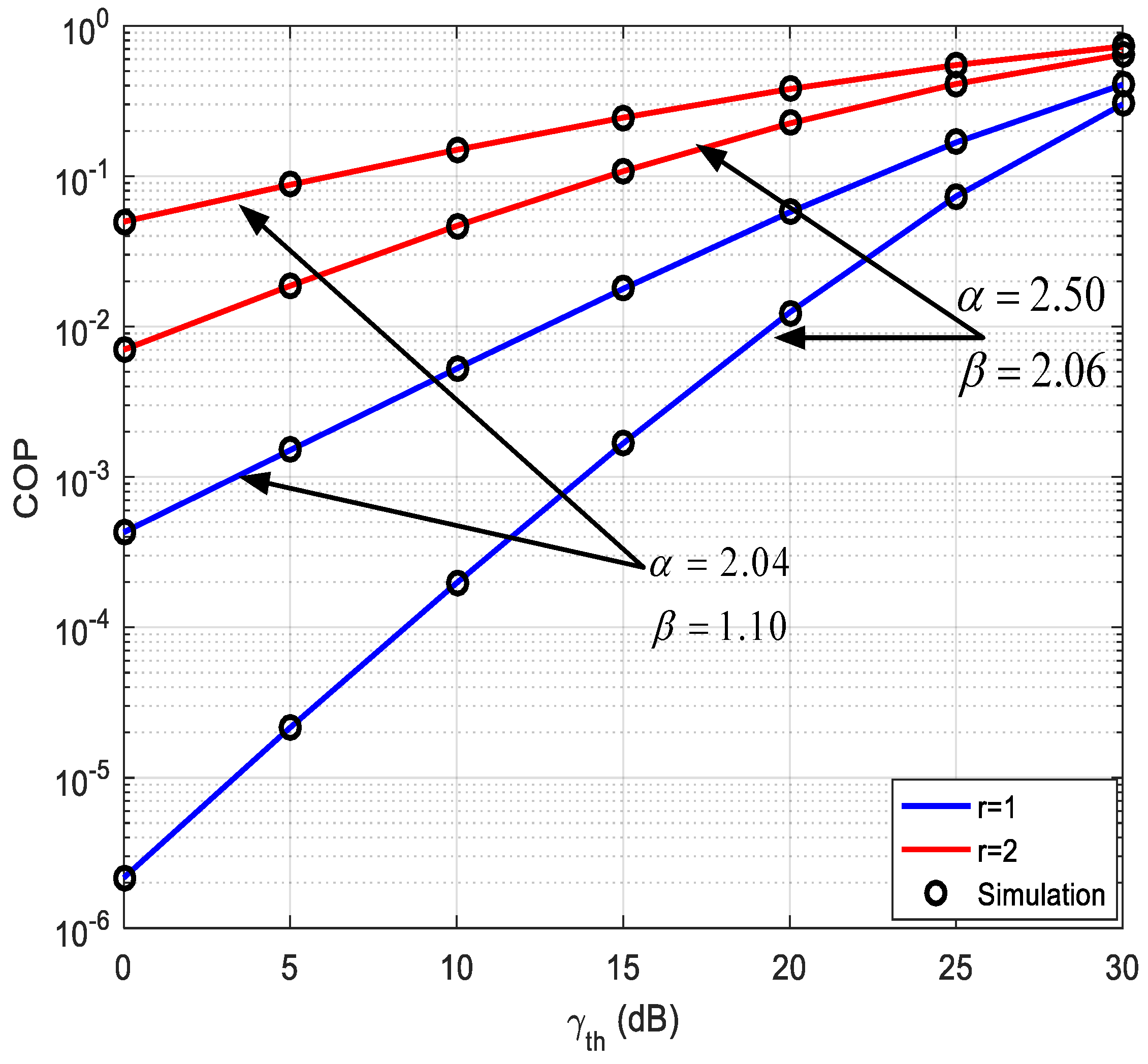
4.1. Connection Outage Probability (COP)

This metric characterizes the attainable reliability performance of the proposed system. It describes a situation, whereby the eavesdropper is unable to decode the confidential message of terrestrial users. This usually occurs when the end-to-end instantaneous SNR of the concerned system falls below a predefined threshold value ${\gamma }_{th}$ and can be formulated as [46]:

$$COP=P_r\left[\gamma \le {\gamma }_{th}\right].$$

(21)

Thus, by substituting (20) into (21), the COP of the concerned system under different detection schemes can be obtained as:

$$\begin{gathered} COP=\frac{{\xi }^2{r}^{\alpha +\beta -2}}{2{\pi }^{r-1}\left(\mathsf{\Gamma }\left(\alpha \right)\mathsf{\Gamma }\left(\alpha \right)\right)}{G}_{r+1,3r+1}^{3r,1}\left(\frac{{\left(\alpha \beta \right)}^r}{r^{2r}{\mu }_r}{\gamma }_{th}|\begin{array}{c}1, {\psi }_1\\ {\psi }_2,0\end{array}\right)+\omega {{\displaystyle \sum }}_{q_1=0}^{m_h-1}\dots {{\displaystyle \sum }}_{q_{N_s}=0}^{m_h-1}\Xi \left(N_u\right){\mathsf{\Delta }}_H^{-\lambda }\times \\ {H}_{1,0:3,1:3,2}^{0,1:1,2:0,3}\left(\begin{array}{c}\left(1,-1,\frac{1}{r}\right)\\ -\end{array}|\begin{array}{c}\left(1-\lambda ,1\right)\left(0,1\right)\left(1,1\right)\\ \left(0,1\right)\end{array}|\begin{array}{c}\left(1-{\xi }^2,1\right)\left(1-\alpha , 1\right)\left(1-\beta ,1\right)\\ \left(-{\xi }^2,1\right)\left(0, \frac{1}{r}\right)\end{array}| \frac{1}{{\Delta }_{H}C},\frac{{\mu }_r^{1/r}}{{\gamma }_{th}^{1/r}M}\right). \end{gathered}$$

(22)

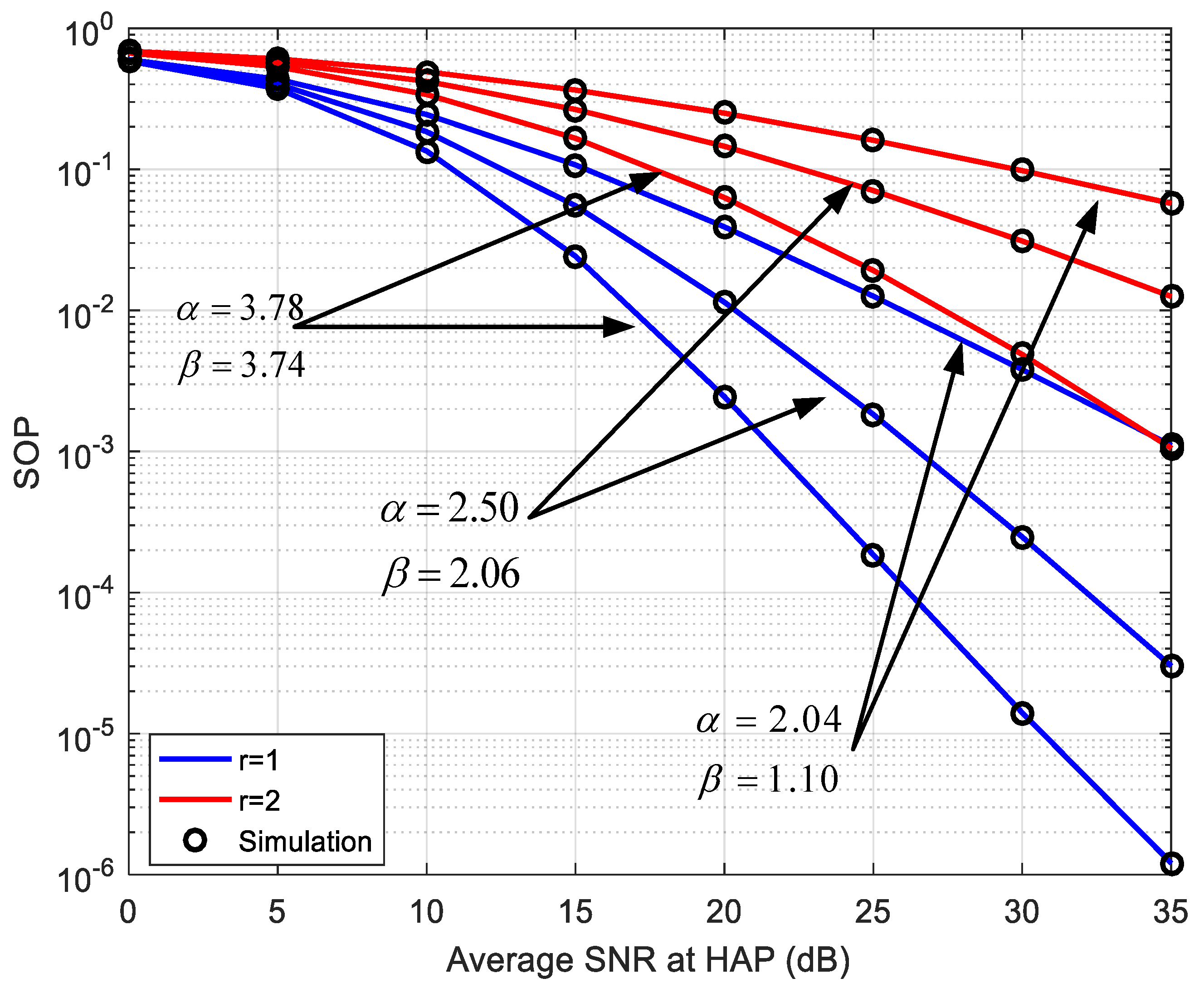
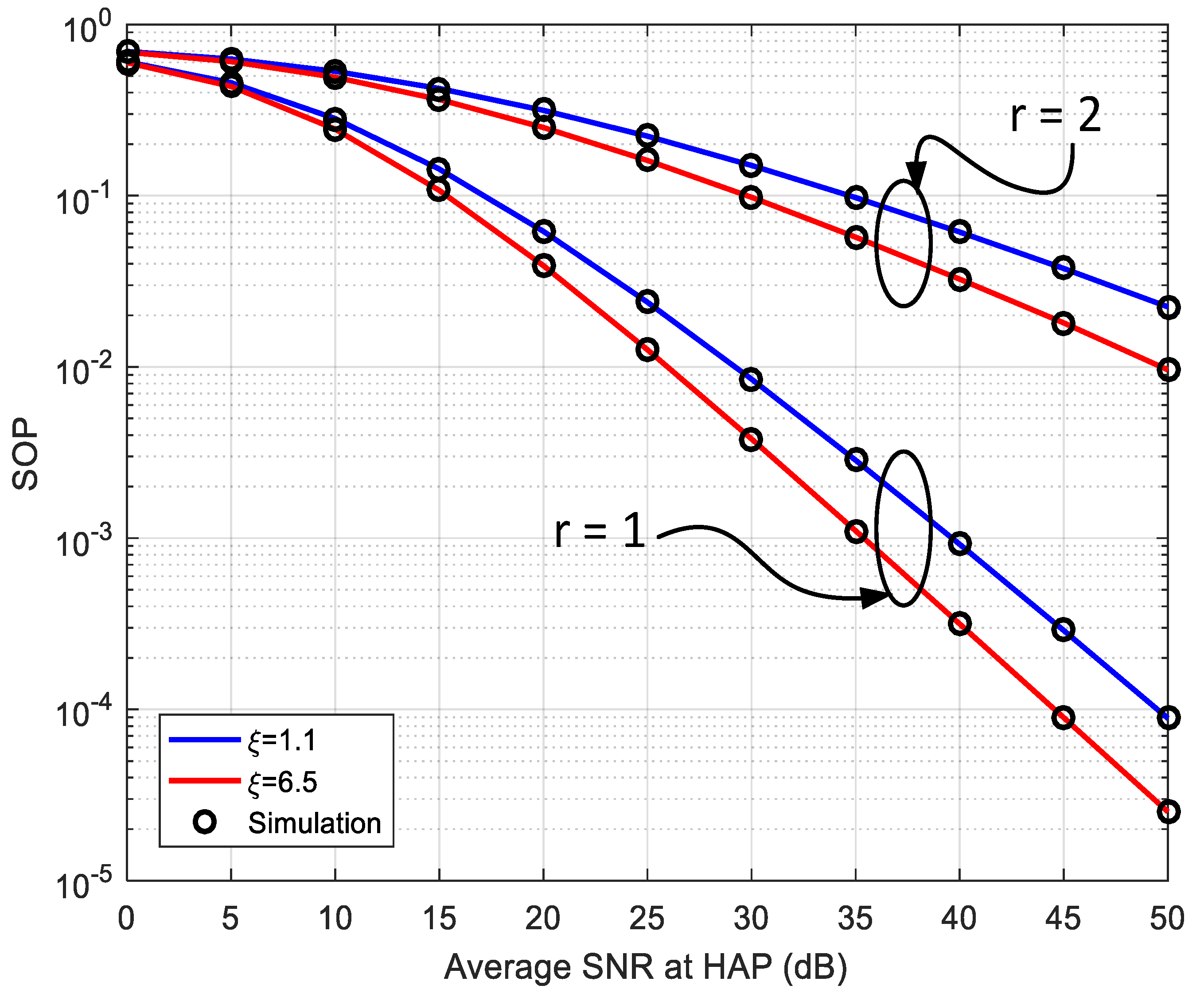
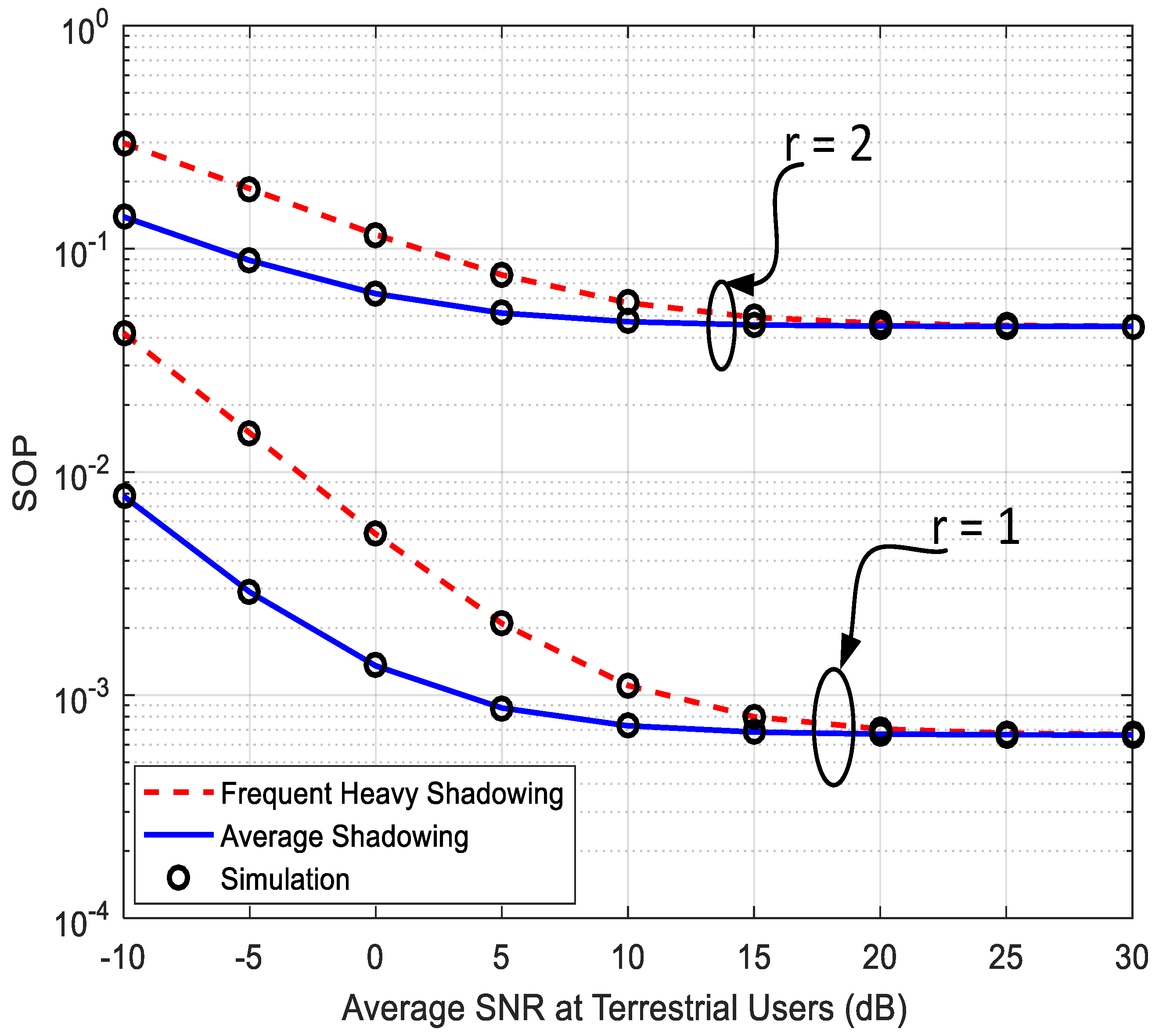
4.2. Secrecy Outage Probability (SOP)

4.2.1. Exact Analysis

These are the most vital performance indices which describe the probability that the instantaneous secrecy capacity falls below a predefined threshold rate of confidential information $R_s$ and can be defined mathematically as follows [6]:

$$SOP={{\displaystyle \int }}_0^{\infty }{F}_{eq}\left(\mathsf{\Theta }\gamma \right)f_e\left(\gamma \right)d\gamma ,$$

(23)

where $\mathsf{\Theta }=e^{R_s}$.

By invoking (12) and (22) into (23), the system SOP can be expressed as:

$$SOP=I_1+I_2.$$

(24)

Thus,

$$I_1=\frac{{\xi }^2{r}^{\alpha +\beta -2}\eta exp\left(-K\right)}{2{\pi }^{r-1}\left(\mathsf{\Gamma }\left(\alpha \right)\mathsf{\Gamma }\left(\alpha \right)\right)}{{\displaystyle \sum }}_{l=0}^{\infty }\frac{{\left(K\eta \right)}^l}{{\left(l!\right)}^2}{{\displaystyle \int }}_0^{\infty }{\gamma }_e{}^l\exp \left(-\eta \gamma \right)G_{r+1,3r+1}^{3r,1}\left(\frac{{\left(\alpha \beta \right)}^r}{r^{2r}{\mu }_r}\gamma \mathsf{\Theta }|\begin{array}{c}1, {\psi }_1\\ {\psi }_2,0\end{array}\right)d\gamma .$$

(25)

By utilizing the integral identity detailed in Reference [38] (Equation (7.813(1))), the $I_1$ term of (25) can be expressed as:

$$I_1=\frac{{\xi }^2{r}^{\alpha +\beta -2}exp\left(-K\right)}{2{\pi }^{r-1}\left(\mathsf{\Gamma }\left(\alpha \right)\mathsf{\Gamma }\left(\alpha \right)\right)}{{\displaystyle \sum }}_{l=0}^{\infty }\frac{K^l}{{\left(l!\right)}^2}{G}_{r+2,3r+1}^{3r,2}\left(\frac{{\left(\alpha \beta \right)}^r\mathsf{\Theta }}{\eta r^{2r}{\mu }_r}|\begin{array}{c}-l,1, {\psi }_1\\ {\psi }_2,0\end{array}\right).$$

(26)

Similarly,

$$\begin{gathered} I_2=\omega \eta exp\left(-K\right){{\displaystyle \sum }}_{l=0}^{\infty }{{\displaystyle \sum }}_{q_1=0}^{m_h-1}\dots {{\displaystyle \sum }}_{q_{N_u}=0}^{m_h-1}\frac{{\left(K\eta \right)}^l\Xi \left(N_u\right){\mathsf{\Delta }}_H^{-\lambda }}{{\left(l!\right)}^2}{{\displaystyle \int }}_0^{\infty }{\gamma }^l\exp \left(-\eta \gamma \right)\times \\ {H}_{1,0:3,1:3,2}^{0,1:1,2:0,3}\left(\begin{array}{c}\left(1,-1,\frac{1}{r}\right)\\ -\end{array}|\begin{array}{c}\left(1-\lambda ,1\right)\left(0,1\right)\left(1,1\right)\\ \left(0,1\right)\end{array}|\begin{array}{c}\left(1-{\xi }^2,1\right)\left(1-\alpha , 1\right)\left(1-\beta ,1\right)\\ \left(-{\xi }^2,1\right)\left(0, \frac{1}{r}\right)\end{array}| \frac{1}{{\Delta }_{H}C},\frac{{\mu }_r^{1/r}}{{\left(\gamma \mathsf{\Theta }\right)}^{1/r}M}\right)d\gamma . \end{gathered}$$

(27)

By converting the H-Fox function to integral form using the identity detailed in Reference [45], (27) can be expressed as:

$$\begin{gathered} I_2=\omega \eta exp\left(-K\right){{\displaystyle \sum }}_{l=0}^{\infty }{{\displaystyle \sum }}_{q_1=0}^{m_h-1}\dots {{\displaystyle \sum }}_{q_{N_u}=0}^{m_h-1}\frac{{\left(K\eta \right)}^l\Xi \left(N_u\right){\mathsf{\Delta }}_H^{-\lambda }}{{\left(l!\right)}^2{\left(2\pi i\right)}^2}{{\displaystyle \int }}_{L_1}^{ }{{\displaystyle \int }}_{L_2}^{ }\mathsf{\Gamma }\left(\frac{t}{r}-s\right)\frac{\mathsf{\Gamma }\left(\lambda +s\right)\mathsf{\Gamma }\left(-s\right)\mathsf{\Gamma }\left(s+1\right)}{\mathsf{\Gamma }\left(1-s\right)}\times \\ \frac{\mathsf{\Gamma }\left({\xi }^2+t\right)\mathsf{\Gamma }\left(\alpha +t\right)\mathsf{\Gamma }\left(\beta +t\right)}{\mathsf{\Gamma }\left({\xi }^2+1+t\right)\mathsf{\Gamma }\left(\frac{t}{r}+1\right)}{\left({\Delta }_{H}C\right)}^{-s}{\left(\frac{{\mathsf{\Theta }}^{1/r}M}{{\mu }_r^{1/r}}\right)}^{-t}\underset{I_3}{\underbrace{{{\displaystyle \int }}_0^{\infty }{\gamma }^{l-t/r}\exp \left(-\eta \gamma \right)d\gamma }} dsdt. \end{gathered}$$

(28)

By applying the integral identity defined in Reference [38] (Equation (3.326(2))), the $I_3$ term of (28) can be solved as:

$$I_3=\mathsf{\Gamma }\left(l-\frac{t}{r}+1\right){\eta }^{-\left(l-\frac{t}{r}+1\right)}.$$

(29)

Putting (29) into (28) and apply the identity given in Reference [45], the $I_2$ term of (28) can be obtained as:

$$\begin{gathered} I_2=\omega exp\left(-K\right){{\displaystyle \sum }}_{l=0}^{\infty }{{\displaystyle \sum }}_{q_1=0}^{m_h-1}\dots {{\displaystyle \sum }}_{q_{N_u}=0}^{m_h-1}\frac{K^l\Xi \left(N_u\right){\mathsf{\Delta }}_H^{-\lambda }}{{\left(l!\right)}^2}\times \\ {H}_{1,0:3,1:3,3}^{0,1:1,2:1,3}\left(\begin{array}{c}\left(1,-1,\frac{1}{r}\right)\\ -\end{array}|\begin{array}{c}\left(1-\lambda ,1\right)\left(0,1\right)\left(0,1\right)\\ \left(0,1\right)\end{array}|\begin{array}{c}\left(1-{\xi }^2,1\right)\left(1-\alpha , 1\right)\left(1-\beta ,1\right)\\ \left(-{\xi }^2,1\right)\left(0, \frac{1}{r}\right)\end{array}| \frac{1}{{\Delta }_{H}C},\frac{{\left(\eta {\mu }_r\right)}^{1/r}}{{\mathsf{\Theta }}^{1/r}M}\right). \end{gathered}$$

(30)

By substituting (26) and (30) into (24), the system SOP can be obtained as:

$$\begin{gathered} SOP=\frac{{\xi }^2{r}^{\alpha +\beta -2}exp\left(-K\right)}{2{\pi }^{r-1}\left(\mathsf{\Gamma }\left(\alpha \right)\mathsf{\Gamma }\left(\alpha \right)\right)}{{\displaystyle \sum }}_{l=0}^{\infty }\frac{K^l}{{\left(l!\right)}^2}{G}_{r+2,3r+1}^{3r,2}\left(\frac{{\left(\alpha \beta \right)}^r\mathsf{\Theta }}{\eta r^{2r}{\mu }_r}|\begin{array}{c} {\psi }_3\\ {\psi }_4\end{array}\right)+\omega exp\left(-K\right){{\displaystyle \sum }}_{l=0}^{\infty }{{\displaystyle \sum }}_{q_1=0}^{m_h-1}\dots {{\displaystyle \sum }}_{q_{N_u}=0}^{m_h-1}\frac{K^l\Xi \left(N_u\right){\mathsf{\Delta }}_H^{-\mathsf{\lambda }}}{{\left(l!\right)}^2} \\ \times H_{1,0:3,1:3,3}^{0,1:1,2:1,3}\left(\begin{array}{c}\left(1,-1,\frac{1}{r}\right)\\ -\end{array}|\begin{array}{c}\left(1-\lambda ,1\right)\left(0,1\right)\left(0,1\right)\\ \left(0,1\right)\end{array}|\begin{array}{c}\left(1-{\xi }^2,1\right)\left(1-\alpha , 1\right)\left(1-\beta ,1\right)\\ \left(-{\xi }^2,1\right)\left(0, \frac{1}{r}\right)\end{array}| \frac{1}{{\Delta }_{H}C},\frac{{\left(\eta {\mu }_r\right)}^{1/r}}{{\mathsf{\Theta }}^{1/r}M}\right), \end{gathered}$$

(31)

where ${\psi }_3=-l,1, {\psi }_1$, and ${\psi }_4={\psi }_2,0$.

4.2.2. Asymptotic Analysis

Due to the complexity of exact closed-form expression of the system SOP given in (31), limited physical insight is provided. As a result of this, the analytical asymptotic expression is derived for the system SOP at high SNR by considering a condition at which ${\mu }_r\to \infty$ and can be derived in closed-form as:

$$\begin{gathered} SO{P}^{\infty }=\frac{{\xi }^2{r}^{\alpha +\beta -2}exp\left(-K\right)}{2{\pi }^{r-1}\left(\mathsf{\Gamma }\left(\alpha \right)\mathsf{\Gamma }\left(\alpha \right)\right)}{{\displaystyle \sum }}_{l=0}^{\infty }{{\displaystyle \sum }}_{t=1}^{3r}\frac{K^l}{{\left(l!\right)}^2}\mathscr{H}{\left(\frac{{\left(\alpha \beta \right)}^r\mathsf{\Theta }}{\eta r^{2r}{\mu }_r}\right)}^{{\psi }_{4,t}}+ \\ \omega \eta exp\left(-K\right){{\displaystyle \sum }}_{l=0}^{\infty }{{\displaystyle \sum }}_{q_1=0}^{m_h-1}\dots {{\displaystyle \sum }}_{q_{N_u}=0}^{m_h-1}\frac{r{\left(K\eta \right)}^l\Xi \left(N_u\right){\mathsf{\Delta }}_H^{-\mathsf{\lambda }}}{{\left(l!\right)}^2\left(2\pi i\right)}{\left(\frac{{\left(\eta {\mu }_r\right)}^{\frac{1}{r}}}{{\mathsf{\Theta }}^{\frac{1}{r}}M}\right)}^{-r}{H}_{4,6}^{5,2}\left(\frac{{\mathsf{\Theta }}^{\frac{1}{r}}M}{{\left(\eta {\mu }_r\right)}^{\frac{1}{r}}}|\begin{array}{c}{\Delta }_1\\ {\Delta }_2\end{array}\right), \end{gathered}$$

(32)

where ${\mathsf{\Delta }}_1=\left\{\left(1,1\right)\left(-l,1/r\right)\left({\xi }^2+1,1\right)\left(1,1/r\right)\right\}$ and ${\Delta }_2=\left\{\left(\lambda ,1\right)\left(1,1\right)\left({\xi }^2,r\right) \left(\alpha ,r\right)\left(\beta ,r\right)\left(0,1\right)\right\}$.

Proof. 

See Appendix A. □

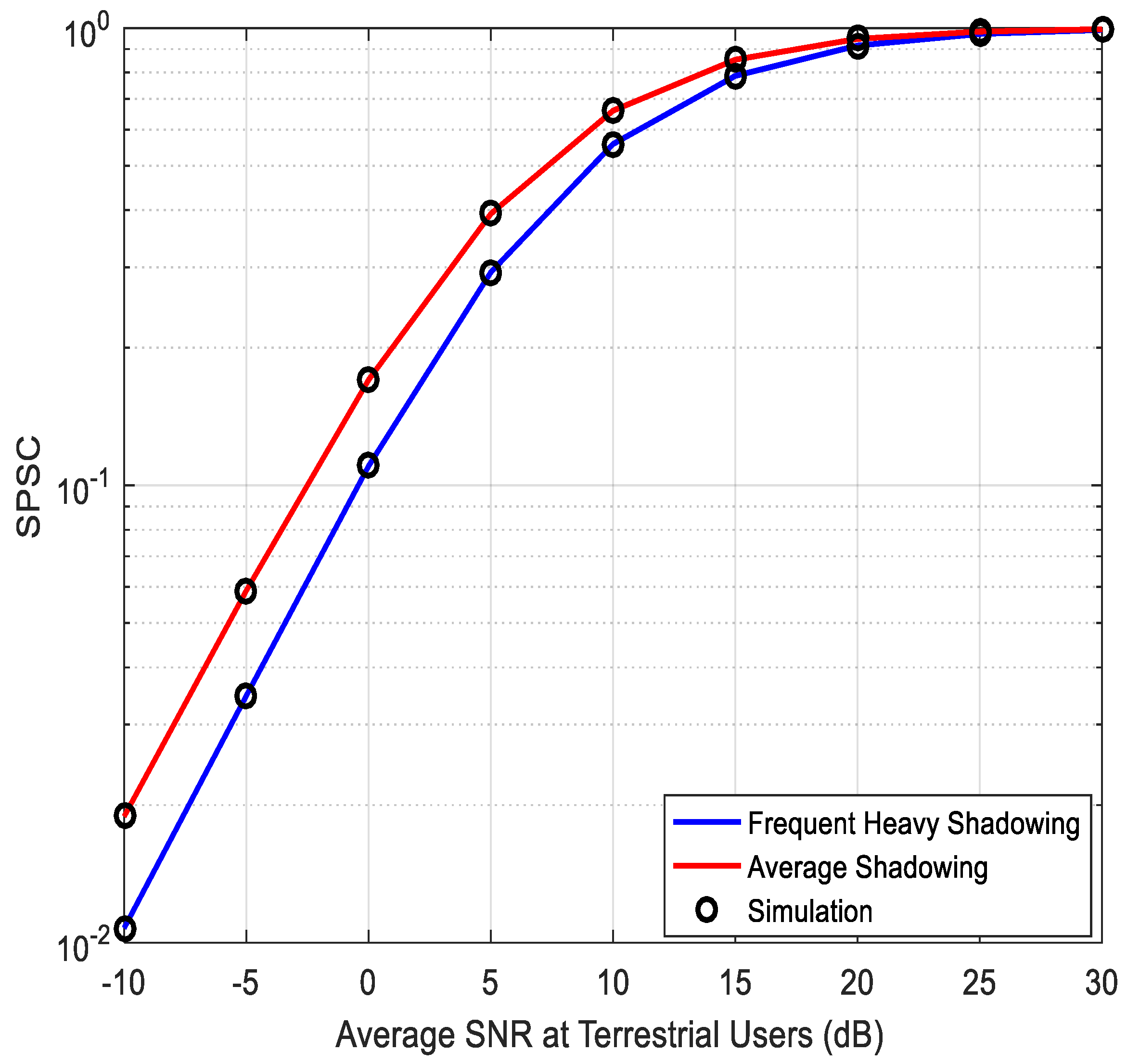
4.3. Strictly Positive Secrecy Capacity (SPSC)

This illustrates the probability of the existence of positive secrecy capacity so as to offer a secure transmission and can be expressed as [32]:

$$SPSC=1-{{\displaystyle \int }}_0^{\infty }{F}_{eq}\left(\gamma \right)f_e\left(\gamma \right)d\gamma .$$

(33)

Thus,

$$SPSC=1-SO{P}_{\mathsf{\Theta }=1}.$$

(34)

5. Numerical Results and Discussions

In this section, numerical results of the system secrecy performance in terms of COP, SOP and SPSC under different detection schemes are presented. The shadowing severity for the Shadowed-Rician distributions are defined as follows: $\left(m=1, b=0.063, \mathsf{\Omega }=0.0007\right)$ for the frequent heavy shadowing (FHS), and $\left(m=5, b=0.251, \mathsf{\Omega }=0.279\right)$ for the average shadowing (AS) [25]. Regarding the influence of atmospheric turbulence, different turbulence conditions are considered, and these include: weak levels $\left(\alpha =3.78, \beta =3.74\right)$, moderate levels $\left(\alpha =2.50, \beta =2.06\right)$, and strong levels $\left(\alpha =2.04, \beta =1.10\right)$ [7]. Except otherwise stated, $R_s=0.01 \mathrm{nats}/\mathrm{s}/\mathrm{Hz}$, $N_u=2$, $C=0.75$, and the system is subjected to strong turbulence and FHS fading conditions.

The COP performance of the system under the variation of threshold SNR ${\gamma }_{th}$ is illustrated in Figure 2 under different atmospheric turbulence. It can be deduced from the results that the increase in atmospheric turbulence significantly deteriorates the system COP performance for the two detection schemes at the HAP. In addition, a similar impact of atmospheric turbulence on the system SOP performance can be observed in Figure 3 as the system SOP gets degraded due to severities of the atmospheric turbulence. In both secrecy performances, it is depicted by the results that heterodyne detection offers the system better performance than IMDD detection. The results also depict that the analytical results perfectly matched with the simulation results, which indicate the accuracy of the derived expressions.

The impact of pointing error on the system SOP performance under the different detection schemes is presented in Figure 4. Under both detections, the lower pointing error value ($\xi =1.1$) causes an increase in the effect of pointing errors, which leads to degradation in the system SOP performance. On the other hand, higher values of PE ($\xi =6.5$) decrease the effect of PE and improve the system SOP. It is observed from the results that the system performance is better under the heterodyne detection compared to the IMDD detection.

In Figure 5, the effect of ${\overline{\gamma }}_e$ level on the system SOP performance is demonstrated under the different detection schemes. It can be seen that the analytical results collaborate perfectly with the simulation results, which proves the accuracy of the derived expressions. Moreover, it can be deduced from the results that the higher the values of ${\overline{\gamma }}_e$, the worse the system SOP performance, with heterodyne detection outperforming the IMDD detection. It can also be observed from the result that the asymptotic results follow the SOP results at high SNR. This shows that the quality of eavesdropper channel improves at higher valves of ${\overline{\gamma }}_e$, which significantly leads to degradation in system SOP performance.

The effect of Rican factor level of the eavesdropper link on the system SOP performance is depicted in Figure 6. It can be observed that the higher value of$K$ factor has lower system SOP performance. This is because, at large values of $K$factor, there is strong LOS for the eavesdropper to wiretap the confidential message from HAP, and this degrades the system SOP performance. The analytical results match well with simulation results, confirming the validity of the derived expressions.

The system SOP performance under different shadowing fading severities is presented in Figure 7. It can be observed that the system becomes degraded as the shadowing fading effect increases from AS to FHS. Under the same channel conditions, the results show that heterodyne detection offers the system better SOP performance compared with IMDD detection. In addition, analytical results of the system SOP closely match with simulation results, showing the accuracy of our derivations.

The effect of the number of terrestrial users on the system SOP performance under strong turbulence condition is presented in Figure 8. It can be deduced that the system SOP performance significantly improves as the number of ground users increases. This is because multiuser diversity gain is achieved, which, in turn, enhances the system SOP performance. The results indicate that the heterodyne detection offers the system better performance compared to the IMDD detection.

The SPSC performance of the system under the different shadowing fading effect is illustrated in Figure 9 under the heterodyne detection at HAP. It can be observed that the system becomes degraded as the shadowing fading effect get severer. The results also demonstrate that the analytical results perfectly agree with the simulation results, which justify the accuracy of the derived expressions.

6. Conclusions

The secrecy performance of a mixed FSO/RF integrated satellite-HAP relaying networks in the presence of an eavesdropper is evaluated. The FSO and RF links are model as Gamma-Gamma distribution and Rican fading distribution, respectively. The exact closed-form expression of the system equivalent end-to-end CDF is derived under different detection schemes. Based on this, the analytical closed form expressions of the concerned system COP, SOP, and SPSC are determined. To obtain more insight about the system performance, the asymptotic analysis of the system SOP is provided. The results shows that the pointing errors, atmospheric turbulence, and shadowing severity significantly degrade the system performance. In addition, the results indicate that heterodyne detection offers the system better performance compared to IM/DD detection. The future work of this paper could be tailored toward the non-orthogonal multiple access (NOMA) for better system spectrum efficiency.