Abstract
In this work, a surface plasmon resonance (SPR) temperature sensor based on a con-joined-tubular anti-resonance optical fiber (CTF) was theoretically designed and analyzed using the finite element method. The CTF cladding was composed of eight pairs of conjoined tubes, and one or two holes of the tubes were selectively coated with gold to generate the SPR effect. Alcohol was injected into the core of the CTF to work as the sensing medium using vapor deposition. The proposed sensing structure exhibited excellent birefringence and produced more than six resonant peaks in different wavebands of the X and Y polarization. The positions of those resonant peaks were sensitive to temperature change, and the simulated sensitivity was about 3.2–3.6 nm/°C. The multiple working wavebands of the proposed sensing structure could be used for self-verification. Moreover, the influence of structural parameters on sensing performance was analyzed in detail. Possessing features of high sensitivity, good birefringence, multiple measuring wavebands, and self-verification, the proposed CTF-based SPR sensor has great potential in practical applications such as biological research and chemical sensing.
1. Introduction
Hollow-core anti-resonant fibers (HC-ARFs), which are based on the anti-resonance effect for energy propagation, have become a research hotspot in the field of microstructure fiber research [1,2,3]. This fiber type usually possesses a single-ring structure and exhibits advantages of simple structure, high transmission quality, and large transmission bandwidth [4,5,6,7,8,9]. As the core surface is usually a negative curvature cycloid, it is also called a hollow-core negative curvature fiber. Along with the development of HC-ARF, more recently, another fiber type, conjoined-tubular anti-resonance fiber (CTF), has been produced, which consists of several untouched conjoined tubes formed by conjoining two air holes. Compared with the traditional single-ring HC-ARF, CTF has a lower loss and a better resistance to bending loss, and it has bright prospects in data transmission and laser applications. In 2018, Gao et al. proposed a CTF with a transmission loss of 2 dB/km at 1512 nm and loss <16 dB/km across the O, E, S, C, L telecom bands (1302–1637 nm) [10,11]. In 2020, Gao et al. used a CTF to challenge the limit of the intrinsic Rayleigh scattering of silica glass material in the visible region [12].
Surface plasmon resonance (SPR) [13,14], caused by collective electronic vibration, is a technology that generally occurs at the interface between two media with opposite dielectric constants. When the phase-matching condition is satisfied at a certain wavelength, the core mode can be completely coupled with the surface plasmon polariton (SPP) mode. Due to unique capabilities such as high sensitivity, real time, and usefulness in unlabeled detection, SPR has experienced rapid development in recent decades and has been widely applied to fields of biological research, food quality detection, chemical and gas analysis, medical diagnostics, and environmental monitoring [15,16,17].
To date, various SPR-based sensors have been proposed, based on the traditional sol-id-core photonic crystal fiber (PCF), among which the U-shaped and D-shaped structures are particularly popular. In 2016, Rahul and Vinod proposed a gold-coated D-shaped PCF refractive index (RI) sensor with an average sensitivity of 7700 nm/RIU and a maximum sensitivity of 9000 nm/RIU [18]. In 2019, Tianshu Li et al. proposed an Ag–graphene-layer-coated H-shaped PCF SPR sensor with a U-shaped groove structure, which obtained a sensitivity as high as 12,600 nm/RIU with a resolution of 7.94 × 10−6 RIU [19]. In 2020, Nelson et al. proposed a highly sensitive RI sensor based on long-range SPR in an H-shaped microstructured optical fiber (MOF), achieving a sensitivity of up to 7540 nm/RIU [20]. Furthermore, to achieve better sensing performance, especially in temperature sensing, the researchers proposed to fill the PCF core with liquid or other materials to enhance the sensitivity. In 2018, Yang et al. designed a hollow-fiber SPR sensor for temperature sensing, whose core was filled with toluene to help realize an extremely high sensitivity of 6.51 nm/°C [21]. In 2021, Tang et al. presented a novel SPR temperature sensor comprising a dielectric/Ag-coated hollow fiber filled with thermosensitive liquid, the sensitivity of which reached 5.21 nm/°C in the range of 20–60 °C [22]. In spite of this excellent sensing performance, most of these reported SPR sensors rely on only a single resonance peak in one polarization direction [15,16,17,18,19,20,21,22]; furthermore, due to the limited range of light sources, the measured data are usually in want of verification.
In this work, an SPR temperature sensor drawing on a CTF structure was designed and simulated. Alcohol was injected into the core of CTF as sensing medium, and the air hole near the core was gold-coated to generate SPR. The proposed sensing structure exhibited excellent nonlinearity and produced more than three resonant peaks along both X and Y polarization, allowing it to work in a much wider waveband and be self-verified. The temperature sensing performance was simulated in the range of 20–50 °C, and a sensitivity as high as 3.45 nm/°C was obtained. Moreover, the influence of structural parameters on sensing performance was analyzed in detail. Possessing features of high sensitivity, good birefringence, multiple measuring wavebands, and self-verification, the proposed sensor has great potential in practical applications such as biological research and chemical sensing.
2. Sensing Principle
In this work, the CTF adopted eight pairs of conjoined tubes; the outer hole diameter of these conjoined tubes is indicated by D, the inner hole diameter is indicated by d, and the hole wall thickness is indicated by T. For the overall fiber structure, the outer diameter (DO) was 160 μm and the inner diameter (DI) was 100 μm. Due to oxidation resistance and excellent SPR application performance, gold was chosen as the metal layer to coat on the inner hole, realized by vapor deposition [23], whose thickness is represented by Tg. Alcohol was injected into the core of CTF as sensing medium by vapor deposition [23]. In this work, two cases are discussed, namely, a single-hole coating (Structure I) and a double-hole coating of opposite distribution (Structure II). The respective fiber cross-section is shown in Figure 1.
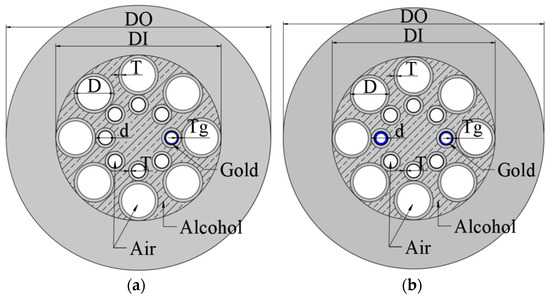
Figure 1.
The cross-sectional structure of the designed sensor: (a) one hole gold-coated; (b) two holes gold-coated.
In this work, we set D to 24 μm, d to 12 μm, and Tg to 400 nm. In order to prevent the leaking mode of CTF from affecting SPR, the inoperable area was calculated according to the anti-resonance formula, which is expressed as follows [24]:
where n1 is the silica RI, n0 is the alcohol RI, m is the order of resonance, and λ is the wavelength. Tm indicates the wall thickness when resonance occurs, at which time the sensor cannot work. To avoid the interference of resonance on sensing, T was set to 1.8 μm.
During the light transmission in CTF, light is limited in the core of CTF by the anti-resonance effect [2]. The gold coating increases the light leakage and produces more evanescent fields to couple with the gold film to excite SPP. When the effective index (neff) of the CTF core mode is equal to that of the gold film SPP, SPR occurs, which induces an increase in the confinement loss (Loss) and produces a resonance peak in the output spectrum. As temperature varies, neff of the CTF core mode changes, resulting in a corresponding change in the resonance peak. Therefore, by observing the location movement of the resonance peak, we can obtain information concerning the temperature variation. Moreover, with the addition of gold coating, structures along the X-axis and Y-axis would be different, which produces a strong birefringence, resulting in different positions of resonance peaks along the X and Y polarization directions. Since gold coating along the Y-axis weakens the birefrigence, in this article, we only discuss cases of gold coating along the X-axis, namely, Structure I and Structure II.
For an incident light, the resonance condition can be described as follows [25]:
where β denotes the real part of the effective index (neff) of the core mode, θ denotes the incident angel of the light, and nk represents the real part of the effective index (neff) of the SPP on the gold film. Upon the occurrence of SPR, Loss can be calculated using the following formula [26,27]:
where Im(neff) is the imaginary part of the mode effective RI (neff), and λ is the wavelength. The temperature sensitivity relative to the shift of peak wavelength Δλpeak and temperature variation ΔT is given by the formula below [21,22,28].
In addition, the dielectric constant of gold expressed by Drude-Lorentz is as follows [29]:
where the high-frequency dielectric constant ε∞ = 5.967 and the weighted coefficient Δε = 1.09; ω refers to the guiding optical angular frequency, ωD refers to the plasmon frequency, γD refers to the damping frequency, ωL refers to the oscillator strength of the Lorenz oscillator, and ΓL refers to the frequency spectrum width of the Lorenz oscillator. In this work, γD/2π = 15.92 THz, ωD/2π = 2113.6 THz, ωD/2π = 650.07 THz, and ΓL/2π = 104.86 THz.
The CTF material was silica, the RI of which can be determined by the Sellmeier equation [30].
where B1 = 0.6961663, B2 = 0.4079426, B3 = 0.8974764, λ1 = 0.0684043 μm, λ2 = 0.1162414 μm, and λ3 = 9.896161 μm. For the adoption of alcohol [31,32] as a sensing medium, its RI change with temperature can be calculated by the equation below [31].
where n0 is the alcohol RI at the reference temperature T0. For simplification, the relationship between the alcohol RI and temperature outlined in Table 1 was used in this work.

Table 1.
Temperature and the corresponding alcohol RI.
3. Simulation and Analysis
3.1. Preliminary Simulation without Temperature Variation
In this work, the COMSOL Multiphysics software was used to simulate the two different gold-coated CTF structures, and the finite element method (FEM) was used to analyze their respective Loss and mode field. The alcohol-filled core RI was set to 1.34800 (T = 50 °C).
Firstly, we simulated the mode field distribution and Loss of Structure I in comparison with the structure without gold-coating. The simulated results along the X polarization are presented in Figure 2a, while those along the Y polarization are presented in Figure 2b. We can see that Loss of the non-gold-coated CTF was negligible compared with its gold-coated counterpart, indicating that Loss was mostly caused by the SPR effect generated by the gold film. It is to be noted that four resonance peaks were formed both along the X and Y polarization directions. Moreover, the peak locations were all different. This is because the structure of CTF resulted in the light being reflected by the outer hole couple into the inner gold-coated hole from various incident angles, leading to the generation of several resonant peaks. This phenomenon is very different from that of the traditional SPR sensors, which generally produce 1–2 resonance peaks [15,16,17,18,19,20,21,22]. An investigation into the mode fields revealed that SPR could occur around the gold-coated hole of Structure I, while it could only occur at a small angle or on a plane in the traditional sensors. For the proposed sensing structure, its generation of more than eight resonance peaks allowed it to have several working wavebands, which is highly advantageous for the sensing performance.
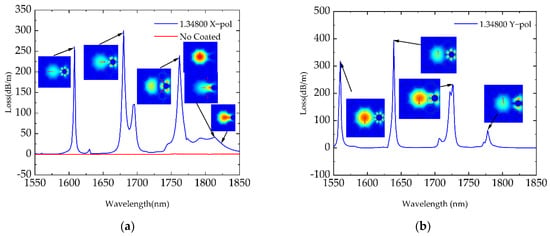
Figure 2.
(a) Mode field distribution and Loss of Structure I in comparison with CTF without coating along the X polarization; (b) mode field distribution and Loss of Structure I along the Y polarization. Arrows in the insets indicate the polarized direction of the electric field.
We further simulated the mode field distribution and Loss of Structure II along the two polarization directions, as shown in Figure 3. We can see that the distribution of the resonance peaks resembled that of Structure I, and the intensity of peaks was obviously stronger. However, in Figure 3a, the Loss spectral band was broadened, and the sub resonance peak was quite stronger in the range of 1650 nm to 1700 nm. This phenomenon was caused by the addition of the second gold-coated hole, which also produced the SPR effect and led to an increase of the Loss and the subpeak, as depicted in the mode field diagram in Figure 3. In other words, the CTF-based sensing structure proposed in this work was able to generate multiple resonance peaks, and its resonance spectral width, subpeaks, and resonance depth could be adjusted by manipulating the gold-coated hole number, thus demonstrating great sensing superiority.
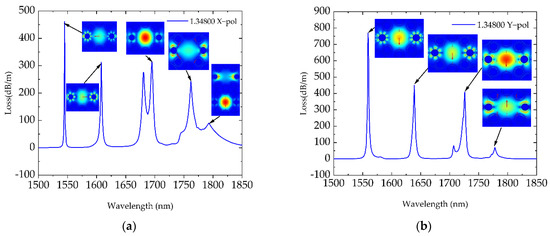
Figure 3.
Mode field distribution and Loss of Structure II (a) along the X polarization and (b) along the Y polarization. Arrows in the insets indicate the polarized direction of the electric field.
3.2. Simulation on Temperature Sensing Performance
Next, to evaluate the sensing performance of the proposed CTF-based sensor, temperature was varied from 20 °C (n = 1.36048) to 50 °C (n = 1.34800) with a step of 10 °C. Because the melting temperature of silicon is about 1670 °C and its RI coefficient is two orders of magnitude lower than that of alcohol [26], the silica RI change was ignored in this work. The Loss of Structure I along the X and Y polarization directions was simulated in the working waveband of 1550–1850 nm, as presented by Figure 4a,b, while that of Structure II was simulated in the working waveband of 1500–1850 nm, as presented by Figure 4c,d. We can see that the multiple resonance peaks exhibited a significant wavelength shift to a longer wavelength direction with the increase in temperature, which is different from the situation of the traditional solid-core PCF SPR sensor [15,16,17,18,19,20]. In traditional sensors, the liquid sensing medium is filled to the position where the cladding contacts the metal. As temperature rises, the liquid RI decreases, leading to a decrease in neff of SPP and core mode and resulting in the phase matching points moving to the shorter wavelength direction. In this work, alcohol was injected into the core of the CTF, and neff of the core mode was close to the liquid RI. When temperature increased, the neff of core mode decreased with the liquid RI, while gold coating induced a decrease in SPP with the increase in wavelength, which resulted in the phase matching points moving to the longer wavelength direction. This obvious wavelength shift of the resonance peak with temperature variation greatly facilitates temperature sensing.
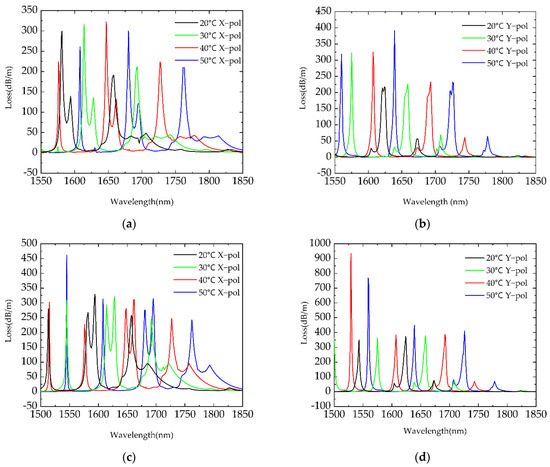
Figure 4.
(Loss of Structure I a) along the X polarization, and (b) along the Y polarization; Loss of Structure II (c) along the X polarization, and (d) along the Y-polarization.
For Structure I and Structure II, two sets of resonance peaks were selected from the X and Y polarization, and their peak wavelengths were fitted with the temperature. The first chosen resonance peak along the X polarization of Structure I is denoted as Structure I X1-pol, and other expressions are given accordingly. The results of fitting diagram are shown in Figure 5a,b. We can see that both fitting lines showed ultra-high linearity. The respective functions of the wavelength shift with temperature are listed in Table 2 in detail, and the temperature sensitivity and R2 values were obtained. It is to be noted that a temperature sensitivity as high as 3.5 nm/°C with R2 of 1 was achieved for Structure II. This confirms the practicality of using these resonance peaks of different wavebands for temperature measurement. Furthermore, the measurement results of different wavebands can be used for self-verification. The self-verification feature of the proposed sensor cannot be achieved by the traditional SPR sensors.
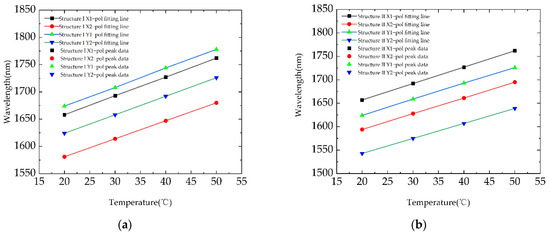
Figure 5.
Fitting diagram of temperature and peak wavelength of (a) Structure I and (b) Structure II.

Table 2.
Fitting function for Structure I and Structure II.
3.3. Model Optimization
Since the structural parameters of the optical fiber have an impact on the performance of the sensor, model optimization was further carried out from three aspects: the thickness of the gold coating Tg, the hole wall thickness T, and the conjoined tube structure (D and d). Since the thermal expansion coefficients of gold and silica are extremely small, the deformation affected by temperature was negligible. Here, we took structure I as our simulation model.
Firstly, Tg was changed to 300 nm, 200 nm, and 100 nm. For the change of Tg, the corresponding Loss at the working waveband of 1550–1850 nm was simulated along X polarization, as shown in Figure 6a,c,e, and along Y polarization, as shown in Figure 6b,d,f. The respective functions of the wavelength shift with temperature are listed in Table 3 in detail, and the temperature sensitivity and R2 values were obtained. Accordingly, a temperature sensitivity ranging from 3.31–3.56 nm/°C with R2 from 0.9998 to 1 was obtained, which is similar to the results obtained at the preliminary parameter setting of Tg = 400 nm (see Table 2). On the other hand, with the decrease in Tg, the resonance peak intensity increased and the sub-peaks weakened, as shown in Figure 6. Therefore, the variation of Tg had little effect on temperature sensitivity, but it could be used to adjust the resonance intensity and the sub-peaks.
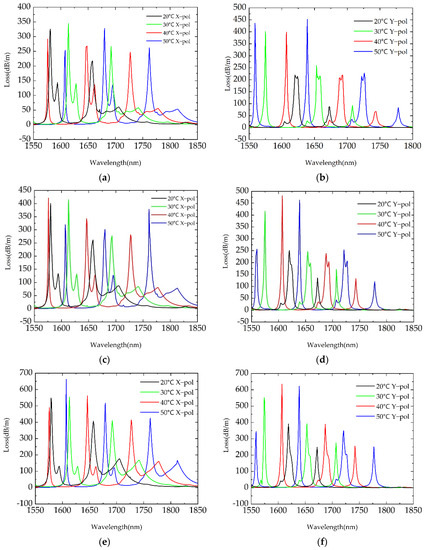
Figure 6.
Loss along X polarization (a) at 300 nm, (c) at 200 nm, and (e) at 100 nm; Loss along Y polarization (b) at 300 nm, (d) at 200 nm, and (f) at 100 nm.

Table 3.
Fitting function for Structure I and Structure II.
Secondly, T was varied to be 1.6 μm, 1.7 μm, and 1.8 μm, and the corresponding Loss spectrum is shown in Figure 7. It can be seen that, as T increased, the resonance peaks of X polarization moved to the longer wavelength direction. For instance, the mode field depicted in the insets moved from 1630 nm to 1810 nm with the increase in T. This phenomenon was due to the change in T as a function of the distance from gold to alcohol and the incident angle. This proves that the hole thickness T can control the distribution of the resonance peaks. In other words, we could adjust T to obtain a suitable working waveband for temperature sensing.
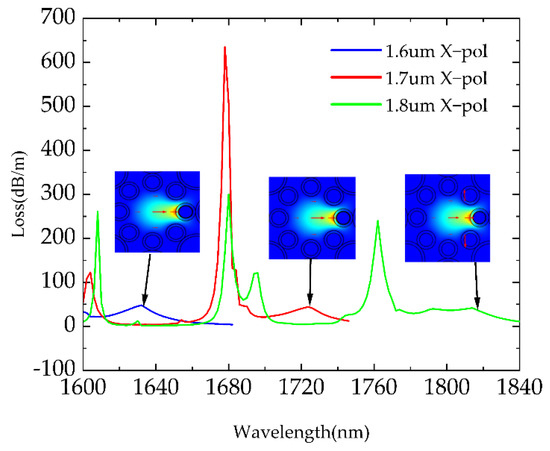
Figure 7.
Loss spectra with the variation of T (1.6 um, 1.7 um, and 1.8 um). Insets indicate the movement of the mode field with the increase in T, where arrows show the polarized direction of the electric field.
Lastly, the impact of different CTF tube structures on sensing performance was analyzed, which was carried out in terms of two cases: with the inner hole larger than the outer hole (d = 20 μm, D = 12 μm), and with the inner hole equal to the outer hole (d = 16 μm, D = 16 μm). The corresponding Loss and mode fields were simulated, as shown in Figure 8. Compared with the previous discussion concerning Structure I (d = 12 μm, D = 24 μm), when d > D, the resonance peak distribution was irregular and the peak intensity became lower; when d = D, the intensity of resonance peaks became even lower. This proves that neither case was suitable for temperature sensing, and the desired tube structure was that which we discussed in the previous section (d < D).
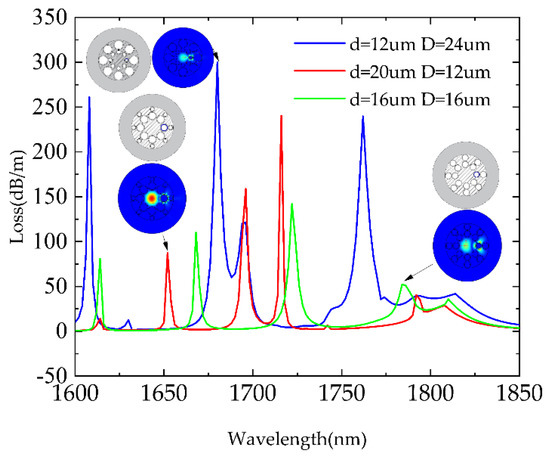
Figure 8.
Loss spectra with different tube structures.
4. Conclusions
This work designed and analyzed an SPR temperature sensor based on CTF. The finite element method was used to simulate the sensing performance of two types of gold-coating structures, both of which exhibited excellent nonlinearity and produced more than three resonant peaks along both X and Y polarization. This property enables the expansion of the range of working wavebands available for temperature sensing and allows for self-verification. Moreover, by adjusting the thickness of the gold coating, the hole wall thickness, and the conjoined tube structure, the influence of structural parameters on sensing performance was analyzed in detail. Possessing features of high sensitivity, good birefringence, multiple measuring wavebands, and self-verification, the proposed CTF-based SPR sensor has great potential in practical applications such as biological research and chemical sensing.
Author Contributions
Conceptualization, Q.W. and T.C.; methodology, T.C.; software, Q.W.; validation, Q.W., T.C., X.Z., X.Y. and F.W.; formal analysis, Q.W.; investigation, Q.W., X.Z., X.Y. and F.W.; resources, Q.W., X.Z., X.Y., F.W. and T.C.; data curation, Q.W.; writing—original draft preparation, Q.W.; writing—review and editing, T.C.; visualization, Q.W., X.Z. and F.W.; supervision, T.C.; project administration, T.C.; funding acquisition, T.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Key Research and Development Program of China (2017YFA0701200), the National Natural Science Foundation of China (61775032), the Fundamental Research Funds for the Central Universities (N2104022, N180704006, N2004021, and N180408018), the Natural Science Foundation of Science and Technology Department of Liaoning Province (2020-BS-046), the Hebei Natural Science Foundation (F2020501040), and the 111 Project (B16009). The authors thank the Liao Ning Revitalization Talents Program.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yu, F.; Knight, J.C. Negative Curvature Hollow-Core Optical Fiber. IEEE J. Sel. Top. Quantum Electron. 2016, 22, 146–155. [Google Scholar] [CrossRef] [Green Version]
- Wei, C.; Weiblen, R.J.; Menyuk, C.R.; Hu, J. Negative curvature fibers. Adv. Opt. Photonics 2017, 9, 504–561. [Google Scholar] [CrossRef]
- Knight, J.C. Anti-Resonant Hollow Core Fibers. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 7 March 2019. [Google Scholar]
- Taranta, A.; Fokoua, E.N.; Mousavi, S.A.; Hayes, J.R.; Bradley, T.D.; Jasion, G.T.; Poletti, F. Exceptional polarization purity in antiresonant hollow-core optical fibres. Nat. Photonics Eng. 2020, 14, 504–510. [Google Scholar] [CrossRef]
- Yan, S.; Lou, S.; Wang, X.; Zhao, T.; Zhang, W. High-birefringence hollow-core anti-resonant THz fiber. Opt. Quantum Electron. 2018, 50, 1–13. [Google Scholar] [CrossRef]
- Yu, F.; Wadsworth, W.J.; Knight, J.C. Knight. Low loss silica hollow core fibers for 3–4 μm spectral region. Opt. Express 2012, 20, 11153–11158. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pryamikov, A.D.; Biriukov, A.S.; Kosolapov, A.F.; Plotnichenko, V.G.; Semjonov, S.L.; Dianov, E.M. Demonstration of a waveguide regime for a silica hollow—Core microstructured optical fiber with a negative curvature of the core boundary in the spectral region > 3.5 μm. Opt. Express 2021, 19, 1441–1448. [Google Scholar] [CrossRef]
- Chen, F.; Jiang, S.; Jin, W.; Bao, H.; Ho, H.L.; Wang, C.; Gao, S. Ethane detection with mid-infrared hollow-core fiber photothermal spectroscopy. Opt. Express 2020, 28, 38115–38126. [Google Scholar] [CrossRef]
- Yao, C.; Xiao, L.; Gao, S.; Wang, Y.; Wang, P.; Kan, R.; Jin, W.; Ren, W. Sub-ppm CO detection in a sub-meter-long hollow-core negative curvature fiber using absorption spectroscopy at 2.3 μm. Sens. Actuators B Chem. 2020, 303, 127238. [Google Scholar] [CrossRef]
- Gao, S.F.; Wang, Y.Y.; Ding, W.; Jiang, D.L.; Gu, S.; Zhang, X.; Wang, P. Hollow-core conjoined-tube negative-curvature fibre with ultralow loss. Nat. Commun. 2018, 9, 2828. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.Y.; Gao, S.F.; Ding, W.; Wang, P. Loss Reduction in Hollow-Core Conjoined-Tube Negative-Curvature Fiber. In Proceedings of the 45th European Conference on Optical Communication, Dublin, Ireland, 22–26 September 2019. [Google Scholar]
- Gao, S.F.; Wang, Y.Y.; Ding, W.; Hong, Y.F.; Wang, P. Conquering the Rayleigh Scattering Limit of Silica Glass Fiber at Visible Wavelengths with a Hollow-Core Fiber Approach. Laser Photonics Rev. 2020, 14, 1900241. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, H.; Park, J.; Kang, S.; Kim, M. Surface plasmon resonance: A versatile technique for biosensor applications. Sensors 2015, 15, 10481–10510. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.; Cheng, T.; Li, S.; Suzuki, T.; Ohishi, Y. Practical sensing approach based on surface plasmon resonance in a photonic crystal fiber. OSA Contin. 2018, 1, 1332–1340. [Google Scholar] [CrossRef]
- Zhou, X.; Li, X.; Cheng, T.; Li, S.; An, G. Graphene enhanced optical fiber SPR sensor for liquid concentration measurement. Opt. Fiber Technol. 2018, 43, 62–66. [Google Scholar] [CrossRef]
- Zhou, X.; Li, X.; Li, S.; An, G.W.; Cheng, T. Magnetic Field Sensing Based on SPR Optical Fiber Sensor Interacting with Magnetic Fluid. IEEE Trans. Instrum. Meas. 2019, 68, 234–239. [Google Scholar] [CrossRef]
- Khanikar, T.; Singh, V.K. Analysis of a highly sensitive side polished hollow fiber plasmonic sensor and its application as a magnetometer. Appl. Opt. 2020, 59, 171–179. [Google Scholar] [CrossRef]
- Gangwar, R.K.; Singh, V.K. Highly Sensitive Surface Plasmon Resonance Based D-Shaped Photonic Crystal Fiber Refractive Index Sensor. Plasmonics 2017, 12, 1367–1373. [Google Scholar] [CrossRef]
- Li, T.; Zhu, L.; Yang, X.; Lou, X.; Yu, L. A Refractive Index Sensor Based on H-Shaped Photonic Crystal Fibers Coated with Ag-Graphene Layers. Sensors 2020, 20, 741. [Google Scholar] [CrossRef] [Green Version]
- Gomez-Cardona, N.; Reyes-Vera, E.; Torres, P. High Sensitivity Refractive Index Sensor Based on the Excitation of Long-Range Surface Plasmon Polaritons in H-Shaped Optical Fiber. Sensors 2020, 20, 2111. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Lu, Y.; Liu, B.; Yao, J. High Sensitivity Hollow Fiber Temperature Sensor Based on Surface Plasmon Resonance and Liquid Filling. IEEE Photonics J. 2018, 10, 1–9. [Google Scholar] [CrossRef]
- Tang, Y.-X.; Zhang, X.; Zhu, X.-S.; Shi, Y.-W. Dielectric layer thickness insensitive EVA/Ag-coated hollow fiber temperature sensor based on long-range surface plasmon resonance. Opt. Express 2021, 29, 368–376. [Google Scholar] [CrossRef]
- Liu, B.-H.; Jiang, Y.-X.; Zhu, X.-S.; Tang, X.-L.; Shi, Y.-W. Hollow fiber surface plasmon resonance sensor for the detection of liquid with high refractive index. Opt. Express 2013, 21, 32349–32357. [Google Scholar] [CrossRef]
- Litchinitser, N.M.; Abeeluck, A.K.; Headley, C.; Eggleton, B.J. Antiresonant reflecting photonic crystal optical waveguides. Opt. Lett. 2002, 27, 1592–1594. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, X.-S.; Shi, Y.-W. Improving the performance of hollow fiber surface plasssmon resonance sensor with one dimensional photonic crystal structure. Opt. Express 2018, 26, 130–140. [Google Scholar] [CrossRef]
- Rifat, A.A.; Mahdiraji, G.A.; Sua, Y.M.; Ahmed, R.; Shee, Y.G.; Adikan, F.M. Highly sensitive multi-core flat fiber surface plasmon resonance refractive index sensor. Opt. Express 2016, 24, 2485–2495. [Google Scholar] [CrossRef]
- Litchinitser, N.M.; Dunn, S.C.; Usner, B.; Eggleton, B.J.; White, T.P.; McPhedran, R.C.; de Sterke, C.M. Resonances in microstructured optical waveguides. Opt. Express 2003, 11, 1243–1251. [Google Scholar] [CrossRef]
- Luan, N.; Wang, R.; Lv, W.; Lu, Y.; Yao, J. Surface plasmon resonance temperature sensor based on photonic crystal fibers randomly filled with silver nanowires. Sensors 2014, 14, 16035–16045. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vial, A.; Grimault, A.S.; Macías, D.; Barchiesi, D.; De La Chapelle, M.L. Improved analytical fit of gold dispersion: Application to the modeling of extinction spectra with a finite-difference time-domain method. Phys. Rev. B 2005, 71, 085416. [Google Scholar] [CrossRef]
- Malitson, I.H. Interspecimen comparison of the refractive index of fused silica. J. Opt. Soc. Am. 1965, 55, 1205–1208. [Google Scholar] [CrossRef]
- Yu, Y.; Li, X.; Hong, X.; Deng, Y.; Song, K.; Geng, Y.; Wei, H.; Tong, W. Some features of the photonic crystal fiber temperature sensor with liquid ethanol filling. Opt. Express 2010, 18, 15383–15388. [Google Scholar] [CrossRef]
- Sani, E.; Dell’Oro, A. Spectral optical constants of ethanol and isopropanol from ultraviolet to far infrared. Opt. Mater. 2016, 60, 137–141. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).