Graphene-Coated Highly Sensitive Photonic Crystal Fiber Surface Plasmon Resonance Sensor for Aqueous Solution: Design and Numerical Analysis
Abstract
1. Introduction
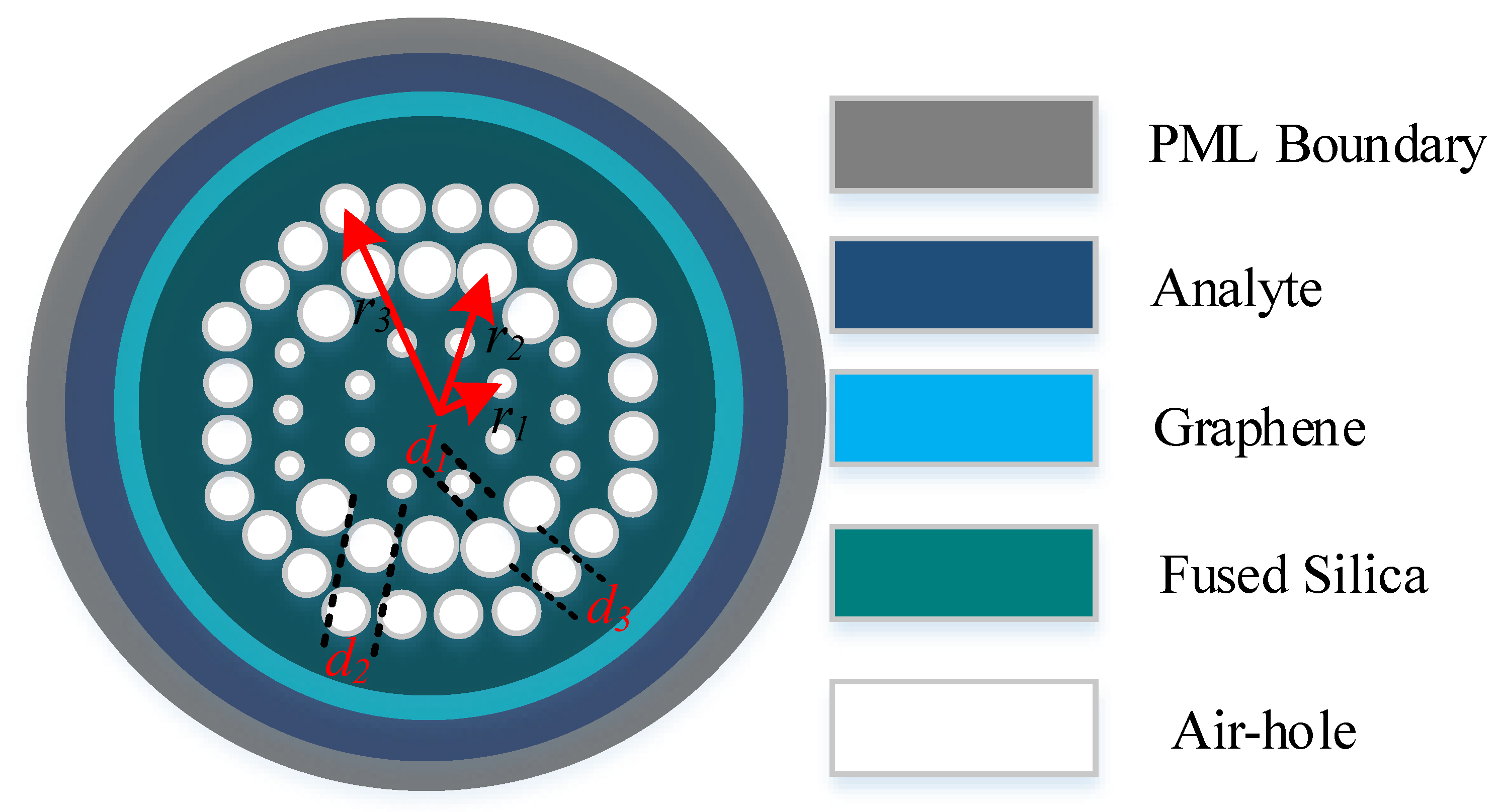
2. Design Methodology
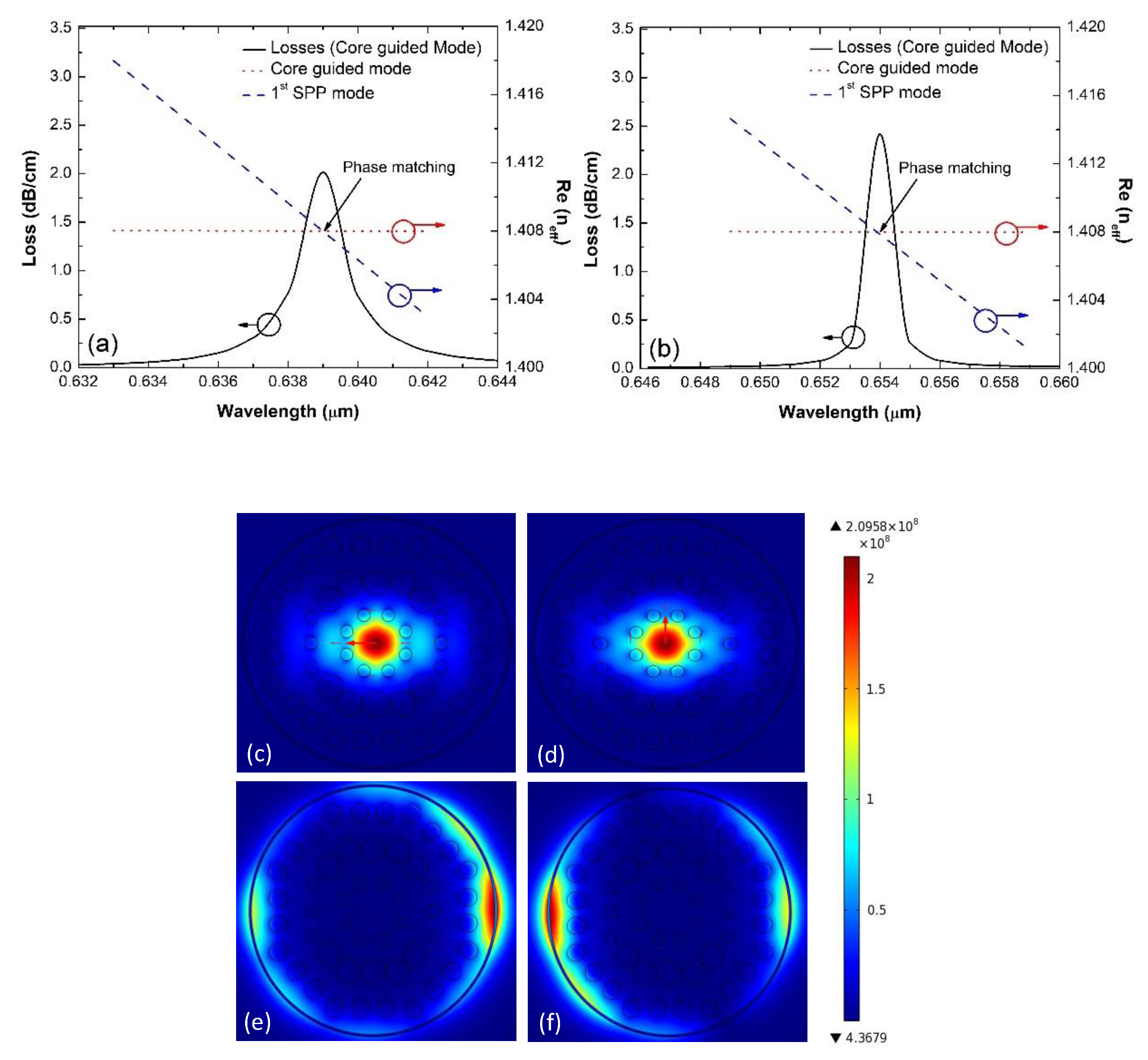
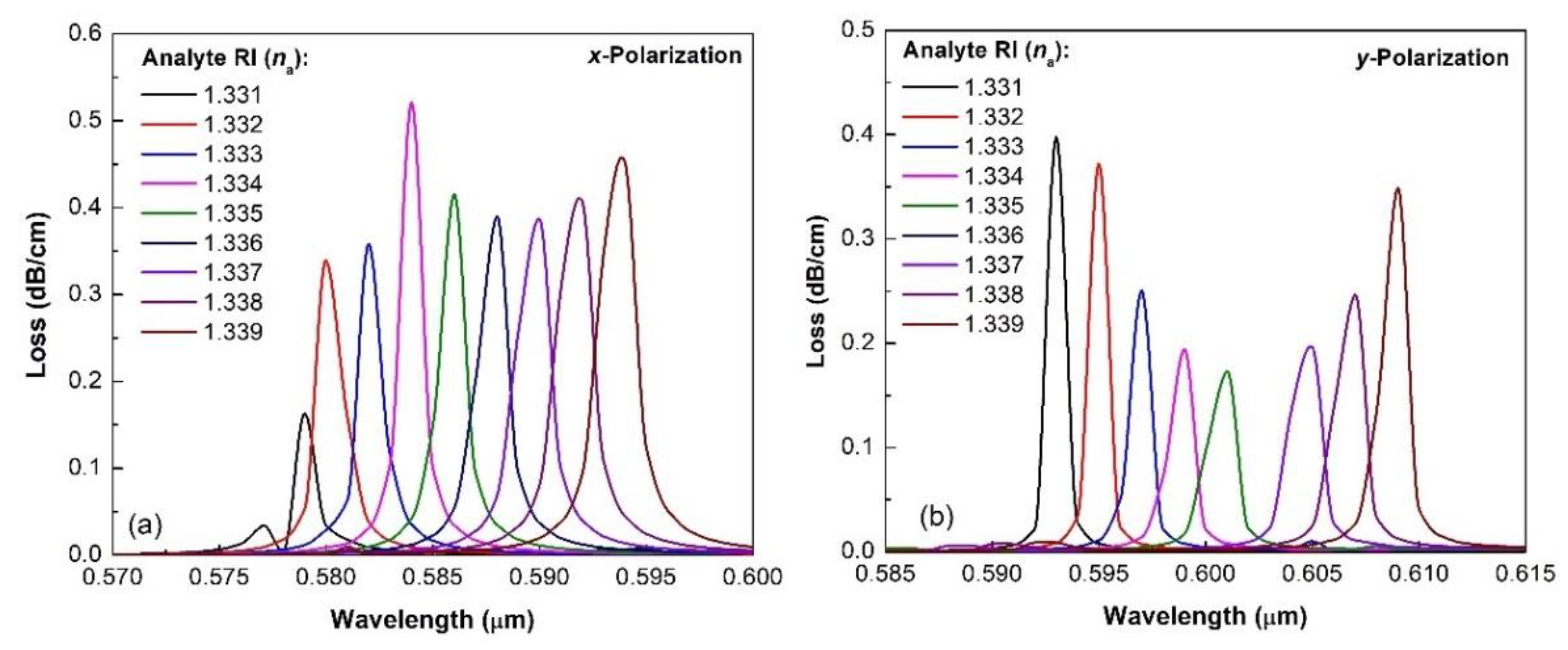
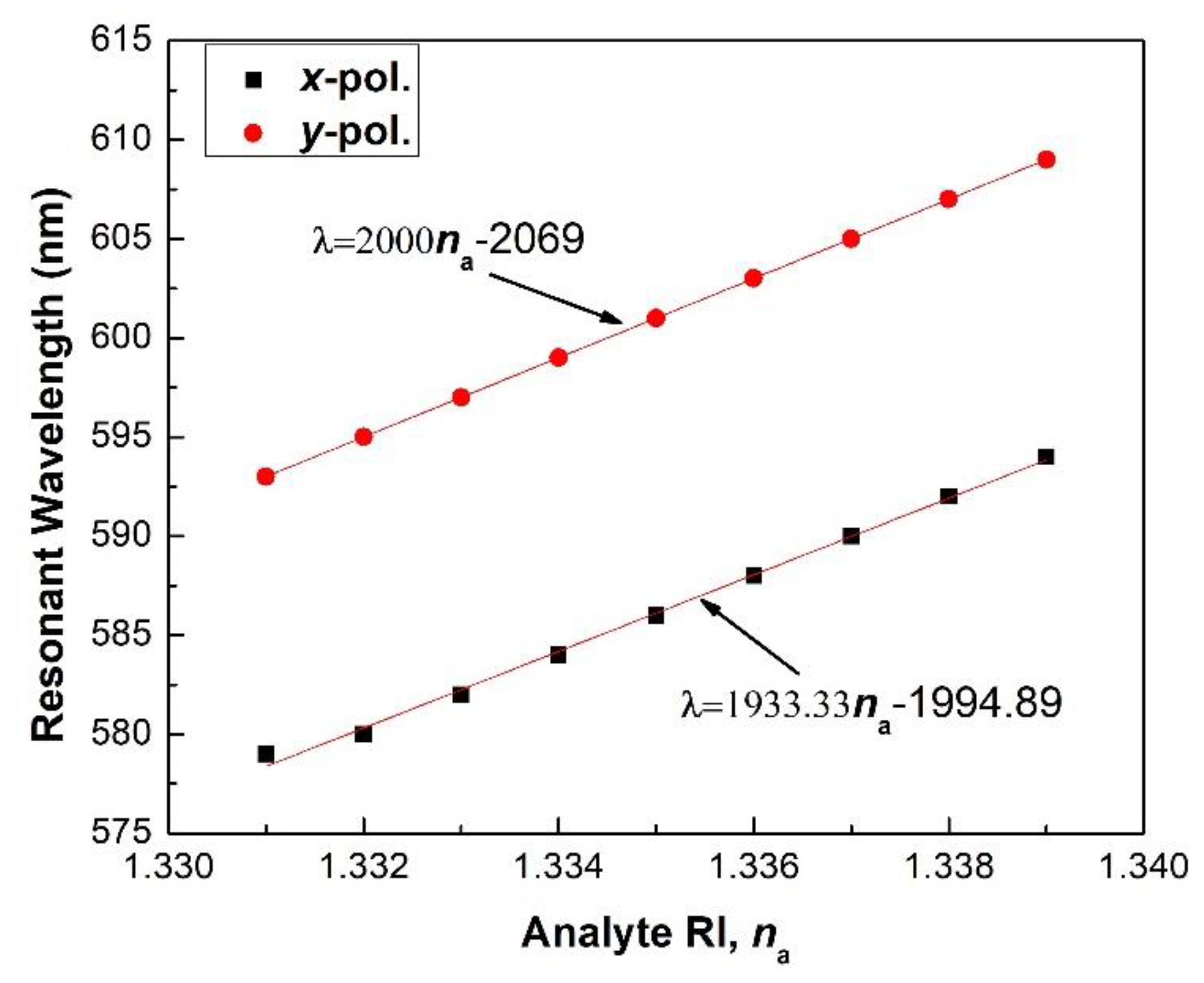
3. Results and Discussion
4. Effect of Graphene Layer Thickness on the Sensitivity
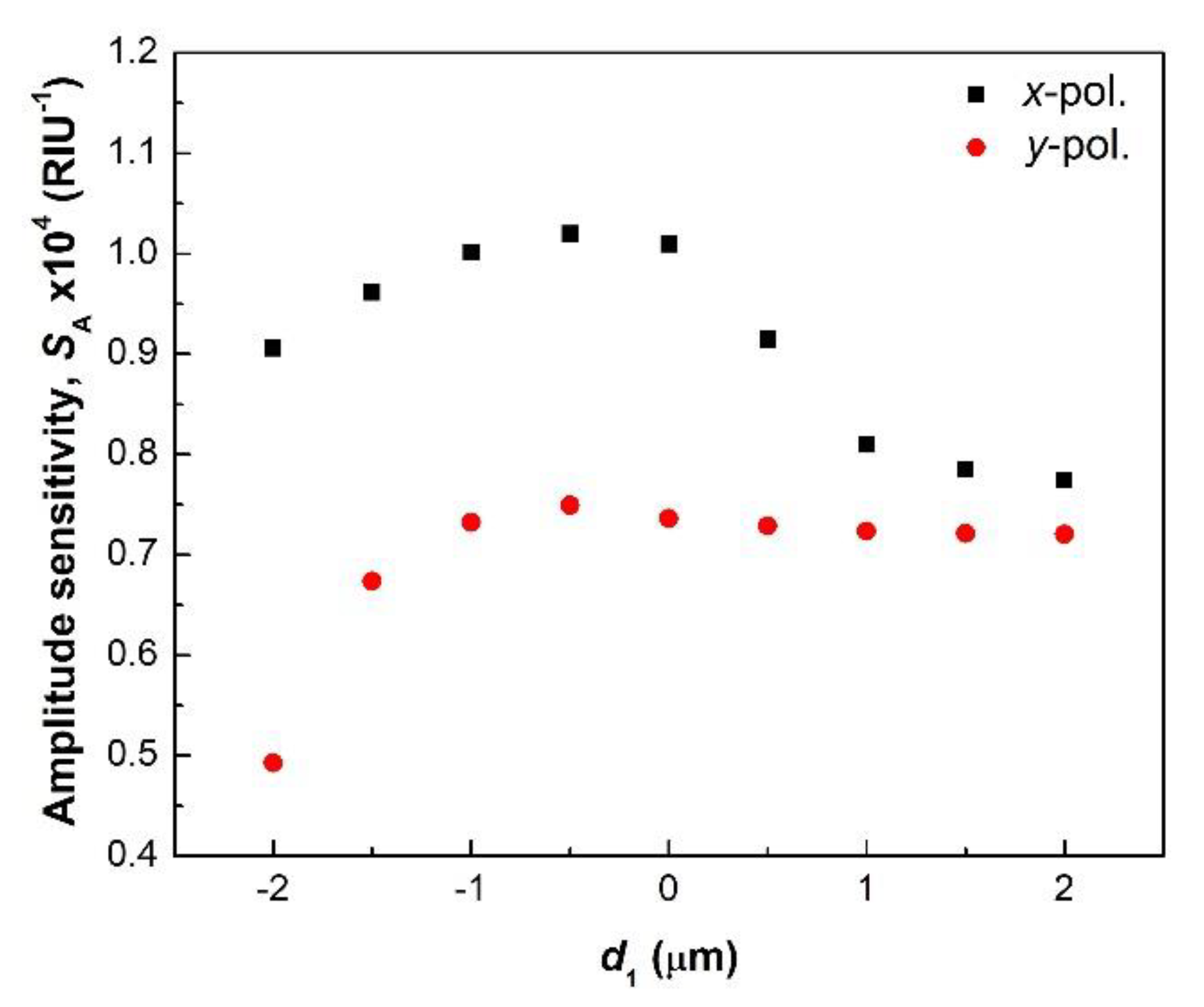
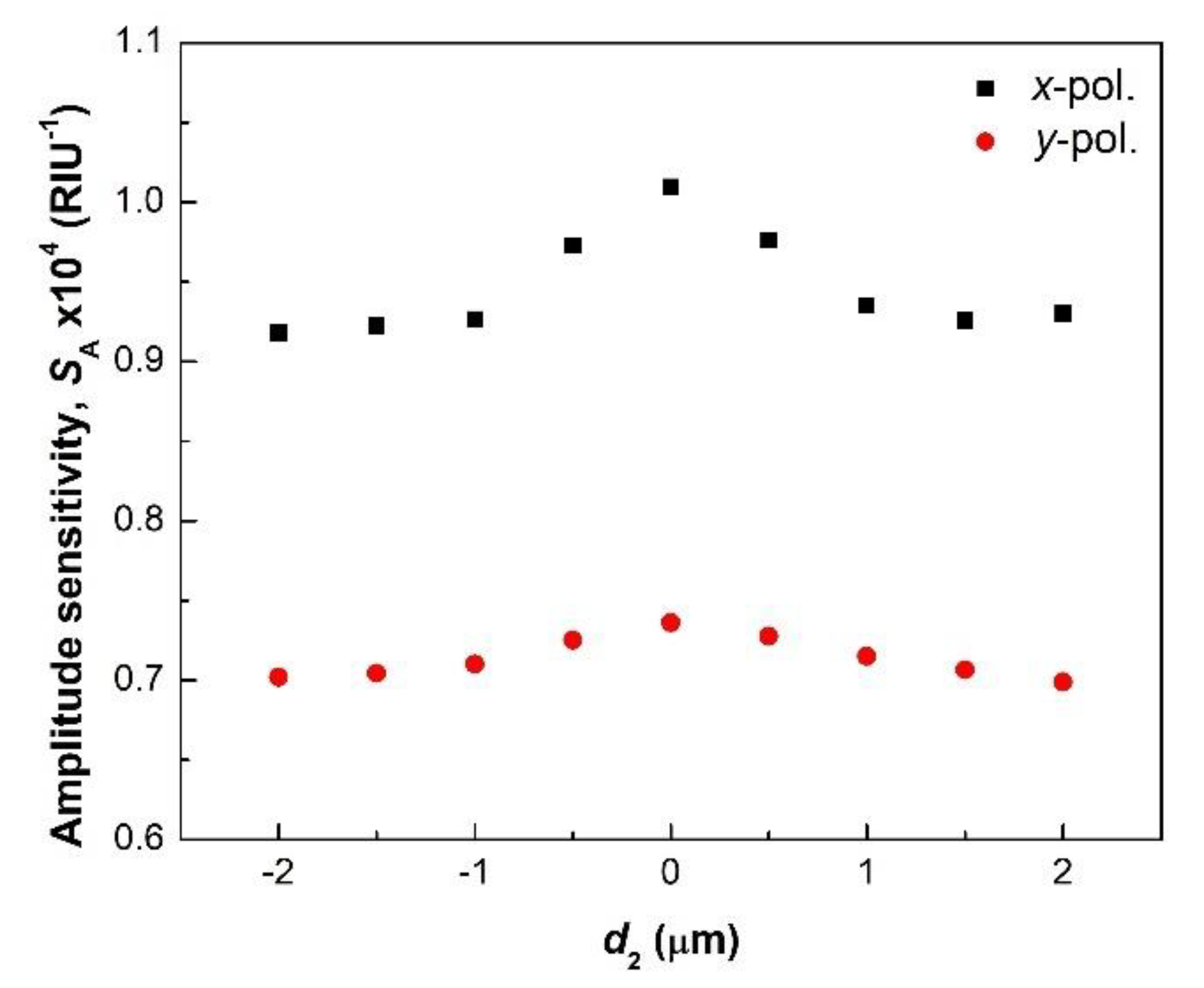
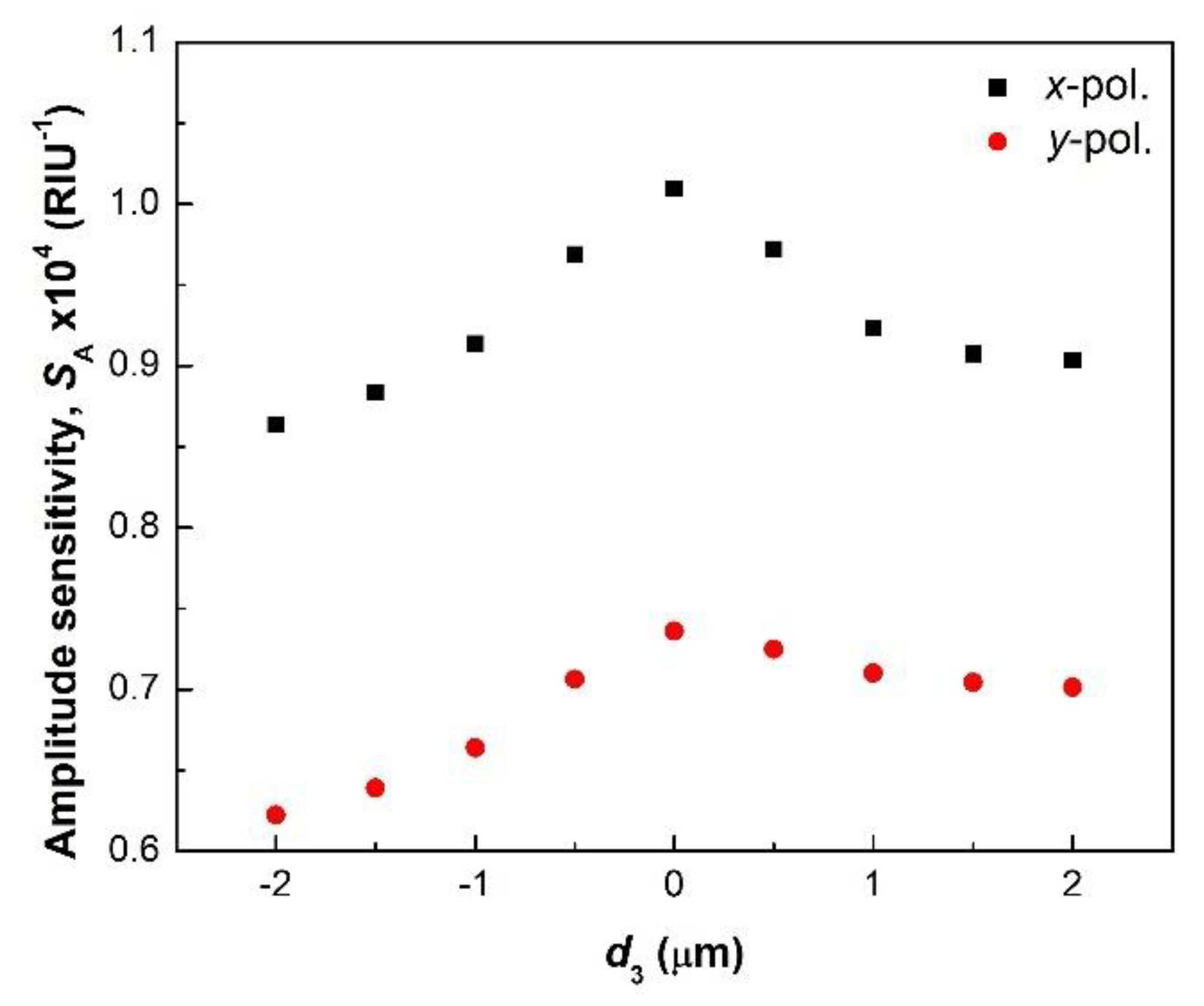
5. Effect of Structural Parameters on the Sensitivity
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Prabowo, B.A.; Purwidyantri, A.; Liu, K.-C. Surface Plasmon Resonance Optical Sensor: A Review on Light Source Technology. Biosensors 2018, 8, 80. [Google Scholar] [CrossRef] [PubMed]
- Jing, J.-Y.; Wang, Q.; Zhao, W.-M.; Wang, B.-T. Long-range surface plasmon resonance and its sensing applications: A review. Opt. Lasers Eng. 2019, 112, 103–118. [Google Scholar] [CrossRef]
- Nguyen, H.H.; Park, J.; Kang, S.; Kim, M. Surface Plasmon Resonance: A Versatile Technique for Biosensor Applications. Sensors 2015, 15, 10481–10510. [Google Scholar] [CrossRef]
- Ritchie, R.H. Plasma Losses by Fast Electrons in Thin Films. Phys. Rev. 1957, 106, 874–881. [Google Scholar] [CrossRef]
- Otto, A. Excitation of nonradiative surface plasma waves in silver by the method of frustrated total reflection. Z. Phys. A Hadron. Nucl. 1968, 216, 398–410. [Google Scholar] [CrossRef]
- Kretschmann, E.; Raether, H. Notizen: Radiative Decay of Non Radiative Surface Plasmons Excited by Light. Z. Nat. A 1968, 23, 2135–2136. [Google Scholar] [CrossRef]
- Rahman, M.S.; Anower, S.; Bin Bashar, L.; Rikta, K.A. Sensitivity analysis of graphene coated surface plasmon resonance biosensors for biosensing applications. Sens. Bio Sens. Res. 2017, 16, 41–45. [Google Scholar] [CrossRef]
- Paliwal, A.; Sharma, A.; Tomar, M.; Gupta, V. Long range surface plasmon resonance (LRSPR) based highly sensitive refractive index sensor using Kretschmann prism coupling arrangement. AIP Conf. Proc. 2016, 1724, 020132. [Google Scholar] [CrossRef]
- Sharma, A.K.; Jha, R.; Gupta, B.D. Fiber-Optic Sensors Based on Surface Plasmon Resonance: A Comprehensive Review. IEEE Sens. J. 2007, 7, 1118–1129. [Google Scholar] [CrossRef]
- Wang, Q.; Jiang, X.; Niu, L.-Y.; Fan, X.-C. Enhanced sensitivity of bimetallic optical fiber SPR sensor based on MoS2 nanosheets. Opt. Lasers Eng. 2020, 128, 105997. [Google Scholar] [CrossRef]
- Cai, S.; Pan, H.; Gonzalez-Vila, A.; Guo, T.; Gillan, D.C.; Wattiez, R.; Caucheteur, C. Selective detection of cadmium ions using plasmonic optical fiber gratings functionalized with bacteria. Opt. Express 2020, 28, 19740–19749. [Google Scholar] [CrossRef] [PubMed]
- Knight, J.; Birks, T.A.; Russell, P.S.J.; Atkin, D.M. All-silica single-mode optical fiber with photonic crystal cladding: Errata. Opt. Lett. 1997, 22, 484–485. [Google Scholar] [CrossRef] [PubMed]
- Russell, P.S. Photonic-Crystal Fibers. J. Light. Technol. 2006, 24, 4729–4749. [Google Scholar] [CrossRef]
- Paul, A.K.; Sarkar, A.K.; Rahman, A.B.S.; Khaleque, A. Twin Core Photonic Crystal Fiber Plasmonic Refractive Index Sensor. IEEE Sens. J. 2018, 18, 5761–5769. [Google Scholar] [CrossRef]
- Habib, A.; Reyes-Vera, E.; Villegas-Aristizabal, J.; Anower, S. Numerical Modeling of a Rectangular Hollow-Core Waveguide for the Detection of Fuel Adulteration in Terahertz Region. Fibers 2020, 8, 63. [Google Scholar] [CrossRef]
- Gómez-Cardona, N.D.; Reyes-Vera, E.; Herrera, R.A.; Torres, P. Novel refractive index sensor based on hybrid long range plasmon in H-shaped optical fiber. Front. Opt. Laser Sci. 2018, 2, JTu2A.97. [Google Scholar] [CrossRef]
- Gomez-Cardona, N.D.; Reyes-Vera, E.; Torres, P. Multi-Plasmon Resonances in Microstructured Optical Fibers: Extending the Detection Range of SPR Sensors and a Multi-Analyte Sensing Technique. IEEE Sens. J. 2018, 18, 7492–7498. [Google Scholar] [CrossRef]
- Rifat, A.A.; Mahdiraji, G.A.; Chow, D.M.; Shee, Y.G.; Ahmed, R.; Adikan, F.R.M. Photonic Crystal Fiber-Based Surface Plasmon Resonance Sensor with Selective Analyte Channels and Graphene-Silver Deposited Core. Sensors 2015, 15, 11499–11510. [Google Scholar] [CrossRef] [PubMed]
- Rifat, A.A.; Haider, F.; Ahmed, R.; Mahdiraji, G.A.; Adikan, F.R.M.; Miroshnichenko, A.E. Highly sensitive selectively coated photonic crystal fiber-based plasmonic sensor. Opt. Lett. 2018, 43, 891–894. [Google Scholar] [CrossRef] [PubMed]
- Hasan, R.; Akter, S.; Rifat, A.A.; Rana, S.; Ali, S. A Highly Sensitive Gold-Coated Photonic Crystal Fiber Biosensor Based on Surface Plasmon Resonance. Photonics 2017, 4, 18. [Google Scholar] [CrossRef]
- Gangwar, R.K.; Singh, V.K. Highly Sensitive Surface Plasmon Resonance Based D-Shaped Photonic Crystal Fiber Refractive Index Sensor. Plasmonics 2017, 12, 1367–1372. [Google Scholar] [CrossRef]
- Haque, E.; Hossain, A.; Ahmed, F.; Namihira, Y. Surface Plasmon Resonance Sensor Based on Modified DD-Shaped Photonic Crystal Fiber for Wider Range of Refractive Index Detection. IEEE Sens. J. 2018, 18, 8287–8293. [Google Scholar] [CrossRef]
- Gomez-Cardona, N.; Reyes-Vera, E.; Torres, P. High Sensitivity Refractive Index Sensor Based on the Excitation of Long-Range Surface Plasmon Polaritons in H-Shaped Optical Fiber. Sensors 2020, 20, 2111. [Google Scholar] [CrossRef] [PubMed]
- Mollah, A.; Islam, S. Novel Single Hole Exposed-Suspended Core Localized Surface Plasmon Resonance Sensor. IEEE Sens. J. 2020, 21, 1. [Google Scholar] [CrossRef]
- Islam, S.; Islam, M.R.; Sultana, J.; Dinovitser, A.; Ng, B.W.-H.; Abbott, D. Exposed-core localized surface plasmon resonance biosensor. J. Opt. Soc. Am. B 2019, 36, 2306. [Google Scholar] [CrossRef]
- Yang, X.; Lu, Y.; Wang, M.; Yao, J. An Exposed-Core Grapefruit Fibers Based Surface Plasmon Resonance Sensor. Sensors 2015, 15, 17106–17114. [Google Scholar] [CrossRef] [PubMed]
- An, G.; Jia, P.; Liang, T.; Hong, Y.; Wang, H.; Ghaffar, A.; Xiong, J. Double-sided Polished Ultra-stable and Ultra-sensitive Optical Fiber Sensor. Plasmonics 2020, 15, 1471–1479. [Google Scholar] [CrossRef]
- Liu, C.; Yang, L.; Lu, X.; Liu, Q.; Wang, F.; Lv, J.; Sun, T.; Mu, H.; Chu, P.K. Mid-infrared surface plasmon resonance sensor based on photonic crystal fibers. Opt. Express 2017, 25, 14227–14237. [Google Scholar] [CrossRef]
- Zhao, L.; Han, H.; Luan, N.; Liu, J.; Song, L.; Hu, Y. A Temperature Plasmonic Sensor Based on a Side Opening Hollow Fiber Filled with High Refractive Index Sensing Medium. Sensors 2019, 19, 3730. [Google Scholar] [CrossRef]
- Islam, S.; Cordeiro, C.M.B.; Sultana, J.; Aoni, R.A.; Feng, S.; Ahmed, R.; Dorraki, M.; Dinovitser, A.; Ng, B.W.-H.; Abbott, D. A Hi-Bi Ultra-Sensitive Surface Plasmon Resonance Fiber Sensor. IEEE Access 2019, 7, 79085–79094. [Google Scholar] [CrossRef]
- Sarker, H.; Faisal, M.; Mollah, A. Slotted photonic crystal fiber-based plasmonic biosensor. Appl. Opt. 2021, 60, 358–366. [Google Scholar] [CrossRef]
- Sharma, P.; Sharan, P. Design of Photonic Crystal-Based Biosensor for Detection of Glucose Concentration in Urine. IEEE Sens. J. 2014, 15, 1035–1042. [Google Scholar] [CrossRef]
- Yousufali; Mollah, A.; Ahmed, K. Multimode Interference-Based Photonic Crystal Fiber Glucose Sensor. Plasmonics 2021, 1–8. [Google Scholar] [CrossRef]
- Weeth, H.J.; Speth, C.F. Estimation of Bovine Plasma Protein from Refractive Index. J. Anim. Sci. 1968, 27, 146–149. [Google Scholar] [CrossRef] [PubMed]
- Wieduwilt, T.; Tuniz, A.; Linzen, S.; Goerke, S.; Dellith, J.; Hübner, U.; Schmidt, M.A. Ultrathin niobium nanofilms on fiber optical tapers—A new route towards low-loss hybrid plasmonic modes. Sci. Rep. 2015, 5, 1–12. [Google Scholar] [CrossRef] [PubMed]
- West, P.R.; Ishii, S.; Naik, G.V.; Emani, N.K.; Shalaev, V.M.; Boltasseva, A. Searching for better plasmonic materials. Laser Photonics Rev. 2010, 4, 795–808. [Google Scholar] [CrossRef]
- Mollah, M.A.; Razzak, S.M.A.; Paul, A.K.; Hasan, M.R. Microstructure optical fiber based plasmonic refractive index sensor. Sens. Bio-Sens. Res. 2019, 24, 100286. [Google Scholar] [CrossRef]
- Amanatiadis, S.A.; Kantartzis, N.V.; Tsiboukis, T.D. A loss-controllable absorbing boundary condition for surface plasmon polaritons propagating onto graphene. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Pisana, S.; Braganca, P.M.; Marinero, E.E.; Gurney, B.A. Graphene magnetic field sensors. IEEE Trans. Magn. 2010, 46, 1910–1913. [Google Scholar] [CrossRef]
- Khan, M.A.; Hristovski, I.R.; Marinaro, G.; Kosel, J. Magnetic composite hydrodynamic pump with laser-induced graphene electrodes. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Fleming, J.W. Dispersion in GeO2–SiO2 glasses. Appl. Opt. 1984, 23, 4486–4493. [Google Scholar] [CrossRef] [PubMed]
- Reyes-Vera, E.; Usuga-Restrepo, J.; Varon, M.; Torres, P. Dual-Core Transversally Chirped Microstructured Optical Fiber for Mode-Converter Device and Sensing Application. In Selected Topics on Optical Fiber Technologies and Applications; Xu, F., Mou, C., Eds.; InTech: London, UK, 2018; ISBN 978-953-51-3813-6. [Google Scholar] [CrossRef][Green Version]
- Bruna, M.; Borini, S.M. Optical constants of graphene layers in the visible range. Appl. Phys. Lett. 2009, 94, 031901. [Google Scholar] [CrossRef]
- Nair, R.R.; Blake, P.; Grigorenko, A.N.; Novoselov, K.S.; Booth, T.J.; Stauber, T.; Peres, N.M.R.; Geim, A.K. Fine Structure Constant Defines Visual Transparency of Graphene. Science 2008, 320, 1308. [Google Scholar] [CrossRef]
- Yang, H.; Liu, M.; Chen, Y.; Guo, L.; Xiao, G.; Liu, H.; Li, J.; Yuan, L. Highly Sensitive Graphene-Au Coated Plasmon Resonance PCF Sensor. Sensors 2021, 21, 818. [Google Scholar] [CrossRef] [PubMed]
- Rifat, A.A.; Mahdiraji, G.A.; Ahmed, R.; Chow, D.M.; Sua, Y.; Shee, Y.; Adikan, F.M. Copper-graphene-based photonic crystal fiber plasmonic biosensor. IEEE Photon. J. 2015, 8, 1–8. [Google Scholar]
- Saitoh, K.; Koshiba, M. Numerical modeling of photonic crystal fibers. J. Light. Technol. 2005, 23, 3580–3590. [Google Scholar] [CrossRef]
- Reyes-Vera, E.; Usuga-Restrepo, J.; Jimenez-Durango, C.; Montoya-Cardona, J.; Gomez-Cardona, N. Design of Low-loss and Highly Birefringent Porous-Core Photonic Crystal Fiber and Its Application to Terahertz Polarization Beam Splitter. IEEE Photon. J. 2018, 10, 1–13. [Google Scholar] [CrossRef]
- Lou, J.; Cheng, T.; Li, S.; Zhang, X. Surface plasmon resonance photonic crystal fiber biosensor based on gold-graphene layers. Opt. Fiber Technol. 2019, 50, 206–211. [Google Scholar] [CrossRef]
- Li, T.; Zhu, L.; Yang, X.; Lou, X.; Yu, L. A Refractive Index Sensor Based on H-Shaped Photonic Crystal Fibers Coated with Ag-Graphene Layers. Sensors 2020, 20, 741. [Google Scholar] [CrossRef] [PubMed]
- Paul, A.K. Design and analysis of photonic crystal fiber plasmonic refractive Index sensor for condition monitoring of transformer oil. OSA Contin. 2020, 3, 2253. [Google Scholar] [CrossRef]
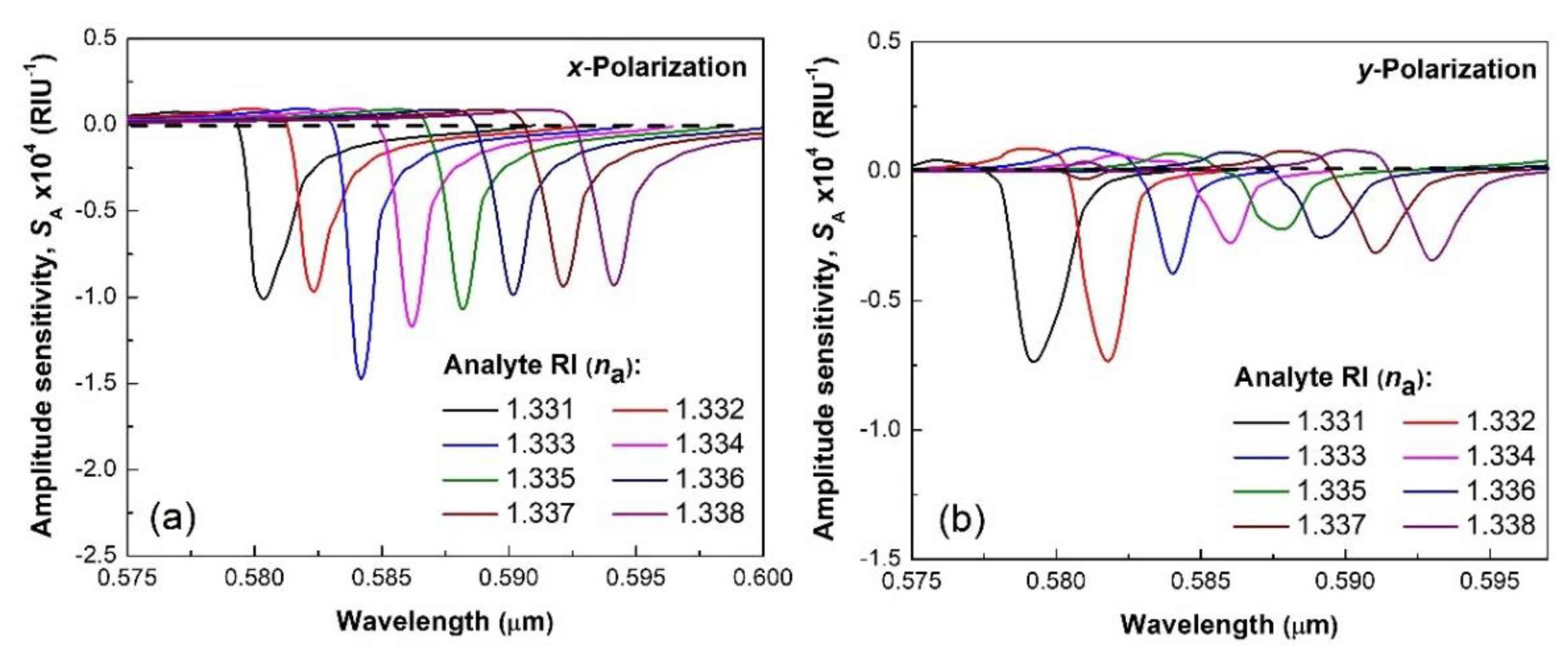
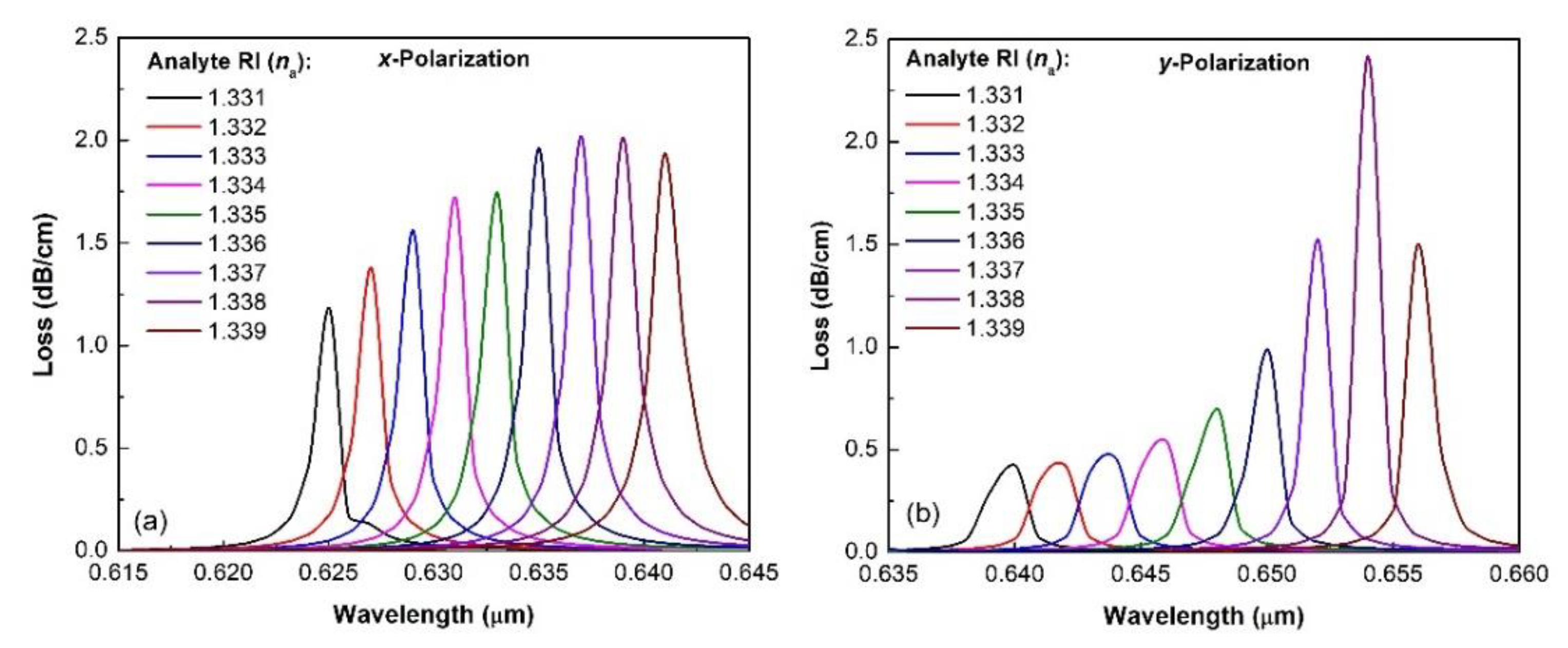
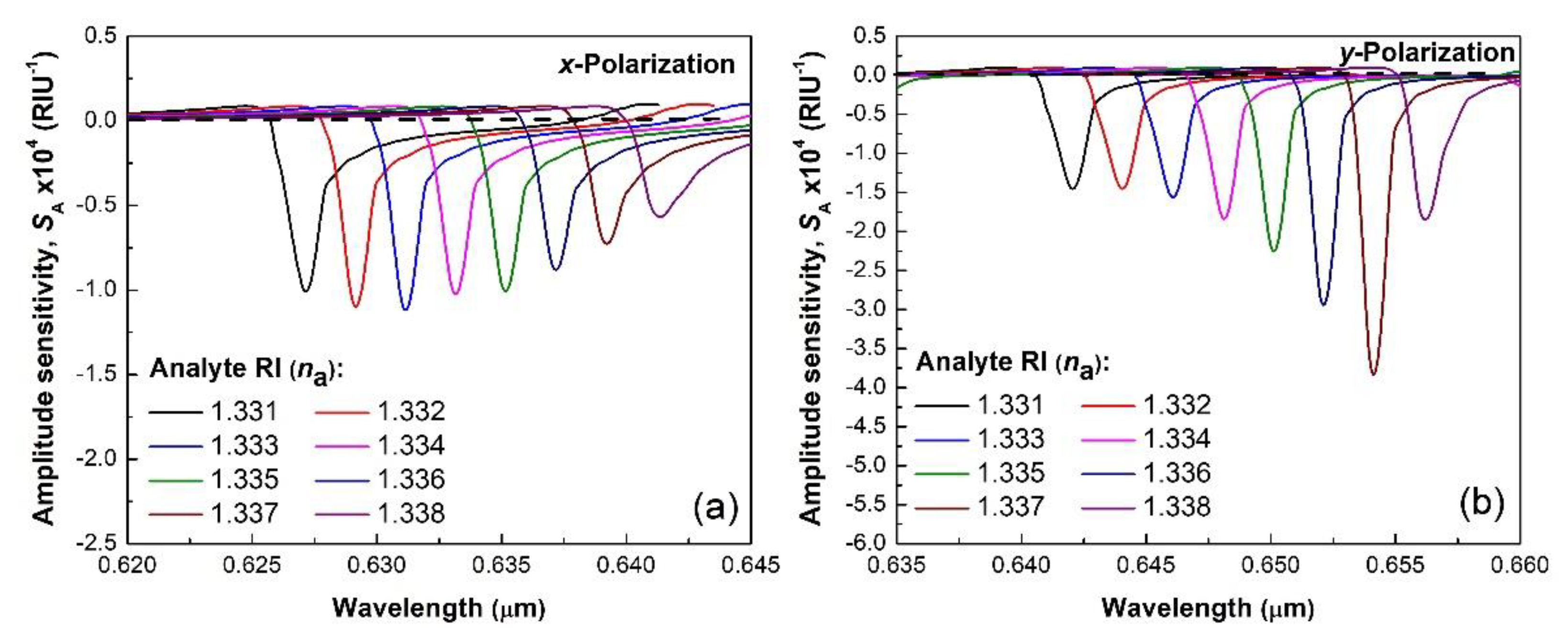
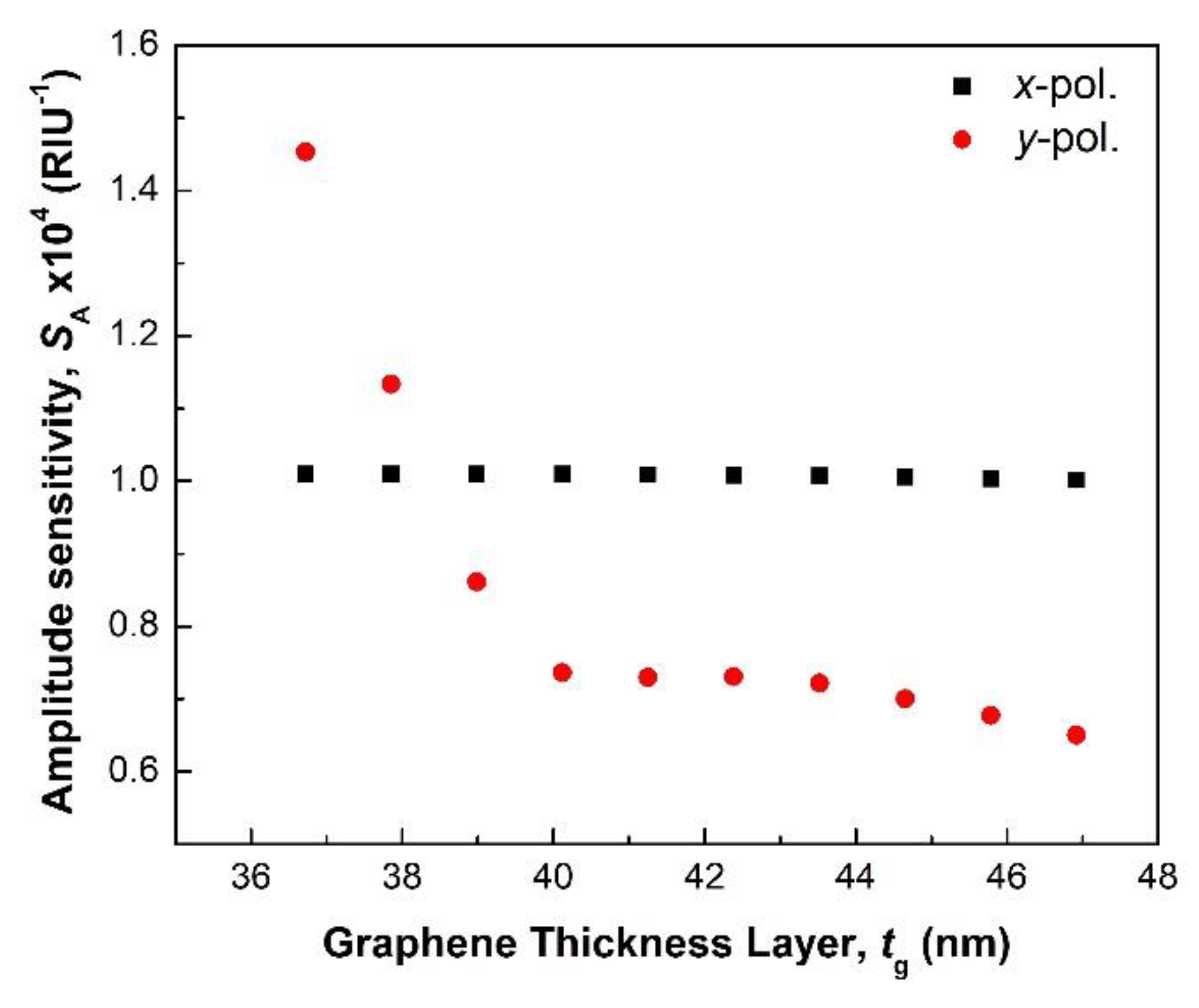
| Constant | u1 | u2 | u3 | v1 | v2 | v3 |
|---|---|---|---|---|---|---|
| Value | 696.163 × 10−3 | 407.9426 × 10−3 | 897.4794 × 10−3 | 469.14826 × 10−5 | 135.120631 × 10−4 | 979.340025 × 10−1 |
| Analyte RI | Peak Loss (dB/cm) | Res. Wa. (µm) | SA (RIU−1) | FWHM (nm) | FOM (RIU−1) |
|---|---|---|---|---|---|
| 1.331 | 0.48008 | 0.579 | 10,258.12 | 1.09 | 1773.70 |
| 0.39771 | 0.593 | 7351.82 | 1.13 | 1769.91 | |
| 1.332 | 0.33946 | 0.580 | 9692.70 | 0.837 | 2310.11 |
| 0.37218 | 0.595 | 7351.82 | 1.10 | 1818.18 | |
| 1.333 | 0.35797 | 0.582 | 14,847.03 | 1.12 | 1726.19 |
| 0.25012 | 0.597 | 3959.30 | 1.09 | 1834.86 | |
| 1.334 | 0.52103 | 0.584 | 11,708.55 | 0.945 | 2046.28 |
| 0.19413 | 0.599 | 2874.76 | 1.12 | 1785.71 | |
| 1.335 | 0.41477 | 0.586 | 10,757.99 | 0.974 | 1984.33 |
| 0.17300 | 0.601 | 2238.46 | 1.0 | 2000.00 | |
| 1.336 | 0.39000 | 0.588 | 10,004.09 | 0.906 | 2134.15 |
| 0.19689 | 0.603 | 2577.17 | 1.57 | 1273.89 | |
| 1.337 | 0.38701 | 0.590 | 9381.33 | 1.03 | 1877.02 |
| 0.19689 | 0.605 | 3205.50 | 1.57 | 1273.89 | |
| 1.338 | 0.41109 | 0.592 | 9381.32 | 1.26 | 1534.39 |
| 0.24646 | 0.607 | 3494.95 | 1.06 | 1886.79 | |
| 1.339 | 0.45793 | 0.594 | 1.60 | 1208.33 | |
| 0.34820 | 0.609 | 1.04 | 1923.08 |
| Ref. | Year | PCF Structure | Plasmonic Material | Pol. | RI Range | SW (nm/RIU) | SA (RIU−1) | FOM (RIU−1) | RES (RIU) |
|---|---|---|---|---|---|---|---|---|---|
| [14] | 2018 | Hybrid | Gold | x | 1.33–1.40 | 9000 | 725.89 | NA * | 1.11 × 10−5 |
| y | 1.33–1.40 | 9000 | 1085 | NA * | 1.11 × 10−5 | ||||
| [18] | 2015 | Hexagonal | Gold and Graphene | y | 1.46–1.49 | 3000 | 418 | NA * | 2.40 × 10−5 |
| [19] | 2018 | Hexagonal | Gold | y | 1.33–1.42 | 11,000 | 1420 | 407 | 9.10 × 10−6 |
| [20] | 2017 | Hexagonal | Gold | y | 1.33–1.36 | 2200 | 266 | NA * | 3.75 × 10−5 |
| [23] | 2020 | H-shaped | Gold | y | 1.33–1.39 | 7540 | NA * | 280 | 1.30 × 10−5 |
| [24] | 2021 | Suspended Core | Gold and TiO2 | y | 1.30–1.412 | 50,000 | 1449 | 335 | 2 × 10−6 |
| [31] | 2019 | Slotted | Gold | x | 1.33–1.43 | 22,000 | 1782.56 | NA * | 4.54 × 10−6 |
| [49] | 2019 | Hexagonal | Gold and Graphene | y | 1.33–1.38 | 8600 | NA * | NA * | 1.16 × 10−5 |
| [50] | 2020 | Hexagonal | Silver and Graphene | x | 1.33–1.41 | 12,600 | 53.37 | NA * | 3.61 × 10−5 |
| [51] | 2020 | Octagonal | Graphene | x | 1.33–1.34 | 1000 | 31,240 | 5000 | 3.20 × 10−6 |
| y | 1.33–1.34 | 1000 | 30,830 | 3.24 × 10−6 | |||||
| This work | 2021 | Octagonal | Graphene | x | 1.33–1.339 | 1933.33 | 14,847.03 | 2310.1 | 5.0 × 10−5 |
| y | 1.33–1.339 | 2000 | 7351.82 | 2000 | 5.0 × 10−5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paul, A.K.; Mollah, M.A.; Hassan, M.Z.; Gomez-Cardona, N.; Reyes-Vera, E. Graphene-Coated Highly Sensitive Photonic Crystal Fiber Surface Plasmon Resonance Sensor for Aqueous Solution: Design and Numerical Analysis. Photonics 2021, 8, 155. https://doi.org/10.3390/photonics8050155
Paul AK, Mollah MA, Hassan MZ, Gomez-Cardona N, Reyes-Vera E. Graphene-Coated Highly Sensitive Photonic Crystal Fiber Surface Plasmon Resonance Sensor for Aqueous Solution: Design and Numerical Analysis. Photonics. 2021; 8(5):155. https://doi.org/10.3390/photonics8050155
Chicago/Turabian StylePaul, Alok Kumar, Md. Aslam Mollah, Md. Zahid Hassan, Nelson Gomez-Cardona, and Erick Reyes-Vera. 2021. "Graphene-Coated Highly Sensitive Photonic Crystal Fiber Surface Plasmon Resonance Sensor for Aqueous Solution: Design and Numerical Analysis" Photonics 8, no. 5: 155. https://doi.org/10.3390/photonics8050155
APA StylePaul, A. K., Mollah, M. A., Hassan, M. Z., Gomez-Cardona, N., & Reyes-Vera, E. (2021). Graphene-Coated Highly Sensitive Photonic Crystal Fiber Surface Plasmon Resonance Sensor for Aqueous Solution: Design and Numerical Analysis. Photonics, 8(5), 155. https://doi.org/10.3390/photonics8050155






