Theoretical Study of Tunable Optical Resonators in Periodic and Quasiperiodic One-Dimensional Photonic Structures Incorporating a Nematic Liquid Crystal
Abstract
1. Introduction
2. Theoretical Model
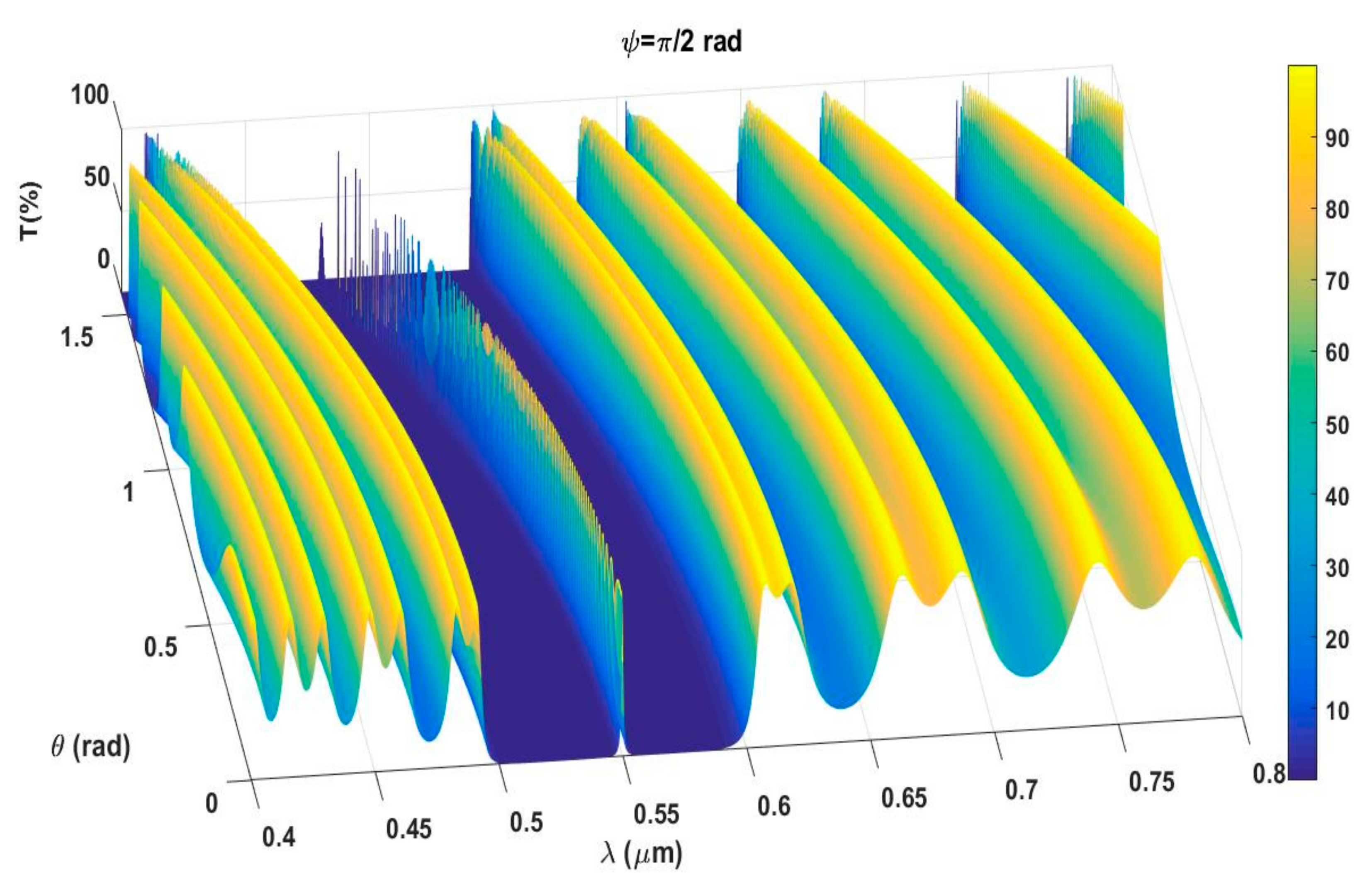
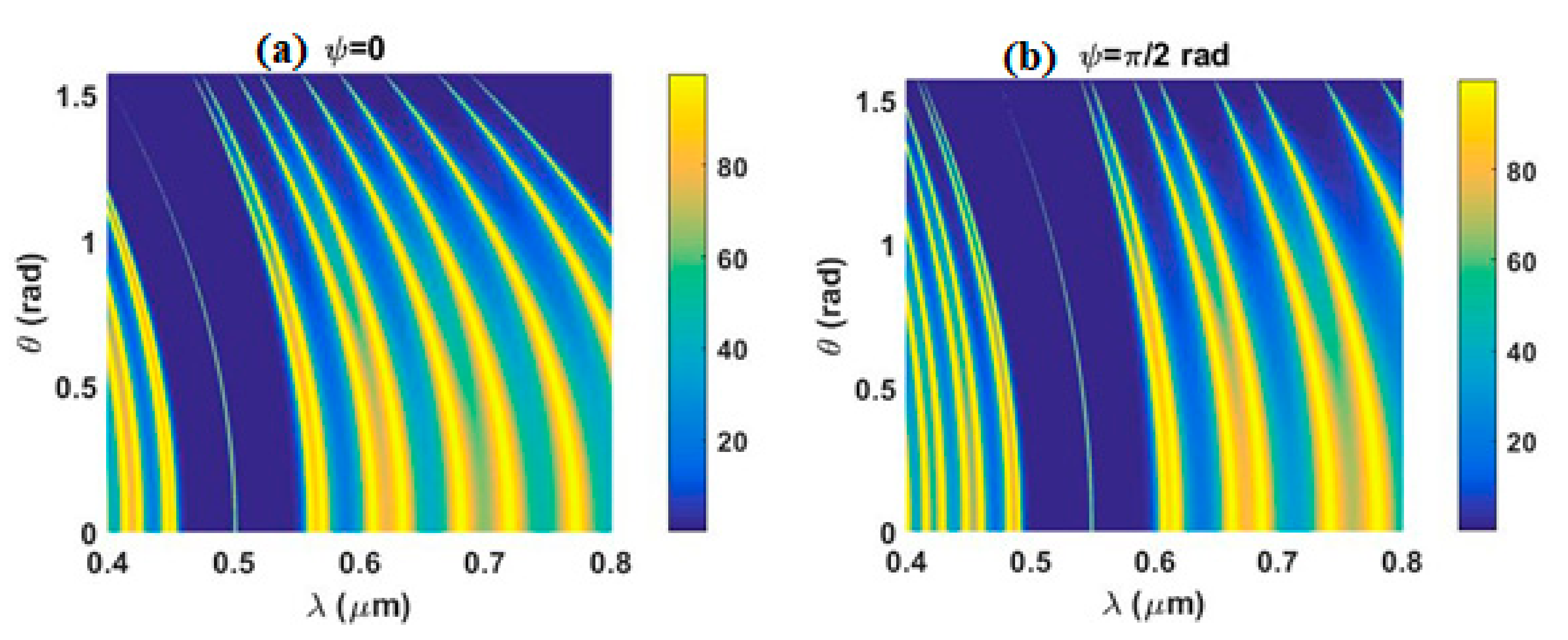
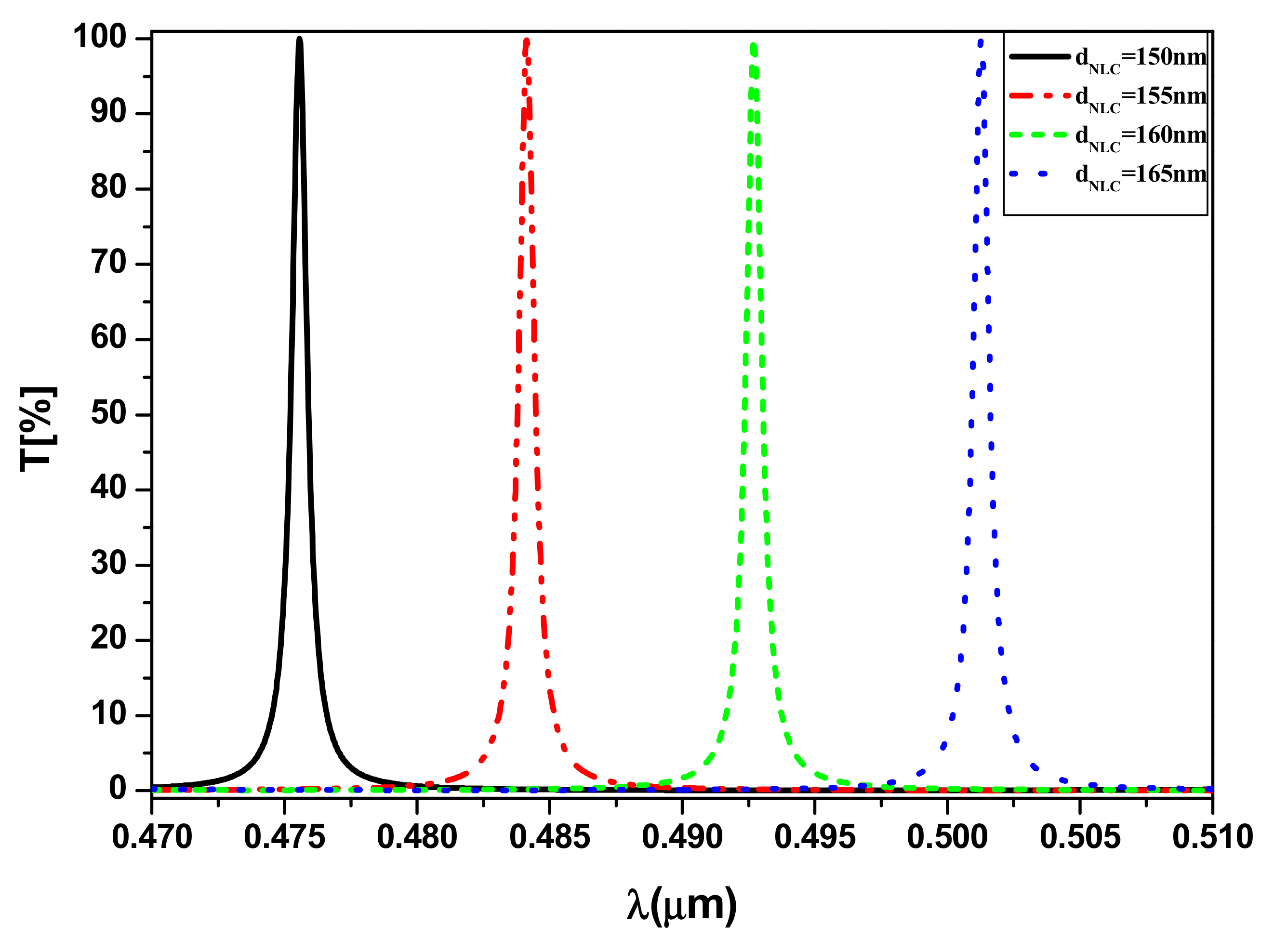
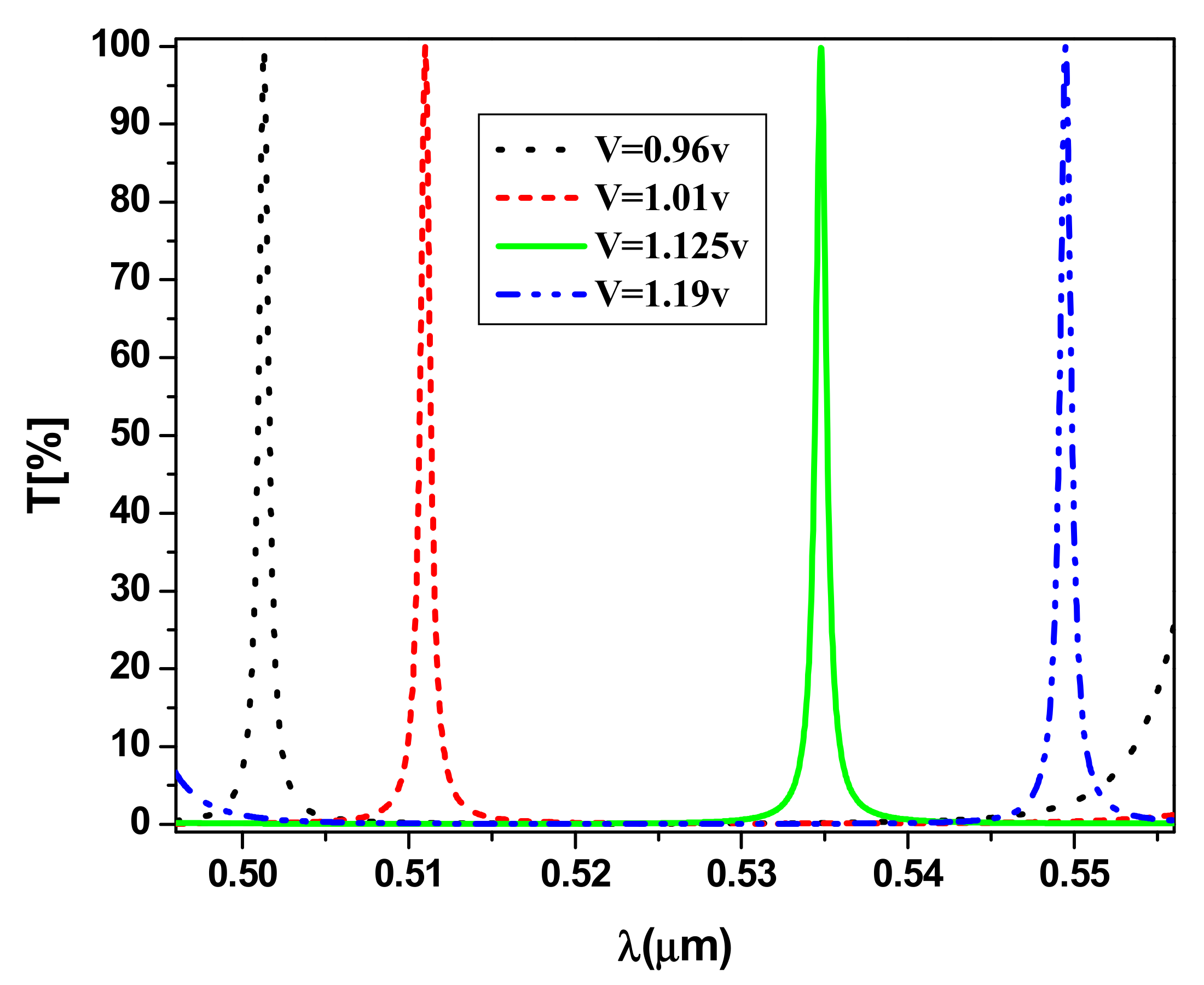
3. Result and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yablonovitch, E. Inhibited Spontaneous Emission in Solid-State Physics and Electronics. Phys. Rev. Lett. 1987, 58, 2059–2062. [Google Scholar] [CrossRef] [PubMed]
- Yablonovitch, E. Photonic band-gap structures. Josa B 1993, 10, 283–295. [Google Scholar] [CrossRef]
- Talebzadeh, R.; Soroosh, M.; Kavian, Y.S.; Mehdizadeh, F. Eight-channel all-optical demultiplexer based on photonic crystal resonant cavities. Optik 2017, 140, 331–337. [Google Scholar] [CrossRef]
- Bhattacharya, P.K. Photonic Crystal Devices. J. Phy. D Appl. Phy. 2007, 40, E01. [Google Scholar]
- Trabelsi, Y. Tunable properties of omnidirectional band gap based on photonic quasicrystals containing superconducting material. Opt. Quantum Electron. 2021, 53, 1–10. [Google Scholar] [CrossRef]
- Lio, G.E.; Palermo, G.; Caputo, R.; De Luca, A. A comprehensive optical analysis of nanoscale structures: From thin films to asymmetric nanocavities. Rsc Adv. 2019, 9, 21429–21437. [Google Scholar] [CrossRef]
- Steurer, W.; Widmer, D.S. Photonic and phononic quasicrystals. J. Phys. D Appl. Phys. 2007, 40, R229. [Google Scholar] [CrossRef]
- Edagawa, K. Photonic crystals, amorphous materials, and quasicrystals. Sci. Technol. Adv. Mater. 2014, 15, 034805. [Google Scholar] [CrossRef]
- Levine, D.; Steinhardt, P.J. Quasicrystals: De_nition and structure. Phys. Rev. B 1986, 34, 596–616. [Google Scholar] [CrossRef]
- Vardeny, Z.V.; Nahata, A.; Agrawal, A. Optics of photonic quasicrystals. Nat. Photonics 2013, 7, 177–187. [Google Scholar] [CrossRef]
- Sahel, S.; Amri, R.; Bouaziz, L.; Gamra, D.; Lejeune, M.; Benlahsen, M.; Bouchriha, H. Optical filters using Cantor quasi-periodic one dimensional photonic crystal based on Si/SiO2. Superlattices Microstruct. 2016, 97, 429–438. [Google Scholar] [CrossRef]
- Trabelsi, Y.; Benali, N.; Bouazzi, Y.; Kanzari, M. Microwave transmission through one-dimensional hybrid quasi-regular (fibonacci and Thue-Morse)/periodic structures. Photonic Sens. 2013, 3, 246–255. [Google Scholar] [CrossRef]
- Trabelsi, Y.; Bouazzi, Y.; Benali, N.; Kanzari, M. Narrow stop band optical filter using one-dimensional regular Fibonacci/Rudin Shapiro photonic quasicrystals. Opt. Quantum Electron. 2016, 48, 1–9. [Google Scholar] [CrossRef]
- Segovia-Chaves, F.; Vinck-Posada, H.; Trabelsi, Y.; Ben Ali, N. Transmittance spectrum in a one-dimensional photonic crystal with Fibonacci sequence superconductor–semiconductor. Opt. Int. J. Light Electron Opt. 2020, 217, 164803. [Google Scholar] [CrossRef]
- Trabelsi, Y. Output multichannel optical filter based on hybrid photonic quasicrystals containing a high-Tc superconductor. Photonics Nanostruct. Fundam. Appl. 2019, 36, 100724. [Google Scholar] [CrossRef]
- Ben Ali, N.; Dhasarathan, V.; AlSaif, H.; Trabelsi, Y.; Nguyen, T.K.; Bouazzi, Y.; Kanzari, M. Design of output-graded narrow polychromatic filter by using photonic quasicrystals. Phys. B Condens. Matter 2020, 582, 411918. [Google Scholar] [CrossRef]
- Nozaki, K.; Baba, T. Quasiperiodic photonic crystal microcavity lasers. Appl. Phys. Lett. 2004, 84, 4875–4877. [Google Scholar] [CrossRef]
- Belhadj, W. Properties of omnidirectional gap and defect mode of one-dimensional graphene-dielectric periodic structures. Opt. Quantum Electron. 2020, 52, 1–20. [Google Scholar] [CrossRef]
- Zeng, C.Z.C.; Luo, C.L.C.; Hao, L.H.L.; Xie, Y.X.Y. The research on magnetic tunable characteristics of photonic crystal defect localized modes with a defect layer of nanoparticle. Chin. Opt. Lett. 2014, 12, S11602–S311604. [Google Scholar] [CrossRef]
- Kłos, J.W.; Krawczyk, M.; Dadoenkova, Y.S.; Dadoenkova, N.N.; Lyubchanskii, I.L. Photonic-magnonic crystals: Multifunctional periodic structures for magnonic and photonic applications. J. Appl. Phys. 2014, 115, 174311. [Google Scholar] [CrossRef]
- Dadoenkova, Y.S.; Dadoenkova, N.N.; Lyubchanskii, I.L.; Kłos, J.W.; Krawczyk, M. Confined states in photonic-magnonic crystals with complex unit cell. J. Appl. Phys. 2016, 120, 073903. [Google Scholar] [CrossRef]
- Dadoenkova, N.N.; Dadoenkova, Y.S.; Panyaev, I.S.; Sannikov, D.G.; Lyubchanskii, I.L. One-dimensional dielectric bi-periodic photonic structures based on ternary photonic crystals. J. Appl. Phys. 2018, 123, 043101. [Google Scholar] [CrossRef]
- Panyaev, I.S.; Yafarova, L.R.; Sannikov, D.G.; Dadoenkova, N.N.; Dadoenkova, Y.S.; Lyubchanskii, I.L. One-dimensional multiperiodic photonic structures: A new route in photonics (four-component media). J. Appl. Phys. 2019, 126, 103102. [Google Scholar] [CrossRef]
- Dionne, J.A.; Sweatlock, L.A.; Atwater, H.A.; Polman, A. Planar metal plasmon waveguides: Frequency-dependent dispersion, propagation, localization, and loss beyond the free electron model. Phys. Rev. B 2005, 72, 075405. [Google Scholar] [CrossRef]
- Wu, J.-J.; Gao, J.-X. Temperature-dependent optical properties of defect mode in dielectric photonic crystal heterostructure containing a superconducting layer. Mater. Chem. Phys. 2016, 171, 91–96. [Google Scholar] [CrossRef]
- Trabelsi, Y.; Ali, N.B.; Kanzari, M. Tunable Narrowband optical filters using superconductor / dielectric generalized Thue-Morse photonic crystals. Microelectron. Eng. 2019, 213, 41–46. [Google Scholar] [CrossRef]
- Liu, Y.; Yi, L. Tunable terahertz multichannel filter based on one-dimensional superconductor-dielectric photonic crystals. J. Appl. Phys. 2014, 116, 223102. [Google Scholar] [CrossRef]
- Aly, A.H. Metallic and Superconducting Photonic Crystal. J. Supercond. Nov. Magn. 2008, 21, 421–425. [Google Scholar] [CrossRef]
- Aly, A.H.; Elsayed, H.A.; Ameen, A.A.; Mohamed, S.H. Tunable properties of one-dimensional photonic crystals that incorporate a defect layer of a magnetized plasma. Int. J. Mod. Phys. B 2017, 31, 1750239. [Google Scholar] [CrossRef]
- Arafa, A.H.; Hussien, E.S.; Sahar, E. Tunability of two dimensional n-doped semiconductor photonic crystals based on the Faraday effect. Opt. Express 2015, 23, 15038–15046. [Google Scholar]
- Lin, Y.-T.; Chang, W.-Y.; Wu, C.-Y.; Zyryanov, V.Y.; Lee, W. Optical properties of one-dimensional photonic crystal with a twisted-nematic defect layer. Opt. Express 2010, 18, 26959–26964. [Google Scholar] [CrossRef]
- Zyryanov, V.Y.; Myslivets, S.A.; Gunyakov, V.A.; Parshin, A.M.; Arkhipkin, V.G.; Shabanov, V.F.; Lee, W. Magnetic-field tunable defect modes in a photonic-crystal/liquid-crystal cell. Opt. Express 2010, 18, 1283–1288. [Google Scholar] [CrossRef]
- D’Alessandro, A.; Asquini, R. Liquid Crystal Devices for Photonic Switching Applications: State of the Art and Future Developments. Mol. Cryst. Liq. Cryst. 2003, 398, 207–221. [Google Scholar] [CrossRef]
- Trabelsi, Y.; Ben Ali, N.; Aly, A.H.; Kanzari, M. Tunable high Tc superconducting photonic band gap resonators based on hybrid quasi-periodic multilayered stacks. Phys. C Supercond. Its Appl. 2020, 576, 1353706. [Google Scholar] [CrossRef]
- Yamamoto, A.; Takeshita, N.; Terakura, C.; Tokura, Y. High pressure effects revisited for the cuprate superconductor family with highest critical temperature. Nat. Commun. 2015, 6, 8990. [Google Scholar] [CrossRef]
- Trabelsi, Y.; Kanzari, M. Omnidirectional reflection from deformed quasiperiodic one-dimensional photonic crystals in high frequency. Phys. Procedia 2009, 2, 947–951. [Google Scholar] [CrossRef]
- Antonella D’Orazio, Infiltrated liquid crystal photonic bandgap devices for switching and tunable filtering. Fiber Integr. Opt. 2010, 22, 161–172.
- Zyryanov, V.Y.; Gunyakov, V.A.; Myslivets, S.A.; Arkhipkin, V.G.; Shabanov, V.F. Electrooptical Switching in a One-Dimensional Photonic Crystal. Mol. Cryst. Liq. Cryst. 2010, 488, 118–126. [Google Scholar] [CrossRef]
- Kowerdziej, R.; Parka, J.; Nyga, P.; Salski, B. Simulation of a tunable metamaterial with nematic liquid crystal layers. Liq. Cryst. 2011, 38, 377–379. [Google Scholar] [CrossRef]
- Alihosseini, F.; Ahmadi, V.; Mir, A. Design and analysis of a tunable liquid crystal switch/filter with metallic nano-slits. Liq. Cryst. 2015, 32, 1638–1642. [Google Scholar] [CrossRef]
- Lio, G.; Ferraro, A. LIDAR and Beam Steering Tailored by Neuromorphic Metasurfaces Dipped in a Tunable Surrounding Medium. Photonics 2021, 8, 65. [Google Scholar] [CrossRef]
- Wu, C.-Y.; Zou, Y.-H.; Timofeev, I.; Lin, Y.-T.; Zyryanov, V.Y.; Hsu, J.-S.; Lee, W. Tunable bi-functional photonic device based on one-dimensional photonic crystal infiltrated with a bistable liquid-crystal layer. Opt. Express 2011, 19, 7349–7355. [Google Scholar] [CrossRef]
- Bouazzi, Y.; Kanzari, M. Optical Fabry–Perot filter based on photonic band gap quasi-periodic one-dimensional multilayer according to the definite Rudin–Shapiro distribution. Opt. Commun. 2012, 285, 2774–2779. [Google Scholar] [CrossRef]
- Trabelsi, Y.; Ali, N.B.; Elhawil, A.; Krishnamurthy, R.; Kanzari, M.; Amiri, I.S.; Yupapin, P. Design of structural gigahertz multichanneled filter by using generalized Fibonacci superconducting photonic quasicrystals. Results Phys. 2019, 13, 10234. [Google Scholar] [CrossRef]
- Wang, Y.-Y.; Chen, L.-W. Tunable negative refraction photonic crystals achieved by liquid crystals. Opt. Express 2006, 14, 10580–10587. [Google Scholar] [CrossRef]
- Vaveliuk, P.; Moraes, F.; Fumeron, S.; Matos, O.M.; Calvo, M.L. Structure of the dielectric tensor in nematic liquid crystals with topological charge. J. Opt. Soc. Am. A 2010, 27, 1466–1472. [Google Scholar] [CrossRef]
- Da, H.-X.; Li, Z.Y. Manipulating Nematic Liquid Crystals-based Magnetophotonic Crystals. In New Developments in Liquid Crystals Book; Tkachenko, G.V., Ed.; I-Tech: Vienna, Austria, 2009; ISBN 978-953-307-015-5. [Google Scholar]
- Asquini, R.; Fratalocchi, A.; D’Alessandro, A.; Assanto, G. Electro-optic routing in a nematic liquid-crystal waveguide. Appl. Opt. 2005, 44, 4136–4143. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trabelsi, Y.; Belhadj, W.; Ben Ali, N.; Aly, A.H. Theoretical Study of Tunable Optical Resonators in Periodic and Quasiperiodic One-Dimensional Photonic Structures Incorporating a Nematic Liquid Crystal. Photonics 2021, 8, 150. https://doi.org/10.3390/photonics8050150
Trabelsi Y, Belhadj W, Ben Ali N, Aly AH. Theoretical Study of Tunable Optical Resonators in Periodic and Quasiperiodic One-Dimensional Photonic Structures Incorporating a Nematic Liquid Crystal. Photonics. 2021; 8(5):150. https://doi.org/10.3390/photonics8050150
Chicago/Turabian StyleTrabelsi, Youssef., Walid. Belhadj, Naim. Ben Ali, and Arafa H. Aly. 2021. "Theoretical Study of Tunable Optical Resonators in Periodic and Quasiperiodic One-Dimensional Photonic Structures Incorporating a Nematic Liquid Crystal" Photonics 8, no. 5: 150. https://doi.org/10.3390/photonics8050150
APA StyleTrabelsi, Y., Belhadj, W., Ben Ali, N., & Aly, A. H. (2021). Theoretical Study of Tunable Optical Resonators in Periodic and Quasiperiodic One-Dimensional Photonic Structures Incorporating a Nematic Liquid Crystal. Photonics, 8(5), 150. https://doi.org/10.3390/photonics8050150




