A Polarization-Insensitive Recirculating Delayed Self-Heterodyne Method for Sub-Kilohertz Laser Linewidth Measurement
Abstract
1. Introduction
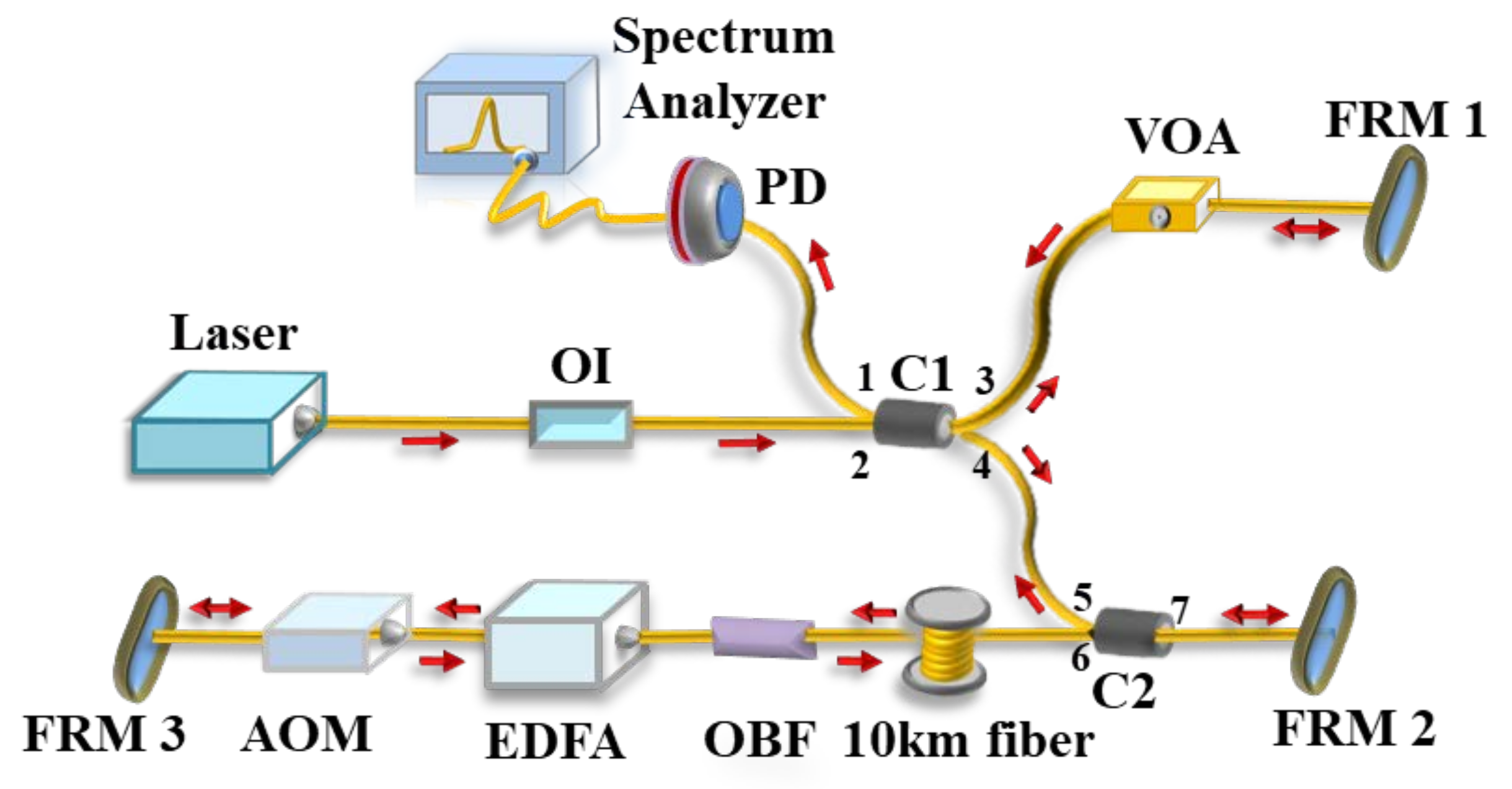
2. Experiment Setup
3. Analysis of Polarization Insensitivity
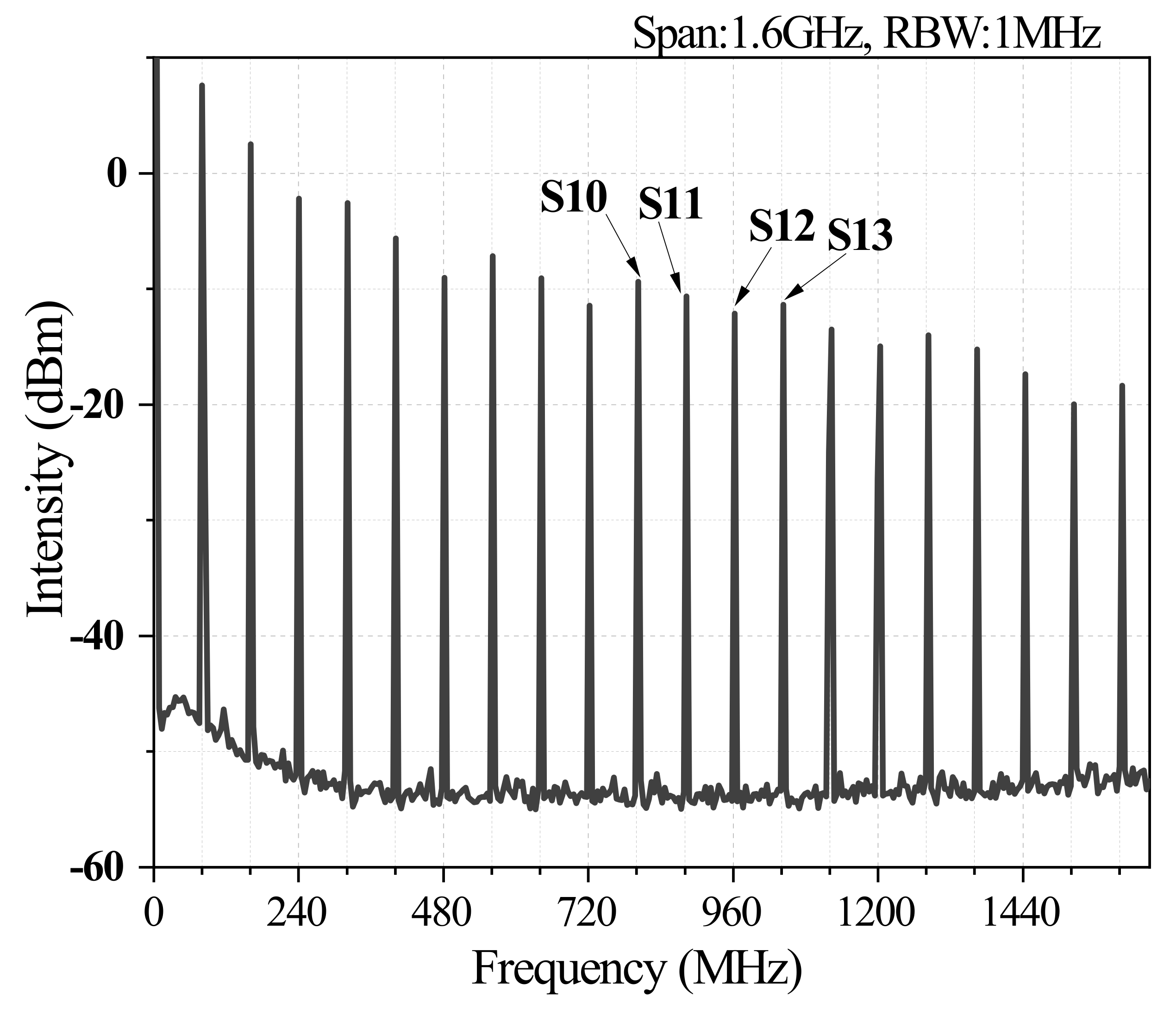
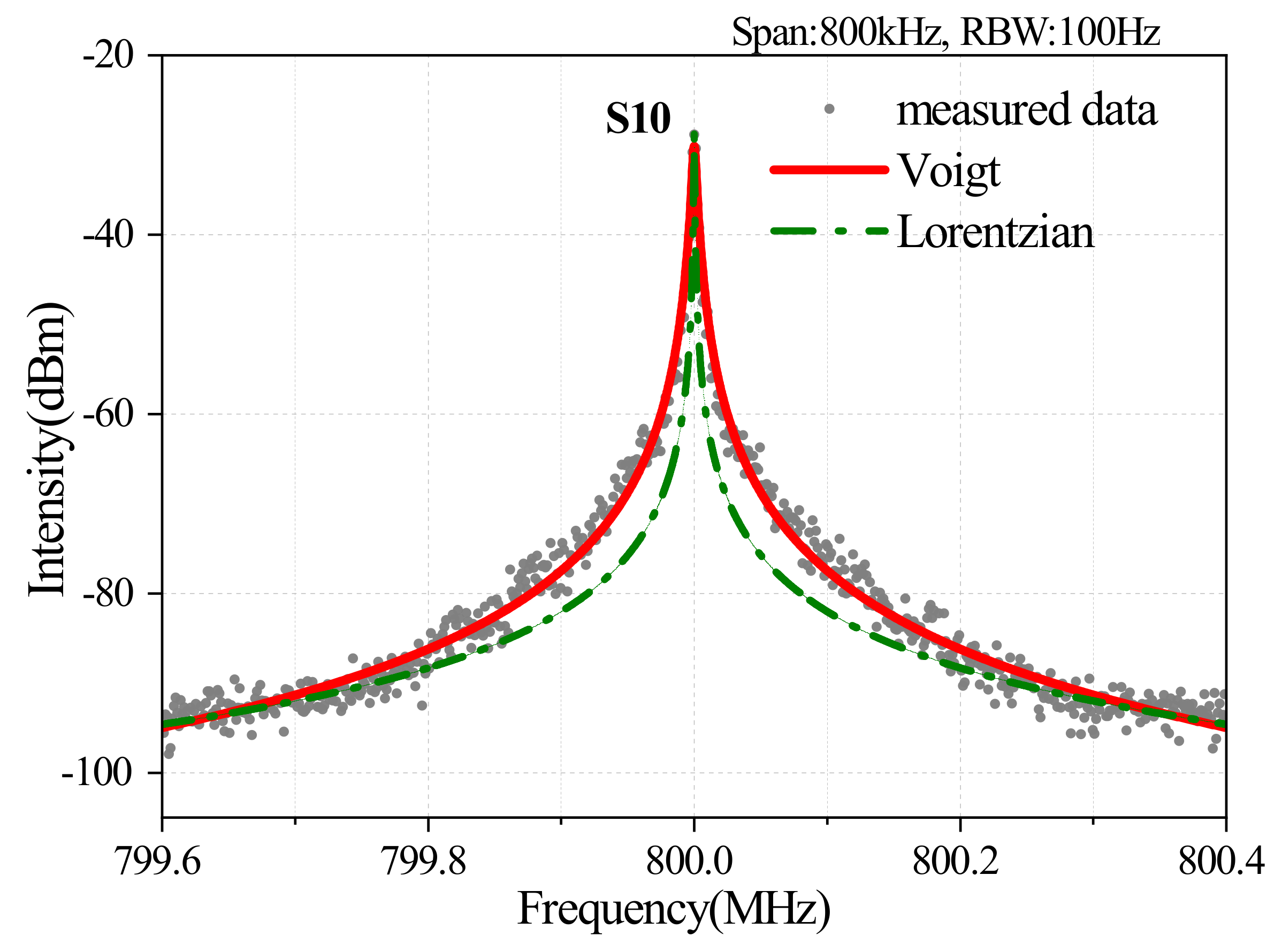
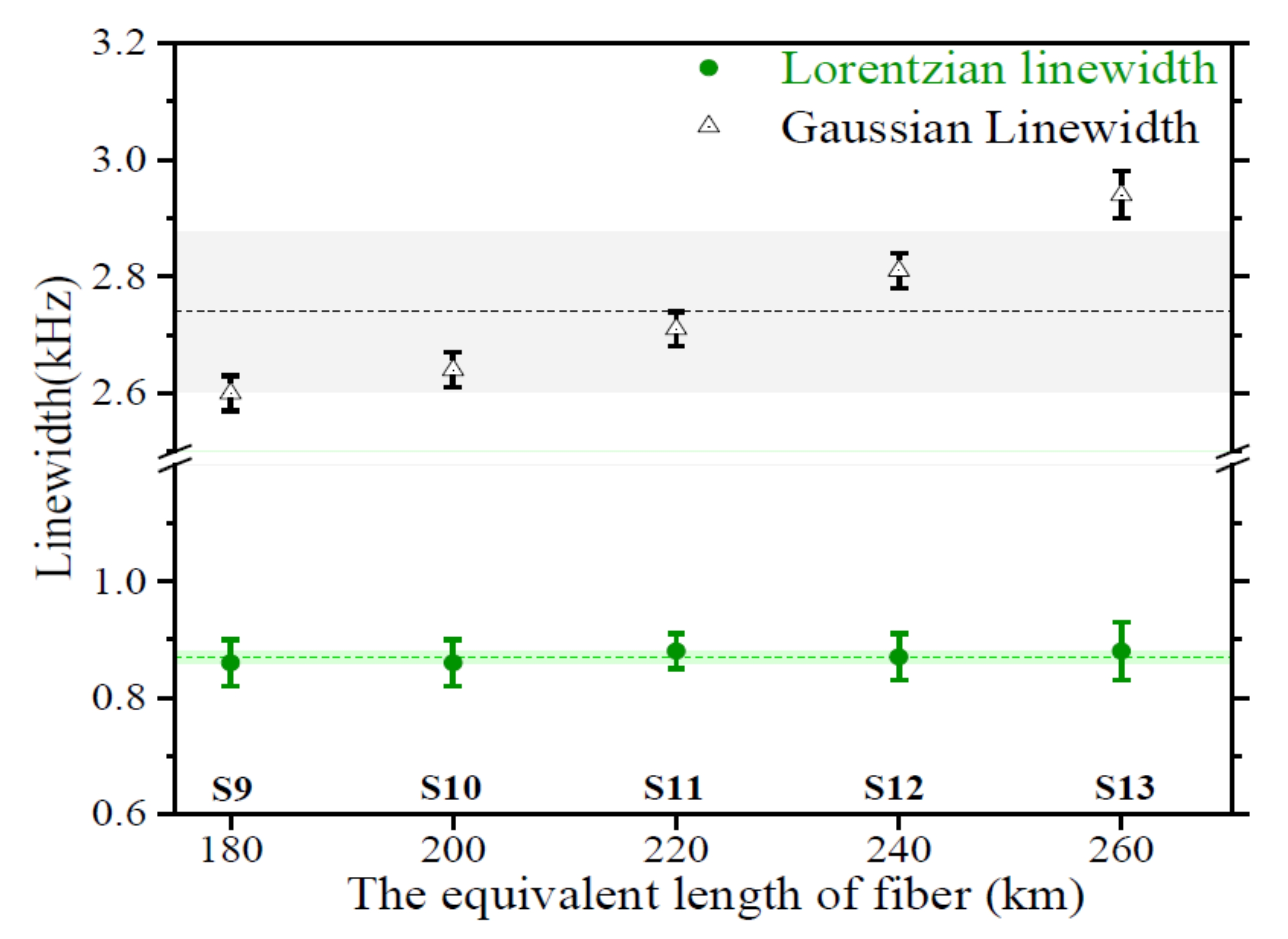
4. Experiment Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kessler, T.; Hagemann, C.; Grebing, C.; Legero, T.; Sterr, U.; Riehle, F.; Martin, M.J.; Chen, L.; Ye, J. A sub-40-mHz-linewidth laser based on a silicon single-crystal optical cavity. Nat. Photonics 2012, 6, 687–692. [Google Scholar] [CrossRef]
- Kapasi, D.P.; Eichholz, J.; Mcrae, T.; Ward, R.L.; Slagmolen, B.J.J.; Legge, S.; Hardman, K.S.; Altin, P.A.; McClelland, D.E. Tunable narrow-linewidth laser at 2 μm wavelength for gravitational wave research. Opt. Express 2020, 28, 3280–3288. [Google Scholar] [CrossRef] [PubMed]
- Deng, X.; Liu, J.; Zang, Q.; Jiao, D.; Gao, J.; Zhang, X.; Wang, D.; Dong, R.; Liu, T. Coherence phase transfer via fiber using heterodyne optical phase locking as optical amplification. Appl. Opt. 2018, 57, 9620–9623. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Du, Y.; Ding, Z.; Liu, K.; Zhou, Y.; Jiang, J. 40-km OFDR based distributed disturbance optical fiber sensor. IEEE Photonics Technol. Lett. 2016, 28, 771–774. [Google Scholar] [CrossRef]
- Okoshi, T.; Kikuchi, K.; Nakayama, A. Novel method for high resolution measurement of laser output spectrum. Electron. Lett. 1980, 16, 630–631. [Google Scholar] [CrossRef]
- Richter, L.E.; Mandelberg, H.I.; Kruger, M.S.; McGrath, P.A. Linewidth determination from self-heterodyne measurements with subcoherence delay times. IEEE J. Quantum Electron. 1986, 22, 2070–2074. [Google Scholar] [CrossRef]
- Peng, Y. A novel scheme for hundred-hertz linewidth measurements with the self-heterodyne method. Chin. Phys. Lett. 2013, 30, 084208. [Google Scholar] [CrossRef]
- Xu, Y.; Xiang, D.; Ou, Z.; Lu, P.; Bao, X. Random Fabry-Perot resonator-based sub-kHz Brillouin fiber laser to improve spectral resolution in linewidth measurement. Opt. Lett. 2015, 40, 1920–1923. [Google Scholar] [CrossRef]
- Yang, C.; Guan, X.; Lin, W.; Zhao, Q.; Tang, G. Efficient 1.6 μm linearly-polarized single-frequency phosphate glass fiber laser. Opt. Express 2017, 25, 29078–29085. [Google Scholar] [CrossRef]
- Mercer, L.B. 1/f frequency noise effects on self-heterodyne linewidth measurements. J. Light. Technol. 1991, 9, 485–493. [Google Scholar] [CrossRef]
- Tsuchida, H. Simple technique for improving the resolution of the delayed self-heterodyne method. Opt. Lett. 1990, 15, 640–642. [Google Scholar] [CrossRef]
- Huang, S.H.; Zhu, T.; Liu, M.; Huang, W. Precise measurement of ultra-narrow laser linewidths using the strong coherent envelope. Sci. Rep. 2017, 7, 41988. [Google Scholar] [CrossRef]
- He, Y.X.; Hu, S.L.; Liang, S.; Li, Y.Y. High-precision narrow laser linewidth measurement based on coherent envelope demodulation. Opt. Fiber Technol. 2019, 50, 200–205. [Google Scholar] [CrossRef]
- Chen, X.P.; Han, M.; Zhu, Y.Z.; Dong, B.; Wang, A.B. Implementation of a loss-compensated recirculating delayed self-heterodyne interferometer for ultranarrow laser linewidth measurement. Appl. Opt. 2006, 45, 7712–7717. [Google Scholar] [CrossRef]
- Wang, Z.H.; Ke, C.J.; Zhong, Y.; Xing, C.; Wang, H.Y.; Yang, K.Y.; Cui, S.; Liu, D.M. Ultra-narrow-linewidth measurement utilizing dual-parameter acquisition through a partially coherent light interference. Opt. Express 2020, 28, 8484–8493. [Google Scholar] [CrossRef]
- Kersey, A.D.; Marrone, M.J.; Dandridge, A. Polarization diversity detection for fiber interferometers using active feedback control of output polarization-mode selection. Opt. Lett. 1990, 15, 1315–1317. [Google Scholar] [CrossRef]
- Confortia, E.; Rodigheria, M.; Sutilib, T.; Galdieria, F.J. Acoustical and 1/f noises in narrow linewidth lasers. Opt. Commun. 2020, 476, 126286. [Google Scholar] [CrossRef]
- Ni, M.; Yang, H.Y.; Xiong, S.D.; Hu, Y.M. Investigation of polarization-induced fading in fiber-optic interferometers with polarizer-based polarization diversity receivers. Appl. Opt 2006, 45, 2387–2390. [Google Scholar]
- Kersey, A.D.; Marrone, M.J.; Davis, M.A. Polarization-insensitive fiber optic Michelson interferometer. Electron. Lett. 1991, 27, 518–520. [Google Scholar] [CrossRef]
- Li, L.; Ma, Q.; Cao, M.; Zhang, G.; Zhang, Y.; Jiang, L.; Gao, C.; Yao, J.; Gong, S.; Li, W. High stability Michelson refractometer based on an in-fiber interferometer followed with a Faraday rotator mirror. Sensors Actuators B 2016, 234, 674–679. [Google Scholar] [CrossRef]
- Huang, S.H.; Zhu, T.; Cao, Z.; Liu, M.; Deng, M.; Liu, J.; Li, X. Laser linewidth measurement based on amplitude difference comparison of coherent envelope. IEEE Photonics Technol. Lett. 2016, 28, 759–762. [Google Scholar] [CrossRef]
- Ludvigsen, H.; Tossavainen, M.; Kaivola, M. Laser linewidth measurements using self-homodyne detection with short delay. Opt. Commun. 1998, 155, 180–186. [Google Scholar] [CrossRef]
- Han, M.; Wang, A. Analysis of a loss-compensated recirculating delayed self-heterodyne interferometer for laser linewidth measurement. Appl. Phys. B 2005, 81, 53–58. [Google Scholar] [CrossRef]
- Chen, M.; Meng, Z.; Wang, J.F.; Chen, W. Ultra-narrow linewidth measurement based on Voigt profile fitting. Opt. Express 2015, 23, 6803–6808. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, J.; Jiao, D.; Deng, X.; Liu, J.; Zhang, L.; Zang, Q.; Zhang, X.; Liu, T.; Zhang, S. A Polarization-Insensitive Recirculating Delayed Self-Heterodyne Method for Sub-Kilohertz Laser Linewidth Measurement. Photonics 2021, 8, 137. https://doi.org/10.3390/photonics8050137
Gao J, Jiao D, Deng X, Liu J, Zhang L, Zang Q, Zhang X, Liu T, Zhang S. A Polarization-Insensitive Recirculating Delayed Self-Heterodyne Method for Sub-Kilohertz Laser Linewidth Measurement. Photonics. 2021; 8(5):137. https://doi.org/10.3390/photonics8050137
Chicago/Turabian StyleGao, Jing, Dongdong Jiao, Xue Deng, Jie Liu, Linbo Zhang, Qi Zang, Xiang Zhang, Tao Liu, and Shougang Zhang. 2021. "A Polarization-Insensitive Recirculating Delayed Self-Heterodyne Method for Sub-Kilohertz Laser Linewidth Measurement" Photonics 8, no. 5: 137. https://doi.org/10.3390/photonics8050137
APA StyleGao, J., Jiao, D., Deng, X., Liu, J., Zhang, L., Zang, Q., Zhang, X., Liu, T., & Zhang, S. (2021). A Polarization-Insensitive Recirculating Delayed Self-Heterodyne Method for Sub-Kilohertz Laser Linewidth Measurement. Photonics, 8(5), 137. https://doi.org/10.3390/photonics8050137




