Ring-Core Photonic Crystal Fiber of Terahertz Orbital Angular Momentum Modes with Excellence Guiding Properties in Optical Fiber Communication
Abstract
1. Introduction
2. PCF Design and Algorithm
3. Simulation Results and Discussions
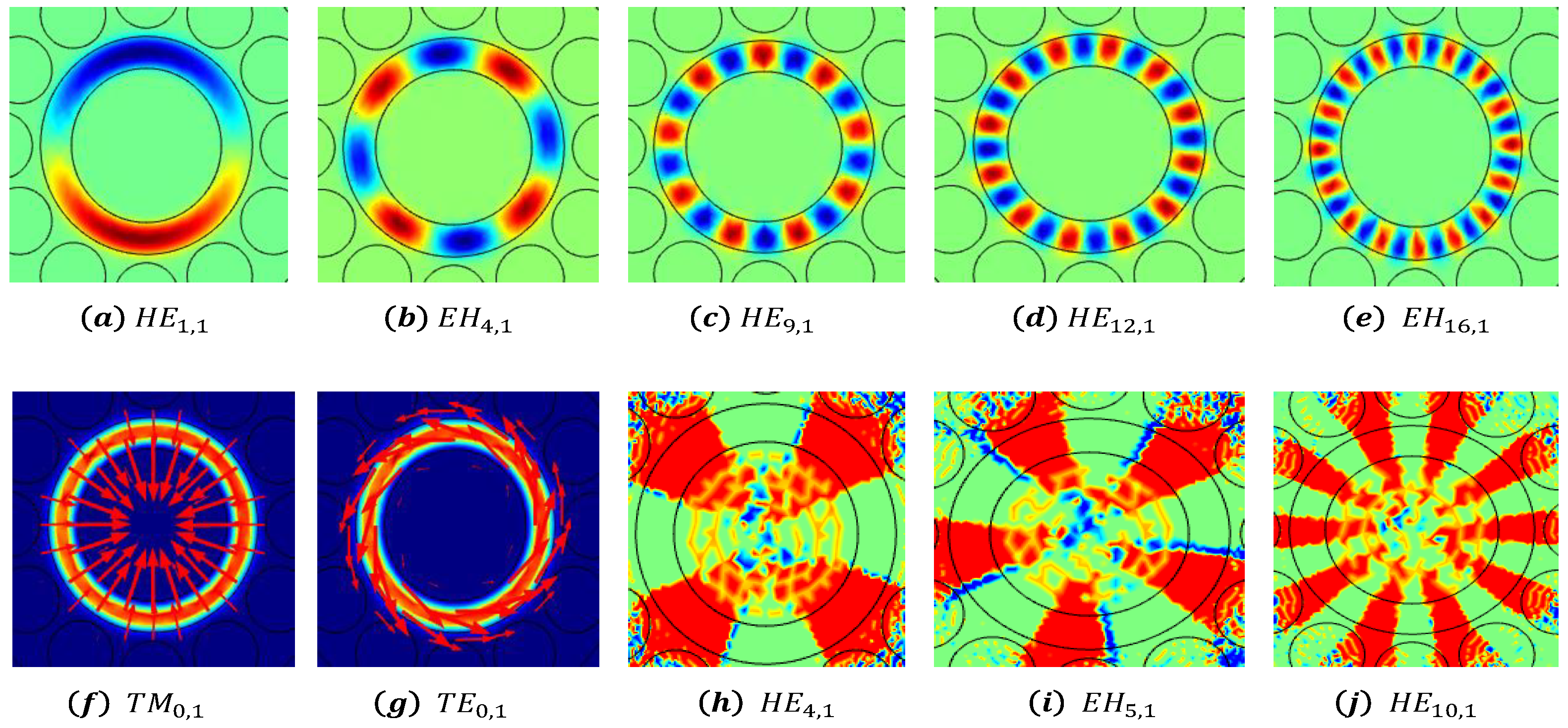
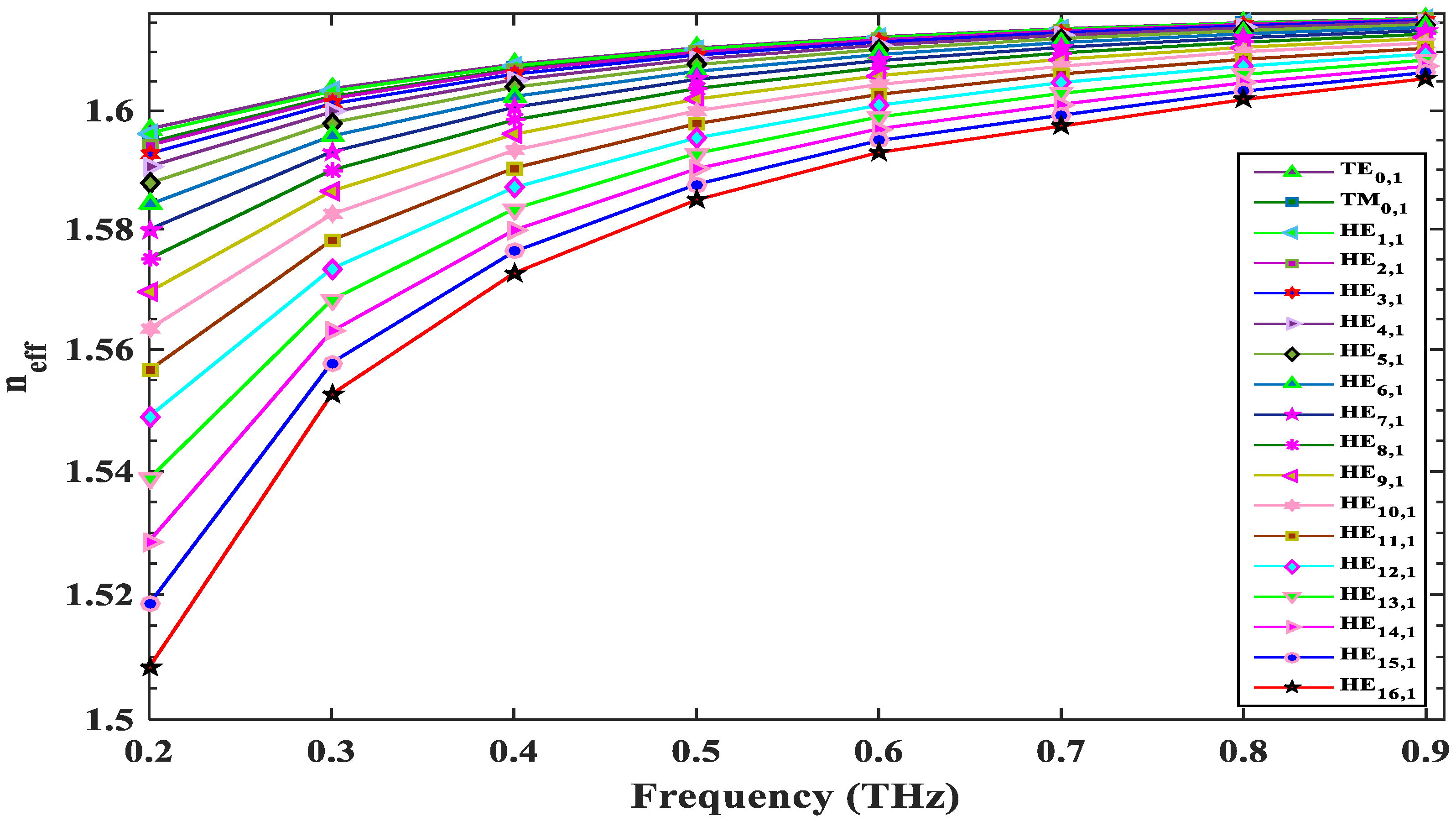
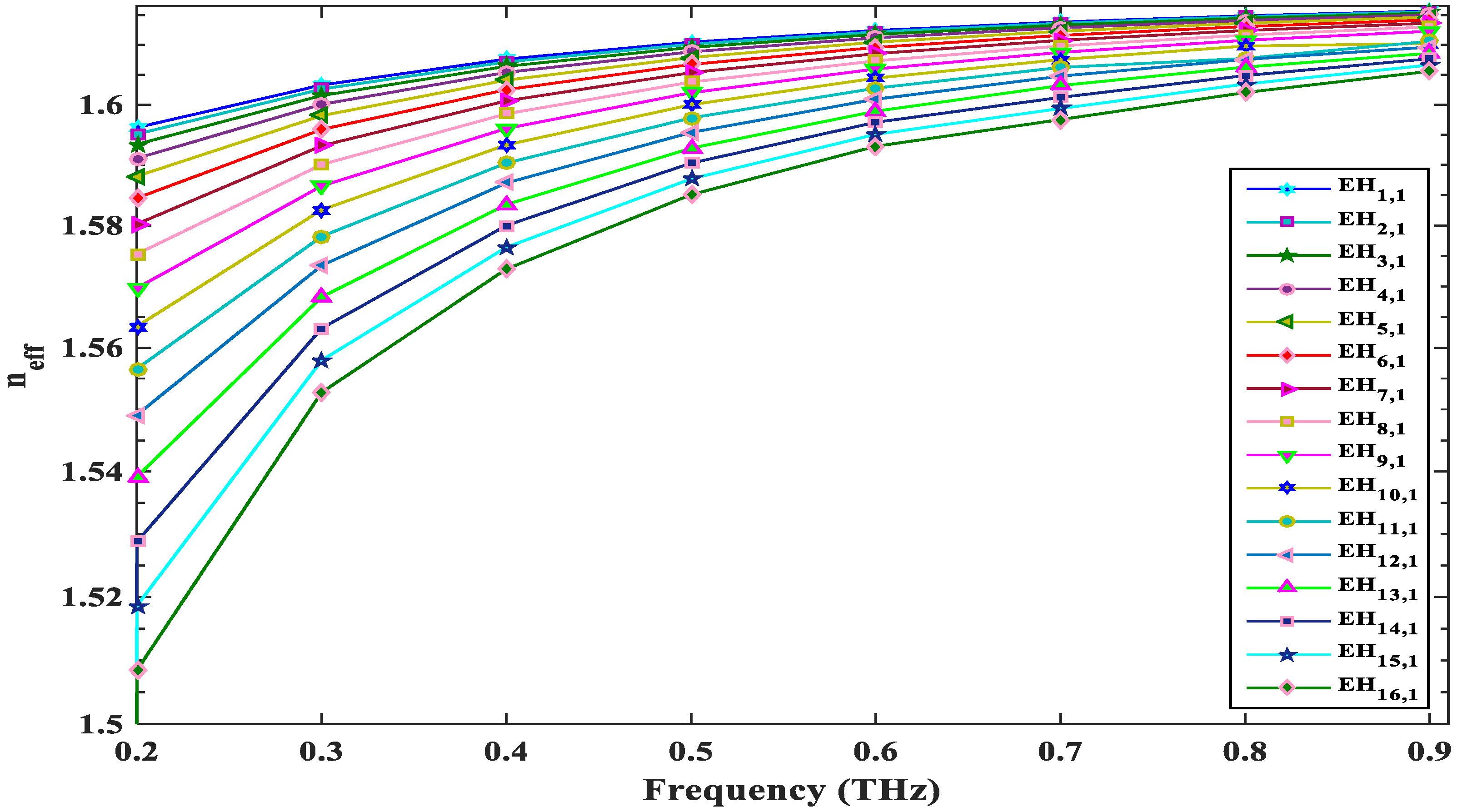
3.1. Effective Refractive Index
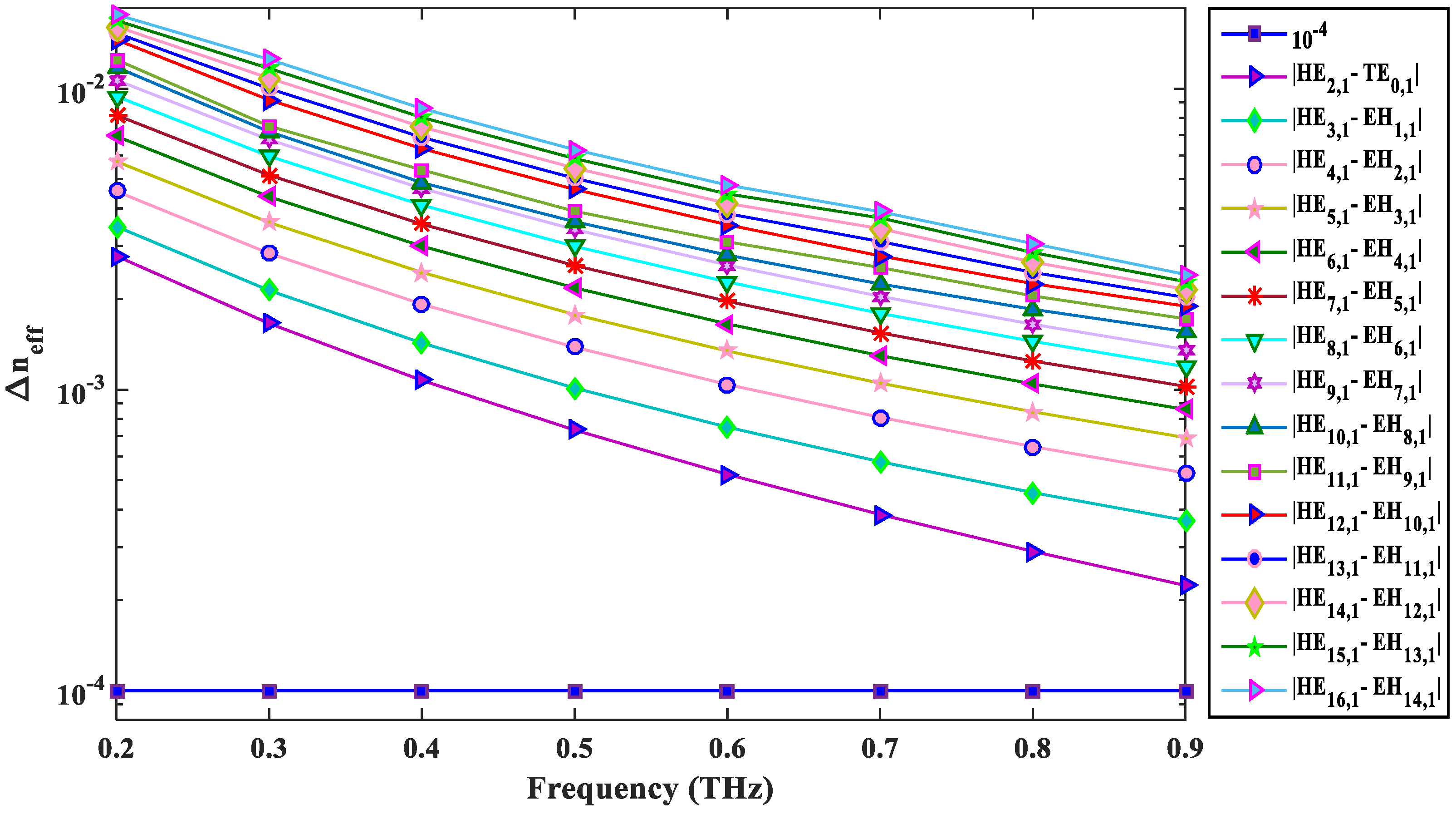
3.2. Effective Refractive Index Difference
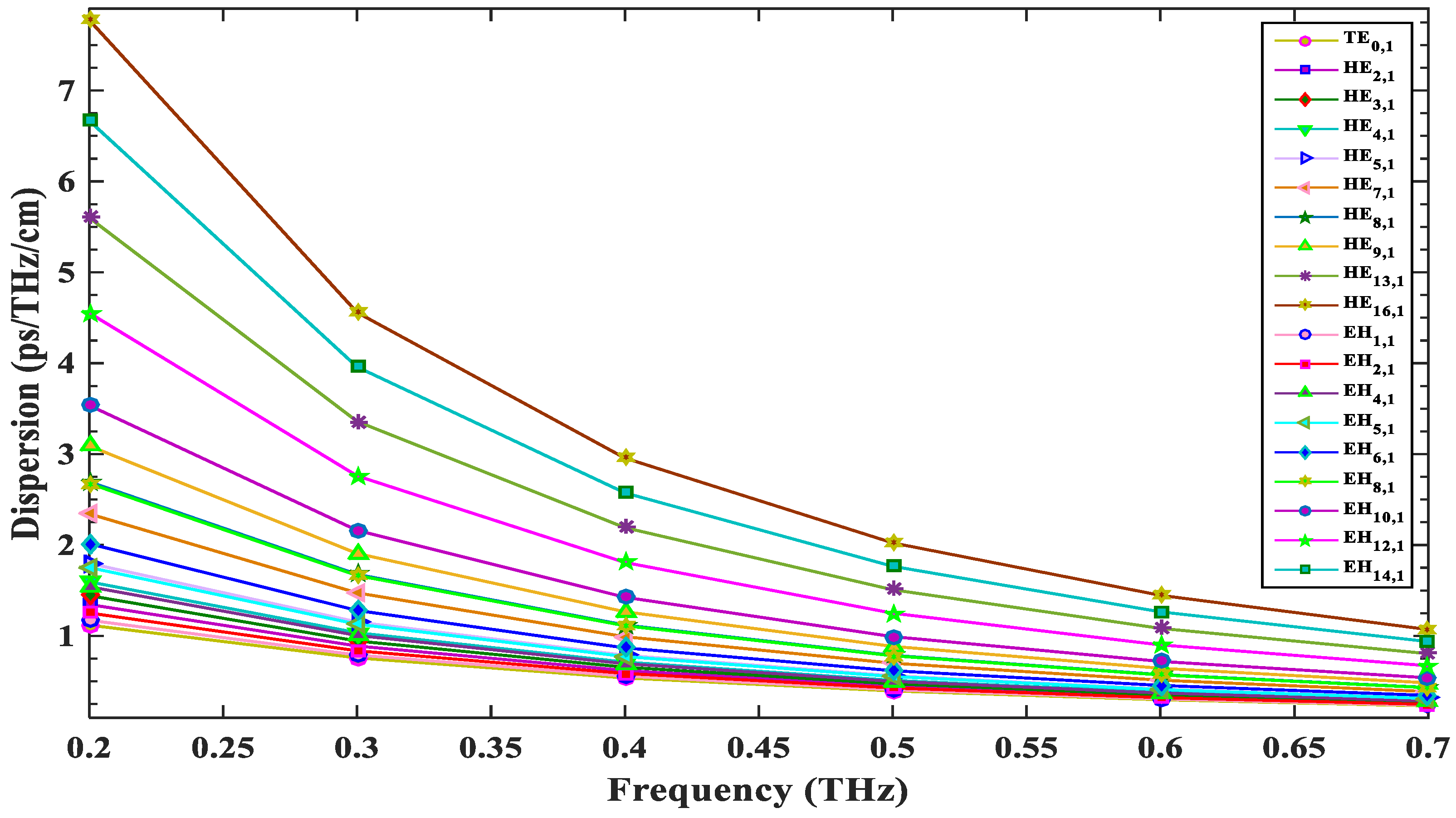
3.3. Dispersion
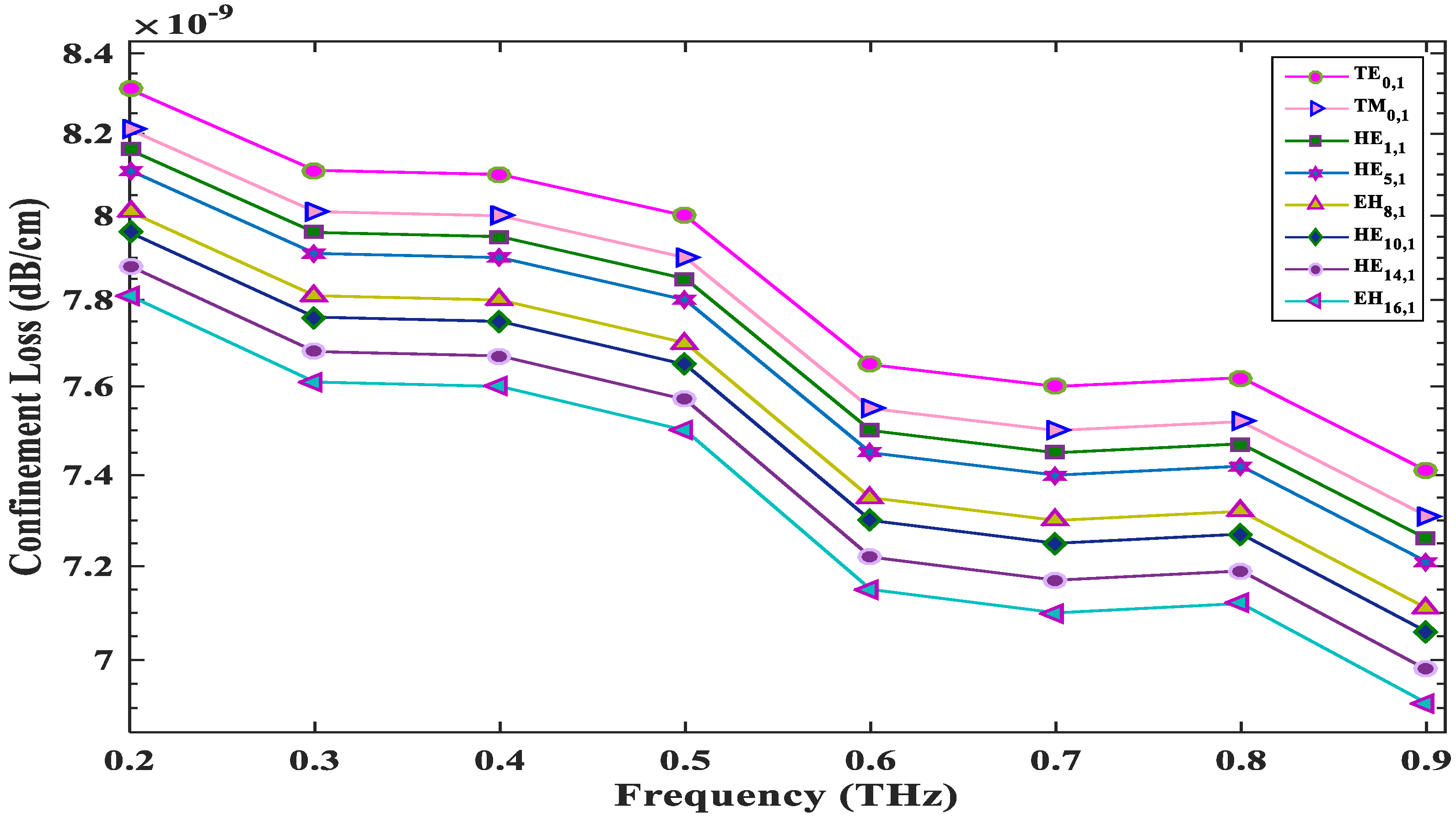
3.4. Confinement Loss
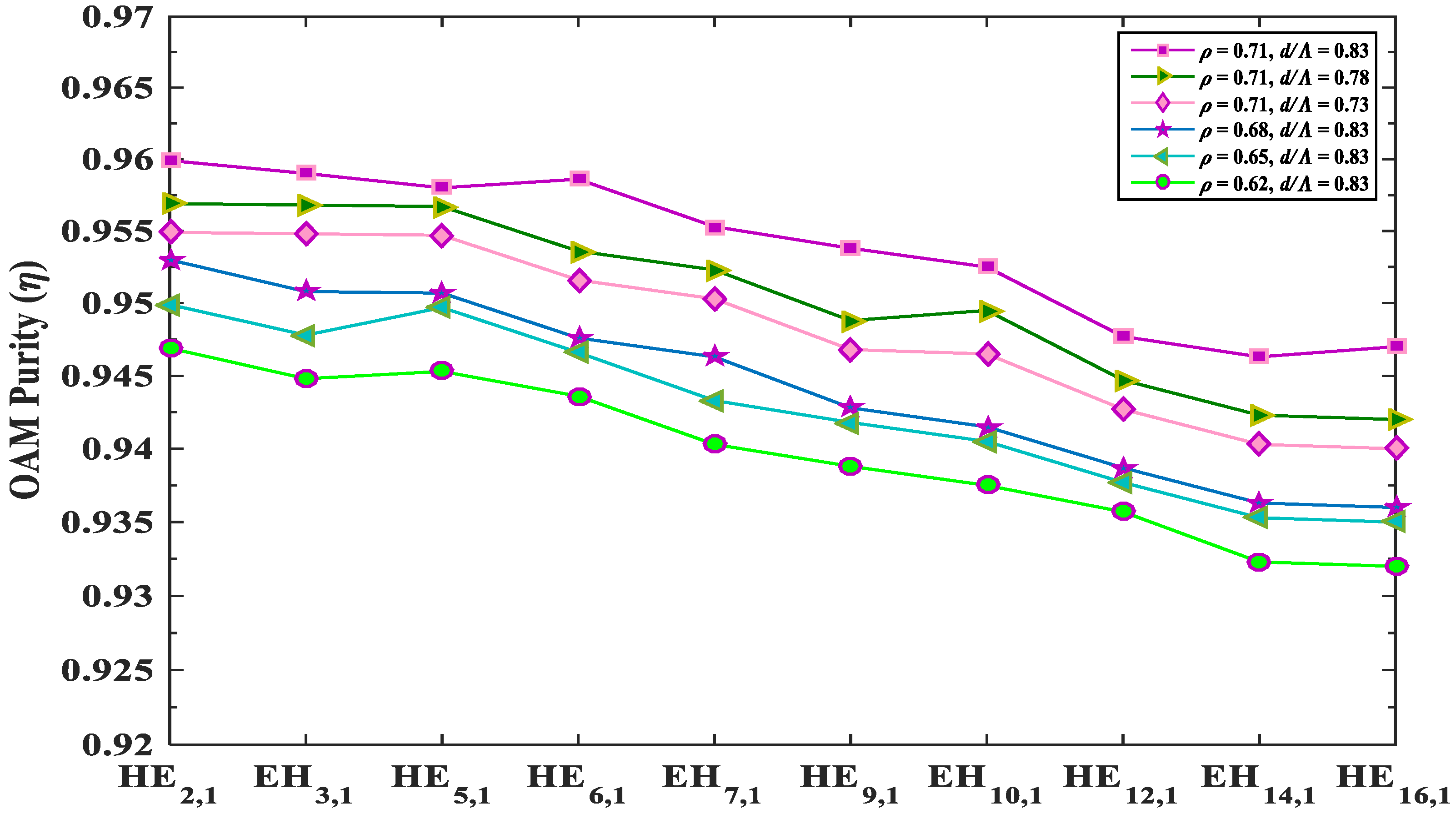
3.5. OAM Purity
4. Fabrication Possibility
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kan, T.; Kasai, K.; Yoshida, M.; Nakazawa, M. 42.3-Tbit/s, 18-Gbaud 64 QAM WDM coherent transmission of 160 km over full C-band using an injection locking technique with a spectral efficiency of 9 bit/s/Hz. In Proceedings of the 2017 Optical Fiber Communications Conference and Exhibition (OFC), Los Angeles, CA, USA, 19–23 March 2017; Volume 25, pp. 1–3. [Google Scholar]
- Nitta, J.; Yoshida, M.; Kimura, K.; Kasai, K.; Hirooka, T.; Nakazawa, M. Single-channel 3.84 Tbit/s, 64 QAM coherent Nyquist pulse transmission over 150 km with a spectral efficiency of 10.6 bit/s/Hz. Opt. Express 2017, 25, 15199–15207. [Google Scholar] [CrossRef]
- Schuh, K.; Buchali, F.; Idler, W.; Eriksson, T.A.; Schmalen, L.; Templ, W.; Altenhain, L.; Dümler, U.; Schmid, R.; Möller, M.; et al. Single carrier 1.2 Tbit/s transmission over 300 km with PM-64 QAM at 100 GBaud. In Optical Fiber Communication Conference; Optical Society of America: Los Angeles, CA, USA, 2017; p. Th5B.5. [Google Scholar]
- Richardson, D.J.; Fini, J.M.; Nelson, L.E. Space-division multiplexing in optical fibers. Nat. Photonics 2013, 7, 354. [Google Scholar] [CrossRef]
- Cui, X.Z.; Yin, X.L.; Chang, H.; Sun, Z.W.; Wang, Y.J.; Tian, Q.H.; Wu, G.H.; Xin, X.J. Analysis of the orbital angular momentum spectrum for Laguerre–Gaussian beams under moderate-to-strong marine-atmospheric turbulent channels. Opt. Commun. 2018, 426, 471–476. [Google Scholar] [CrossRef]
- Wang, J. Advances in communications using optical vortices. Photonics Res. 2016, 4, B14–B28. [Google Scholar] [CrossRef]
- Fürhapter, S.; Jesacher, A.; Bernet, S.; Ritsch-Marte, M. Spiral phase contrast imaging in microscopy. Opt. Express 2005, 13, 689–694. [Google Scholar] [CrossRef]
- Padgett, M.; Bowman, R. Tweezers with a twist. Nat. Photonics 2011, 5, 343–348. [Google Scholar] [CrossRef]
- Erhard, M.; Fickler, R.; Krenn, M.; Zeilinger, A. Twisted photons: New quantum perspectives in high dimensions. Light Sci. Appl. 2018, 7, 17146. [Google Scholar] [CrossRef]
- Padgett, M.J. Orbital angular momentum 25 years on. Opt. Express 2017, 25, 11265–11274. [Google Scholar] [CrossRef]
- Durnin, J.J.J.M.; Miceli, J.J., Jr.; Eberly, J.H. Diffraction-free beams. Phys. Rev. Lett. 1987, 58, 1499. [Google Scholar] [CrossRef]
- Sueda, K.; Miyaji, G.; Miyanaga, N.; Nakatsuka, M. Laguerre-Gaussian beam generated with a multilevel spiral phase plate for highintensity laser pulses. Opt. Express 2004, 12, 3548–3553. [Google Scholar] [CrossRef]
- Huang, H.; Milione, G.; Lavery, M.P.; Xie, G.; Ren, Y.; Cao, Y.; Ahmed, N.; Nguyen, T.A.; Nolan, D.A.; Li, M.J.; et al. Mode division multiplexing using an orbital angular momentum mode sorter and MIMO-DSP over a graded-index few-mode optical fiber. Sci. Rep. 2015, 5, 1–7. [Google Scholar] [CrossRef]
- Yan, Y.; Xie, G.; Lavery, M.P.; Huang, H.; Ahmed, N.; Bao, C.; Ren, Y.; Cao, Y.; Li, L.; Zhao, Z.; et al. High-capacity millimeter-wave communications with orbital angular momentum multiplexing. Nat. Commun. 2014, 5, 1–9. [Google Scholar] [CrossRef]
- Li, S.; Wang, J. Compensation of a distorted N-fold orbital angular momentum multicasting link using adaptive optics. Opt. Lett. 2016, 41, 1482–1485. [Google Scholar] [CrossRef]
- Ramachandran, S.; Gregg, P.; Kristensen, P.; Golowich, S.E. On the scalability of ring fiber designs for OAM multiplexing. Opt. Express 2015, 23, 3721–3730. [Google Scholar] [CrossRef] [PubMed]
- Brunet, C.; Ung, B.; Wang, L.; Messaddeq, Y.; LaRochelle, S.; Rusch, L.A. Design of a family of ring-core fibers for OAM transmission studies. Opt. Express 2015, 23, 10553–10563. [Google Scholar] [CrossRef]
- Ye, J.; Li, Y.; Han, Y.; Deng, D.; Guo, Z.; Gao, J.; Sun, Q.; Liu, Y.; Qu, S. Excitation and separation of vortex modes in the twisted air-core fiber. Opt. Express 2016, 24, 8310–8316. [Google Scholar] [CrossRef]
- Zhang, Z.; Gan, J.; Heng, X.; Wu, Y.; Li, Q.; Qian, Q.; Chen, D.; Yang, Z. Optical fiber design with orbital angular momentum light purity higher than 99.9%. Opt. Express 2015, 23, 29331–29341. [Google Scholar] [CrossRef] [PubMed]
- Yan, Y.; Wang, J.; Zhang, L.; Yang, J.Y.; Fazal, I.M.; Ahmed, N.; Shamee, B.; Willner, A.E.; Birnbaum, K.; Dolinar, S. Fiber coupler for generating orbital angular momentum modes. Opt. Lett. 2011, 36, 4269–4271. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Ren, G.; Zhu, B.; Gao, Y.; Yin, B.; Wang, J.; Jian, S. Guiding terahertz orbital angular momentum beams in multimode Kagome hollow-core fibers. Opt. Lett. 2017, 42, 179–182. [Google Scholar] [CrossRef]
- Yao, A.M.; Padgett, M.J. Orbital angular momentum: Origins, behavior, and applications. Adv. Opt. Photonics 2011, 3, 161–204. [Google Scholar] [CrossRef]
- Xie, Z.; Wang, X.; Ye, J.; Feng, S.; Sun, W.; Akalin, T.; Zhang, Y. Spatial terahertz modulator. Sci. Rep. 2013, 3, 3347. [Google Scholar] [CrossRef]
- Liu, C.; Wei, X.; Niu, L.; Wang, K.; Yang, Z.; Liu, J. Discrimination of orbital angular momentum modes of the terahertz vortex beam using a diffractive mode transformer. Opt. Express 2016, 24, 12534–12541. [Google Scholar] [CrossRef]
- He, J.; Wang, X.; Hu, D.; Ye, J.; Feng, S.; Kan, Q.; Zhang, Y. Generation and evolution of the terahertz vortex beam. Opt. Express 2013, 21, 20230–20239. [Google Scholar] [CrossRef] [PubMed]
- Imai, R.; Kanda, N.; Higuchi, T.; Konishi, K.; Kuwata-Gonokami, M. Generation of broadband terahertz vortex beams. Opt. Lett. 2014, 39, 3714–3717. [Google Scholar] [CrossRef]
- Ramachandran, S.; Kristensen, P. Optical vortices in fiber. Nanophotonics 2013, 2, 455–474. [Google Scholar] [CrossRef]
- Atakaramians, S.; Afshar, S.; Monro, T.M.; Abbott, D. Terahertz dielectric waveguides. Adv. Opt. Photonics 2013, 5, 169–215. [Google Scholar] [CrossRef]
- Li, H.; Atakaramians, S.; Lwin, R.; Tang, X.; Yu, Z.; Argyros, A.; Kuhlmey, B.T. Flexible single-mode hollow-core terahertz fiber with metamaterial cladding. Optica 2016, 3, 941–947. [Google Scholar] [CrossRef]
- Navarro-Cía, M.; Melzer, J.E.; Harrington, J.A.; Mitrofanov, O. Silver-coated Teflon tubes for waveguiding at 1–2 THz. J. Infrared Millim. Terahertz Waves 2015, 36, 542–555. [Google Scholar] [CrossRef]
- Litchinitser, N.M.; Abeeluck, A.K.; Headley, C.; Eggleton, B.J. Antiresonant reflecting photonic crystal optical waveguides. Opt. Lett. 2002, 27, 1592–1594. [Google Scholar] [CrossRef]
- Lu, W.; Lou, S.; Argyros, A. Investigation of flexible low-loss hollow-core fibres with tube-lattice cladding for terahertz radiation. IEEE J. Sel. Top. Quantum Electron. 2015, 22, 214–220. [Google Scholar] [CrossRef]
- Anthony, J.; Leonhardt, R.; Leon-Saval, S.G.; Argyros, A. THz propagation in kagome hollow-core microstructured fibers. Opt. Express 2011, 19, 18470–18478. [Google Scholar] [CrossRef]
- Lai, C.H.; Hsueh, Y.C.; Chen, H.W.; Huang, Y.J.; Chang, H.C.; Sun, C.K. Low-index terahertz pipe waveguides. Opt. Lett. 2009, 34, 3457–3459. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, J.; Gong, C.; Tian, H.; Sun, L.; Chen, P.; Lin, L.; Liu, W. 3D printed low-loss THz waveguide based on Kagome photonic crystal structure. Opt. Express 2016, 24, 22454–22460. [Google Scholar] [CrossRef]
- Hasan, M.R.; Anower, M.S.; Islam, M.A.; Razzak, S.M.A. Polarization-maintaining low-loss porous-core spiral photonic crystal fiber for terahertz wave guidance. Appl. Opt. 2016, 55, 4145–4152. [Google Scholar] [CrossRef]
- Nandam, A.; Shin, W. Spiral photonic crystal fiber structure for supporting orbital angular momentum modes. Optik 2018, 169, 361–367. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, X.; Li, H.; Deng, Y.; Zhang, X.; Xi, L.; Tang, X.; Zhang, W. A design strategy of the circular photonic crystal fiber supporting good quality orbital angular momentum mode transmission. Opt. Commun. 2017, 397, 59–66. [Google Scholar] [CrossRef]
- Hassan, M.M.; Kabir, M.A.; Hossain, M.N.; Biswas, B.; Paul, B.K.; Ahmed, K. Photonic crystal fiber for robust orbital angular momentum transmission: Design and investigation. Opt. Quantum Electron. 2020, 52, 8. [Google Scholar] [CrossRef]
- Kim, M.; Kim, S. Photonic Quasi-crystal Fiber for Orbital Angular Momentum Modes with Ultra-flat Dispersion. Curr. Opt. Photonics 2019, 3, 298–303. [Google Scholar]
- Zhang, H.; Han, D.; Xi, L.; Zhang, Z.; Zhang, X.; Li, H.; Zhang, W. Two-layer erbium-doped air-core circular photonic crystal fiber amplifier for orbital angular momentum mode division multiplexing system. Crystals 2019, 9, 156. [Google Scholar] [CrossRef]
- Israk, M.F.; Razzak, M.A.; Ahmed, K.; Hassan, M.M.; Kabir, M.A.; Hossain, M.N.; Paul, B.K.; Dhasarathan, V. Ring-based coil structure photonic crystal fiber for transmission of Orbital Angular Momentum with large bandwidth: Outline, investigation and analysis. Opt. Commun. 2020, 473, 126003. [Google Scholar] [CrossRef]
- Huang, S.H.; Ma, Q.C.; Chen, W.C.; Liu, H.Z.; Xing, X.B.; Cui, H.; Luo, Z.C.; Xu, W.C.; Luo, A.P. Microstructure ring fiber for supporting higher-order orbital angular momentum modes with flattened dispersion in broad waveband. Appl. Phys. B 2019, 125, 197. [Google Scholar] [CrossRef]
- Wang, W.; Wang, N.; Li, K.; Geng, Z.; Jia, H. A novel dual guided modes regions photonic crystal fiber with low crosstalk supporting 56 OAM modes and 4 LP modes. Opt. Fiber Technol. 2020, 57, 102213. [Google Scholar] [CrossRef]
- Monfared, Y.E.; Mojtahedinia, A.; Javan, A.M.; Kashani, A.M. Highly nonlinear enhanced-core photonic crystal fiber with low dispersion for wavelength conversion based on four-wave mixing. Front. Optoelectron. 2013, 6, 297–302. [Google Scholar] [CrossRef]
- COMSOL AB. Comsol Multiphysics® v. 5.4 www.comsol.com; COMSOL AB: Stockholm, Sweden, 2018. [Google Scholar]
- Bjarklev, A. Microdeformation losses of single-mode fibers with step-index profiles. J. Light. Technol. 1986, 4, 341–346. [Google Scholar] [CrossRef]
- Zhou, G.; Zhou, G.; Chen, C.; Xu, M.; Xia, C.; Hou, Z. Design and analysis of a microstructure ring fiber for orbital angular momentum transmission. IEEE Photonics J. 2016, 8, 1–12. [Google Scholar] [CrossRef]
- Kabir, M.A.; Hassan, M.M.; Hossain, M.N.; Paul, B.K.; Ahmed, K. Design and performance evaluation of photonic crystal fibers of supporting orbital angular momentum states in optical transmission. Opt. Commun. 2020, 467, 125731. [Google Scholar] [CrossRef]
- Islam, M.S.; Sultana, J.; Ahmed, K.; Islam, M.R.; Dinovitser, A.; Ng, B.W.H.; Abbott, D. A novel approach for spectroscopic chemical identification using photonic crystal fiber in the terahertz regime. IEEE Sens. J. 2017, 18, 575–582. [Google Scholar] [CrossRef]
- Islam, M.; Hossain, M.A.; Haque, F. A Comparative Analysis between Low Loss Kagome Structured THz Hollow Core and Porous Core PCF. AIUB J. Sci. Eng. 2017, 16, 95–100. [Google Scholar]
- Xu, M.; Zhou, G.; Chen, C.; Zhou, G.; Sheng, Z.; Hou, Z.; Xia, C. A novel microstructured fiber for OAM mode and LP mode simultaneous transmission. J. Opt. 2018, 47, 428–436. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, W.; Xi, L.; Tang, X.; Zhang, X.; Zhang, X. A new type circular photonic crystal fiber for orbital angular momentum mode transmission. IEEE Photonics Technol. Lett. 2016, 28, 1426–1429. [Google Scholar] [CrossRef]
- Kabir, M.A.; Hassan, M.M.; Ahmed, K.; Rajan, M.M.; Aly, A.H.; Hossain, M.N.; Paul, B.K. Novel spider web photonic crystal fiber for robust mode transmission applications with supporting orbital angular momentum transmission property. Opt. Quantum Electron. 2020, 52, 1–17. [Google Scholar] [CrossRef]
- Hassan, M.M.; Kabir, M.A.; Hossain, M.N.; Nguyen, T.K.; Paul, B.K.; Ahmed, K.; Dhasarathan, V. Numerical analysis of circular core shaped photonic crystal fiber for orbital angular momentum with efficient transmission. Appl. Phys. B 2020, 126, 1–8. [Google Scholar] [CrossRef]
- El Hamzaoui, H.; Ouerdane, Y.; Bigot, L.; Bouwmans, G.; Capoen, B.; Boukenter, A.; Girard, S.; Bouazaoui, M. Sol-gel derived ionic copper-doped microstructured optical fiber: A potential selective ultraviolet radiation dosimeter. Opt. Express 2012, 20, 29751–29760. [Google Scholar] [CrossRef] [PubMed]
- Tandjè, A.; Yammine, J.; Dossou, M.; Bouwmans, G.; Baudelle, K.; Vianou, A.; Andresen, E.R.; Bigot, L. Ring-core photonic crystal fiber for propagation of OAM modes. Opt. Lett. 2019, 44, 1611–1614. [Google Scholar] [CrossRef] [PubMed]
- Brunet, C.; Vaity, P.; Messaddeq, Y.; LaRochelle, S.; Rusch, L.A. Design, fabrication and validation of an OAM fiber supporting 36 states. Opt. Express 2014, 22, 26117–26127. [Google Scholar] [CrossRef]
- Kumar, V.R.K.; George, A.K.; Reeves, W.H.; Knight, J.C.; Russell, P.S.J.; Omenetto, F.G.; Taylor, A.J. Extruded soft glass photonic crystal fiber for ultra-broad supercontinuum generation. Opt. Express 2002, 10, 1520–1525. [Google Scholar] [CrossRef]

| Year | Author | Lattice | Material | Number of OAM Modes | Operating Bandwidth | Reference |
|---|---|---|---|---|---|---|
| 2016 | H. Li et al. | Kagome | Polymer | 3 | 700 GHz | [21] |
| 2019 | H. Zhang et al. | Circular | Erbium | 14 | 560 nm | [41] |
| 2020 | M. F. Israk et al. | Coil | Schott | 56 | 1900 nm | [42] |
| 2019 | S. H. Huang et al. | Circular | Schott & phosphate glass | 146 and 70 | 900 nm | [43] |
| 2020 | W. Wang et al. | Circular | Schott | 56 + 4 | 300 nm | [44] |
| Reference | Operating Bandwidth Range | Supported OAM Modes | The Lowest Confinement Loss (dB/cm) | The Lowest Dispersion Variation |
|---|---|---|---|---|
| [21] | 0.20–0.90 THz | 3 | ≈ | - |
| [37] | 1.30–2.00 m | 14 | 5.095 × | 10.35 ps/km/nm |
| [38] | 1.25–2.00 m | >42 | 9.52 × | - |
| [39] | 1.20–1.95 m | 26 | 3.19 × | 3.8684 ps/km/nm |
| [42] | 0.60–2.50 m | 56 | 1.74 × | 36.907 ps/km/nm |
| [43] | 1.10–2.00 m | 146 | - | 2.92 ps/km/nm |
| [44] | 1.52–1.58 m | 30 | ≈ | - |
| [48] | 0.80–2.00 m | 42 | 1.131 × | 3.7980 ps/km/nm |
| [52] | 1.40–1.70 m | 56 | <4.91 × | - |
| [53] | 1.25–1.81 m | 14 | 3.434 × | <46.38 ps/km/nm |
| [54] | 0.80–1.80 m | 26 | 1.030 × | 7.8337 ps/km/nm |
| [55] | 1.00–2.00 m | 38 | 1.534 × | 0.916 ps/km/nm |
| This work | 0.20–0.90 THz | 58 | 6.91 × | 0.8881 ps/THz/cm |
| Key Parameters | Numerical Values |
|---|---|
| Number of Supported OAM modes | 58 |
| Operating Bandwidth | 0.20–0.90 THz |
| Effective refractive index difference | > |
| Dispersion | 0.23–7.77 ps/THz/cm |
| Confinement Loss | 6.91 × –8.21 × dB/cm |
| OAM Purity | 0.9320–0.9599 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Zahrani, F.A.; Kabir, M.A. Ring-Core Photonic Crystal Fiber of Terahertz Orbital Angular Momentum Modes with Excellence Guiding Properties in Optical Fiber Communication. Photonics 2021, 8, 122. https://doi.org/10.3390/photonics8040122
Al-Zahrani FA, Kabir MA. Ring-Core Photonic Crystal Fiber of Terahertz Orbital Angular Momentum Modes with Excellence Guiding Properties in Optical Fiber Communication. Photonics. 2021; 8(4):122. https://doi.org/10.3390/photonics8040122
Chicago/Turabian StyleAl-Zahrani, Fahad Ahmed, and Md. Anowar Kabir. 2021. "Ring-Core Photonic Crystal Fiber of Terahertz Orbital Angular Momentum Modes with Excellence Guiding Properties in Optical Fiber Communication" Photonics 8, no. 4: 122. https://doi.org/10.3390/photonics8040122
APA StyleAl-Zahrani, F. A., & Kabir, M. A. (2021). Ring-Core Photonic Crystal Fiber of Terahertz Orbital Angular Momentum Modes with Excellence Guiding Properties in Optical Fiber Communication. Photonics, 8(4), 122. https://doi.org/10.3390/photonics8040122






