Quantum Reinforcement Learning with Quantum Photonics
Abstract
1. Introduction
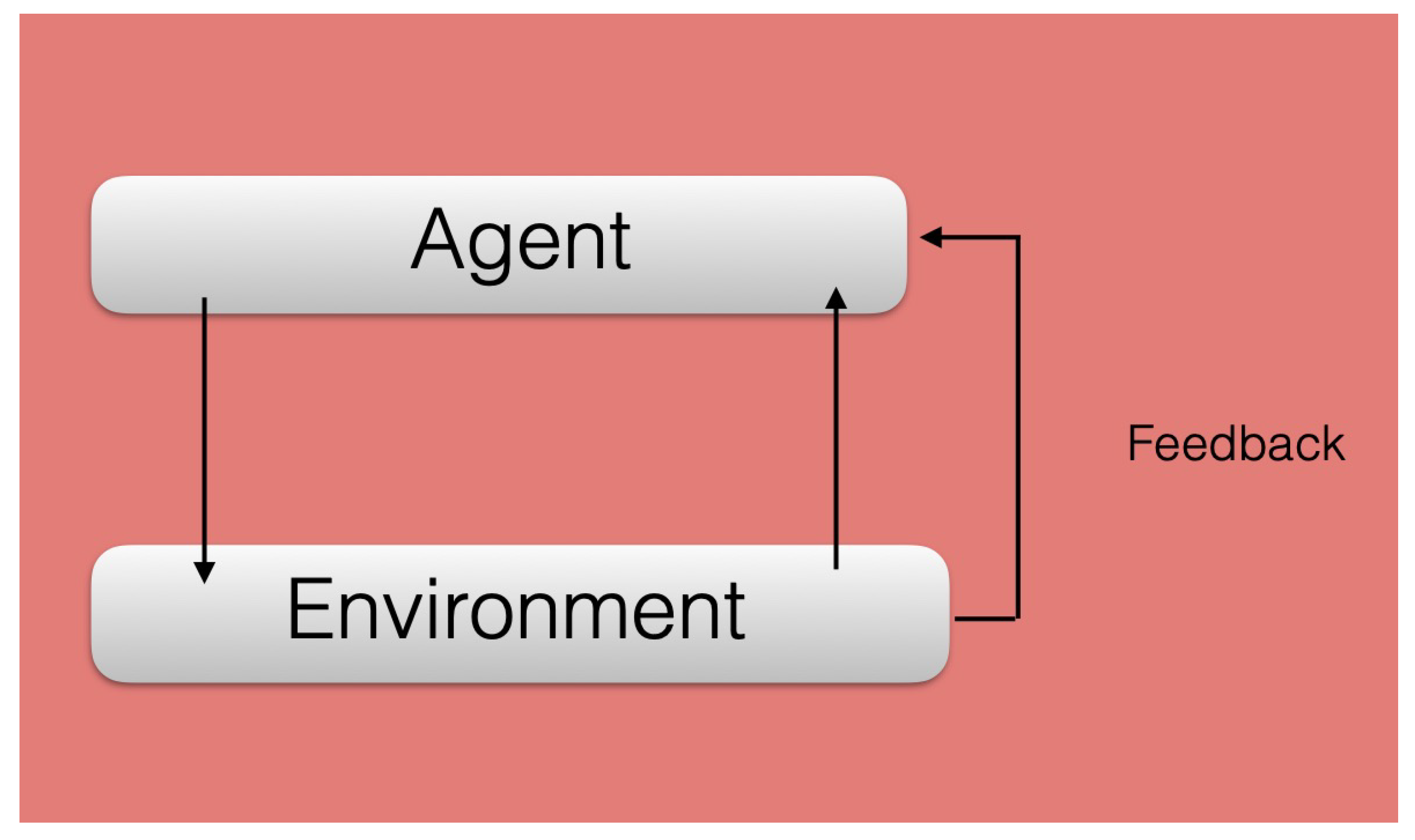
2. Quantum Reinforcement Learning
3. Measurement-Based Adaptation Protocol with Quantum Reinforcement Learning Implemented with Quantum Photonics
3.1. Theoretical Proposal
3.2. Implementation with Quantum Photonics
4. Further Developments of Quantum Reinforcement Learning with Quantum Photonics
5. Conclusions
Funding
Conflicts of Interest
References
- Russell, S.; Norvig, P. Artificial Intelligence: A Modern Approach; Pearson: London, UK, 2009. [Google Scholar]
- Wittek, P. Quantum Machine Learning; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Schuld, M.; Petruccione, F. Supervised Learning with Quantum Computers; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Schuld, M.; Sinayskiy, I.; Petruccione, F. An introduction to quantum machine learning. Contemp. Phys. 2015, 56, 172. [Google Scholar] [CrossRef]
- Biamonte, J.; Wittek, P.; Pancotti, N.; Rebentrost, P.; Wiebe, N.; Lloyd, S. Quantum machine learning. Nature 2017, 549, 074001. [Google Scholar] [CrossRef] [PubMed]
- Dunjko, V.; Briegel, H.J. Machine learning & artificial intelligence in the quantum domain: A review of recent progress. Rep. Prog. Phys. 2018, 81, 074001. [Google Scholar] [PubMed]
- Schuld, M.; Sinayskiy, I.; Petruccione, F. The quest for a Quantum Neural Network. Quantum Inf. Process. 2014, 13, 2567. [Google Scholar] [CrossRef]
- Lamata, L. Quantum machine learning and quantum biomimetics: A perspective. Mach. Learn. Sci. Technol. 2020, 1, 033002. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Dong, D.; Chen, C.; Li, H.; Tarn, T.-J. Quantum Reinforcement Learning. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2008, 38, 1207. [Google Scholar] [CrossRef]
- Paparo, G.D.; Dunjko, V.; Makmal, A.; Martin-Delgado, M.A.; Briegel, H.J. Quantum Speedup for Active Learning Agents. Phys. Rev. X 2014, 4, 031002. [Google Scholar] [CrossRef]
- Dunjko, V.; Taylor, J.M.; Briegel, H.J. Quantum-Enhanced Machine Learning. Phys. Rev. Lett. 2016, 117, 130501. [Google Scholar] [CrossRef]
- Lamata, L. Basic protocols in quantum reinforcement learning with superconducting circuits. Sci. Rep. 2017, 7, 1609. [Google Scholar] [CrossRef]
- Cárdenas-López, F.A.; Lamata, L.; Retamal, J.C.; Solano, E. Multiqubit and multilevel quantum reinforcement learning with quantum technologies. PLoS ONE 2018, 13, e0200455. [Google Scholar] [CrossRef]
- Albarrán-Arriagada, F.; Retamal, J.C.; Solano, E.; Lamata, L. Measurement-based adaptation protocol with quantum reinforcement learning. Phys. Rev. A 2018, 98, 042315. [Google Scholar] [CrossRef]
- Yu, S.; Albarrán-Arriagada, F.; Retamal, J.C.; Wang, Y.-T.; Liu, W.; Ke, Z.-J.; Meng, Y.; Li, Z.-P.; Tang, J.-S.; Solano, E.; et al. Reconstruction of a Photonic Qubit State with Reinforcement Learning. Adv. Quantum Technol. 2019, 2, 1800074. [Google Scholar] [CrossRef]
- Albarrán-Arriagada, F.; Retamal, J.C.; Solano, E.; Lamata, L. Reinforcement learning for semi-autonomous approximate quantum eigensolver. Mach. Learn. Sci. Technol. 2020, 1, 015002. [Google Scholar] [CrossRef]
- Olivares-Sánchez, J.; Casanova, J.; Solano, E.; Lamata, L. Measurement-Based Adaptation Protocol with Quantum Reinforcement Learning in a Rigetti Quantum Computer. Quantum Rep. 2020, 2, 293–304. [Google Scholar] [CrossRef]
- Melnikov, A.A.; Nautrup, H.P.; Krenn, M.; Dunjko, V.; Tiersch, M.; Zeilinger, A.; Briegel, H.J. Active learning machine learns to create new quantum experiments. Proc. Natl. Acad. Sci. USA 2018, 115, 1221. [Google Scholar] [CrossRef]
- Flamini, F.; Hamann, A.; Jerbi, S.; Trenkwalder, L.M.; Nautrup, H.P.; Briegel, H.J. Photonic architecture for reinforcement learning. New J. Phys. 2020, 22, 045002. [Google Scholar] [CrossRef]
- Fösel, T.; Tighineanu, P.; Weiss, T.; Marquardt, F. Reinforcement Learning with Neural Networks for Quantum Feedback. Phys. Rev. X 2018, 8, 031084. [Google Scholar] [CrossRef]
- Bukov, M. Reinforcement learning for autonomous preparation of Floquet-engineered states: Inverting the quantum Kapitza oscillator. Phys. Rev. B 2018, 98, 224305. [Google Scholar] [CrossRef]
- Bukov, M.; Day, A.G.R.; Sels, D.; Weinberg, P.; Polkovnikov, A.; Mehta, P. Reinforcement Learning in Different Phases of Quantum Control. Phys. Rev. X 2018, 8, 031086. [Google Scholar] [CrossRef]
- Melnikov, A.A.; Sekatski, P.; Sangouard, N. Setting up experimental Bell test with reinforcement learning. arXiv 2020, arXiv:2005.01697. [Google Scholar]
- Mackeprang, J.; Dasari, D.B.R.; Wrachtrup, J. A Reinforcement Learning approach for Quantum State Engineering. arXiv 2019, arXiv:1908.05981. [Google Scholar]
- Schäfer, F.; Kloc, M.; Bruder, C.; Lörch, N. A differentiable programming method for quantum control. arXiv 2002, arXiv:2002.08376. [Google Scholar] [CrossRef]
- Sgroi, P.; Palma, G.M.; Paternostro, M. Reinforcement learning approach to non-equilibrium quantum thermodynamics. arXiv 2020, arXiv:2004.07770. [Google Scholar]
- Wallnöfer, J.; Melnikov, A.A.; Dür, W.; Briegel, H.J. Machine learning for long-distance quantum communication. arXiv 2019, arXiv:1904.10797. [Google Scholar]
- Zhang, X.-M.; Wei, Z.; Asad, R.; Yang, X.-C.; Wang, X. When does reinforcement learning stand out in quantum control? A comparative study on state preparation. npj Quantum Inf. 2019, 5, 85. [Google Scholar] [CrossRef]
- Xu, H.; Li, J.; Liu, L.; Wang, Y.; Yuan, H.; Wang, X. Generalizable control for quantum parameter estimation through reinforcement learning. npj Quantum Inf. 2019, 5, 82. [Google Scholar] [CrossRef]
- Sweke, R.; Kesselring, M.S.; van Nieuwenburg, E.P.L.; Eisert, J. Reinforcement Learning Decoders for Fault-Tolerant Quantum Computation. arXiv 2018, arXiv:1810.07207. [Google Scholar] [CrossRef]
- Andreasson, P.; Johansson, J.; Liljestr, S.; Granath, M. Quantum error correction for the toric code using deep reinforcement learning. Quantum 2019, 3, 183. [Google Scholar] [CrossRef]
- Nautrup, H.P.; Delfosse, N.; Dunjko, V.; Briegel, H.J.; Friis, N. Optimizing Quantum Error Correction Codes with Reinforcement Learning. Quantum 2019, 3, 215. [Google Scholar] [CrossRef]
- Fitzek, D.; Eliasson, M.; Kockum, A.F.; Granath, M. Deep Q-learning decoder for depolarizing noise on the toric code. Phys. Rev. Res. 2020, 2, 023230. [Google Scholar] [CrossRef]
- Fösel, T.; Krastanov, S.; Marquardt, F.; Jiang, L. Efficient cavity control with SNAP gates. arXiv 2020, arXiv:2004.14256. [Google Scholar]
- McKiernan, K.A.; Davis, E.; Alam, M.S.; Rigetti, C. Automated quantum programming via reinforcement learning for combinatorial optimization. arXiv 2019, arXiv:1908.08054. [Google Scholar]
- Garcia-Saez, A.; Riu, J. Quantum Observables for continuous control of the Quantum Approximate Optimization Algorithm via Reinforcement Learning. arXiv 2019, arXiv:1911.09682. [Google Scholar]
- Khairy, K.; Shaydulin, R.; Cincio, L.; Alexeev, Y.; Balaprakash, P. Learning to Optimize Variational Quantum Circuits to Solve Combinatorial Problems. arXiv 2019, arXiv:1911.11071. [Google Scholar] [CrossRef]
- Yao, J.; Bukov, M.; Lin, L. Policy Gradient based Quantum Approximate Optimization Algorithm. arXiv 2020, arXiv:2002.01068. [Google Scholar]
- Flamini, F.; Spagnolo, N.; Sciarrino, F. Photonic quantum information processing: A review. Rep. Prog. Phys. 2019, 82, 016001. [Google Scholar] [CrossRef]
- Cai, X.-D.; Wu, D.; Su, Z.-E.; Chen, M.-C.; Wang, X.-L.; Li, L.; Liu, N.-L.; Lu, C.-Y.; Pan, J.-W. Entanglement-Based Machine Learning on a Quantum Computer. Phys. Rev. Lett. 2015, 114, 110504. [Google Scholar] [CrossRef]
- Briegel, H.J.; De las Cuevas, G. Projective simulation for artificial intelligence. Sci. Rep. 2012, 2, 1. [Google Scholar] [CrossRef]
Biography
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lamata, L. Quantum Reinforcement Learning with Quantum Photonics. Photonics 2021, 8, 33. https://doi.org/10.3390/photonics8020033
Lamata L. Quantum Reinforcement Learning with Quantum Photonics. Photonics. 2021; 8(2):33. https://doi.org/10.3390/photonics8020033
Chicago/Turabian StyleLamata, Lucas. 2021. "Quantum Reinforcement Learning with Quantum Photonics" Photonics 8, no. 2: 33. https://doi.org/10.3390/photonics8020033
APA StyleLamata, L. (2021). Quantum Reinforcement Learning with Quantum Photonics. Photonics, 8(2), 33. https://doi.org/10.3390/photonics8020033




