Dual-Band, Polarization-Insensitive, Ultrathin and Flexible Metamaterial Absorber Based on High-Order Magnetic Resonance
Abstract
:1. Introduction
2. Metamaterial Structure and Methods
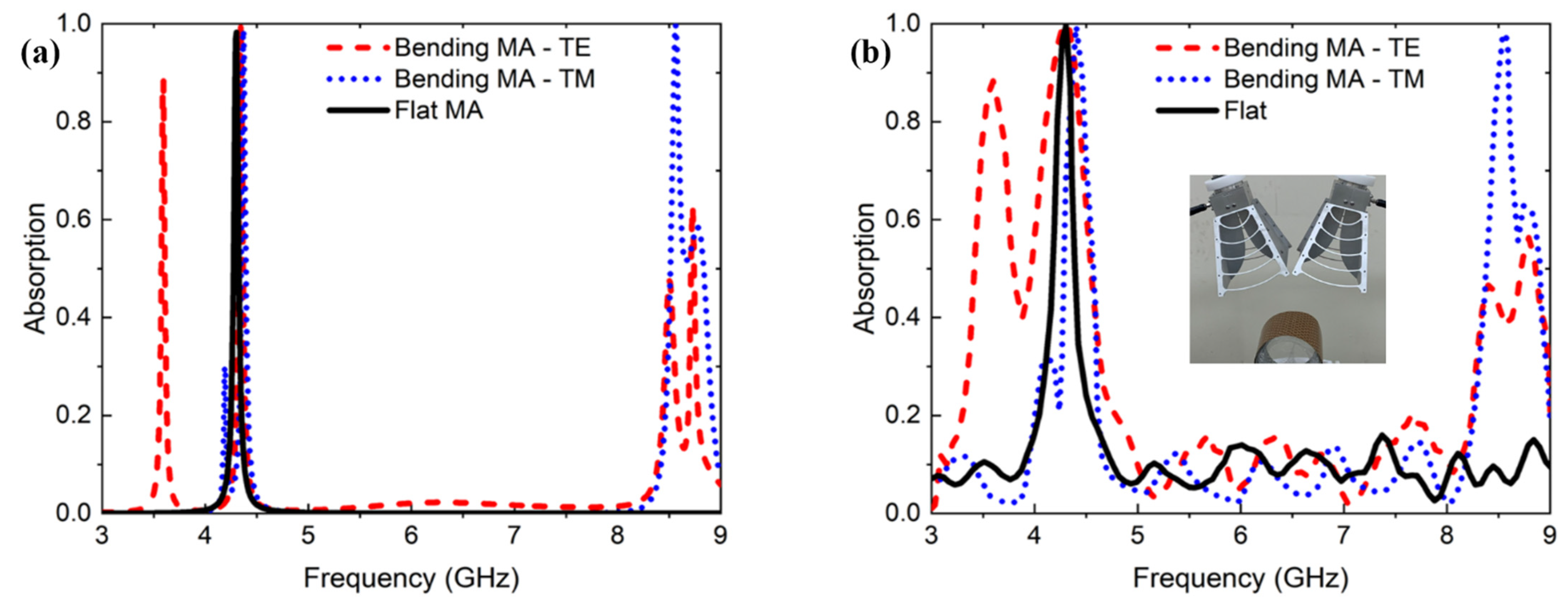
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sreekanth, K.V.; Alapan, Y.; ElKabbash, M.; Ilker, E.; Hinczewski, M.; Gurkan, U.A.; Luca, A.D.; Strangi, G. Extreme sensitivity biosensing platform based on hyperbolic metamaterials. Nat. Mater. 2016, 15, 621–627. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Palermo, G.; Sreekanth, K.V.; Maccaferri, N.; Lio, G.E.; Nicoletta, G.; Angelis, F.D.; Hinczewski, M.; Strangi, G. Hyperbolic dispersion metasurfaces for molecular biosensing. Nanophotonics 2021, 10, 295–314. [Google Scholar] [CrossRef]
- Ma, L.; Chen, D.; Zheng, W.; Li, J.; Zahra, S.; Liu, Y.; Zhou, Y.; Huang, Y.; Wen, G. Advanced electromagnetic metamaterials for temperature sensing applications. Front. Phys. 2021, 9, 195. [Google Scholar] [CrossRef]
- Liao, Y.L.; Zhao, Y. Ultra-narrowband dielectric metamaterial absorber with ultra-sparse nanowire grids for sensing applications. Sci. Rep. 2020, 10, 1–7. [Google Scholar]
- Montoya, J.A.; Tian, Z.B.; Krishna, S.; Padilla, W.J. Ultra-thin infrared metamaterial detector for multicolor imaging applications. Opt. Express 2017, 25, 23343–23355. [Google Scholar] [CrossRef]
- Haxha, S.; AbdelMalek, F.; Ouerghi, F.; Charlton, M.D.B.; Aggoun, A.; Fang, X.J.S.R. Metamaterial superlenses operating at visible wavelength for imaging applications. Sci. Rep. 2018, 8, 1–15. [Google Scholar]
- Karaaslan, M.; Bağmancı, M.; Ünal, E.; Akgol, O.; Sabah, C. Microwave energy harvesting based on metamaterial absorbers with multi-layered square split rings for wireless communications. Opt. Commun. 2017, 392, 31–38. [Google Scholar] [CrossRef]
- Alkurt, F.O.; Altintas, O.; Ozakturk, M.; Karaaslan, M.; Akgol, O.; Unal, E.; Sabah, C. Enhancement of image quality by using metamaterial inspired energy harvester. Phys. Lett. A 2020, 384, 126041. [Google Scholar] [CrossRef]
- Landy, N.I.; Sajuyigbe, S.; Mock, J.J.; Smith, D.R.; Padilla, W.J. Perfect metamaterial absorber. Phys. Rev. Lett. 2008, 100, 207402. [Google Scholar] [CrossRef]
- Yoo, Y.J.; Zheng, H.Y.; Kim, Y.J.; Rhee, J.Y.; Kang, J.H.; Kim, K.W.; Cheong, H.; Kim, Y.H.; Lee, Y. Flexible and elastic metamaterial absorber for low frequency, based on small-size unit cell. Appl. Phys. Lett. 2014, 105, 041902. [Google Scholar] [CrossRef]
- Khuyen, B.X.; Tung, B.S.; Kim, Y.J.; Hwang, J.S.; Kim, K.W.; Rhee, J.Y.; Lam, V.D.; Kim, Y.H.; Lee, Y. Ultra-subwavelength thickness for dual/triple-band metamaterial absorber at very low frequency. Sci. Rep. 2018, 8, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Lio, G.E.; Ferraro, A.; Giocondo, M.; Caputo, R.; De Luca, A. Color gamut behavior in epsilon near-zero nanocavities during propagation of gap surface plasmons. Adv. Opt. Mater. 2020, 8, 2000487. [Google Scholar] [CrossRef]
- Zhong, M. Design and measurement of a narrow band metamaterial absorber in terahertz range. Opt. Mater. 2020, 100, 109712. [Google Scholar] [CrossRef]
- Cheng, Y.; Yang, H.; Cheng, Z.; Wu, N. Perfect metamaterial absorber based on a split-ring-cross resonator. Appl. Phys. A 2011, 102, 99–103. [Google Scholar] [CrossRef]
- Assimonis, S.D.; Fusco, V. Polarization insensitive, wide-angle, ultra-wideband, flexible, resistively loaded, electromagnetic metamaterial absorber using conventional inkjet-printing technology. Sci. Rep. 2019, 9, 1–15. [Google Scholar]
- Elsharabasy, A.; Bakr, M.; Deen, M.J. Wide-angle, wide-band, polarization-insensitive metamaterial absorber for thermal energy harvesting. Sci. Rep. 2020, 10, 1–10. [Google Scholar] [CrossRef]
- Liu, J.; Ma, W.Z.; Chen, W.; Yu, G.X.; Chen, Y.S.; Deng, X.C.; Yang, C.F. Numerical analysis of an ultra-wideband metamaterial absorber with high absorptivity from visible light to near-infrared. Opt. Express 2020, 28, 23748–23760. [Google Scholar] [CrossRef]
- Liu, H.; Wang, Z.H.; Li, L.; Fan, Y.X.; Tao, Z.Y. Vanadium dioxide-assisted broadband tunable terahertz metamaterial absorber. Sci. Rep. 2019, 9, 1–10. [Google Scholar]
- Hu, F.; Wang, L.; Quan, B.; Xu, X.; Li, Z.; Wu, Z.; Pan, X. Design of a polarization insensitive multiband terahertz metamaterial absorber. J. Phys. D Appl. Phys. 2013, 46, 195103. [Google Scholar] [CrossRef]
- Wang, W.; Wang, K.; Yang, Z.; Liu, J. Experimental demonstration of an ultra-flexible metamaterial absorber and its application in sensing. J. Phys. D Appl. Phys. 2017, 50, 135108. [Google Scholar] [CrossRef]
- Sadeqi, A.; Nejad, H.R.; Sonkusale, S. Low-cost metamaterial-on-paper chemical sensor. Opt. Express 2017, 25, 16092–16100. [Google Scholar] [CrossRef] [PubMed]
- Tasolamprou, A.C.; Mentzaki, D.; Viskadourakis, Z.; Economou, E.N.; Kafesaki, M.; Kenanakis, G. Flexible 3D printed conductive metamaterial units for electromagnetic applications in microwaves. Materials 2020, 13, 3879. [Google Scholar] [CrossRef]
- Borah, D.; Bhattacharyya, N.S. Design, fabrication and characterization of flexible and ultrathin microwave metamaterial absorber. In Proceedings of the 2017 International Conference on Innovations in Electronics, Signal Processing and Communication (IESC), Shillong, India, 6–7 April 2017; pp. 190–193. [Google Scholar]
- Amiri, M.; Tofigh, F.; Shariati, N.; Lipman, J.; Abolhasan, M. Wide-angle metamaterial absorber with highly insensitive absorption for TE and TM modes. Sci. Rep. 2020, 10, 1–13. [Google Scholar] [CrossRef]
- Song, Z.; Wang, K.; Li, J.; Liu, Q.H. Broadband tunable terahertz absorber based on vanadium dioxide metamaterials. Opt. Express 2018, 26, 7148–7154. [Google Scholar] [CrossRef]
- Bai, J.; Zhang, S.; Fan, F.; Wang, S.; Sun, X.; Miao, Y.; Chang, S. Tunable broadband THz absorber using vanadium dioxide metamaterials. Opt. Commun. 2019, 452, 292–295. [Google Scholar] [CrossRef]
- Ma, J.; Wang, J.; Hu, Z.D.; Zhang, Z.; Pan, L.; Di Falco, A. High-efficiency and ultrabroadband flexible absorbers based on transversely symmetrical multi-layer structures. AIP Adv. 2019, 9, 115007. [Google Scholar] [CrossRef] [Green Version]
- Yang, D.; Xia, Y. Experimental verification of multi-band metamaterial absorber with double structured layers. Mater. Res. Express 2020, 7, 035801. [Google Scholar] [CrossRef]
- Zhao, L.; Liu, H.; He, Z.; Dong, S. Theoretical design of twelve-band infrared metamaterial perfect absorber by combining the dipole, quadrupole, and octapole plasmon resonance modes of four different ring-strip resonators. Opt. Express 2018, 26, 12838–12851. [Google Scholar] [CrossRef]
- Wang, J.; Lang, T.; Hong, Z.; Xiao, M.; Yu, J. Design and fabrication of a triple-band terahertz metamaterial absorber. Nanomaterials 2021, 11, 1110. [Google Scholar] [CrossRef] [PubMed]
- Jung, S.; Kim, Y.J.; Yoo, Y.J.; Hwang, J.S.; Khuyen, B.X.; Chen, L.Y.; Lee, Y. High-order resonance in a multiband metamaterial absorber. J. Electron. Mater. 2020, 49, 1677–1688. [Google Scholar] [CrossRef]
- Huang, X.; Lu, C.; Rong, C.; Hu, Z.; Liu, M. Multiband ultrathin polarization-insensitive terahertz perfect absorbers with complementary metamaterial and resonator based on high-order electric and magnetic resonances. IEEE Photonics J. 2018, 10, 1–11. [Google Scholar] [CrossRef]
- Khuyen, B.X.; Tung, B.S.; Tung, N.T.; Hien, N.T.; Kim, Y.J.; Chen, L.Y.; Lee, Y.; Linh, P.T.; Lam, V.D. Realization for dual-band high-order perfect absorption, based on metamaterial. J. Phys. D Appl. Phys. 2019, 53, 105502. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Nguyen, T.A.H.; Dinh, T.N.; Bui, X.K.; Bui, S.T.; Nguyen, X.C.; Nguyen, B.T.; Vu, D.L. Multiband metamaterial absorber in a ring structure base on high-order magnetic resonance. Commun. Phys. 2021, 31, 199. [Google Scholar] [CrossRef]
- CST Microwave Studio 2015, License ID: 52856-1. Dassault Systèmes. Available online: http://www.cst.com (accessed on 15 June 2021).
- Chen, X.; Grzegorczyk, T.M.; Wu, B.-I.; Pacheco, J., Jr.; Kong, J.A. Robust method to retrieve the constitutive effective parameters of metamaterials. Phys. Rev. E 2004, 70, 016608. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, T.Q.H.; Nguyen, T.K.T.; Cao, T.N.; Nguyen, H.; Bach, L.G. Numerical study of a broadband metamaterial absorber using a single split circle ring and lumped resistors for X-band applications. AIP Adv. 2020, 10, 035326. [Google Scholar] [CrossRef]
- Zhou, J.; Economon, E.N.; Koschny, T.; Soukoulis, C.M. Unifying approach to left-handed material design. Opt. Lett. 2006, 31, 3620–3622. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.Z.; Cheng, Z.Z.; Mao, X.S.; Gong, R.Z. Ultra-thin multi-band polarization-insensitive microwave metamaterial absorber based on multiple-order responses using a single resonator structure. Materials 2017, 10, 1241. [Google Scholar] [CrossRef] [Green Version]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ha, D.T.; Tung, B.S.; Khuyen, B.X.; Pham, T.S.; Tung, N.T.; Tung, N.H.; Hoa, N.T.; Lam, V.D.; Zheng, H.; Chen, L.; et al. Dual-Band, Polarization-Insensitive, Ultrathin and Flexible Metamaterial Absorber Based on High-Order Magnetic Resonance. Photonics 2021, 8, 574. https://doi.org/10.3390/photonics8120574
Ha DT, Tung BS, Khuyen BX, Pham TS, Tung NT, Tung NH, Hoa NT, Lam VD, Zheng H, Chen L, et al. Dual-Band, Polarization-Insensitive, Ultrathin and Flexible Metamaterial Absorber Based on High-Order Magnetic Resonance. Photonics. 2021; 8(12):574. https://doi.org/10.3390/photonics8120574
Chicago/Turabian StyleHa, Duong Thi, Bui Son Tung, Bui Xuan Khuyen, Thanh Son Pham, Nguyen Thanh Tung, Nguyen Hoang Tung, Nguyen Thi Hoa, Vu Dinh Lam, Haiyu Zheng, Liangyao Chen, and et al. 2021. "Dual-Band, Polarization-Insensitive, Ultrathin and Flexible Metamaterial Absorber Based on High-Order Magnetic Resonance" Photonics 8, no. 12: 574. https://doi.org/10.3390/photonics8120574
APA StyleHa, D. T., Tung, B. S., Khuyen, B. X., Pham, T. S., Tung, N. T., Tung, N. H., Hoa, N. T., Lam, V. D., Zheng, H., Chen, L., & Lee, Y. (2021). Dual-Band, Polarization-Insensitive, Ultrathin and Flexible Metamaterial Absorber Based on High-Order Magnetic Resonance. Photonics, 8(12), 574. https://doi.org/10.3390/photonics8120574








