Improving Multiphoton Microscopy by Combining Spherical Aberration Patterns and Variable Axicons
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Setup
2.2. Imaging Protocol
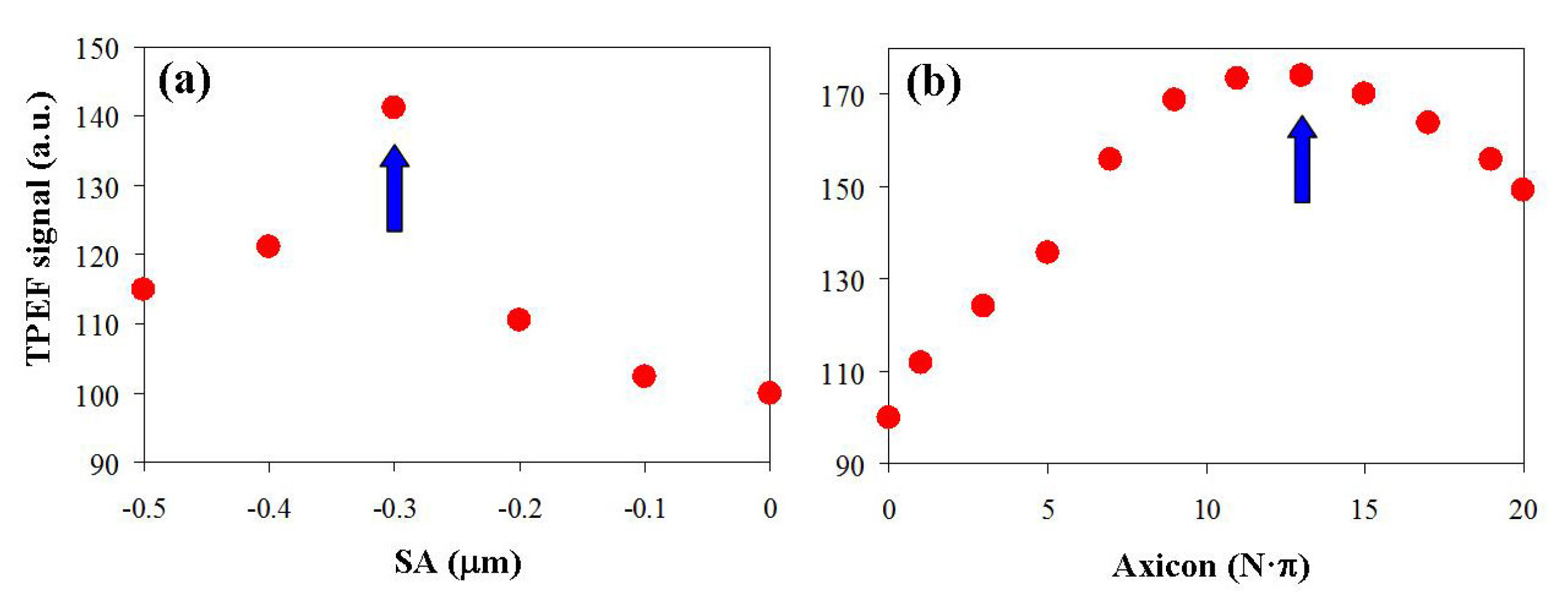
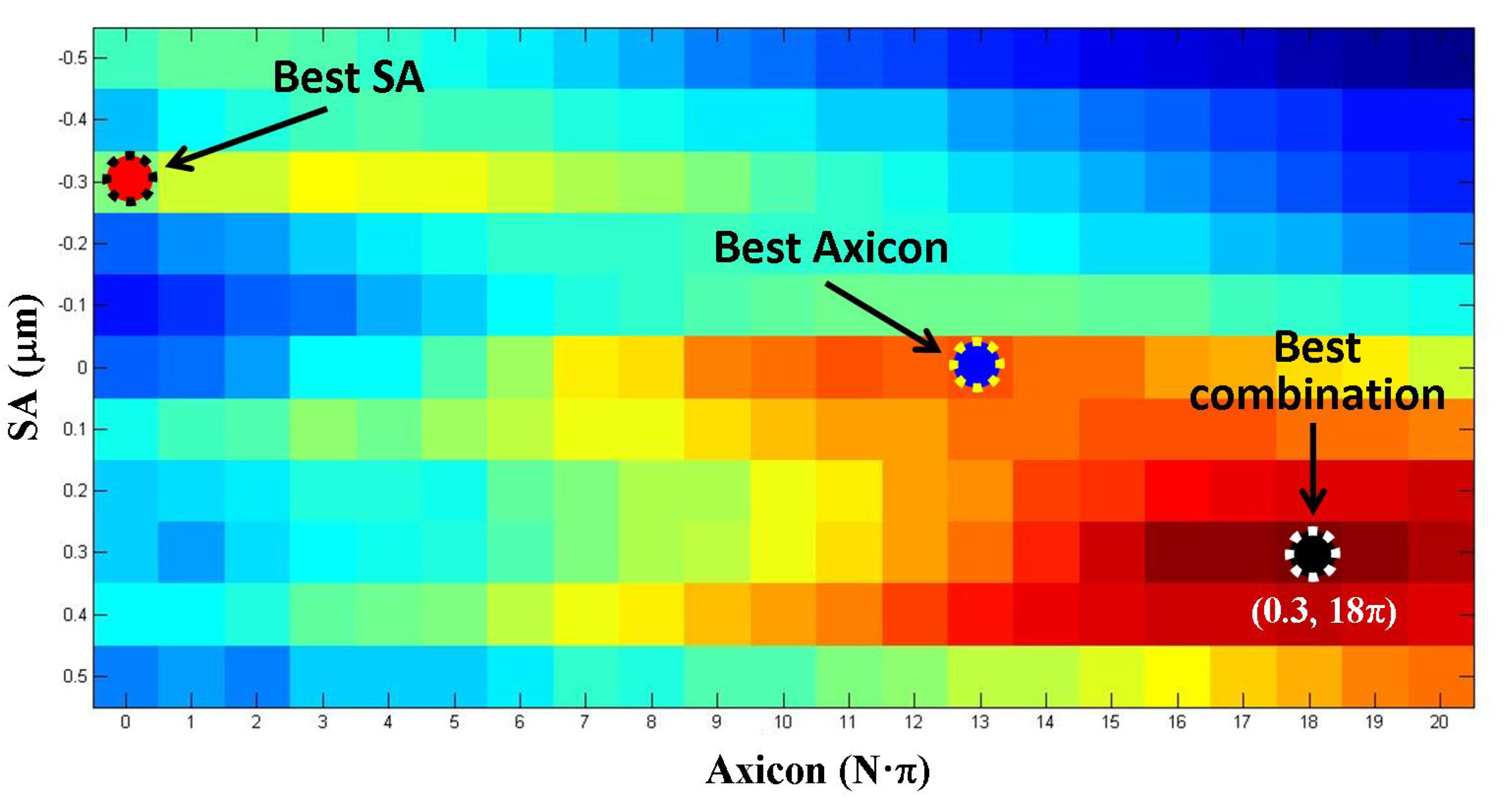
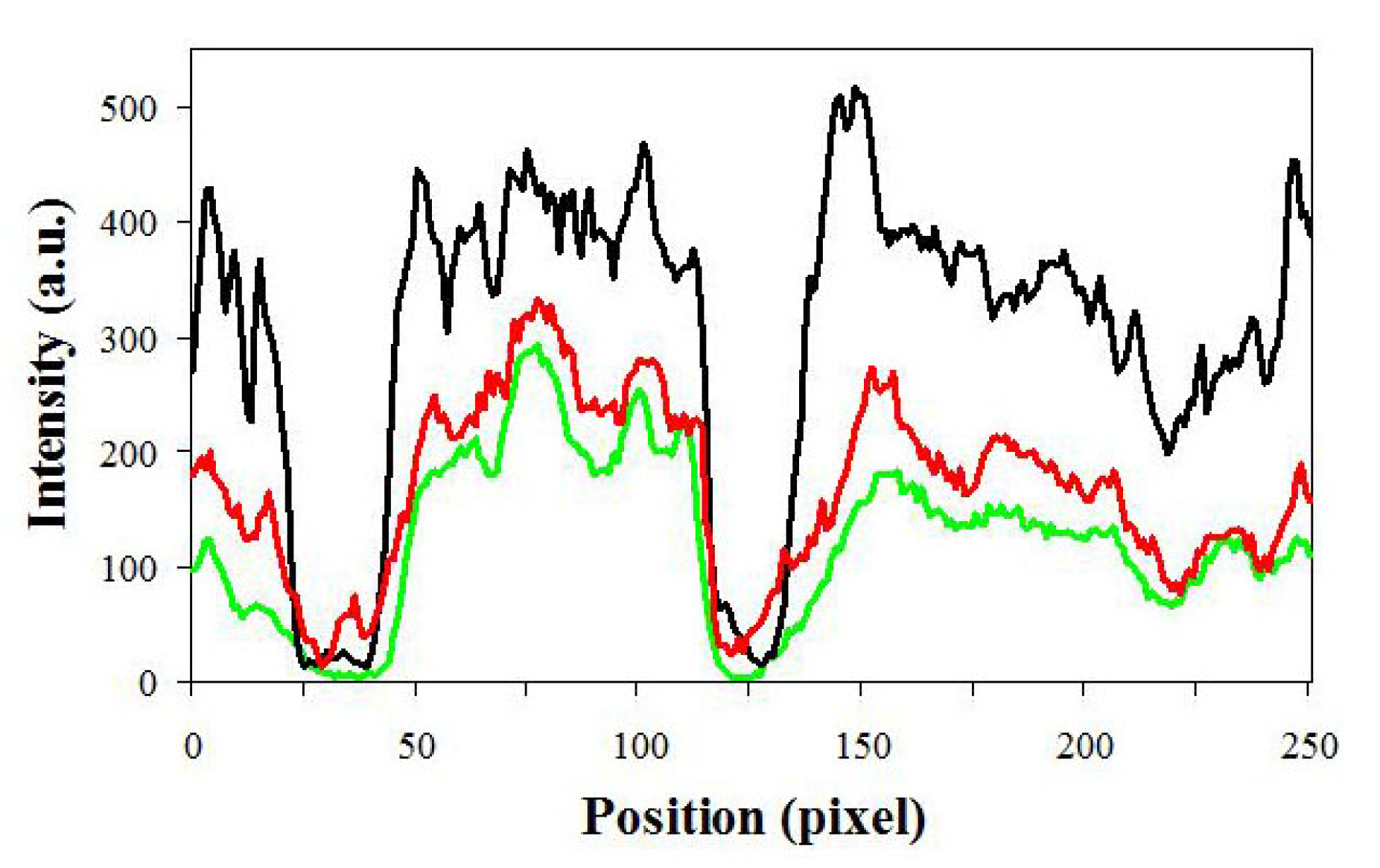
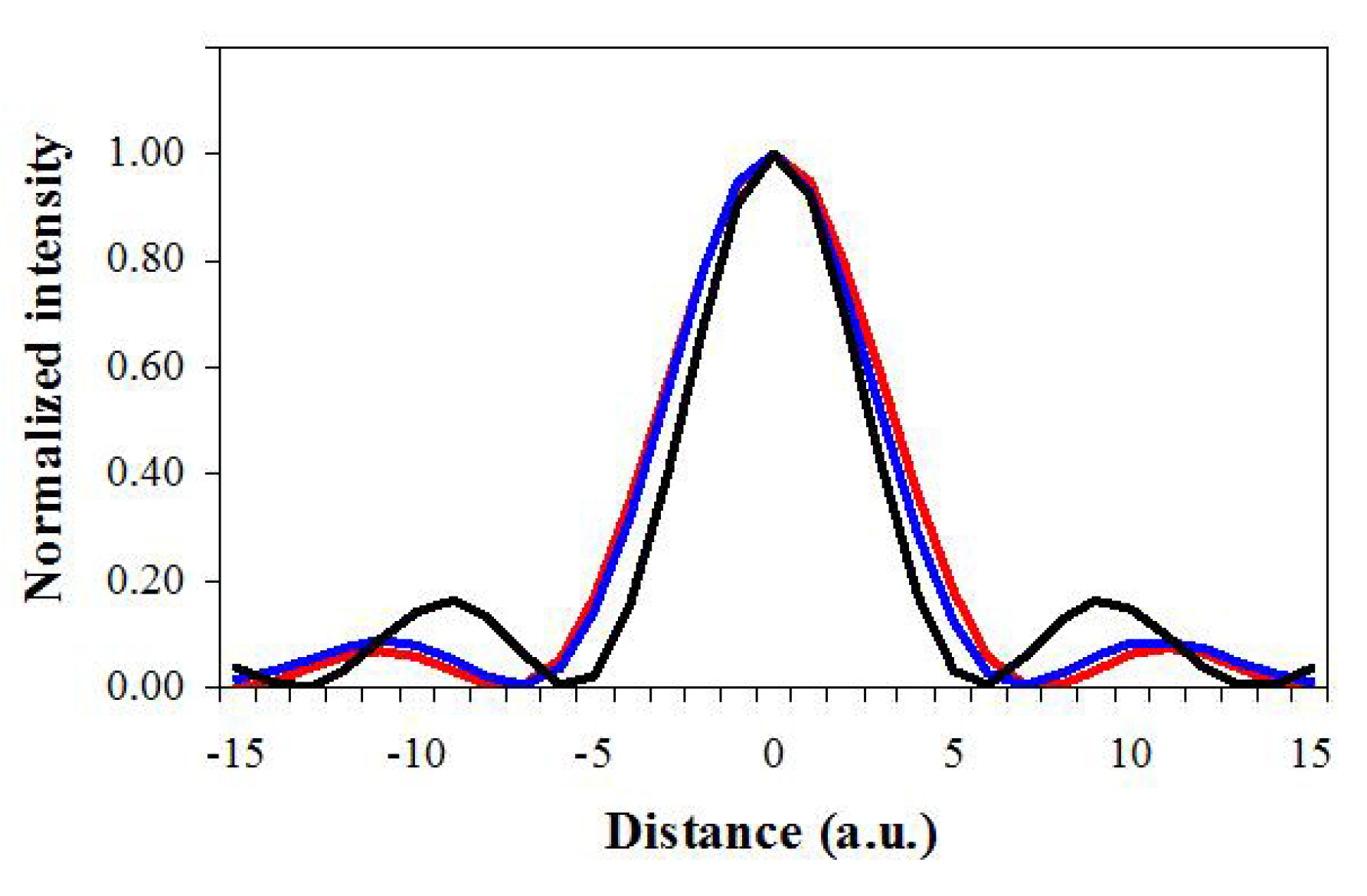
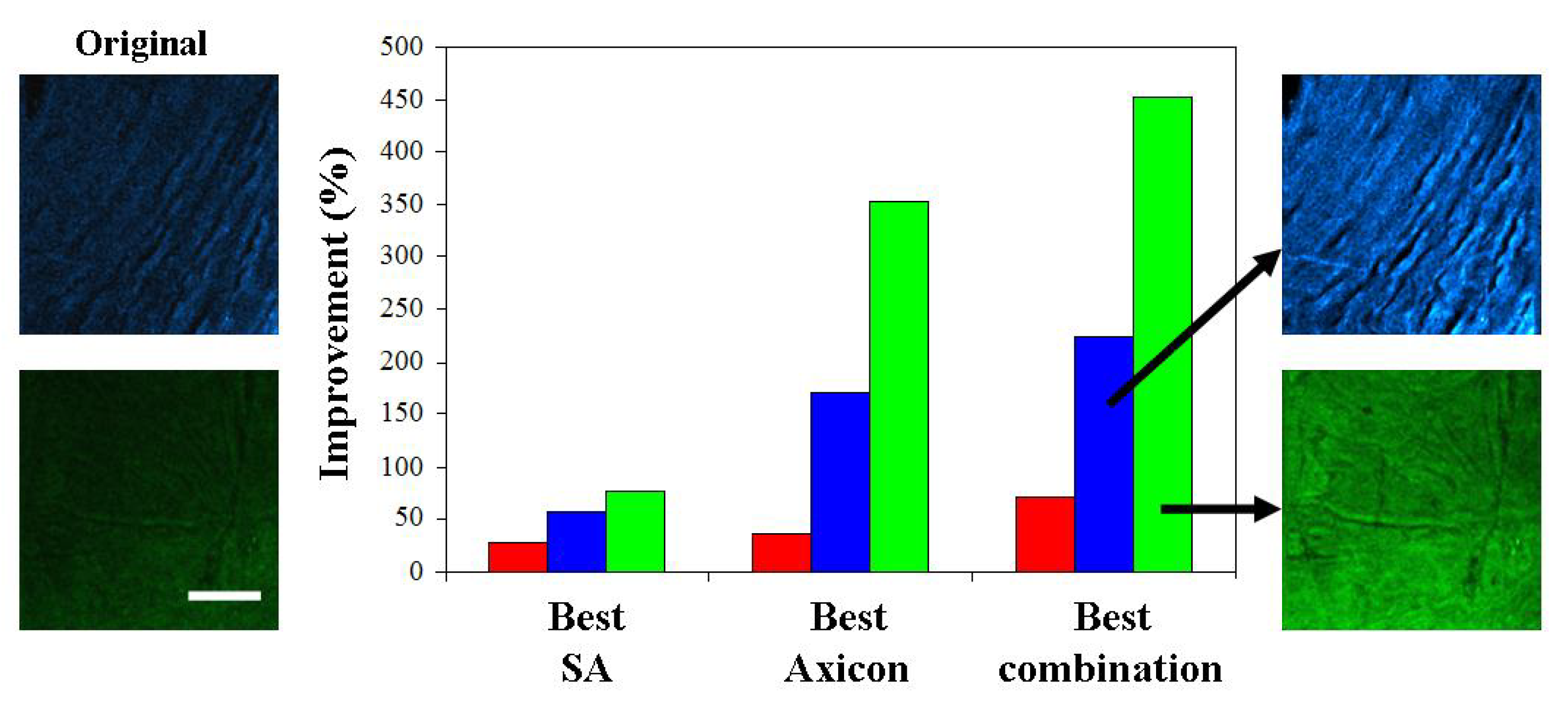
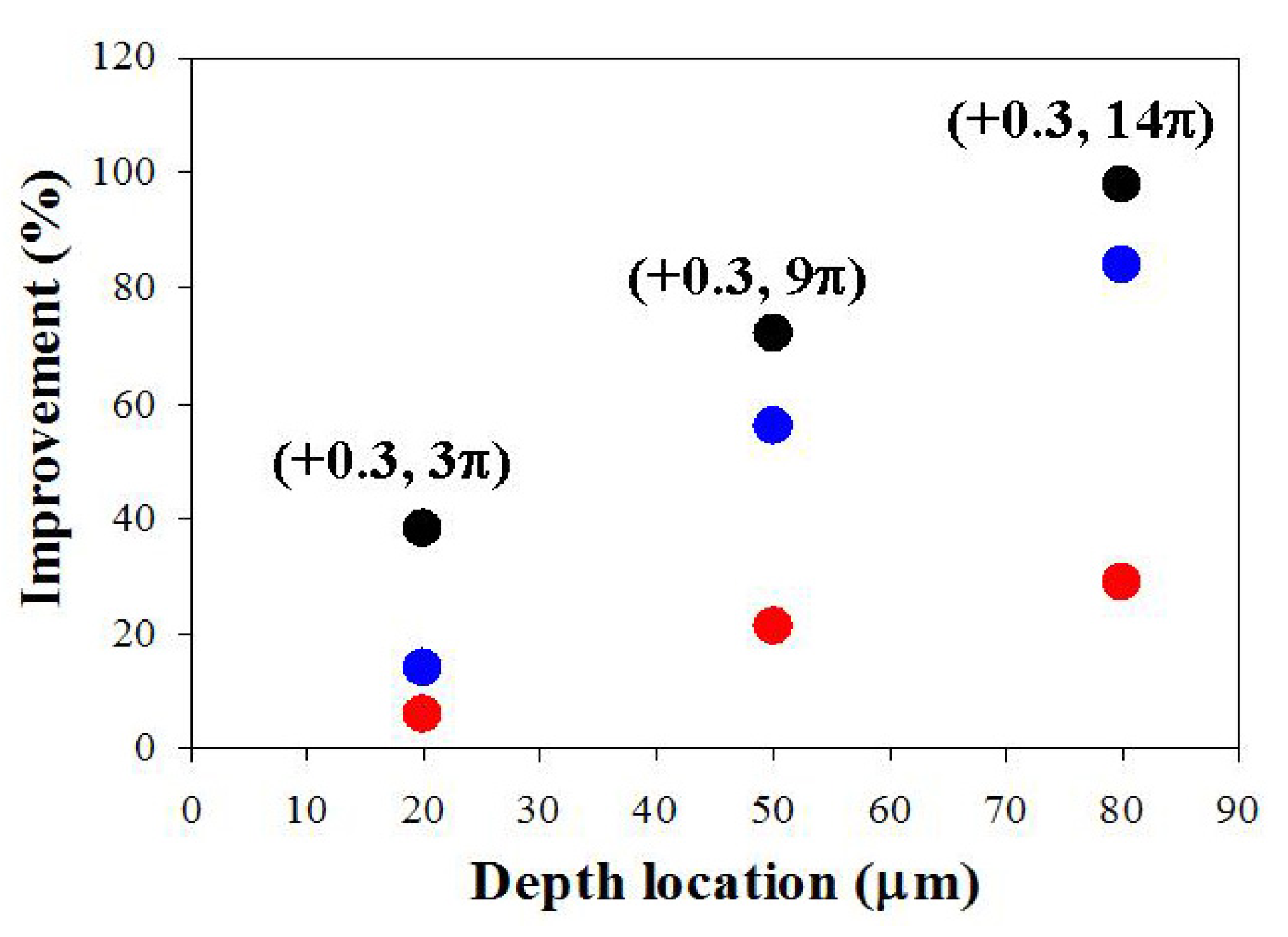
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Denk, W.; Strickler, J.H.; Webb, W.W. Two-photon laser scanning fluorescence microscopy. Science 1990, 248, 73–76. [Google Scholar] [CrossRef]
- Guo, Y.; Ho, P.P.; Savage, H.; Harris, D.; Sacks, P.; Schantz, S.; Liu, F.; Zhadin, N.; Alfano, R.R. Second-harmonic tomography of tissues. Opt. Lett. 1997, 22, 1323–1325. [Google Scholar] [CrossRef]
- Sherman, L.; Ye, J.Y.; Albert, O.; Norris, T.B. Adaptive correction of depth-induced aberrations in multiphoton scanning microscopy using a deformable mirror. J. Microsc. 2002, 206, 65–71. [Google Scholar] [CrossRef]
- Booth, M.J. Adaptive optical microscopy: The ongoing quest for a perfect image. Light Sci. Appl. 2014, 3, e165. [Google Scholar] [CrossRef]
- Débarre, D.; Botcherby, E.J.; Watanabe, T.; Srinivas, S.; Booth, M.J.; Wilson, T. Image-based adaptive optics for two-photon microscopy. Opt. Lett. 2009, 34, 2495–2497. [Google Scholar] [CrossRef]
- Skorsetz, M.; Artal, P.; Bueno, J.M. Performance evaluation of a sensor-less adaptive optics multiphoton microscope. J. Microsc. 2015, 261, 249–258. [Google Scholar] [CrossRef] [PubMed]
- Bueno, J.M.; Skorsetz, M.; Palacios, R.; Gualda, E.J.; Artal, P. Multiphoton imaging microscopy at deeper layers with adaptive optics control of spherical aberration. J. Biomed. Opt. 2014, 19, 011007. [Google Scholar] [CrossRef]
- Lo, W.; Sun, Y.; Lin, S.-J.; Jee, S.-H.; Dong, C.-Y. Spherical aberration correction in multiphoton fluorescence imaging using objective correction collar. J. Biomed. Opt. 2005, 10, 034006. [Google Scholar] [CrossRef]
- Muriello, P.A.; Dunn, K.W. Improving signal levels in intravital multiphoton microscopy using an objective correction collar. Opt. Commun. 2008, 281, 1806–1812. [Google Scholar] [CrossRef] [PubMed]
- Matsumoto, N.; Inoue, T.; Matsumoto, A.; Okazaki, S. Correction of depth-induced spherical aberration for deep observation using two-photon excitation fluorescence microscopy with spatial light modulator. Biomed. Opt. Express 2015, 6, 2575–2587. [Google Scholar] [CrossRef] [PubMed]
- Botcherby, E.J.; Juskaitis, R.; Wilson, T. Scanning two photon fluorescence microscopy with extended depth of field. Opt. Commun. 2006, 268, 253–260. [Google Scholar] [CrossRef]
- Thériault, G.; De Koninck, Y.; McCarthy, N. Extended depth of field microscopy for rapid volumetric two-photon imaging. Opt. Express 2013, 21, 10095–10104. [Google Scholar] [CrossRef]
- Dufour, P.; Piché, M.; De Koninck, Y.; McCarthy, N. Two-photon excitation fluorescence microscopy with a high depth of field using an axicon. Appl. Opt. 2006, 45, 9246–9252. [Google Scholar] [CrossRef] [PubMed]
- Thériault, G.; Cottet, M.; Castonguay, A.; McCarthy, N.; De Koninck, Y. Extended two-photon microscopy in live samples with Bessel beams: Steadier focus, faster volume scans, and simpler stereoscopic imaging. Front. Cell. Neurosci. 2014, 8, 139. [Google Scholar]
- Dumin, J.; Miceli, J.J., Jr.; Eberly, J.H. Diffraction-free beams. Phys. Rev. Lett. 1987, 58, 1499–1501. [Google Scholar]
- Lu, R.; Tanimoto, M.; Koyama, M.; Ji, N. 50 Hz volumetric functional imaging with continuously adjustable depth of focus. Biomed. Opt. Express 2018, 9, 1964–1976. [Google Scholar] [CrossRef]
- Vasara, A.; Turunen, J.; Friberg, A.T. Realization of general nondiffracting beams with computer-generated holograms. J. Opt. Soc. Am. A 1989, 6, 1748–1754. [Google Scholar] [CrossRef]
- Davis, J.A.; Carcole, E.; Cottrell, D.M. Nondiffracting interference patterns generated with programmable spatial light modulators. Appl. Opt. 1996, 35, 599–602. [Google Scholar] [CrossRef]
- Bowman, R.; Muller, N.; Zambrana-Puyalto, X.; Jedrkiewicz, O.; Di Trapani, P.; Padgett, M.J. Efficient generation of Bessel beam arrays by means of an SLM. Eur. Phys. J. Spec. Top. 2011, 199, 159–166. [Google Scholar] [CrossRef]
- Trichili, A.; Mhlanga, T.; Ismail, Y.; Roux, F.; McLaren, M.; Zghal, M.; Forbes, A. Detection of Bessel beams with digital axicons. Opt. Express 2014, 22, 17553–17560. [Google Scholar] [CrossRef]
- Chattrapiban, N.; Rogers, E.; Cofield, D.; Hill, W., III; Roy, R. Generation of nondiffracting Bessel beams by use of a spatial light modulator. Opt. Lett. 2003, 28, 2183–2185. [Google Scholar] [CrossRef] [PubMed]
- García-Martínez, P.; Sánchez-López, M.M.; Davis, J.A.; Cottrell, D.M.; Sand, D.; Moreno, I. Generation of Bessel beam arrays through Dammann gratings. Appl. Opt. 2012, 51, 1375–1381. [Google Scholar] [CrossRef]
- Ventura, M.E.M.; Tapang, G.A.; Saloma, C.A. Robust Bessel beam scanning without mechanical movement. Proc. SPIE 2016, 9896, 989618. [Google Scholar]
- Vuillemin, N.; Mahou, P.; Débarre, D.; Gacoin, T.; Tharaux, P.-L.; Schanne-Klein, M.-C.; Supatto, W.; Beaurepaire, E. Efficient second-harmonic imaging of collagen in histological slides using Bessel beam excitation. Sci. Rep. 2016, 6, 29863. [Google Scholar] [CrossRef] [PubMed]
- Lu, R.; Sun, W.; Liang, Y.; Kerlin, A.; Bierfeld, J.; Seelig, J.D.; Wilson, D.E.; Scholl, B.; Nohar, B.; Tanomoto, M.; et al. Video-rate volumetric functional imaging of the brain at synaptic resolution. Nat. Neurosci. 2017, 20, 620–628. [Google Scholar] [CrossRef] [PubMed]
- Lu, R.; Liang, Y.; Meng, G.; Zhou, P.; Svoboda, K.; Paninski, L.; Ji, N. Rapid mesoscale volumetric imaging of neural activity with synaptic resolution. Nat. Methods 2020, 17, 291–294. [Google Scholar] [CrossRef]
- Bueno, J.M.; Skorsetz, M.; Bonora, S.; Artal, P. Wavefront correction in two-photon microscopy with a multiactuator adaptive lens. Biomed. Opt. Express 2018, 26, 14278–14287. [Google Scholar] [CrossRef]
- Hunter, J.J.; Cookson, C.J.; Kisilak, M.L.; Bueno, J.M.; Campbell, M.C.W. Characterizing image quality in a scanning laser ophthalmoscope with differing pinholes and induced scattered light. J. Opt. Soc. Am. A 2007, 24, 1284–1295. [Google Scholar] [CrossRef][Green Version]
- Fahrbach, F.O.; Gurchenkov, V.; Alessandri, K.; Nassoy, P.; Rohrbach, A. Light-sheet microscopy in thick media using scanned Bessel beams and two-photon fluorescence excitation. Opt. Express 2013, 21, 13824–13839. [Google Scholar] [CrossRef]
- Sheppard, C.J.R.; Castello, M.; Tortarolo, G.; Slenders, E.; Deguchi, T.; Koho, S.V.; Vicidomini, G.; Diaspro, A. Image scanning microscopy with multiphoton excitation or Bessel beam illumination. J. Opt. Soc. Am. A 2020, 37, 1639–1649. [Google Scholar] [CrossRef]
- Wright, A.J.; Burns, D.; Patterson, B.A.; Poland, S.P.; Valentine, G.J.; Girkin, J.M. Exploration of the optimisation algorithms used in the implementation of adaptive optics in confocal and multiphoton microscopy. Microsc. Res. Tech. 2005, 67, 36–44. [Google Scholar] [CrossRef]
- Olivier, N.; Débarre, D.; Beaurepaire, E. Dynamic aberration correction for multiharmonic microscopy. Opt. Lett. 2009, 34, 3145–3147. [Google Scholar] [CrossRef]
- Ávila, F.J.; Gambín, A.; Artal, P.; Bueno, J.M. In vivo two-photon microscopy of the human eye. Sci. Rep. 2019, 9, 10121. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bueno, J.M.; Hernández, G.; Skorsetz, M.; Artal, P. Improving Multiphoton Microscopy by Combining Spherical Aberration Patterns and Variable Axicons. Photonics 2021, 8, 573. https://doi.org/10.3390/photonics8120573
Bueno JM, Hernández G, Skorsetz M, Artal P. Improving Multiphoton Microscopy by Combining Spherical Aberration Patterns and Variable Axicons. Photonics. 2021; 8(12):573. https://doi.org/10.3390/photonics8120573
Chicago/Turabian StyleBueno, Juan M., Geovanni Hernández, Martin Skorsetz, and Pablo Artal. 2021. "Improving Multiphoton Microscopy by Combining Spherical Aberration Patterns and Variable Axicons" Photonics 8, no. 12: 573. https://doi.org/10.3390/photonics8120573
APA StyleBueno, J. M., Hernández, G., Skorsetz, M., & Artal, P. (2021). Improving Multiphoton Microscopy by Combining Spherical Aberration Patterns and Variable Axicons. Photonics, 8(12), 573. https://doi.org/10.3390/photonics8120573




