Maintaining Constant Pulse-Duration in Highly Dispersive Media Using Nonlinear Potentials
Abstract
:1. Introduction
2. Methods and Theory
2.1. Control-Pulse Formulation
2.2. Deviation from Stationary Propagation
3. Results
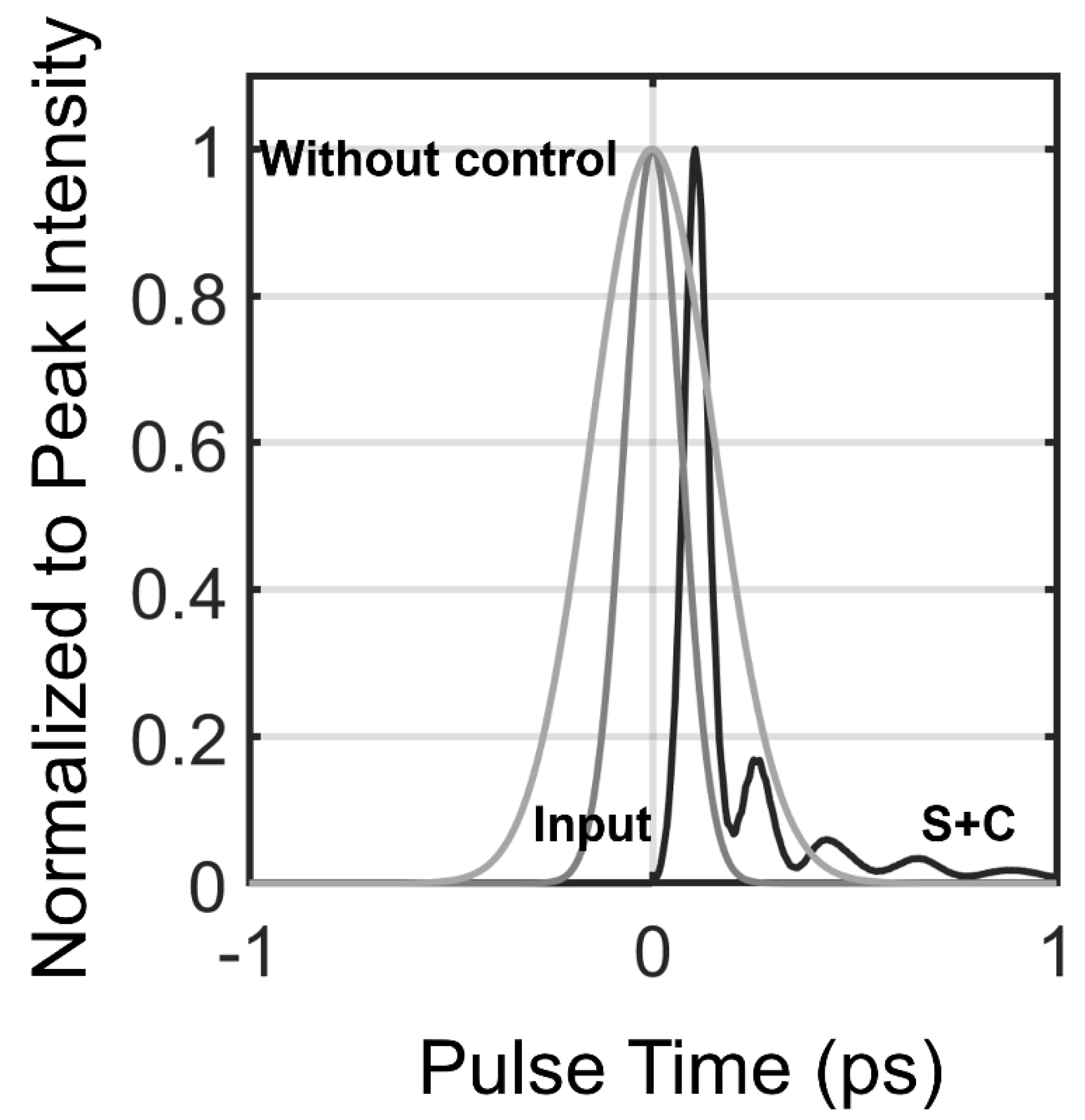
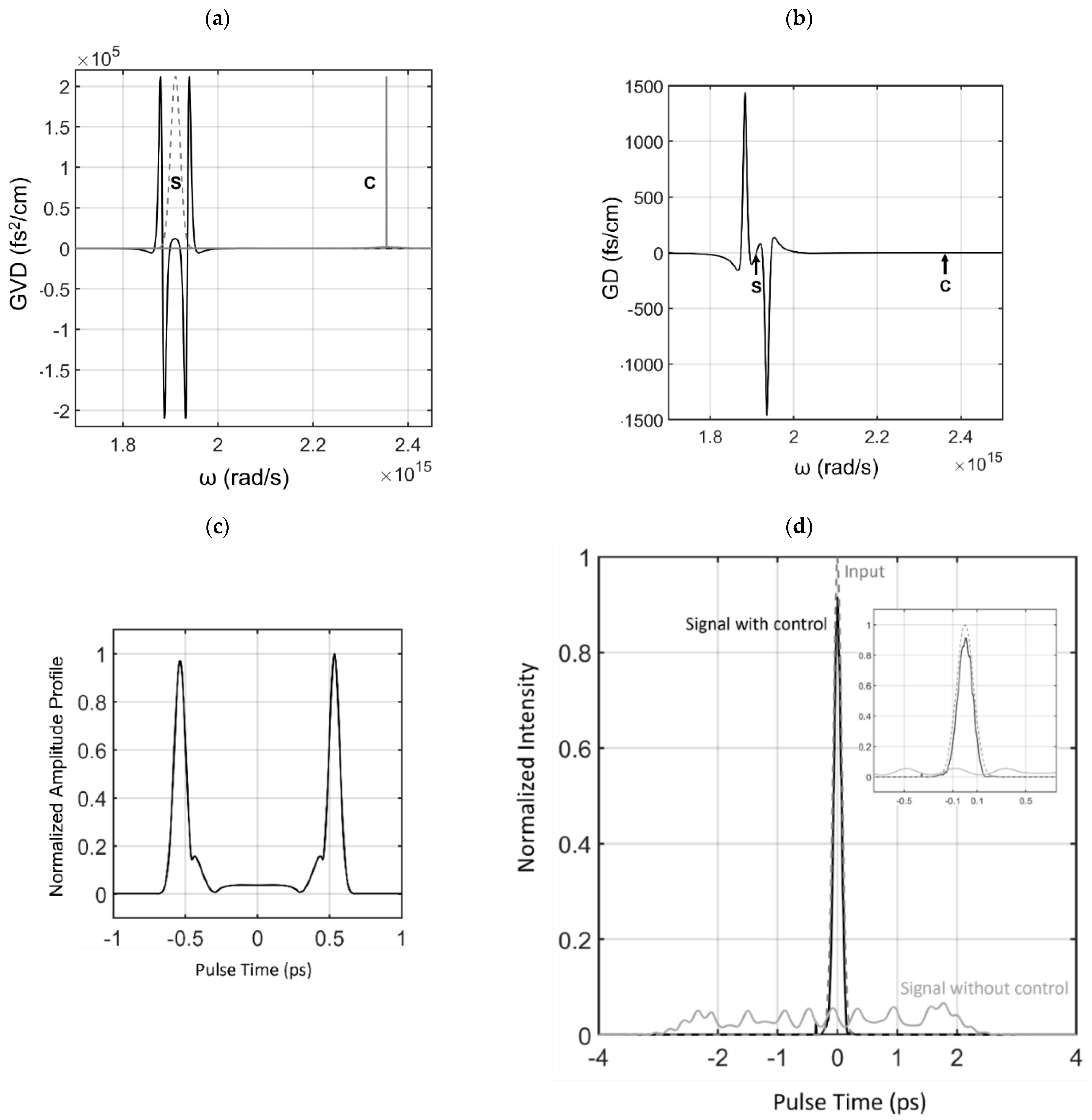
3.1. Example 1: Near Stationary Pulses in Turbulent Dispersive Media
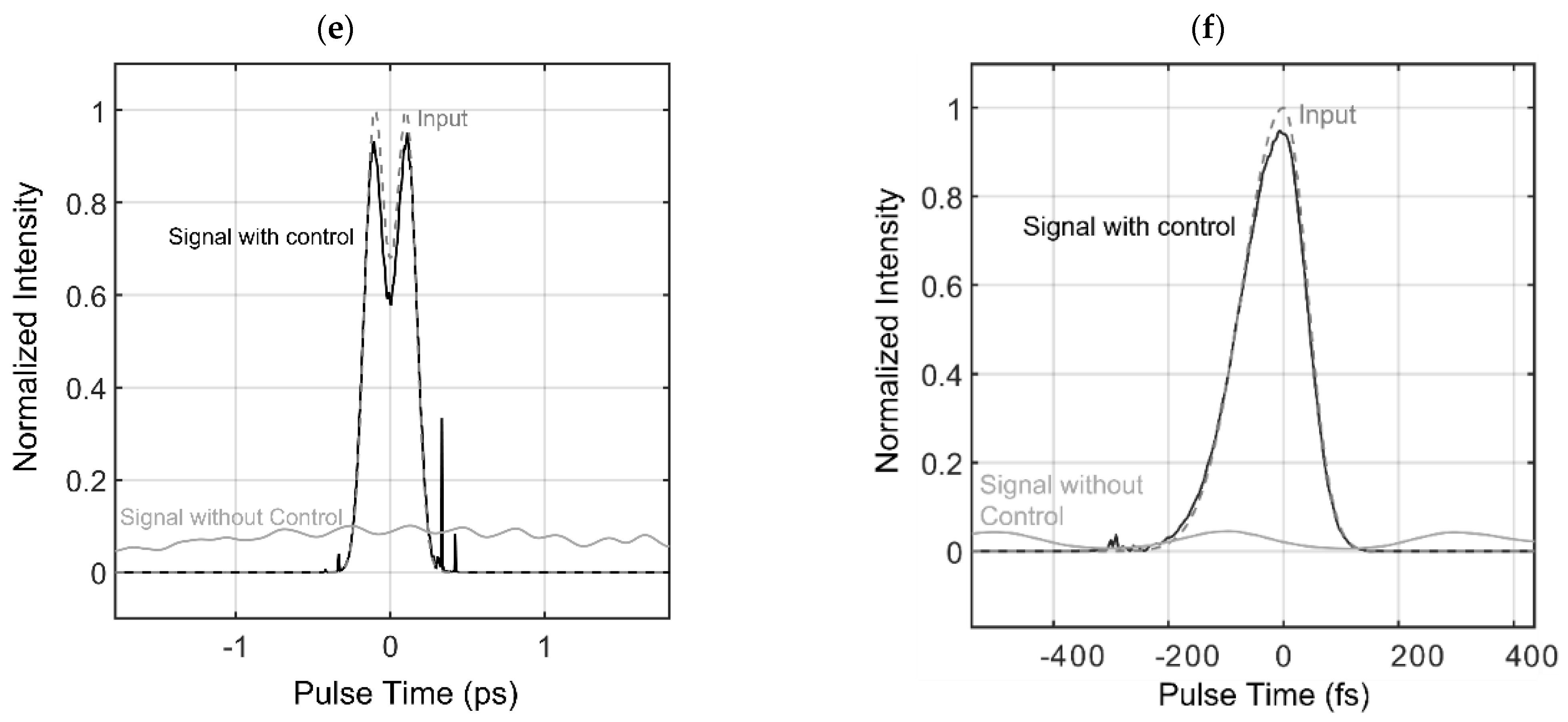
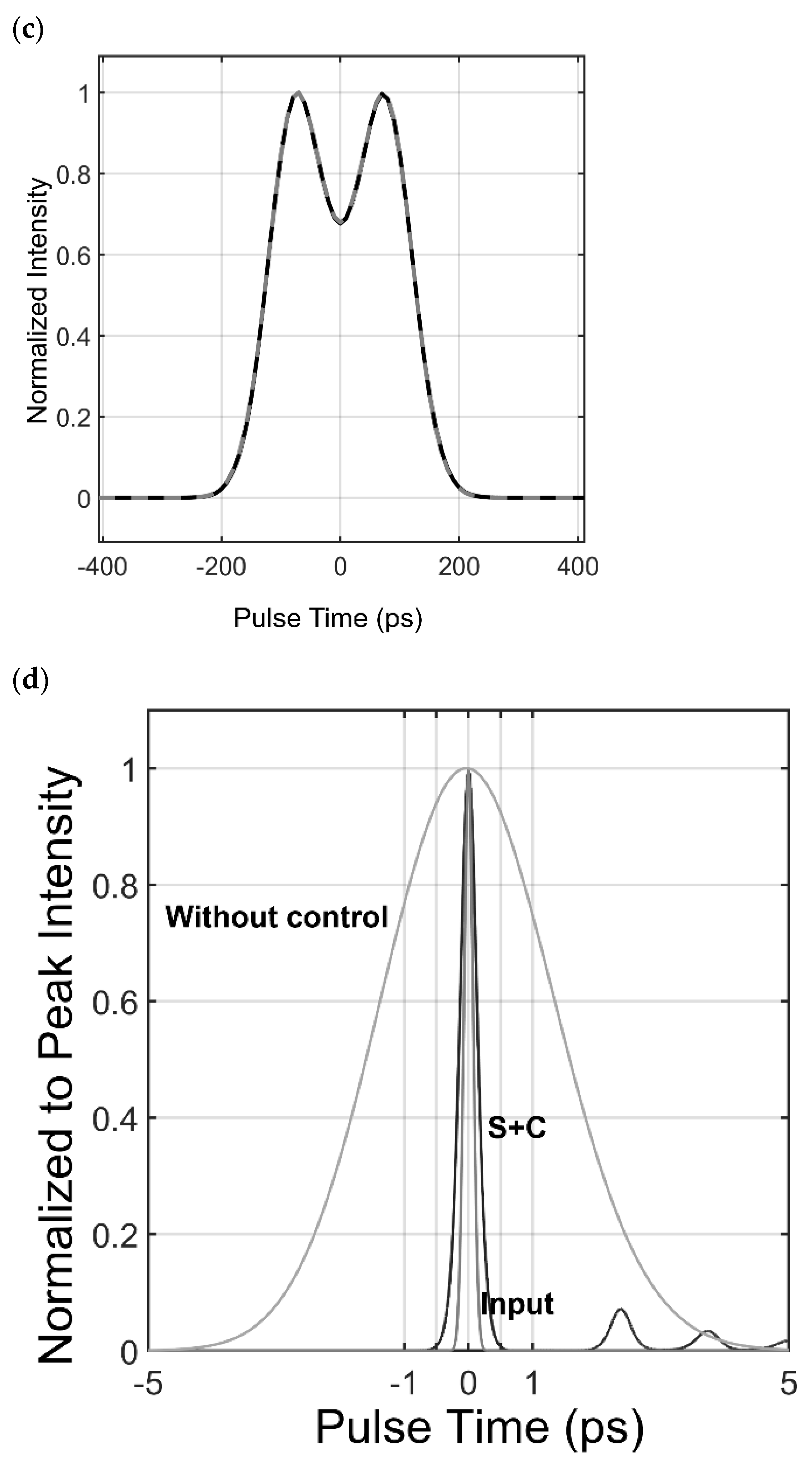
3.2. Example 2: Preventing Dispersive Effects in Practical Telecom Fiber
3.2.1. Asymmetric Dispersion across Signal Pulse
3.2.2. Asymmetric Dispersion across Signal Pulse and Significant Presence of Dispersive Effects for Control Pulse
4. Discussion
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Wavelength Shift of Signal Pulse and Other Effects on Signal Pulse from Waveform Distortion of the Control Pulse
Appendix B. p-Values for Control Pulses
| Figure Label of Illustrated Signal Pulse | Approx. p-Value (1/m) |
|---|---|
| 1d | 0 |
| 1e | 1.2 × 103 |
| 1f | 9.8 × 103 |
| 2b | 0 |
| 2c | 2.0 |
| 2d | 0 |

References
- Hasegawa, A.; Tappert, F. Transmission of stationary nonlinear optical pulses in dispersive dielectric fibers. II. Normal dispersion. Appl. Phys. Lett. 1973, 23, 171–172. [Google Scholar] [CrossRef]
- Grahelj, D.; Igor, P. Solitons in Optics; University of Ljubljana: Ljubljana, Slovenia, 2010. [Google Scholar]
- Dudley, J.M.; Genty, G.; Coen, S. Supercontinuum generation in photonic crystal fiber. Rev. Mod. Phys. 2006, 78, 1135–1184. [Google Scholar] [CrossRef]
- Sahin, E.; Blanco-Redondo, A.; Xing, P.; Ng, D.K.T.; Png, C.E.; Tan, D.T.H.; Eggleton, B.J. Bragg Soliton Compression and Fission on CMOS-Compatible Ultra-Silicon-Rich Nitride. Laser Photonics Rev. 2019, 13, 1900114. [Google Scholar] [CrossRef]
- Eggleton, B.J.; de Sterke, C.M.; Slusher, R.E. Nonlinear pulse propagation in Bragg gratings. J. Opt. Soc. Am. B 1997, 14, 2980–2993. [Google Scholar] [CrossRef]
- Liu, Y.; Fu, S.; Malomed, B.A.; Khoo, I.C.; Zhou, J. Ultrafast optical signal processing with Bragg structures. Appl. Sci. 2017, 7, 556. [Google Scholar] [CrossRef]
- Tucker, R.S.; Riding, J.L. Optical Ring-Resonator Random-Access Memories. J. Light. Technol. 2008, 26, 320–328. [Google Scholar] [CrossRef]
- De Goede, M.; Dijkstra, M.; Obregón, R.; Ramón-Azcón, J.; Martínez, E.; Padilla, L.; Mitjans, F.; Garcia-Blanco, S.M. Al2O3 microring resonators for the detection of a cancer biomarker in undiluted urine. Opt. Express 2019, 27, 18508. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Heideman, R.; Hoekman, M.; Schreuder, E. TriPleX-based integrated optical ring resonators for lab-on-a-chip and environmental detection. IEEE J. Sel. Top. Quantum Electron. 2012, 18, 1583–1596. [Google Scholar] [CrossRef]
- Yebo, N.A.; Taillaert, D.; Roels, J.; Lahem, D.; Debliquy, M.; Van Thourhout, D.; Baets, R. Silicon-on-insulator (SOI) ring resonator-based integrated optical hydrogen sensor. IEEE Photonics Technol. Lett. 2009, 21, 960–962. [Google Scholar] [CrossRef] [Green Version]
- Bogaerts, W.; de Heyn, P.; van Vaerenbergh, T.; de Vos, K.; Kumar Selvaraja, S.; Claes, T.; Dumon, P.; Bienstman, P.; van Thourhout, D.; Baets, R. Silicon microring resonators. Laser Photonics Rev. 2012, 6, 47–73. [Google Scholar] [CrossRef]
- Pittman, T.B.; Franson, J.D. Cyclical quantum memory for photonic qubits. Phys. Rev. A-At. Mol. Opt. Phys. 2002, 66, 4. [Google Scholar] [CrossRef] [Green Version]
- Leung, P.M.; Ralph, T.C. Quantum memory scheme based on optical fibers and cavities. Phys. Rev. A-At. Mol. Opt. Phys. 2006, 74, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Vavulin, D.N.; Sukhorukov, A.A. Effect of loss on single photon parametric amplification. Opt. Commun. 2017, 390, 117–122. [Google Scholar] [CrossRef]
- Bonneau, D.; Mendoza, G.J.; O’Brien, J.L.; Thompson, M.G. Effect of loss on multiplexed single-photon sources. New J. Phys. 2015, 17, 1–15. [Google Scholar] [CrossRef]
- Zhang, J.; Fauchet, P.M.; Painter, O.J.; Agrawal, G.P. Nonlinear optical phenomena in silicon waveguides. Opt. Express 2006, 15, 16604–16644. [Google Scholar]
- Uppu, R.; Wolterink, T.A.W.; Tentrup, T.B.H.; Pinkse, P.W.H. Quantum optics of lossy asymmetric beam splitters. Opt. Express 2016, 24, 16440. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Islam, M.N.; Sucha, G.; Bar-Joseph, I.; Wegener, M.; Gordon, J.P.; Chemla, D.S. Femtosecond distributed soliton spectrum in fibers. J. Opt. Soc. Am. B 2008, 6, 1149. [Google Scholar] [CrossRef]
- Trillo, S.; Wabnitz, S.; Wright, E.M.; Stegeman, G.I. Optical solitary waves induced by cross-phase modulation. Opt. Lett. 1988, 13, 871–873. [Google Scholar] [CrossRef]
- Nishizawa, N.; Goto, T. Characteristics of pulse trapping by use of ultrashort soliton pulses in optical fibers across the zero-dispersion wavelength. Opt. Express 2002, 10, 1151. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.F.; Mussot, A.; Conforti, M.; Zeng, X.L.; Kudlinski, A. Bouncing of a dispersive wave in a solitonic cage. Opt. Lett. 2015, 40, 3320. [Google Scholar] [CrossRef] [PubMed]
- Deng, Z.; Liu, J.; Huang, X.; Zhao, C.; Wang, X. Active control of adiabatic soliton fission by external dispersive wave at optical event horizon. Opt. Express 2017, 25, 28556. [Google Scholar] [CrossRef]
- Wang, S.F.; Mussot, A.; Conforti, M.; Bendahmane, A.; Zeng, X.L.; Kudlinski, A. Optical event horizons from the collision of a soliton and its own dispersive wave. Phys. Rev. A-At. Mol. Opt. Phys. 2015, 92, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Agrawal, G.P. Applications of Nonlinear Fiber Optics; Elsevier: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Zhang, T.R.; Choo, H.R.; Downer, M.C. Phase and group velocity matching for second harmonic generation of femtosecond pulses. Appl. Opt. 1990, 29, 3927. [Google Scholar] [CrossRef] [PubMed]
- Willenberg, B.; Brunner, F.; Phillips, C.R.; Keller, U. High-power picosecond deep-UV source via group velocity matched frequency conversion. Optica 2020, 7, 485. [Google Scholar] [CrossRef]
- Essiambre, R.J.; Mestre, M.A.; Ryf, R.; Gnauck, A.H.; Tkach, R.W.; Chraplyvy, A.R.; Sun, Y.; Jiang, X.; Lingle, R. Experimental observation of inter-modal cross-phase modulation in few-mode fibers. IEEE Photonics Technol. Lett. 2013, 25, 535–538. [Google Scholar] [CrossRef]
- Malomed, B.A.; Mostofi, A.; Chu, P.L. Transformation of a dark soliton into a bright pulse. J. Opt. Soc. Am. B 2000, 17, 507. [Google Scholar] [CrossRef]
- Dong, Y.; Wang, D.; Wang, Y.; Ding, J. Matching group velocity of bright and/or dark solitons via double-dark resonances. Phys. Lett. Sect. A Gen. At. Solid State Phys. 2018, 382, 2006–2012. [Google Scholar] [CrossRef]
- Wu, T.L.; Chao, C.H. A novel ultraflattened dispersion photonic crystal fiber. IEEE Photonics Technol. Lett. 2005, 17, 67–69. [Google Scholar]
- Lee, S.; Ha, W.; Park, J.; Kim, S.; Oh, K. A new design of low-loss and ultra-flat zero dispersion photonic crystal fiber using hollow ring defect. Opt. Commun. 2012, 285, 4082–4087. [Google Scholar] [CrossRef]
- Hilligsøe, K.M.; Andersen, T.V.; Paulsen, H.N.; Nielsen, C.K.; Mølmer, K.; Keiding, S.; Hansen, K.P.; Kristiansen, R.E.; Larsen, J.J. Supercontinuum generation in a photonic crystal fiber with two closely lying zero dispersion wavelengths. OSA Trends Opt. Photonics Ser. 2004, 96 A, 1567–1568. [Google Scholar]
- Westbrook, P.S.; Nicholson, J.W.; Feder, K.S.; Li, Y.; Brown, T. Supercontinuum generation in a fiber grating. Appl. Phys. Lett. 2004, 85, 4600–4602. [Google Scholar] [CrossRef]
- Sollapur, R.; Kartashov, D.; Zürch, M.; Hoffmann, A.; Grigorova, T.; Sauer, G.; Hartung, A.; Schwuchow, A.; Bierlich, J.; Kobelke, J.; et al. Resonance-enhanced multi-octave supercontinuum generation in antiresonant hollow-core fibers. Light Sci. Appl. 2017, 6, e17124. [Google Scholar] [CrossRef] [Green Version]
- Runge, A.F.J.; Qiang, Y.L.; Alexander, T.J.; Rafat, M.Z.; Hudson, D.D.; Blanco-Redondo, A.; de Sterke, C.M. Infinite hierarchy of solitons: Interaction of Kerr nonlinearity with even orders of dispersion. Phys. Rev. Res. 2021, 3, 1–8. [Google Scholar] [CrossRef]
- Michael, L.B.; Ghavami, M.; Kohno, R. Multiple pulse generator for ultra-wideband communication using Hermite polynomial based orthogonal pulses. In Proceedings of the 2002 IEEE Conference on Ultra Wideband Systems and Technologies (IEEE Cat. No.02EX580), Baltimore, MD, USA, 21–23 May 2002; pp. 47–51. [Google Scholar]
- Zia, H. Simulation of white light generation and near light bullets using a novel numerical technique. Commun. Nonlinear Sci. Numer. Simul. 2018, 54, 356–376. [Google Scholar] [CrossRef] [Green Version]
- Steinberg, A.M.; Chiao, R.Y. Dispersionless, highly superluminal propagation in. Phys. Rev. A 1994, 49, 2071–2075. [Google Scholar] [CrossRef] [PubMed]
- Sharping, J.E.; Okawachi, Y.; Gaeta, A.L. Wide bandwidth slow light using a Raman fiber amplifier. Opt. Express 2005, 13, 6092. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, G.P.; Baldeck, P.L.; Alfano, R.R. Optical wave breaking and pulse compression due to cross-phase modulation in optical fibers. Opt. Lett. 1989, 14, 137–139. [Google Scholar] [CrossRef] [PubMed]
- Zia, H. Enhanced pulse compression within sign-alternating dispersion waveguides. Photonics 2021, 8, 50. [Google Scholar] [CrossRef]
- England, D.; Bouchard, F.; Fenwick, K.; Bonsma-Fisher, K.; Zhang, Y.; Bustard, P.J.; Sussman, B.J. Perspectives on all-optical Kerr switching for quantum optical applications. Appl. Phys. Lett. 2021, 119, 160501. [Google Scholar] [CrossRef]
- Matsuda, N. Deterministic reshaping of single-photon spectra using cross-phase modulation. Sci. Adv. 2016, 2, e1501223. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tournois, P. Acousto-optic programmable dispersive filter for adaptive compensation of group delay time dispersion in laser systems. Opt. Commun. 1997, 140, 245–249. [Google Scholar] [CrossRef]
- Verluise, F.; Laude, V.; Cheng, Z.; Spielmann, C.; Tournois, P. Amplitude and phase control of ultrashort pulses by use of an acousto-optic programmable dispersive filter: Pulse compression and shaping. Opt. Lett. 2000, 25, 575. [Google Scholar] [CrossRef] [PubMed]
- Fastlite. Dazzler. 2021. Available online: https://fastlite.com/produits/dazzler-ultrafast-pulse-shaper/ (accessed on 6 December 2021).

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zia, H. Maintaining Constant Pulse-Duration in Highly Dispersive Media Using Nonlinear Potentials. Photonics 2021, 8, 570. https://doi.org/10.3390/photonics8120570
Zia H. Maintaining Constant Pulse-Duration in Highly Dispersive Media Using Nonlinear Potentials. Photonics. 2021; 8(12):570. https://doi.org/10.3390/photonics8120570
Chicago/Turabian StyleZia, Haider. 2021. "Maintaining Constant Pulse-Duration in Highly Dispersive Media Using Nonlinear Potentials" Photonics 8, no. 12: 570. https://doi.org/10.3390/photonics8120570
APA StyleZia, H. (2021). Maintaining Constant Pulse-Duration in Highly Dispersive Media Using Nonlinear Potentials. Photonics, 8(12), 570. https://doi.org/10.3390/photonics8120570





