Hyperchaos in a Bose-Hubbard Chain with Rydberg-Dressed Interactions
Abstract
1. Introduction
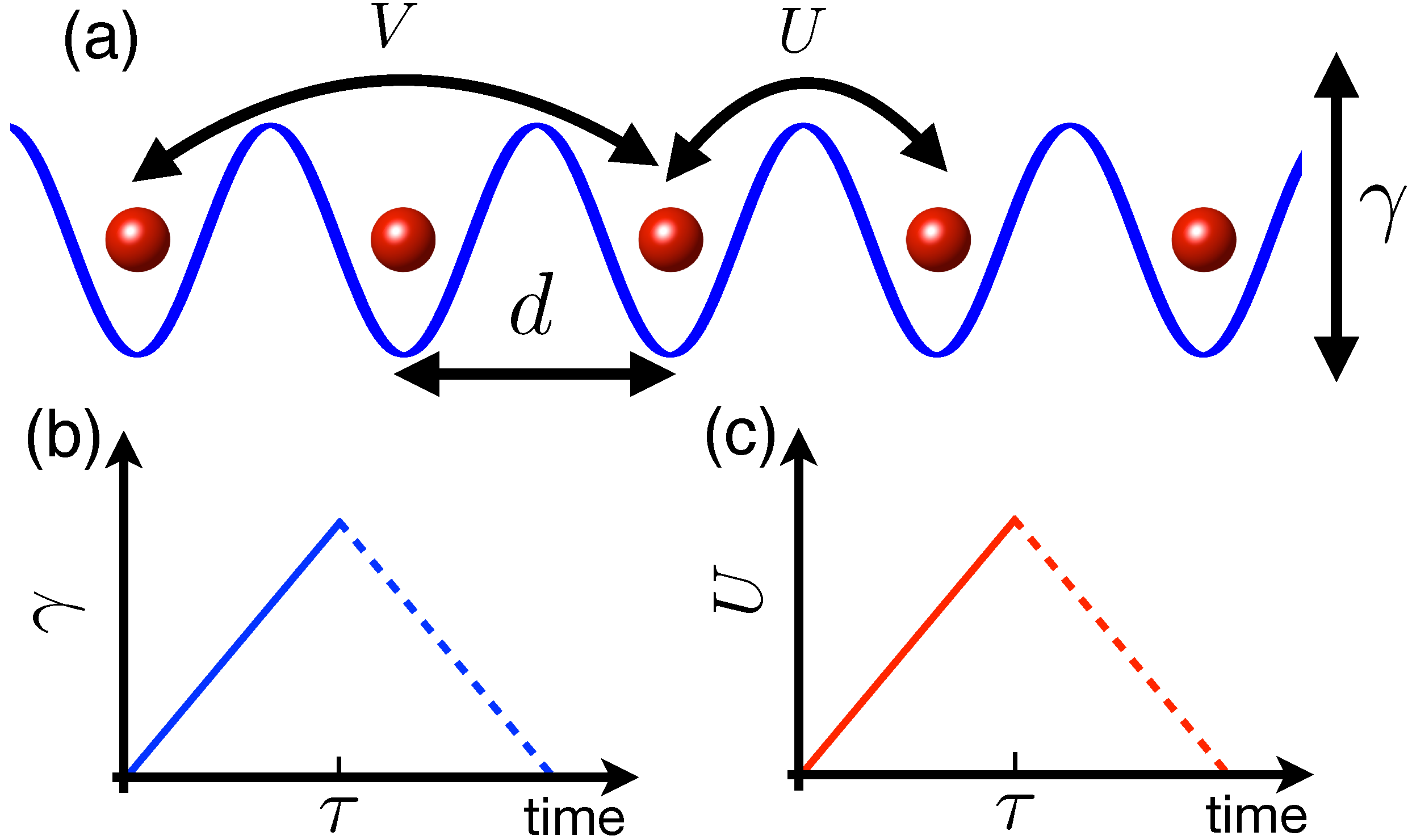
2. Model and Method
2.1. Extended Bose-Hubbard Model in the Semiclassical Limit
2.2. Nonlinear Eigenenergies and Bogoliubov Spectra
2.3. Poincaré Sections and Lyapunov Exponents
2.4. Quenching Schemes
3. Stability of the Ground State
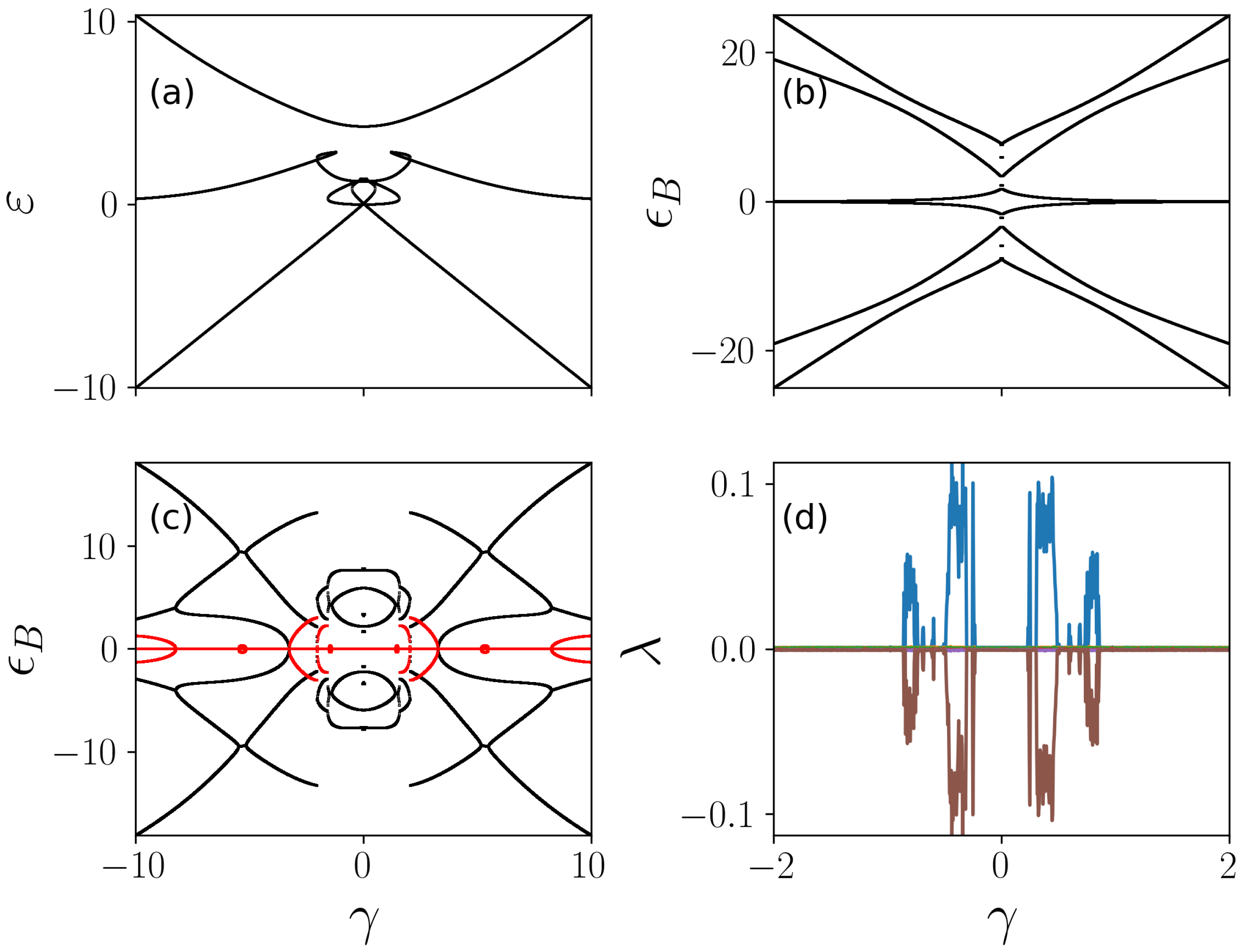
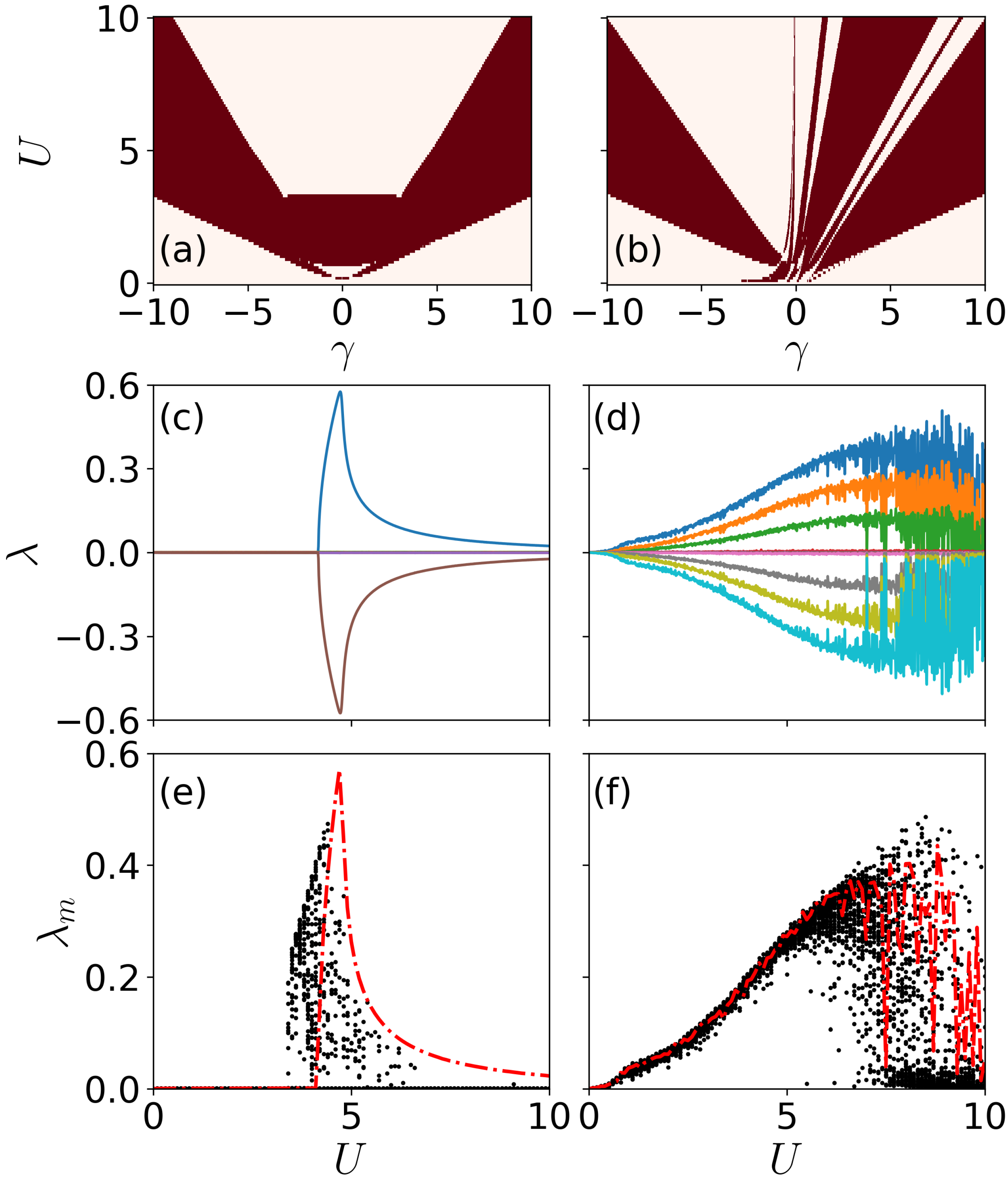
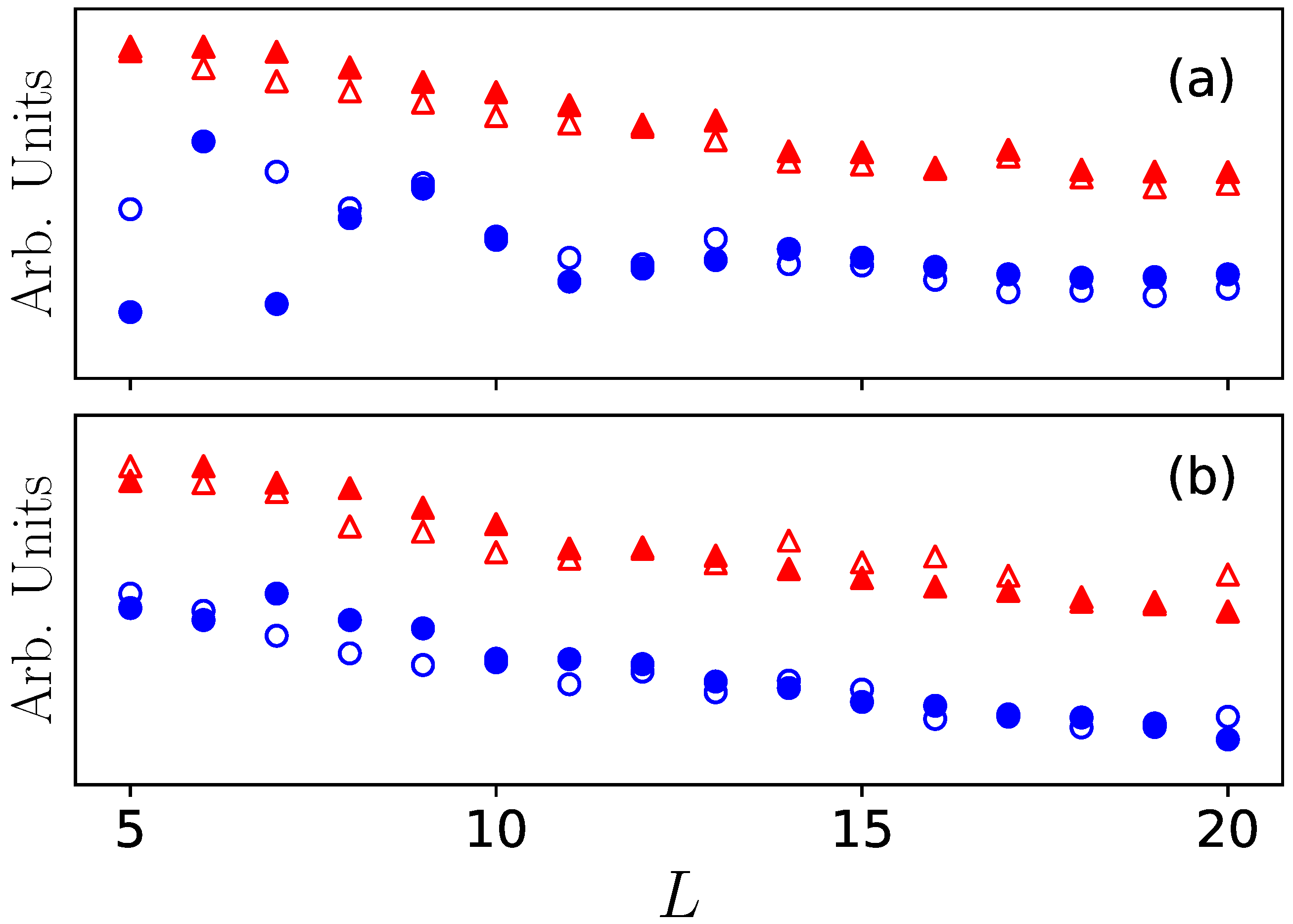
3.1. Eigenenergies, Bogoliubov Spectra, and Lyapunov Exponents
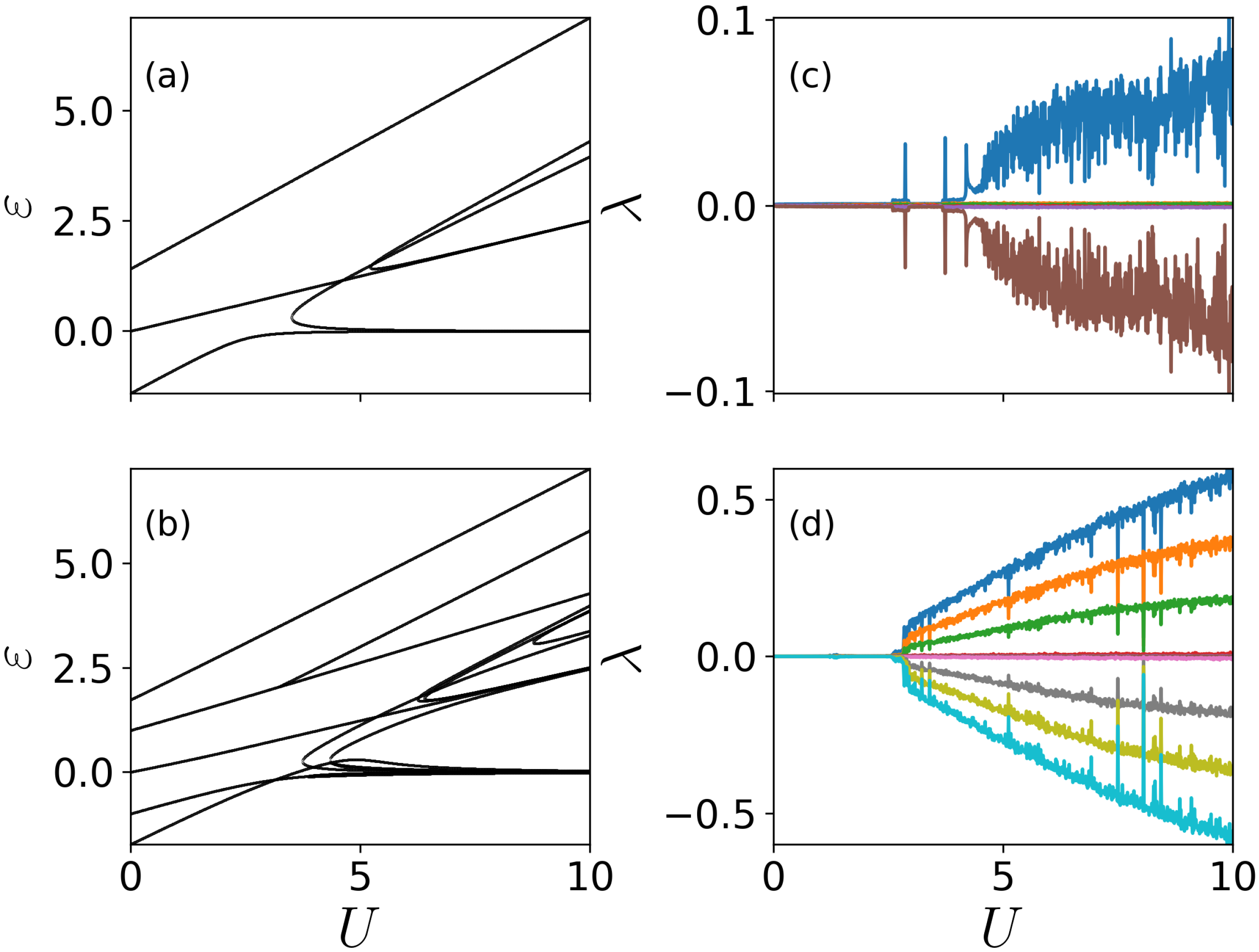
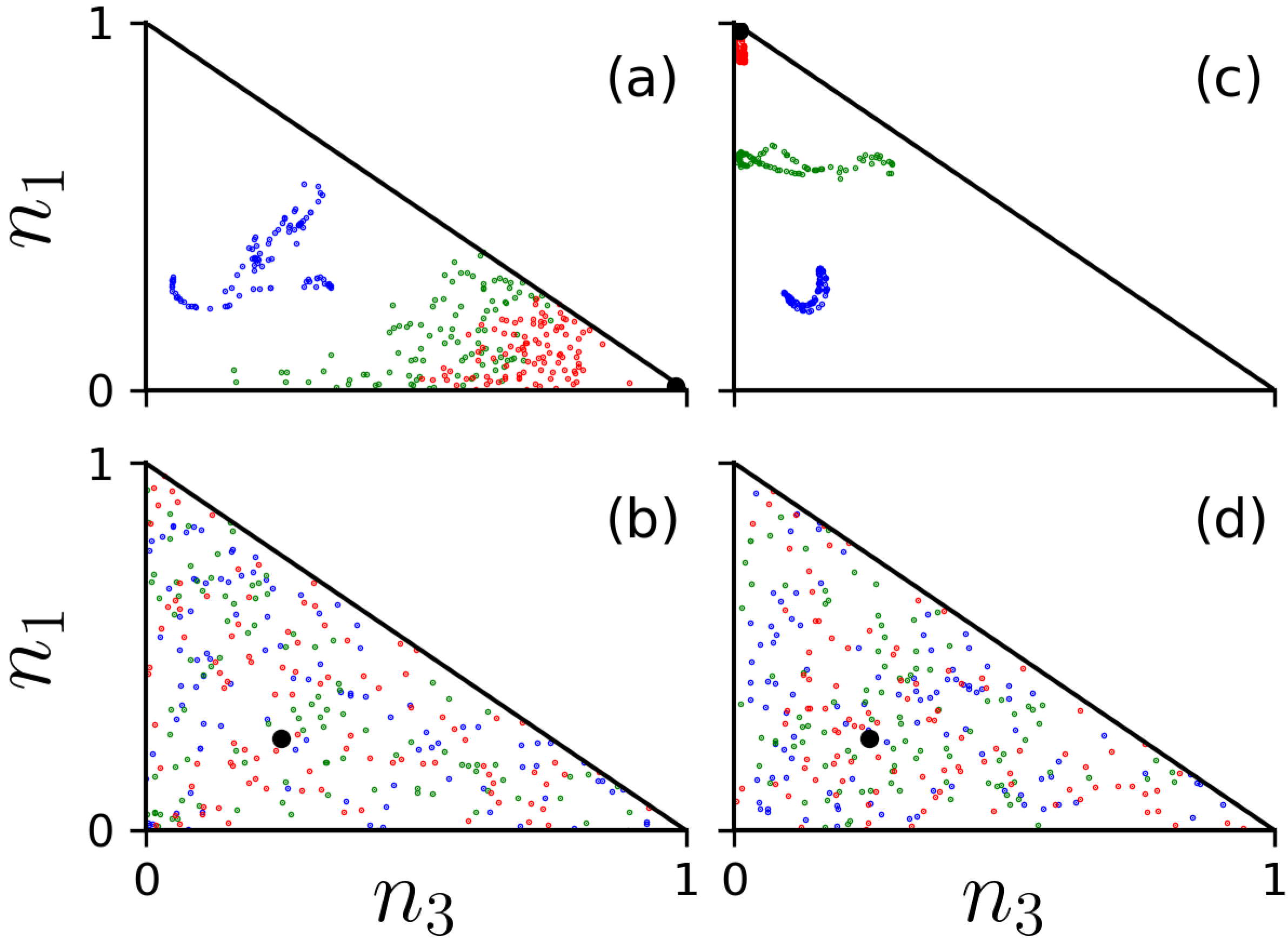
3.2. Quench Dynamics
4. Stability of the Localized State
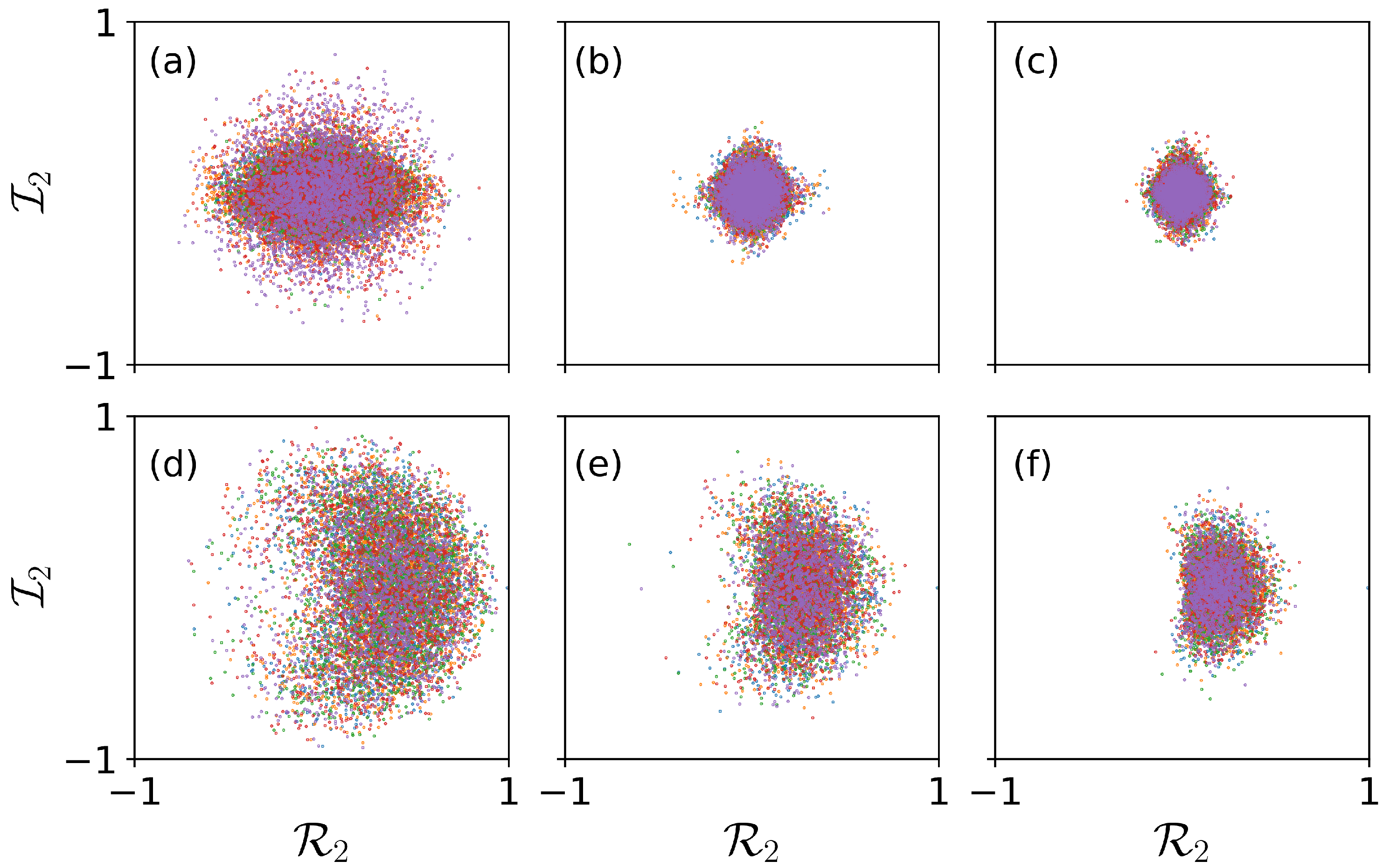
4.1. Bogoliubov Spectra and Lyapunov Exponents
4.2. Quench Dynamics
5. Discussion
6. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Robert, P.S.; Zoran, H. Effects of Interactions on Bose-Einstein Condensation of an Atomic Gas. In Physics of Quantum Fluids: New Trends and Hot Topics in Atomic and Polariton Condensates; Alberto, B., Michele, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 341–359. [Google Scholar]
- Pethick, C.J.; Smith, H. Microscopic theory of the Bose gas. In Bose–Einstein Condensation in Dilute Gases; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Leonardo, F.; Chiara, F.; Jessica, E.L.; Massimo, I. Bose-Einstein condensate in an optical lattice with tunable spacing: Transport and static properties. Opt. Express 2005, 13, 4303–4313. [Google Scholar]
- Smerzi, A.; Fantoni, S.; Giovanazzi, S.; Shenoy, S.R. Quantum coherent atomic tunneling between two trapped bose-einstein condensates. Phys. Rev. Lett. 1997, 79, 4950–4953. [Google Scholar] [CrossRef]
- Manjun, M.R.; Navarro, R.; Carretero-González, R. Solitons riding on solitons and the quantum newton’s cradle. Phys. Rev. E 2016, 93, 022202. [Google Scholar]
- Anderson, B.P.; Haljan, P.C.; Regal, C.A.; Feder, D.L.; Collins, L.A.; Clark, C.W.; Cornell, E.A. Watching dark solitons decay into vortex rings in a bose-einstein condensate. Phys. Rev. Lett. 2001, 86, 2926–2929. [Google Scholar] [CrossRef] [PubMed]
- Zachary, D.; Michael, B.; Christopher, S.; Lene Vestergaard, H. Observation of quantum shock waves created with ultra- compressed slow light pulses in a bose-einstein condensate. Science 2001, 293, 663–668. [Google Scholar]
- Denschlag, J.; Simsarian, J.E.; Feder, D.L.; Clark, C.W.; Collins, L.A.; Cubizolles, J.; Deng, L.; Hagley, E.W.; Helmerson, K.; Phillips, W.D.; et al. Generating solitons by phase engineering of a bose-einstein condensate. Science 2000, 287, 97–101. [Google Scholar] [CrossRef] [PubMed]
- Burger, S.; Bongs, K.; Dettmer, S.; Ertmer, W.; Sengstock, K.; Sanpera, A.; Shlyapnikov, G.V.; Lewenstein, M. Dark solitons in bose-einstein condensates. Phys. Rev. Lett. 1999, 83, 5198–5201. [Google Scholar] [CrossRef]
- Cornish, S.L.; Thompson, S.T.; Wieman, C.E. Formation of bright matter-wave solitons during the collapse of attractive bose-einstein condensates. Phys. Rev. Lett. 2006, 96, 170401. [Google Scholar] [CrossRef]
- Khaykovich, L.; Schreck, F.; Ferrari, G.; Bourdel, T.; Cubizolles, J.; Carr, L.D.; Castin, Y.; Salomon, C. Formation of a matter-wave bright soliton. Science 2002, 296, 1290–1293. [Google Scholar] [CrossRef]
- Strecker, K.E.; Partridge, G.B.; Truscott, A.G.; Hulet, R.G. Formation and propagation of matter-wave soliton trains. Nature 2002, 417, 150–153. [Google Scholar] [CrossRef]
- Kinoshita, T.; Wenger, T.; Weiss, D.S. A quantum newton’s cradle. Nature 2006, 440, 900–903. [Google Scholar] [CrossRef]
- Xia, B.; Hai, W.; Chong, G. Stability and chaotic behavior of a two-component Bose-Einstein condensate. Phys. Lett. Sect. A Gen. At. Solid State Phys. 2006, 351, 136–142. [Google Scholar] [CrossRef]
- Liu, B.; Fu, L.B.; Yang, S.P.; Liu, J. Josephson oscillation and transition to self-trapping for Bose-Einstein condensates in a triple-well trap. Phys. Rev. A 2007, 75, 033601. [Google Scholar] [CrossRef]
- Graefe, E.M.; Korsch, H.J.; Witthaut, D. Mean-field dynamics of a Bose-Einstein condensate in a time-dependent triple-well trap: Nonlinear eigenstates, Landau-Zener models, and stimulated Raman adiabatic passage. Phys. Rev. A 2006, 73, 013617. [Google Scholar] [CrossRef]
- Viscondi, T.F.; Furuya, K. Dynamics of a Bose-Einstein condensate in a symmetric triple-well trap. J. Phys. A Math. Theor. 2011, 44, 175301. [Google Scholar] [CrossRef]
- Li, L.; Wang, B.; Lü, X.Y.; Wu, Y. Chaos-related Localization in Modulated Lattice Array. Annalen der Physik 2018, 530, 1700218. [Google Scholar] [CrossRef]
- Chong, G.; Hai, W.; Xie, Q. Controlling chaos in a weakly coupled array of Bose-Einstein condensates. Phys. Rev. E 2005, 71, 016202. [Google Scholar] [CrossRef]
- Liu, J.; Fu, L.; Ou, B.Y.; Chen, S.G.; Choi, D.I.; Wu, B.; Niu, Q. Theory of nonlinear Landau-Zener tunneling. Phys. Rev. A 2002, 66, 023404. [Google Scholar] [CrossRef]
- Liu, J.; Wu, B.; Niu, Q. Nonlinear Evolution of Quantum States in the Adiabatic Regime. Phys. Rev. Lett. 2003, 90, 170404. [Google Scholar] [CrossRef]
- Albiez, M.; Gati, R.; Fölling, J.; Hunsmann, S.; Cristiani, M.; Oberthaler, M.K. Direct observation of tunneling and nonlinear self-trapping in a single bosonic josephson junction. Phys. Rev. Lett. 2005, 95, 010402. [Google Scholar] [CrossRef]
- Zibold, T.; Nicklas, E.; Gross, C.; Oberthaler, M.K. Classical bifurcation at the transition from rabi to Josephson dynamics. Phys. Rev. Lett. 2010, 105, 204101. [Google Scholar] [CrossRef]
- Gotlibovych, I.; Schmidutz, T.F.; Gaunt, A.L.; Navon, N.; Smith, R.P.; Hadzibabic, Z. Observing properties of an interacting homogeneous bose-einstein condensate: Heisenberg-limited momentum spread, interaction energy, and free-expansion dynamics. Phys. Rev. A 2014, 89, 061604. [Google Scholar] [CrossRef]
- Gaunt, A.L.; Schmidutz, T.F.; Gotlibovych, I.; Smith, R.P.; Hadzibabic, Z. Bose-einstein condensation of atoms in a uniform potential. Phys. Rev. Lett. 2013, 110, 200406. [Google Scholar] [CrossRef] [PubMed]
- Schmidutz, T.F.; Gotlibovych, I.; Gaunt, A.L.; Smith, R.P.; Navon, N.; Hadzibabic, Z. Quantum joule-thomson effect in a saturated homogeneous bose gas. Phys. Rev. Lett. 2014, 112, 040403. [Google Scholar] [CrossRef]
- Buonsante, P.; Penna, V. Some remarks on the coherent-state variational approach to nonlinear boson models. J. Phys. A Math. Theor. 2008, 41, 175301. [Google Scholar] [CrossRef]
- Hai, W.; Rong, S.; Zhu, Q. Discrete chaotic states of a Bose-Einstein condensate. Phys. Rev. E 2008, 78, 066214. [Google Scholar] [CrossRef] [PubMed]
- Sinha, S.; Sinha, S. Chaos and Quantum Scars in Bose-Josephson Junction Coupled to a Bosonic Mode. Phys. Rev. Lett. 2020, 125, 134101. [Google Scholar] [CrossRef] [PubMed]
- Boukobza, E.; Moore, M.G.; Cohen, D.; Vardi, A. Nonlinear phase dynamics in a driven bosonic josephson junction. Phys. Rev. Lett. 2010, 104, 240402. [Google Scholar] [CrossRef]
- Pedri, P.; Santos, L. Two-Dimensional Bright Solitons in Dipolar Bose-Einstein Condensates. Phys. Rev. Lett. 2005, 95, 200404. [Google Scholar] [CrossRef] [PubMed]
- Tikhonenkov, I.; Malomed, B.A.; Vardi, A. Anisotropic Solitons in Dipolar Bose-Einstein Condensates. Phys. Rev. Lett. 2008, 100, 090406. [Google Scholar] [CrossRef] [PubMed]
- Nath, R.; Pedri, P.; Santos, L. Phonon Instability with Respect to Soliton Formation in Two-Dimensional Dipolar Bose-Einstein Condensates. Phys. Rev. Lett. 2009, 102, 050401. [Google Scholar] [CrossRef]
- Cuevas, J.; Malomed, B.A.; Kevrekidis, P.G.; Frantzeskakis, D.J. Solitons in quasi-one-dimensional Bose-Einstein condensates with competing dipolar and local interactions. Phys. Rev. A 2009, 79, 053608. [Google Scholar] [CrossRef]
- Young-S, L.E.; Muruganandam, P.; Adhikari, S.K. Dynamics of quasi-one-dimensional bright and vortex solitons of a dipolar Bose–Einstein condensate with repulsive atomic interaction. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 101001. [Google Scholar] [CrossRef]
- Lahaye, T.; Pfau, T.; Santos, L. Mesoscopic ensembles of polar bosons in triple-well potentials. Phys. Rev. Lett. 2010, 104, 170404. [Google Scholar] [CrossRef]
- Xiong, B.; Fischer, U.R. Interaction-induced coherence among polar bosons stored in triple-well potentials. Phys. Rev. A 2013, 88, 063608. [Google Scholar] [CrossRef]
- Gallemí, A.; Guilleumas, M.; Mayol, R.; Sanpera, A. Role of anisotropy in dipolar bosons in triple-well potentials. Phys. Rev. A 2013, 88, 063645. [Google Scholar] [CrossRef]
- Köberle, P.; Cartarius, H.; Fabčič, T.; Main, J.; Wunner, G. Bifurcations, order and chaos in the bose–einstein condensation of dipolar gases. New J. Phys. 2009, 11, 023017. [Google Scholar] [CrossRef]
- Andreev, P.A. Quantum hydrodynamic theory of quantum fluctuations in dipolar bose–einstein condensate. Chaos An Interdiscip. J. Nonlinear Sci. 2021, 31, 023120. [Google Scholar] [CrossRef]
- Xiong, B.; Gong, J.; Pu, H.; Bao, W.; Li, B. Symmetry breaking and self-trapping of a dipolar Bose-Einstein condensate in a double-well potential. Phys. Rev. A 2009, 79, 013626. [Google Scholar] [CrossRef]
- Abad, M.; Guilleumas, M.; Mayol, R.; Pi, M.; Jezek, D.M. A dipolar self-induced bosonic Josephson junction. Europhys. Lett. 2011, 94, 10004. [Google Scholar] [CrossRef]
- Wang, C.; Kevrekidis, P.G.; Frantzeskakis, D.J.; Malomed, B.A. Effects of long-range nonlinear interactions in double-well potentials. Phys. D Nonlinear Phenom. 2011, 240, 805–813. [Google Scholar] [CrossRef]
- Adhikari, S.K. Self-trapping of a dipolar Bose-Einstein condensate in a double well. Phys. Rev. A 2014, 89, 043609. [Google Scholar] [CrossRef]
- Zhang, A.-X.; Xue, J.-K. Dipolar-induced interplay between inter-level physics and macroscopic phase transitions in triple-well potentials. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 145305. [Google Scholar] [CrossRef]
- Fortanier, R.; Zajec, D.; Main, J.; Wunner, G. Dipolar Bose–Einstein condensates in triple-well potentials. J. Phys. B At. Mol. Opt. Phys. 2013, 46, 235301. [Google Scholar] [CrossRef][Green Version]
- Bouchoule, I.; Molmer, K. Spin squeezing of atoms by the dipole interaction in virtually excited Rydberg states. Phys. Rev. A 2002, 65, 041803. [Google Scholar] [CrossRef]
- Henkel, N.; Nath, R.; Pohl, T. Three-dimensional roton excitations and supersolid formation in rydberg-excited bose-einstein condensates. Phys. Rev. Lett. 2010, 104, 195302. [Google Scholar] [CrossRef] [PubMed]
- Honer, J.; Weimer, H.; Pfau, T.; Büchler, H.P. Collective many-body interaction in rydberg dressed atoms. Phys. Rev. Lett. 2010, 105, 160404. [Google Scholar] [CrossRef]
- Pupillo, G.; Micheli, A.; Boninsegni, M.; Lesanovsky, I.; Zoller, P. Strongly correlated gases of rydberg-dressed atoms: Quantum and classical dynamics. Phys. Rev. Lett. 2010, 104, 223002. [Google Scholar] [CrossRef] [PubMed]
- Johnson, J.E.; Rolston, S.L. Interactions between Rydberg-dressed atoms. Phys. Rev. A 2010, 82, 033412. [Google Scholar] [CrossRef]
- Li, W.; Hamadeh, L.; Lesanovsky, I. Probing the interaction between Rydberg-dressed atoms through interference. Phys. Rev. A 2012, 85, 053615. [Google Scholar] [CrossRef]
- DeSalvo, B.J.; Aman, J.A.; Gaul, C.; Pohl, T.; Yoshida, S.; Burgdörfer, J.; Hazzard, K.R.A.; Dunning, F.B.; Killian, T.C. Rydberg-blockade effects in autler-townes spectra of ultracold strontium. Phys. Rev. A 2016, 93, 022709. [Google Scholar] [CrossRef]
- Hsueh, C.-H.; Wang, C.-W.; Wu, W.-C. Vortex structures in a rotating rydberg-dressed bose-einstein condensate with the lee-huang-yang correction. Phys. Rev. A 2020, 102, 063307. [Google Scholar] [CrossRef]
- Maucher, F.; Henkel, N.; Saffman, M.; Królikowski, W.; Skupin, S.; Pohl, T. Rydberg-induced solitons: Three-dimensional self-trapping of matter waves. Phys. Rev. Lett. 2011, 106, 170401. [Google Scholar] [CrossRef] [PubMed]
- Cinti, F.; MacRì, T.; Lechner, W.; Pupillo, G.; Pohl, T. Defect-induced supersolidity with soft-core bosons. Nat. Commun. 2014, 5, 4235. [Google Scholar] [CrossRef] [PubMed]
- Hsueh, C.H.; Tsai, Y.C.; Wu, W.C. Excitations of one-dimensional supersolids with optical lattices. Phys. Rev. A 2016, 93, 063605. [Google Scholar] [CrossRef]
- McCormack, G.; Nath, R.; Li, W. Dynamical excitation of maxon and roton modes in a Rydberg-Dressed Bose-Einstein Condensate. Phys. Rev. A 2020, 102, 023319. [Google Scholar] [CrossRef]
- Lauer, A.; Muth, D.; Fleischhauer, M. Transport-induced melting of crystals of Rydberg dressed atoms in a one-dimensional lattice. New J. Phys. 2012, 14, 095009. [Google Scholar] [CrossRef][Green Version]
- Lan, Z.; Minar, J.; Levi, E.; Li, W.; Lesanovsky, I. Emergent Devil’s Staircase without Particle-Hole Symmetry in Rydberg Quantum Gases with Competing Attractive and Repulsive Interactions. Phys. Rev. Lett. 2015, 115, 203001. [Google Scholar] [CrossRef]
- Angelone, A.; Mezzacapo, F.; Pupillo, G. Superglass Phase of Interaction-Blockaded Gases on a Triangular Lattice. Phys. Rev. Lett. 2016, 116, 135303. [Google Scholar] [CrossRef]
- Chougale, Y.; Nath, R. Ab initio calculation of Hubbard parameters for Rydberg-dressed atoms in a one-dimensional optical lattice. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 144005. [Google Scholar] [CrossRef]
- Li, Y.; Geißler, A.; Hofstetter, W.; Li, W. Supersolidity of lattice bosons immersed in strongly correlated Rydberg dressed atoms. Phys. Rev. A 2018, 97, 023619. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, Y.; Nath, R.; Li, W. Quench dynamics of Rydberg-dressed bosons on two-dimensional square lattices. Phys. Rev. A 2020, 101, 013427. [Google Scholar] [CrossRef]
- Barbier, M.; Geißler, A.; Hofstetter, W. Decay-dephasing-induced steady states in bosonic rydberg-excited quantum gases in an optical lattice. Phys. Rev. A 2019, 99, 033602. [Google Scholar] [CrossRef]
- Jau, Y.Y.; Hankin, A.M.; Keating, T.; Deutsch, I.H.; Biedermann, G.W. Entangling atomic spins with a Rydberg-dressed spin-flip blockade. Nat. Phys. 2016, 12, 3487. [Google Scholar] [CrossRef]
- Zeiher, J.; van Bijnen, R.; Schauß, P.; Hild, S.; Choi, J.Y.; Pohl, T.; Bloch, I.; Gross, C. Many-body interferometry of a Rydberg-dressed spin lattice. Nat. Phys. 2016, 12, 3835. [Google Scholar] [CrossRef]
- Zeiher, J.; Choi, J.Y.; Rubio-Abadal, A.; Pohl, T.; Van Bijnen, R.; Bloch, I.; Gross, C. Coherent many-body spin dynamics in a long-range interacting Ising chain. Phys. Rev. X 2017, 7, 041063. [Google Scholar] [CrossRef]
- Guardado-Sanchez, E.; Spar, B.M.; Schauss, P.; Belyansky, R.; Young, J.T.; Bienias, P.; Gorshkov, A.V.; Iadecola, T.; Bakr, W.S. Quench Dynamics of a Fermi Gas with Strong Long-Range Interactions. arXiv 2020, arXiv:2010.05871. [Google Scholar]
- Borish, V.; Marković, O.; Hines, J.A.; Rajagopal, S.V.; Schleier-Smith, M. Transverse-Field Ising Dynamics in a Rydberg-Dressed Atomic Gas. Phys. Rev. Lett. 2020, 124, 063601. [Google Scholar] [CrossRef]
- McCormack, G.; Nath, R.; Li, W. Nonlinear dynamics of Rydberg-dressed Bose-Einstein condensates in a triple-well potential. Phys. Rev. A 2020, 102, 063329. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Andreev, A.V.; Balanov, A.G.; Fromhold, T.M.; Greenaway, M.T.; Hramov, A.E.; Li, W.; Makarov, V.V.; Zagoskin, A.M. Emergence and control of complex behaviors in driven systems of interacting qubits with dissipation. NPJ Quantum Inf. 2021, 7, 1–7. [Google Scholar] [CrossRef]
- Eckel, S.; Lee, J.G.; Jendrzejewski, F.; Murray, N.; Clark, C.W.; Lobb, C.J.; Phillips, W.D.; Edwards, M.; Campbell, G.K. Hysteresis in a quantized superfluid ’atomtronic’ circuit. Nature 2014, 506, 200–203. [Google Scholar] [CrossRef] [PubMed]
- Trenkwalder, A.; Spagnolli, G.; Semeghini, G.; Coop, S.; Landini, M.; Castilho, P.; Pezzè, L.; Modugno, G.; Inguscio, M.; Smerzi, A.; et al. Quantum phase transitions with parity-symmetry breaking and hysteresis. Nat. Phys. 2016, 12, 826–829. [Google Scholar] [CrossRef]
- Bürkle, R.; Vardi, A.; Cohen, D.; Anglin, J.R. Probabilistic hysteresis in integrable and chaotic isolated hamiltonian systems. Phys. Rev. Lett. 2019, 123, 114101. [Google Scholar] [CrossRef]
- Scully, M.O.; Zubairy, M.S. Quantum Optics, 1st ed.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Castro, E.R.; Chávez-Carlos, J.; Roditi, I.; Santos, L.F.; Hirsch, J.G. Quantum-classical correspondence of a system of interacting bosons in a triple-well potential. arXiv 2021, arXiv:2105.10515. [Google Scholar] [CrossRef]
- Dey, A.; Cohen, D.; Vardi, A. Adiabatic Passage through Chaos. Phys. Rev. Lett. 2018, 121, 250405. [Google Scholar] [CrossRef] [PubMed]
- Dey, A.; Cohen, D.; Vardi, A. Many-body adiabatic passage: Quantum detours around chaos. Phys. Rev. A 2019, 99, 033623. [Google Scholar] [CrossRef]
- Datseris, G. Dynamicalsystems.jl: A julia software library for chaos and nonlinear dynamics. J. Open Source Softw. 2018, 3, 598. [Google Scholar] [CrossRef]
- Baier, G.; Klein, M. Maximum hyperchaos in generalized Hénon maps. Phys. Lett. A 1990, 151, 281–284. [Google Scholar] [CrossRef]
- Baier, G.; Sahle, S. Design of hyperchaotic flows. Phys. Rev. E 1995, 51, R2712–R2714. [Google Scholar] [CrossRef]
- Kapitaniak, T.; Thylwe, K.-E.; Cohen, I.; Wojewoda, J. Chaos-hyperchaos transition. Chaos Solitons Fractals 1995, 5, 2003–2011. [Google Scholar] [CrossRef]
- Tarkhov, A.E.; Wimberger, S.; Fine, B.V. Extracting lyapunov exponents from the echo dynamics of bose-einstein condensates on a lattice. Phys. Rev. A 2017, 96, 023624. [Google Scholar] [CrossRef]
- Lerose, A.; Pappalardi, S. Bridging entanglement dynamics and chaos in semiclassical systems. Phys. Rev. A 2020, 102, 032404. [Google Scholar] [CrossRef]
- Pausch, L.; Carnio, E.G.; Rodríguez, A.; Buchleitner, A. Chaos and Ergodicity across the Energy Spectrum of Interacting Bosons. Phys. Rev. Lett. 2021, 126, 150601. [Google Scholar] [CrossRef]
- Kollath, C.; Roux, G.; Biroli, G.; Läuchli, A.M. Statistical properties of the spectrum of the extended Bose-Hubbard model. J. Stat. Mech. 2010, 2010, P08011. [Google Scholar] [CrossRef]
- Chen, Y.; Cai, Z. Persistent oscillations versus thermalization in the quench dynamics of quantum gases with long-range interactions. Phys. Rev. A 2020, 101, 023611. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
McCormack, G.; Nath, R.; Li, W. Hyperchaos in a Bose-Hubbard Chain with Rydberg-Dressed Interactions. Photonics 2021, 8, 554. https://doi.org/10.3390/photonics8120554
McCormack G, Nath R, Li W. Hyperchaos in a Bose-Hubbard Chain with Rydberg-Dressed Interactions. Photonics. 2021; 8(12):554. https://doi.org/10.3390/photonics8120554
Chicago/Turabian StyleMcCormack, Gary, Rejish Nath, and Weibin Li. 2021. "Hyperchaos in a Bose-Hubbard Chain with Rydberg-Dressed Interactions" Photonics 8, no. 12: 554. https://doi.org/10.3390/photonics8120554
APA StyleMcCormack, G., Nath, R., & Li, W. (2021). Hyperchaos in a Bose-Hubbard Chain with Rydberg-Dressed Interactions. Photonics, 8(12), 554. https://doi.org/10.3390/photonics8120554




