A Novel Liquid Crystal-Filled, Dual-Core Photonic Crystal Fiber Polarization Beam Splitter Covering the E + S + C + L + U Communication Band

Abstract

This paper proposes a novel liquid crystal-filled, dual core photonic crystal fiber polarization beam splitter (LC-DC-PCF PBS) based on the coupled mode theory of DC-PCF. The mode birefringence of odd and even modes, coupling lengths (CLs) of the X-polarization (X-pol) and Y-polarization (Y-pol), and the corresponding coupling length ratio (CLR) of the proposed LC-DC-PCF PBS filled without LC E7 and with LC E7 are compared. The change rules of the CLs of the X-pol and Y-pol and CLR of the proposed LC-DC-PCF with wavelengths for different cladding microstructure parameters were investigated. The relationships between the X-pol and Y-pol normalized output powers in core A of the proposed LC-DC-PCF PBS and the propagation length at the wavelength of 1.604 μm are discussed. Finally, by studying the change of extinction ratio (ER) with wavelength, the LC-DC-PCF PBS ER of 60.3 and 72.2 dB at wavelengths 1.386 and 1.619 μm are achieved, respectively. The final splitting length (L_S) is 94 μm, and the splitting bandwidth is 349 nm (1.352~1.701 μm), covering the whole of the E + S + C + L + U communication bands. The proposed LC-DC-PCF PBS has good beam-splitting performance, such as ultra-short L_S and ultra-wide splitting bandwidth, with potential applications in laser, sensing, and communication systems.

1. Introduction

In the late 1990s, J.C. Knight et al. proposed and successfully fabricated the first photonic crystal fiber (PCF), whose cladding was composed of micron-sized air holes arranged according to certain rules [1,2,3]. In the following 20 years, due to the flexible cladding microstructure of PCF and the maturity of fiber post-processing technology, the PCF has experienced incredible development in various fields of optics and photonics [4,5,6,7,8,9,10]. Especially after all six optical fiber communication windows O (1260–1360 nm), E (1360–1460 nm), S (1460–1530 nm), C (1530–1565 nm), L (1565–1625 nm), and U (1625–1675 nm) are proposed, PCF has more significant advantages in the field of multi window optical fiber communication.

In recent years, researchers worldwide have conducted a great deal of research on the dual-core photonic crystal fiber (DC-PCF) [11,12,13,14,15]. A large number of studies have shown that a polarization beam splitter (PBS) with excellent performance can be obtained by using the coupled mode theory of DC-PCF and fiber post-processing technology, such as filling with liquid crystal (LC), liquid, or precious metal materials in some fixed air holes of DC-PCF [16,17,18,19,20,21,22,23]. However, the commonly used precious metal filling materials are generally gold or silver materials, which are expensive, and the deposition process is complex. Complex methods such as high-pressure chemical vapor deposition and radio frequency magnetron sputtering are usually needed. Compared with gold and silver materials, LC or liquid filling materials have a lower price and simpler filling process, so many researchers have favored them in recent years. In 2016, Wang et al. proposed a DC-PCF PBS filled with LC E7 in all the air holes of the cladding, where the shortest splitting length (L_S) was 890.5 μm and the widest splitting bandwidth was 150 nm, which almost covers all the S + C + L communication bands [24]. In 2017, Hagras et al. reported an ultra-compact DC-PCF PBS filled with LC E7 in six big air holes of the cladding. The L_S and splitting bandwidth of the DC-PCF PBS were 111.2 μm and 88 nm, respectively [25]. In 2018, Younis et al. designed a DC-PCF PBS whose left core was surrounded by LC E7-filled air holes. At wavelengths 1.3 and 1.55 μm, the splitting bandwidths of the DC-PCF PBS were always 3 nm, and L_S were 5.678 and 7.178 mm, respectively [26]. In 2019, Xu et al. proposed a DC-PCF PBS based on rare metal, Ti, and liquid filling in the cladding air holes. The proposed DC-PCF PBS offered an ultra-short length of 83.9 µm, a high extinction ratio (ER) of 44.05 dB, but the splitting bandwidth was only 32.1 nm [27]. However, the above-mentioned DC-PCF PBS, LC, or liquid are always filled in multiple air holes, and some DC-PCF PBS also involves filling multiple materials simultaneously or even filling rare metals, which will lead to increased fabrication difficulty and fabrication cost. In addition, it is difficult for the above-mentioned DC-PCF PBS to obtain a shorter L_S and a wider splitting bandwidth at the same time.

In this paper, we propose a novel LC-filled DC-PCF (LC-DC-PCF) PBS based on the DC-PCF-coupled mode theory. With the full vector-finite element method (FV-FEM), the differences of the effective refractive indices of odd and even modes, mode birefringence of odd and even modes, coupling length (CL) of the X-polarization (X-pol) and Y-polarization (Y-pol), and coupling length ratio (CLR) in LC-DC-PCF filled without and with LC E7 are simulated and compared. Furthermore, the influences of structural parameters on the CLs of the X-pol and Y-pol and CLR are analyzed. Finally, a LC-DC-PCF PBS with ultra-short L_S (94 µm) and ultra-wide splitting bandwidth (349 nm) is obtained, covering the whole of the E + S + C + L + U communication bands.

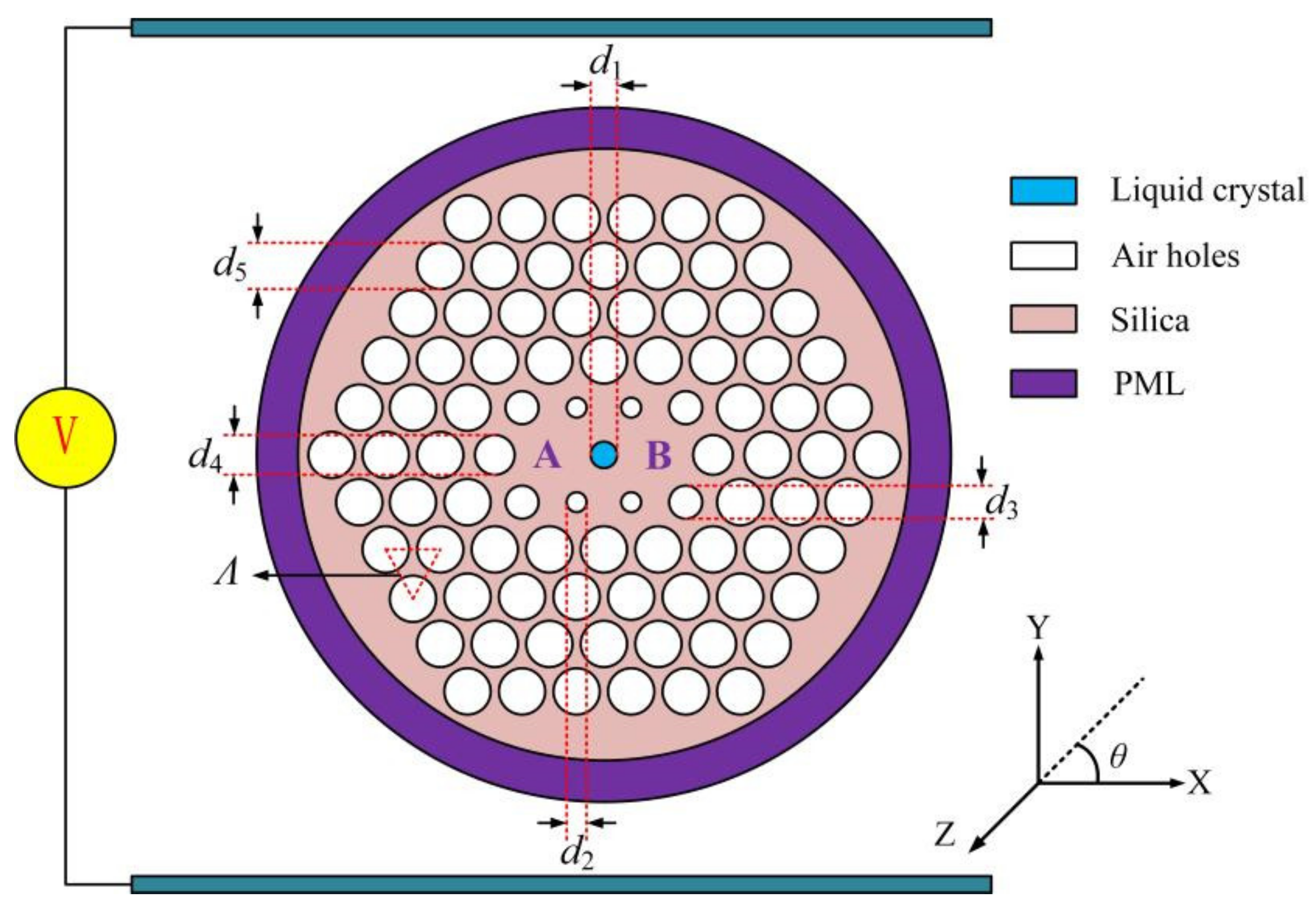
2. Design of the LC-DC-PCF PBS

The cross-sectional structure of the proposed LC-DC-PCF PBS is shown in Figure 1. From Figure 1, the most central air hole with the diameter of d₁ is filled with the LC E7 to obtain high mode birefringence. Near the most central air hole, one air hole is missing in the X-positive direction, and the other is missing in the X-negative direction to form cores A and B, respectively. To obtain higher mode birefringence, there are three different sizes of air holes around cores A and B, with diameters of d₂, d₃, and d₄, respectively. The diameter of the remaining air hole is d₅, and the distance between any two air holes is Λ. The proposed LC-DC-PCF is arranged in a triangular lattice, and the background material is silica. A perfectly matched layer (PML) is added to the outermost layer of the proposed LC-DC-PCF to absorb radiation energy [28]. The refractive indices of the silica material and PML are n_silica and n_silica + 0.05, respectively. In addition, it also can be seen from Figure 1 that cores A and B of the proposed LC-DC-PCF are two symmetrical cores with the same structure.

The refractive index of the n_silica at different wavelengths can be obtained by the Sellmeier equation [29]:

$$n_{\mathrm{silica}}(\lambda )=\sqrt{1+\frac{{\mathrm{A}}_1{\lambda }^2}{{\lambda }^2-B_1^2}+\frac{{\mathrm{A}}_2{\lambda }^2}{{\lambda }^2-B_2^2}+\frac{{\mathrm{A}}_3{\lambda }^2}{{\lambda }^2-B_3^2}},$$

(1)

where λ is the wavelength of the incident light in the free space. Each coefficient in the Sellmeier equation for n_silica can be obtained from Ref. [29].

The ordinary refractive index n_o and the extraordinary refractive index n_e of the LC E7 can be described by the extended Cauchy equation [30]:

$$n_{\mathrm{o}}=D_{\mathrm{o}}+\frac{E_{\mathrm{o}}}{{\lambda }^2}+\frac{F_{\mathrm{o}}}{{\lambda }^4},$$

(2)

$$n_{\mathrm{e}}=D_{\mathrm{e}}+\frac{E_{\mathrm{e}}}{{\lambda }^2}+\frac{F_{\mathrm{e}}}{{\lambda }^4},$$

(3)

where D_o, E_o, F_o, D_e, E_e, and F_e have some specific functional relationships with temperature, which can be obtained from Ref. [30]. The temperature T is 25 °C D_o = 1.4994, E_o = 0.007 μm², F_o = 0.0004 μm⁴, D_e = 1.6933, E_e = 0.0078 μm², and F_e = 0.0028 μm⁴. Here, we set the T to a fixed value of 25 °C.

The relative permittivity of the LC E7 is defined as [31]

$${\epsilon }_r=\left(\begin{array}{ccc}{n}_{\mathrm{o}}^2{\sin }^2(\theta )+n_{\mathrm{e}}^2{\cos }^2(\theta )& (n_{\mathrm{e}}^2-n_{\mathrm{o}}^2)\cos (\theta )\sin (\theta )& 0\\ (n_{\mathrm{e}}^2-n_{\mathrm{o}}^2)\cos (\theta )\sin (\theta )& n_{\mathrm{o}}^2{\cos }^2(\theta )+n_{\mathrm{e}}^2{\sin }^2(\theta )& 0\\ 0& 0& n_{\mathrm{o}}^2\end{array}\right),$$

(4)

where θ is the angle between the direction vector of the LC E7 material and the X-axis. θ can be controlled by an external electric field, such as placing the proposed LC-DC-PCF between two electrodes, as shown in Figure 1. The LC E7 molecules can usually be arranged in three forms by modulating the external electric field: the long axis of the LC E7 molecules is parallel to the X-axis, that is, θ is equal to 0°. θ between the long axis of the LC E7 molecule and the X-axis is 45°. The long axis of the LC E7 molecule is perpendicular to the X-axis; that is, θ is equal to 90°. Here, we set θ to the most commonly used fixed value of 90° [31].

The even mode birefringence (B_e) and odd mode birefringence (B_o) can be defined as [32]

$$B_{\mathrm{e}}=\left|n_{\mathrm{even}}^{\mathrm{X}}-n_{\mathrm{even}}^{\mathrm{Y}}\right|,$$

(5)

$$B_{\mathrm{o}}=\left|n_{\mathrm{odd}}^{\mathrm{X}}-n_{\mathrm{odd}}^{\mathrm{Y}}\right|,$$

(6)

where $n_{\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{n}}^{\mathrm{X}}$, $n_{\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{n}}^{\mathrm{Y}}$, $n_{\mathrm{o}\mathrm{d}\mathrm{d}}^{\mathrm{X}}$, and $n_{\mathrm{o}\mathrm{d}\mathrm{d}}^{\mathrm{Y}}$ represent the effective refractive indices of the even and odd modes of the X-pol and Y-pol, respectively.

Because the DC structures of DC-PCF are completely symmetrical and the medium distribution is the same, the dual-core mode coupling equation can be expressed as [33]

$$\frac{d{a}_1(z)}{dz}=i\beta a_1(z)+iK{a}_2(z),$$

(7)

$$\frac{d{a}_2(z)}{dz}=i\beta a_2(z)+iK{a}_1(z),$$

(8)

where β is the propagation constant of the DC, K is the coupling coefficient of the dual core, and z represents the transmission direction and distance.

By setting a series of initial condition parameters, combined with the fact that the DC-PCF has even mode and odd mode in the X-pol and Y-pol, respectively, the mode coupling equation is solved, and the CLs of the DC-PCF can be obtained.

The CLs of the X-pol and Y-pol of the LC-DC-PCF PBS can be calculated as [34]

$$C{L}_{\mathrm{X}}=\frac{\lambda }{2\left|(n_{\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{n}}^{\mathrm{X}}-n_{\mathrm{o}\mathrm{d}\mathrm{d}}^{\mathrm{X}})\right|},$$

(9)

$$C{L}_{\mathrm{Y}}=\frac{\lambda }{2\left|(n_{\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{n}}^{\mathrm{Y}}-n_{\mathrm{o}\mathrm{d}\mathrm{d}}^{\mathrm{Y}})\right|},$$

(10)

where CL_X and CL_Y represent the CL of the X-pol and Y-pol, respectively.

The CLR can be calculated by [35]

$$CLR=\frac{C{L}_{\mathrm{Y}}}{C{L}_{\mathrm{X}}},$$

(11)

According to the previous studies, when the optimal CLR = 2 or 1/2 and the CL_X and CL_Y are shorter, it is easier for the PBS to have the shortest L_S [36].

Because cores A and B of the proposed LC-DC-PCF have symmetrical and identical structures, only incident light from cores A or B should be considered [37]. Here, we assume that the incident light is incident from core A. The normalized output power (P_out) in the X-pol and Y-pol in the core A can be described as [38]

$$P_{\mathrm{out}, \mathrm{A}}^{\mathrm{X}, \mathrm{Y}}=P_{\mathrm{i}\mathrm{n}}{\cos }^2(\frac{\pi }{2}\frac{L_{\mathrm{P}}}{C{L}_{\mathrm{X},\mathrm{Y}}}),$$

(12)

where P_in is the input power of the incident light, and L_P is the propagation length of the LC-DC-PCF PBS. According to Equation (10), L_P will change periodically. According to previous studies, the shortest L_P is also the shortest L_S [39].

The ER of the core A can be calculated as [40].

$$E{R}_{\mathrm{A}}=10{\log }_{10}\frac{P_{\mathrm{o}\mathrm{u}\mathrm{t}, \mathrm{A}}^{\mathrm{X}}}{P_{\mathrm{o}\mathrm{u}\mathrm{t}, \mathrm{A}}^{\mathrm{Y}}},$$

(13)

For the PBS, the ER is a significant indicator with which to judge and characterize the performance of the PBS. In practical application, when the ER reaches 20 dB, the power of the polarization light is 100 times that of the other, which is enough to separate two orthogonal polarization lights. Generally speaking, the wavelength range with the ER greater than 20 dB is the splitting bandwidth of the PBS [41].

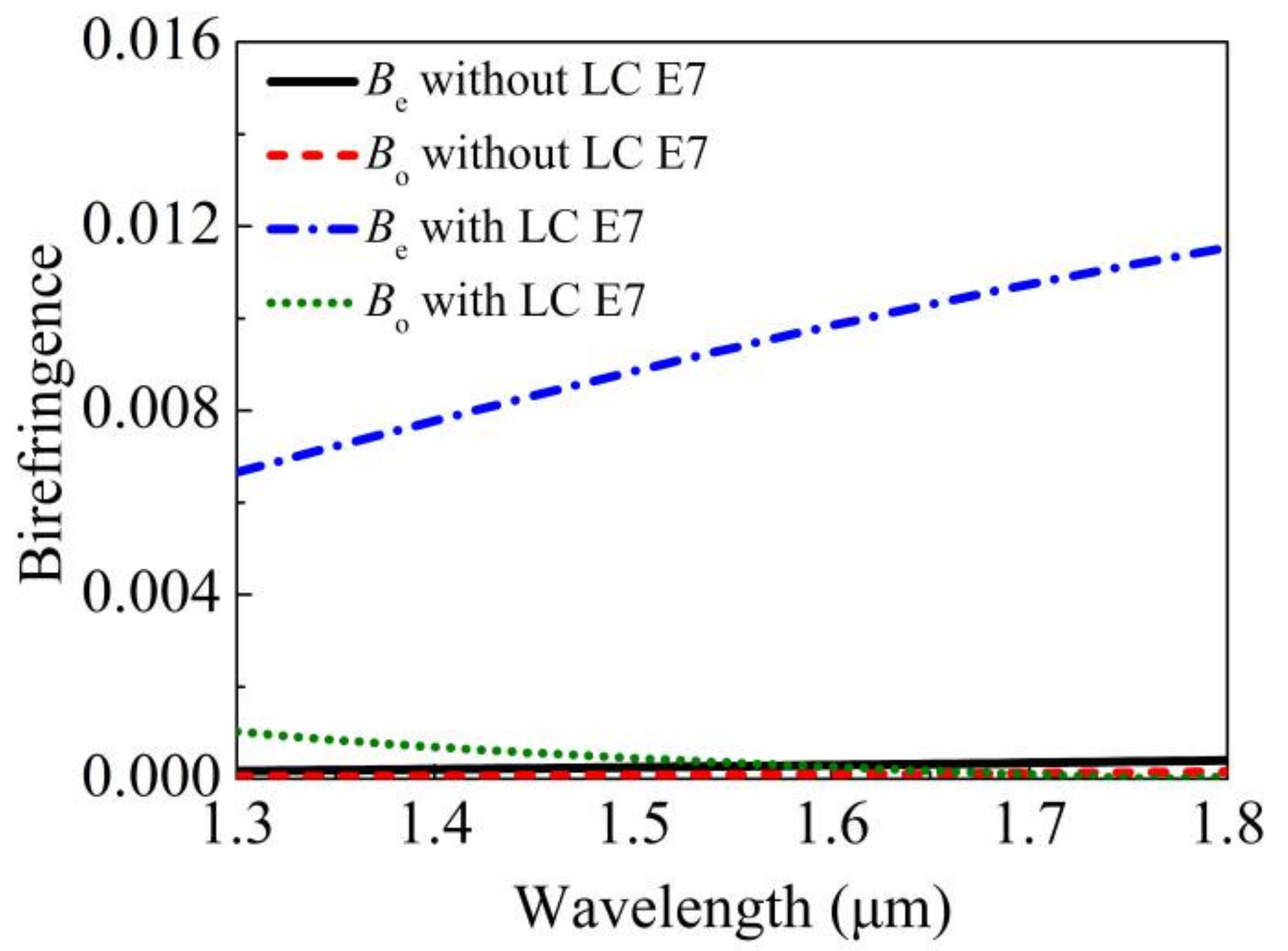
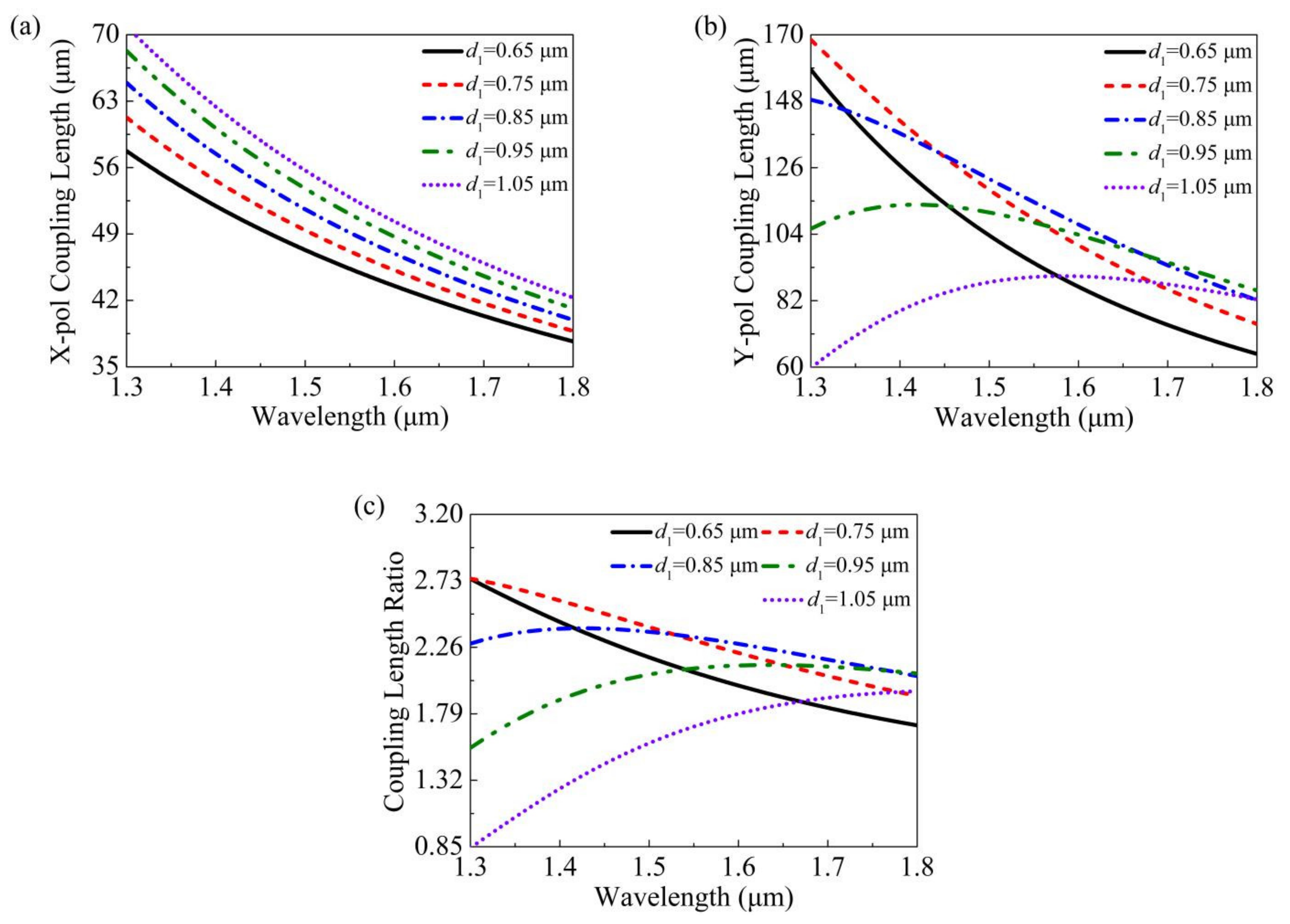
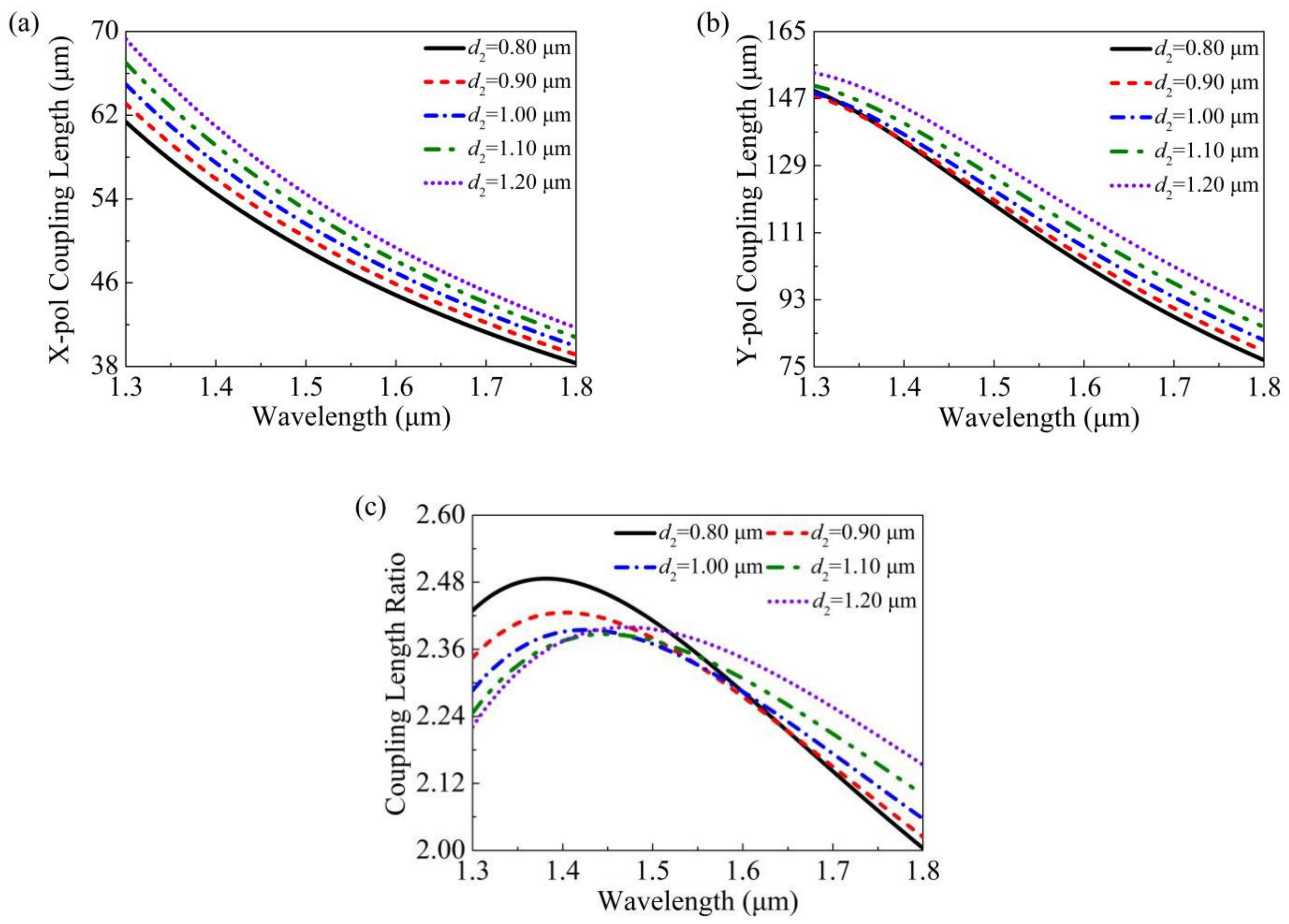
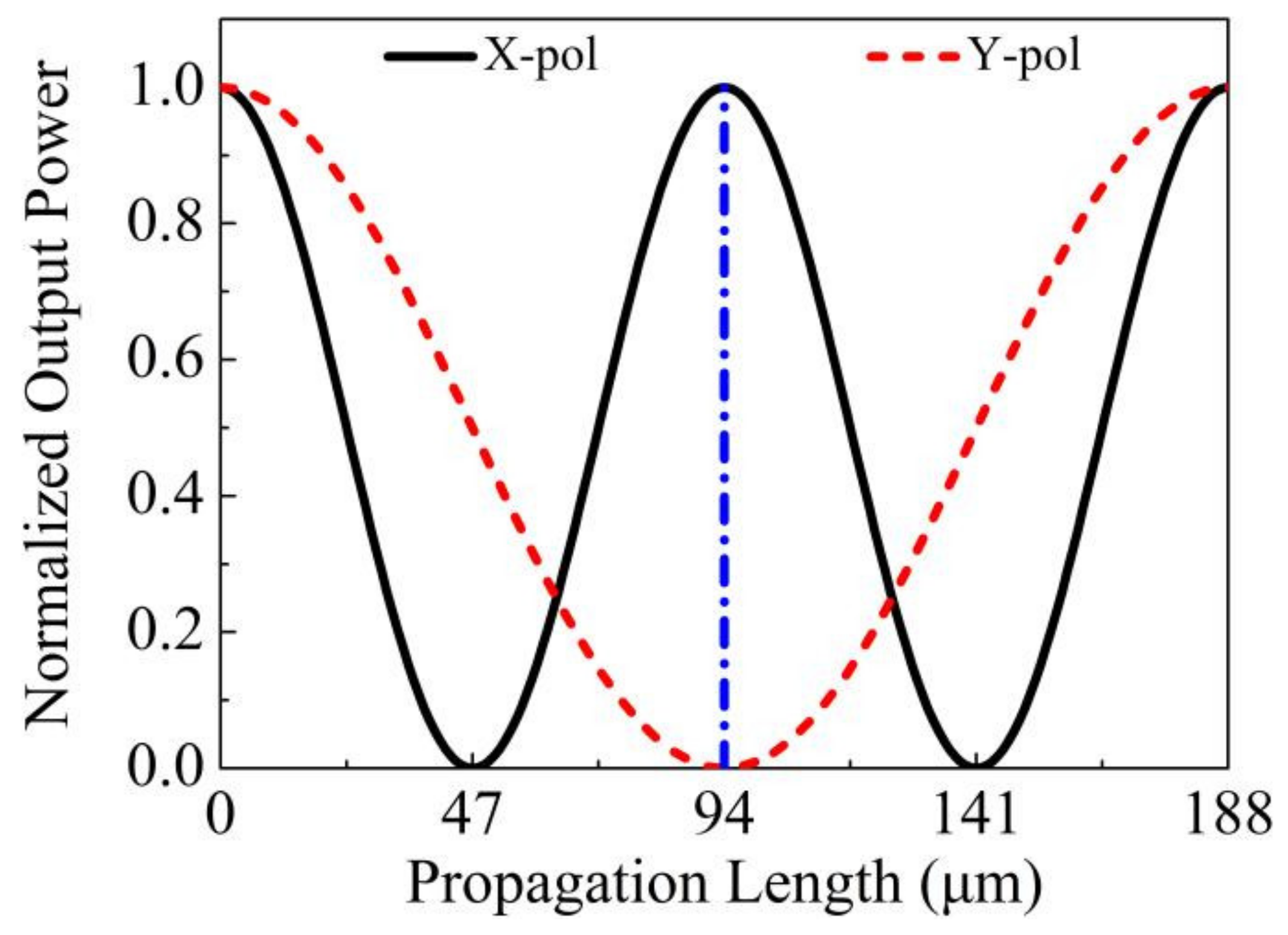
3. Simulation Results

The initial structural parameters of the LC-DC-PCF are set as follows: d₁ = 0.85 μm, d₂ = 1.00 μm, d₃ = 1.50 μm, d₄ = 1.60 μm, d₅ = 1.65 μm, and Λ = 2.10 μm. The relationships between the effective refractive indices of the X-pol and Y-pol even and odd modes of the LC-DC-PCF and the wavelength are shown in Figure 2a,b when the LC-DC-PCF is filled without and with LC E7, respectively. From Figure 2a, when the LC-DC-PCF is filled without LC E7, the effective refractive indices of the X-pol and Y-pol even and odd modes decrease with the increase in wavelength. The effective refractive index curves of the X-pol and Y-pol even modes are very close, and those of the X-pol and Y-pol odd modes are virtually overlapped. In other words, the effective refractive index differences between the X-pol and Y-pol even modes or X-pol and Y-pol odd modes are very small. Therefore, the values of the B_e and B_o are also very small. From Figure 2b, when the LC-DC-PCF is filled with LC E7, the effective refractive indices of the X-pol and Y-pol even and odd modes decrease with the increase in wavelength. This change trend is similar to that filled without LC E7. The effective refractive index curves of the X-pol and Y-pol odd modes are also nearly overlapped. However, the effective refractive index values of the X-pol and Y-pol even modes have an obvious change, respectively. In other words, the effective refractive index difference between X-pol and Y-pol odd modes is also very small, but the effective refractive index difference between X-pol and Y-pol even modes is a larger value. Therefore, the B_o will still be small, but the B_e will be large. The B_e and B_o of the LC-DC-PCF are shown in Figure 3 when the LC-DC-PCF is filled without and with LC E7. From Figure 3, the B_e and B_o are kept very small with the wavelength increase when the LC-DC-PCF is filled without LC E7. When the LC-DC-PCF is filled with LC E7, the B_o still keeps a small value, but the B_e increases. B_e varies from 6.7 × 10⁻³ to 1.2 × 10⁻² in the wavelength range of 1.3~1.8 μm, which is a relatively large mode birefringence compared with many previous studies. According to the above analysis, a large B_e can be introduced by filling LC E7 in the most central air hole.

To further explain the above phenomenon, Figure 4a,b shows the mode field distributions of the X-pol and Y-pol even and odd modes at wavelengths 1.3 and 1.8 μm, respectively, when the LC-DC-PCF is filled with LC E7. From Figure 4a,b, when the LC-DC-PCF is filled with LC E7, the mode field energies of the X-pol and Y-pol odd modes are mainly distributed in cores A and B at wavelengths 1.3 and 1.8 μm, respectively. According to previous work, this is the same as that of conventional DC-PCF. However, no matter at 1.3 or 1.8 μm, most of the mode field energy of the X-pol and Y-pol even modes is still distributed in cores A and B, but a small part is distributed in the most central air hole filled with LC E7. This is also why B_e is larger when the LC E7 is filled into the most central air hole. Therefore, the most central air hole filled with LC E7 can be regarded as a modulation core. At wavelengths 1.3 and 1.8 μm, the energy percentages of mode field energy of the X-pol and Y-pol even modes transmitted in the modulation core are 6.79%, 1.23%, and 6.96%, 3.46%, respectively. It can be seen from Figure 4a,b that the energy transmitted in cores A and B is much greater than that in modulation core. Therefore, the CL_X, CL_Y, and CLR can be analyzed using the DC-PCF coupling mode theory [42] and Equations (9)–(11).

Figure 5a,b shows the CL_X, CL_Y, and CLR of the LC-DC-PCF when the LC-DC-PCF is filled without and with LC E7, respectively. From Figure 5a, when the LC-DC-PCF is filled without LC E7, the CL_X, CL_Y, and CLR decrease approximately linearly with the wavelength increase. However, the difference between CL_X and CL_Y is small, which leads to smaller values and smaller changes of CLR. This phenomenon can be deduced from the results shown in Figure 2a and Equations (9)–(11). In addition, at a wavelength of 1.8 μm, the minimum values of the CL_X and CL_Y are 151 and 167 μm, respectively. At wavelengths of 1.3 and 1.8 μm, the largest and smallest CLR are 1.102 and 1.125, respectively. From Figure 5b, when the LC-DC-PCF is filled with LC E7, although the CL_X and CL_Y decrease approximate linearly with the increase in wavelength, the difference between the CL_X and CL_Y decreases gradually. However, the minimum difference is also much larger than when the LC-DC-PCF is filled without LC E7. With the increase in wavelength, CLR has a trend of increasing first and then decreasing. This is because the introduction of the modulation core produces a large B_e, leading to a large change in the effective refractive index of the X-pol and Y-pol even modes, which leads to the corresponding change of the CL_X, CL_Y, and CLR. At 1.3 μm, the maximum values of the CL_X and CL_Y are 65 and 148 μm, respectively. Additionally, in the wavelength range of 1.3~1.8 μm, the minimum and maximum values of CLR are 2.057 and 2.395, respectively. Therefore, when the LC-DC-PCF is filled with LC E7, the maximum CL_X and CL_Y are smaller than the minimum CL_X and CL_Y when the LC-DC-PCF is filled without LC E7, and the CLR value in the range of 1.3~1.8 μm is closer to the optimal CLR = 2. In other words, the LC-DC-PCF is filled with LC E7; if CLR = 2 is obtained at a certain wavelength in the communication band and the CL_X and CL_Y have a small value, the proposed LC-DC-PCF PBS may obtain better beam splitting characteristics. Therefore, in the following, we will discuss the change rule of the CL_X, CL_Y, and CLR of the proposed LC-DC-PCF with the change of each structural parameter.

The change rules of the CL_X, CL_Y, and CLR of the proposed LC-DC-PCF with wavelengths for different d₁ are shown in Figure 6a–c. From Figure 6a, when d₁ increases from 0.65 to 1.05 μm, the CL_X increases gradually in the whole wavelength range of 1.3~1.8 μm. However, the increased extent of the CL_X at a short wavelength is larger than that at a long wavelength. From Figure 6b, when d₁ increases from 0.65 to 0.75 μm, the CL_Y also increases gradually in the whole wavelength range of 1.3~1.8 μm. However, when d₁ increases from 0.75~0.95 μm, the CL_Y decreases gradually at the short wavelength, and the decreasing range is larger, while the CL_Y increases gradually at the long wavelength and the increasing range is smaller. When d₁ increases from 0.95 to 1.05 μm, the CL_Y decreases gradually in the wavelength range of 1.3~1.8 μm, while the CL_Y has a larger decrease at a short wavelength and a smaller decrease at a long wavelength. On the whole, the change range of the CL_Y in the short wavelength is larger than that in the long wavelength when d₁ increases from 0.75 to 1.05 μm. From Figure 6c, the CLR also increases in the whole wavelength range of 1.3~1.8 μm with the increase in d₁ from 0.65 to 0.75 μm, then decreases in the short wavelength and increases in the long wavelength with the increase in d₁ from 0.75 to 0.95 μm, and finally decreases in the whole wavelength range of 1.3~1.8 μm with the increase in d₁ from 0.95 to 1.05 μm. On the whole, the CLR occurs to fluctuate in the range from 0.84 to 2.74. When d₁ is 0.85 μm, the minimum and maximum of the CLR are 2.3948 and 2.0568, respectively, and the difference between them is 0.338.

The change rules of the CL_X, CL_Y, and CLR of the proposed LC-DC-PCF with wavelengths for different d₂ are shown in Figure 7a–c. From Figure 7a, when d₂ increases from 0.80 to 1.20 μm, the CL_X maintains a relatively stable increase in the whole wavelength range of 1.3~1.8 μm. However, overall, the changing amplitude of the CL_X is not very large. From Figure 7b, when d₂ increases from 0.80 to 1.00 μm, the CL_Y changes little at the short wavelength but increases steadily at the long wavelength. The CL_Y also maintains a relatively stable increase in the whole wavelength range of 1.3~1.8 μm when d₂ increases from 1.00 to 1.20 μm. However, on the whole, the changing amplitude of the CL_Y is slightly larger than that of the CL_X. According to the change rule of the CL_X and the CL_Y with d₂, the CLR decreases gradually at the short wavelength and increases gradually at the long wavelength when d₂ increases from 1.00 to 1.20 μm. In addition, it is found that the larger the d₂, the smaller the difference between the minimum and maximum CLR. When d₂ is 1.20 μm, the minimum and maximum of the CLR are 2.3994 and 2.1534, respectively, and the difference between them is only 0.246.

The change rules of the CL_X, CL_Y, and CLR of the proposed LC-DC-PCF with wavelengths for different d₃ are shown in Figure 8a–c. From Figure 8a,b, the CL_X and CL_Y decrease gradually when d₃ increases from 1.30 to 1.70 μm in the whole wavelength range of 1.3~1.8 μm. The decreasing amplitude of the CL_Y is slightly larger than that of the CL_X. Thus, it can be seen from Figure 8c that the CLR maintains a relatively stable decrease when d₃ increases from 1.30 to 1.70 μm in the whole wavelength range of 1.3~1.8 μm. In addition, we also find that the larger the d₃, the smaller the difference between the minimum and maximum CLR. When d₃ is 1.70 μm, the minimum and maximum of the CLR are 2.2541 and 1.9409, respectively, and the difference between them is only 0.3132.

The change rules of the CL_X, CL_Y, and CLR of the proposed LC-DC-PCF with wavelengths for different d₄ are shown in Figure 9a–c. From Figure 9a,b, the CL_X and CL_Y gradually decrease when d₄ increases from 1.40 to 1.80 μm in the whole wavelength range of 1.3~1.8 μm. The decreasing amplitude of the CL_X and CL_Y is nearly the same. Therefore, as shown in Figure 9c, the CLR has a small change when d₄ increases from 1.40 to 1.80 μm in the whole wavelength range of 1.3~1.8 μm. In addition, when d₄ is 1.40 μm and 1.8 μm, the minimum and maximum of the CLR are 2.0436, 2.3835, and 2.0653, 2.3996, respectively. The maximum difference of the CLR is only 0.0217.

The change rules of the CL_X, CL_Y, and CLR of the proposed LC-DC-PCF with wavelengths for different d₅ are shown in Figure 10a–c. From Figure 10a,b, the curves under different d₅ are virtually coincident, that is to say, the CL_X and CL_Y do not change when d₅ increases from 1.40 to 1.80 μm in the whole wavelength range of 1.3~1.8 μm. Certainly, the CLR will not change with the change of d₅ in the whole wavelength range of 1.3~1.8 μm.

The change rules of the CL_X, CL_Y, and CLR of the proposed LC-DC-PCF with wavelengths for different Λ are shown in Figure 11a–c. From Figure 11a it can be seen that the CL_X increases gradually in the whole wavelength range of 1.3~1.8 μm when Λ increases from 1.90 to 2.30 μm. From Figure 11b, although the CL_Y also increases gradually in the whole wavelength range of 1.3~1.8 μm when Λ increases from 1.90 to 2.30 μm, the increasing amplitude of the CL_Y is larger at the shorter wavelength and smaller at the longer wavelength. Hence, when Λ increases from 1.90 to 2.30 μm, the CLR increases gradually, but the increased amplitude of the CLR is larger at the shorter wavelength and smaller at the longer wavelength. When Λ is 1.90 μm, the maximum and minimum of the CLR are 2.0778 and 1.9035, respectively, and the difference between them is only 0.1743. When Λ is 2.30 μm, the maximum and minimum of the CLR are 2.2349 and 2.8137, respectively, and the difference between them can reach 0.5877. That is to say, the difference between the maximum and minimum of the CLR becomes larger when Λ increases from 1.90 to 2.30 μm.

4. Discussion

According to the above analysis, considering the influences of structural parameters on the CL_X, CL_Y, and CLR of the proposed LC-DC-PCF, a set of final parameters is set as d₁ = 1.00 μm, d₂ = 0.90 μm, d₃ = 1.50 μm, d₄ = 1.65 μm, d₅ = 1.70 μm, and Λ = 2.10 μm. The relationships of the CL_X, CL_Y, and CLR of the proposed LC-DC-PCF with wavelengths obtained under the final parameters are shown in Figure 12. From Figure 12, the CL_X decreases with the increase in wavelength, while the CL_Y first increases and then decreases with the increase in wavelength. At the same time, we notice that the CL_X and CL_Y have a relatively small length, and the maximum length is only 98.4 μm. With the increase in wavelength, the CLR first presents a gradual upward trend, but the upward trend gradually decreases and finally has a nearly flat change. When the wavelength is equal to 1.604 μm, the CLR is equal to 2. Before the wavelength of 1.604 μm, the range of the CLR change is 1.22~2.0. After the wavelength of 1.604 μm, the range of the CLR change is only 2.0~2.036.

We mentioned earlier that, when the CLR = 2 and the CL_X and CL_Y are shorter, the proposed PBS is easier to obtain the shortest L_S. Therefore, the relationships between the X-pol and Y-pol P_out in the core A of the proposed LC-DC-PCF PBS and L_P at the wavelength of 1.604 μm are shown in Figure 13. From Figure 13, when the L_P is 0 μm, P_out of the X-pol and Y-pol is the maximum because the initial incident light enters the core A. When L_P is 94 μm, P_out of the X-pol reaches the maximum again, while P_out of the Y-pol reaches 0 for the first time. This shows that only X-pol light exists in core A, and Y-pol light only exists in core B. When L_P is 188 μm, P_out of the X-pol and Y-pol is once again maximum. It indicates that both the X-pol and Y-pol light completely exist in core A again, just as in the initial incident. That is enough to show that P_out of the X-pol and Y-pol changes periodically with the increase in L_P. That is to say, the X-pol and Y-pol light propagate periodically in cores A and B. When the X-pol and Y-pol light are separated to cores A and B for the first time, respectively, the corresponding L_P = 94 μm is the shortest L_S.

When L_P is 94 μm, the relationship of the ER in the core A of the proposed LC-DC-PCF with wavelengths is shown in Figure 14. It can be seen from Figure 14 that with the increase in wavelength, the ER first increases and then reaches the first maximum peak value of 60.3 dB at the wavelength of 1.386 μm. Then, as the wavelength continues to increase, the ER first decreases and then increases; a relatively gentle ER valley is formed between 1.386 and 1.619 μm, and then reaches the second maximum peak value of 72.2 dB at the wavelength of 1.619 μm. After 1.619 μm, the ER decreases gradually with the increase in wavelength. Between 1.352 and 1.701 μm, the ER is greater than 20 dB. In other words, the splitting bandwidth of the proposed LC-DC-PCF PBS can reach 349 nm (1.352~1.701 μm), which can cover the whole of the E + S + C + L + U communication bands.

The comparisons between the proposed LC-DC-PCF PBS and reported DC-PCF PBS are shown in

Table 1. Comparisons between the proposed LC-DC-PCF PBS and reported DC-PCF PBS.

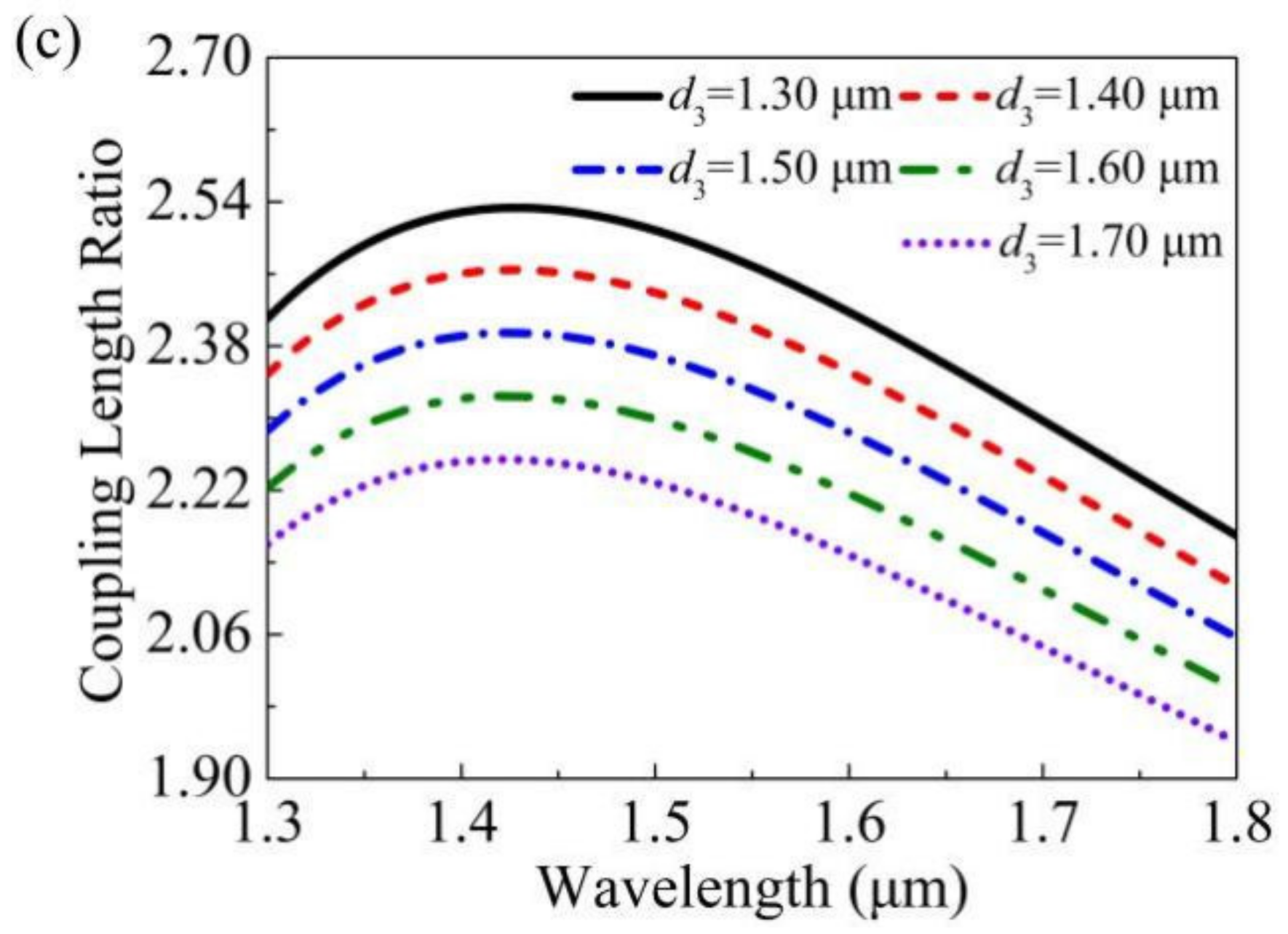
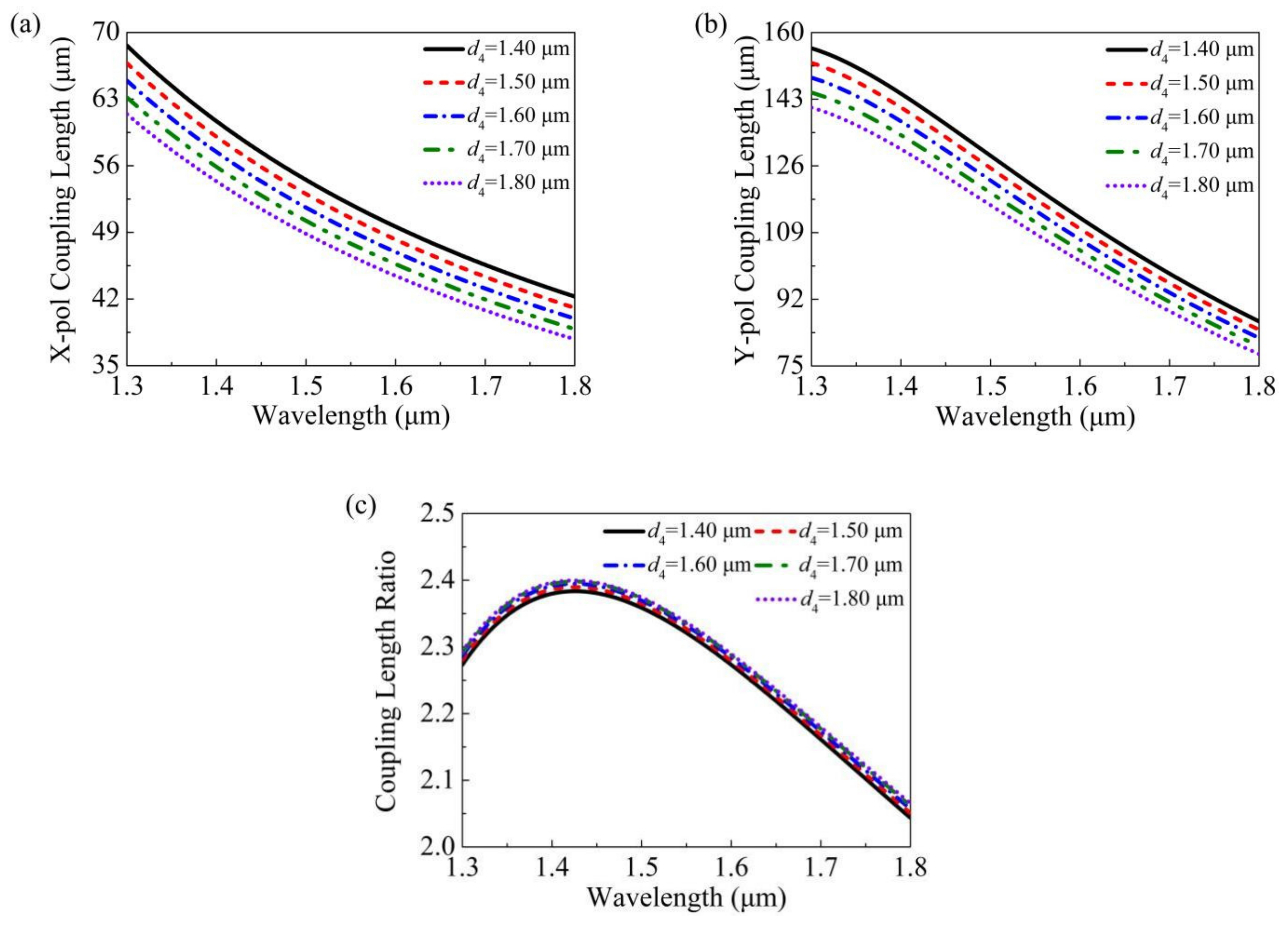
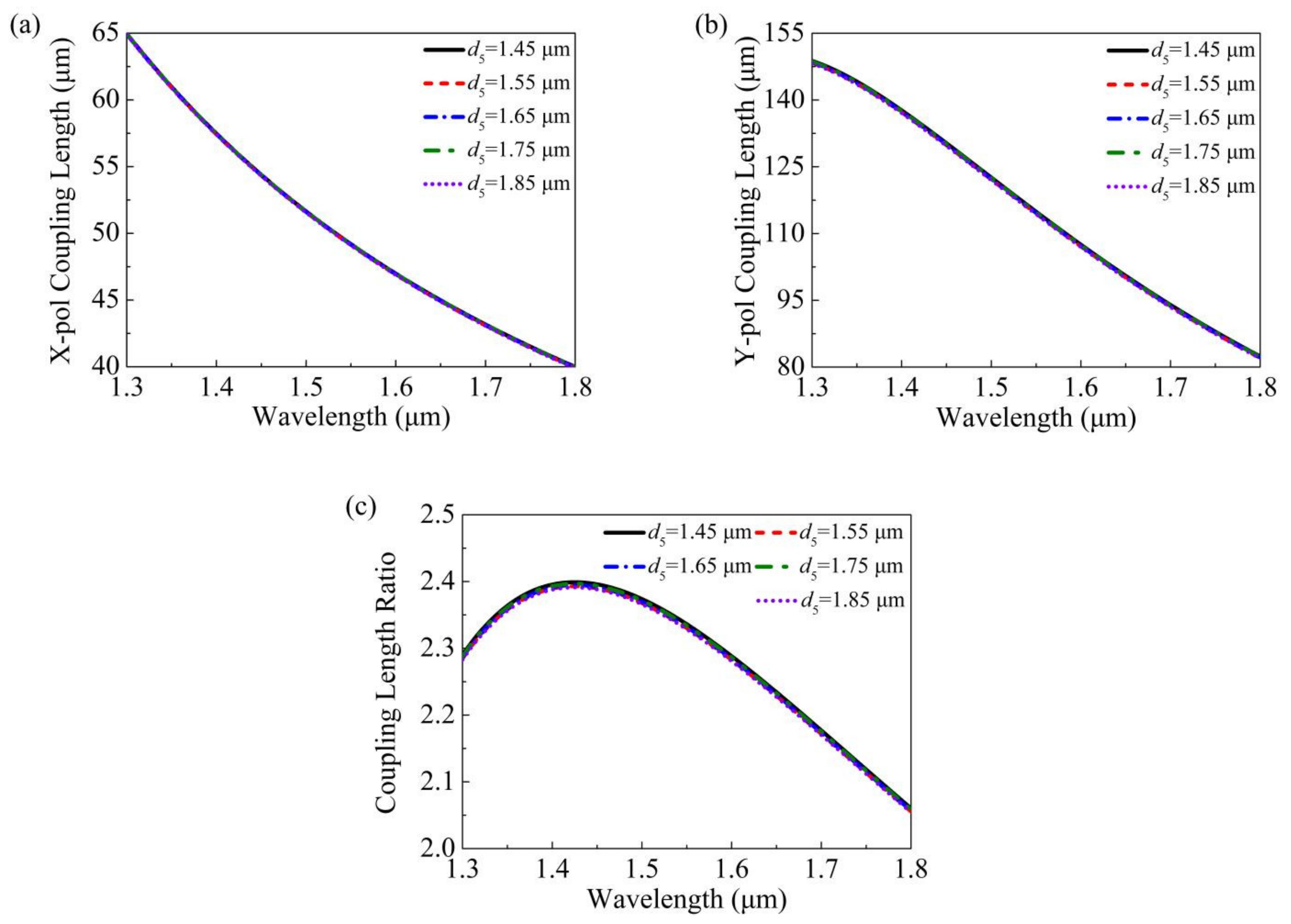
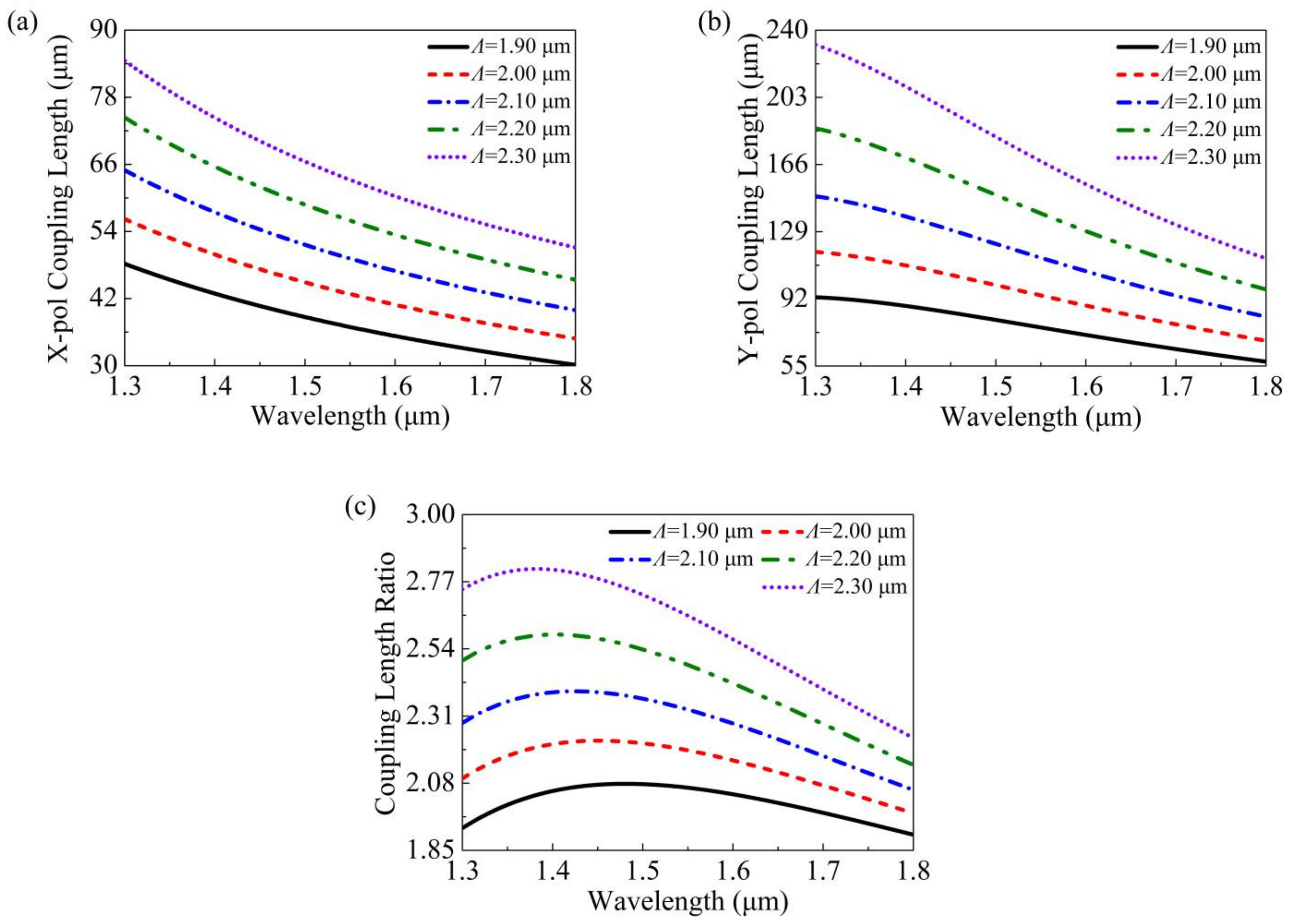
Ref.	Structural Characteristics	Splitting Bandwidth	LS	Max ER
[16]	Filling liquid crystal E7 in one air hole	250 nm	175 μm	80.7 dB
[24]	Filling liquid crystal E7 in all air holes	150 nm	890.5 μm	45 dB
[25]	Filling liquid crystal E7 in six air holes and filling As2S3 in one air hole	88 nm	111.2 μm	55 dB
[26]	Filling liquid crystal E7 in six air holes	3 nm	5678 μm	<30 dB
[27]	Filling liquid (ethanol) in six air holes and filling Ti in two air holes	32.1 nm	83.9 μm	44.05 dB
[38]	Filling elliptical gold wire in one air hole	70 nm	1079 μm	174.92 dB
[39]	Coating gold film in one air hole	318 nm	188 μm	<82dB
[40]	Filling silver wire in one air hole	250 nm	577.5 μm	42 dB
This work	Filling liquid crystal E7 in one air hole	349 nm	94 μm	72.2 dB

. From Table 1, since the cost of liquid crystal E7 is significantly lower than that of gold, from the perspective of structural fabrication and cost reduction, the proposed LC-DC-PCF PBS in this work is only filling liquid crystal E7 in one air hole, does not fill other materials, and does not contain elliptical air holes, which not only reduces the fabrication difficulty but also reduces the fabrication cost. In addition, only L_S of the DC-PCF PBS reported in Ref. [27] is slightly shorter than that of the proposed LC-DC-PCF PBS, but the splitting bandwidth of the proposed LC-DC-PCF PBS is more than ten times that of the DC-PCF PBS reported in Ref. [27]. Moreover, the maximum ER of the DC-PCF PBS reported in Refs. [16,38,39] is slightly higher than that of the proposed LC-DC-PCF PBS, but the proposed LC-DC-PCF PBS has the widest splitting bandwidth and the shortest L_S compared with other results reported in Refs. [16,38,39]. Because the splitting bandwidth of the DC-PCF PBS is the wavelength range corresponding to the ER greater than 20 dB, even if the maximum ER of a certain wavelength is large, the final splitting bandwidth is not necessarily the widest, so it is only necessary to compare the L_S and splitting bandwidth. To summarize, it can be seen that the proposed LC-DC-PCF PBS in this work can obtain a shorter L_S and wider splitting bandwidth at the same time and has a lower cost and simpler fabrication process.

The fabrication methods of the PCF mainly include the stack-and-draw method, femtosecond laser drilling method, 3D-printing method, etc., [3,43,44,45]. In addition, the technology of selectively filling LC in some or all of the air holes has also been very mature; in the past three years, there have been many reports on the practical fabrication of PCFs selectively filled with LC material [46,47,48,49,50]. In this work, the fabrication steps of the proposed LC-DC-PCF are as follows: first, the proposed LC-DC-PCF is fabricated by the stack-and-draw method. With this method, the high-purity silica glass tubes of different diameters and wall thicknesses are arranged according to the designed structure. Two high-purity silica solid rods with the same diameter are used to replace the high-purity silica glass tubes on the left and right sides of the most central high-purity silica glass tubes, respectively, to form the LC-DC-PCF preform, and then the LC-DC-PCF preform is drawn into the designed LC-DC-PCF. In the fabrication process, parameters such as temperature, air pressure, and traction speed must be controlled simultaneously to obtain the LC-DC-PCF with an excellent final structure. Finally, the LC E7 is selectively filled in the central air hole of the proposed LC-DC-PCF by femtosecond laser-assisted selective infiltration technology. Among them, the technology mainly includes several steps, such as UV curable, normal splicing, laser cutting, capillary infiltration, etc.

In the actual fabrication process for the proposed LC-DC-PCF, some unnecessary tolerances will inevitably occur in the diameter of the air hole, which will lead to a ±1% change in the final L_S. When the final L_S changes ±1%, the relationships of the ER in the core A of the proposed LC-DC-PCF with wavelength are shown in Figure 15. From Figure 15, when the final L_S changes -1% and +1%, the wavelength ranges with ER greater than 20 dB are 1.346~1.713 μm and 1.357~1.689 μm, respectively, which can cover the whole of the E + S + C + L + U communication band. This indicates that the proposed LC-DC-PCF has good fabrication fault tolerance.

5. Conclusions

In summary, a novel LC-DC-PCF PBS based on the DC-PCF-coupled mode theory is proposed. Using the FV-FEM, the effective refractive indices of the X-pol and Y-pol even and odd modes, the B_e and B_o, the CL_X, CL_Y, and CLR of the LC-DC-PCF filled without and with LC E7 are analyzed and compared. By optimizing the influences of cladding microstructure parameters on the CL_X, CL_Y, and CLR of the LC-DC-PCF, the CLR is exactly equal to 2 at a wavelength of 1.604 μm. The relationships between the X-pol and Y-pol P_out in core A of the proposed LC-DC-PCF PBS and L_P at the wavelength of 1.604 μm are investigated. The ERs in core A achieve 60.3 and 72.2 dB at wavelengths 1.386 and 1.619 µm, respectively. The final L_S is 94 μm, and the splitting bandwidth can reach 349 nm (1.352~1.701 μm), covering the whole of the E + S + C + L + U communication bands. The proposed LC-DC-PCF PBS has an ultra-short L_S and ultra-wide splitting bandwidth, so it can be applied in laser, sensing, and communication systems.