Abstract
With the rapid development of virtual/augmented reality and cloud services, the capacity demand for optical communication systems is ever-increasing. To further increase system capacity, current researches focus on efficient and reliable system management, in which the transmission performance should be accurately estimated. The wavelength-dependent gain effects of erbium-doped fiber amplifiers (EDFAs) have a great impact on transmission performance, and therefore a precise EDFA gain model is required. In this paper, we firstly summarize the underlying principles and structures of EDFA, and introduce the gain performance and challenges in modeling. Then, we review the EDFA gain modeling methods. We categorize these researches into analytical modeling methods and machine learning (ML)-based modeling methods, and discuss their feasibilities and performances. In addition, we discuss the remaining problems for applying the models in a system and the possible directions for future investigations.
1. Introduction
To support various emerging Internet applications such as virtual/augmented reality, cloud services and video streaming, the optical transmission system is facing the ever-rising demand for increasing capacity. Over the past few years, advanced technologies including probability constellation shaping and forward error correction have been widely applied, and have brought the system capacity close to the theoretical limit [1]. Moreover, numerous current researches to further improve the system capacity are proposed through optimizations in the physical layer [2] or efficient resource allocation in the controlling layer [3].
To realize the above-mentioned optimization techniques, accurately modeling erbium-doped fiber amplifiers (EDFAs) in optical networks is of vital importance. Firstly, to optimize operations in the physical layer such as optical power optimization [4], the system is planned based on an accurate physical layer model, in which the EDFA model is an important component. Secondly, for resource allocation algorithms in the controlling layer such as routing and wavelength assignment (RWA) [5], the quality of transmission (QoT) of the system should be strictly controlled to ensure an error-free transmission. QoT is degraded due to multiple physical impairments experienced by signals [6], and it should be accurately estimated for system management. One of the keys for QoT estimation is EDFA modeling, since some physical impairments are crucially related to EDFAs [7,8]. The gain of EDFA determines the signal power level of each channel, which further affects the magnitude of nonlinear impairments in fiber. Besides, the amplified spontaneous emission (ASE) noise generated by the EDFA is a major noise in optical systems. Therefore, an EDFA model that calculates its gain and noise power is needed for advanced system management, while the modeling accuracy is a decisive factor for the reliability of management algorithms [9].
The gain of EDFA can be characterized as a complicated function of its input wavelength, input signal configuration and control settings, etc. Firstly, the EDFA gain spectrum is nonflat in the static state due to wavelength-dependent effects such as spectral hole burning (SHB) [10,11] and saturation [12]. Secondly, the EDFA gain spectrum varies under diverse signal configurations due to the variation of the population inversion. Further dynamic gain excursion may occur due to the enabled pump power adjustment under certain control settings [13].
The ASE noise power of EDFA can be calculated based on a physical model, and it is mainly determined by the gain and noise figure (NF) [14,15]. For traditional methods, accurate gain and NF modeling is the basis of the ASE noise power calculation. Complex characterizations of the gain and noise figure, such as wavelength-dependent properties, lead to a complex characterization of ASE noise. In addition, ASE noise accumulates over multi-span propagation, which makes the modeling more difficult. For data-driven-based methods, ASE noise power is strongly correlated with gain and has similar characterizations. Some ASE noise models can be derived using schemes that are similar to gain modeling schemes [16,17]. Models that simultaneously calculate the signal power and ASE noise power have also been proposed [18,19].
Currently, many researches primarily focus on EDFA gain modeling. In this paper, we summarize the EDFA gain characterization and review the recent progress of modeling techniques. The rest of the paper is organized as follows.
In Section 2, we review the underlying principles and structures of EDFA, and introduce the gain characterization.
In Section 3, we discuss the scheme and performance of analytical EDFA gain models.
In Section 4, we discuss the scheme and performance of machine learning (ML)-based EDFA gain models.
In Section 5, we discuss the future possible directions for EDFA gain modeling.
In Section 6, the conclusions for this paper is provided.
2. Principle and Characterization of EDFA
The core component for amplifying optical signal powers in EDFA is erbium-doped fiber (EDF). The doped erbium (Er3+) ions in EDF can be limited to a two-level system [20,21], processing transitions between the upper energy level (i.e., level) and the lower energy level (i.e., level). When signals of about 1550 nm wavelength and pump lights of 980 nm or 1480 nm wavelength are injected, Er3+ ions process transitions in mainly three approaches, as shown in Figure 1 [22].
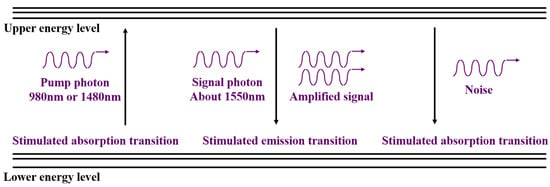
Figure 1.
Limited two-level system of erbium-doped fiber.
With the excitation of pump lights, Er3+ ions at a lower energy level jump to an upper energy level through stimulated absorption transition, forming a population inversion. Meanwhile, with the excitation of signal lights, Er3+ ions at the upper energy level jump to the lower energy level through stimulated emission transition, emitting photons identical to the incident ones. During this process, the signal powers are amplified. The rest of the Er3+ ions at the upper energy level jump to the lower energy level through spontaneous emission transition, emitting photons with a random phase and wavelength. Some of these photons can be captured and amplified in EDF, therefore generating the ASE noise, which is the major noise in current optical communication systems.
Under a steady-state condition, these three transition processes reach dynamic equilibrium, which indicates that the fractional population on both the lower level and the upper level can be regarded as constant. Denoting and as the fractional population of the lower/upper state along the EDF, they are given by [21]:
where is the spontaneous lifetime of the upper level, and is the density of active atoms within an active volume of the cross-sectional area . , , and indicate the forward pump power, backward pump power, signal power and ASE noise power at wavelength , respectively. Optical power can be expressed in units of photons per unit of time. The power evolution of the forward pump, backward pump, signal and ASE noise along the EDF can be described by:
where , and are the background loss of the forward pump, backward pump, and signal, respectively. Similarly, , and are the absorption/emission cross-sections for the two pumps and the signal. , and are the signal overlap factors for the two pumps and the signal. The parameters can be obtained by complex experimental measurements of EDF, and the equations can be solved with the fourth-order Runge–Kutta method [20].
Based on the EDF, combining pump light sources and other passive optical structures, an EDFA is packaged for signal amplification in optical systems [23]. The basic structure of EDFA is shown in Figure 2, containing the EDF, pump source laser, isolator, coupler and filter. The isolator is used to transmit signals in one direction only [24]. The coupler is used to combine the injected pump lights and signal lights. The filter is used to remove the generated noise. The forward pumping scheme, backward pumping scheme and bidirectional pumping scheme are all feasible structures for EDFAs. For a more general consideration, a bidirectional pumping structure is shown here.

Figure 2.
Basic structure of erbium-doped fiber amplifier.
However, to achieve a better performance such as lower noise power, and to meet diverse requirements in various systems such as wide-band amplification, some additional optimized structures for EDFA are proposed [25,26,27,28]. In most typical commercial EDFAs, a two-stage amplification is applied to improve the amplifying efficiency and reduce the NF [29]. A gain flattening filter (GFF) is used to mitigate the power non-flatness of EDF due to wavelength-dependent parameters such as absorption/emission cross-sections and overlap factors [30,31]. Additionally, three different operation modes are commonly enabled in EDFAs [32], including automatic gain control (AGC), automatic power control (APC), and automatic pump current control (ACC). In the AGC mode, a fixed average gain is maintained by dynamically adjusting the pump power. In the APC mode, a fixed average output power is maintained by dynamically adjusting the pump power. In the ACC mode, a fixed pump laser current is maintained.
In such typical commercial EDFAs, modeling the gain performance remains a challenge due to the following reasons. Firstly, the gain model itself is rather complicated due to the underlying physics and mathematics. It is wavelength-dependent, and further dynamic excursion occurs when the input signal varies (i.e., loaded channel reconfiguration and signal power fluctuation), especially for EDFAs under the AGC and APC modes. Secondly, the gain models for EDFAs of different makes are inconsistent. Various physical designs such as controlling loops and filters are utilized in EDFAs to meet diverse requirements such as the gain setting ranges and the transmitting bands. Therefore, the models are difficult to uniformly derive. Thirdly, fabrication errors cause inaccuracy in gain models. EDFAs of the same make may also possess different characterizations due to fabrication errors in the inner structure. These subtle discrepancies are difficult to describe and correct. To achieve a reliable EDFA model, several approaches have been investigated. They are summarized and discussed in the following sections.
3. Analytical EDFA Gain Models
Traditional methods provide interpretable analytical models to calculate the EDFA gain spectrum. These models obtain device parameters and calculate the gain based on theories of the underlying modules. Two approaches for analytical modeling, respectively derived from physical principles of the EDF and the AGC mode, are discussed as follows.
Equations (3)–(6) mentioned in Section 2 provide a detailed analysis for the signal power evolution along EDF. It is capable of modeling the gain characterization for the inner structure of an EDFA only. The equation requires tens of underlying parameters, which are difficult to realize practically. In [20], the simplification of the equation is discussed, and based on experimentally measured monochromatic absorption data, an EDF modeling result within a 0.5-dB error is achieved. In [22], the analytical models for different scenarios are summarized. However, these models are far from being practical applications due to their high complexity and limited consideration of the EDFA structure. First, the transcendental equation is rather complicated, and some of the parameters are difficult to obtain in packaged EDFA. Furthermore, additional components in EDFAs, such as the GFF, may influence the shape of the gain spectrum. The diverse designs of vendors, such as the different structure designs and the different filter shapes, make these influences difficult to uniformly estimate. Therefore, even though the model provides detailed insights into the power evolution in EDF, it is difficult to derive an accurate model of the overall gain in typical commercial EDFAs through this equation.
Another analytical model for EDFA gain characterization is a simplified center of mass (CM) model. It provides a simple expression for measuring the dynamic gain excursion caused by AGC, which is the commonly used operation mode in optical systems [33]. The model is given as:
where represents the gain experienced by the wavelength {} when a set of n wavelengths {} is input into the EDFA, represents the gain for wavelength when all of the WDM channels are input into the EDFA, and represents the gain for wavelength when only is input into the EDFA. The equation calculates an approximative gain excursion as AGC EDFA adjusting the pump power to maintain the constant average gain. Only a few easily measured EDFA gain spectra under certain input conditions are needed in the equation.
The CM model is capable of estimating the gain of AGC EDFAs under diverse input signals and can be easily generalized for multiple devices. However, its accuracy is limited since some internal effects are ignored. First, the CM model ideally assumes a constant shape of the EDFA gain spectrum, which is inconsistent with the situation in actual systems. Besides, the model focuses on gain excursion caused by the loaded channel configuration, while ignoring the fluctuation of channel powers. Therefore, the model is practically easily obtained but with a relatively low accuracy.
In general, analytical estimating methods provide interpretable models but cannot comprehensively consider all internal effects of the EDFA. In addition, analytical models have some common defects when deployed in practical systems. For deployed optical links, it is difficult to obtain the internal parameters required by the model. Additionally, the aging of devices can lead to a time-varying change of EDFAs, and analytical models lack the ability to track this change. These defects remain a limitation factor for applying analytical models in practical systems.
4. ML-Based EDFA Gain Models
With data-driven approaches, ML-based models provide the mapping relationship between input and output features, which is proved to achieve an exceptional performance when the physics and mathematics are too difficult to present. Currently, ML-based methods are the main research direction for EDFA gain modeling, and several studies have been explored.
In these modeling processes, data collection is the key. Datasets of EDFA gain spectra (or output power spectra) under various input conditions are required. Actually, for the commonly used C-band EDFAs, dozens of channels are utilized, so the configuration of the input signal can be very diverse, which leads to a complex feature space. Furthermore, the EDFA gain performance under different inputs varies case by case, so huge datasets containing various situations are needed to cover the complex features in modeling. In current studies, such huge datasets are usually automatically collected in the experimental system, which is a rather time-consuming process. A typical experimental setup is shown in Figure 3. Optical signals are generated by a comb source or an ASE noise source, which is filtered by a wavelength selective switch (WSS) to select the active channels and finetune the shape of the channel power spectrum. The filtered optical signal is used as the input of the device under test (DUT), whose input and output power spectra are captured by optical channel monitors (OCM). A controller is used to control all the devices and automate the data collecting process. After the experimental data collection, the data samples are fed into ML-based training schemes. Several ML-based schemes for training the EDFA gain model have been proposed.
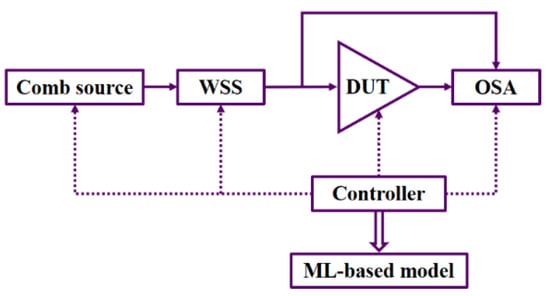
Figure 3.
Experimental setup of EDFA data collection.
First, the neural network (NN)-based EDFA gain model is investigated. In [34], a multilayer perceptron (MLP) NN model that contains two hidden layers is used to estimate the EDFA gain excursion on different input signal configurations. The input layer of the NN model represents the channel input powers, total input power and gain setting, and the output layer of the NN model represents the gain offset from the full-loaded gain profile. About 50,000 data samples of gain profiles corresponding to diverse channel loadings are measured under different EDFA gain settings and total input powers. Trained on this dataset, the model shows a maximum gain prediction error of 0.18 dB and a standard deviation of the prediction error of 0.019 dB. In [35], a set of NNs are used to estimate the output power spectrum of EDFA based on its input power spectrum. A separate NN model that contains four hidden layers is created for each output channel. The input layer of the NN model represents the channel input powers, and the output layer of the NN model represents the output power for the specific channel. Trained on data samples of EDFA input and output spectra under different channel loadings, the model achieves a root mean square error (RMSE) of 0.08 dB, 0.18 dB, and 0.27 dB under input power dynamic ranges of +/− 3, 6, and 9 dB, respectively. These NN-based models can accurately predict the gain spectrum for a specific EDFA under diverse channel configurations with an acceptable complexity.
To generalize the EDFA gain model to multiple devices of the same make, an NN-based modeling approach is further proposed in [36]. An NN model containing two hidden layers is utilized. The input layer of the NN model represents the channel input powers, total input and output powers, and the output layer of the NN model represents the channel output powers. Jointly trained on a minimum dataset of 1600 measured spectra on each amplifier, a unified generalized model is used to estimate the gain of three EDFAs of the same make. The generalized model achieves a mean square error (MSE) below 0.06 dB2. The model accurately predicts the EDFA gain spectrum under diverse channel configurations. Furthermore, it is generalizable to different amplifier operation regimes and can be extended to multiple physical devices of the same make.
To further reduce the modeling error and training complexity for completely data-driven NN models, hybrid ML models that combine the analytical calculations and the ML-based schemes have been proposed. In [37], a hybrid ML gain model for an EDFA under AGC mode is discussed. Equation (3), which estimates the gain offset of an AGC EDFA, is used as prior knowledge and fed into the NN model. A separate NN that contains four hidden layers is built for each output channel. The input layer of the NN model represents the channel input powers and the analytically estimated output channel powers, and the output layer of the NN model represents the output power for the specific channel. Compared to the simple NN models, the hybrid ML scheme increases the modeling accuracy by 10.5%, reduces the training sample size by 33% and reduces the training time by 37%. In [38], the hybrid ML gain model for an EDFA under ACC mode is discussed. It is assumed that the gain curve of an ACC EDFA is solely defined by a given average population inversion. Therefore, an arbitrary nonflat input power condition can be simplified to a corresponding flat input power condition with the same population inversion. This relationship of input powers is delivered by an extended Saleh equation [20]. Through linear regressions, the gain spectrum for flat input powers can be delivered by an experimentally measured look-up table. The model shows 0.05 dB of RMS error in the EDFA gain prediction and 0.15 dB of RMS error in the output power prediction after 12 cascaded EDFAs.
In general, ML-based EDFA gain models can achieve a high accuracy without considering the underlying principles, but some of them still require a large dataset measured on each specific device, especially when the EDFA is under AGC or APC mode. For further applications in systems with a low modeling complexity, the generalizability of ML-based models should be optimized, while new modeling schemes are needed to reduce the huge amount of required data.
5. Future Work
To support the performance estimation, system management and optimization in optical networks, an accurate EDFA gain model is needed. In practical systems, the requirement for EDFA gain models is to estimate the nonflat gain spectrum under the different input signals and operating conditions of each EDFA.
In this paper, we review EDFA gain modeling techniques. Analytical approaches provide interpretable models, but with a limited accuracy. ML-based approaches provide accurate models, but require huge datasets in most scenarios. Therefore, there are still some challenges in EDFA gain modeling, and possible directions for future investigations are discussed as follows:
- Analytical models that consider all modules and effects. The current analytical models only represent the principle of a component in EDFA, which is an important cause of its inaccuracy. Therefore, to model the gain performance of the overall EDFA, all the inner modules need to be considered in analytical models.
- ML-based modeling schemes using small datasets. The main factor in modeling that leads to a high complexity is the time-consuming data collection process, as most ML-based EDFA models require a large dataset. Therefore, to reduce the cost of the ML-based modeling process, new modeling schemes that trained on a small dataset are needed.
- ML-based modeling schemes with a better generalizability. Although EDFAs without the same make may possess similar characterizations, their gain model cannot be easily generalized to other devices in current ML-based schemes, which restricts the deployment of the model in the system. Therefore, new modeling schemes with a better generalizability should be studied.
- ML-based modeling schemes to accurately estimate both the gain and the ASE noise. Some ML-based models can be used to estimate the signal power and the noise power of EDFA simultaneously [18,19]. Currently, simple NNs are utilized for these models, and a large dataset is needed. To optimize the modeling scheme for a lower modeling error and training complexity, theoretical knowledge for both the gain and the noise characterizations should be considered in the models.
- Modeling schemes for online correcting and tracking. In the proposed analytical models, multiple parameters cannot be accurately corrected to track the time-varying change online. In the proposed ML-based models, online tracking might be feasible, but sufficient data is difficult to obtain online. Therefore, efficient online monitoring techniques and tracking schemes based on small online datasets are expected.
6. Conclusions
In this paper, we review and discuss EDFA gain modeling techniques. First, we explain the significance for EDFA gain modeling. Then, we review the basic theory of EDFA and explain its gain performance. Afterwards, the analytical models and the ML-based models are introduced, and the modeling performances are analyzed. Finally, we summarize the challenges and possible directions for future investigations in EDFA gain modeling.
Author Contributions
Conceptualization, Y.L., X.L., L.Y., W.H. and Q.Z.; investigation, M.C. and Y.Z.; writing—original draft preparation, Y.L., X.L. and Q.Z.; writing—review and editing, Y.L., X.L., L.L. and Q.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Key R&D Program of China, grant number 2018YFB1801200, NSFC, grant number 61801291, Shanghai Rising-Star Program, grant number 19QA1404600.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Roberts, K.; Zhuge, Q.; Monga, I.; Gareau, S.; Laperle, C. Beyond 100 Gb/s: Capacity, Flexibility, and Network Optimization. J. Opt. Commun. Netw. 2017, 9, C12–C24. [Google Scholar] [CrossRef]
- Gerstel, O.; Jinno, M.; Lord, A.; Yoo, S.B. Elastic optical networking: A new dawn for the optical layer? IEEE Commun. Mag. 2012, 50, s12–s20. [Google Scholar] [CrossRef]
- Roberts, I.; Kahn, J.M.; Boertjes, D. Convex Channel Power Optimization in Nonlinear WDM Systems Using Gaussian Noise Model. J. Light. Technol. 2016, 34, 3212–3222. [Google Scholar] [CrossRef]
- Yankov, M.P.; de Moura, U.C.; da Ros, F. Power evolution prediction and optimization in a multi-span system based on component-wise system modeling. In Proceedings of the 2020 European Conference on Optical Communications (ECOC), Brussels, Belgium, 7–9 December 2020; pp. 1–4. [Google Scholar]
- Zang, H.; Jue, J.P.; Mukherjee, B. A review of routing and wavelength assignment approaches for wavelength-routed optical WDM networks. Opt. Netw. Mag. 2000, 1, 47–60. [Google Scholar]
- Pointurier, Y. Design of Low-Margin Optical Networks. J. Opt. Commun. Netw. 2016, 9, A9–A17. [Google Scholar] [CrossRef]
- Mahajan, A.; Christodoulopoulos, K.; Martinez, R.; Spadaro, S.; Munoz, R. Modeling EDFA Gain Ripple and Filter Penalties with Machine Learning for Accurate QoT Estimation. J. Light. Technol. 2020, 38, 2616–2629. [Google Scholar] [CrossRef]
- Seve, E.; Pesic, J.; Pointurier, Y. Accurate QoT Estimation by Means of a Reduction of EDFA Characteristics Uncertainties with Machine Learning. In Proceedings of the 2020 International Conference on Optical Network Design and Modeling (ONDM), Barcelona, Spain, 18–21 May 2020; pp. 1–3. [Google Scholar]
- Yu, J.; Zhu, S.; Gutterman, C.L.; Zussman, G.; Kilper, D.C. Machine-learning-based EDFA gain estimation. J. Opt. Commun. Netw. 2021, 13, B83. [Google Scholar] [CrossRef]
- Nishihara, M.; Sugaya, Y.; Ishikawa, E. Impact of Spectral Hole Burning in Multi-Channel Amplification of EDFA. In Proceedings of the Optical Fiber Communication Conference, Los Angeles, CA, USA, 22 February 2004; p. FB1. [Google Scholar]
- Desurvire, E.; Zyskind, J.L.; Simpson, J.R. Spectral gain hole-burning at 1.53 μm in erbium-doped fiber amplifiers. IEEE Photon. Technol. Lett. 1990, 2, 246–248. [Google Scholar] [CrossRef]
- Desurvire, E. Analysis of gain difference between forward- and backward-pumped erbium-doped fiber amplifiers in the saturation regime. IEEE Photon. Technol. Lett. 1992, 4, 711–714. [Google Scholar] [CrossRef]
- Ishii, K.; Tanizawa, K.; Kurumida, J.; Namiki, S. Experimental Study of Wavelength-dependent Dynamic Gain Offsets of AGC WDM EDFA. In Proceedings of the 2013 18th OptoElectronics and Communications Conference Held Jointly with Photonics in Switching, Kyoto, Japan, 30 June–4 July 2013; p. WS3_1. [Google Scholar]
- Masuda, H.; Aida, K.; Nakagawa, K. Noise figure monitoring of a cascaded in-line erbium-doped fiber amplifier. IEEE Photon. Technol. Lett. 1993, 5, 1436–1438. [Google Scholar] [CrossRef]
- Xiang, Y.; Tang, M.; Wu, Q.; Zhou, H.; Yong, B.; Fu, S.; Liu, D. A Joint OSNR and Nonlinear Distortions Estimation Method for Optical Fiber Transmission System. IEEE Photon. J. 2018, 10, 1–11. [Google Scholar] [CrossRef]
- You, Y.; Jiang, Z.; Janz, C. OSNR prediction using machine learning-based EDFA models. In Proceedings of the 2019 European Conference on Optical Communication (ECOC), Dublin, Ireland, 22–26 September 2019; pp. 1–3. [Google Scholar]
- Yankov, M.P.; Kaminski, P.M.; Hansen, H.E.; Da Ros, F. SNR optimization of multi-span fiber optic communication systems employing EDFAs with non-flat gain and noise figure. arXiv 2021, arXiv:2106.03639. [Google Scholar]
- Cho, J.; Chandrasekhar, S.; Sula, E.; Olsson, S.; Burrows, E.; Raybon, G.; Ryf, R.; Fontaine, N.; Antona, J.-C.; Grubb, S.; et al. maximizing fiber cable capacity under a supply power constraint using deep neural networks. In Proceedings of the Optical Fiber Communication Conference (OFC) 2020, San Diego, CA, USA, 10–12 March 2020; p. W1K.2. [Google Scholar]
- Cho, J.; Raybon, G.; Burrows, E.; Antona, J.-C.; Fontaine, N.; Ryf, R.; Chen, H.; Chandrasekhar, S.; Sula, E.; Olsson, S.; et al. Optimizing gain shaping filters with neural networks for maximum cable capacity under electrical power constraints. In Proceedings of the 2020 European Conference on Optical Communications (ECOC), Brussels, Belgium, 7–9 December 2020; pp. 1–4. [Google Scholar]
- Saleh, A.; Jopson, R.; Evankow, J.; Aspell, J. Modeling of gain in erbium-doped fiber amplifiers. IEEE Photon. Technol. Lett. 1990, 2, 714–717. [Google Scholar] [CrossRef]
- Lei, C.; Feng, H.; Messaddeq, Y.; Larochelle, S. Investigation of Bi-Directionally, Dual-Wavelength Pumped Extended L-Band EDFAs. IEEE Photon. Technol. Lett. 2020, 32, 1227–1230. [Google Scholar] [CrossRef]
- Giles, C.; Desurvire, E. Modeling erbium-doped fiber amplifiers. J. Light. Technol. 1991, 9, 271–283. [Google Scholar] [CrossRef] [Green Version]
- Pedersen, B.; Dakss, M.; Thompson, B.; Miniscalco, W.; Wei, T.; Andrews, L. Experimental and theoretical analysis of efficient erbium-doped fiber power amplifiers. IEEE Photon. Technol. Lett. 1991, 3, 1085–1087. [Google Scholar] [CrossRef]
- Nishida, Y.; Yamada, M.; Kanamori, T.; Kobayashi, K.; Temmyo, J.; Sudo, S.; Ohishi, Y. Development of an efficient praseodymium-doped fiber amplifier. IEEE J. Quantum Electron. 1998, 34, 1332–1339. [Google Scholar] [CrossRef]
- Richards, D.; Jackel, J.; Ali, M. A theoretical investigation of dynamic all-optical automatic gain control in multichannel EDFA’s and EDFA cascades. IEEE J. Sel. Top. Quantum Electron. 1997, 3, 1027–1036. [Google Scholar] [CrossRef]
- Luo, G.; Zyskind, J.; Sun, Y.; Srivastava, A.; Sulhoff, J.; Wolf, C.; Ali, M. Performance degradation of all-optical gain-clamped EDFAs due to relaxation-oscillations and spectral-hole burning in amplified WDM networks. IEEE Photon. Technol. Lett. 1997, 9, 1346–1348. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Zhang, Y.; Soh, Y.C.; Wen, C. Design and analysis of dynamic erbium-doped fiber amplifier gain-clamping systems with feedback control. J. Opt. Soc. Am. B 2007, 24, 1739–1748. [Google Scholar] [CrossRef]
- Wei, H.; Tong, Z.; Jian, S. Use of a genetic algorithm to optimize multistage erbium-doped fiber-amplifier systems with complex structures. Opt. Express 2004, 12, 531–544. [Google Scholar] [CrossRef] [PubMed]
- Lei, C.; Feng, H.; Messaddeq, Y.; LaRochelle, S. Investigation of C-band pumping for extended L-band EDFAs. J. Opt. Soc. Am. B 2020, 37, 2345. [Google Scholar] [CrossRef]
- Lancry, M.; Costes, S.; Lopez, T.; Poumellec, B. Reliable lifetime prediction of gain flattening filters. Adv. Photonics 2014, 5, 2. [Google Scholar] [CrossRef]
- Sommer, R.L.; Fortenberry, R.; Flintham, B.; Johnson, P. Multiple filter functions integrated into multi-port GFF components. In Proceedings of the OFC/NFOEC 2007 Conference on Optical Fiber Communication and the National Fiber Optic Engineers Conference, Anaheim, CA, USA, 25–29 March 2007; pp. 1–3. [Google Scholar]
- Hashimoto, M.; Yoshida, M.; Tanaka, H. The characteristics of WDM systems with hybrid AGC EDFA in the photonics network. In Proceedings of the Optical Fiber Communication Conference and Exhibit, Anaheim, CA, USA, 17–22 March 2002; pp. 517–518. [Google Scholar] [CrossRef]
- Ishii, K.; Kurumida, J.; Namiki, S. Experimental Investigation of Gain Offset Behavior of Feedforward-Controlled WDM AGC EDFA under Various Dynamic Wavelength Allocations. IEEE Photon. J. 2016, 8, 1–13. [Google Scholar] [CrossRef]
- You, Y.; Jiang, Z.; Janz, C. Machine Learning-Based EDFA Gain Model. In Proceedings of the 2018 European Conference on Optical Communication (ECOC), Rome, Italy, 23–27 September 2018; pp. 1–3. [Google Scholar]
- Zhu, S.; Gutterman, C.L.; Mo, W.; Li, Y.; Zussman, G.; Kilper, D. Machine Learning Based Prediction of Erbium-Doped Fiber WDM Line Amplifier Gain Spectra. In Proceedings of the 2018 European Conference on Optical Communication (ECOC), Rome, Italy, 23–27 September 2018; pp. 1–3. [Google Scholar]
- Da Ros, F.; de Moura, U.C.; Yankov, M.P. Machine learning-based EDFA gain model generalizable to multiple physical devices. In Proceedings of the 2020 European Conference on Optical Communications (ECOC), Brussels, Belgium, 7–9 December 2020; pp. 1–4. [Google Scholar]
- Zhu, S.; Gutterman, C.; Montiel, A.D.; Yu, J.; Ruffini, M.; Zussman, G.; Kilper, D. Hybrid Machine Learning EDFA Model. In Proceedings of the Optical Fiber Communication Conference (OFC) 2020, San Diego, CA, USA, 10–12 March 2020; p. T4B.4. [Google Scholar]
- Meseguer, A.C.; Antona, J.-C.; Bononi, A.; Cho, J.; Grubb, S.; Pecci, P.; Courtois, O.; Letellier, V. Highly accurate measurement-based gain model for constant-pump EDFA for non-flat WDM inputs. In Proceedings of the Optical Fiber Communication Conference (OFC) 2021, San Diego, CA, USA, 6–11 June 2021; p. M5C.4. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).