Numerical Study of Parallel Optoelectronic Reservoir Computing to Enhance Nonlinear Channel Equalization
Abstract
:1. Introduction
2. The Parallel Reservoir Computing
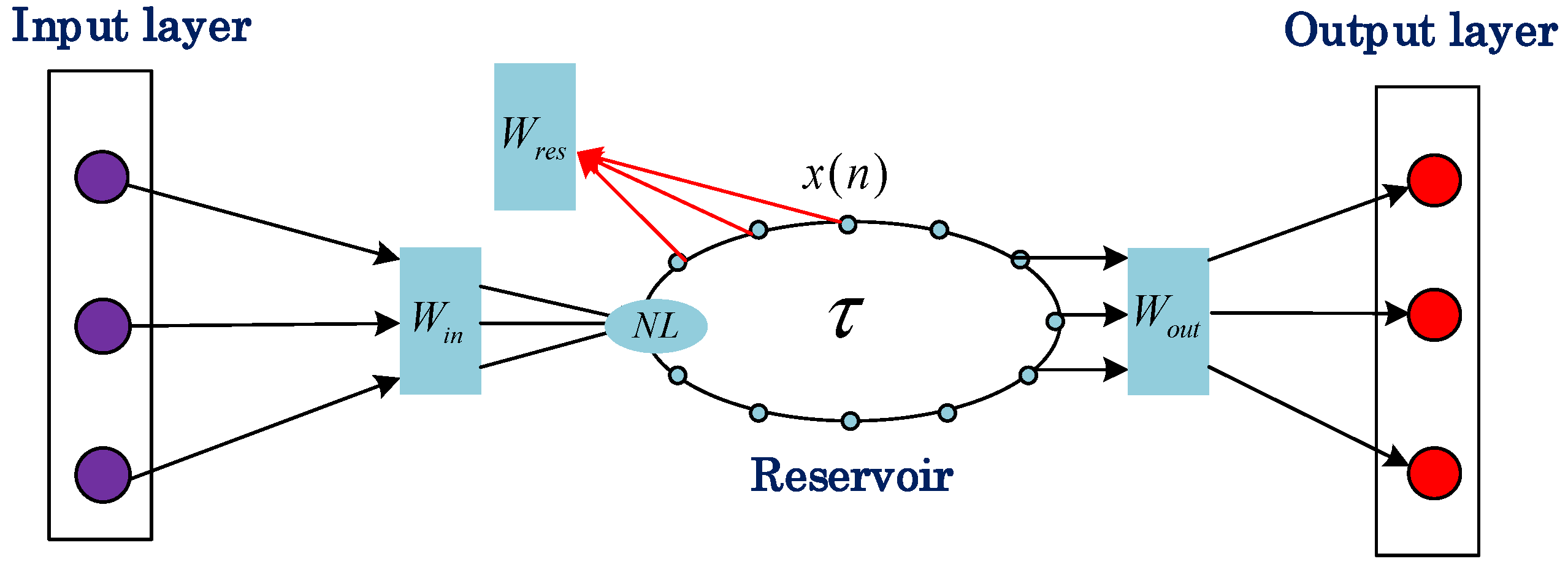
2.1. Basic Concepts of Reservoir Computing
2.2. Proposed Scheme of Optoelectronic Reservoir Computing
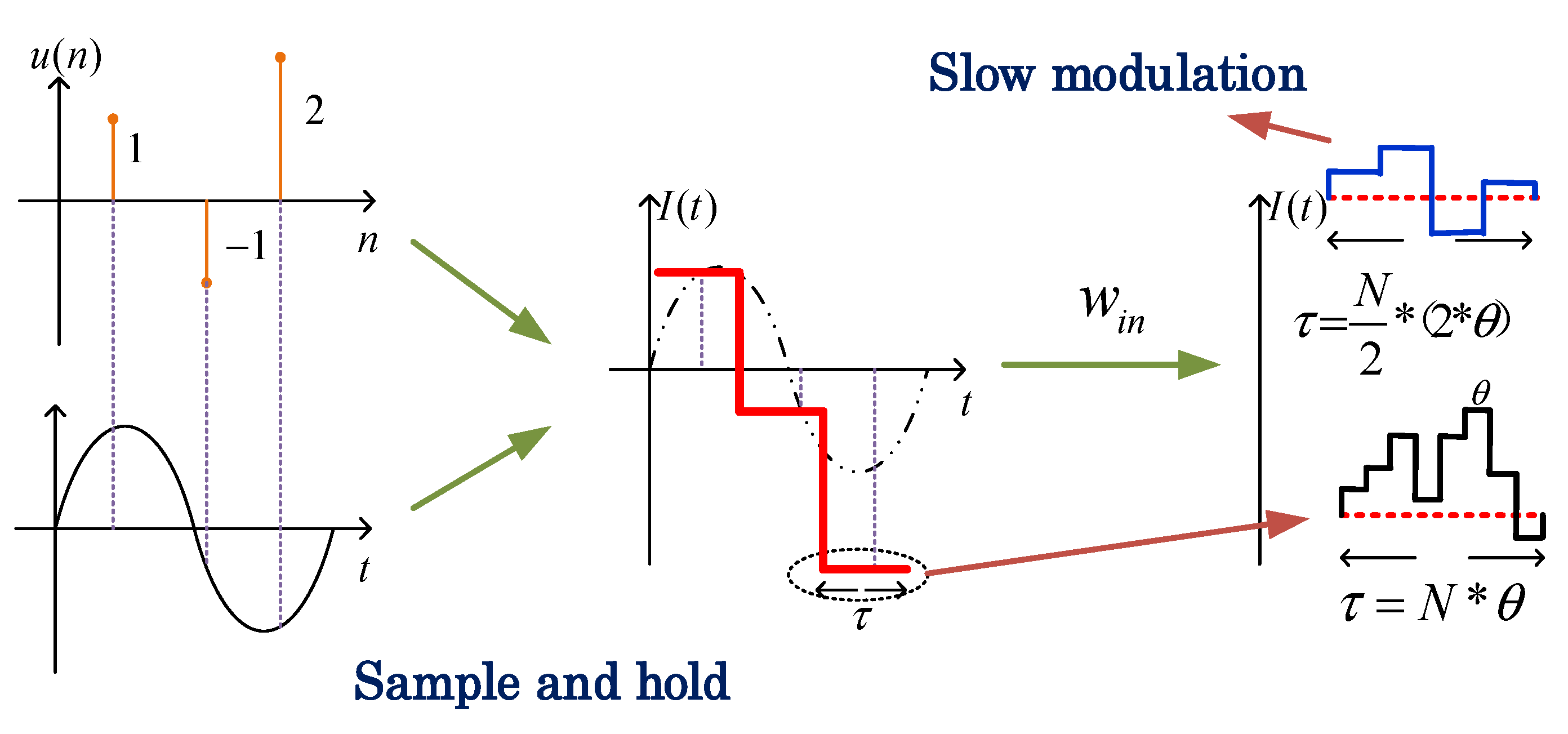
2.3. Input Signal Processing
3. Numerical Setup and Results
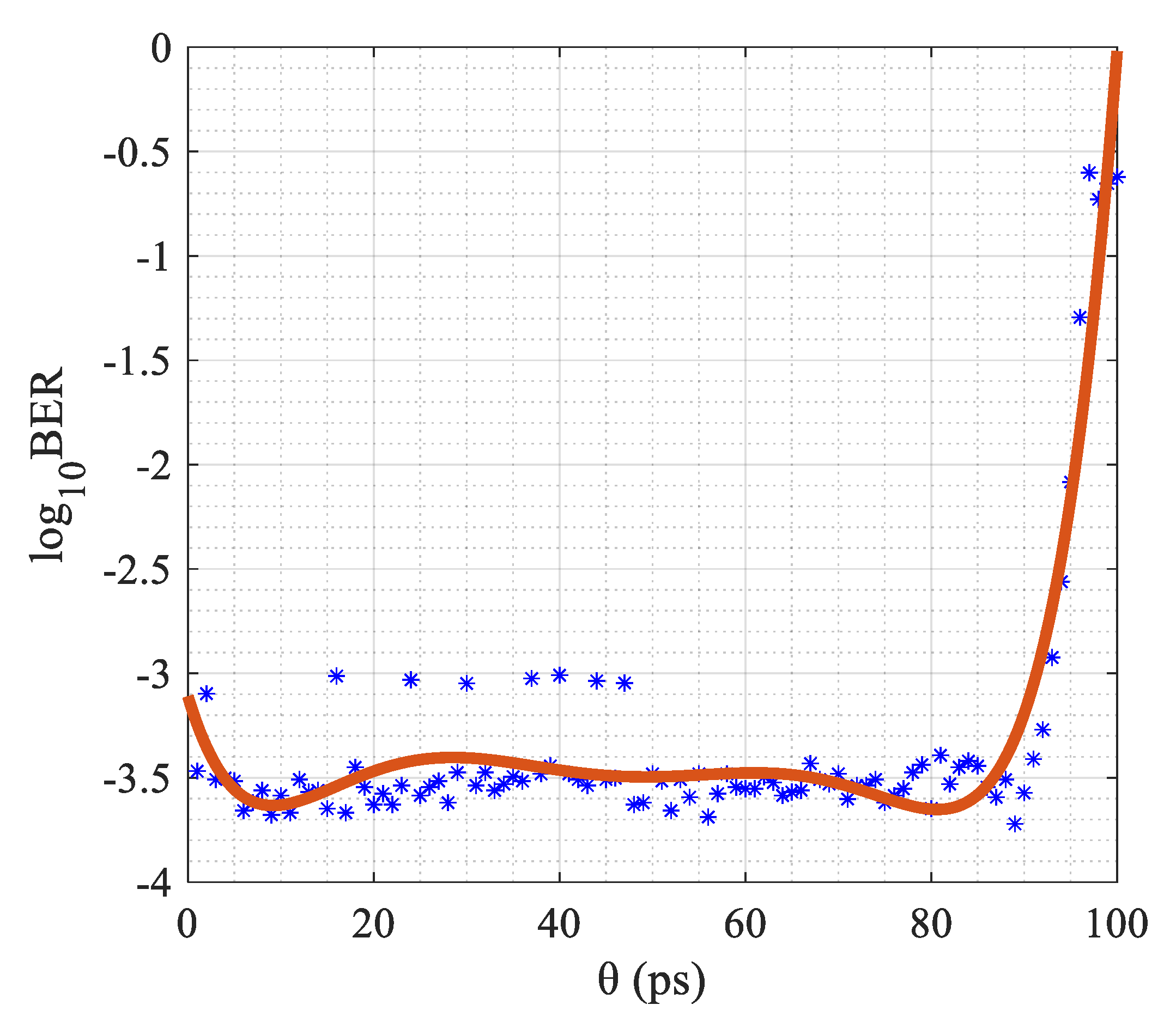
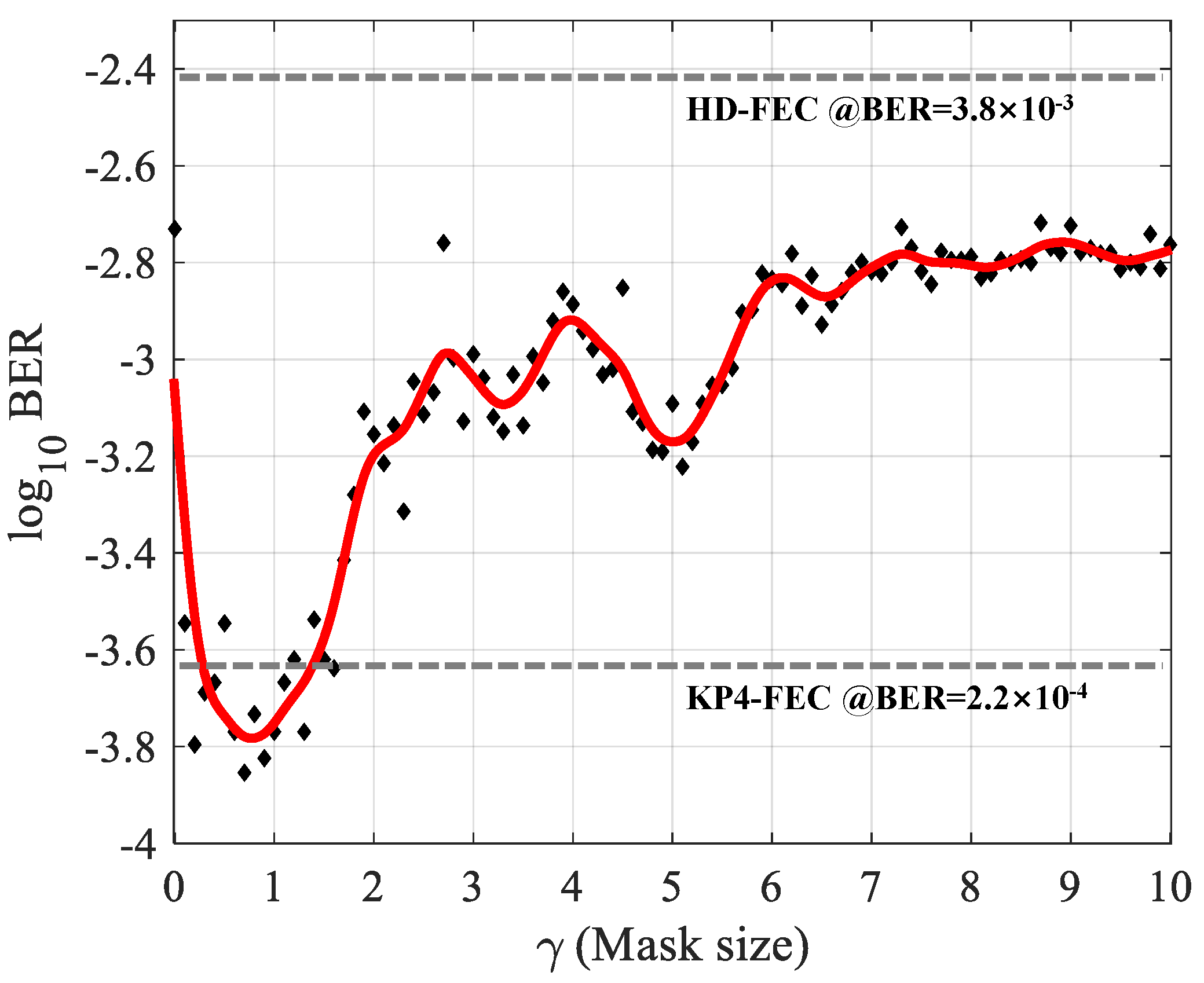
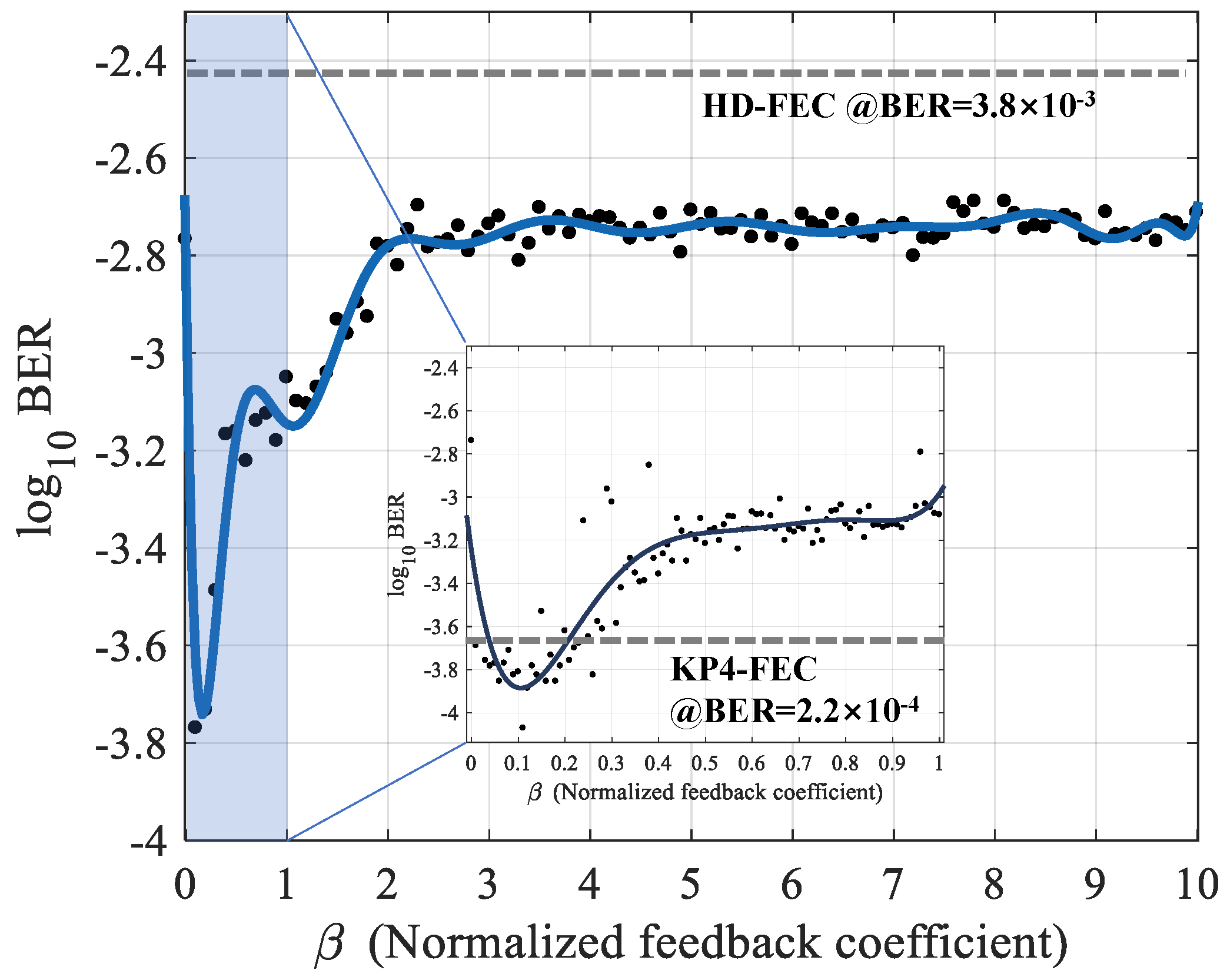
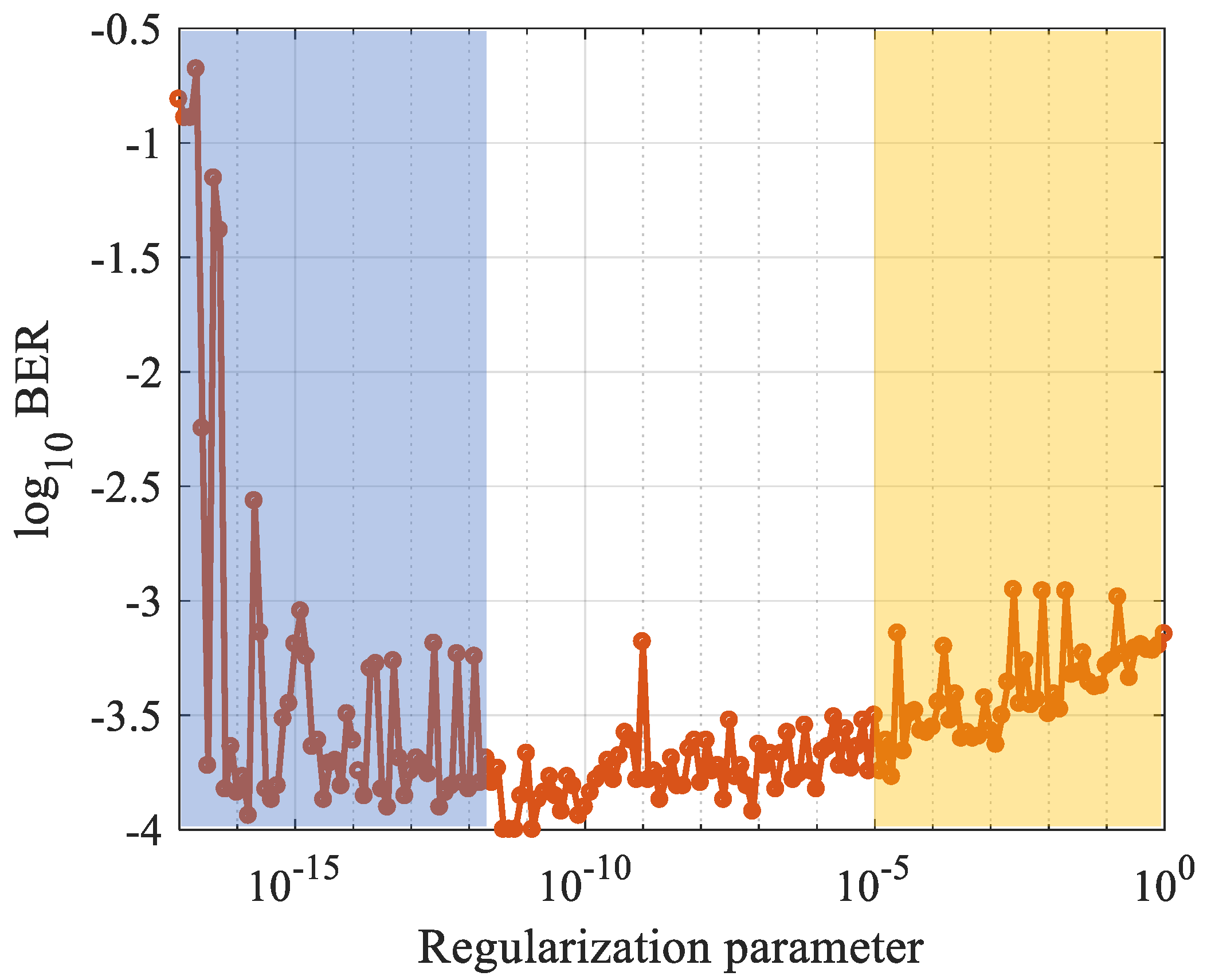
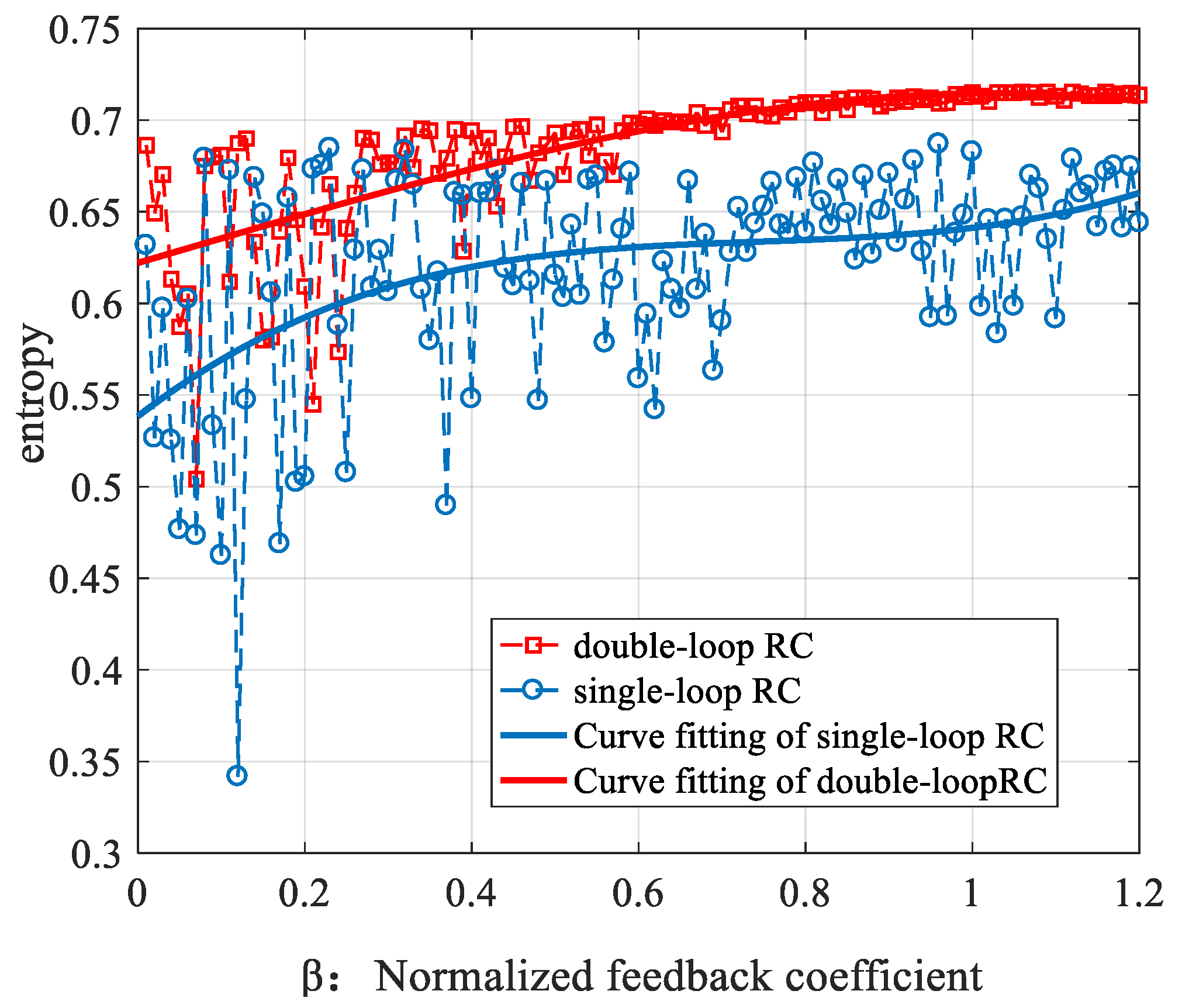
3.1. Parameters Optimization
3.2. Results and Comparisons
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mitra, R.; Bhatia, V. Chebyshev Polynomial-Based Adaptive Predistorter for Nonlinear LED Compensation in VLC. IEEE Photonics Technol. Lett. 2016, 28, 1053–1056. [Google Scholar] [CrossRef]
- Belabad, A.R.; Motamedi, S.A.; Sharifian, S. An Adaptive Digital Predistortion for Compensating Nonlinear Distortions in RF Power Amplifier with Memory Effects. Integration 2017, 57, 184–191. [Google Scholar] [CrossRef]
- Giacoumidis, E.; Lin, Y.; Wei, J.; Aldaya, I.; Tsokanos, A.; Barry, L.P. Harnessing machine learning for fiber-induced nonlinearity mitigation in long-haul coherent optical OFDM. Futur. Internet 2018, 11, 2. [Google Scholar] [CrossRef] [Green Version]
- Zerguine, A.; Bettayeb, M.; Cowan, C.F.N. Hybrid LMS–LMF algorithm for adaptive echo cancellation. IEE Proc. Vis. Image Signal Process. 1999, 146, 173–180. [Google Scholar] [CrossRef]
- He, F.; Zhu, M.; Liu, W.; Liu, T.; Wang, L. Decision of optimum open-pit slope angle based on artificial neural network. In Proceedings of the 2010 International Symposium on Computational Intelligence and Design, Hangzhou, China, 29–31 October 2010; pp. 56–59. [Google Scholar]
- Das, G.; Pattnaik, P.K.; Padhy, S.K. Artificial Neural Network trained by Particle Swarm Optimization for non-linear channel equalization. Expert Syst. Appl. 2014, 41, 3491–3496. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Appeltant, L.; Soriano, M.C.; Van der Sande, G.; Danckaert, J.; Massar, S.; Dambre, J.; Schrauwen, B.; Mirasso, C.; Fischer, I. Information processing using a single dynamical node as complex system. Nat. Commun. 2011, 2, 468. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Paquot, Y.; Duport, F.; Smerieri, A.; Dambre, J.; Schrauwen, B.; Haelterman, M.; Massar, S. Optoelectronic reservoir computing. Sci. Rep. 2012, 2, 287. [Google Scholar] [CrossRef] [PubMed]
- Duport, F.; Schneider, B.; Smerieri, A.; Haelterman, M.; Massar, S. All-optical reservoir computing. Opt. Express 2012, 20, 22783–22795. [Google Scholar] [CrossRef] [PubMed]
- Vandoorne, K.; Dierckx, W.; Schrauwen, B.; Verstraeten, D.; Baets, R.; Bienstman, P.; Van Campenhout, J. Toward optical signal processing using Photonic Reservoir Computing. Opt. Express 2008, 16, 11182–11192. [Google Scholar] [CrossRef] [PubMed]
- Nguimdo, R.M.; Verschaffelt, G.; Danckaert, J.; der Sande, G.V. Fast photonic information processing using semiconductor lasers with delayed optical feedback: Role of phase dynamics. Opt. Express 2014, 22, 8672–8686. [Google Scholar] [CrossRef] [PubMed]
- Hasnain, S.A.; Mahapatra, R. On-chip parallel photonic reservoir computing using multiple delay lines. In Proceedings of the 2020 IEEE 32nd International Symposium on Computer Architecture and High Performance Computing (SBAC-PAD), Porto, Portugal, 8–11 September 2020; Volume 28–34. [Google Scholar]
- Chen, Y.; Yi, L.; Ke, J.; Yang, Z.; Yang, Y.; Huang, L.; Zhuge, Q.; Hu, W. Reservoir computing system with double optoelectronic feedback loops. Opt. Express 2019, 27, 27431–27440. [Google Scholar] [CrossRef] [PubMed]
- Xia, G.Q.; Hou, Y.S.; Wu, Z.M. Prediction performance of reservoir computing using a semiconductor laser with double optical feedback. In Proceedings of the 2018 Conference on Lasers and Electro-Optics Pacific Rim (CLEO-PR), Hong Kong, China, 29 July–3 August 2018; Volume 1–2. [Google Scholar]
- Yue, D.-Z.; Wu, Z.-M.; Hou, Y.-S.; Hu, C.-X.; Jiang, Z.-F.; Xia, G.-Q. Reservoir Computing Based on Two Parallel Reservoirs Under Identical Electrical Message Injection. IEEE Photon J. 2021, 13, 1–11. [Google Scholar]
- Tezuka, M.; Kanno, K.; Bunsen, M. Reservoir computing with a slowly modulated mask signal for pre-processing using a mutually coupled optoelectronic system. Jpn. J. Appl. Phys. 2016, 50, 08RE06. [Google Scholar] [CrossRef]
- Wiener, N.; Teichmann, T. Nonlinear Problems in Random Theory. Phys. Today 1959, 12, 52. [Google Scholar] [CrossRef]
- Qi, N.; Zhang, Z.; Liu, L.; Liu, J.; Wu, N.; Xiao, X.; Chiang, P.Y. The design techniques for high-speed PAM4 clock and data recovery. In IEEE International Conference on Integrated Circuits. In Proceedings of the Technologies and Applications (ICTA), Beijing, China, 21–23 November 2018; pp. 142–143. [Google Scholar]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 2000, 42, 80–86. [Google Scholar] [CrossRef]
- Choi, C.-S.; Lee, H.; Kaneda, N.; Chen, Y.-K. Concatenated non-binary LDPC and HD-FEC codes for 100Gb/s optical transport systems. In Proceedings of the 2012 IEEE International Symposium on Circuits and Systems (ISCAS), Seoul, Korea, 20–23 May 2012; pp. 1783–1786. [Google Scholar]
- Stojanovic, N.; Prodaniuc, C.; Zhang, L.; Wei, J. 210/225 Gbit/s PAM-6 transmission with BER below KP4-FEC/EFEC and at Least 14 dB link budget. In Proceedings of the 2018 European Conference on Optical Communication (ECOC), Roma, Italy, 23–27 September 2018; pp. 1–3. [Google Scholar]
- Stojanovic, M.; Catipovic, J.; Proakis, J.G. Adaptive multichannel combining and equalization for underwater acoustic communications. J. Acoust. Soc. Am. 1993, 94, 1621–1631. [Google Scholar] [CrossRef]
- De Figueiredo, R. The Volterra and Wiener theories of nonlinear systems. Proc. IEEE 1982, 70, 316–317. [Google Scholar] [CrossRef]



| Parameters | Symbol | Value |
|---|---|---|
| Size of RC | N | 50, 100 |
| Time constant of the high-pass filtering | τH | 19.89 × 10−12 s |
| Time constant of the low-pass filtering | τL | 51.34 × 10−12 s |
| Half-wave voltage of the modulator | Vπ | 5 V |
| Parameters (unit) | Symbol | Typical RC | Proposed RC |
|---|---|---|---|
| Size of RC | N1 | 150 | 50 |
| N2 | \ | 100 | |
| Input gain | γ | 0.5 | 0.7 |
| Feedback gain | β | 0.47 | 0.11 |
| Delay time (s) | τ1 | 1.2 × 10−5 | 4 × 10−6 |
| τ2 | \ | 8 × 10−6 | |
| Bias voltage (V) | φ1 | –4π | 3.5π |
| φ2 | \ | −2.5π | |
| Scale factor of feedback | α1 | 0.9 | 0.7 |
| α2 | \ | 0.55 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, X.; Zhang, L.; Pang, X.; Gu, X.; Yu, X. Numerical Study of Parallel Optoelectronic Reservoir Computing to Enhance Nonlinear Channel Equalization. Photonics 2021, 8, 406. https://doi.org/10.3390/photonics8100406
Feng X, Zhang L, Pang X, Gu X, Yu X. Numerical Study of Parallel Optoelectronic Reservoir Computing to Enhance Nonlinear Channel Equalization. Photonics. 2021; 8(10):406. https://doi.org/10.3390/photonics8100406
Chicago/Turabian StyleFeng, Xingxing, Lu Zhang, Xiaodan Pang, Xiazhen Gu, and Xianbin Yu. 2021. "Numerical Study of Parallel Optoelectronic Reservoir Computing to Enhance Nonlinear Channel Equalization" Photonics 8, no. 10: 406. https://doi.org/10.3390/photonics8100406
APA StyleFeng, X., Zhang, L., Pang, X., Gu, X., & Yu, X. (2021). Numerical Study of Parallel Optoelectronic Reservoir Computing to Enhance Nonlinear Channel Equalization. Photonics, 8(10), 406. https://doi.org/10.3390/photonics8100406







