Progress of Waveguide Ring Resonators Used in Micro-Optical Gyroscopes
Abstract
1. Introduction
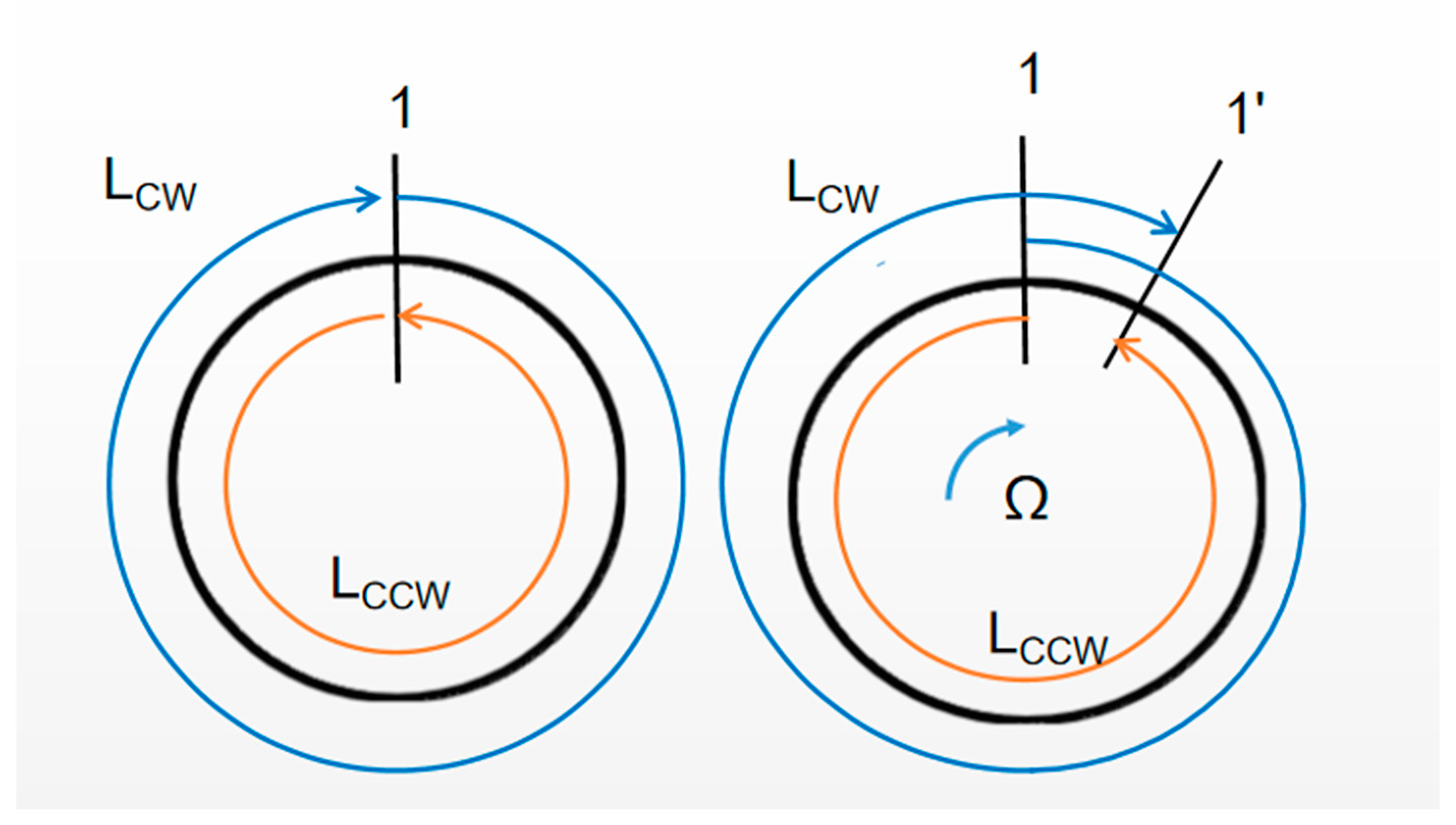
2. Waveguide Ring Resonators for MOGs
2.1. Progress of Waveguide Ring Resonator Used in MOGs
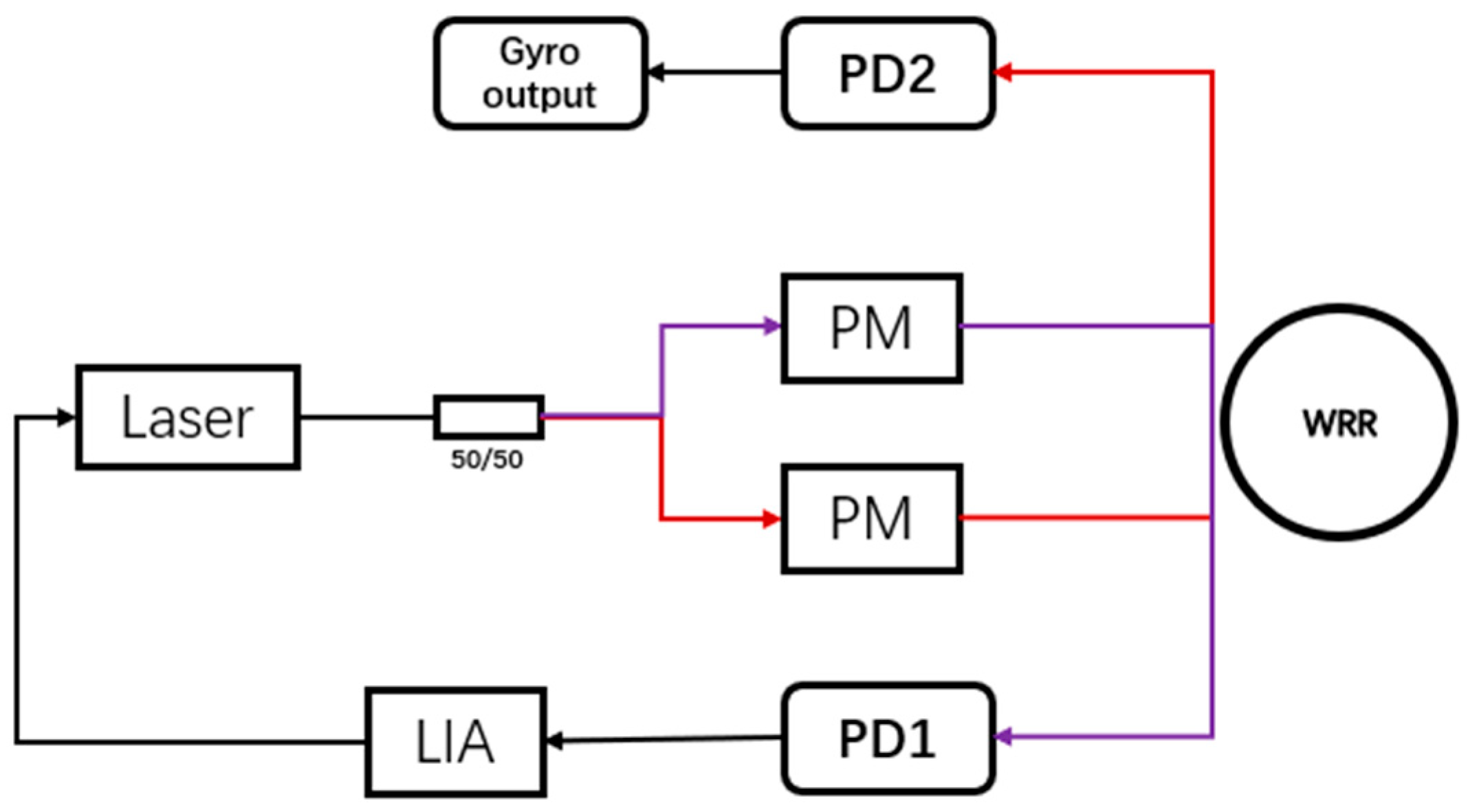
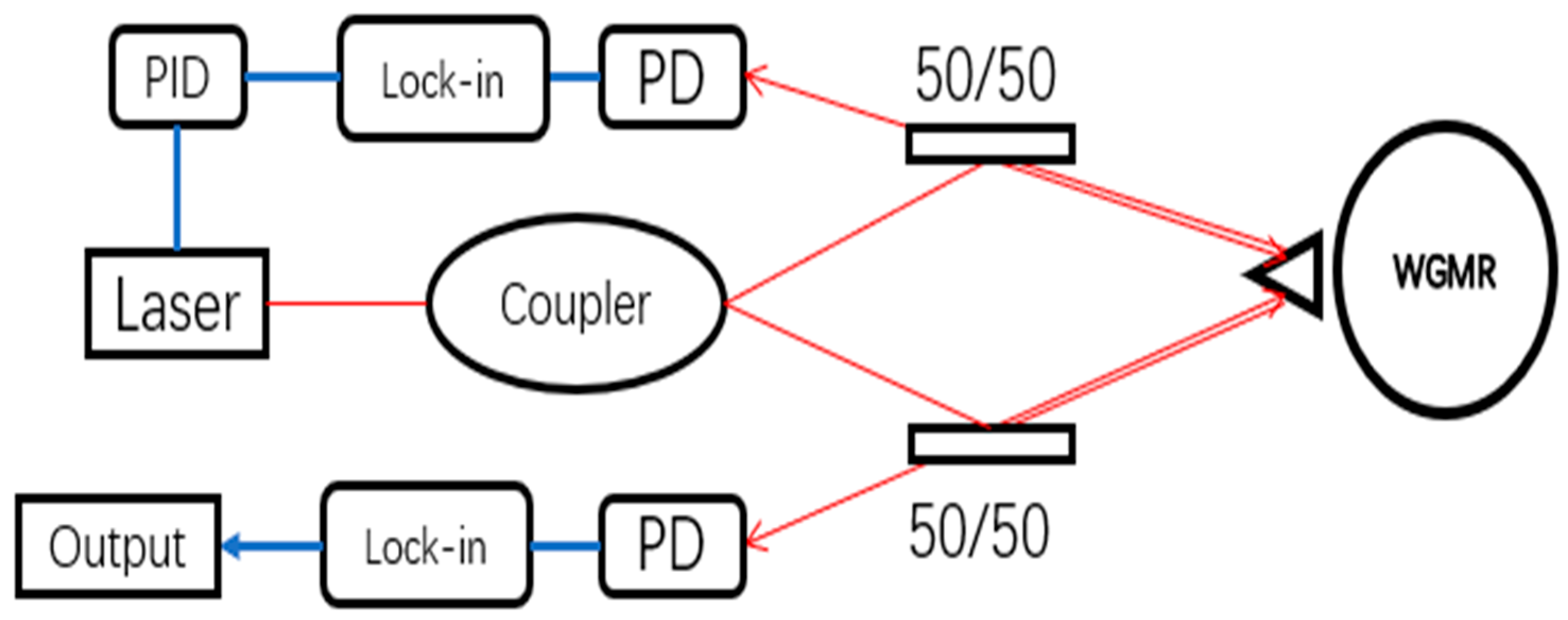
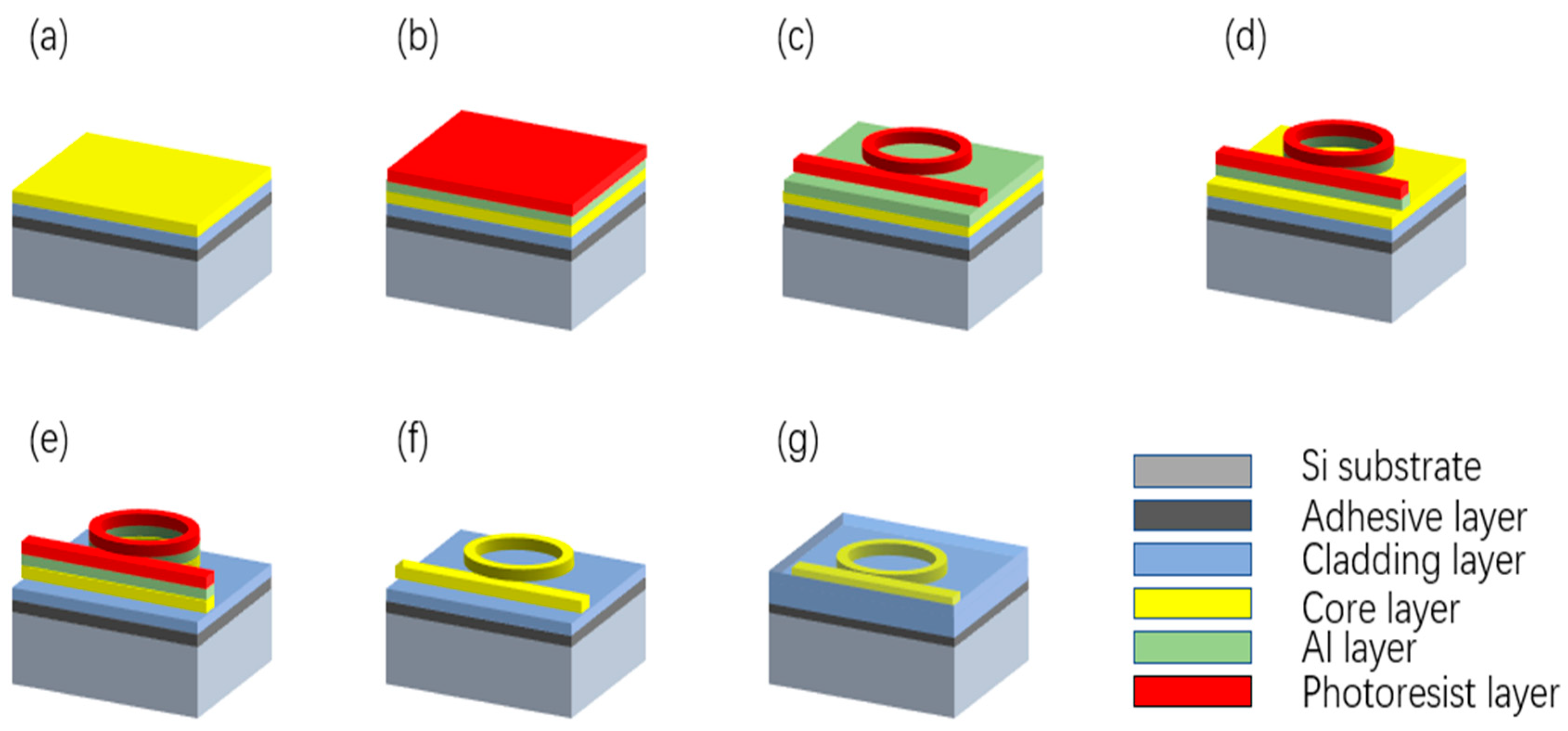
2.1.1. Silica Waveguide Ring Resonator
2.1.2. Indium Phosphide Waveguide Ring Resonator
2.1.3. Calcium Fluoride Waveguide Ring Resonator
2.1.4. Polymer Waveguide Ring Resonator
2.2. New Architectures of Ring Resonators for MOGs
2.2.1. Double-Ring Resonators for MOGs
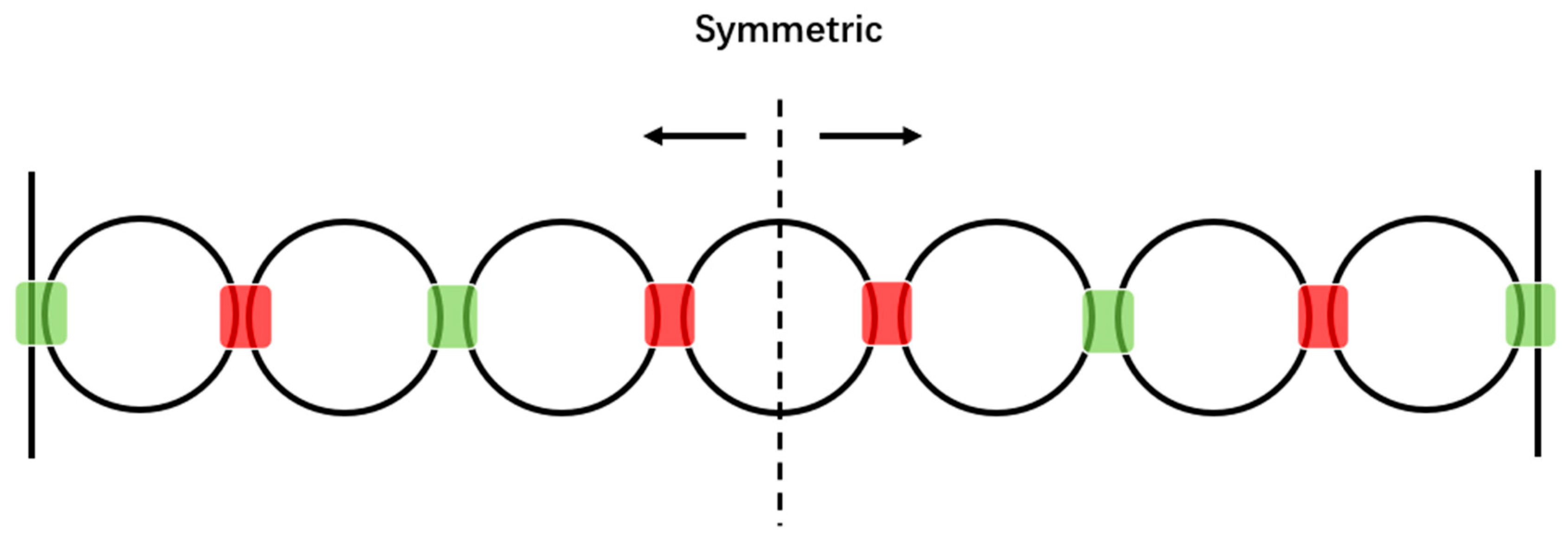
2.2.2. Multiple Ring Resonators for MOGs
2.3. WRRs Candidates for MOGs
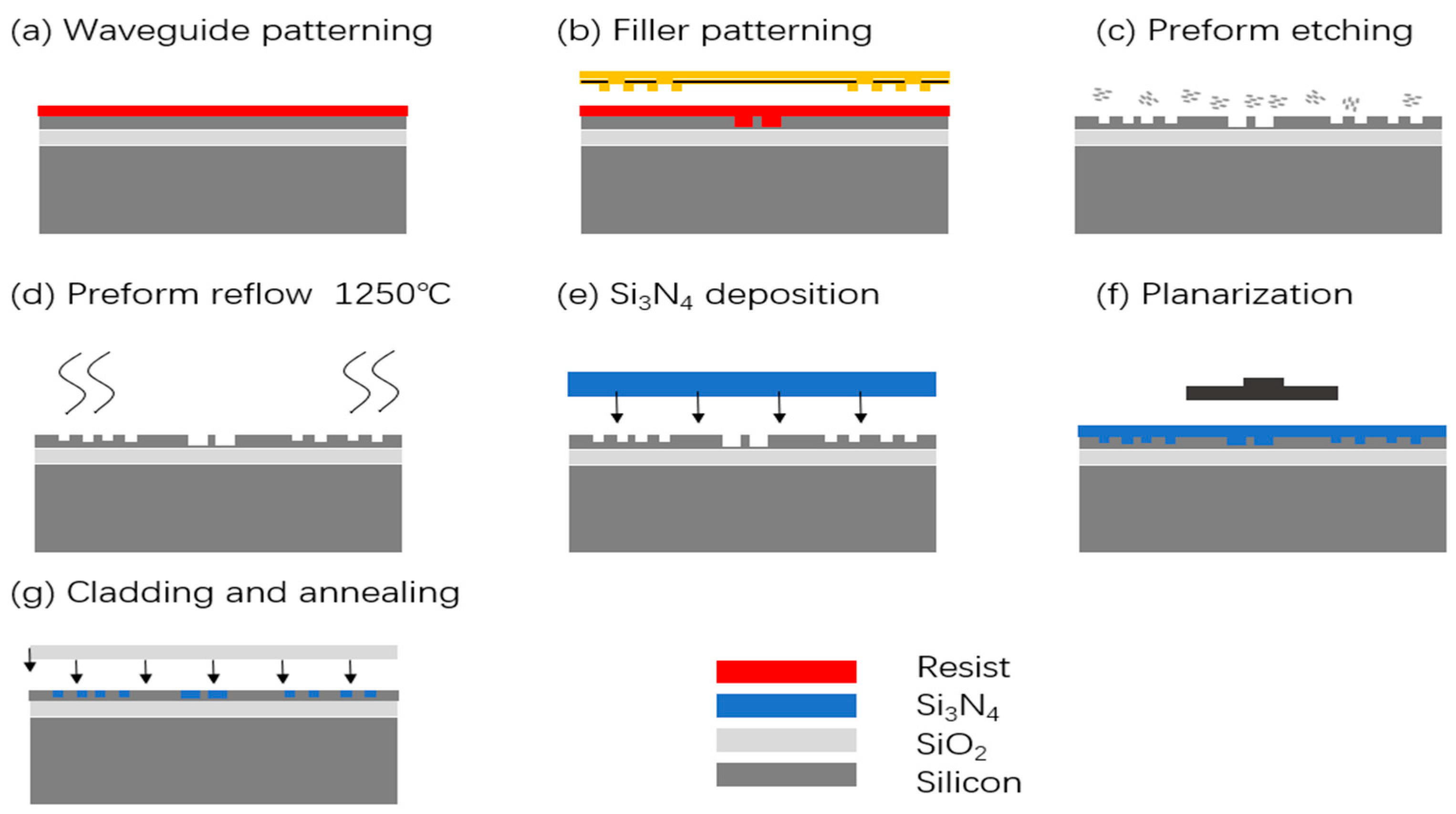
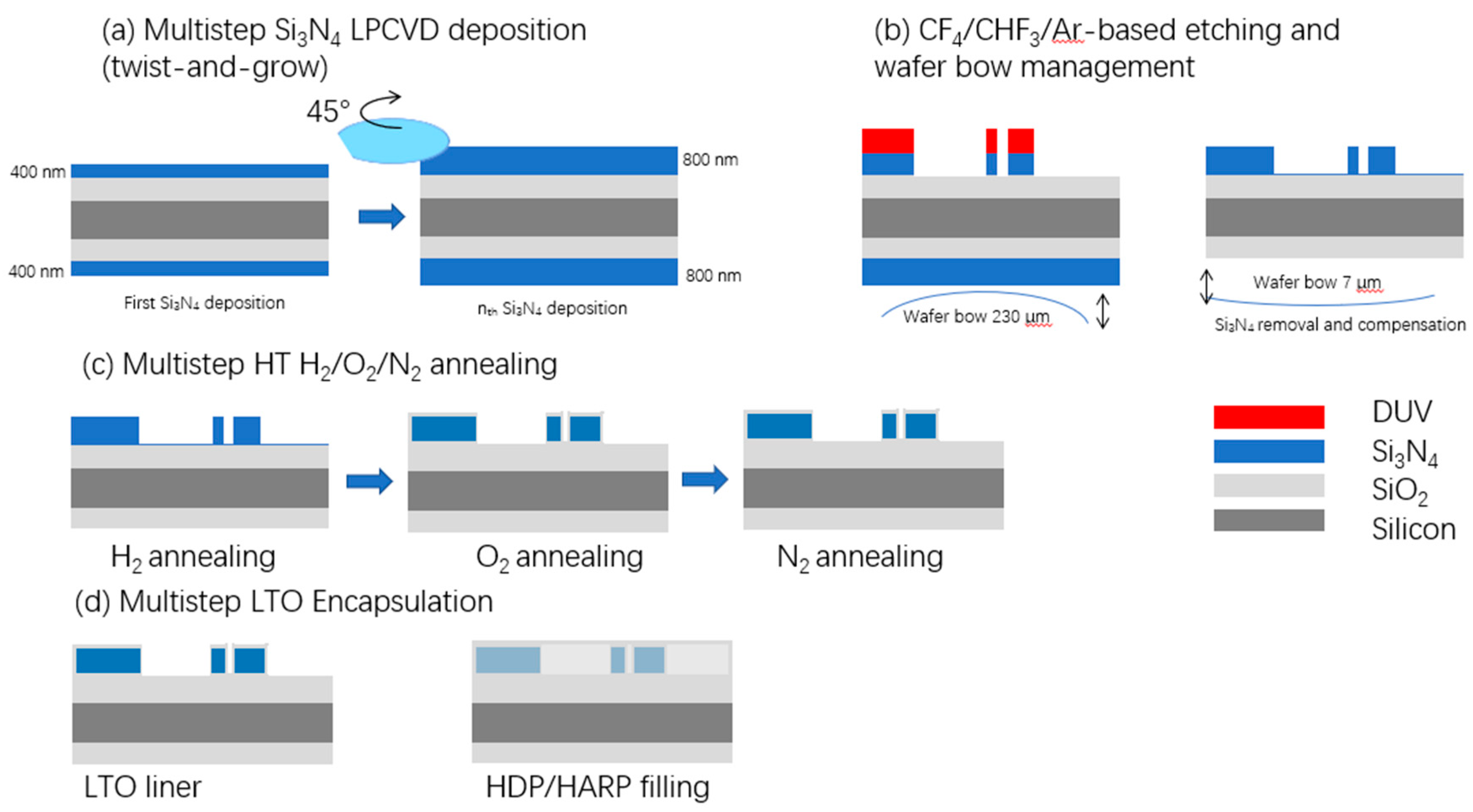
2.3.1. Silicon Nitride Waveguide Resonant Ring
2.3.2. Lithium Niobate Waveguide Ring Resonator
2.3.3. CaF2 Waveguide Ring Resonator
2.3.4. Magnesium Fluoride Waveguide Ring Resonator
2.3.5. Titanium Dioxide Waveguide Ring Resonator
2.4. Summary
3. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ezekiel, S.; Balsamo, S. Passive ring resonator laser gyroscope. Appl. Phys. Lett. 1977, 30, 478–480. [Google Scholar] [CrossRef]
- Venediktov, V.Y.; Filatov, Y.V.; Shalymov, E.V. Passive Ring Resonator Micro-Optical Gyroscopes. Quantum Electron. 2016, 46, 437–446. [Google Scholar] [CrossRef]
- Suzuki, K.; Takiguchi, K.; Hotate, K. Monolithically Integrated Resonator Microoptic Gyro on Silica Planar Lightwave Circuit. J. Lightwave Tech. 2000, 18, 66–72. [Google Scholar] [CrossRef]
- Chow, W.W.; Gea-Banacloche, J.; Pedrotti, L.M.; Sanders, V.E.; Schleich, W.; Scully, M.O. The Ring Laser Gyro. Rev. Mod. Phys. 1985, 57, 61. [Google Scholar] [CrossRef]
- Huai-Yong, Y.; Chun-Xi, Z.; Li-Shuang, F.; Zhen, Z.; Ling-Fei, H. Sio2 Waveguide Resonator Used in an Integrated Optical Gyroscope. Chin. Phys. Lett. 2009, 26, 054210. [Google Scholar] [CrossRef]
- Ma, H.; He, Z.; Hotate, K. Reduction of Backscattering Induced Noise by Carrier Suppression in Waveguide-Type Optical Ring Resonator Gyro. J. Lightwave Tech. 2011, 29, 85–90. [Google Scholar] [CrossRef]
- Huilan Liu, L.F.; Jiao, Z.; Li, R. Polarization Noise and Reduction Technology in Micro Optical Gyroscope. In Proceedings of the 2011 6th IEEE International Conference on Nano/Micro Engineered and Molecular Systems, Kaohsiung, Taiwan, 20–23 February 2011. [Google Scholar]
- Li, X.; Zhang, J.; Ma, H.; Jin, Z. Test and Analysis of the Optical Kerr-Effect in Resonant Micro-Optic Gyros. IEEE Photon. J. 2014, 6, 1–7. [Google Scholar]
- Cutler, C.C.; Newton, S.A.; Shaw, H.J. Limitation of Rotation Sensing by Scattering. Opt. Lett. 1980, 5, 488–490. [Google Scholar] [CrossRef]
- Hsiao, H.-K.; Winick, K. Planar Glass Waveguide Ring Resonators with Gain. Opt. Express 2007, 15, 17783–17797. [Google Scholar] [CrossRef]
- Hotate, K.; Higashiguchi, M. Eigenstate of Polarization in a Fiber Ring Resonator and its Effect in an Optical Passive Ring-Resonator Gyro. Appl. Opt. 1986, 25, 2606–2612. [Google Scholar]
- Zhi, Y.; Feng, L.; Lei, M.; Wang, K. Low-Delay, High-Bandwidth Frequency-Locking Loop Of Resonator Integrated Optic Gyro With Triangular Phase Modulation. Appl. Opt. 2013, 52, 8024–8031. [Google Scholar] [CrossRef]
- Strandjord, L.K.; Sanders, G.A. Effects of Imperfect Serrodyne Phase Modulation in Resonator Fiber Optic Gyroscopes. In Proceedings of the SPIE’s 1994 International Symposium on Optics, Imaging, and Instrumentation, San Diego, CA, USA, 24–29 July 1994; International Society for Optics and Photonics: Bellingham, WA, USA. [Google Scholar]
- Ma, H.; Zhang, X.; Jin, Z.; Ding, C. Waveguide-Type O Passive Ring Resonator Gyro Using Phase Modulation Spectroscopy Technique. Opt. Eng. 2006, 45, 080506-080506-3. [Google Scholar] [CrossRef]
- Ying, D.; Ma, H.; Jin, Z. Resonator Fiber Optic Gyro Using the Triangle Wave Phase Modulation Technique. Opt. Commun. 2008, 281, 580–586. [Google Scholar] [CrossRef]
- Mao, H.; Ma, H.; Jin, Z. Resonator Micro-Optic Gyroscope Based on the Double Phase Modulation Technique. In Proceedings of the Conference on Lasers and Electro.-Optics, San Jose, CA, USA, 16–21 May 2010; Optical Society of America: Washington, DC, USA. [Google Scholar]
- Lei, M.; Feng, L.; Zhi, Y. Sensitivity Improvement of Resonator Integrated Optic Gyroscope by Double-Electrode Phase Modulation. Appl. Opt. 2013, 52, 7214–7219. [Google Scholar] [CrossRef] [PubMed]
- Zhi, Y.; Feng, L.; Wang, J.; Tang, Y. Reduction of Backscattering Noise in a Resonator Integrated Optic Gyro by Double Triangular Phase Modulation. Appl. Opt. 2015, 54, 114–122. [Google Scholar] [CrossRef] [PubMed]
- Feng, L.S.; Lei, M.; Liu, H.; Zhi, Y.; Wang, J. Suppression of Backreflection Noise in a Resonator Integrated Optic Gyro by Hybrid Phase-Modulation Technology. Appl. Opt. 2013, 52, 1668–1675. [Google Scholar] [CrossRef]
- Ma, H.; Zhang, J.; Wang, L.; Jin, Z. Double Closed-Loop Resonant Micro Optic Gyro Using Hybrid Digital Phase Modulation. Opt. Express 2015, 23, 15088–15097. [Google Scholar] [CrossRef]
- Guillén-Torres, M.Á.; Cretu, E.; Jaeger, N.A.; Chrostowski, L. Ring Resonator Optical Gyroscopes—Parameter Optimization and Robustness Analysis. J. Lightwave Tech. 2012, 30, 1802–1817. [Google Scholar] [CrossRef]
- Zhang, J.; Li, H.; Ma, H.; Jin, Z. High. Finesse Silica Waveguide Ring Resonators for Resonant Micro-Optic Gyroscopes. In Proceedings of the 25th International Conference on Optical Fiber Sensors, Jeju, South Korea, 24–28 April 2017; International Society for Optics and Photonics: Bellingham, WA, USA, 2017. [Google Scholar]
- Spencer, D.T.; Bauters, J.F.; Heck, M.J.; Bowers, J.E. Integrated Waveguide Coupled Si_3n_4 Resonators in the Ultrahigh-Q Regime. Optica 2014, 1, 153. [Google Scholar] [CrossRef]
- Tian, H.; Liu, J.; Dong, B.; Skehan, J.C.; Zervas, M.; Kippenberg, T.J.; Bhave, S.A. Hybrid. Integrated Photonics Using Bulk Acoustic Resonators. Nat. Commun. 2020, 11, 3073. [Google Scholar] [CrossRef]
- Madani, A.; Kleinert, M.; Stolarek, D.; Zimmermann, L.; Ma, L.; Schmidt, O.G. Vertical Optical Ring Resonators Fully Integrated With Nanophotonic Waveguides on Silicon-on-Insulator Substrates. Opt. Lett. 2015, 40, 3826–3829. [Google Scholar] [CrossRef] [PubMed]
- Ciminelli, C.; Dell’Olio, F.; Campanella, C.E.; Armenise, M.N. Photonic Technologies for Angular Velocity Sensing. Adv. Opt. Photon. 2010, 2, 370–404. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, H.; Li, H.; Jin, Z. Single-Polarization Fiber-Pigtailed High-Finesse Silica Waveguide Ring Resonator for a Resonant Micro-Optic Gyroscope. Opt. Lett. 2017, 42, 3658–3661. [Google Scholar] [CrossRef]
- Ciminelli, C.; D’Agostino, D.; Carnicella, G.; Dell’Olio, F.; Conteduca, D.; Ambrosius, H.P.; Smit, M.K.; Armenise, M.N. A High.-InP Resonant Angular Velocity Sensor for a Monolithically Integrated Optical Gyroscope. Photon. J. IEEE 2016, 8, 1–18. [Google Scholar] [CrossRef]
- Liang, W.; Ilchenko, V.S.; Savchenkov, A.A.; Dale, E.; Eliyahu, D.; Matsko, A.B.; Maleki, L. Resonant Microphotonic Gyroscope. Optica 2017, 4, 114–117. [Google Scholar] [CrossRef]
- Qian, G.; Zhang, T.; Zhang, L.J.; Tang, J.; Zhang, X.Y.; Lu, Y.; Wan, F.H. Demonstrations of Centimeter-Scale Polymer Resonator for Resonant Integrated Optical Gyroscope. Sens. Actuators Phys. 2016, 237, 29–34. [Google Scholar] [CrossRef]
- D’Agostino, D.; Carnicella, G.; Ciminelli, C.; Thijs, P.; Veldhoven, P.J.; Ambrosius, H.; Smit, M. Low-Loss Passive Waveguides in a Generic Inp Foundry Process Via Local Diffusion of Zinc. Opt. Express 2015, 23, 25143–25157. [Google Scholar] [CrossRef]
- Wang, M.; Yang, Y.; Meng, L.; Jin, X.; Dong, Y.; Zhang, L.; Wang, K. Fabrication and Packaging for High-Q Caf2 Crystalline Resonators with Modal Modification. Chin. Opt. Lett. 2019, 17, 111401. [Google Scholar] [CrossRef]
- Grudinin, I.S.; Matsko, A.B.; Maleki, L. On the Fundamental Limits of Q Factor of Crystalline Dielectric Resonators. Opt. Express 2007, 15, 3390–3395. [Google Scholar] [CrossRef]
- Matsko, A.B.; Savchenkov, A.A.; Ilchenko, V.S.; Maleki, L. Optical Gyroscope with Whispering Gallery Mode Optical Cavities. Opt. Commun. 2004, 233, 107–112. [Google Scholar] [CrossRef]
- Lefèvre, H.C. Fundamentals of the Interferometric Fiber-Optic Gyroscope. Opt. Rev. 1997, 4, A20–A27. [Google Scholar]
- Matsko, A.B.; Savchenkov, A.A.; Strekalov, D.; Ilchenko, V.S.; Yu, N.; Maleki, L. Fabrication, Characterization and Applications of Crystalline Whispering Gallery Mode Resonators. In Proceedings of the International Conference on Transparent Optical Networks, Rome, Italy, 1–5 July 2007; pp. 50–54. [Google Scholar]
- Li, R.-Z.; Zhang, T.; Yu, Y.; Jiang, Y.J.; Zhang, X.Y.; Wang, L.D. Flexible Multilayer Substrate Based Optical Waveguides: Applications to Optical Sensing. Sens. Actuators Phys. 2014, 209, 57–61. [Google Scholar] [CrossRef]
- Tazawa, H.; Kuo, Y.H.; Dunayevskiy, I.; Luo, J.; Jen, A.K.Y.; Fetterman, H.R.; Steier, W.H. Ring Resonator-Based Electrooptic Polymer Traveling-Wave Modulator. J. Lightwave Tech. 2006, 24, 3514–3519. [Google Scholar] [CrossRef]
- Ren, J.; Wang, L.; Han, X.; Cheng, J.; Lv, H.; Wang, J.; Jian, X.; Zhao, M.; Jia, L. Organic Silicone Sol-Gel Polymer as a Noncovalent Carrier of Receptor Proteins for Label-Free Optical Biosensor Application. ACS Appl. Mater. Interfaces 2013, 5, 386–394. [Google Scholar] [CrossRef] [PubMed]
- Rabiei, P.; Steier, W.H. Tunable Polymer Double Micro-Ring Filters. IEEE Photon. Tech. Lett. 2003, 15, 1255–1257. [Google Scholar] [CrossRef]
- Sanghadasa, M.; Ashley, P.R.; Lindsay, G.A.; Bramson, M.D.; Tawney, J. Backscatter Compensation in IFOG Based Inertial Measurement Units With Polymer Phase Modulators. J. Lightwave Tech. 2009, 27, 806–813. [Google Scholar]
- Steinberg, B.Z.; Scheuer, J.; Boag, A. Rotation-Induced Superstructure in Slow-Light Waveguides With Mode-Degeneracy: Optical Gyroscopes with Exponential Sensitivity. J. Opt. Soc. Am. B 2007, 24, 1216–1224. [Google Scholar] [CrossRef]
- Campanella, C.E.; De Leonardis, F.; Passaro, V.M. Fiber Bragg Grating Ring Resonators Under Rotation for Angular Velocity Sensing. Appl. Opt. 2015, 54, 4789–4796. [Google Scholar] [CrossRef]
- Khial, P.P.; White, A.D.; Hajimiri, A. Nanophotonic Optical Gyroscope with Reciprocal Sensitivity Enhancement. Nat. Photon. 2018, 12, 671–675. [Google Scholar] [CrossRef]
- Grant, M.J.; Digonnet, M.J.F. Double-Ring Resonator Optical Gyroscopes. J. Lightwave Tech. 2018, 36, 2708–2715. [Google Scholar] [CrossRef]
- Sorrentino, C.; Toland, J.R. Ultra-Sensitive Chip Scale Sagnac Gyroscope Based on Periodically Modulated Coupling of a Coupled Resonator Optical Waveguide. Opt. Express 2012, 20, 354–363. [Google Scholar] [CrossRef] [PubMed]
- Kovach, A.; Chen, D.; He, J.; Choi, H.; Dogan, A.H.; Ghasemkhani, M.; Armani, A.M. Emerging Material Systems for Integrated Optical Kerr Frequency Combs. Adv. Opt. Photon. 2020, 12, 135–222. [Google Scholar] [CrossRef]
- Sacher, W.D.; Huang, Y.; Lo, G.Q.; Poon, J.K. Multilayer Silicon Nitride-on-Silicon Integrated Photonic Platforms and Devices. J. Lightwave Tech. 2015, 33, 901–910. [Google Scholar] [CrossRef]
- Anderson, M.H.; Lihachev, G.; Weng, W.; Liu, J.; Kippenberg, T.J. Zero-Dispersion Kerr Solitons In Optical Microresonators. arXiv 2020, arXiv:2007.14507. [Google Scholar]
- Pfeiffer, M.H.; Kordts, A.; Brasch, V.; Zervas, M.; Geiselmann, M.; Jost, J.D.; Kippenberg, T.J. Photonic Damascene Process for Integrated High-Q Microresonator Based Nonlinear Photonics. Optica 2016, 3, 20–25. [Google Scholar] [CrossRef]
- Pfeiffer, M.H.; Kordts, A.; Brasch, V.; Zervas, M.; Geiselmann, M.; Jost, J.D.; Kippenberg, T.J. Ultra-Smooth Silicon Nitride Waveguides Based on the Damascene Reflow Process: Fabrication and Loss Origins. Optica 2018, 5, 20–25. [Google Scholar] [CrossRef]
- Pfeiffer, M.H.P.; Herkommer, C.; Liu, J.; Morais, T.; Zervas, M.; Geiselmann, M.; Kippenberg, T.J. Photonic Damascene Process. for Low-Loss, High.-Confinement Silicon Nitride Waveguides. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 1–11. [Google Scholar] [CrossRef]
- El Dirani, H.; Youssef, L.; Petit-Etienne, C.; Kerdiles, S.; Grosse, P.; Monat, C.; Sciancalepore, C. Ultralow-Loss Tightly Confining Si3n4 Waveguides and High-Q Microresonators. Opt. Express 2019, 27, 30726–30740. [Google Scholar] [CrossRef]
- Huffman, T.A.; Brodnik, G.M.; Pinho, C.; Gundavarapu, S.; Baney, D.; Blumenthal, D.J. Integrated Resonators in an Ultralow Loss Si3N4/SiO2 Platform for Multifunction Applications. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 1–9. [Google Scholar] [CrossRef]
- Ferraro, P.; Grilli, S.; De Natale, P. Ferroelectric Crystals for Photonic Applications; Springer: Cham, Switzerland, 2008. [Google Scholar]
- Chang, L.; Li, Y.; Volet, N.; Wang, L.; Peters, J.; Bowers, J.E. Thin Film Wavelength Converters for Photonic Integrated Circuits. Optica 2016, 3, 531–535. [Google Scholar] [CrossRef]
- Krasnokutska, I.; Tambasco, J.-L.J.; Peruzzo, A. Tunable Large Free Spectral Range Microring Resonators in Lithium Niobate on Insulator. Sci. Rep. 2019, 9, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Wang, C.; Cheng, R.; Shams-Ansari, A.; Lončar, M. Monolithic Ultra-High-Q Lithium Niobate Microring Resonator. Optica 2017, 4, 1536–1537. [Google Scholar] [CrossRef]
- Savchenkov, A.A.; Liang, W.; Ilchenko, V.; Matsko, A.; Maleki, L. Crystalline Waveguides for Optical Gyroscopes. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 1–11. [Google Scholar] [CrossRef]
- Liu, G.; Ilchenko, V.S.; Su, T.; Ling, Y.-C.; Feng, S.; Shang, K.; Zhang, Y.; Liang, W.; Savchenkov, A.A.; Matsko, A.B.; et al. Low-Loss Prism-Waveguide Optical Coupling for Ultrahigh-Q Low-Index Monolithic Resonators. Optica 2018, 5, 219–226. [Google Scholar] [CrossRef]
- Piels, M.; Bauters, J.F.; Davenport, M.L.; Heck, M.J.; Bowers, J.E. Low-Loss Silicon Nitride AWG Demultiplexer Heterogeneously Integrated With Hybrid. III–V/Silicon Photodetectors. J. Lightwave Tech. 2014, 32, 817–823. [Google Scholar] [CrossRef]
- Weigel, P.O.; Savanier, M.; DeRose, C.T.; Pomerene, A.T.; Starbuck, A.L.; Lentine, A.L.; Mookherjea, S. Lightwave Circuits in Lithium Niobate through Hybrid. Waveguides with Silicon Photonics. Sci. Rep. 2016, 6, 22301. [Google Scholar] [CrossRef] [PubMed]



| Gyros | Q factor | Diameter | Bias Stability (deg/h) | Sensitivity (deg/h) |
|---|---|---|---|---|
| Silica micro gyro [27] | 1.46 × 107 | 2.5 cm | 0.004 | 3.74 |
| InP Micro gyro [28] | 6 × 105 | 3 mm | A few | 150 |
| CaF2 Micro gyro [29] | 1 × 109 | 7 mm | 3 | - |
| Polymer Micro gyro [30] | 1 × 105 | 1 cm | - | 324 |
| Material | Q factor | Diameter | Loss | Integration | Sensitivity (deg/h) |
|---|---|---|---|---|---|
| Si3N4 [53] | 1 × 107 | 220 μm | 3 dB/m | ▲▲▲ | - |
| Si3N4 [54] | 6.2 × 108 | 18 mm | 0.2–0.5 dB/m | ▲▲▲ | 0.03 |
| LN [58] | 1 × 107 | 180 μm | >10 dB/m | ▲▲ | - |
| CaF2 [59] | 5 × 109 | 3.8 mm | - | ▲ | 0.01 |
| MgF2 [60] | 1.9 × 109 | 2.66 mm | 3.8 dB | ▲ | 0.05 |
| TiO2 [25] | 310 | 16 μm | - | ▲ | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Z.; He, Y.; Yan, W.; Yang, F.; Han, W.; Li, Z. Progress of Waveguide Ring Resonators Used in Micro-Optical Gyroscopes. Photonics 2020, 7, 96. https://doi.org/10.3390/photonics7040096
Feng Z, He Y, Yan W, Yang F, Han W, Li Z. Progress of Waveguide Ring Resonators Used in Micro-Optical Gyroscopes. Photonics. 2020; 7(4):96. https://doi.org/10.3390/photonics7040096
Chicago/Turabian StyleFeng, Zuo, Yuming He, Wei Yan, Fuhua Yang, Weihua Han, and Zhaofeng Li. 2020. "Progress of Waveguide Ring Resonators Used in Micro-Optical Gyroscopes" Photonics 7, no. 4: 96. https://doi.org/10.3390/photonics7040096
APA StyleFeng, Z., He, Y., Yan, W., Yang, F., Han, W., & Li, Z. (2020). Progress of Waveguide Ring Resonators Used in Micro-Optical Gyroscopes. Photonics, 7(4), 96. https://doi.org/10.3390/photonics7040096






