Ellipticity of High-Order Harmonics Generated by Aligned Homonuclear Diatomic Molecules Exposed to an Orthogonal Two-Color Laser Field
Abstract
1. Introduction
2. Theory
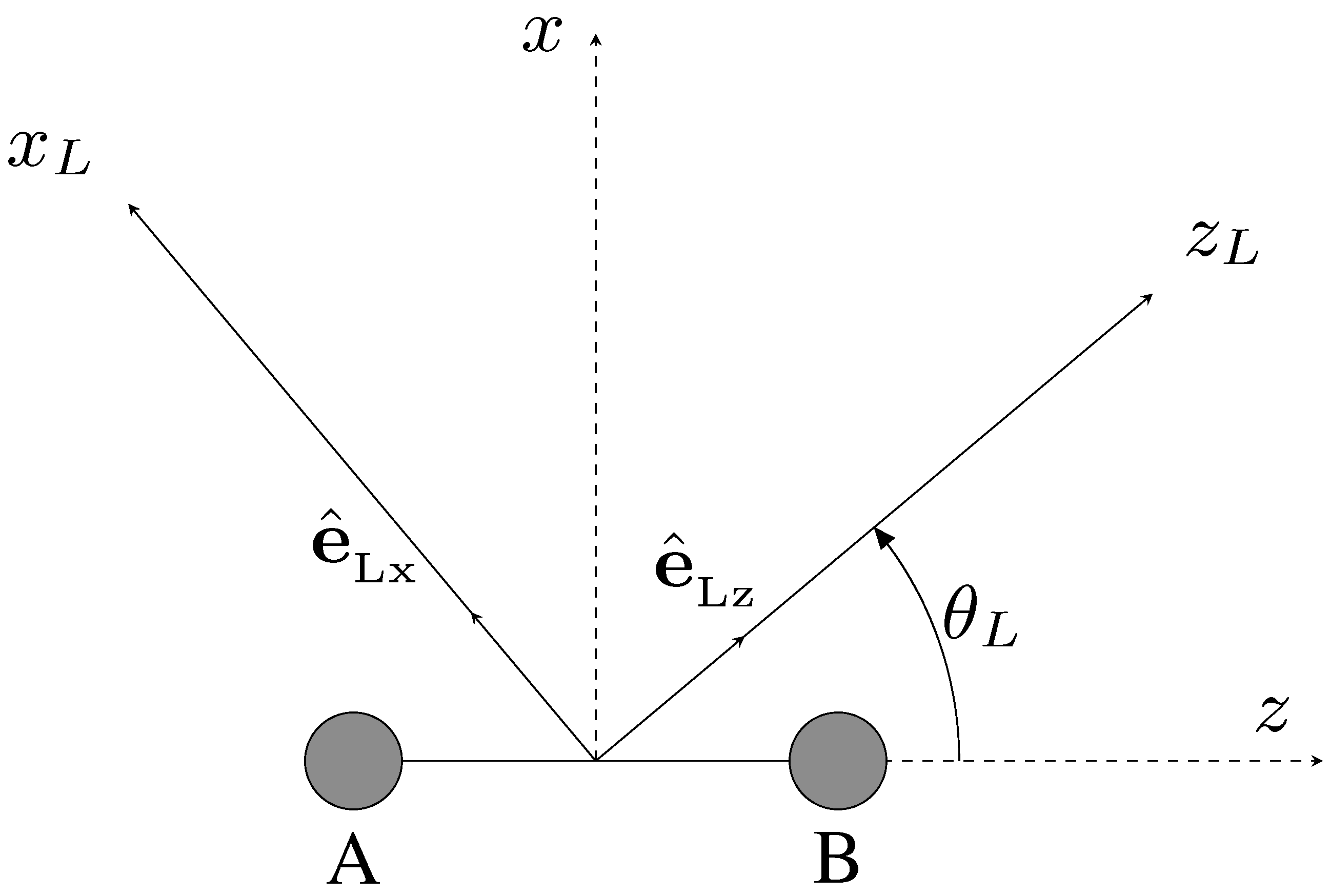
2.1. Definition of the OTC Field, Diatomic Molecules and the Geometry of the HHG Process
2.2. Harmonic Emission Rate
2.3. Harmonic Ellipticity
2.4. Interference Minima Conditions
2.5. Simple Man’s Model
3. Numerical Results
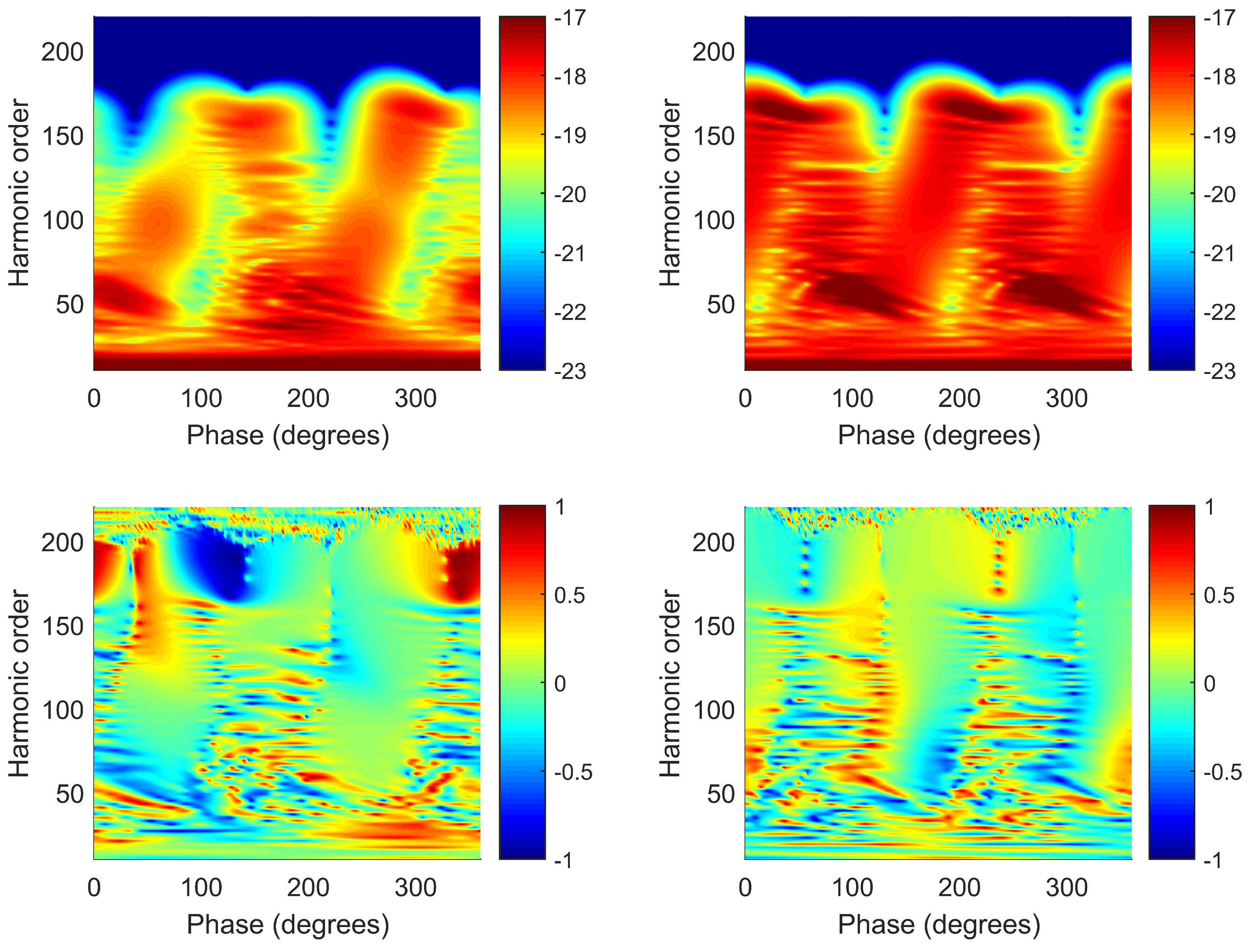
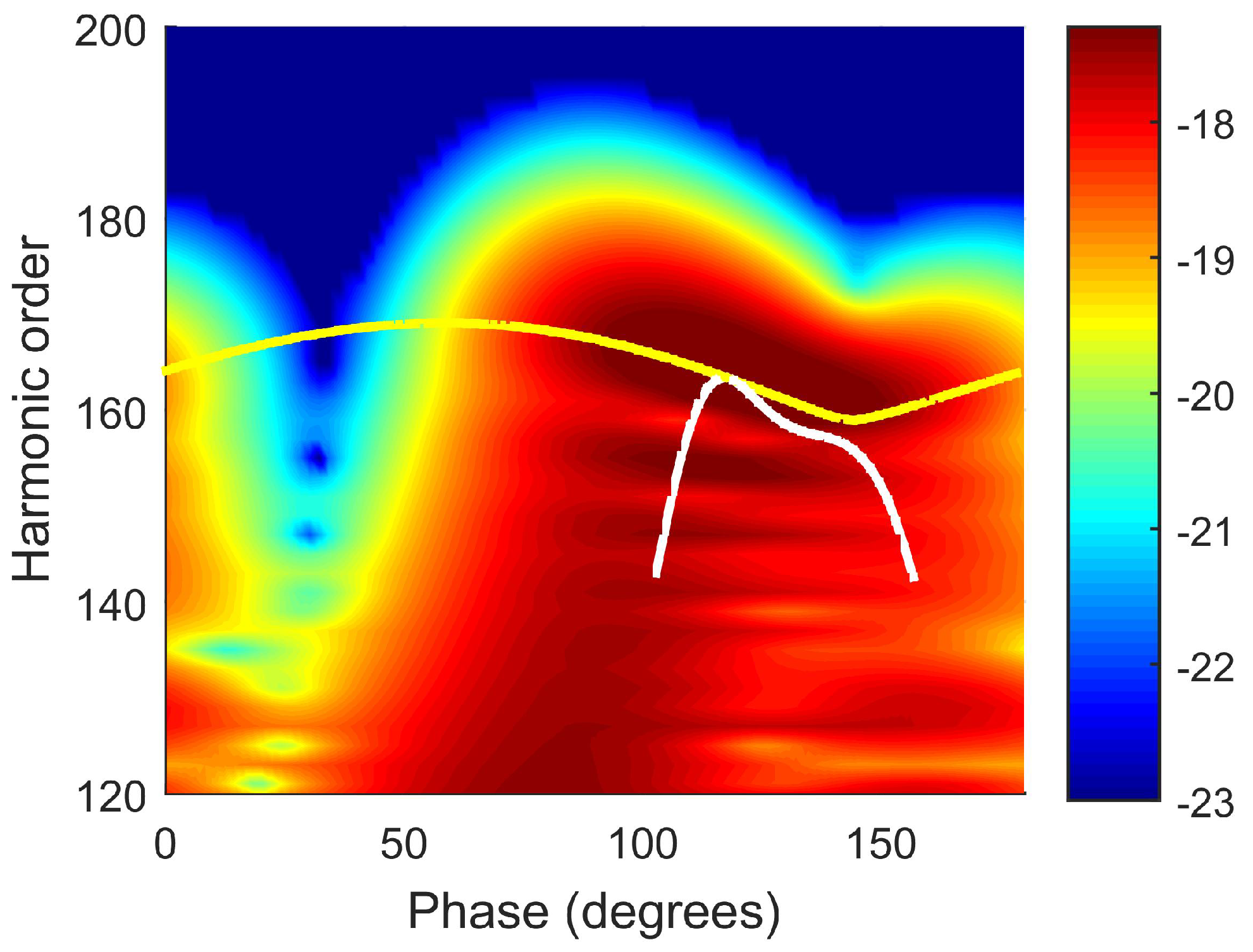
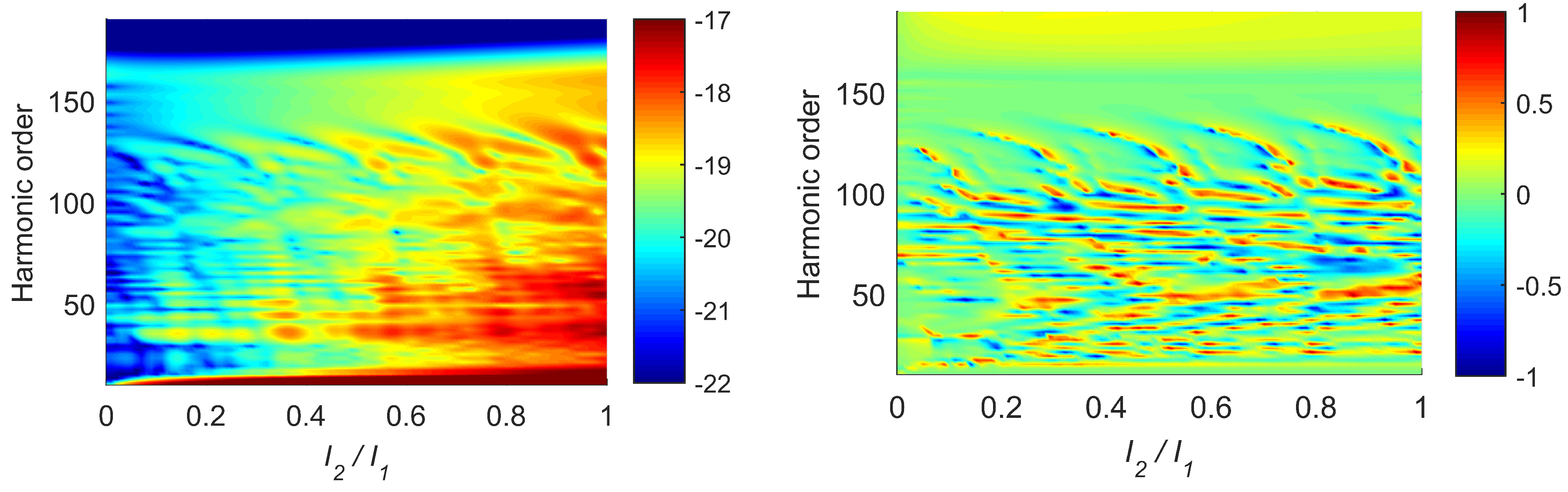
3.1. Harmonic Emission Rate and Ellipticity as Functions of the Relative Phase
3.1.1. – OTC Field
3.1.2. – OTC Field
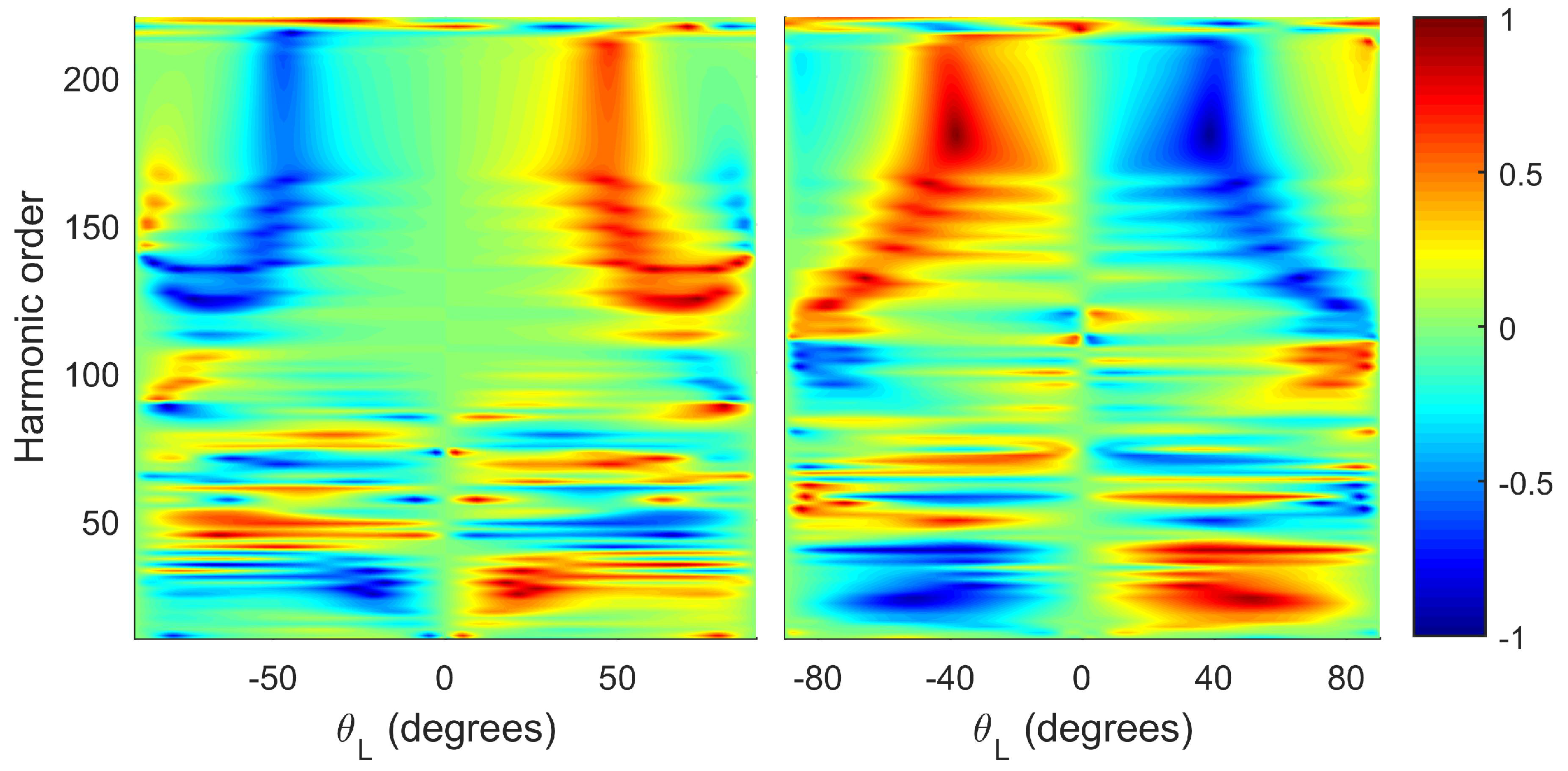
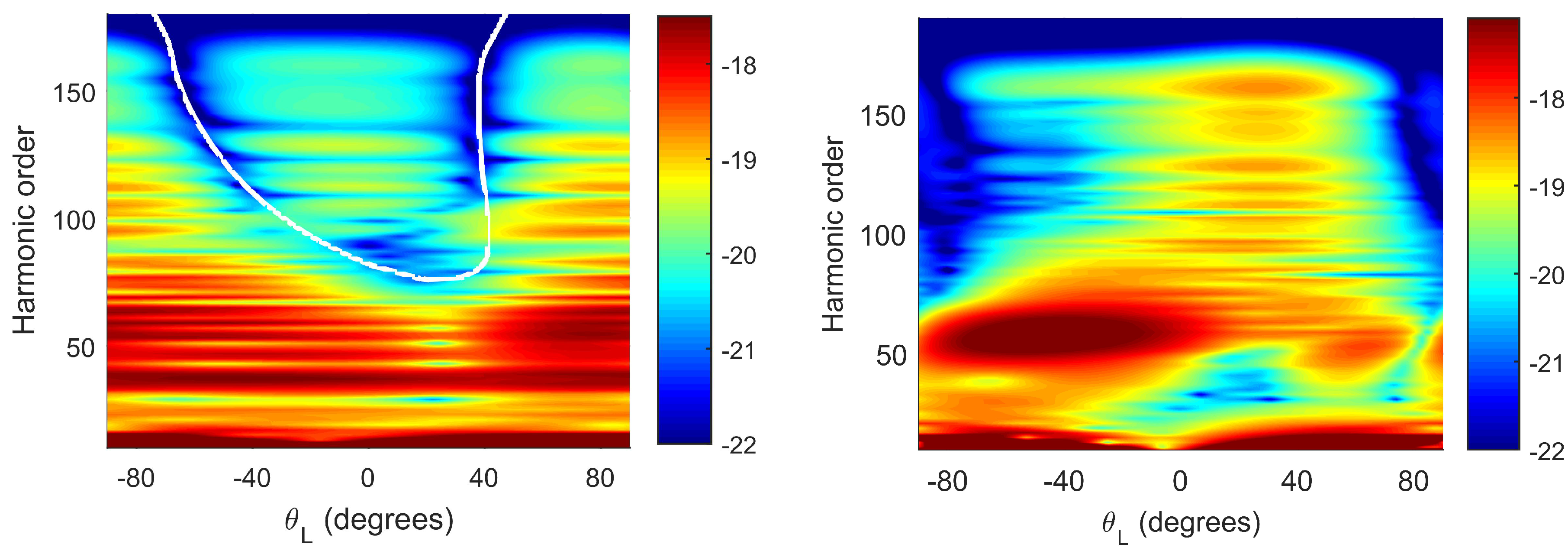
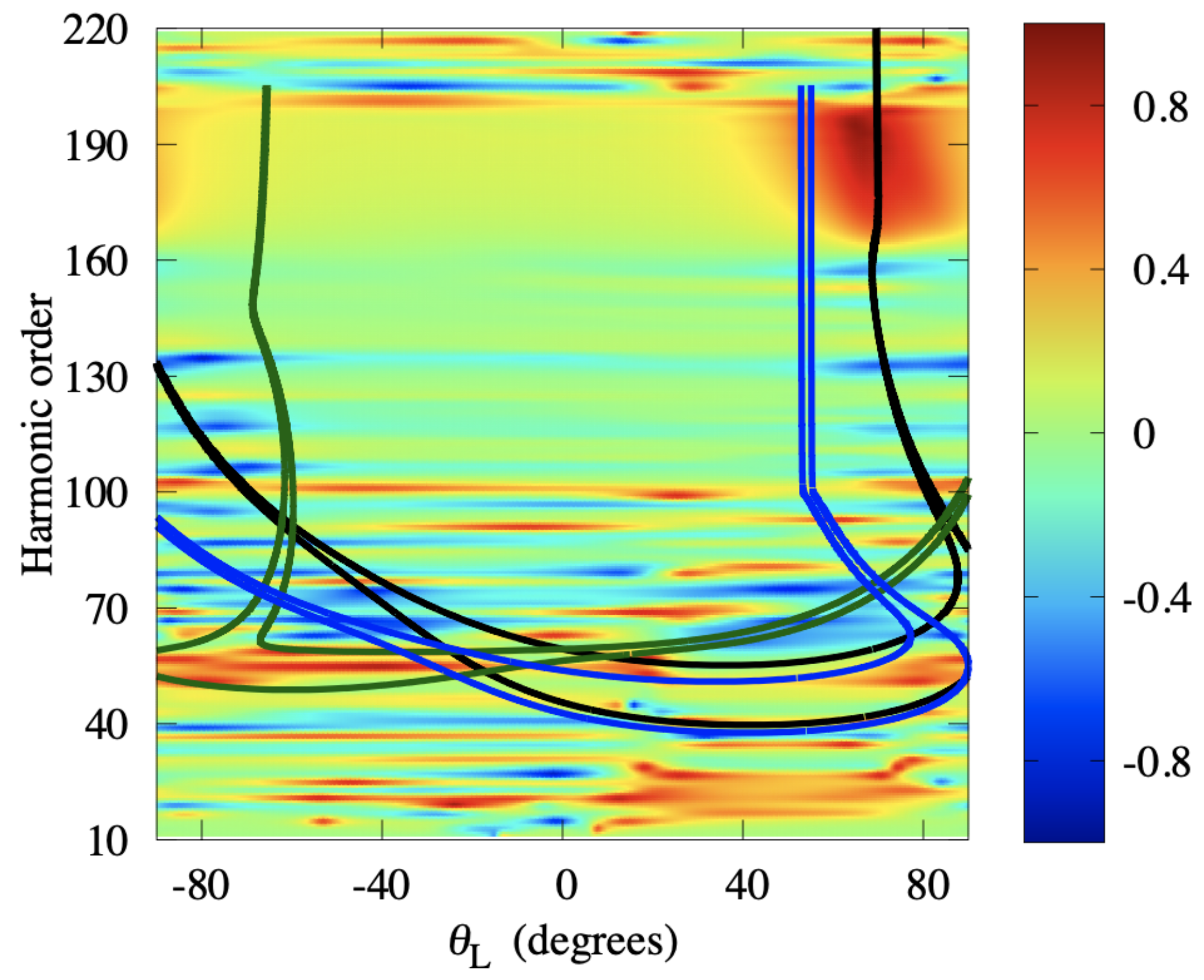
3.2. Harmonic Emission Rate and Ellipticity as Functions of the Molecular Orientation Angle
3.2.1. – OTC Field
3.2.2. – OTC Field
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Saddle-Point Method and Quantum-Orbit Theory

References
- Corkum, P.B. Plasma perspective on strong field multiphoton ionization. Phys. Rev. Lett. 1993, 71, 1994–1997. [Google Scholar] [CrossRef] [PubMed]
- Lewenstein, M.; Balcou, P.; Ivanov, M.Y.; L’Huillier, A.; Corkum, P.B. Theory of high-harmonic generation by low-frequency laser fields. Phys. Rev. A 1994, 49, 2117–2132. [Google Scholar] [CrossRef] [PubMed]
- Becker, W.; Grasbon, F.; Kopold, R.; Milošević, D.B.; Paulus, G.G.; Walther, H. Above-Threshold Ionization: From Classical Features to Quantum Effects. Adv. At. Mol. Opt. Phys. 2002, 48, 35–98. [Google Scholar] [CrossRef]
- Kohler, M.; Pfeifer, T.; Hatsagortsyan, K.; Keitel, C. Frontiers of Atomic High-Harmonic Generation. Adv. At. Mol. Opt. Phys. 2012, 61, 159–208. [Google Scholar] [CrossRef]
- Becker, W.; Liu, X.; Ho, P.J.; Eberly, J.H. Theories of photoelectron correlation in laser-driven multiple atomic ionization. Rev. Mod. Phys. 2012, 84, 1011–1043. [Google Scholar] [CrossRef]
- Eichmann, H.; Egbert, A.; Nolte, S.; Momma, C.; Wellegehausen, B.; Becker, W.; Long, S.; McIver, J.K. Polarization-dependent high-order two-color mixing. Phys. Rev. A 1995, 51, R3414–R3417. [Google Scholar] [CrossRef] [PubMed]
- Long, S.; Becker, W.; McIver, J.K. Model calculations of polarization-dependent two-color high-harmonic generation. Phys. Rev. A 1995, 52, 2262–2278. [Google Scholar] [CrossRef]
- Zuo, T.; Bandrauk, A.D. High-order harmonic generation in intense laser and magnetic fields. J. Nonlinear Opt. Phys. Mat. 1995, 04, 533–546. [Google Scholar] [CrossRef]
- Milošević, D.B.; Becker, W.; Kopold, R. Generation of circularly polarized high-order harmonics by two-color coplanar field mixing. Phys. Rev. A 2000, 2000. 61, 063403. [Google Scholar] [CrossRef]
- Fleischer, A.; Kfir, O.; Diskin, T.; Sidorenko, P.; Cohen, O. Spin angular momentum and tunable polarization in high-harmonic generation. Nat. Photon. 2014, 8, 543–549. [Google Scholar] [CrossRef]
- Ke, Q.; Zhou, Y.; Tan, J.; He, M.; Liang, J.; Zhao, Y.; Li, M.; Lu, P. Direct probing of tunneling time in strong-field ionization processes by time-dependent wave packets. Opt. Express 2019, 27, 32193–32209. [Google Scholar] [CrossRef] [PubMed]
- Baykusheva, D.; Wörner, H.J. Chiral Discrimination through Bielliptical High-Harmonic Spectroscopy. Phys. Rev. X 2018, 8, 031060. [Google Scholar] [CrossRef]
- Neufeld, O.; Ayuso, D.; Decleva, P.; Ivanov, M.Y.; Smirnova, O.; Cohen, O. Ultrasensitive Chiral Spectroscopy by Dynamical Symmetry Breaking in High Harmonic Generation. Phys. Rev. X 2019, 9, 031002. [Google Scholar] [CrossRef]
- Ayuso, D.; Neufeld, O.; Ordonez, A.F.; Decleva, P.; Lerner, G.; Cohen, O.; Ivanov, M.Y.; Smirnova, O. Locally and globally chiral fields for ultimate control of chiral light matter interaction. Nat. Photon. 2019, 13, 866–871. [Google Scholar] [CrossRef]
- Levesque, J.; Mairesse, Y.; Dudovich, N.; Pépin, H.; Kieffer, J.C.; Corkum, P.B.; Villeneuve, D.M. Polarization State of High-Order Harmonic Emission from Aligned Molecules. Phys. Rev. Lett. 2007, 99, 243001. [Google Scholar] [CrossRef]
- Ferré, A.; Handschin, C.; Dumergue, M.; Burgy, F.; Comby, A.; Descamps, D.; Fabre, B.; Garcia, G.A.; Géneaux, R.; Merceron, L.; et al. A table-top ultrashort light source in the extreme ultraviolet for circular dichroism experiments. Nat. Photon. 2015, 9, 93–98. [Google Scholar] [CrossRef]
- Hickstein, D.D.; Dollar, F.J.; Grychtol, P.; Ellis, J.L.; Knut, R.; Hernández-García, C.; Zusin, D.; Gentry, C.; Shaw, J.M.; Fan, T.; et al. Non-collinear generation of angularly isolated circularly polarized high harmonics. Nat. Photon. 2015, 9, 743–750. [Google Scholar] [CrossRef]
- Hernández-García, C.; Durfee, C.G.; Hickstein, D.D.; Popmintchev, T.; Meier, A.; Murnane, M.M.; Kapteyn, H.C.; Sola, I.J.; Jaroń-Becker, A.; Becker, A. Schemes for generation of isolated attosecond pulses of pure circular polarization. Phys. Rev. A 2016, 93, 043855. [Google Scholar] [CrossRef]
- Smirnova, O.; Patchkovskii, S.; Mairesse, Y.; Dudovich, N.; Villeneuve, D.; Corkum, P.; Ivanov, M.Y. Attosecond circular dichroism spectroscopy of polyatomic molecules. Phys. Rev. Lett. 2009, 102, 063601. [Google Scholar] [CrossRef]
- Zhou, X.; Lock, R.; Wagner, N.; Li, W.; Kapteyn, H.C.; Murnane, M.M. Elliptically polarized high-order harmonic emission from molecules in linearly polarized laser fields. Phys. Rev. Lett. 2009, 102, 073902. [Google Scholar] [CrossRef]
- Milošević, D.B.; Becker, W. X-ray harmonic generation by orthogonally polarized two-color fields: Spectral shape and polarization. Phys. Rev. A 2019, 100, 031401. [Google Scholar] [CrossRef]
- Kim, I.J.; Kim, C.M.; Kim, H.T.; Lee, G.H.; Lee, Y.S.; Park, J.Y.; Cho, F.J.; Nam, C.H. Highly Efficient High-Harmonic Generation in an Orthogonally Polarized Two-Color Laser Field. Phys. Rev. Lett. 2005, 94, 243901. [Google Scholar] [CrossRef]
- Milošević, D.B.; Becker, W. Generation of elliptically polarized soft x rays using high-order harmonic generation with orthogonal two-color laser fields. J. Phys. Conf. Ser. 2020, 1508, 012001. [Google Scholar] [CrossRef]
- Neufeld, O.; Podolsky, D.; Cohen, O. Floquet group theory and its application to selection rules in harmonic generation. Nat. Commun. 2019, 10, 405. [Google Scholar] [CrossRef] [PubMed]
- Zhai, C.; Shao, R.; Lan, P.; Wang, B.; Zhang, Y.; Yuan, H.; Njoroge, S.M.; He, L.; Lu, P. Ellipticity control of high-order harmonic generation with nearly orthogonal two-color laser fields. Phys. Rev. A 2020, 101, 053407. [Google Scholar] [CrossRef]
- Neufeld, O.; Cohen, O. Background-Free Measurement of Ring Currents by Symmetry-Breaking High-Harmonic Spectroscopy. Phys. Rev. Lett. 2019, 123, 103202. [Google Scholar] [CrossRef] [PubMed]
- Neufeld, O.; Cohen, O. Probing ultrafast electron correlations in high harmonic generation. Phys. Rev. Res. 2020, 2, 033037. [Google Scholar] [CrossRef]
- Watanabe, S.; Kondo, K.; Nabekawa, Y.; Sagisaka, A.; Kobayashi, Y. Two-Color Phase Control in Tunneling Ionization and Harmonic Generation by a Strong Laser Field and Its Third Harmonic. Phys. Rev. Lett. 1994, 73, 2692–2695. [Google Scholar] [CrossRef]
- Bordo, E.; Kfir, O.; Zayko, S.; Neufeld, O.; Fleischer, A.; Ropers, C.; Cohen, O. Interlocked attosecond pulse trains in slightly bi-elliptical high harmonic generation. J. Phys. Photon. 2020, 2, 034005. [Google Scholar] [CrossRef]
- Milošević, D.B.; Becker, W. High-order harmonic generation by bi-elliptical orthogonally polarized two-color fields. Phys. Rev. A 2020, 102, 023107. [Google Scholar] [CrossRef]
- Lein, M.; Hay, N.; Velotta, R.; Marangos, J.P.; Knight, P.L. Role of the Intramolecular Phase in High-Harmonic Generation. Phys. Rev. Lett. 2002, 88, 183903. [Google Scholar] [CrossRef] [PubMed]
- Odžak, S.; Milošević, D.B. Interference effects in high-order harmonic generation by homonuclear diatomic molecules. Phys. Rev. A 2009, 79, 023414. [Google Scholar] [CrossRef]
- Odžak, S.; Milošević, D.B. Dressed-bound-state molecular strong-field approximation: Application to high-order harmonic generation by heteronuclear diatomic molecules. J. Opt. Soc. Am. B 2012, 29, 2147–2155. [Google Scholar] [CrossRef]
- Itatani, J.; Levesque, J.; Zeidler, D.; Niikura, H.; Pépin, H.; Kieffer, J.C.; Corkum, P.B.; Villeneuve, D.M. Tomographic imaging of molecular orbitals. Nature (Lond.) 2004, 432, 867–871. [Google Scholar] [CrossRef]
- Niikura, H.; Dudovich, N.; Villeneuve, D.M.; Corkum, P.B. Mapping Molecular Orbital Symmetry on High-Order Harmonic Generation Spectrum Using Two-Color Laser Fields. Phys. Rev. Lett. 2010, 105, 053003. [Google Scholar] [CrossRef]
- Niikura, H.; Wörner, H.J.; Villeneuve, D.M.; Corkum, P.B. Probing the Spatial Structure of a Molecular Attosecond Electron Wave Packet Using Shaped Recollision Trajectories. Phys. Rev. Lett. 2011, 107, 093004. [Google Scholar] [CrossRef]
- Shafir, D.; Soifer, H.; Bruner, B.D.; Dagan, M.; Mairesse, Y.; Patchkovskii, S.; Ivanov, M.Y.; Smirnova, O.; Dudovich, N. Resolving the time when an electron exits a tunnelling barrier. Nature 2012, 485, 243–346. [Google Scholar] [CrossRef]
- Das, T.; Augstein, B.B.; Figueira de Morisson Faria, C. High-order-harmonic generation from diatomic molecules in driving fields with nonvanishing ellipticity: A generalized interference condition. Phys. Rev. A 2013, 88, 023404. [Google Scholar] [CrossRef]
- Liu, X.; Zhu, X.; Li, L.; Li, Y.; Zhang, Q.; Lan, P.; Lu, P. Selection rules of high-order-harmonic generation: Symmetries of molecules and laser fields. Phys. Rev. A 2016, 94, 033410. [Google Scholar] [CrossRef]
- Chen, C.; Ren, D.X.; Han, X.; Yang, S.P.; Chen, Y.J. Time-resolved harmonic emission from aligned molecules in orthogonal two-color fields. Phys. Rev. A 2018, 98, 063425. [Google Scholar] [CrossRef]
- Zhai, C.; Zhang, X.; Zhu, X.; He, L.; Zhang, Y.; Wang, B.; Zhang, Q.; Lan, P.; Lu, P. Single-shot molecular orbital tomography with orthogonal two-color fields. Opt. Express 2018, 26, 2775–2784. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Lein, M. High-order harmonic generation from diatomic molecules in an orthogonally polarized two-color laser field. Phys. Rev. A 2019, 100, 043401. [Google Scholar] [CrossRef]
- Ansari, Z.; Böttcher, M.; Manschwetus, B.; Rottke, H.; Sandner, W.; Verhoef, A.; Lezius, M.; Paulus, G.G.; Saenz, A.; Milošević, D.B. Interference in strong-field ionization of a two-centre atomic system. New J. Phys. 2008, 10, 093027. [Google Scholar] [CrossRef][Green Version]
- Busuladžić, M.; Gazibegović-Busuladžić, A.; Milošević, D.B.; Becker, W. Angle-Resolved High-Order Above-Threshold Ionization of a Molecule: Sensitive Tool for Molecular Characterization. Phys. Rev. Lett. 2008, 100, 203003. [Google Scholar] [CrossRef] [PubMed]
- Okunishi, M.; Itaya, R.; Shimada, K.; Prümper, G.; Ueda, K.; Busuladžić, M.; Gazibegović-Busuladžić, A.; Milošević, D.B.; Becker, W. Angle-resolved high-order above-threshold ionization spectra for N2 and O2: Measurements and the strong-field approximation. J. Phys. B 2008, 41, 201004. [Google Scholar] [CrossRef]
- Okunishi, M.; Itaya, R.; Shimada, K.; Prümper, G.; Ueda, K.; Busuladžić, M.; Gazibegović-Busuladžić, A.; Milošević, D.B.; Becker, W. Two-Source Double-Slit Interference in Angle-Resolved High-Energy Above-Threshold Ionization Spectra of Diatoms. Phys. Rev. Lett. 2009, 103, 043001. [Google Scholar] [CrossRef]
- Kang, H.; Quan, W.; Wang, Y.; Lin, Z.; Wu, M.; Liu, H.; Liu, X.; Wang, B.B.; Liu, H.J.; Gu, Y.Q.; et al. Structure Effects in Angle-Resolved High-Order Above-Threshold Ionization of Molecules. Phys. Rev. Lett. 2010, 104, 203001. [Google Scholar] [CrossRef]
- Gazibegović-Busuladžić, A.; Hasović, E.; Busuladžić, M.; Milošević, D.B.; Kelkensberg, F.; Siu, W.K.; Vrakking, M.J.J.; Lépine, F.; Sansone, G.; Nisoli, M.; et al. Above-threshold ionization of diatomic molecules by few-cycle laser pulses. Phys. Rev. A 2011, 84, 043426. [Google Scholar] [CrossRef]
- Quan, W.; Lai, X.-Y.; Chen, Y.-J.; Wang, C.-L.; Hu, Z.-L.; Liu, X.-J.; Hao, X.-L.; Chen, J.; Hasović, E.; Busuladžić, M.; et al. Resonancelike enhancement in high-order above-threshold ionization of molecules. Phys. Rev. A 2013, 88, 021401. [Google Scholar] [CrossRef]
- Sun, R.P.; Lai, X.Y.; Yu, S.G.; Wang, Y.L.; Xu, S.P.; Quan, W.; Liu, X.J. Tomographic extraction of the internuclear separation based on two-center interference with aligned diatomic molecules. Phys. Rev. Lett. 2019, 122, 193202. [Google Scholar] [CrossRef]
- Habibović, D.; Gazibegović-Busuladžić, A.; Busuladžić, M.; Čerkić, A.; Milošević, D.B. Strong-field ionization of homonuclear diatomic molecules using orthogonally polarized two-color laser fields. Phys. Rev. A 2020, 102, 023111. [Google Scholar] [CrossRef]
- Milošević, D.B. Strong-field approximation for ionization of a diatomic molecule by a strong laser field. Phys. Rev. A 2006, 74, 063404. [Google Scholar] [CrossRef]
- Odžak, S.; Hasović, E.; Milošević, D.B. Strong-field-approximation theory of high-order harmonic generation by polyatomic molecules. Phys. Rev. A 2016, 93, 043413. [Google Scholar] [CrossRef]
- Odžak, S.; Hasović, E.; Milošević, D.B. High-order harmonic generation in polyatomic molecules induced by a bicircular laser field. Phys. Rev. A 2016, 94, 033419. [Google Scholar] [CrossRef]
- Atkins, P.W.; Friedman, R.S. Molecular Quantum Mechanics; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Wahl, A.C. Analytic Self Consistent Field Wavefunctions and Computed Properties for Homonuclear Diatomic Molecules. J. Chem. Phys. 1964, 41, 2600–2611. [Google Scholar] [CrossRef]
- Milošević, D.B.; Ehlotzky, F. Scattering and Reaction Processes in Powerful Laser Fields. Adv. At. Mol. Opt. Phys. 2003, 49, 373–532. [Google Scholar] [CrossRef]
- Milošević, D.B. A semi-classical model for high-harmonic generation. In Super-Intense Laser-Atom Physics; Piraux, B., Rza̧żewski, K., Eds.; Kluwer: Dordrecht, The Netherlands, 2001; pp. 229–238. [Google Scholar]
- Becker, W.; Chen, J.; Chen, S.G.; Milošević, D.B. Dressed-state strong-field approximation for laser-induced molecular ionization. Phys. Rev. A 2007, 76, 033403. [Google Scholar] [CrossRef]
- Odžak, S.; Milošević, D.B. Ellipticity and the offset angle of high harmonics generated by homonuclear diatomic molecules. J. Phys. B 2011, 44, 125602. [Google Scholar] [CrossRef]
- Odžak, S.; Milošević, D.B. Elliptic dichroism, ellipticity and the offset angle of high harmonics generated by arbitrary homonuclear diatomic molecules. Laser Phys. 2012, 22, 1780–1786. [Google Scholar] [CrossRef]
- Odžak, S.; Milošević, D.B. Role of ellipticity in high-order harmonic generation by homonuclear diatomic molecules. Phys. Rev. A 2010, 82, 023412. [Google Scholar] [CrossRef]
- Odžak, S.; Milošević, D.B. Molecular high-order harmonic generation: Analysis of a destructive interference condition. J. Phys. B 2009, 42, 071001. [Google Scholar] [CrossRef]
- Gallagher, T.F. Above-Threshold Ionization in Low-Frequency Limit. Phys. Rev. Lett. 1988, 61, 2304–2307. [Google Scholar] [CrossRef] [PubMed]
- Corkum, P.B.; Burnett, N.H.; Brunel, F. Above-threshold ionization in the long-wavelength limit. Phys. Rev. Lett. 1989, 62, 1259–1262. [Google Scholar] [CrossRef]
- Schafer, K.J.; Yang, B.; DiMauro, L.F.; Kulander, K.C. Above threshold ionization beyond the high harmonic cutoff. Phys. Rev. Lett. 1993, 70, 1599–1602. [Google Scholar] [CrossRef] [PubMed]
- Fetić, B.; Milošević, D.B. High-order above-threshold ionization of the H2+ ion: The role of internuclear distance. Phys. Rev. A 2019, 99, 043426. [Google Scholar] [CrossRef]
- Salières, P.; Carré, B.; Le Déroff, L.; Grasbon, F.; Paulus, G.G.; Walther, H.; Kopold, R.; Becker, W.; Milošević, D.B.; Sanpera, A.; et al. Feynman’s Path-integral approach for intense-laser-atom interactions. Science 2001, 292, 902–905. [Google Scholar] [CrossRef]
- Milošević, D.B. Cut-off law for high-harmonic generation by an elliptically polarized laser field. J. Phys. B 2000, 33, 2479–2488. [Google Scholar] [CrossRef]
- Kopold, R.; Milošević, D.B.; Becker, W. Rescattering processes for elliptical polarization: A quantum trajectory analysis. Phys. Rev. Lett. 2000, 84, 3831–3834. [Google Scholar] [CrossRef]
- Milošević, D.B.; Bauer, D.; Becker, W. Quantum-orbit theory of high-order atomic processes in intense laser fields. J. Mod. Opt. 2006, 53, 125–134. [Google Scholar] [CrossRef]
- Milošević, D.B. Strong-field approximation and quantum orbits. In Computational Strong-Field Quantum Dynamics: Intense Light-Matter Interactions; Bauer, D., Ed.; De Gruyter Textbook: Berlin, Germany, 2016; Chap. VII; pp. 199–221. [Google Scholar]
- Milošević, D.; Becker, W. Role of long quantum orbits in high-order harmonic generation. Phys. Rev. A 2002, 66, 063417. [Google Scholar] [CrossRef]
- Milošević, D.B. Quantum-orbit analysis of high-order harmonic generation by bicircular field. J. Mod. Opt. 2019, 66, 47–58. [Google Scholar] [CrossRef]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Habibović, D.; Milošević, D.B. Ellipticity of High-Order Harmonics Generated by Aligned Homonuclear Diatomic Molecules Exposed to an Orthogonal Two-Color Laser Field. Photonics 2020, 7, 110. https://doi.org/10.3390/photonics7040110
Habibović D, Milošević DB. Ellipticity of High-Order Harmonics Generated by Aligned Homonuclear Diatomic Molecules Exposed to an Orthogonal Two-Color Laser Field. Photonics. 2020; 7(4):110. https://doi.org/10.3390/photonics7040110
Chicago/Turabian StyleHabibović, Dino, and Dejan B. Milošević. 2020. "Ellipticity of High-Order Harmonics Generated by Aligned Homonuclear Diatomic Molecules Exposed to an Orthogonal Two-Color Laser Field" Photonics 7, no. 4: 110. https://doi.org/10.3390/photonics7040110
APA StyleHabibović, D., & Milošević, D. B. (2020). Ellipticity of High-Order Harmonics Generated by Aligned Homonuclear Diatomic Molecules Exposed to an Orthogonal Two-Color Laser Field. Photonics, 7(4), 110. https://doi.org/10.3390/photonics7040110




