Nonlinear Optical Study in a Set of Dibenzylideneacetone Derivatives with Potential for Optical Frequency Conversion
Abstract
1. Introduction
2. Materials and Methods
2.1. Compounds
2.2. Optical Measurements
2.3. Theoretical
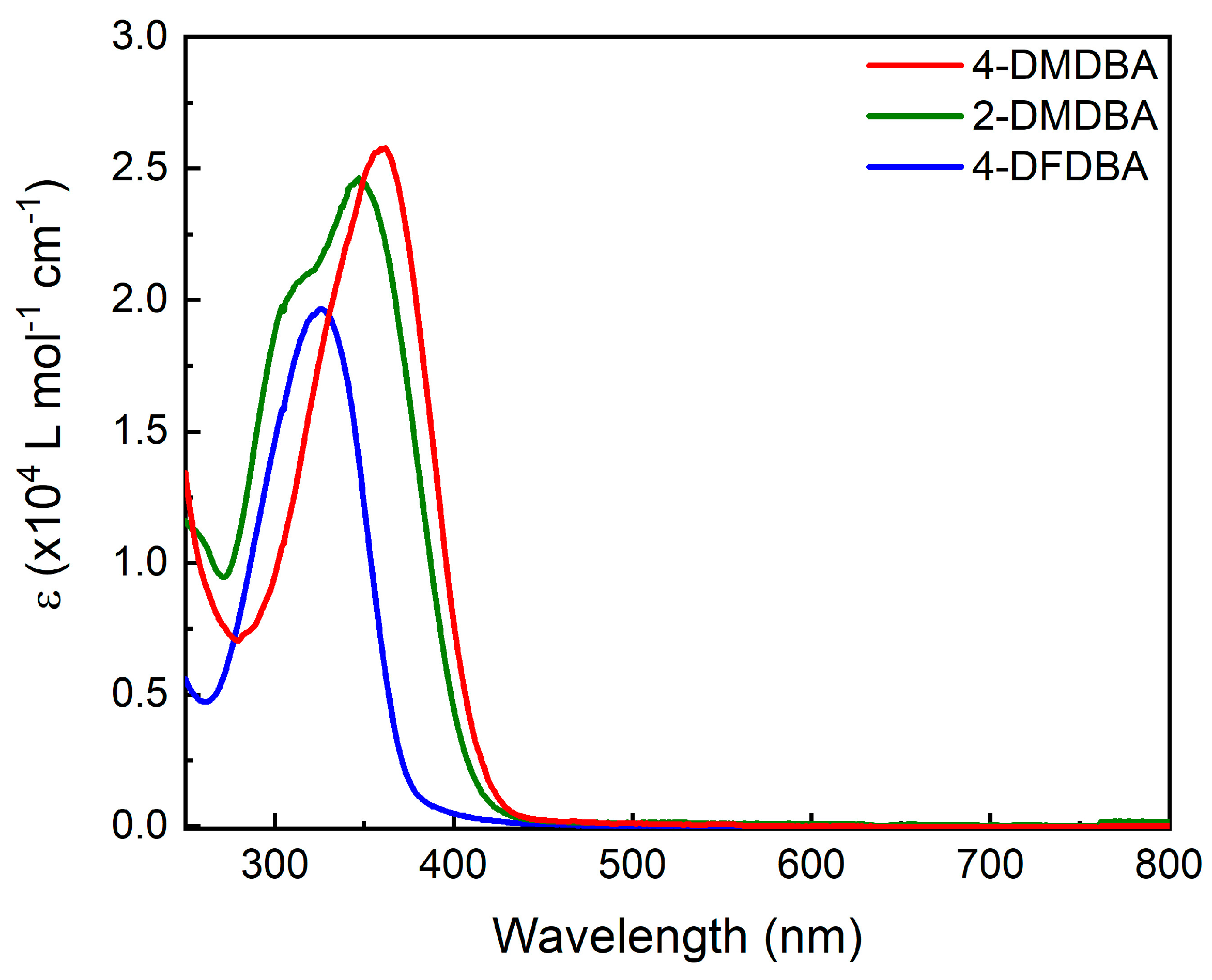
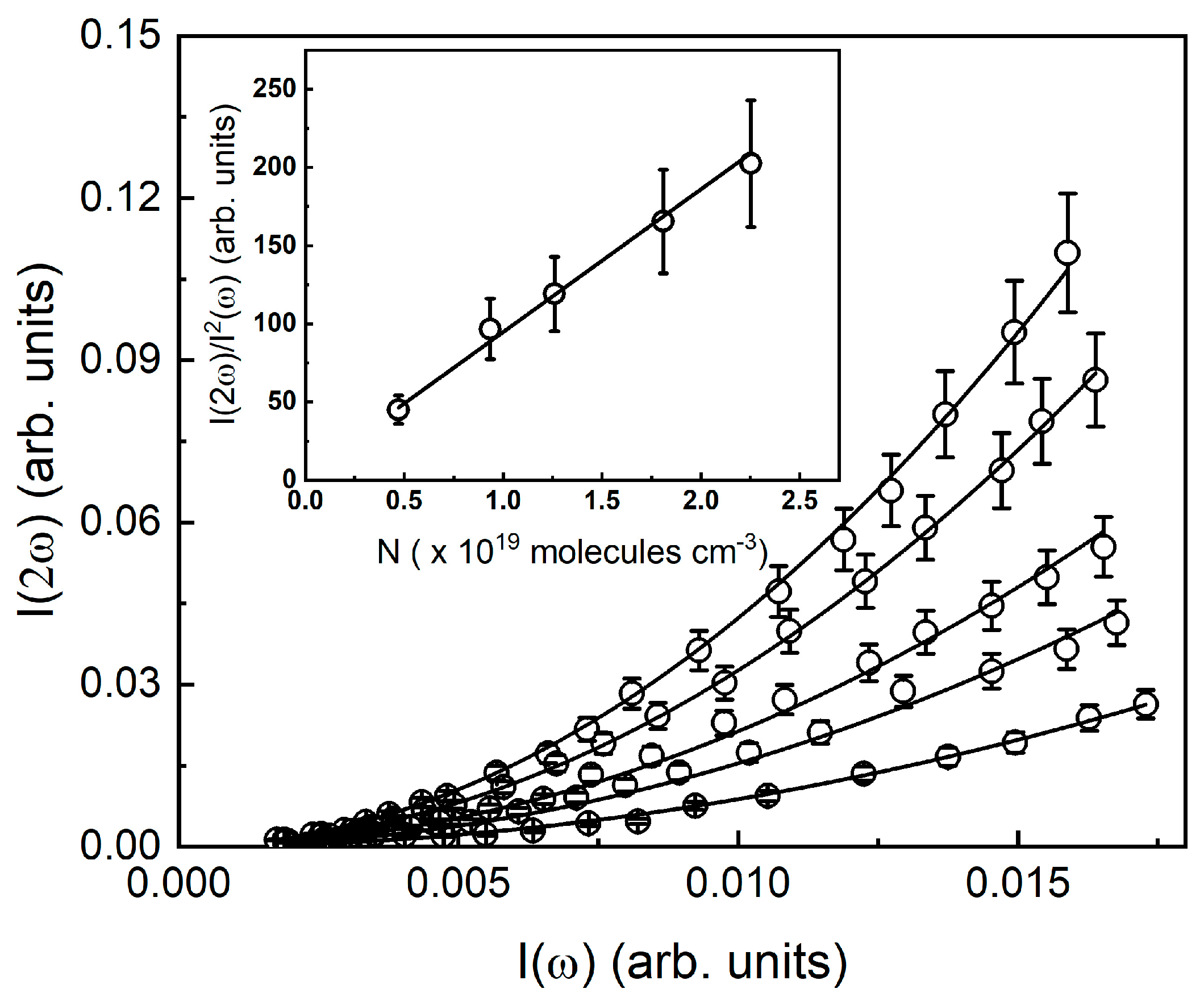
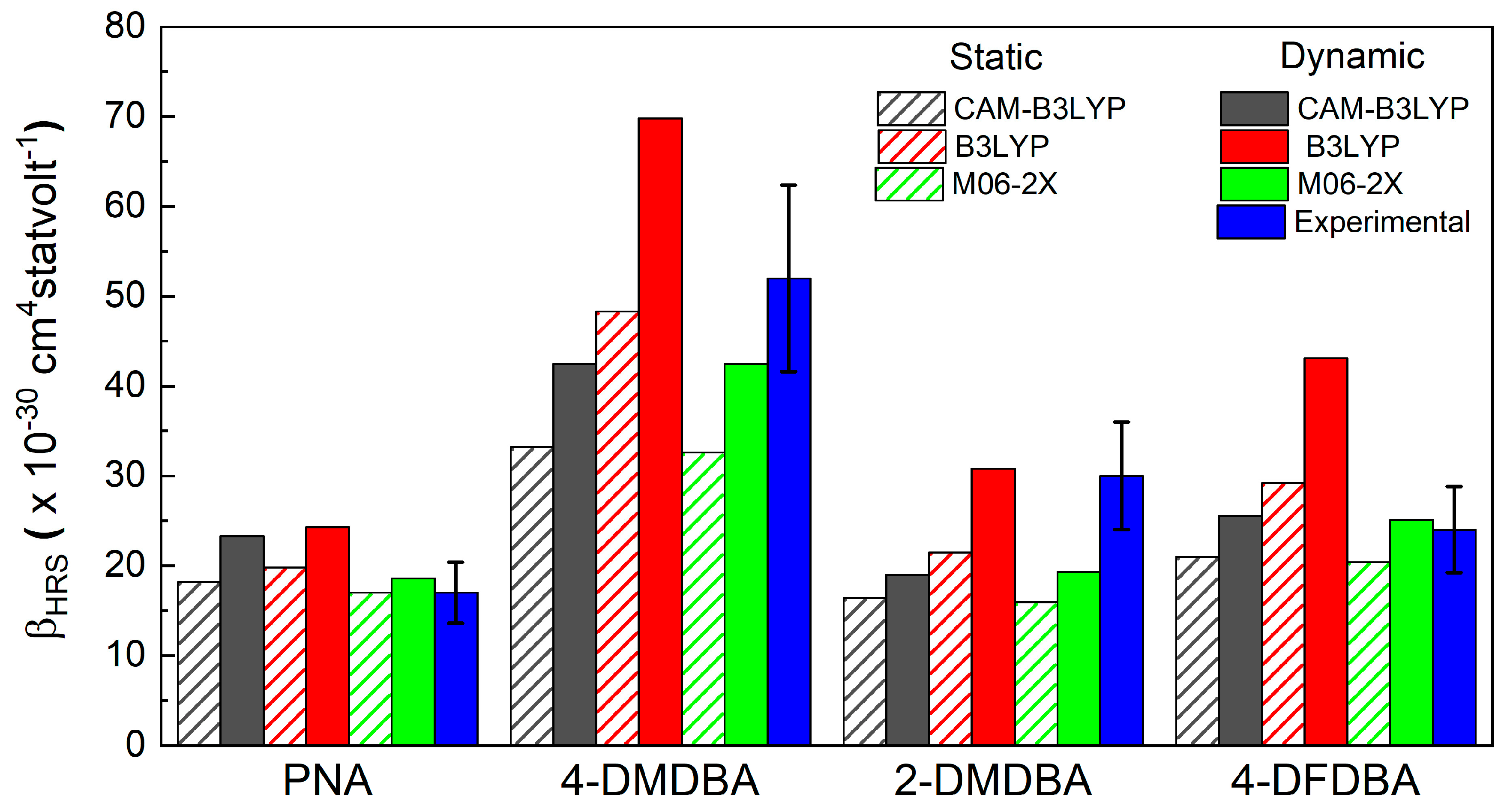
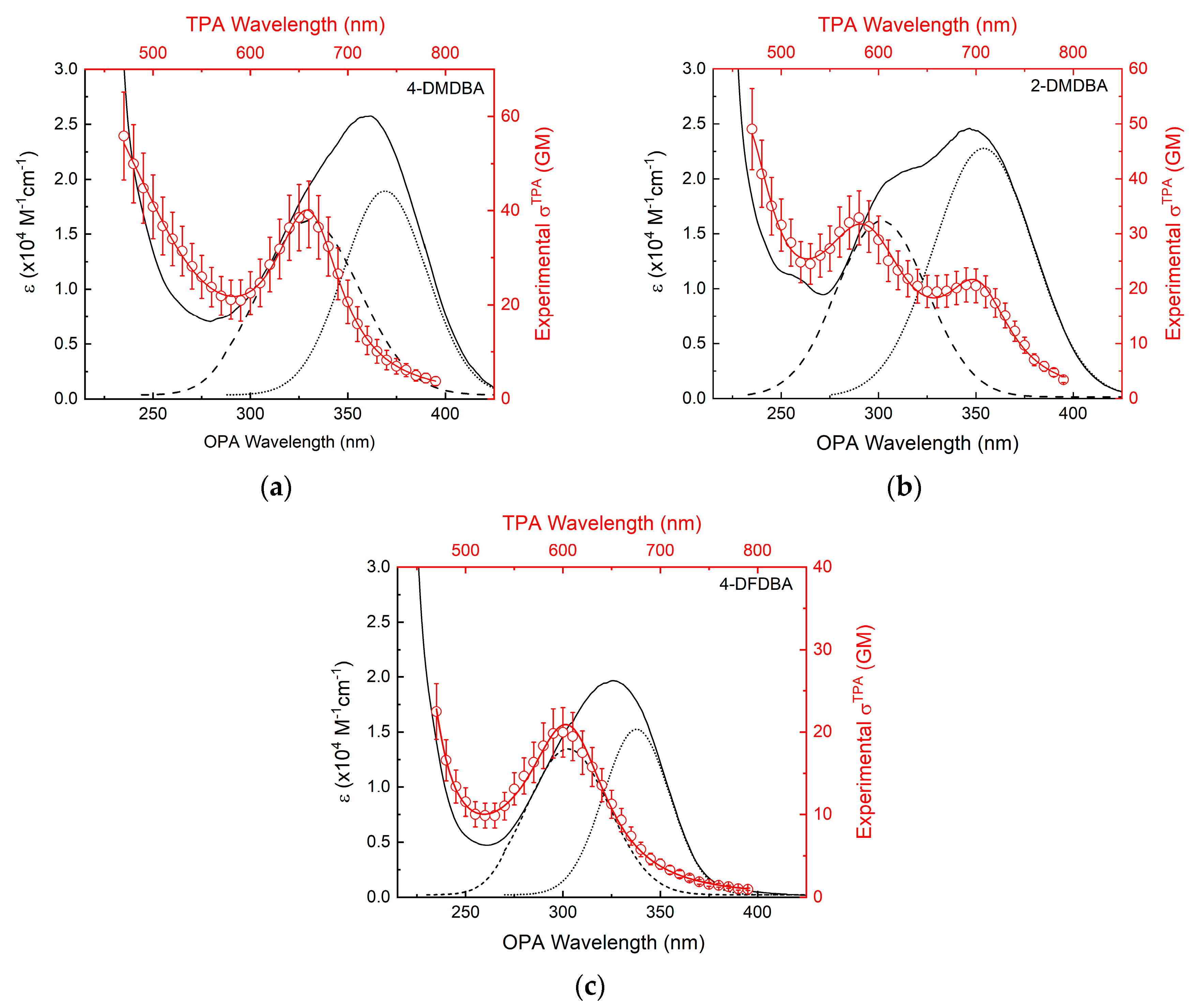
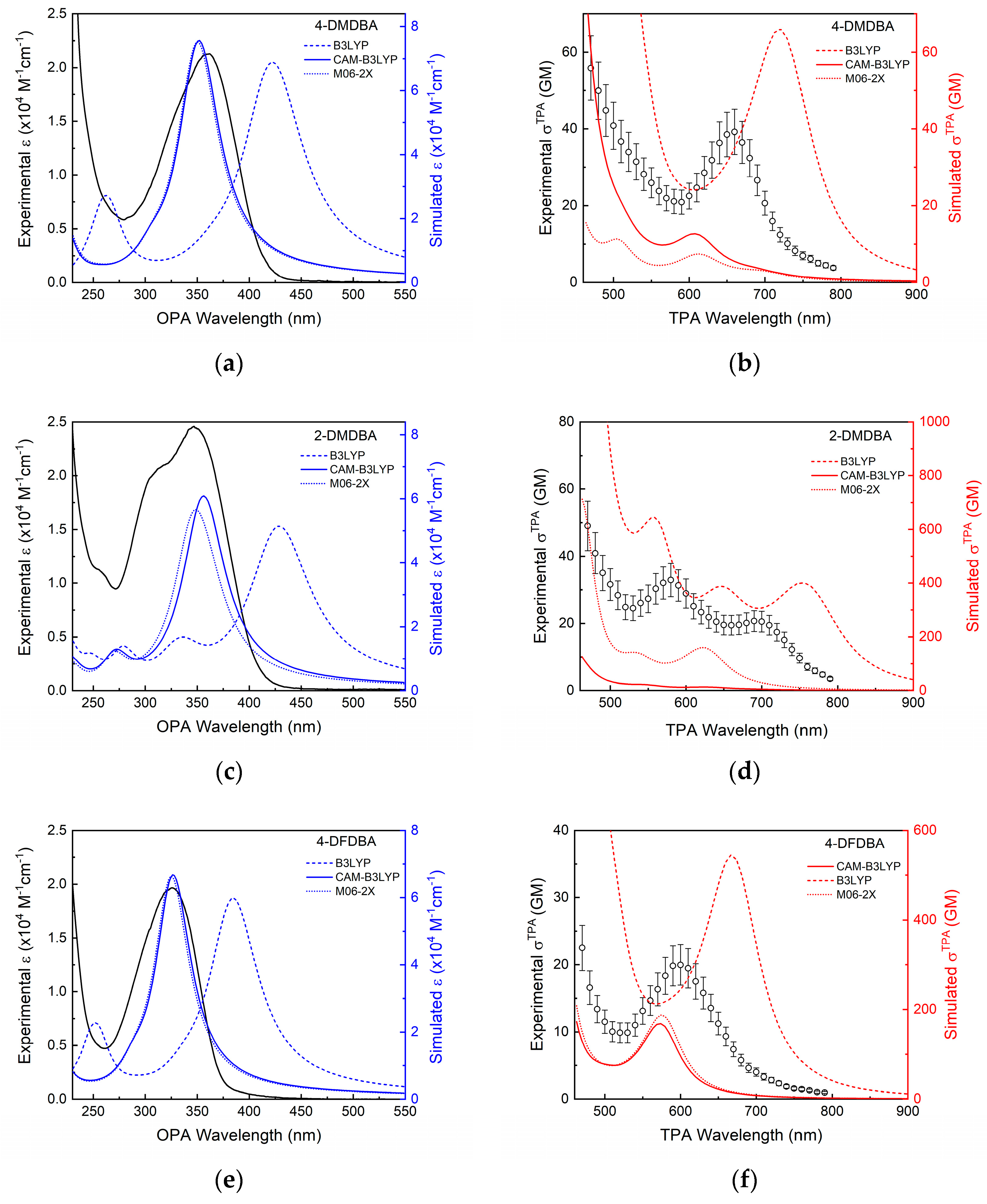
3. Results and Discussion
3.1. First Molecular Hyperpolarizability
3.2. Two-Photon Absorption
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mohammed, N.; Wiles, A.A.; Belsley, M.; Fernandes, S.S.; Cariello, M.; Rotello, V.M.; Raposo, M.M.M.; Cooke, G. Synthesis and characterisation of push–pull flavin dyes with efficient second harmonic generation (SHG) properties. RSC Adv. 2017, 7, 24462–24469. [Google Scholar] [CrossRef]
- Zhang, H.; Liao, Q.; Wang, X.; Xu, Z.; Fu, H. Self-assembled organic hexagonal micro-prisms with high second harmonic generation efficiency for photonic devices. Nanoscale 2015, 7, 10186–10192. [Google Scholar] [CrossRef] [PubMed]
- Xing, X.-S.; Sa, R.-J.; Li, P.-X.; Zhang, N.-N.; Zhou, Z.-Y.; Liu, B.-W.; Liu, J.; Wang, M.-S.; Guo, G.-C. Second-order nonlinear optical switching with a record-high contrast for a photochromic and thermochromic bistable crystal. Chem. Sci. 2017, 8, 7751–7757. [Google Scholar] [CrossRef] [PubMed]
- Chai, Z.; Hu, X.; Wang, F.; Niu, X.; Xie, J.; Gong, Q. Ultrafast All-Optical Switching. Adv. Opt. Mater. 2017, 5, 1600665. [Google Scholar] [CrossRef]
- Song, Y.; Chen, Y.; Jiang, X.; Liang, W.; Wang, K.; Liang, Z.; Ge, Y.; Zhang, F.; Wu, L.; Zheng, J.; et al. Nonlinear Few-Layer Antimonene-Based All-Optical Signal Processing: Ultrafast Optical Switching and High-Speed Wavelength Conversion. Adv. Opt. Mater. 2018, 6, 1701287. [Google Scholar] [CrossRef]
- Kulyk, B.; Kerasidou, A.P.; Soumahoro, L.; Moussallem, C.; Gohier, F.; Frère, P.; Sahraoui, B. Optimization and diagnostic of nonlinear optical features of π-conjugated benzodifuran-based derivatives. RSC Adv. 2016, 6, 14439–14447. [Google Scholar] [CrossRef]
- Rosenne, S.; Grinvald, E.; Shirman, E.; Neeman, L.; Dutta, S.; Bar-Elli, O.; Ben-Zvi, R.; Oksenberg, E.; Milko, P.; Kalchenko, V.; et al. Self-assembled organic nanocrystals with strong nonlinear optical response. Nano Lett. 2015, 15, 7232–7237. [Google Scholar] [CrossRef]
- Hales, J.M.; Barlow, S.; Kim, H.; Mukhopadhyay, S.; Brédas, J.-L.; Perry, J.W.; Marder, S.R. Design of organic chromophores for all-optical signal processing applications. Chem. Mater. 2013, 26, 549–560. [Google Scholar] [CrossRef]
- Chen, S.; Li, Y.; Yang, W.; Chen, N.; Liu, H.; Li, Y. Synthesis and tuning optical nonlinear properties of molecular crystals of benzothiadiazole. J. Phys. Chem. C 2010, 114, 15109–15115. [Google Scholar] [CrossRef]
- Desiraju, G.R. Crystal engineering: From molecule to crystal. J. Am. Chem. Soc. 2013, 135, 9952–9967. [Google Scholar] [CrossRef]
- Ostroverkhova, O. Handbook of Organic Materials for Optical and (Opto) Electronic Devices: Properties and Applications; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Verbiest, T.; Houbrechts, S.; Kauranen, M.; Clays, K.; Persoons, A. Second-order nonlinear optical materials: Recent advances in chromophore design. J. Mater. Chem. 1997, 7, 2175–2189. [Google Scholar] [CrossRef]
- Beaujean, P.; Bondu, F.; Plaquet, A.; Garcia-Amorós, J.; Cusido, J.; Raymo, F.M.; Castet, F.; Rodriguez, V.; Champagne, B. Oxazines: A new class of second-order nonlinear optical switches. J. Am. Chem. Soc. 2016, 138, 5052–5062. [Google Scholar] [CrossRef] [PubMed]
- Miniewicz, A.; Bartkiewicz, S.; Wojaczynska, E.; Galica, T.; Zalesny, R.; Jakubas, R. Second harmonic generation in nonlinear optical crystals formed from propellane-type molecules. J. Mater. Chem. C 2019, 7, 1255–1262. [Google Scholar] [CrossRef]
- Luo, Y.; Yuan, C.; Xu, J.; Li, Y.; Liu, H.; Semin, S.; Rasing, T.; Yang, W.; Li, Y. Controlling the growth of molecular crystal aggregates with distinct linear and nonlinear optical properties. ACS Appl. Mater. Interfaces 2017, 9, 30862–30871. [Google Scholar] [CrossRef] [PubMed]
- Beverina, L.; Fu, J.; Leclercq, A.; Zojer, E.; Pacher, P.; Barlow, S.; Van Stryland, E.W.; Hagan, D.J.; Brédas, J.-L.; Marder, S.R.; et al. Two-photon absorption at telecommunications wavelengths in a dipolar chromophore with a pyrrole auxiliary donor and thiazole auxiliary acceptor. J. Am. Chem. Soc. 2005, 127, 7282–7283. [Google Scholar] [CrossRef]
- Liu, X.; Wang, D.; Gao, H.; Yang, Z.; Xing, Y.; Cao, H.; He, W.; Wang, H.; Gu, J.; Hu, H. Click chemistry functionalization improving the wideband optical-limiting performance of fullerene derivatives. Phys. Chem. Chem. Phys. 2016, 18, 7341–7348. [Google Scholar] [CrossRef]
- Bouit, P.A.; Kamada, K.; Feneyrou, P.; Berginc, G.; Toupet, L.; Maury, O.; Andraud, C. Two-photon absorption-related properties of functionalized BODIPY dyes in the infrared range up to telecommunication wavelengths. Adv. Mater. 2009, 21, 1151–1154. [Google Scholar] [CrossRef]
- Kiran, M.S.; Anand, B.; Sai, S.S.S.; Rao, G.N. Second-and third-order nonlinear optical properties of bis-chalcone derivatives. J. Photochem. Photobiol. A Chem. 2014, 290, 38–42. [Google Scholar] [CrossRef]
- Shetty, T.C.S.; Raghavendra, S.; Kumar, C.C.; Dharmaprakash, S. Crystal structure and nonlinear optical absorption of a new chalcone derivative: A promising candidate for optical switching. Appl. Phys. B 2016, 122, 205. [Google Scholar] [CrossRef]
- Reddy, N.S.K.; Badam, R.; Sattibabu, R.; Molli, M.; Muthukumar, V.S.; Sai, S.S.S.; Rao, G.N. Synthesis, characterization and nonlinear optical properties of symmetrically substituted dibenzylideneacetone derivatives. Chem. Phys. Lett. 2014, 616, 142–147. [Google Scholar] [CrossRef]
- Rajashekar, B.; Sowmendran, P.; Sai, S.S.S.; Rao, G.N. Synthesis, characterization and two-photon absorption based broadband optical limiting in diarylideneacetone derivative. J. Photochem. Photobiol. A Chem. 2012, 238, 20–23. [Google Scholar] [CrossRef]
- Badaeva, E.A.; Timofeeva, T.V.; Masunov, A.; Tretiak, S. Role of donor- acceptor strengths and separation on the two-photon absorption response of cytotoxic dyes: A TD-DFT Study. J. Phys. Chem. A 2005, 109, 7276–7284. [Google Scholar] [CrossRef] [PubMed]
- Karuppasamy, P.; Sivasubramani, V.; Pandian, M.S.; Ramasamy, P. Growth and characterization of semi-organic third order nonlinear optical (NLO) potassium 3,5-dinitrobenzoate (KDNB) single crystals. RSC Adv. 2016, 6, 109105–109123. [Google Scholar] [CrossRef]
- Thanigaimani, K.; Arshad, S.; Khalib, N.C.; Razak, I.A.; Arunagiri, C.; Subashini, A.; Sulaiman, S.F.; Hashim, N.S.; Ooi, K.L. A new chalcone structure of (e)-1-(4-bromophenyl)-3-(napthalen-2-yl) prop-2-en-1-one: Synthesis, structural characterizations, quantum chemical investigations and biological evaluations. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2015, 149, 90–102. [Google Scholar] [CrossRef]
- Prasad, A.A.; Muthu, K.; Meenatchi, V.; Rajasekar, M.; Agilandeshwari, R.; Meena, K.; Manonmoni, J.V.; Meenakshisundaram, S. Optical, vibrational, NBO, first-order molecular hyperpolarizability and Hirshfeld surface analysis of a nonlinear optical chalcone. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2015, 140, 311–327. [Google Scholar] [CrossRef]
- Franzen, P.L.; Misoguti, L.; Zilio, S.C. Hyper-Rayleigh scattering with picosecond pulse trains. Appl. Opt. 2008, 47, 1443–1446. [Google Scholar] [CrossRef]
- Abegão, L.M.; Fonseca, R.D.; Santos, F.A.; Souza, G.B.; Barreiros, A.L.B.; Barreiros, M.L.; Alencar, M.; Mendonça, C.R.; Silva, D.L.; De Boni, L.; et al. Second-and third-order nonlinear optical properties of unsubstituted and mono-substituted chalcones. Chem. Phys. Lett. 2016, 648, 91–96. [Google Scholar] [CrossRef]
- Abegão, L.M.; Fonseca, R.D.; Santos, F.A.; Rodrigues, J.J.; Kamada, K.; Mendonça, C.R.; Piguel, S.; De Boni, L. First molecular electronic hyperpolarizability of series of π-conjugated oxazole dyes in solution: An experimental and theoretical study. RSC Adv. 2019, 9, 26476–26482. [Google Scholar] [CrossRef]
- Clays, K.; Persoons, A. Hyper-Rayleigh scattering in solution. Phys. Rev. Lett. 1991, 66, 2980. [Google Scholar] [CrossRef]
- Hendrickx, E.; Clays, K.; Persoons, A. Hyper-Rayleigh scattering in isotropic solution. Acc. Chem. Res. 1998, 31, 675–683. [Google Scholar] [CrossRef]
- Verbiest, T.; Clays, K.; Rodriguez, V. Second-Order Nonlinear Optical Characterization Techniques: An Introduction; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Brasselet, S.; Zyss, J. Multipolar molecules and multipolar fields: Probing and controlling the tensorial nature of nonlinear molecular media. JOSA B 1998, 15, 257–288. [Google Scholar] [CrossRef]
- Sheik-Bahae, M.; Said, A.A.; Wei, T.-H.; Hagan, D.J.; Van Stryland, E.W. Sensitive measurement of optical nonlinearities using a single beam. IEEE J. Quantum Electron. 1990, 26, 760–769. [Google Scholar] [CrossRef]
- Gross, E.; Kohn, W. Time-dependent density-functional theory. In Advances in Quantum Chemistry; Elsevier: Amsterdam, The Netherlands, 1990; Volume 21, pp. 255–291. [Google Scholar]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Rev. B.01; Gaussian Inc: Wallingford, CT, USA, 2016. [Google Scholar]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785. [Google Scholar] [CrossRef] [PubMed]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
- Tomasi, J.; Mennucci, B.; Cances, E. The IEF version of the PCM solvation method: An overview of a new method addressed to study molecular solutes at the QM ab initio level. J. Mol. Struct. THEOCHEM 1999, 464, 211–226. [Google Scholar] [CrossRef]
- Pielak, K.; Bondu, F.; Sanguinet, L.; Rodriguez, V.; Champagne, B.; Castet, F. Second-order nonlinear optical properties of multiaddressable indolinooxazolidine derivatives: Joint computational and hyper-Rayleigh scattering investigations. J. Phys. Chem. C 2017, 121, 1851–1860. [Google Scholar] [CrossRef]
- Hirata, S.; Head-Gordon, M. Time-dependent density functional theory within the Tamm–Dancoff approximation. Chem. Phys. Lett. 1999, 314, 291–299. [Google Scholar] [CrossRef]
- Ohta, K.; Yamada, S.; Kamada, K.; Slepkov, A.D.; Hegmann, F.A.; Tykwinski, R.R.; Shirtcliff, L.D.; Haley, M.M.; Sałek, P.; Gel’mukhanov, F.; et al. Two-photon absorption properties of two-dimensional π-conjugated chromophores: Combined experimental and theoretical study. J. Phys. Chem. A 2010, 115, 105–117. [Google Scholar] [CrossRef]
- Woodford, J.; Pauley, M.; Wang, C. Solvent dependence of the first molecular hyperpolarizability of p-nitroaniline revisited. J. Phys. Chem. A 1997, 101, 1989–1992. [Google Scholar] [CrossRef]
- Muhammad, S.; Al-Sehemi, A.G.; Irfan, A.; Chaudhry, A.R.; Gharni, H.; AlFaify, S.; Shkir, M.; Asiri, A.M. The impact of position and number of methoxy group (s) to tune the nonlinear optical properties of chalcone derivatives: A dual substitution strategy. J. Mol. Model. 2016, 22, 73. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Thomas, K.J.; Thayumanavan, S.; Bardeen, C.J. Dependence of the Two-Photon Absorption Cross Section on the Conjugation of the Phenylacetylene Linker in Dipolar Donor-Bridge-Acceptor Chromophores. J. Phys. Chem. A 2005, 109, 9767–9774. [Google Scholar] [CrossRef] [PubMed]
- Kiran, A.J.; Rai, N.S.; Chandrasekharan, K.; Kalluraya, B.; Rotermund, F. Substituent dependence of third-order optical nonlinearity in chalcone derivatives. Jpn. J. Appl. Phys. 2008, 47, 6312. [Google Scholar] [CrossRef]
- Santos, F.A.; Abegão, L.M.; Fonseca, R.D.; Alcântara, A.M.; Mendonça, C.R.; Valle, M.S.; Alencar, M.; Kamada, K.; De Boni, L.; Rodrigues, J., Jr. Bromo-and chloro-derivatives of dibenzylideneacetone: Experimental and theoretical study of the first molecular hyperpolarizability and two-photon absorption. J. Photochem. Photobiol. A Chem. 2019, 369, 70–76. [Google Scholar] [CrossRef]
- Vivas, M.G.; Silva, D.L.; De Boni, L.; Bretonniere, Y.; Andraud, C.; Laibe-Darbour, F.; Mulatier, J.-C.; Zaleśny, R.; Bartkowiak, W.; Canuto, S.; et al. Experimental and theoretical study on the one-and two-photon absorption properties of novel organic molecules based on phenylacetylene and azoaromatic moieties. J. Phys. Chem. B 2012, 116, 14677–14688. [Google Scholar] [CrossRef]
- Day, P.N.; Nguyen, K.A.; Pachter, R. TDDFT Study of One-and Two-Photon Absorption Properties: Donor- π- Acceptor Chromophores. J. Phys. Chem. B 2005, 109, 1803–1814. [Google Scholar] [CrossRef]
- Friese, D.H.; Mikhaylov, A.; Krzeszewski, M.; Poronik, Y.M.; Rebane, A.; Ruud, K.; Gryko, D.T. Pyrrolo [3, 2-b] pyrroles—From Unprecedented Solvatofluorochromism to Two-Photon Absorption. Chem. A Eur. J. 2015, 21, 18364–18374. [Google Scholar] [CrossRef]
- Masunov, A.; Tretiak, S. Prediction of two-photon absorption properties for organic chromophores using time-dependent density-functional theory. J. Phys. Chem. B 2004, 108, 899–907. [Google Scholar] [CrossRef]
- Rudberg, E.; Sałek, P.; Helgaker, T.; Ågren, H. Calculations of two-photon charge-transfer excitations using Coulomb-attenuated density-functional theory. J. Chem. Phys. 2005, 123, 184108. [Google Scholar] [CrossRef]
- Castet, F.; Rodriguez, V.; Pozzo, J.-L.; Ducasse, L.; Plaquet, A.; Champagne, B. Design and characterization of molecular nonlinear optical switches. Acc. Chem. Res. 2013, 46, 2656–2665. [Google Scholar] [CrossRef] [PubMed]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santos, F.A.; Abegão, L.M.G.; Fonseca, R.D.; Alcântara, A.M.; Mendonça, C.R.; Alencar, M.A.R.C.; Valle, M.S.; Kamada, K.; De Boni, L.; Rodrigues, J.J., Jr. Nonlinear Optical Study in a Set of Dibenzylideneacetone Derivatives with Potential for Optical Frequency Conversion. Photonics 2020, 7, 8. https://doi.org/10.3390/photonics7010008
Santos FA, Abegão LMG, Fonseca RD, Alcântara AM, Mendonça CR, Alencar MARC, Valle MS, Kamada K, De Boni L, Rodrigues JJ Jr. Nonlinear Optical Study in a Set of Dibenzylideneacetone Derivatives with Potential for Optical Frequency Conversion. Photonics. 2020; 7(1):8. https://doi.org/10.3390/photonics7010008
Chicago/Turabian StyleSantos, Francisco A., Luis M. G. Abegão, Ruben D. Fonseca, Aline M. Alcântara, Cleber R. Mendonça, Márcio A. R. C. Alencar, Marcelo S. Valle, Kenji Kamada, Leonardo De Boni, and José J. Rodrigues, Jr. 2020. "Nonlinear Optical Study in a Set of Dibenzylideneacetone Derivatives with Potential for Optical Frequency Conversion" Photonics 7, no. 1: 8. https://doi.org/10.3390/photonics7010008
APA StyleSantos, F. A., Abegão, L. M. G., Fonseca, R. D., Alcântara, A. M., Mendonça, C. R., Alencar, M. A. R. C., Valle, M. S., Kamada, K., De Boni, L., & Rodrigues, J. J., Jr. (2020). Nonlinear Optical Study in a Set of Dibenzylideneacetone Derivatives with Potential for Optical Frequency Conversion. Photonics, 7(1), 8. https://doi.org/10.3390/photonics7010008





