Tunable Mode Converter Device Based on Photonic Crystal Fiber with a Thermo-Responsive Liquid Crystal Core
Abstract
1. Introduction
2. Materials and Methods
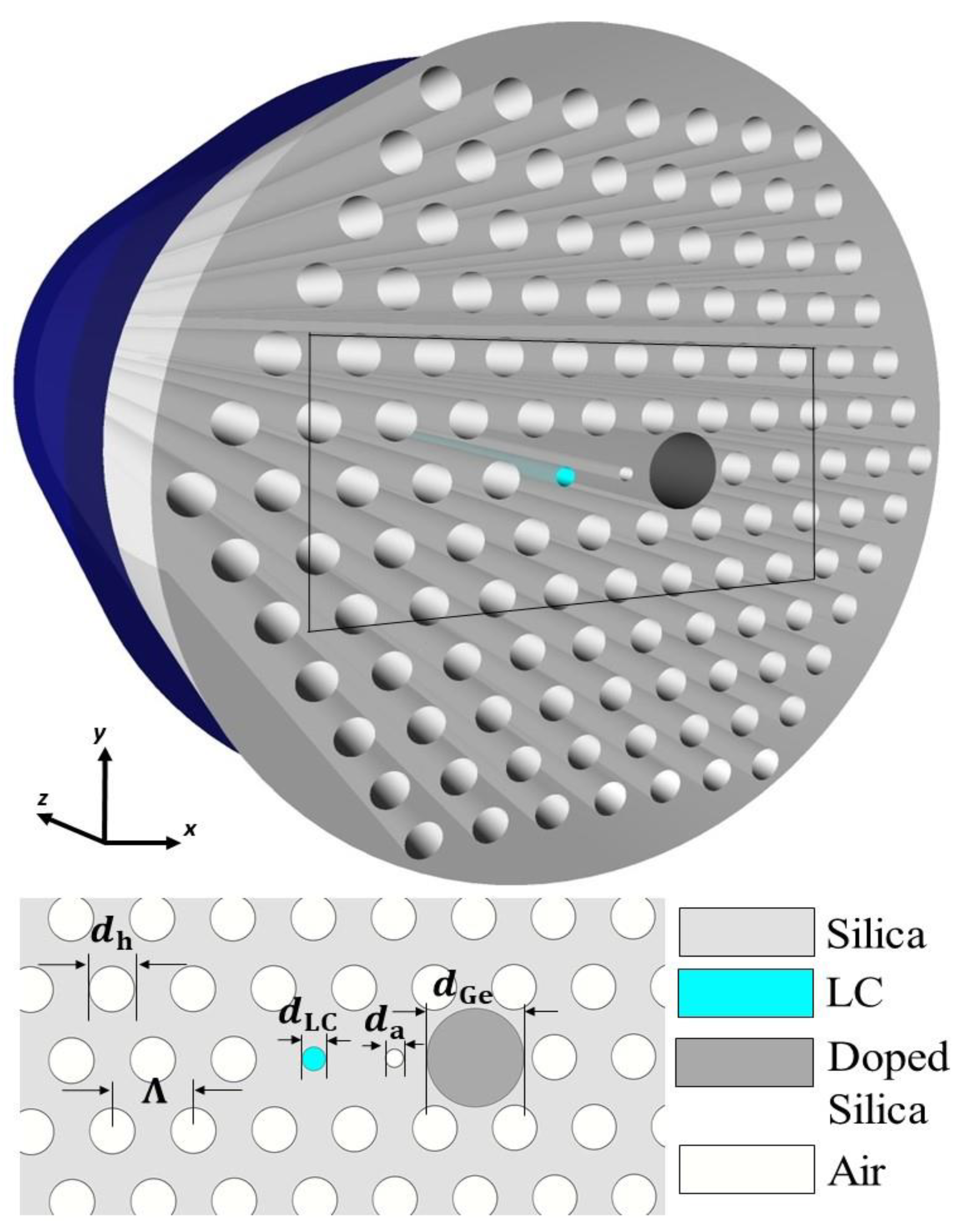
2.1. Structure Design
2.2. Working Principle
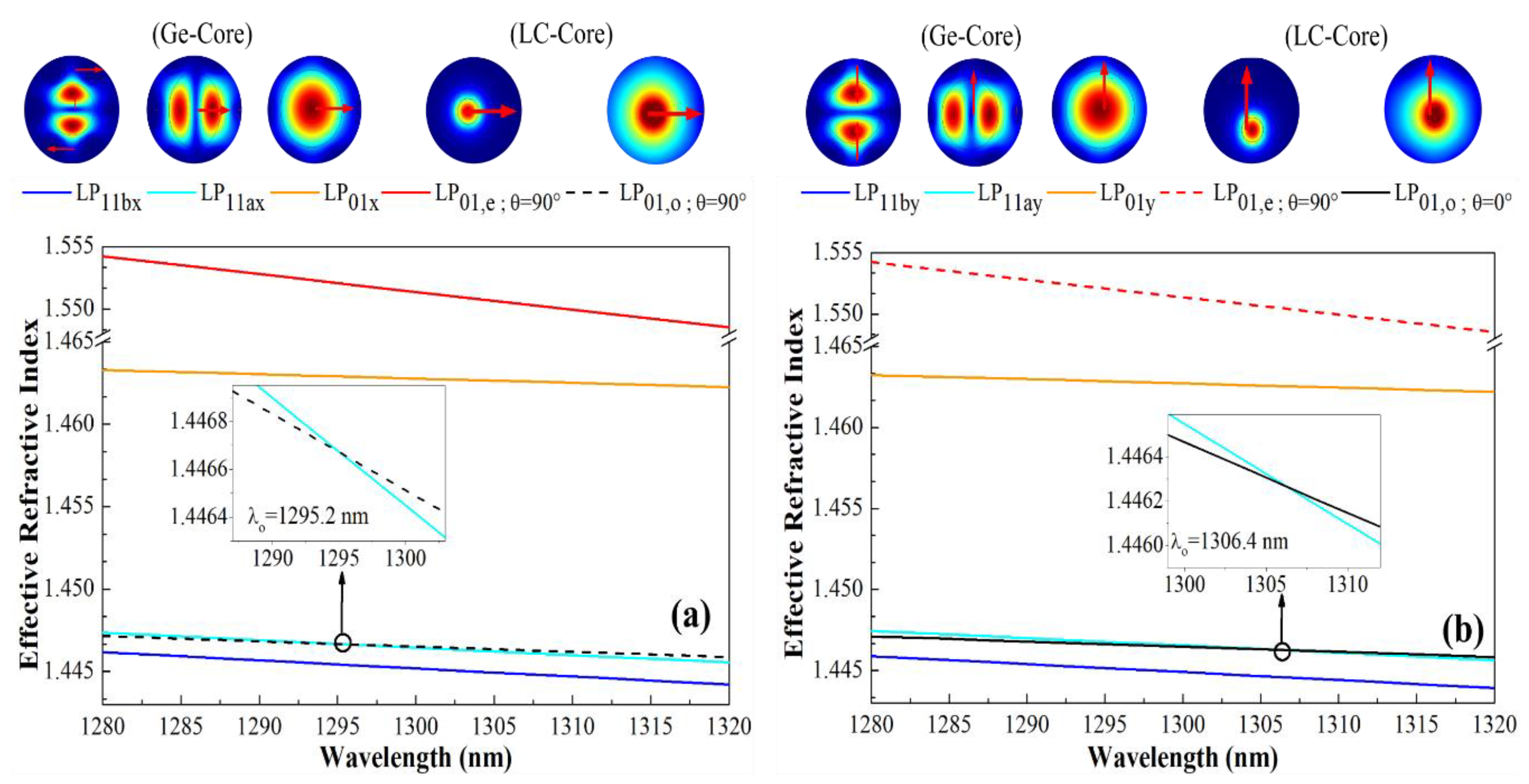
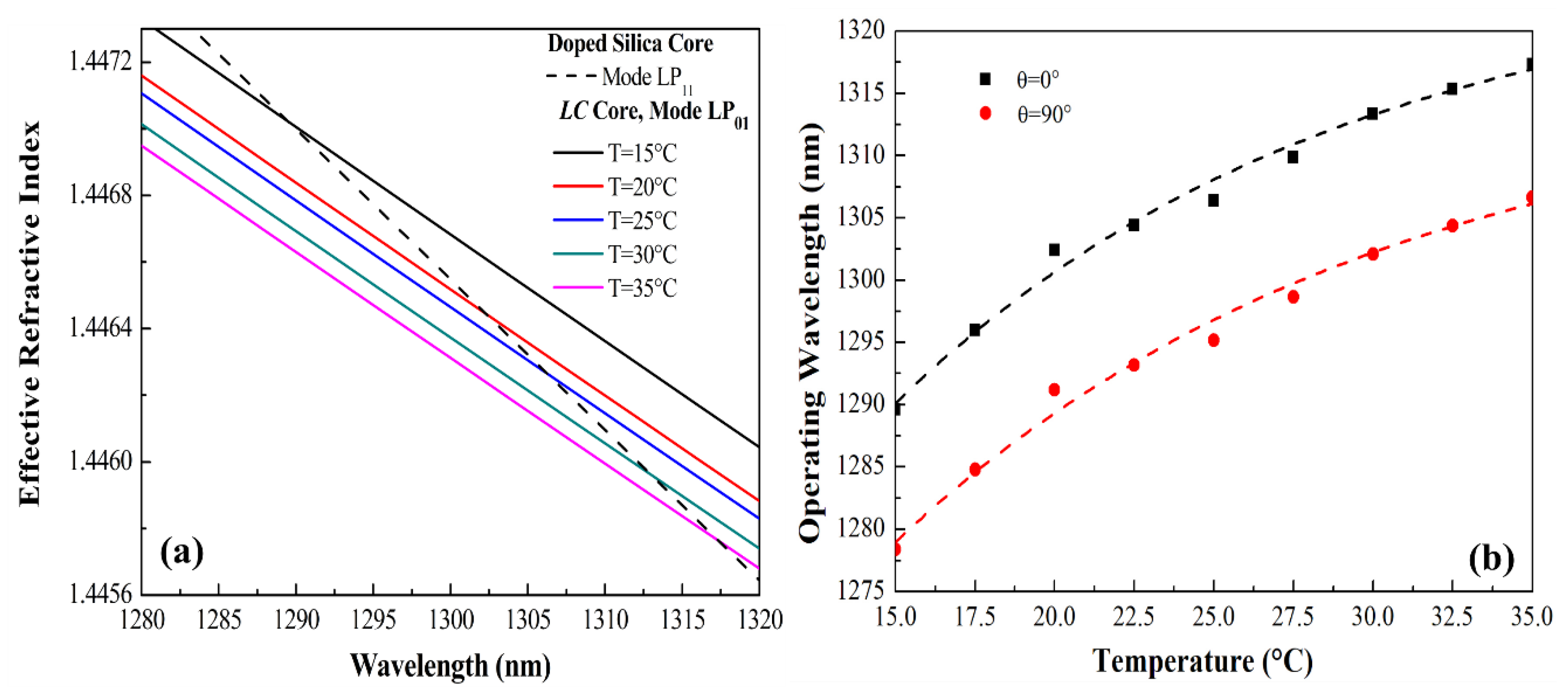
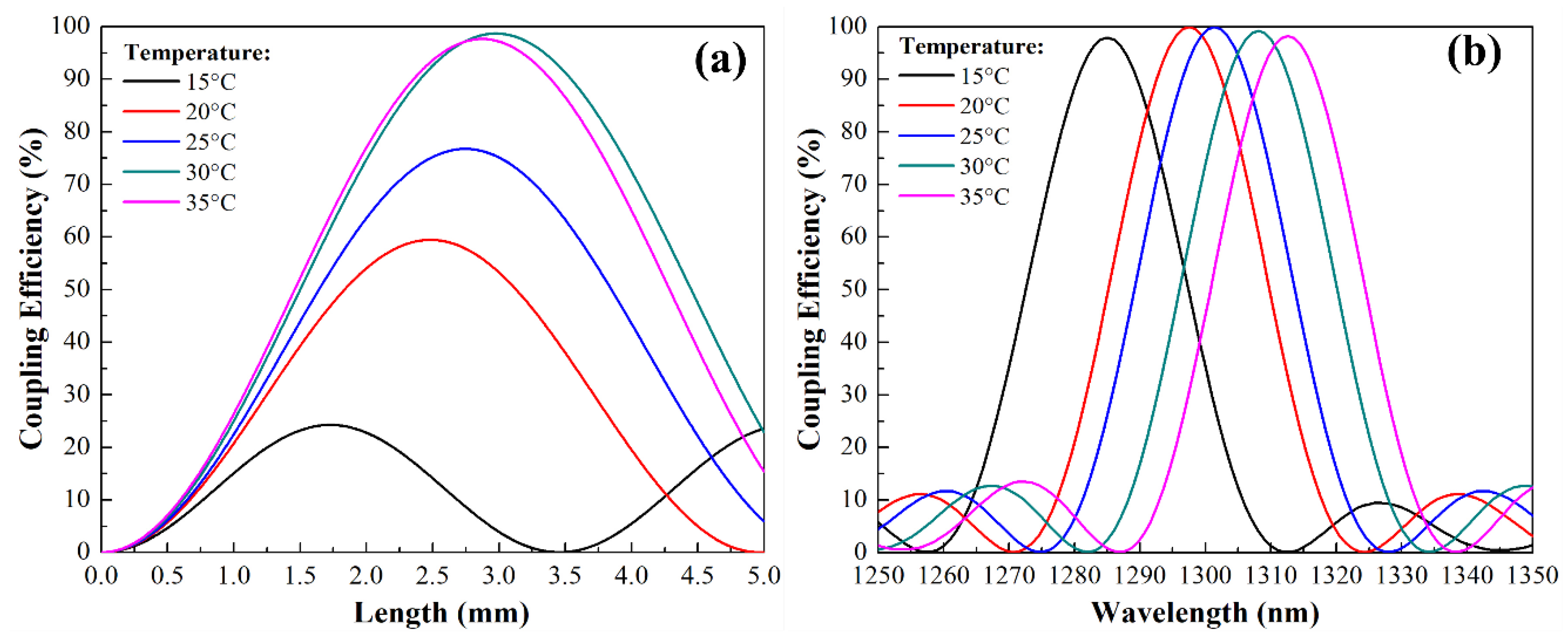
3. Results and Discussion
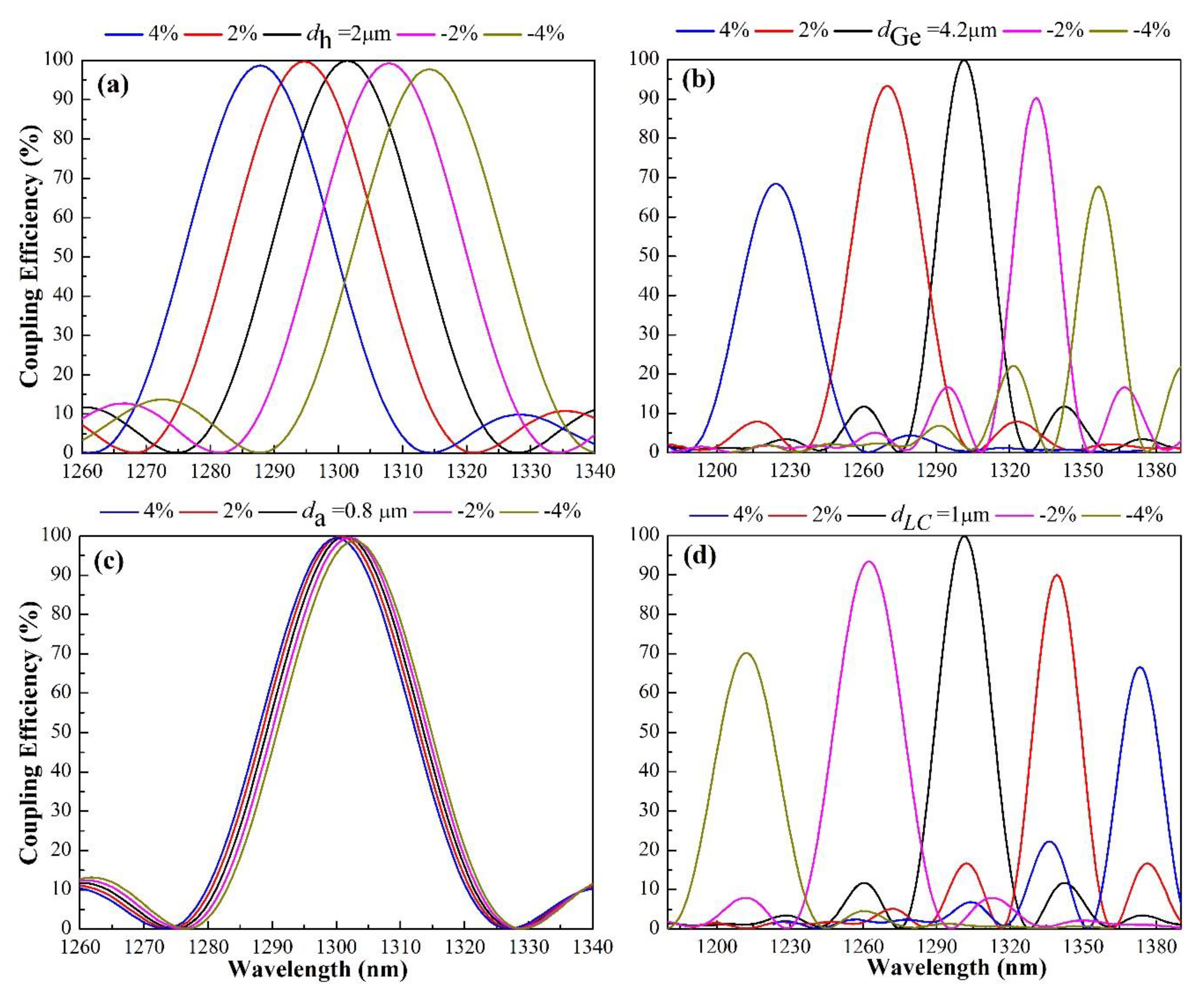
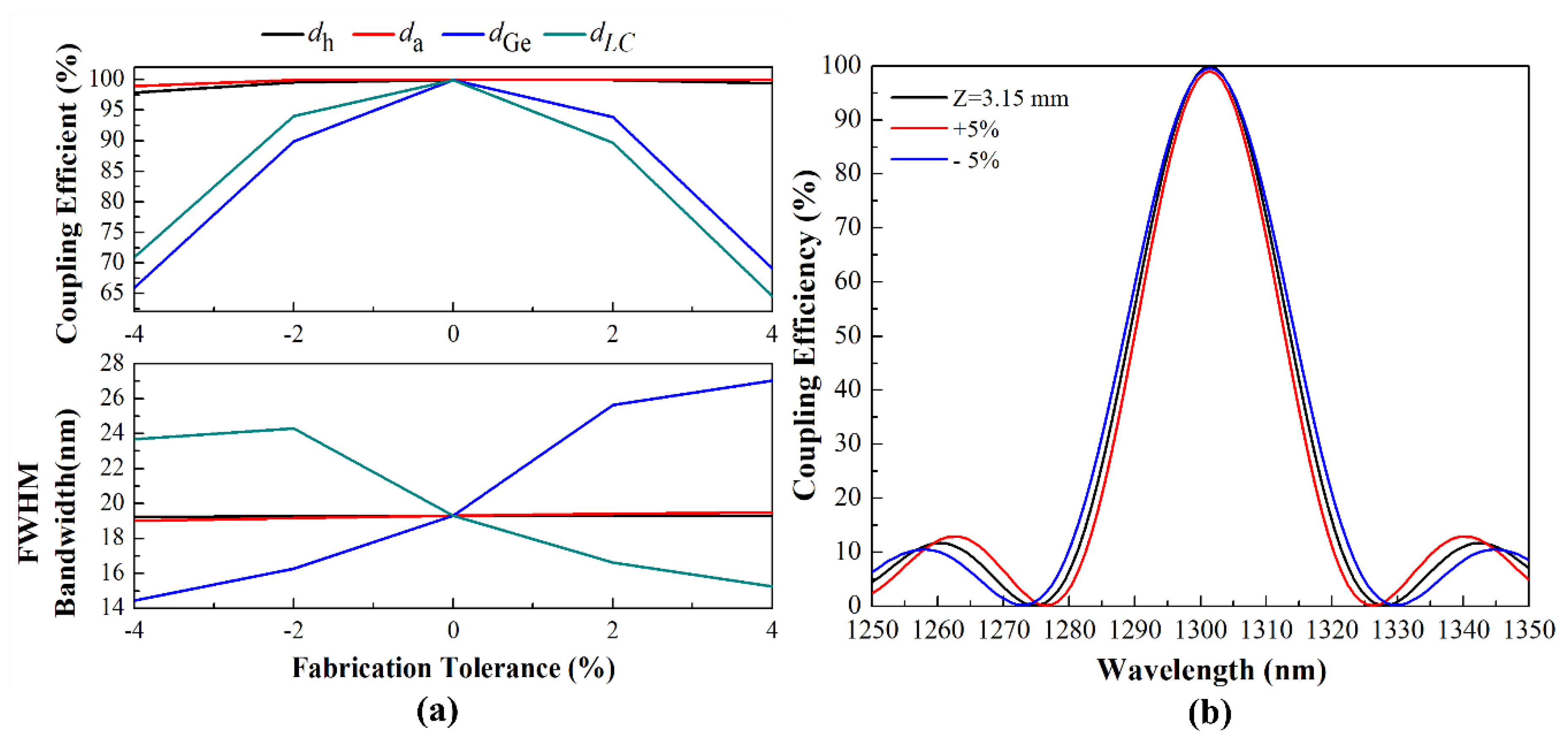
4. Fabrication Tolerance Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Botero-Valencia, J.; Castaño-Londoño, L.; Marquez-Viloria, D. Trends in the Internet of Things. TecnoLógicas 2019, 22, 1–2. [Google Scholar] [CrossRef][Green Version]
- Agrell, E.; Karlsson, M.; Chraplyvy, A.R.; Richardson, D.J.; Krummrich, P.M.; Winzer, P.; Roberts, K.; Fischer, J.K.; Savory, S.J.; Eggleton, B.J.; et al. Roadmap of optical communications. J. Opt. 2016, 18, 1–40. [Google Scholar] [CrossRef]
- Richardson, D.J.; Fini, J.M.; Nelson, L.E. Space-division multiplexing in optical fibres. Nat. Photonics 2013, 7, 354–362. [Google Scholar] [CrossRef]
- Spiess, J.; Joens, Y.T.; Dragnea, R.; Spencer, P. Using Big Data to Improve Customer Experience and Business Performance. Bell Labs Tech. J. 2014, 18, 3–17. [Google Scholar] [CrossRef]
- Sillard, P. New fibers for ultra-high capacity transport. Opt. Fiber Technol. 2011, 17, 495–502. [Google Scholar] [CrossRef]
- Wei, Y.; Ebendorff-Heidepriem, H.; Zhao, J. Recent Advances in Hybrid Optical Materials: Integrating Nanoparticles within a Glass Matrix. Adv. Opt. Mater. 2019, 7, 1900702. [Google Scholar] [CrossRef]
- Desurvire, E.; Simpson, J.R.; Becker, P.C. High-gain erbium-doped traveling-wave fiber amplifier. Opt. Lett. 1987, 12, 888. [Google Scholar] [CrossRef]
- Miura, J. Recent advances of optical amplification technology. Opt. Metro Netw. Short Haul Syst. IX 2017, 10129, 1012903. [Google Scholar] [CrossRef]
- Fang, X.; Claus, R.O. Polarization-independent all-fiber wavelength-division multiplexer based on a Sagnac interferometer. Opt. Lett. 1995, 20, 2146. [Google Scholar] [CrossRef]
- Delgado Mendinueta, J.; Shinada, S.; Furukawa, H.; Wada, N. Ultra-High-Capacity Optical Packet Switching Networks with Coherent Polarization Division Multiplexing QPSK/16QAM Modulation Formats. Photonics 2017, 4, 27. [Google Scholar] [CrossRef]
- Liu, X.; Chandrasekhar, S.; Winzer, P.J. Digital Signal Processing Techniques Enabling Multi-Tb\/s Superchannel Transmission: An overview of recent advances in DSP-enabled superchannels. IEEE Signal Process. Mag. 2014, 31, 16–24. [Google Scholar] [CrossRef]
- Melián, B.; Laguna, M.; Moreno-Pérez, J.A. Capacity expansion of fiber optic networks with WDM systems: Problem formulation and comparative analysis. Comput. Oper. Res. 2004, 31, 461–472. [Google Scholar] [CrossRef]
- Yerolatsitis, S.; Gris-Sánchez, I.; Birks, T.A. Adiabatically-tapered fiber mode multiplexers. Opt. Express 2014, 22, 608–617. [Google Scholar] [CrossRef]
- Yunhe, Z.; Liu, Y.; Jianxiang, W.; Tingyun, W. Mode converter based on the long period fiber gratings written in two mode fiber. Opt. Express 2016, 24, 6186–6195. [Google Scholar]
- Gao, Y.; Sun, J.; Chen, G.; Sima, C. Demonstration of simultaneous mode conversion and demultiplexing for mode and wavelength division multiplexing systems based on tilted few-mode fiber Bragg gratings. Opt. Express 2015, 23, 9959. [Google Scholar] [CrossRef]
- Ali, M.M.; Jung, Y.; Lim, K.-S.; Islam, M.R.; Alam, S.-U.; Richardson, D.J.; Ahmad, H. Characterization of Mode Coupling in Few-Mode FBG with Selective Mode Excitation. IEEE Photonics Technol. Lett. 2015, 27, 1713–1716. [Google Scholar] [CrossRef]
- Chen, M.-Y.; Zhou, J. Mode converter based on mode coupling in an asymmetric dual-core photonic crystal fibre. J. Opt. A Pure Appl. Opt. 2008, 10, 115304. [Google Scholar] [CrossRef]
- Lin, G.; Dong, X. Design of broadband LP01↔LP02 mode converter based on special dual-core fiber for dispersion compensation. Appl. Opt. 2012, 51, 4388–4393. [Google Scholar] [CrossRef]
- Reyes-Vera, E.; Úsuga, J.; Acevedo-Echeverry, J.; Gómez-Cardona, N.; Varón, M. Performance analysis of a modal converter based on an asymmetric dual-core photonic crystal fiber. Opt. Pura Apl. 2017, 50, 251–257. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y.; Cai, S.; Lan, M.; Yu, S.; Gu, W. Mode converter based on dual-core all-solid photonic bandgap fiber. Photonics Res. 2015, 3, 220–223. [Google Scholar] [CrossRef]
- Cai, S.; Yu, S.; Wang, Y.; Lan, M.; Gao, L.; Gu, W. Hybrid Dual-Core Photonic Crystal Fiber for Spatial Mode Conversion. IEEE Photonics Technol. Lett. 2016, 28, 339–342. [Google Scholar] [CrossRef]
- Reyes Vera, E.E.; Usuga Restrepo, J.E.; Gómez Cardona, N.E.; Varón, M. Mode selective coupler based in a dual-core photonic crystal fiber with non-identical cores for spatial mode conversion. In Latin America Optics and Photonics Conference; Optical Society of America: Washington, DC, USA, 2016; p. LTu3C.1. [Google Scholar]
- Yu, Y.; Sun, B. Ultra-Wide-Bandwidth Tunable Magnetic Fluid-Filled Hybrid Connected Dual-Core Photonic Crystal Fiber Mode Converter. Crystals 2018, 8, 95. [Google Scholar] [CrossRef]
- Markos, C.; Travers, J.C.; Abdolvand, A.; Eggleton, B.J.; Bang, O. Hybrid photonic-crystal fiber. Rev. Mod. Phys. 2017, 89. [Google Scholar] [CrossRef]
- Alexander Schmidt, M.; Argyros, A.; Sorin, F. Hybrid Optical Fibers—An Innovative Platform for In-Fiber Photonic Devices. Adv. Opt. Mater. 2016, 4, 13–36. [Google Scholar] [CrossRef]
- Reyes-Vera, E.; Cordeiro, C.M.B.; Torres, P. Highly sensitive temperature sensor using a Sagnac loop interferometer based on a side-hole photonic crystal fiber filled with metal. Appl. Opt. 2017, 56, 156–162. [Google Scholar] [CrossRef]
- Markos, C.; Yuan, W.; Vlachos, K.; Town, G.E.; Bang, O. Label-free biosensing with high sensitivity in dual-core microstructured polymer optical fibers. Opt. Express 2011, 19, 7790. [Google Scholar] [CrossRef]
- Muñoz-Hernández, T.; Reyes-Vera, E.; Torres, P. Tunable Whispering Gallery Mode Photonic Device Based on Microstructured Optical Fiber with Internal Electrodes. Sci. Rep. 2019, 9, 12083. [Google Scholar] [CrossRef]
- Du, F.; Lu, Y.-Q.; Wu, S.-T. Electrically tunable liquid-crystal photonic crystal fiber. Appl. Phys. Lett. 2004, 85, 2181–2183. [Google Scholar] [CrossRef]
- Woliński, T.R.; Czapla, A.; Ertman, S.; Tefelska, M.; Domański, A.W.; Nowinowski-Kruszelnicki, E.; Dąbrowski, R. Tunable highly birefringent solid-core photonic liquid crystal fibers. Opt. Quantum Electron. 2007, 39, 1021–1032. [Google Scholar] [CrossRef]
- Kuhlmey, B.T.; Eggleton, B.J.; Wu, D.K.C. Fluid-filled solid-core photonic bandgap fibers. J. Light. Technol. 2009, 27, 1617–1630. [Google Scholar] [CrossRef]
- Li, J.; Gauzia, S.; Wu, S.-T. High temperature-gradient refractive index liquid crystals. Opt. Express 2004, 12, 2002. [Google Scholar] [CrossRef] [PubMed]
- Saitoh, K.; Florous, N.J.; Varshney, S.K.; Koshiba, M. Tunable Photonic Crystal Fiber Couplers With a Thermo-Responsive Liquid Crystal Resonator. J. Light. Technol. 2008, 26, 663–669. [Google Scholar] [CrossRef]
- Younis, B.M.; Heikal, A.M.; Hameed, M.F.O.; Obayya, S.S.A. Highly wavelength-selective asymmetric dual-core liquid photonic crystal fiber polarization splitter. J. Opt. Soc. Am. B 2018, 35, 1020. [Google Scholar] [CrossRef]
- Chen, H.L.; Li, S.G.; Fan, Z.K.; An, G.W.; Li, J.S.; Han, Y. A Novel Polarization Splitter Based on Dual-Core Photonic Crystal Fiber with a Liquid Crystal Modulation Core. IEEE Photonics J. 2014, 6, 1–9. [Google Scholar] [CrossRef]
- Khan, K.R.; Bidnyk, S.; Hall, T.J. Tunable all optical switch implemented in a liquid crystal filled dual-core photonic crystal fiber. Prog. Electromagn. Res. M 2012, 22, 179–189. [Google Scholar] [CrossRef]
- Xu, Z.; Li, B.; Hu, D.J.J.; Wu, Z.; Ertman, S.; Wolinski, T.; Tong, W.; Shum, P.P. Hybrid photonic crystal fiber for highly sensitive temperature measurement. J. Opt. 2018, 20, 075801. [Google Scholar] [CrossRef]
- Li, J.; Wu, S.-T.; Brugioni, S.; Meucci, R.; Faetti, S. Infrared refractive indices of liquid crystals. J. Appl. Phys. 2005, 97, 073501. [Google Scholar] [CrossRef]
- Knight, J.C.; Birks, T.A.; Cregan, R.F.; Russell, P.S.J.; de Sandro, J.-P. Photonic crystals as optical fibres—Physics and applications. Opt. Mater. 1999, 11, 143–151. [Google Scholar] [CrossRef]
- Birks, T.A.; Knight, J.C.; Russell, P.S.; Atkin, D.M. All-silica single-mode optical fiber with photonic crystal cladding. Opt. Lett. 1996, 21, 1547–1549. [Google Scholar] [CrossRef]
- Ebendorff-Heidepriem, H.; Monro, T.M. Extrusion of complex preforms for microstructured optical fibers. Opt. Express 2007, 15, 15086. [Google Scholar] [CrossRef]
- Knight, J.C.; Arriaga, J.; Birks, T.A.; Ortigosa-Blanch, A.; Wadsworth, W.J.; Russell, P.S.J. Anomalous dispersion in photonic crystal fiber. IEEE Photonics Technol. Lett. 2000, 12, 807–809. [Google Scholar] [CrossRef]
- Zhou, G.; Hou, Z.; Li, S.; Hou, L. Fabrication of glass photonic crystal fibers with a die-cast process. Appl. Opt. 2006, 45, 4433–4436. [Google Scholar] [CrossRef]
- Wiederhecker, G.S.; Cordeiro, C.M.B.; Couny, F.; Benabid, F.; Maier, S.A.; Knight, J.C.; Cruz, C.H.B.; Fragnito, H.L. Field enhancement within an optical fibre with a subwavelength air core. Nat. Photonics 2007, 1, 115–118. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, Y.; Zhang, L.; Shao, Y.; Zhang, F.; Liao, C.; Wang, Y. Tunable Electro-Optical Modulator Based on a Photonic Crystal Fiber Selectively Filled with Liquid Crystal. J. Light. Technol. 2019, 37, 1903–1908. [Google Scholar] [CrossRef]
- Wahle, M.; Kitzerow, H.-S. Liquid crystal assisted optical fibres. Opt. Express 2014, 22, 262. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Wang, R.; Cox, F.M.; Kuhlmey, B.T.; Large, M.C.J. Selective coating of holes in microstructured optical fiber and its application to in-fiber absorptive polarizers. Opt. Express 2007, 15, 16270–16278. [Google Scholar] [CrossRef]
- Huang, Y.; Xu, Y.; Yariv, A. Fabrication of functional microstructured optical fibers through a selective-filling technique. Appl. Phys. Lett. 2004, 85, 5182–5184. [Google Scholar] [CrossRef]
- Vieweg, M.; Gissibl, T.; Pricking, S.; Kuhlmey, B.T.; Wu, D.C.; Eggleton, B.J.; Giessen, H. Ultrafast nonlinear optofluidics in selectively liquid-filled photonic crystal fibers. Opt. Express 2010, 18, 25232. [Google Scholar] [CrossRef]
- Lee, D.L. Electromagnetic Principles of Integrated Optics, 1st ed.; Wiley: Hoboken, NJ, USA, 1986; ISBN 978-0471879787. [Google Scholar]
- Snyder, A.W.; Love, J.D. Optical Waveguide Theory; Springer: Boston, MA, USA, 1984; ISBN 978-0-412-24250-2. [Google Scholar]
- Reyes-Vera, E.; Usuga-Restrepo, J.; Jimenez-Durango, C.; Montoya-Cardona, J.; Gomez-Cardona, N. Design of Low-loss and Highly Birefringent Porous-Core Photonic Crystal Fiber and Its Application to Terahertz Polarization Beam Splitter. IEEE Photonics J. 2018, 10, 1–13. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, K.; Jin, W.; Chiang, K.S. Widely Wavelength-Tunable Mode Converter Based on Polymer Waveguide Grating. IEEE Photonics Technol. Lett. 2015, 27, 1985–1988. [Google Scholar] [CrossRef]
- Taher, A.B.; Di Bin, P.; Bahloul, F.; Tartaret-Josnière, E.; Jossent, M.; Février, S.; Attia, R. Adiabatically tapered microstructured mode converter for selective excitation of the fundamental mode in a few mode fiber. Opt. Express 2016, 24, 1376. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Liu, Y.; Liu, Z.; Zhao, Y.; Wang, T.; Shen, L.; Chen, S. Mode converter based on the long-period fiber gratings written in the six-mode fiber. In Proceedings of the 2017 16th International Conference on Optical Communications and Networks (ICOCN), Wuzhen, China, 7–10 August 2017; pp. 1–3. [Google Scholar] [CrossRef]
- Han, S.; Wang, Z.; Liu, Y.; Li, H.; Liang, H.; Wang, Z. Mode Couplers and Converters Based on Dual-Core Hollow-Core Photonic Bandgap Fiber. IEEE Photonics J. 2018, 10, 1–8. [Google Scholar] [CrossRef]
| Description | Tunable | Range | Bandwidth | Length | Ref. |
|---|---|---|---|---|---|
| Mode converted based on mode coupling in an asymmetric dual-core PCF | No | 1550 nm | 14 nm | 12.7 mm | [17] |
| Mode converter based on dual-core all-solid PCF | No | 1550 nm | 47.8 nm (max.) | 6.437 mm | [20] |
| Mode Converter Based on Polymer Waveguide Grating | Yes | 1560 nm to 1592 nm | 4 nm | 5.07 mm | [53] |
| Hybrid dual-core PCF | No | 1550 nm | 43 nm (max.) | 3.21 mm | [21] |
| Adiabatically tapered MOF mode converter | No | 1550 nm | NP 1 | 21 mm | [54] |
| Mode converter based on the LPFG written in the two-mode fiber | Yes | 1500 nm to 1540 nm (max.) | 18 nm (max.) | 24 mm | [55] |
| Dual core Hollow-Core PBGF | No | 1965 nm | 200 nm | 7.6 mm | [56] |
| Magnetic Fluid-Filled Hybrid Connect Dual-Core PCF mode converter | Yes | 1.33 μm–1.85 μm 1.38 μm–1.75 μm | 0.52 μm 0.37 μm | 0.835 mm | [23] |
| Tunable mode converter device based on PCF with a thermo-responsive LC-core | Yes | 1278 nm to 1317 nm | 19.938 nm | 3.15 mm | This work |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montoya Cardona, J.A.; Gomez Cardona, N.D.; Gonzalez Valencia, E.; Torres Trujillo, P.; Reyes Vera, E. Tunable Mode Converter Device Based on Photonic Crystal Fiber with a Thermo-Responsive Liquid Crystal Core. Photonics 2020, 7, 3. https://doi.org/10.3390/photonics7010003
Montoya Cardona JA, Gomez Cardona ND, Gonzalez Valencia E, Torres Trujillo P, Reyes Vera E. Tunable Mode Converter Device Based on Photonic Crystal Fiber with a Thermo-Responsive Liquid Crystal Core. Photonics. 2020; 7(1):3. https://doi.org/10.3390/photonics7010003
Chicago/Turabian StyleMontoya Cardona, Jorge Andres, Nelson Dario Gomez Cardona, Esteban Gonzalez Valencia, Pedro Torres Trujillo, and Erick Reyes Vera. 2020. "Tunable Mode Converter Device Based on Photonic Crystal Fiber with a Thermo-Responsive Liquid Crystal Core" Photonics 7, no. 1: 3. https://doi.org/10.3390/photonics7010003
APA StyleMontoya Cardona, J. A., Gomez Cardona, N. D., Gonzalez Valencia, E., Torres Trujillo, P., & Reyes Vera, E. (2020). Tunable Mode Converter Device Based on Photonic Crystal Fiber with a Thermo-Responsive Liquid Crystal Core. Photonics, 7(1), 3. https://doi.org/10.3390/photonics7010003







