Near-IR Plasmons in Micro and Nanoparticles with a Semiconductor Core
Abstract
1. Introduction
2. Materials and Methods
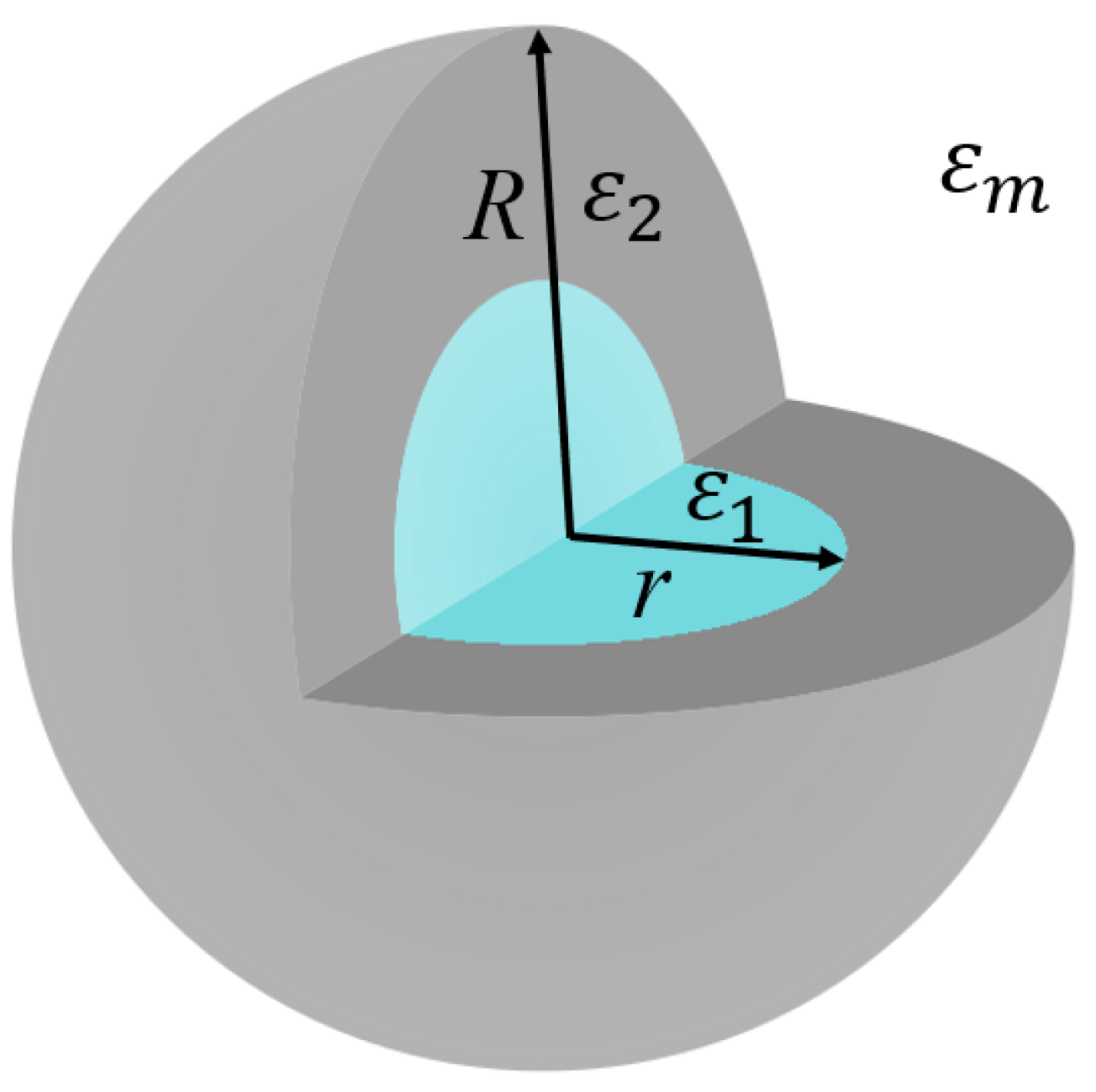
2.1. Mie Theory for Core@Shell Particles
2.2. Polarizability of Core@Shell Shapes
3. Results and Discussion
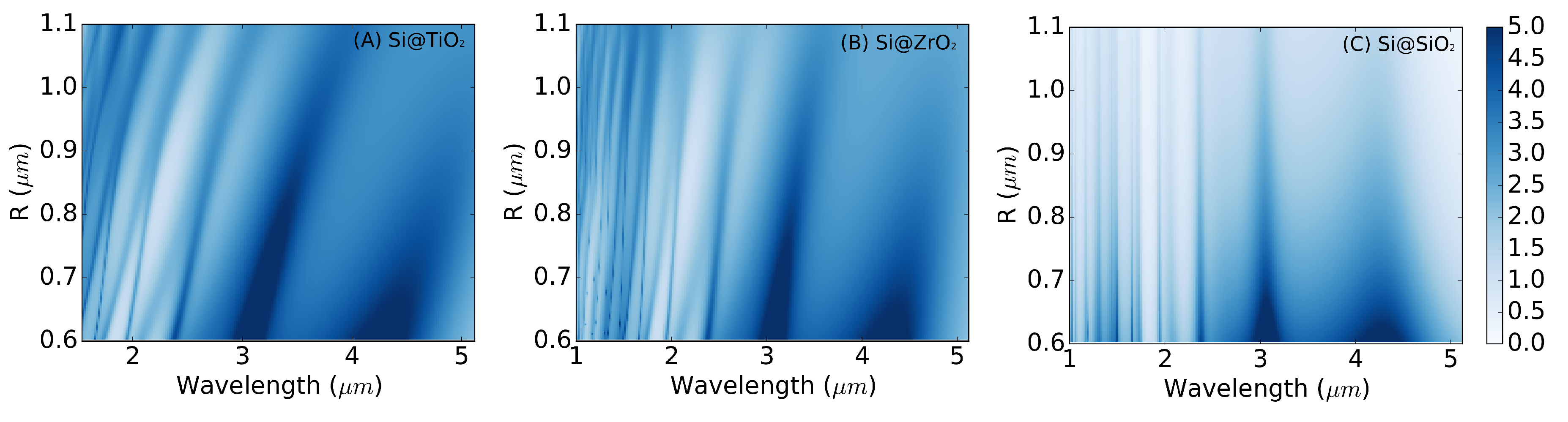
3.1. Semiconductor@Oxide Microparticles
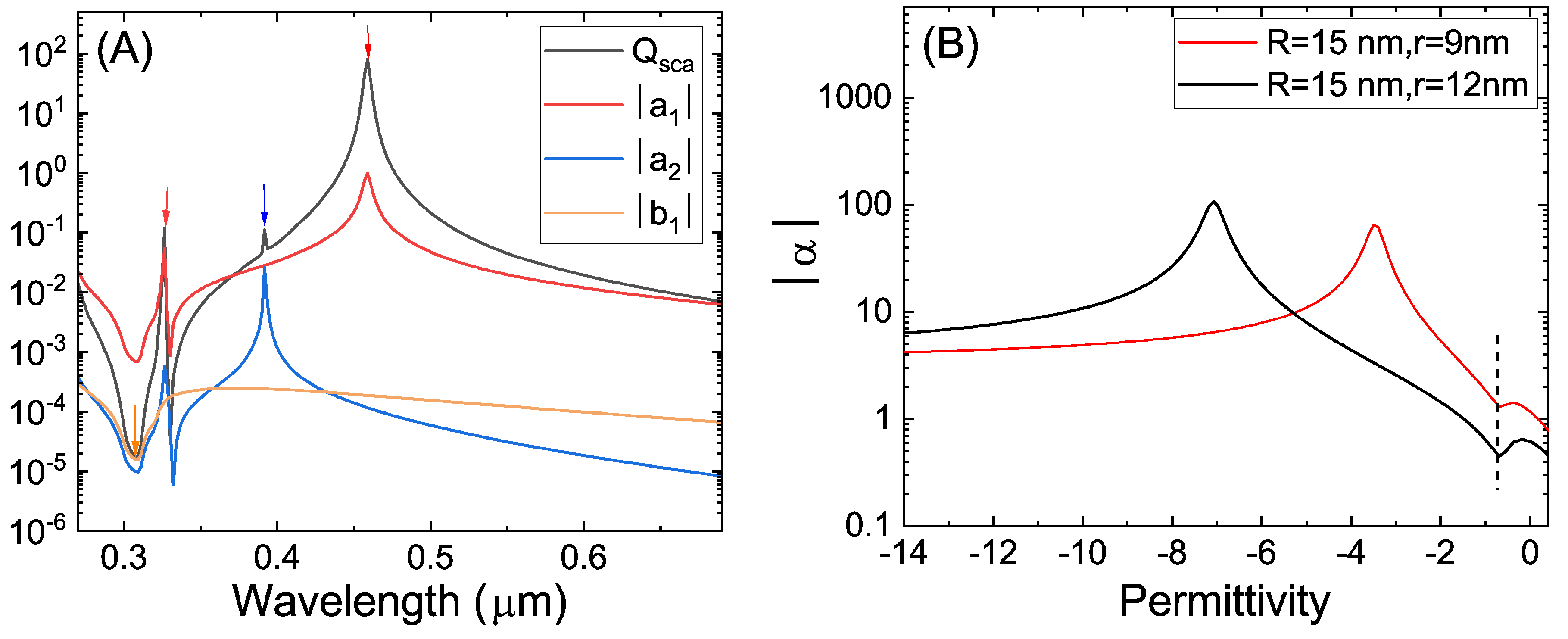
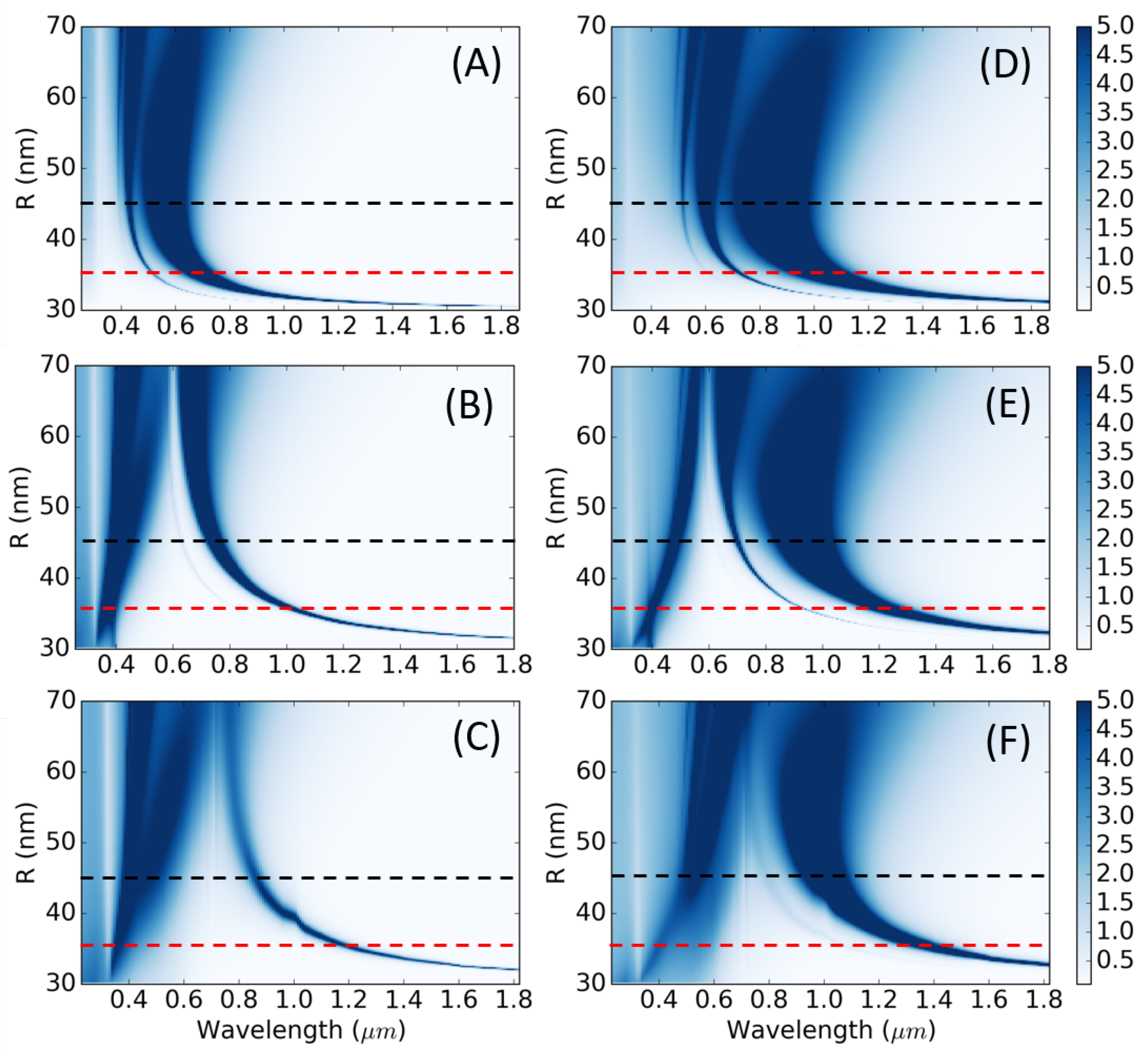
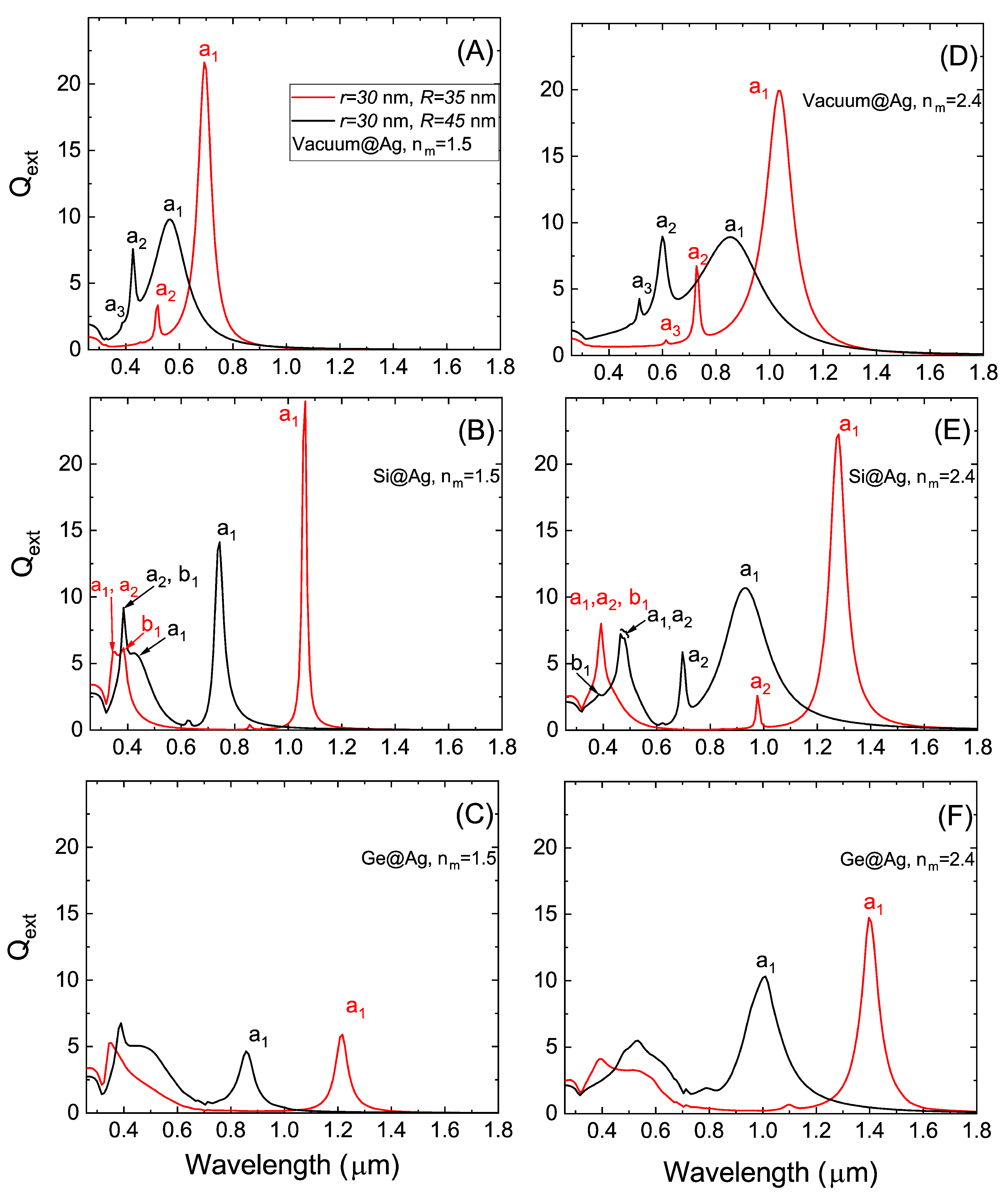
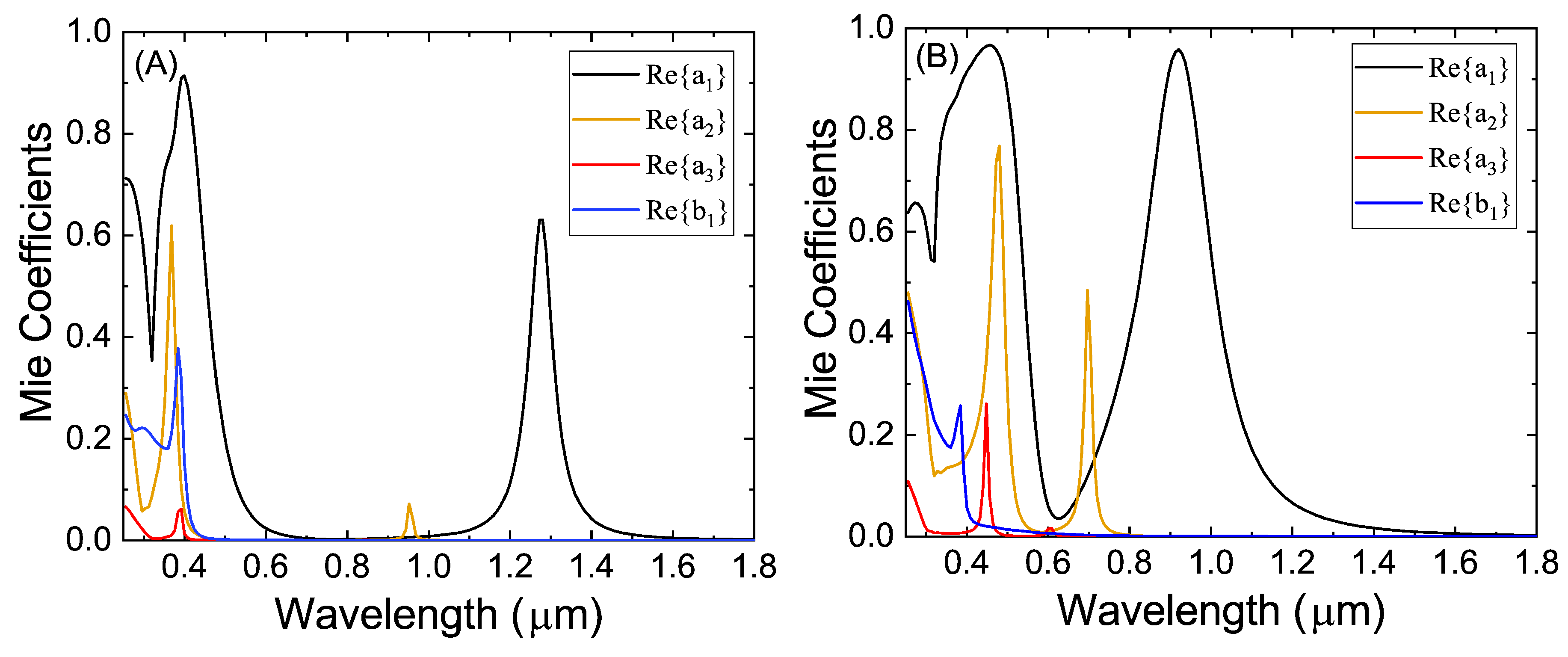
3.2. Semiconductor@Metallic Nanoparticles
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Agrawal, A.; Cho, S.H.; Zandi, O.; Ghosh, S.; Johns, R.W.; Milliron, D.J. Localized surface plasmon resonance in semiconductor nanocrystals. Chem. Rev. 2018, 118, 3121–3207. [Google Scholar] [CrossRef]
- Lu, L.; Kobayashi, A.; Tawa, K.; Ozaki, Y. Silver nanoplates with special shapes: controlled synthesis and their surface plasmon resonance and surface-enhanced Raman scattering properties. Chem. Mater. 2006, 18, 4894–4901. [Google Scholar] [CrossRef]
- Chen, J.; Shi, S.; Su, R.; Qi, W.; Huang, R.; Wang, M.; Wang, L.; He, Z. Optimization and application of reflective LSPR optical fiber biosensors based on silver nanoparticles. Sensors 2015, 15, 12205–12217. [Google Scholar] [CrossRef] [PubMed]
- Aslan, K.; Wu, M.; Lakowicz, J.R.; Geddes, C.D. Fluorescent core- shell Ag@SiO2 nanocomposites for metal-enhanced fluorescence and single nanoparticle sensing platforms. J. Am. Chem. Soc. 2007, 129, 1524–1525. [Google Scholar] [CrossRef] [PubMed]
- West, P.R.; Ishii, S.; Naik, G.V.; Emani, N.K.; Shalaev, V.M.; Boltasseva, A. Searching for better plasmonic materials. Laser Photonics Rev. 2010, 4, 795–808. [Google Scholar] [CrossRef]
- Naik, G.V.; Boltasseva, A. Semiconductors for plasmonics and metamaterials. Phys. Status Solidi 2010, 4, 295–297. [Google Scholar] [CrossRef]
- Paniagua-Domínguez, R.; López-Tejeira, F.; Marqués, R.; Sánchez-Gil, J.A. Metallo-dielectric core–shell nanospheres as building blocks for optical three-dimensional isotropic negative-index metamaterials. New J. Phys. 2011, 13, 123017. [Google Scholar] [CrossRef]
- Mendelsberg, R.J.; Garcia, G.; Li, H.; Manna, L.; Milliron, D.J. Understanding the plasmon resonance in ensembles of degenerately doped semiconductor nanocrystals. J. Phys. Chem. 2012, 116, 12226–12231. [Google Scholar] [CrossRef]
- Naik, G.V.; Shalaev, V.M.; Boltasseva, A. Alternative plasmonic materials: beyond gold and silver. Adv. Mater. 2013, 25, 3264–3294. [Google Scholar] [CrossRef]
- Tang, J.; Thakore, V.; Ala-Nissila, T. Plasmonically Enhanced Reflectance of Heat Radiation from Low-Bandgap Semiconductor Microinclusions. Sci. Rep. 2017, 7, 5696. [Google Scholar] [CrossRef]
- Conley, K.; Thakore, V.; Ala-Nissila, T. Plasmonically Enhanced Spectrally-Sensitive Coatings for Gradient Heat Flux Sensors. In Proceedings of the 2018 Progress in Electromagnetics Research Symposium (PIERS-Toyama), Toyama, Japan, 1–4 August 2018; pp. 2435–2441. [Google Scholar]
- Atwater, H.A.; Polman, A. Plasmonics for improved photovoltaic devices. Nat. Mater. 2010, 9, 205. [Google Scholar] [CrossRef] [PubMed]
- Pala, R.A.; White, J.; Barnard, E.; Liu, J.; Brongersma, M.L. Design of plasmonic thin-film solar cells with broadband absorption enhancements. Adv. Mater. 2009, 21, 3504–3509. [Google Scholar] [CrossRef]
- Aden, A.L.; Kerker, M. Scattering of electromagnetic waves from two concentric spheres. J. Appl. Phys. 1951, 22, 1242–1246. [Google Scholar] [CrossRef]
- Bohren, C.F.; Huffman, D.R. A Potpourri of Particles. In Absorption and Scattering of Light by Small Particles; John Wiley & Sons: Hoboken, NJ, USA, 1983; pp. 181–183. [Google Scholar]
- Kreibig, U. Electronic properties of small silver particles: The optical constants and their temperature dependence. J. Phys. Met. Phys. 1974, 4, 999. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics; Wiley: New York, NY, USA, 1976. [Google Scholar]
- Prodan, E.; Radloff, C.; Halas, N.J.; Nordlander, P. A hybridization model for the plasmon response of complex nanostructures. Science 2003, 302, 419–422. [Google Scholar] [CrossRef]
- Sheverdin, A.; Valagiannopoulos, C. Core-shell nanospheres under visible light: Optimal absorption, scattering, and cloaking. Phys. Rev. 2019, 99, 075305. [Google Scholar] [CrossRef]
- Ruan, Z.; Fan, S. Design of subwavelength superscattering nanospheres. Appl. Phys. Lett. 2011, 98, 043101. [Google Scholar] [CrossRef]
- Laaksonen, K.; Suomela, S.; Puisto, S.; Rostedt, N.; Ala-Nissila, T.; Nieminen, R. Influence of high-refractive-index oxide cores on optical properties of metal nanoshells. J. Opt. Soc. Am. 2014, 31, 494–502. [Google Scholar] [CrossRef]
- Streetman, B.G.; Banerjee, S. Solid State Electronic Devices; Prentice-Hall of India: New Delhi, India, 2001; p. 524. [Google Scholar]
- Palik, E.D. Handbook of Optical Constants of Solids; Academic Press: Cambridge, MA, USA, 1998; Volume 3, pp. 5–114. [Google Scholar]
- Wood, D.L.; Nassau, K. Refractive index of cubic zirconia stabilized with yttria. Appl. Opt. 1982, 21, 2978–2981. [Google Scholar] [CrossRef]
- Halas, N.J.; Lal, S.; Chang, W.S.; Link, S.; Nordlander, P. Plasmons in strongly coupled metallic nanostructures. Chem. Rev. 2011, 111, 3913–3961. [Google Scholar] [CrossRef]
- Johnson, P.B.; Christy, R.W. Optical constants of the noble metals. Phys. Rev. 1972, 6, 4370. [Google Scholar] [CrossRef]
- Sihvola, A.; Tzarouchis, D.C.; Ylä-Oijala, P.; Wallén, H. Properties of Hybridized Modes in Core–Shell Scatterers. In Proceedings of the 2018 2nd URSI Atlantic Radio Science Meeting (AT-RASC), Meloneras, Spain, 28 May–1 June 2018; pp. 1–3. [Google Scholar]
- Tzarouchis, D.C.; Sihvola, A. General scattering characteristics of resonant core–shell spheres. IEEE Trans. Antennas Propag. 2017, 66, 323–330. [Google Scholar] [CrossRef]
- Prodan, E.; Nordlander, P. Plasmon hybridization in spherical nanoparticles. J. Chem. Phys. 2004, 120, 5444–5454. [Google Scholar] [CrossRef] [PubMed]
- Brandl, D.W.; Oubre, C.; Nordlander, P. Plasmon hybridization in nanoshell dimers. J. Chem. Phys. 2005, 123, 024701. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seyedheydari, F.; Conley, K.; Ala-Nissila, T. Near-IR Plasmons in Micro and Nanoparticles with a Semiconductor Core. Photonics 2020, 7, 10. https://doi.org/10.3390/photonics7010010
Seyedheydari F, Conley K, Ala-Nissila T. Near-IR Plasmons in Micro and Nanoparticles with a Semiconductor Core. Photonics. 2020; 7(1):10. https://doi.org/10.3390/photonics7010010
Chicago/Turabian StyleSeyedheydari, Fahime, Kevin Conley, and Tapio Ala-Nissila. 2020. "Near-IR Plasmons in Micro and Nanoparticles with a Semiconductor Core" Photonics 7, no. 1: 10. https://doi.org/10.3390/photonics7010010
APA StyleSeyedheydari, F., Conley, K., & Ala-Nissila, T. (2020). Near-IR Plasmons in Micro and Nanoparticles with a Semiconductor Core. Photonics, 7(1), 10. https://doi.org/10.3390/photonics7010010





