Image Encryption System Based on a Nonlinear Joint Transform Correlator for the Simultaneous Authentication of Two Users
Abstract
1. Introduction
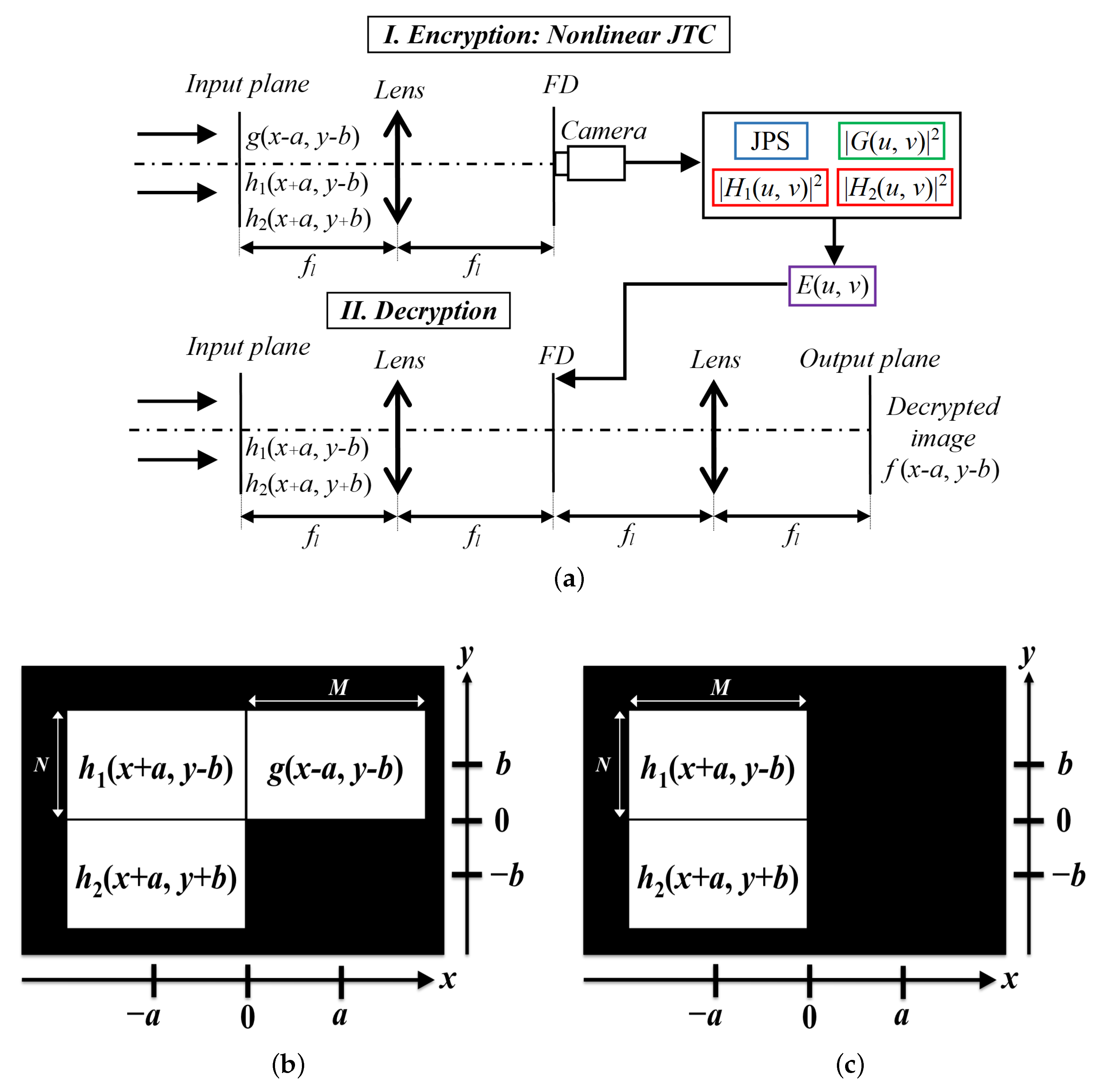
2. Encryption, Decryption, and Authentication Stages
2.1. Encryption Stage
2.2. Decryption and Authentication Stages
3. Computational Simulations
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Javidi, B.; Carnicer, A.; Yamaguchi, M.; Nomura, T.; Pérez-Cabré, E.; Millán, M.; Nishchal, N.; Torroba, R.; Barrera, J.; He, W.; et al. Roadmap on optical security. J. Opt. 2016, 18, 083001. [Google Scholar] [CrossRef]
- Chen, W.; Javidi, B.; Chen, X. Advances in optical security systems. Adv. Opt. Photonics 2014, 6, 120–155. [Google Scholar] [CrossRef]
- Millán, M.S.; Pérez-Cabré, E. Optical data encryption. In Optical and Digital Image Processing: Fundamentals and Applications; Cristóbal, G., Schelkens, P., Thienpont, H., Eds.; Wiley-VCH Verlag GmbH & Co.: Hoboken, NJ, USA, 2011; pp. 739–767. [Google Scholar]
- Millán, M.S.; Pérez-Cabré, E.; Vilardy, J.M. Nonlinear techniques for secure optical encryption and multifactor authentication. In Advanced Secure Optical Image Processing for Communications; Al Falou, A., Ed.; IOP Publishing: Bristol, UK, 2018; pp. 8-1–8-33. [Google Scholar]
- Réfrégier, P.; Javidi, B. Optical image encryption based on input plane and Fourier plane random encoding. Opt. Lett. 1995, 20, 767–769. [Google Scholar] [CrossRef] [PubMed]
- Goodman, J.W. Introduction to Fourier Optics; McGraw-Hill: New York, NY, USA, 1996. [Google Scholar]
- Nomura, T.; Javidi, B. Optical encryption using a joint transform correlator architecture. Opt. Eng. 2000, 39, 2031–2035. [Google Scholar]
- Rueda, E.; Barrera, J.F.; Henao, R.; Torroba, R. Optical encryption with a reference wave in a joint transform correlator architecture. Opt. Commun. 2009, 282, 3243–3249. [Google Scholar] [CrossRef]
- Rueda, E.; Barrera, J.F.; Henao, R.; Torroba, R. Lateral shift multiplexing with a modified random mask in a joint transform correlator encrypting architecture. Opt. Eng. 2009, 48, 027006. [Google Scholar] [CrossRef]
- Barrera, J.F.; Rueda, E.; Rios, C.; Tebaldi, M.; Bolognini, N.; Torroba, R. Experimental opto-digital synthesis of encrypted sub-samples of an image to improve its decoded quality. Opt. Commun. 2011, 284, 4350–4355. [Google Scholar] [CrossRef]
- Barrera, J.F.; Tebaldi, M.; Rios, C.; Rueda, E.; Bolognini, N.; Torroba, R. Experimental multiplexing of encrypted movies using a JTC architecture. Opt. Express 2012, 20, 3388–3393. [Google Scholar] [CrossRef]
- Vilardy, J.M.; Millán, M.S.; Pérez-Cabré, E. Improved decryption quality and security of a joint transform correlator-based encryption system. J. Opt. 2013, 15, 025401. [Google Scholar] [CrossRef]
- Vilardy, J.M.; Millán, M.S.; Pérez-Cabré, E. Nonlinear optical security system based on a joint transform correlator in the Fresnel domain. Appl. Opt. 2014, 53, 1674–1682. [Google Scholar] [CrossRef]
- Vilardy, J.M.; Millán, M.S.; Pérez-Cabré, E. Joint transform correlator-based encryption system using the Fresnel transform and nonlinear filtering. Proc. SPIE 2013, 8785, 87853. [Google Scholar]
- Shen, X.; Lin, C.; Zou, X.; Cai, J. Nonlinear optical cryptosystem based on joint Fresnel transform correlator under vector wave illumination. J. Opt. 2015, 17, 055701. [Google Scholar]
- Barrera, J.F.; Jaramillo, A.; Vélez, A.; Torroba, R. Experimental analysis of a joint free space cryptosystem. Opt. Lasers Eng. 2016, 83, 126–130. [Google Scholar]
- Dou, S.; Shen, X.; Zhou, B.; Wang, L.; Lin, C. Experimental research on optical image encryption system based on joint Fresnel transform correlator. Opt. Laser Technol. 2019, 112, 56–64. [Google Scholar] [CrossRef]
- Vilardy, J.M.; Torres, Y.; Millán, M.S.; Pérez-Cabré, E. Generalized formulation of an encryption system based on a joint transform correlator and fractional Fourier transform. J. Opt. 2014, 16, 125405. [Google Scholar] [CrossRef]
- Vilardy, J.M.; Millán, M.S.; Pérez-Cabré, E. Sistema de cifrado de imágenes basado en un correlador de transformadas conjuntas fraccionario y filtrado no lineal. Opt. Pura Appl. 2014, 47, 35–41. [Google Scholar] [CrossRef]
- Wang, Q.; Guo, Q.; Lei, L.; Zhou, J. Optical image encryption based on joint fractional transform correlator architecture and digital holography. Opt. Eng. 2013, 52, 048201. [Google Scholar] [CrossRef]
- Jaramillo, A.; Barrera, J.F.; Vélez, A.; Torroba, R. Fractional optical cryptographic protocol for data containers in a noise-free multiuser environment. Opt. Lasers Eng. 2018, 102, 119–125. [Google Scholar] [CrossRef]
- Vilardy, J.M.; Millán, M.S.; Pérez-Cabré, E. Nonlinear image encryption using a fully phase nonzero-order joint transform correlator in the Gyrator domain. Opt. Lasers Eng. 2017, 89, 88–94. [Google Scholar] [CrossRef]
- Millán, M.S.; Pérez-Cabré, E.; Javidi, B. Multifactor authentication reinforces optical security. Opt. Lett. 2006, 31, 721–723. [Google Scholar] [CrossRef]
- Pérez-Cabré, E.; Millán, M.S.; Javidi, B. Near infrared multifactor identification tags. Opt. Express 2007, 15, 15615–15627. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Cabré, E.; Mohammed, E.A.; Millán, M.S.; Saadon, H.L. Photon-counting multifactor optical encryption and authentication. J. Opt. 2015, 17, 025706. [Google Scholar] [CrossRef]
- Horrillo, S.; Pérez-Cabré, E.; Millán, M.S. Information compression for remote readable ID tags. J. Opt. 2010, 12, 115404. [Google Scholar] [CrossRef][Green Version]
- Ahouzi, E.; Zamrani, W.; Azami, N.; Lizana, A.; Campos, J.; Yzuel, M.J. Optical triple random-phase encryption. Opt. Eng. 2017, 56, 113114. [Google Scholar] [CrossRef]
- Hai, H.; Pan, S.; Liao, M.; Lu, D.; He, W.; Peng, X. Cryptanalysis of random-phase-encoding-based optical cryptosystem via deep learning. Opt. Express 2019, 27, 21204–21213. [Google Scholar] [CrossRef] [PubMed]
- Towghi, N.; Javidi, B.; Luo, Z. Fully phase encrypted image processor. J. Opt. Soc. Am. A 1999, 16, 1915–1927. [Google Scholar] [CrossRef]
- Frauel, Y.; Castro, A.; Naughton, T.J.; Javidi, B. Resistance of the double random phase encryption against various attacks. Opt. Express 2007, 15, 10253–10265. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vilardy O., J.M.; Millán, M.S.; Pérez-Cabré, E. Image Encryption System Based on a Nonlinear Joint Transform Correlator for the Simultaneous Authentication of Two Users. Photonics 2019, 6, 128. https://doi.org/10.3390/photonics6040128
Vilardy O. JM, Millán MS, Pérez-Cabré E. Image Encryption System Based on a Nonlinear Joint Transform Correlator for the Simultaneous Authentication of Two Users. Photonics. 2019; 6(4):128. https://doi.org/10.3390/photonics6040128
Chicago/Turabian StyleVilardy O., Juan M., María S. Millán, and Elisabet Pérez-Cabré. 2019. "Image Encryption System Based on a Nonlinear Joint Transform Correlator for the Simultaneous Authentication of Two Users" Photonics 6, no. 4: 128. https://doi.org/10.3390/photonics6040128
APA StyleVilardy O., J. M., Millán, M. S., & Pérez-Cabré, E. (2019). Image Encryption System Based on a Nonlinear Joint Transform Correlator for the Simultaneous Authentication of Two Users. Photonics, 6(4), 128. https://doi.org/10.3390/photonics6040128





