An Optoelectronic Targeting System for Measuring the Distribution of Projectile Motion Based on the Subdivision of a Light Screen

Abstract

This paper proposes a cost-effective, compact, noncontacting optoelectronic targeting system for measuring the distribution of projectile motion. The major elements of this system include a light emitting diode (LED) array, photodiode detecting array, double-layered aperture arrays, adaptive threshold circuit, and date acquisition. Through cooperating with double-layered aperture arrays, the system effectively reduces the radiation width of the light source to the photodiode detecting surface, and filters out the influence of incident light from the adjacent apertures on both sides above each photodiode to the corresponding photodiode detecting surface. It realizes that the response of the photodiode array corresponds to the coordinates of the light screen one by one. Through the sensitivity analysis of the light screen of the system, the system detecting threshold when the projectile passes through the light screen is calculated, and the corresponding adaptive threshold circuit is designed to prevent misjudgment when the system works. The measuring error of the system can reach ±2 mm by experimental verification. Compared with other projectile’s distribution measuring systems, the proposed system has the advantages of having high precision, convenient debugging, is nondestructive, and is a noncontact system.

1. Introduction

The distribution measurement of projectile motion is a significant evaluation indicator for the development, acceptance, and finalization of weapons [1,2,3,4,5]. At present, according to whether the projectile is in contact with the measuring system, the distribution measuring methods of the projectile are mainly divided into contact measurements and noncontact measurements [6,7,8,9,10]. A contact measurement usually uses aluminum foil or a steel plate to form a target to measure the distribution of projectiles. This method is simple in structure and low in cost, but the measuring system made by this method is one-off and has poor repeatability [11]. In noncontact measurement, a parallel light screen shaped by a laser or light emitting diode (LED) is used as the light source to illuminate the sensor array and the coordinates of the projectile are measured by the response of the sensor array to the signal produced when the projectile passes through the light screen (i.e., the over-target signal of the projectile) [12,13,14,15]. However, this method usually requires a high cost to customize the specially processed Fresnel lens or convex lens combination; it also needs to design the mechanical structure in which to fix them to form the precise collimating optical system. The collimating system forms the light source with the divergence angle into the parallel light screen, which is used as a measuring light screen. Therefore, this method has very high requirements for the parallelism of the light screen, and its collimation directly affects the accuracy of the measuring results. In addition, during the process of system debugging, the optical path needs to be checked and calibrated, which increases the complexity of design and installation of the system. At the same time, because the mechanical structure of the collimating optical system will occupy a certain volume of the system to reduce the area of the measuring light screen, the utilization of the target surface is low [16,17,18,19].

In order to solve the above problems in the distribution measurement of projectile motion, this paper proposes an optoelectronic measuring system based on a LED aperture photodiode (hereinafter referred to as PD) structure to measure the distributed coordinate of the projectile. Based on the principle of dot-matrix optoelectronic coordinate measuring technology [20,21,22], this method selects an LED with small volume and low cost as the light source, double-layered aperture arrays are designed to shape the light source, and the shaped light is irradiated to the detecting surface composed of the PD array to form a large-area measuring light screen. This enables accurate measuring of the distributed coordinates of the projectile [23]. In addition, since the proposed system does not need to add an optical system to shape the beam at the position of the light source, the optical structure of the system is greatly simplified, saving costs, and the installation is facilitated. At the same time, higher utilization of the target surface is achieved.

2. Principle

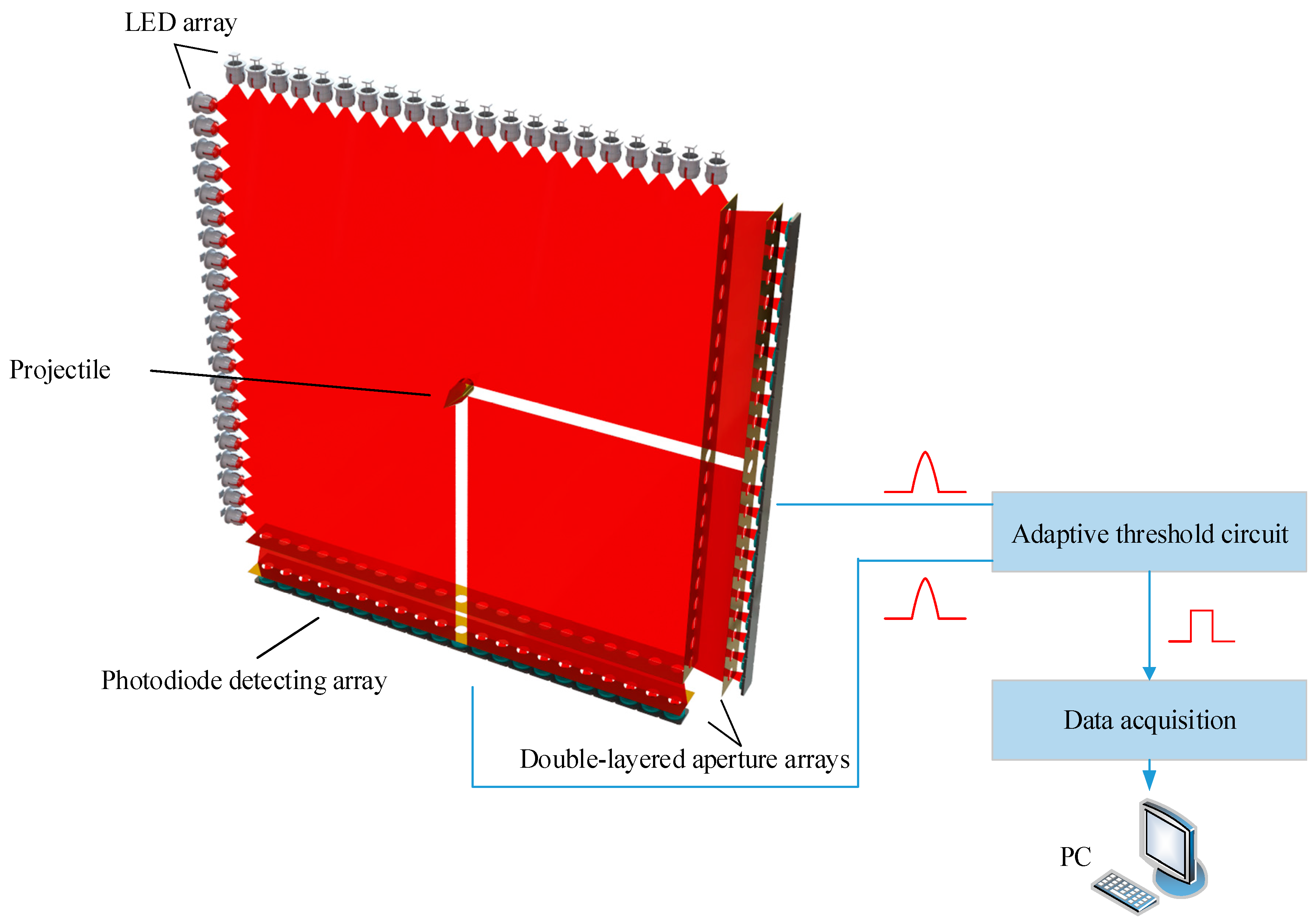
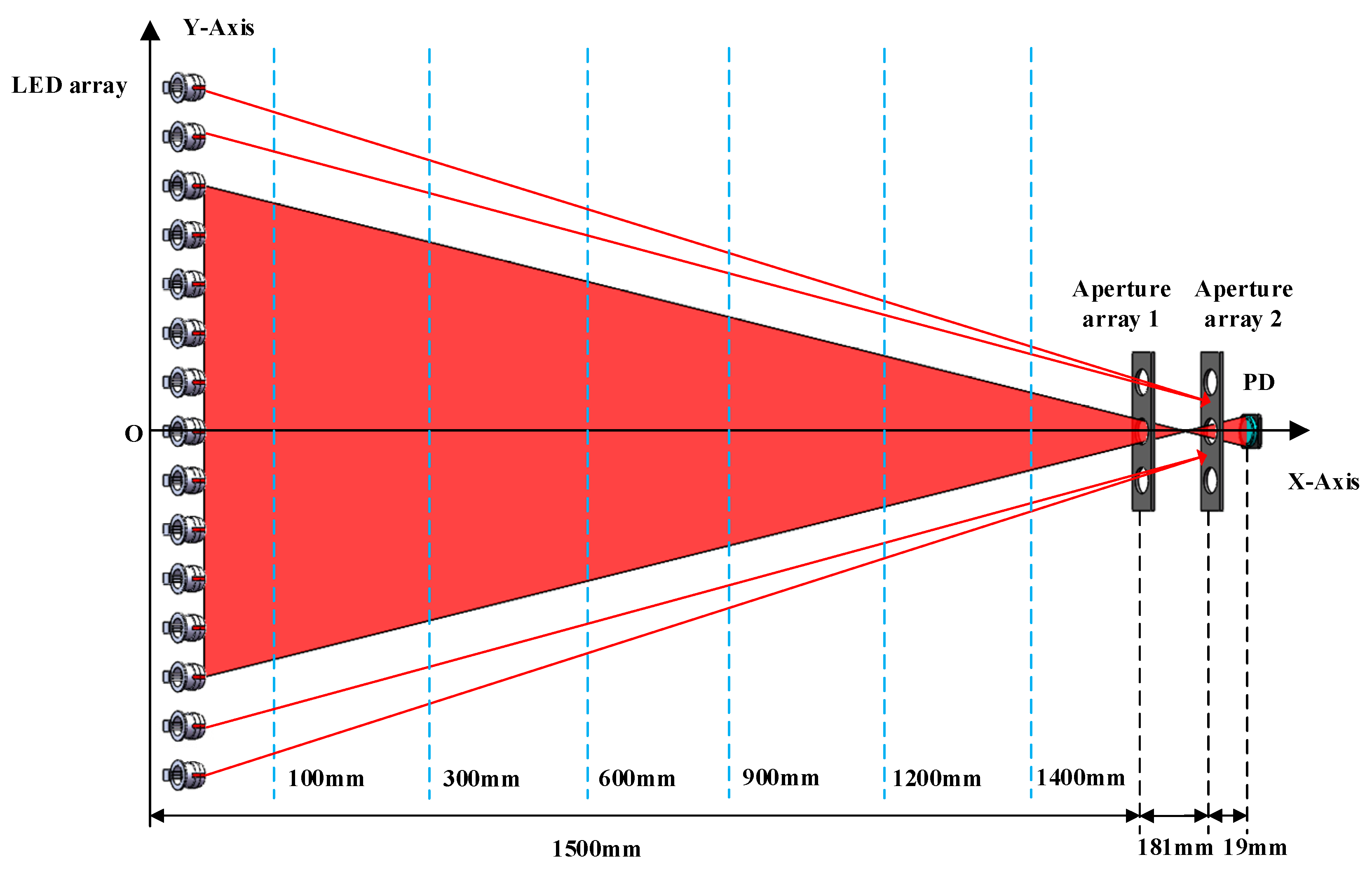
The major elements of this system include the LED array, PD detecting array, double-layered aperture arrays, adaptive threshold circuit, and date acquisition. The proposed system is shown in Figure 1. The LED array is used as the light source to produce the light screen. After the light screen with divergence angle is subdivided by the double-layered aperture arrays, it is irradiated to the PD array, and the PD array as a detecting module has a one-to-one correspondence with the LED array in space. Through this form of radiation, a large-area targeting surface of the two-dimensional orthogonal light screen is formed. When the projectile passes through the light screen, the PD at the corresponding position of the detecting array will receive the slightly changed optical signal, because when the projectile blocks the light, it is amplified and converted by the adaptive threshold circuit to form the over-target digital signal of the projectile. The signal is sent to the computer by the data acquisition system, and the PD coordinates that generate the response signal are used as the coordinates for the projectile impact point.

3. Mathematical Analysis

Due to the inherent divergent angle of the LED, the detecting surface of a single PD will receive different angles of optical radiation. When the projectile passes through a certain position of the light screen, multiple PD detectors will respond. If the aperture array is added above the PD detecting array to limit the detecting field of view of a single PD detecting surface, the number of LEDs in the light source that can affect the response of the single PD detector can be reduced. Therefore, it is necessary to establish a mathematical model for the aperture array, calculate the optimal position of the aperture array, and realize the correspondence between the response of the PD detecting array and the coordinates of the light screen.

3.1. Mathematical Abstraction

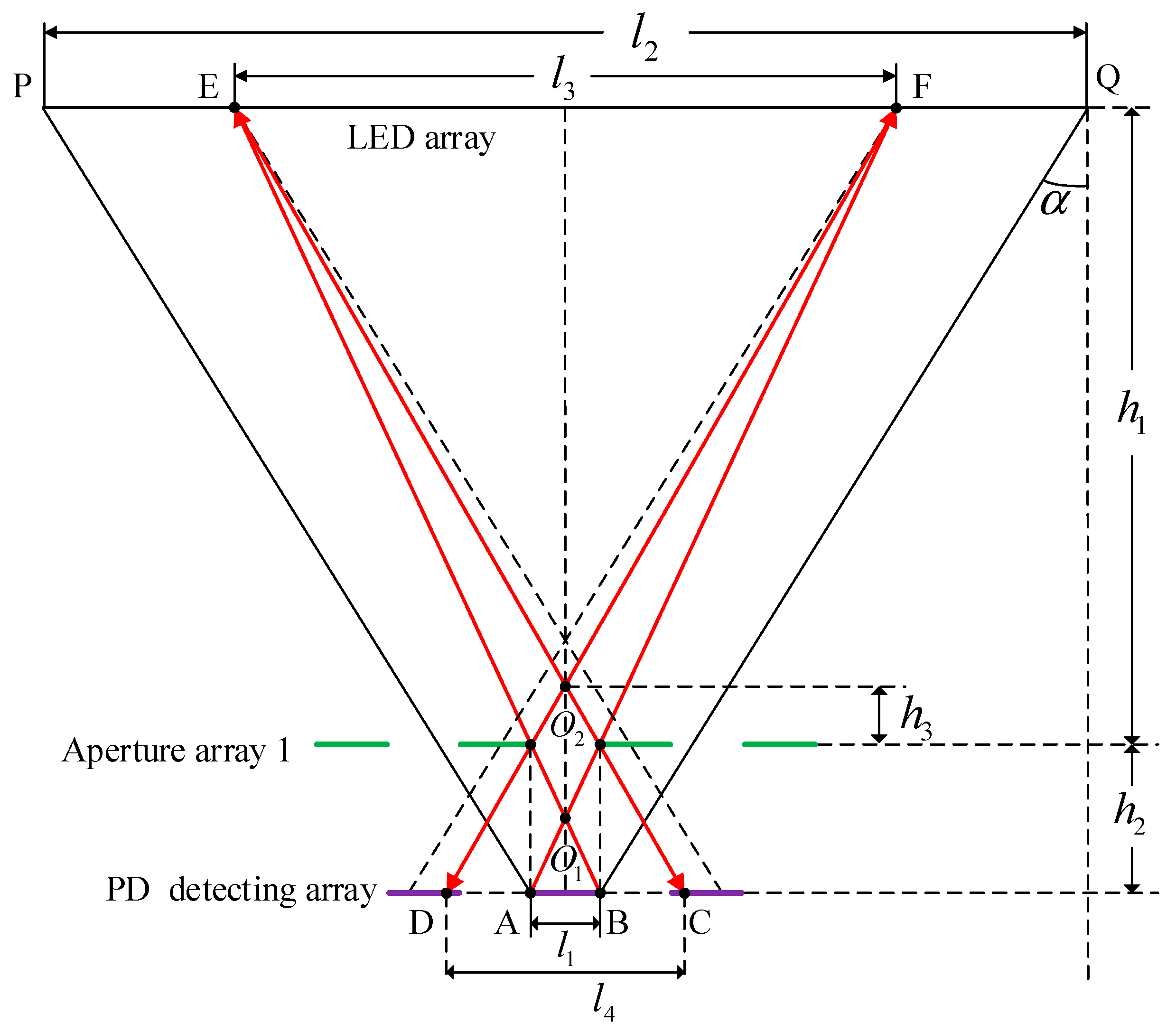
Taking a single PD at a random position in the detecting array as the research object, the mathematical model of a single-layered aperture array is established, as shown in Figure 2. AB is the diameter of the effective photosurface in the single PD detector, which is equal to the diameter of a single aperture, and α is the half divergence angle of the LED. When there is no aperture array, the width PQ of the LED array that can affect a single PD detector is $l_2=2(h_1+h_2)\tan \alpha +l_1$. After adding a single-layered aperture array 1 to limit the light screen, the width EF of the single PD’s field of view is $l_3=(1+\frac{2h_1}{h_2})l_1$. According to the geometric relationship in Figure 2, $\frac{l_1}{l_3}=\frac{h_3}{h_1-h_3}$ and $\frac{l_1}{l_4}=\frac{h_3}{h_2+h_3}$ are known, and the maximum width that the LED array radiates to the detecting array in the range of EF is:

$$l_4=\left(3+\frac{2h_2}{h_1}\right)l_1$$

(1)

Under the condition that the effective length of the light screen ($h_1=1.5\mathrm{m}$) and the diameter of a single PD detecting surface ($l_1=3\mathrm{mm}$) are known, in order to ensure the compact structure of the aperture PD module, when the distance between the aperture array 1 and the PD array is $h_2=200\mathrm{mm}$, the width of the single PD’s field of view is $l_3=50\mathrm{mm}$, and the width in which the LED array radiates to the detection array in the range of $l_3$ is $l_4=9.8\mathrm{mm}$.

The change of the optical power of a single PD detector is not only related to the aperture that is right above it, but it is also affected by the incident light of the adjacent apertures according to Figure 2. In view of this, aperture array 2 is added between aperture array 1 and the detecting array. This not only effectively reduces the width in which the LED array radiates to the detecting array, but also filters out the influence of incident light from the adjacent apertures on the detector. As shown in Figure 3, this makes sure that the light with the maximum oblique angle does not affect the detector. Based on this condition, the distance between the two aperture arrays is analyzed and calculated. Here, $\frac{l_1}{l_4^{\prime }}=\frac{h_3^{\prime }+h_4}{h_2+h_3^{\prime }}$, $\frac{l_4^{\prime }}{l_3}=\frac{h_2+h_3^{\prime }}{h_1-h_3^{\prime }}$, and $\frac{d-l_1}{\raisebox{1ex}{$l_2$}\!\left/ \!\raisebox{-1ex}{$2$}\right.-\raisebox{1ex}{$l_1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}=\frac{h_2-h_4}{h_1+h_2}$ are known from the geometric relationship in Figure 3. After adding aperture array 2, the width in which the LED array radiates to the detecting array is:

$$l_4^{\prime }=\left[\frac{2h_2^2+3h_1{h}_2-2h_1{h}_4-h_2{h}_4}{h_1{h}_2+h_2{h}_4}\right]l_1$$

(2)

The relationship between the horizontal distance $d$ of the two PDs and the vertical distance $h_4$ of the double-layered aperture arrays is:

$$h_4=h_2-\frac{d-l_1}{\tan \alpha }$$

(3)

3.2. Calculation of PD Spacing

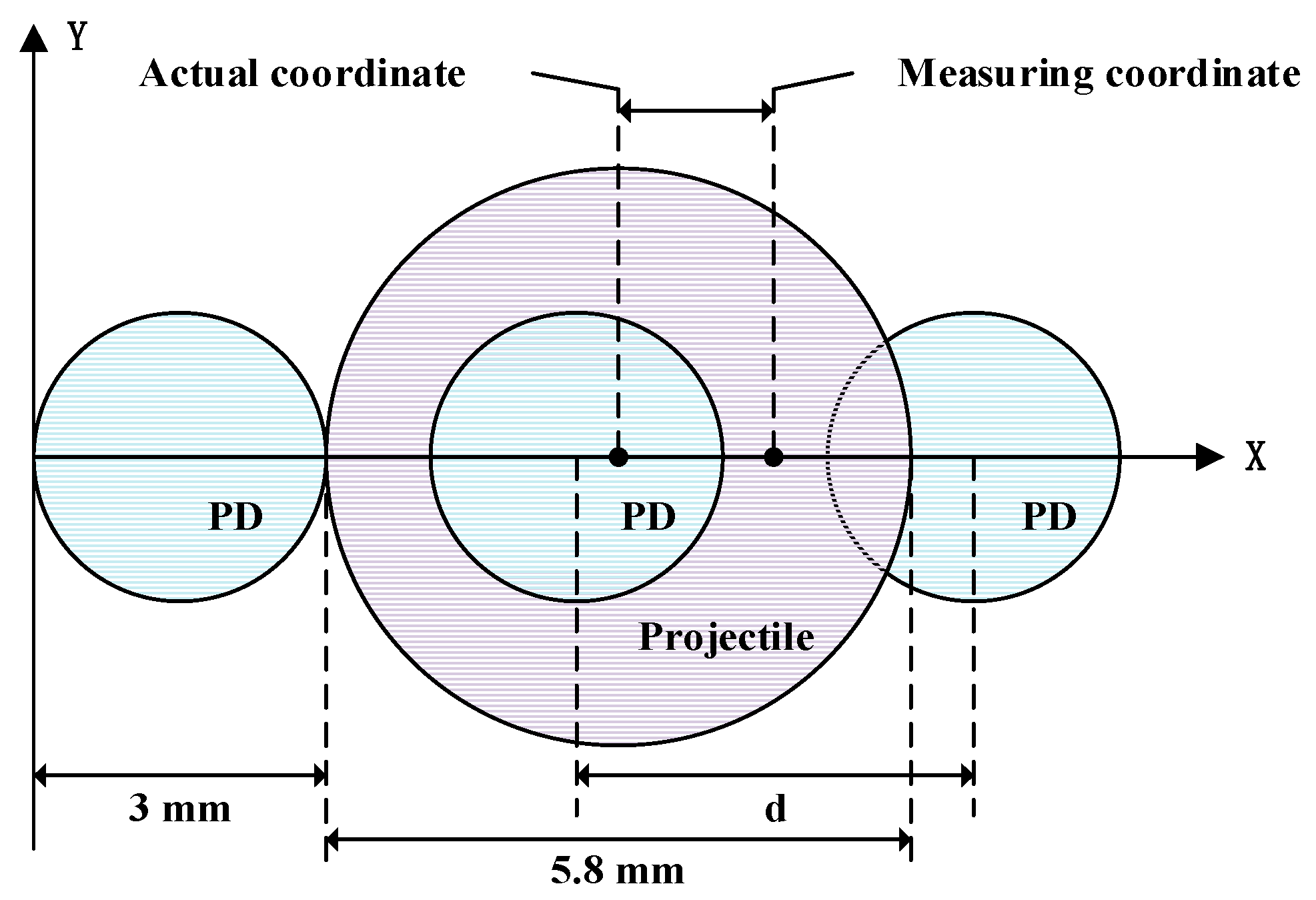
According to Equation (3), in order to obtain the vertical distance $h_4$ of the double-layered aperture arrays, the horizontal distance $d$ of the two PDs must be calculated first. Taking a 5.8 mm projectile as the example, several PD responses are triggered when the projectile passes through the light screen, then the measured coordinate after the processing of the recognition algorithm is the coordinate of the center positions of several PDs. As shown in Figure 4, supposing the edge of the projectile happens to not trigger the PD next to it, the coordinate error generated at this time is the largest. In order to ensure that the coordinate measurement error is less than 2 mm, Equation (4) can be obtained from Figure 4:

$$\frac{3}{2}d-4.4\le 2\mathrm{mm}$$

(4)

When the horizontal distance $d$ of the two PDs is $d\le 4.2\mathrm{mm}$, the measurement error is less than 2 mm.

Based on the above mathematical derivation, when the distance between each PD is $d=4\mathrm{mm}$, it meets the measuring error of no more than 2 mm. According to Equations (2) and (3), the ultimate distance of the double-layered aperture arrays is $h_4=181\mathrm{mm}$ and the maximum radiation width of the detecting array is $l_3^{\prime }=3.58\mathrm{mm}$. This shows that each PD detector responds only to the incident light in the aperture corresponding to itself.

4. Analysis of System Optical Characteristics

4.1. Uniformity Measurement of Light Screen

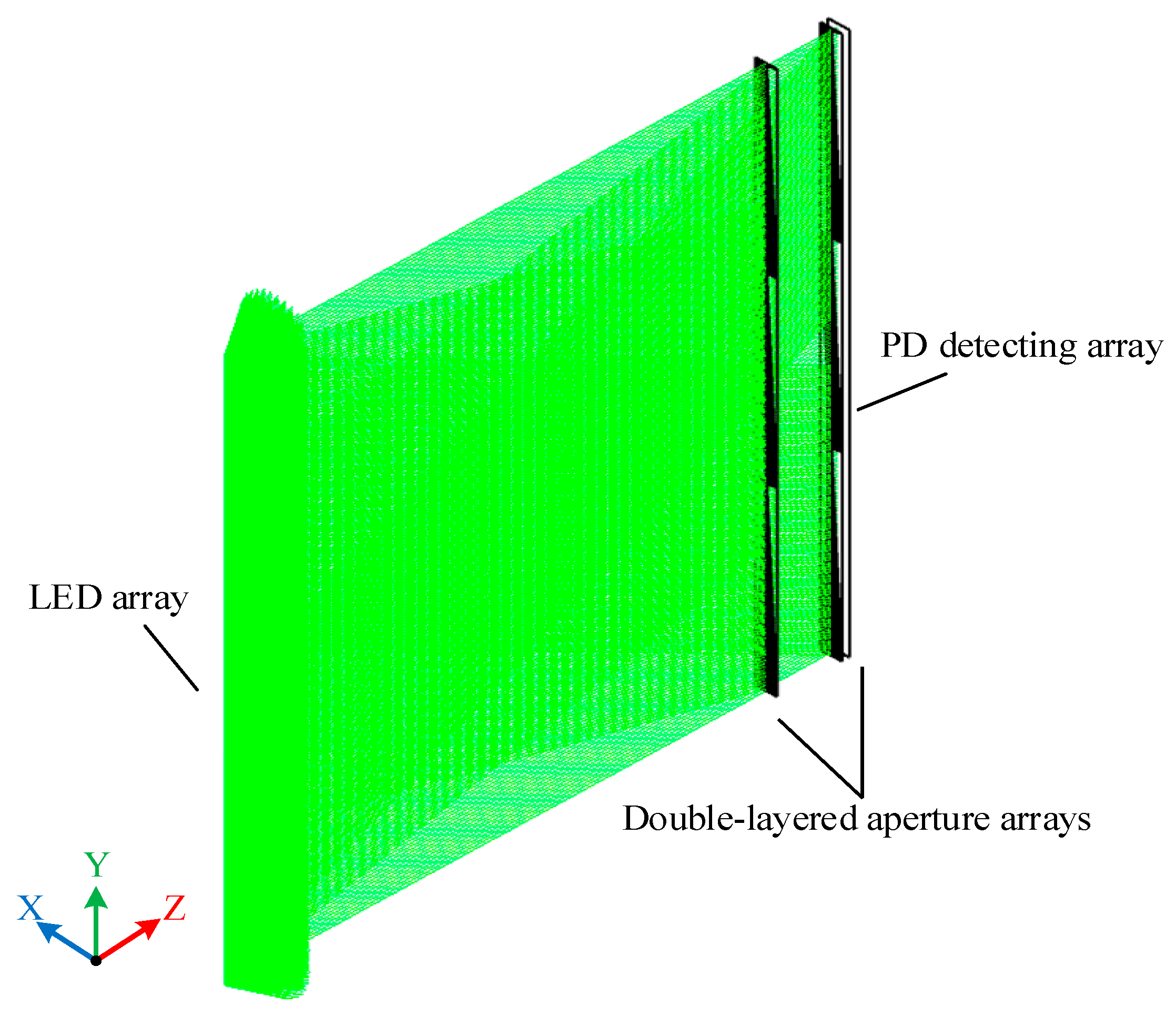
Optical simulation of the system is carried out using Zemax. In the nonsequential mode of Zemax, the source_diode model is selected as the component of the LED array, and its half divergence angle ${\theta }_{1/2}$ is set to 3°. The LED array is centered on the origin of Zemax’s coordinate axis, and the source_diode is placed at intervals of 4 mm on both sides along the Y axis, which makes the length of the LED array reach 1600 mm. Along the Z axis, in order to ensure that the effective length of the light screen is 1500 mm, the mechanical model of the double-layered aperture arrays is placed at a distance of 1500 mm from the LED array. The specific parameters are consistent with the results of the mathematical modeling in the previous section (i.e., the distance of the double-layered aperture arrays is 181 mm, the distance between each aperture is 4 mm along the Y axis, and each aperture has a diameter of 3 mm; the total length of the double-layered aperture arrays is 1600 mm, which corresponds to the LED array). The PD detecting array is placed at a distance of 1700 mm from the LED array; each detector of the PD detecting array has a diameter of 3 mm and corresponds to each aperture. It is responsible for receiving the radiation of the light source after being restricted by the double-layer aperture.

Optical simulation of the system is shown in Figure 5. After the light screen of the LED array is subdivided by the double-layered aperture arrays, the light spot array is formed at a position 1700 mm from the light source. According to the mathematical modeling in the previous section, due to the effect of the double-layered aperture arrays on shaping and filtering of the light screen, each PD detector receives the light intensity only from the corresponding position of the radiation of the light source, and it effectively filters out the influence of incident light from the adjacent apertures on each PD detector. The uniformity of the light intensity before and after the addition of the double-layered aperture array is shown in Figure 6. After the light screen is reshaped by the double layer aperture arrays, the light intensity that is irradiated by the LED array to the PD detecting array is reduced, but it improves the uniformity of the light intensity received by PD detecting array and the measured accuracy of the system, so it can be used as an effective targeting surface for measurement.

4.2. Analysis of Detection Sensitivity

After adding the design of the double-layered aperture arrays, the system’s measuring accuracy improves, but the detecting sensitivity is compromised to some extent due to the reduced optical power received by the PD detecting array. When the projectile passes through the light screen, the variation in optical power is converted by the signal conditioning circuit, the voltage of which is:

$$V_{(t)}=\Delta {\varphi }_{(t)}\cdot \epsilon \cdot \gamma \cdot R$$

(5)

In Equation (5), $\Delta {\varphi }_{(t)}$ is the variation of optical power caused by the projectile passing through the light screen, and R is the resistance that converts the PD detector’s current signal to the voltage signal. For the same system, the photoelectric conversion sensitivity ε of the PD detector is the same as the gain γ of the signal conditioning circuit, and the amplitude of the voltage signal generated by the PD detector depends on the amount of light blocked by the projectile passing through the light screen. To enable the PD detector to detect the projectile’s over-target signal at a random position in the light screen, at this random position, the $V_{(t)}$ produced by the projectile passing through the light screen must be greater than the detecting threshold set by the system. Therefore, the minimum variation of optical power when the circuit can output an effective projectile’s over-target signal is the detecting sensitivity of the system.

Based on the simulation model in Section 4.1, a sensitivity model is established by Zemax. It is used to ensure that the PD at the corresponding position responds to the variation in optical power when the projectile passes through the random position within the light screen. The PD detector of the random position at a distance of 1700 mm from the LED array is used as a measuring object. 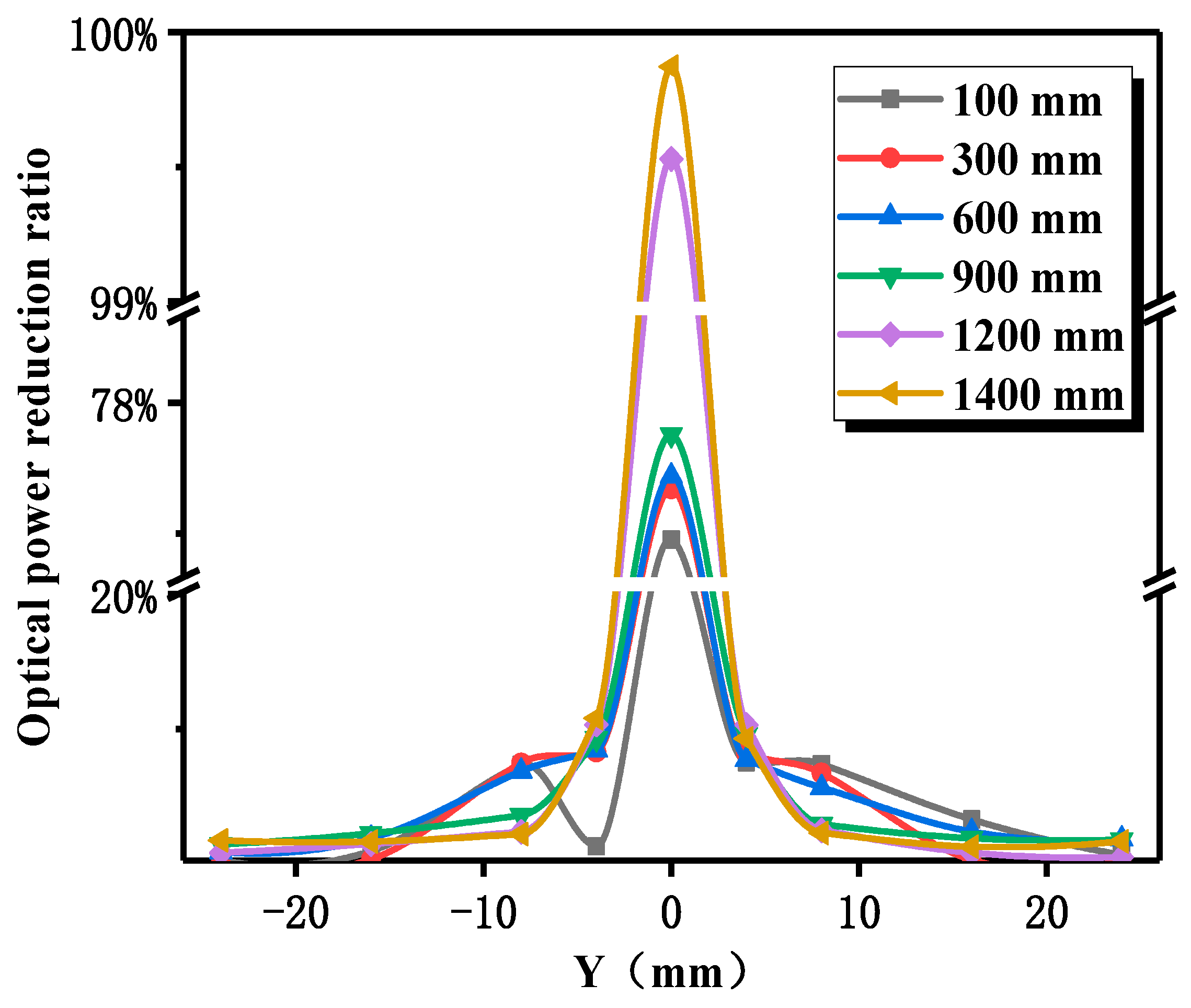When there is no projectile passing through the light screen, the PD receives the optical power as $P_1=1.8228\times {10}^{-4}\mathrm{W}$ after being restricted by the double-layered apertures. Then, the simulation obtains the optical power of the PD detector when the 5.8 mm projectile passes through the light screen at different positions of the dotted line, as shown in Figure 7. The rate of decrease in optical power received by the PD detector relative to $P_1$ when the projectile passes through the light screen at different positions is calculated (the data curve is shown in Figure 8). The characteristics are: (1) Along the Y-axis direction, when the Y-coordinate is 0 mm (the projectile is facing and coaxial with the PD detector), the variation of optical power is the largest and far higher than the position on both sides of the Y-direction, and it decreases rapidly along both sides of Y-direction. (2) The closer the projectile is to the PD detector; the larger the variation of the optical power received by the PD detector; that is, the farther away from the PD detector array in the system, the smaller the detection sensitivity.

Analysis of Figure 8 shows that if the detecting threshold for generating the projectile’s over-target signal is set to 1/5 of the peak voltage (that is, when optical power of the PD detector drops to 1/5 of the peak value), the signal conditioning circuit generates the projectile’s over-target pulse signal. This can reduce the number of PD detectors responding when the projectile passes through the light screen to ensure the effective response of the PD detectors within the error range +2 mm, and can improve the measured accuracy of the projectile’s distributed coordinates.

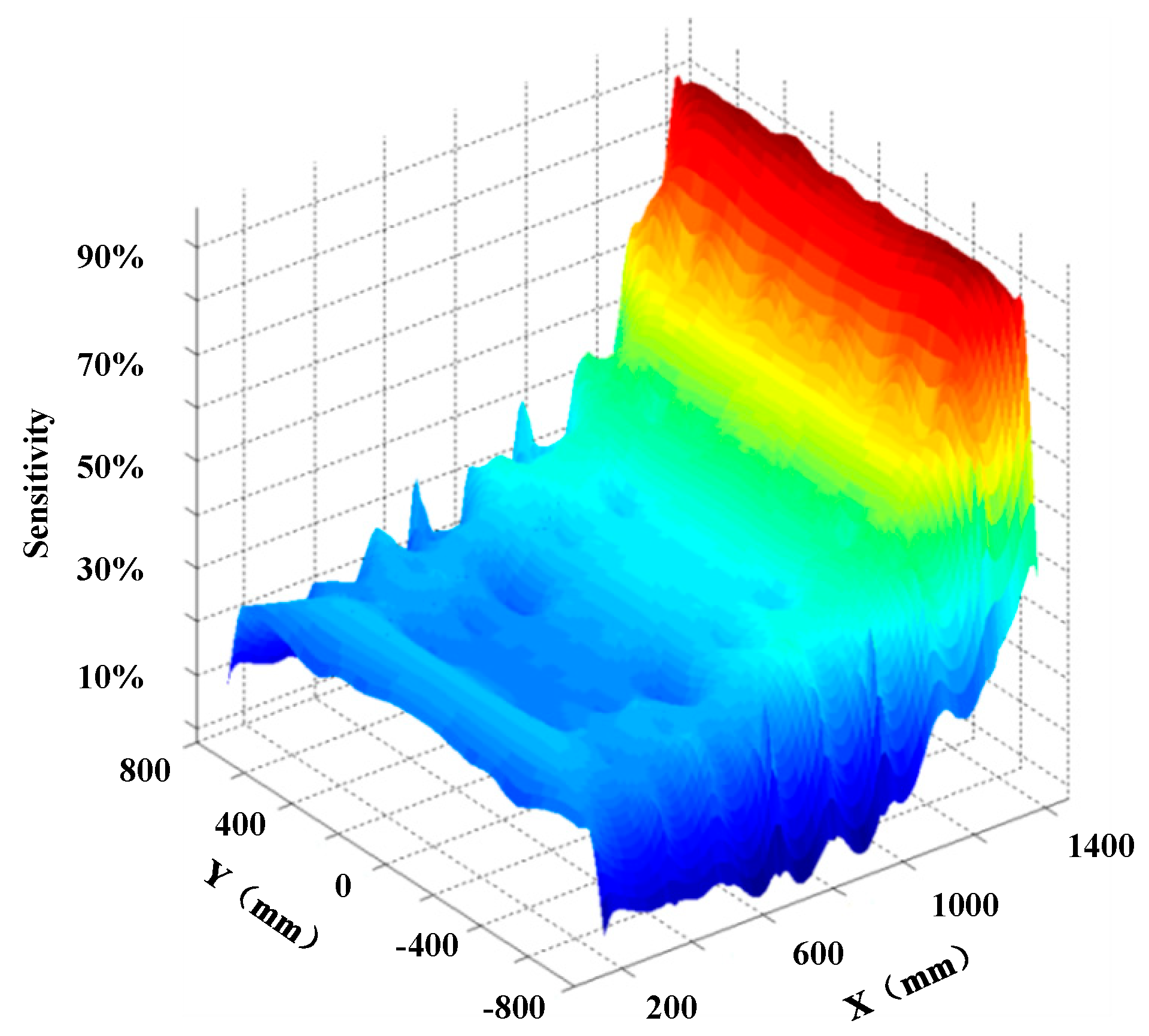
The sensitivity distribution of the effective light screen is drawn according to the percentage of the corresponding optical power variation obtained by the projectile passing through different positions in the light screen. As shown in Figure 9, the detection sensitivity decreases as the distance between the position of the PD and the projectile increases. However, the sensitivity distribution along the Y-axis is mainly uniform at the same distance from the PD detector array. Due to the edge effect of the LED array, the sensitivity at both ends is low. Therefore, in the measuring system, the two ends of the LEDs array should be larger than the effective targeting surface by a certain distance to ensure consistent detecting sensitivity along the Y-axis within the effective targeting surface of the light screen.

5. Adaptive Threshold Circuit

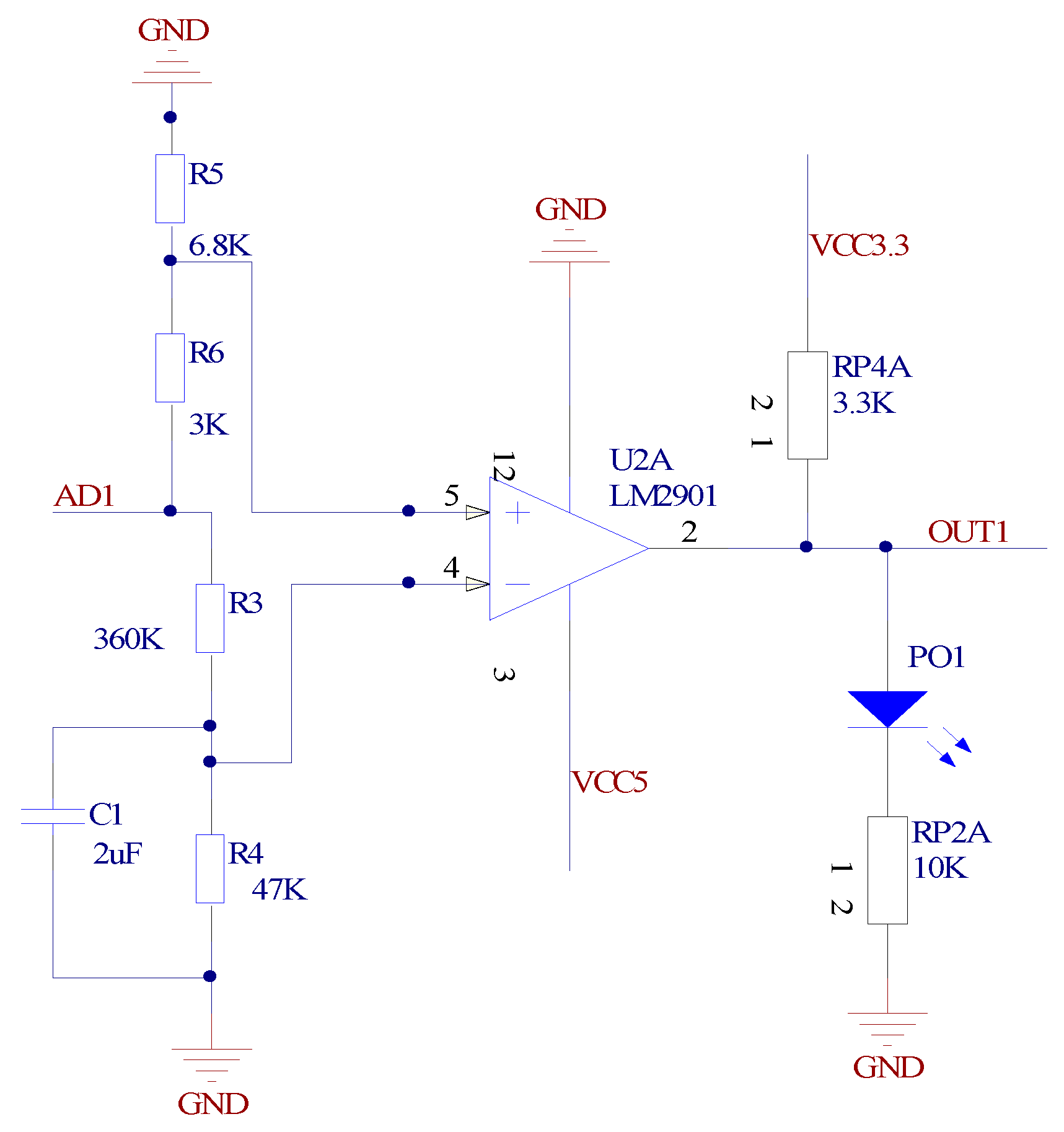
The reliable detection of a projectile’s distributed coordinates depends on the accurate response of the detecting circuit, the fast response speed of the PD detector, and low noise of the detecting circuit. These are effective means to improve the sensitivity of the measuring system. Due to the different sensitivities of thousands of PD detectors, the optical power received by the detectors is also different; setting a fixed detecting threshold in the circuit will affect the discrimination result. Therefore, the adaptive threshold circuit is designed to detect the projectile’s over-target signal, so as to effectively avoid misjudgment when the threshold of the comparison voltage signal is higher than the amplitude of the projectile’s over-target signal.

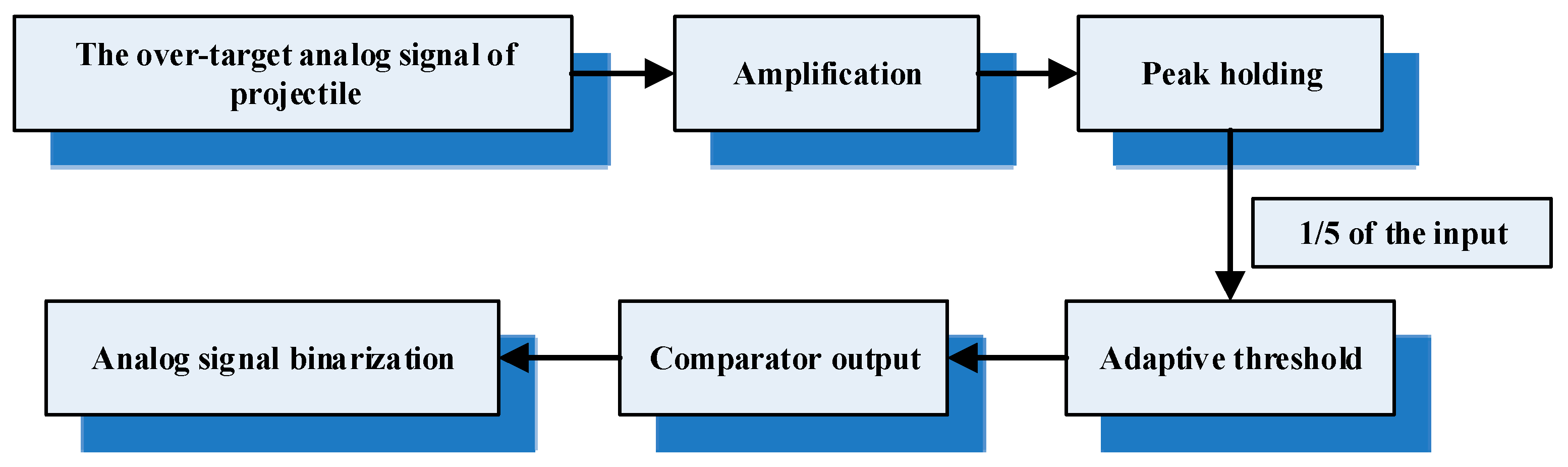
The adaptive threshold circuit converts the changing optical signal into the current signal, which is amplified and shaped into the over-target analog signal of the projectile. After binary processing, the analog signal is converted into a digital pulse signal, which is easy to be processed by FPGA (Field Programmable Gate Array) in the date acquisition module. The design flow is shown in Figure 10 and the circuit for generating the over-target pulse signal is shown in Figure 11.

When no projectile passes through the light screen, the optical power received by the PD detector is converted and amplified to the output of the peak voltage $V_0$. Since the capacitor C₁ has the delay characteristic in charge and discharge, the threshold voltage is kept constant when the projectile passes through the light screen. The threshold voltage $V_T$ at which the output signal of the comparator is inverted by two sets of resistors is:

$$V_T=\frac{R_4/(R_3+R_4)}{R_5/(R_5+R_6)}{V}_0$$

(6)

From Equation (4), it can be seen that the PD detector’s threshold voltage depends on its peak voltage. According to the simulation results in the previous section, the detecting threshold of the projectile’s over-target signal is 1/5 of the PD detector’s peak voltage. When the projectile passes through the light screen and the signal amplitude drops to 4/5 of the peak value, the output signal level of comparator changes from high to low. When the projectile leaves the light screen and the signal amplitude rises to 4/5 of the peak value, the output signal of the comparator is flipped again; thereby it can convert the over-target analog signal of the projectile into the digital pulse signal. The adaptive threshold circuit is shown in Figure 12.

After binary processing, the high level for the projectile’s over-target pulse signal is 3.3 V, and its low level is 0 V. The measuring waveform is shown in Figure 13. Through this circuit, misjudgment is avoided and the measurement accuracy is improved.

6. Experiment

The acquisition daughter board of the system is shown in Figure 14. When the projectile passes through the light screen, it may cause a response from the multiple adjacent detectors; the coordinate identification method is shown in Figure 15. In the X-axis, it is assumed that the projectile passing through the light screen will cause the response of detectors 47–49 in acquisition daughter board 1, while the coordinate of the projectile is: $(200+1\times 4+3\times 4÷2)=210\mathrm{mm}$. The identified method for determining the projectile’s coordinates in the Y-axis is the same.

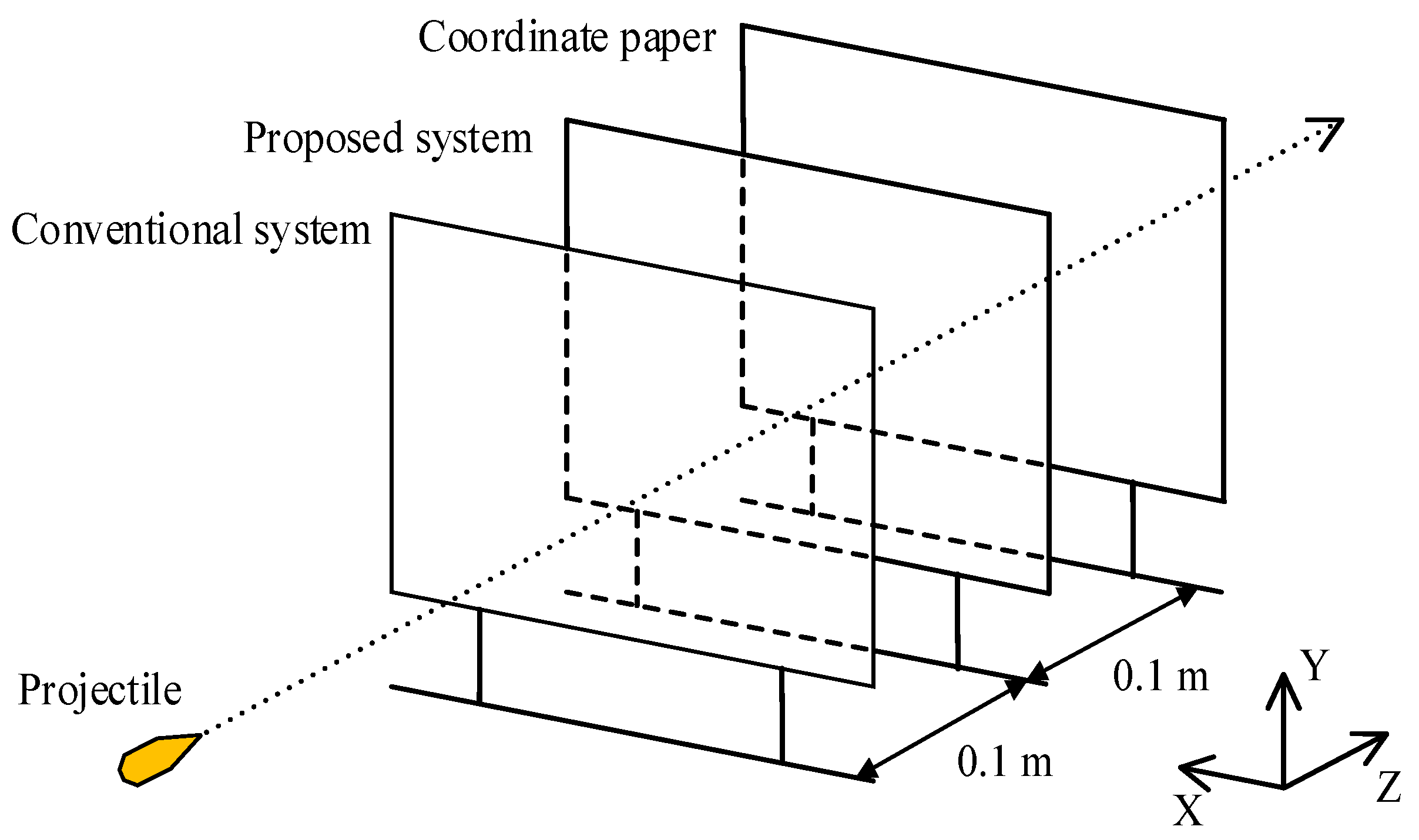
In order to verify the measuring performance of the proposed system, it is compared with a conventional optoelectronic system and a coordinate paper. Among them, the conventional optoelectronic system uses the noncontact optoelectronic measuring method mentioned in the introduction; that is, it uses the optical lens to shape the semiconductor laser with the divergence angle into the parallel light screen and irradiates it into the sensor array to form the measuring light screen. The coordinates of the projectile are measured by the response of the sensor array to the signal produced when the projectile passes through the light screen. The accuracy of the coordinate paper is 0.1 mm, and its measuring result is used as the standard value for comparison with the other two systems in the experiment.

The three methods are installed in the target district in sequence, and the position of the layout is shown in Figure 16. Firstly, coordinate calibration was carried out for the three systems to make sure the coordinate axes of the three methods was unified, and the experiment was carried out using a simulation gun (the diameter of projectile is 5.8 mm). The measuring results of the conventional optoelectronic system and the proposed system were compared with those of the coordinate paper, and the results are shown in

Table 1. Simulated projectile coordinate data.

No.	Position/mm		Position/mm		Position/mm		Error 1/mm		Error 2/mm
	Conventional System		Proposed System		Coordinate Paper
	X-axis	Y-axis	X-axis	Y-axis	X-axis	Y-axis	△x	△y	△x	△y
1	560	784	562	784	562.5	783.2	2.5	−0.8	0.5	−0.8
2	894	548	892	544	891.8	544.3	−2.2	−3.7	−0.2	0.3
3	712	436	710	436	710.9	436.5	−1.1	0.5	0.9	0.5
4	584	734	580	734	580.2	733.8	−3.8	−0.2	0.2	−0.2
5	472	1080	474	1080	474	1078.3	2	−1.7	0	−1.7
6	924	636	922	638	922.5	637.1	−1.5	1.1	0.5	−0.9
7	250	184	250	186	249.7	186.3	−0.3	2.3	−0.3	0.3
8	298	1466	300	1470	300.2	1468.5	2.2	2.5	0.2	−1.5
9	1404	272	1400	274	1401.7	273.6	−2.3	1.6	1.7	−0.4
10	1454	1392	1452	1396	1452.3	1395.5	−1.7	3.5	0.3	−0.5

. Among these, error 1 is the deviation between the measuring coordinates of the conventional system and the measuring coordinates of the coordinate paper, and error 2 is the deviation between the measuring coordinates of the proposed system and the measuring coordinates of the coordinate paper. According to the data in Table 1, the range of the conventional optoelectronic system’s deviation is larger, and its error is within ±4 mm. The standard deviation of X’s coordinates is 0.88 mm, and the standard deviation of Y’s coordinates is 1.14 mm. The range of the proposed system’s deviation is smaller, and its error is less than ±2 mm. The standard deviation of X’s coordinates is 0.47 mm, and the standard deviation of Y’s coordinates is 0.49 mm. The reason for the large fluctuant range of the traditional optoelectronic system’s deviation is speculated to be because the measuring light screen is not completely parallel. The experiment proves that the measuring accuracy of the proposed system is higher than the conventional optoelectronic system

7. Conclusions

This investigation proposed a novel optoelectronic targeting system that combines geometrical optics and electronic circuits. The system can be used to undertake nondestructive and noncontact measuring of distributed projectile coordinates. For projectiles with a diameter greater than 5.8 mm, the measuring error is not more than ±2 mm. Compared with other photoelectric measuring systems of projectile distribution, the optical structure of the proposed system is simple and the materials required by this system are easy to obtain and cost-competitive. Further, it has the advantages of high precision and convenient debugging. The follow-up work of this paper will continue; after transferring the projectile’s coordinates collected by the system to the PC terminal, we will compile the algorithm to display the data frame-by-frame using flash animation. This will provide a more convenient reference for evaluating the performance of weapons.

In the future, the proposed system could further reduce the size of the PD and the spacing between the PDs, increase the number of PD arrays, and achieve higher precision on the basis of satisfying the effective recognition of the projectile’s over-target signal. A larger light screen target will be obtained to meet the measuring requirements of different caliber projectiles. The goal is to develop a measuring system of projectile distribution that can achieve calibration level on a weapons test field.