Optical Image Encryption Using a Nonlinear Joint Transform Correlator and the Collins Diffraction Transform
Abstract
:1. Introduction
2. Collins Diffraction Transform (CDT)
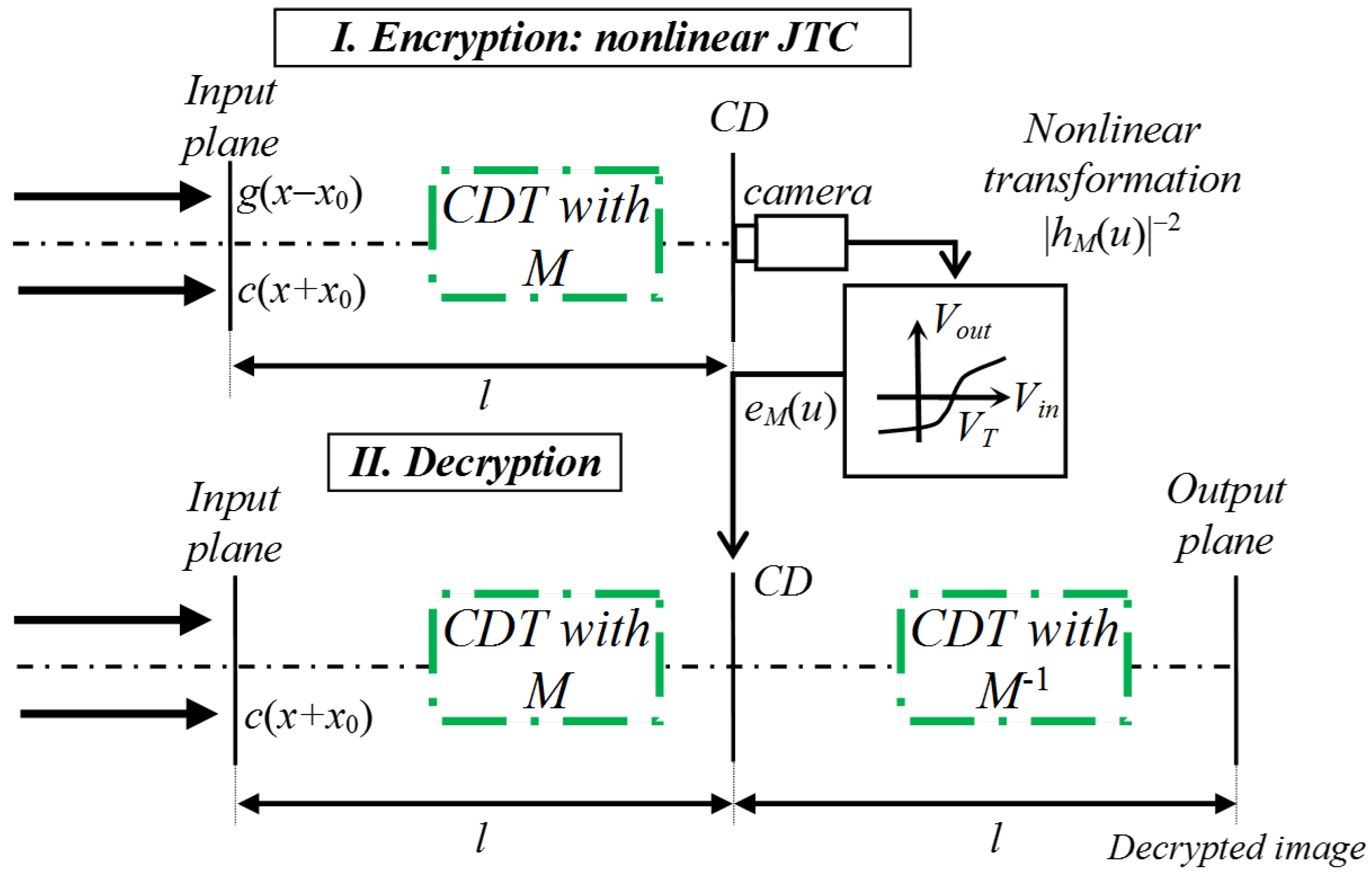
3. Optical Image Encryption System Based on a Nonlinear JTC Architecture in the Collins Diffraction Domain
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Réfrégier, P.; Javidi, B. Optical image encryption based on input plane and Fourier plane random encoding. Opt. Lett. 1995, 20, 767–769. [Google Scholar] [CrossRef] [PubMed]
- Millán, M.S.; Pérez-Cabré, E. Optical data encryption. In Optical and Digital Image Processing: Fundamentals and Applications; Cristóbal, G., Schelkens, P., Thienpont, H., Eds.; Wiley-VCH Verlag GmbH & Co.: Hoboken, NJ, USA, 2011; pp. 739–767. [Google Scholar]
- Javidi, B.; Carnicer, A.; Yamaguchi, M.; Nomura, T.; Pérez-Cabré, E.; Millán, M.; Nishchal, N.; Torroba, R.; Barrera, J.; He, W.; et al. Roadmap on optical security. J. Opt. 2016, 18, 083001. [Google Scholar] [CrossRef]
- Millán, M.S.; Pérez-Cabré, E.; Vilardy, J.M. Nonlinear techniques for secure optical encryption and multifactor authentication. In Advanced Secure Optical Image Processing for Communications; Al Falou, A., Ed.; IOP Publishing: Bristol, UK, 2018; pp. 8-1–8-33. [Google Scholar]
- Matoba, O.; Javidi, B. Encrypted optical memory system using three-dimensional keys in the Fresnel domain. Opt. Lett. 1999, 24, 762–764. [Google Scholar] [CrossRef] [PubMed]
- Situ, G.; Zhang, J. Double random phase encoding in the Fresnel domain. Opt. Lett. 2004, 29, 1584–1586. [Google Scholar] [CrossRef] [PubMed]
- Unnikrishnan, G.; Joseph, J.; Singh, K. Optical encryption by double-random phase encoding in the fractional Fourier domain. Opt. Lett. 2000, 25, 887–889. [Google Scholar] [CrossRef] [PubMed]
- Goodman, J.W. Introduction to Fourier Optics; McGraw-Hill: New York, NY, USA, 1996. [Google Scholar]
- Nomura, T.; Javidi, B. Optical encryption using a joint transform correlator architecture. Opt. Eng. 2000, 39, 2031–2035. [Google Scholar]
- Frauel, Y.; Castro, A.; Naughton, T.J.; Javidi, B. Resistance of the double random phase encryption against various attacks. Opt. Express 2007, 15, 10253–10265. [Google Scholar] [CrossRef]
- Guo, C.; Liu, S.; Sheridan, J.T. Iterative phase retrieval algorithms. Part II: Attacking optical encryption systems. Appl. Opt. 2015, 54, 4709–4719. [Google Scholar] [CrossRef]
- Barrera, J.F.; Vargas, C.; Tebaldi, M.; Torroba, R. Chosen-plaintext attack on a joint transform correlator encrypting system. Opt. Commun. 2010, 283, 3917–3921. [Google Scholar] [CrossRef]
- Barrera, J.F.; Vargas, C.; Tebaldi, M.; Torroba, R.; Bolognini, N. Known-plaintext attack on a joint transform correlator encrypting system. Opt. Lett. 2010, 35, 3553–3555. [Google Scholar] [CrossRef]
- Zhang, C.; Liao, M.; He, W.; Peng, X. Ciphertext-only attack on a joint transform correlator encryption system. Opt. Express 2013, 21, 28523–28530. [Google Scholar] [CrossRef] [PubMed]
- Rueda, E.; Barrera, J.F.; Henao, R.; Torroba, R. Optical encryption with a reference wave in a joint transform correlator architecture. Opt. Commun. 2009, 282, 3243–3249. [Google Scholar] [CrossRef]
- Vilardy, J.M.; Millán, M.S.; Pérez-Cabré, E. Improved decryption quality and security of a joint transform correlator-based encryption system. J. Opt. 2013, 15, 025401. [Google Scholar] [CrossRef]
- Vilardy, J.M.; Millán, M.S.; Pérez-Cabré, E. Nonlinear optical security system based on a joint transform correlator in the Fresnel domain. Appl. Opt. 2014, 53, 1674–1682. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barrera, J.F.; Jaramillo, A.; Vélez, A.; Torroba, R. Experimental analysis of a joint free space cryptosystem. Opt. Lasers Eng. 2016, 83, 126–130. [Google Scholar]
- Vilardy, J.M.; Torres, Y.; Millán, M.S.; Pérez-Cabré, E. Generalized formulation of an encryption system based on a joint transform correlator and fractional Fourier transform. J. Opt. 2014, 16, 125405. [Google Scholar] [CrossRef]
- Vilardy, J.M.; Millán, M.S.; Pérez-Cabré, E. Sistema de cifrado de imágenes basado en un correlador de transformadas conjuntas fraccionario y filtrado no lineal. Ópt. Pura Apl. 2014, 47, 35–41. [Google Scholar] [CrossRef]
- Jaramillo, A.; Barrera, J.F.; Vélez, A.; Torroba, R. Fractional optical cryptographic protocol for data containers in a noise-free multiuser environment. Opt. Lasers Eng. 2018, 102, 119–125. [Google Scholar] [CrossRef]
- Vilardy, J.M.; Millán, M.S.; Pérez-Cabré, E. Nonlinear image encryption using a fully phase nonzero-order joint transform correlator in the Gyrator domain. Opt. Lasers Eng. 2017, 89, 88–94. [Google Scholar] [CrossRef] [Green Version]
- Kwak, C.H.; Javidi, B. Generalized description of double random phase encoding by Collins diffraction transformation. J. Opt. 2019, 21, 015703. [Google Scholar] [CrossRef]
- Kwak, C.H.; Kim, G.Y.; Javidi, B. Volume holographic optical encryption and decryption in photorefractive LiNbO3:Fe crystal. Opt. Commun. 2019, 437, 95–103. [Google Scholar] [CrossRef]
- Collins, S.A. Lens-system diffraction integral written in terms of matrix optics. J. Opt. Soc. Am. 1970, 60, 1168–1177. [Google Scholar] [CrossRef]
- Alieva, T.; Bastiaans, M.J. Properties of the linear canonical integral transformation. J. Opt. Soc. A 2007, 24, 3658–3665. [Google Scholar] [CrossRef] [PubMed]
- Bernardo, L.M. ABCD matrix formalism of fractional Fourier optics. Opt. Eng. 1996, 35, 732–740. [Google Scholar] [CrossRef]
- Healy, J.J.; Kutay, M.A.; Ozaktas, H.M.; Sheridan, J.T. Linear Canonical Transforms: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Ozaktas, H.M.; Zalevsky, Z.; Kutay, M.A. The Fractional Fourier Transform: With Applications in Optics and Signal Processing; Wiley: Hoboken, NJ, USA, 2001. [Google Scholar]
- Rodrigo, J.A.; Alieva, T.; Calvo, M.L. Gyrator transform: Properties and applications. Opt. Express 2007, 15, 2190–2203. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vilardy O., J.M.; Perez, R.A.; Torres M., C.O. Optical Image Encryption Using a Nonlinear Joint Transform Correlator and the Collins Diffraction Transform. Photonics 2019, 6, 115. https://doi.org/10.3390/photonics6040115
Vilardy O. JM, Perez RA, Torres M. CO. Optical Image Encryption Using a Nonlinear Joint Transform Correlator and the Collins Diffraction Transform. Photonics. 2019; 6(4):115. https://doi.org/10.3390/photonics6040115
Chicago/Turabian StyleVilardy O., Juan M., Ronal A. Perez, and Cesar O. Torres M. 2019. "Optical Image Encryption Using a Nonlinear Joint Transform Correlator and the Collins Diffraction Transform" Photonics 6, no. 4: 115. https://doi.org/10.3390/photonics6040115
APA StyleVilardy O., J. M., Perez, R. A., & Torres M., C. O. (2019). Optical Image Encryption Using a Nonlinear Joint Transform Correlator and the Collins Diffraction Transform. Photonics, 6(4), 115. https://doi.org/10.3390/photonics6040115




