Excitation Schemes of Plasmonic Angular Ring Resonator-Based Band-Pass Filters Using a MIM Waveguide
Abstract
:1. Introduction
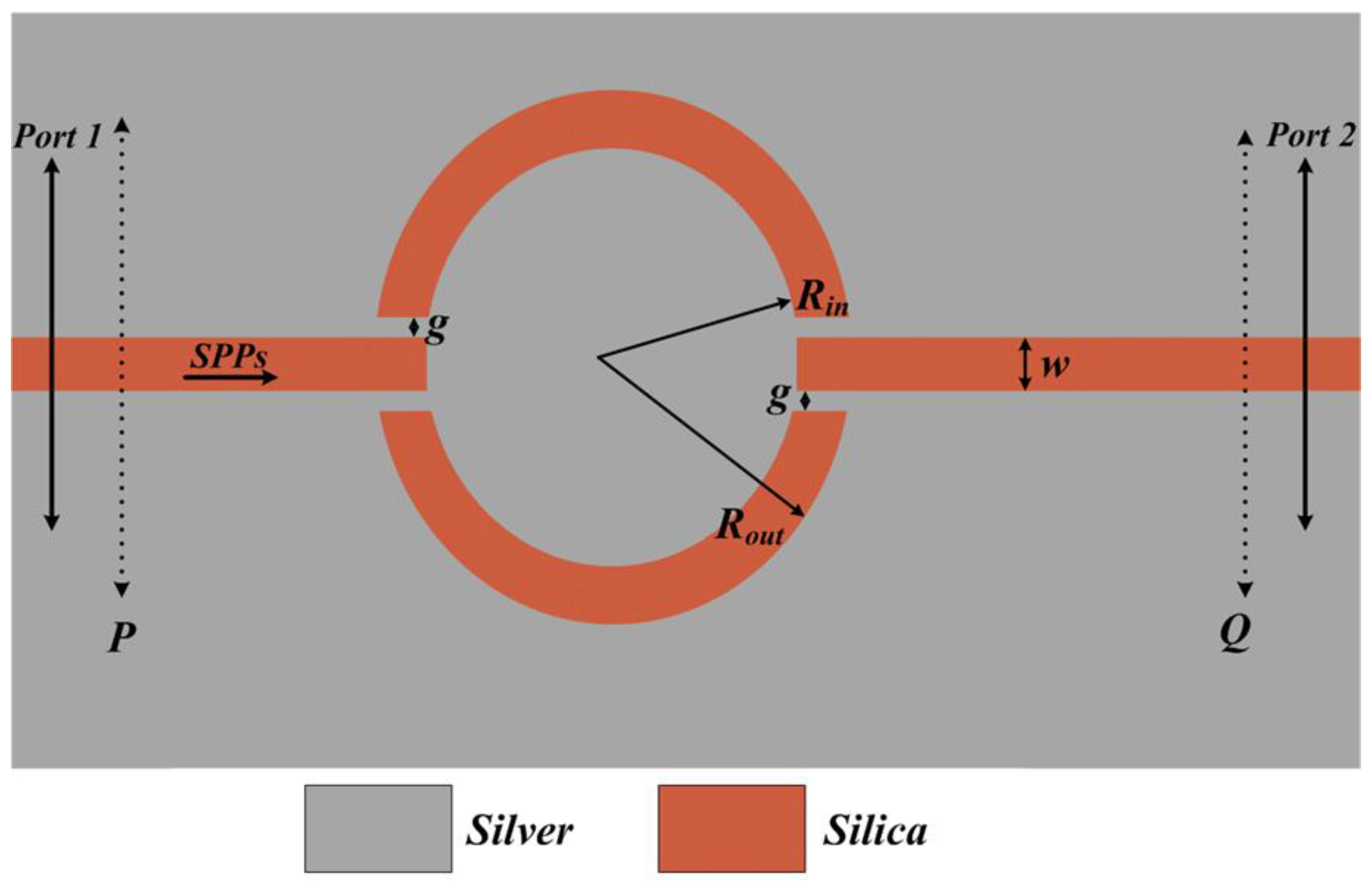
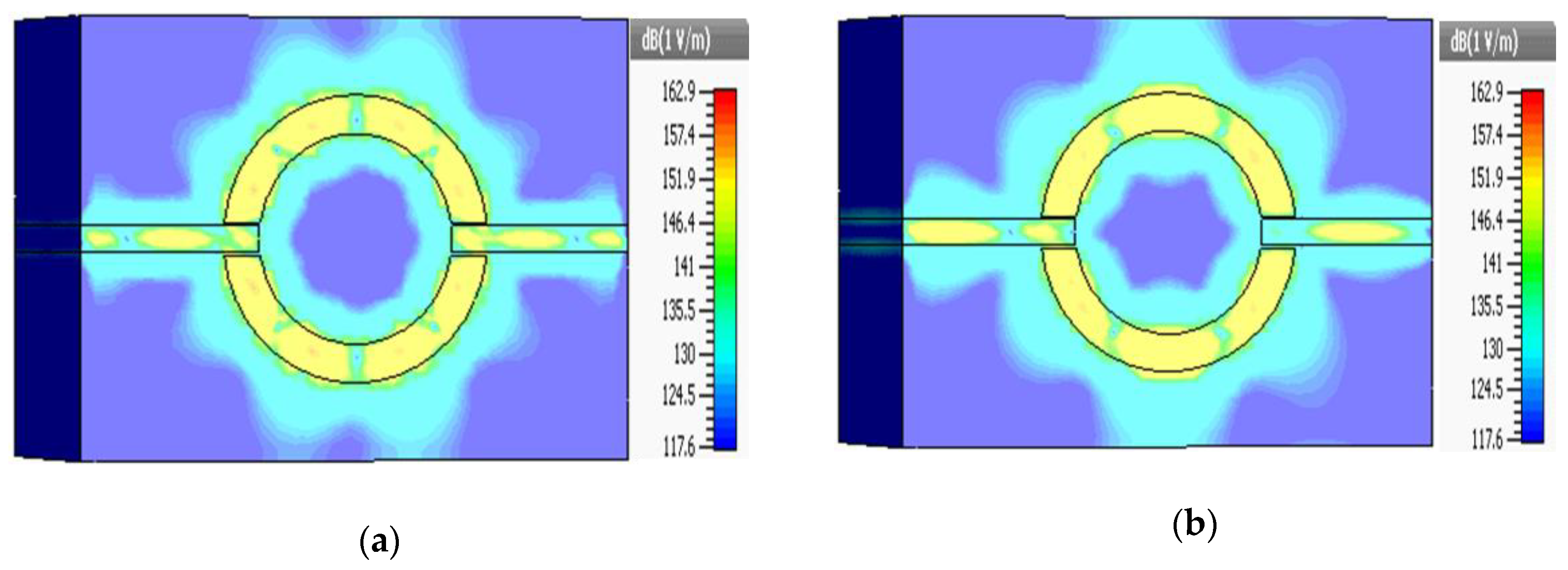
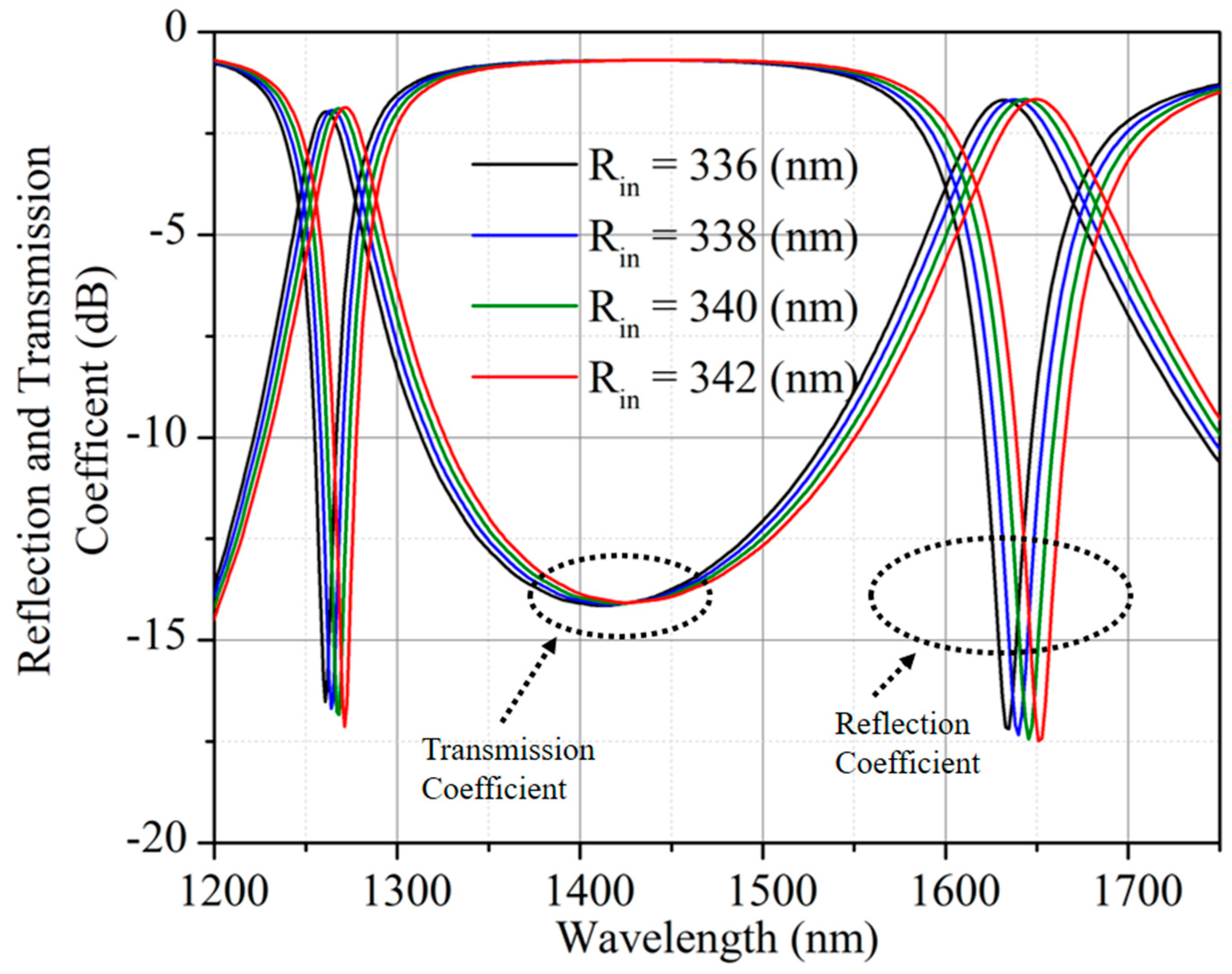
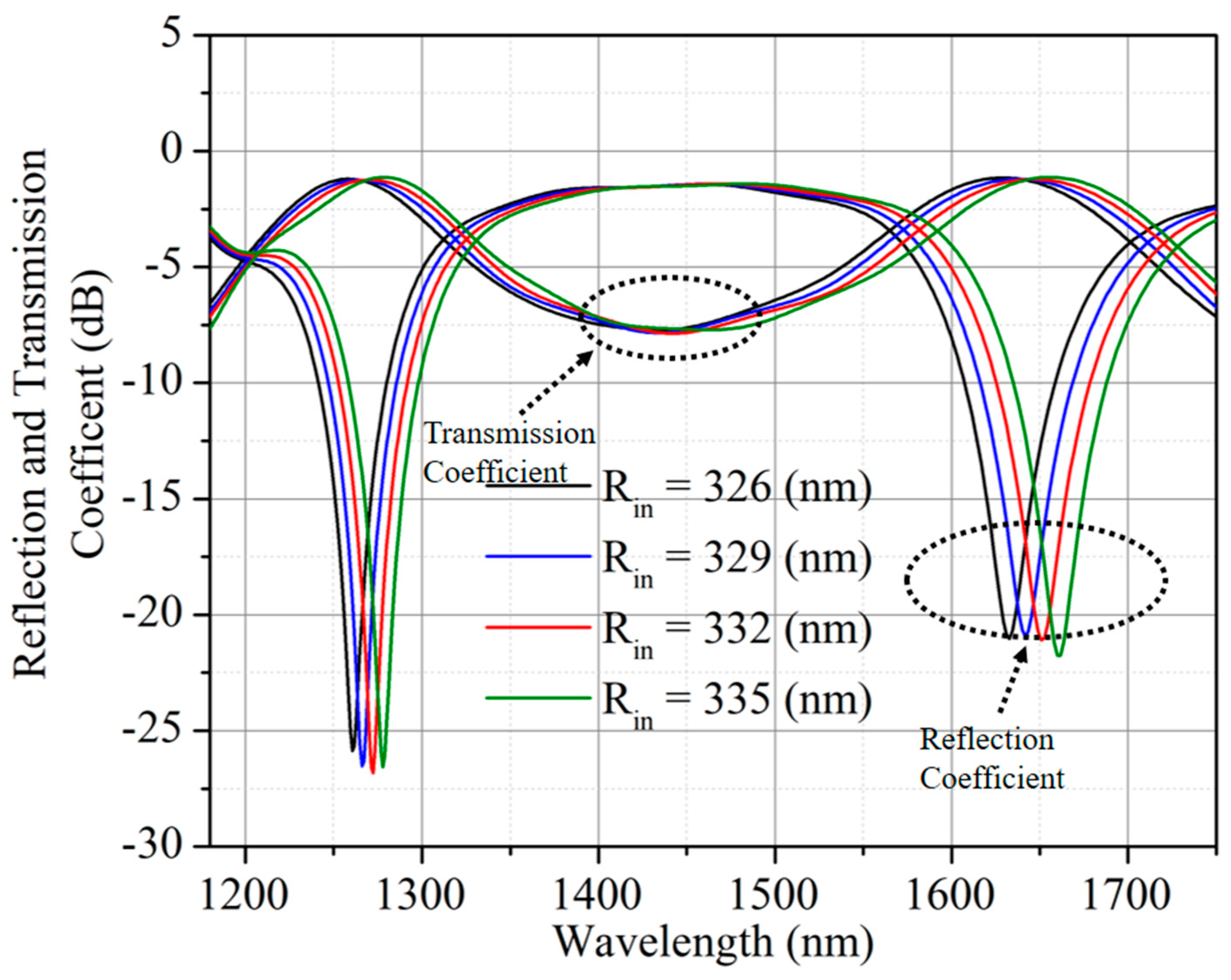
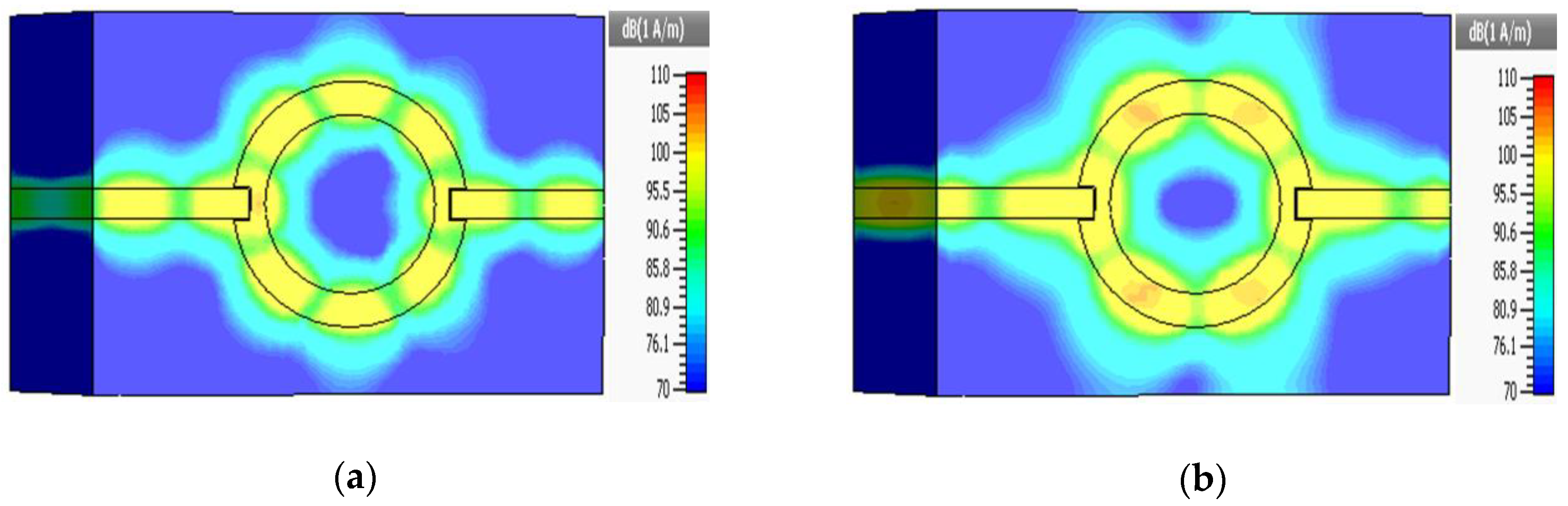
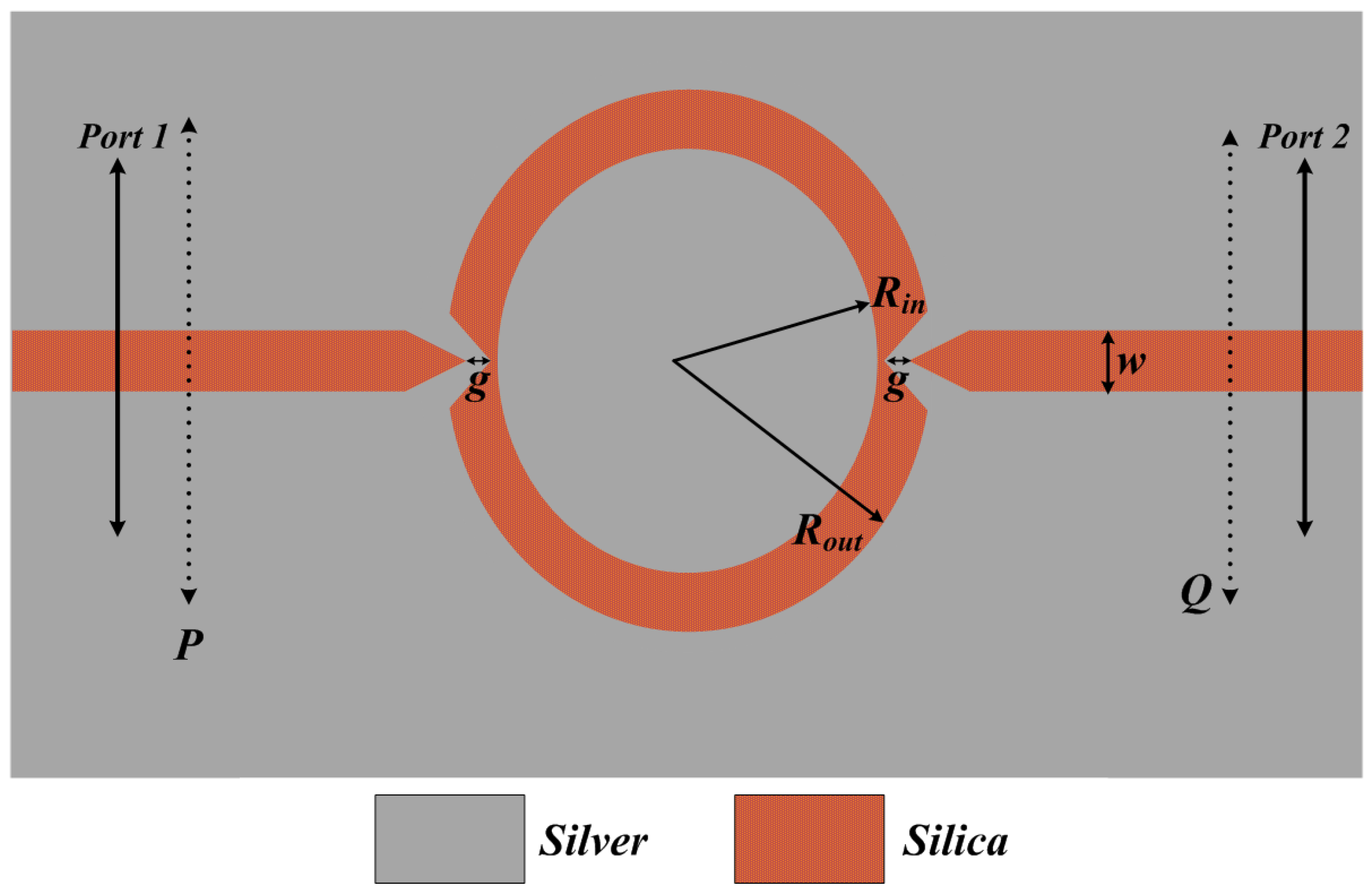
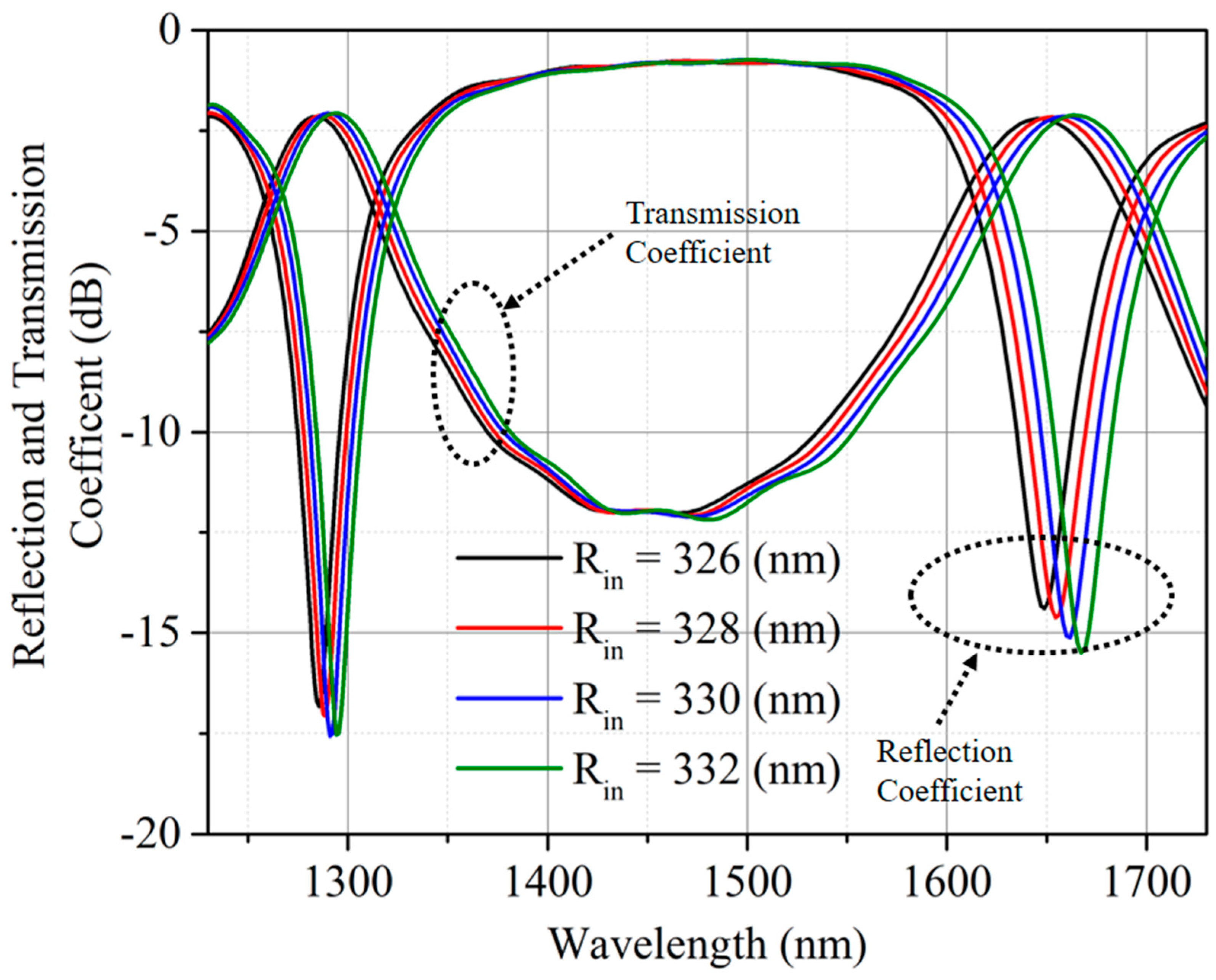
2. Geometry and Operation of Angular Ring Resonator (A) Using MIM Waveguide
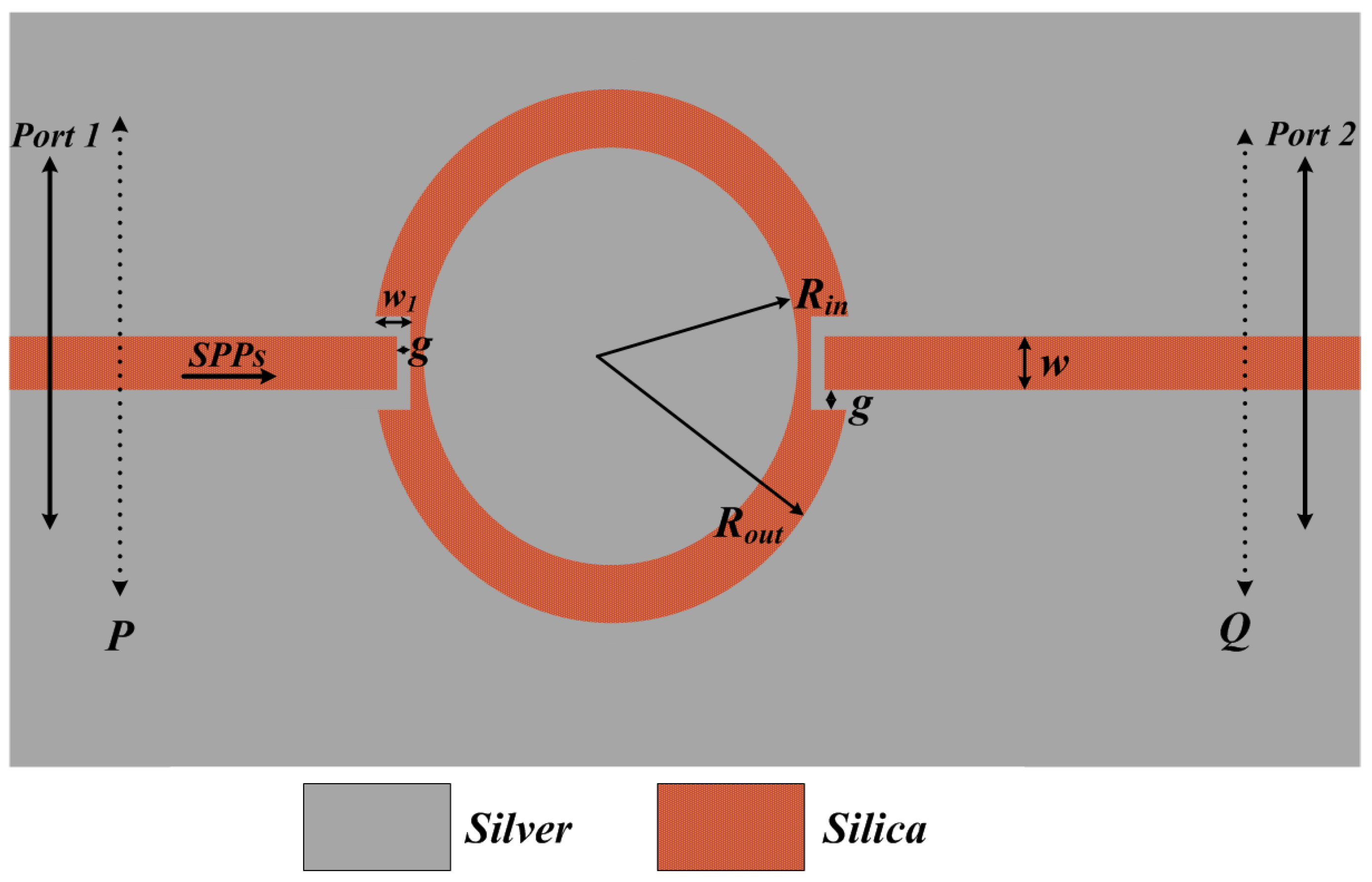
3. Geometry and Operation of Angular Ring Resonator (B) Using MIM Waveguide
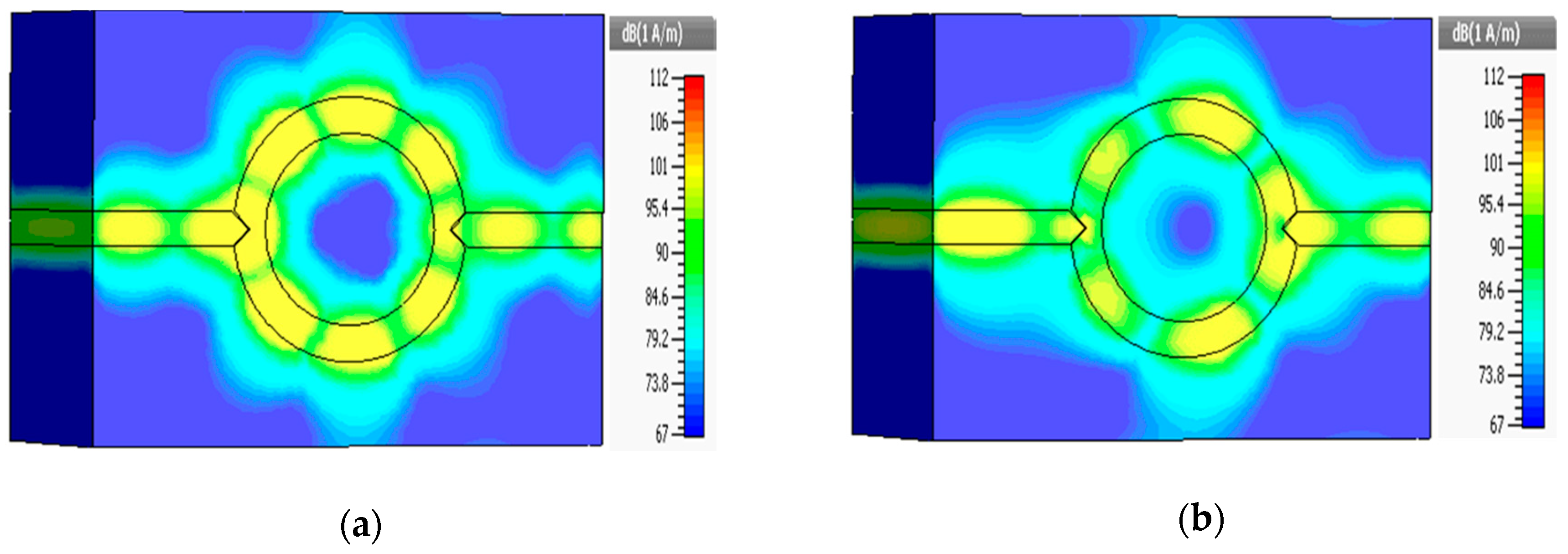
4. Geometry and Operation of Angular Ring Resonator (C) Using MIM Waveguide
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tang, L.; Latif, S.; Miller, D.B. Plasmonic device in Si CMOS. In Proceedings of the LEOS 2008 21st Annual Meeting of the IEEE Lasers and Electro-Optics Society, Acapulco, Mexico, 9–13 November 2008; pp. 139–140. [Google Scholar]
- Duan, H.; Dominguez, A.I.F.; Bosman, M.; Maier, S.A.; Yang, J.K.W. Nanoplasmonics: Classical down to the Nanometer Scale. Nano Lett. 2012, 12, 1683–1689. [Google Scholar] [CrossRef] [PubMed]
- Onbasli, M.C.; Okyay, A.K. Nanoantenna Couplers for Metal-Insulator-Metal Waveguide Interconnects. In Proceedings of the SPIE, San Diego, CA, USA, 10 September 2010; Volume 7757, p. 77573R-1-11. [Google Scholar]
- Barnes, W.L.; Dereux, A.; Ebbesen, T.W. Surface plasmon subwavelength optics. Nature 2003, 424, 824–830. [Google Scholar] [CrossRef] [PubMed]
- Conway, J.A.; Sahni, S.; Szkopek, T. Plasmonic interconnects versus conventional interconnects: A comparison of latency, crosstalk and energy costs. Opt. Express 2007, 15, 4474–4484. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.H.; Wang, Q.J.; Shum, P.; Huang, X.G. A Simple Nanometeric Plasmonic Narrow-Band Filter Structure Based on Metal-Insulator-Metal Waveguide. IEEE Trans. Nanotechnol. 2011, 10, 1371–1376. [Google Scholar] [CrossRef]
- Chityala, R.K. Nanoplasmonic concurrent dual-band antennas using metal-insulator-metal step impedance resonators. Microw. Opt. Technol. Lett. 2019. [Google Scholar] [CrossRef]
- Masashi, M.; Akira, K.; Yusuke, N.; Junichi, T. Electromechanically Tunable Plasmonic Nanowires Operating in Visible Wavelengths. ACS Photonics 2016, 3, 2268–2274. [Google Scholar]
- Randhawa, S.; Krasavin, A.V.; Holmgaard, T.; Renger, J.; Bozhevolnyi, S.I.; Zayats, A.V.; Quidant, R. Experimental demonstration of dielectric-loaded plasmonic waveguide disk resonators at telecom wavelengths Experimental demonstration of dielectric-loaded plasmonic waveguide disk resonators at telecom wavelengths. Appl. Phys. Lett. 2011, 98, 161102. [Google Scholar] [CrossRef]
- Smith, C.L.C.; Stenger, N.; Kristensen, A.; Mortensen, N.A. Gap and channeled plasmons in tapered grooves: A review. R. Soc. Chem. 2015, 7, 79–82. [Google Scholar] [CrossRef] [PubMed]
- Veronis, G.; Fan, S.; Veronis, G.; Fan, S. Bends and splitters in metal-dielectric-metal subwavelength plasmonic waveguides Bends and splitters in metal-dielectric-metal subwavelength plasmonic waveguides. Appl. Phys. Lett. 2005, 87, 131102. [Google Scholar] [CrossRef]
- Liu, D.; Wang, J.; Zhang, F.; Pan, Y.; Lu, J.; Ni, X. Tunable Plasmonic Band-Pass Filter with Dual Side-Coupled Circular Ring Resonators. Sensors 2017, 17, 585. [Google Scholar] [CrossRef] [PubMed]
- Lezec, H.J.; Degiron, A.; Devaux, E.; Linke, R.A.; Martin-Moreno, L.; Garcia-Vidal, F.J.; Ebbesen, T.W. Beaming light from a subwavelength aperture. Science 2002, 297, 820–822. [Google Scholar] [CrossRef] [PubMed]
- Pile, D.F.P.; Gramotnev, D.K. Plasmonic subwavelength waveguides: Next to zero losses at sharp bends. Opt. Lett. 2005, 30, 1186–1188. [Google Scholar] [CrossRef] [PubMed]
- Taylor, P.; Li, C.; Qi, D.; Xin, J.; Hao, F. Metal-insulator-metal plasmonic waveguide for low- distortion slow light at telecom frequencies. J. Modern Opt. 2014, 61, 37–41. [Google Scholar]
- Fitrakis, E.P.; Kamalakis, T. Slow-light dark solitons in insulator-insulator-metal plasmonic waveguides. J. Opt. Soc. Am. B 2010, 27, 1071–1076. [Google Scholar] [CrossRef]
- Li, M.; Pernice, W.H.P.; Xiong, C.; Hochberg, M.; Tang, H.X. Harnessing optical forces in integrated photonic circuits. Nat. Lett. 2008, 456, 480–484. [Google Scholar] [CrossRef] [PubMed]
- Gopalakrishnan, G.K.; Chang, K. Novel excitation schemes for the microstrip ring resonator with lower insertion loss. Electron. Lett. 1994, 30, 148–149. [Google Scholar] [CrossRef]
- Vishwanath, M.; Khan, H.; Thirupathaiah, K. Concurrent dual-band filters using plasmonic MIM waveguide ring resonator. ARPN J. Eng. Appl. Sci. 2018, 13, 1813–1818. [Google Scholar]
- Rahman, M.Z.U.; Krishna, K.M.; Reddy, K.K.; Babu, M.V.; Mirza, S.S.; Fathima, S.Y. Ultra-Wide-Band Band-Pass Filters Using Plasmonic MIM Waveguide-Based Ring Resonators. IEEE Photonics Technol. Lett. 2018, 30, 1715–1718. [Google Scholar] [CrossRef]
- Palik, E.D. Handbook of Optical Constants of Solids; Academic Press: New York, NY, USA, 1985. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mittapalli, V.; Khan, H. Excitation Schemes of Plasmonic Angular Ring Resonator-Based Band-Pass Filters Using a MIM Waveguide. Photonics 2019, 6, 41. https://doi.org/10.3390/photonics6020041
Mittapalli V, Khan H. Excitation Schemes of Plasmonic Angular Ring Resonator-Based Band-Pass Filters Using a MIM Waveguide. Photonics. 2019; 6(2):41. https://doi.org/10.3390/photonics6020041
Chicago/Turabian StyleMittapalli, Vishwanath, and Habibulla Khan. 2019. "Excitation Schemes of Plasmonic Angular Ring Resonator-Based Band-Pass Filters Using a MIM Waveguide" Photonics 6, no. 2: 41. https://doi.org/10.3390/photonics6020041
APA StyleMittapalli, V., & Khan, H. (2019). Excitation Schemes of Plasmonic Angular Ring Resonator-Based Band-Pass Filters Using a MIM Waveguide. Photonics, 6(2), 41. https://doi.org/10.3390/photonics6020041




