Modeling of Ultra-Long Span Bidirectional Raman Transmission Link Using Three-Segment Hybrid Fiber Core Structure

Abstract

Ultra-long span unrepeatered systems using distributed Raman amplification are cost-effective solutions for bridging moderate transmission distances. However, there are two major limiting factors: nonlinear Kerr effect-induced nonlinear signal distortion and optical signal-to-noise ratio degradation due to spontaneous Raman noise. In this report, we proposed a model of three-segment hybrid fiber effective core area structure and developed a model covering: (1) generalized mathematical formulations, (2) analysis of three-segment Raman amplified link, and (3) simulation model of data transmission. The proposed model showed an improvement of the Raman gain profile, a reduction of the negative impact of the nonlinear Kerr effect, and an enhancement of the optical signal-to-noise ratio. A numerical simulation of the transmission performance of the three-segment hybrid structure was compared to conventional single-segment single fiber core structure on 80 Gb/s differential quadrature phase-shift keying (DQPSK) modulated data signals over a propagation distance of 390 km. The required optical signal-to-noise ratio was reduced by 2.71 dB to achieve the target error rate without using forward error correction. The numerical model and simulation of various data rates up to 100 Gb/s consistently showed that an improvement in transmission performance could be achieved by using three-segment hybrid fiber effective core area structure.

1. Introduction

Over the years, there has been continual exponential growth in the demand for optical fiber transmission for applications in the areas of inter-island hopping and coastal festoon systems; additionally, the use of single ultra-long span terrestrial links in the range of several hundred kilometers is rising. Over medium-range transmission distances, ultra-long span unrepeatered systems that use distributed Raman amplification represent an uncomplicated and cost-effective solution that does not require in-line active components. Improvements in fiber optic core design and material characteristics [1], including the availability of large effective core area fibers [2] and very-low loss fibers [3], have enhanced the transmission performance and extended the propagation distance of unrepeatered systems without additional in-line active devices.

In order to restore signal power at the receiver end after propagating several hundred kilometers, unrepeatered ultra-long single-span systems require high Raman gains in both forward and backward directions to compensate for very large accumulated fiber attenuation [4,5]. There are two major limiting factors in such systems: the first factor is nonlinear Kerr effect-induced nonlinearity, such as self-phase modulation in a single-channel systems, cross-phase modulation, and four-wave mixing for a multi-channel systems; the second factor is optical signal-to-noise ratio (OSNR) degradation due to spontaneous Raman noise accumulation caused by high Raman pump power from both the forward and backward directions [6,7].

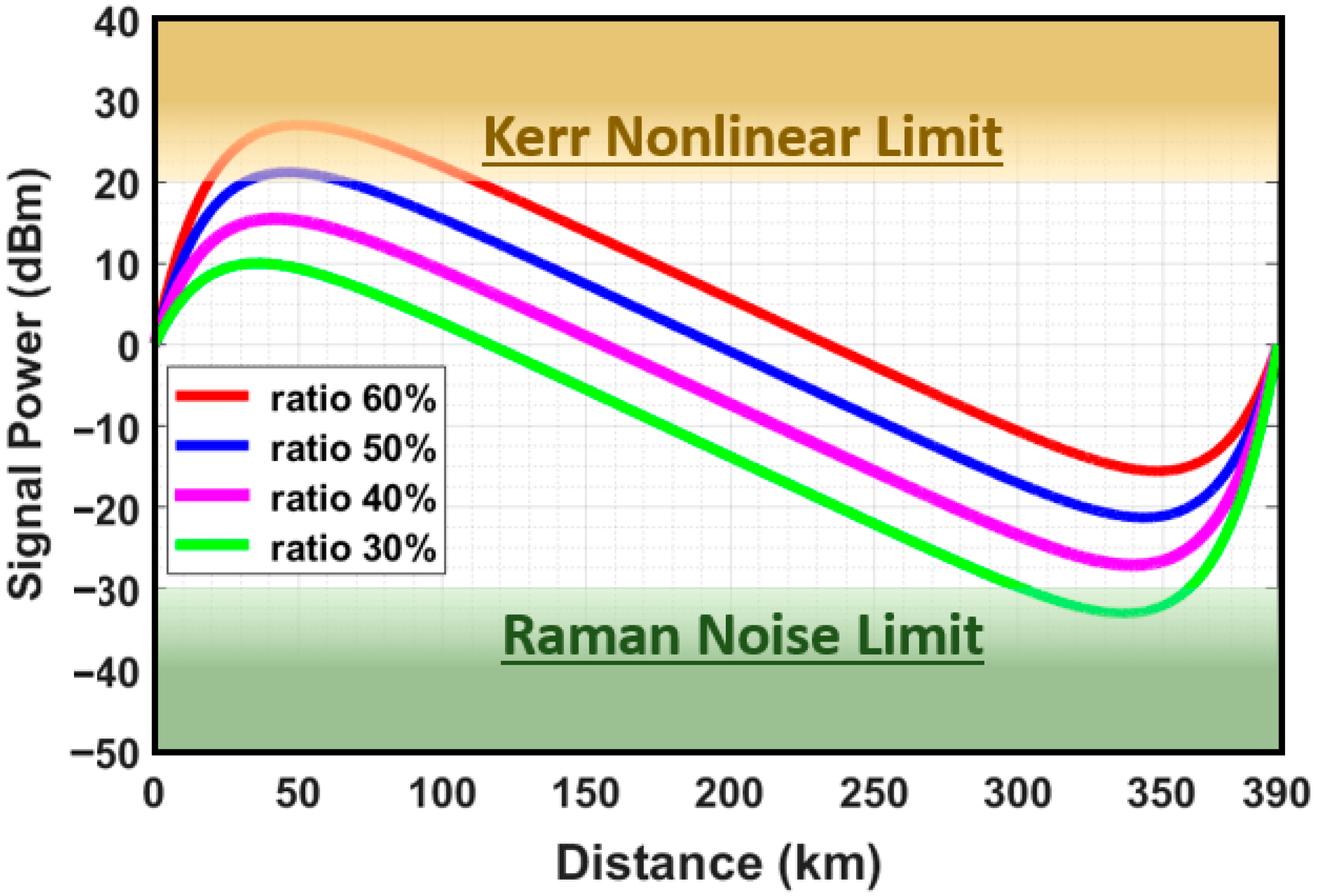
Figure 1 illustrates the typical profile of signal power transmission along an ultra-long span based on [8] with modifications and recalculations for various pump power ratios over a very-long span length (in this case 390 km); additional details will be provided in the following sections. Figure 1 also shows the upper and lower signal power boundaries as two limiting factors that need to be addressed to improve transmission quality and provide an achievable propagation distance. The change of pump power ratio, which is the ratio between the forward pump power over the total pump power, will only shift the signal power profile in the vertical-axis direction, which means a trade-off between the Kerr nonlinear limit and the Raman noise limit will still exist. Therefore, to improve transmission performance, a solution that can modify the gain profile of bidirectional distributed Raman amplification and simultaneously reduce the Kerr nonlinear limit and the Raman noise limit is required.

In this article, a hybrid fiber effective core area consisting of a three-segment structure is proposed as an alternative to the conventional single fiber effective core area in a single-segment structure. The introduction of a three-segment hybrid fiber effective core area is expected to increase flexibility in the Raman gain profile structure, reduce the negative impact of the nonlinear Kerr effect due to high signal power, and improve the OSNR by means of the reduction of Raman optical pump-induced amplified spontaneous emissions. In order to directly analyze the influence of the two factors, we built an analytical model covering mathematical formulation, analysis of bidirectional Raman amplification, and data transmission simulation on various data rates. The current model using a single-channel signal amplified by single-wavelength Raman pumps, which can be expanded to a multi-channel and multi-wavelength Raman pumps system based on the same principle.

The system design for the overall length is based on the previous reports on the ultra-long span systems. The span configuration without an in-line active device has been reported as over 304 [2], 333.6 [9], and 365 km [3] for various bit rates. The span configuration with in-line active support has been reported as over 402 km [10] using in-line remote optically pumped amplifier (ROPA), and as over 500 km [11] using parallel fibers for pump power delivery. Since our objective is to design an ultra-long span system without an in-line active device, a reasonable target distance would be between 365 and 402 km. This target distance shows improvement over the results of previous studies on cases span configuration without in-line active devices and approaching the results on cases span configuration with in-line active devices. Our preliminary analytical model on unrepeatered ultra-long span system using a bidirectional pumped distributed Raman amplifier was described in [12], the impact of the size of the fiber effective core area on the transmission performance was analyzed in [13], and the transmission simulation of various data rates was reported in [14]. Our previous report [14] showed the simulation results for an overall 390-km length DBPSK-modulated signal on the conventional single-segment single fiber effective core area structure. Therefore, in this article, we use a 390-km span length and explore the benefits of using a three-segment hybrid fiber effective core area structure, and we extend the transmission capacity by using DQPSK-modulated signals.

The proposed three-segment hybrid fiber core structure is an alternative option as a simple solution for the deployment of a new transmission link in a green field but will have high costs for upgrading from existing fiber links. Other solutions commonly used to overcome fiber nonlinearity in ultra-long span system are high-order (second-order or third-order) distributed Raman amplification schemes that have the ability to deliver Raman pump power that penetrates deeper into the fiber along the transmission link. As reported in [15], the optical signal is counter-directionally amplified by a powerful third-order Raman fiber laser (RFL) located at the receiver side. In the experiment, the RFL delivers 4.9 W at 1276 nm as the primary pump wavelength. The pump energy is transferred from the initial wavelength to a band around 1360 nm and then to 1425 and 1455 nm as amplification wavelength along the fiber transmission line through a cascaded Raman amplification scheme. In this backward pump configuration, the optical pump power at 1425 and 1455 nm provides 27 dB Raman gain to the optical signal. Using a backward pumping only configuration has a drawback on the increase in signal power variation and noise. As reported in [16], the experimental results show that bi-directionally pumped second-order Raman amplification scheme based on a random distributed feedback (DFB) fiber laser configuration can achieve low signal power variation and improves transmission performance compared to conventional Raman amplification schemes. There is no relative intensity noise (RIN) increase on the signal using this scheme even with bidirectional pumping.

Another technology enabling extended reach is remote amplification. Recent experimental work [17] has shown that single-carrier 400 Gb/s unrepeatered transmission can achieve 443.1 km by using bidirectional pumping remote optically pumped amplifiers (ROPAs) supported by parallel fibers for pump power delivery. ROPA is typically placed 60 to 140 km away from the receive site and also transmit side in some cases. The addition of a ROPA within the span at a distance from the Raman pumps improves the OSNR significantly and reduce the signal power variation along the fiber where the signal power is very low near the receiving end. In a conventional configuration, the energy necessary for creating optical amplification is brought to the ROPA by optical pump waves launched backward into the line fiber from the receiving end. Actually, this is the residual pump power that was not consumed to build the distributed Raman gain inside the line fiber that is used to pump the ROPAs. In an extreme configuration, extra fiber parallel to the transmission line fiber within the same cable can be dedicated to the sole purpose of transporting the optical Raman pumps from the terminal end to the ROPAs.

Finally, the transmission performance of an unrepeatered ultra-long span system over a transmission distance of 390-km will be evaluated using numerical simulation. The bit error rate (BER) performance improvement of the three-segment hybrid fiber effective core area configuration compared to the conventional single fiber effective core area is examined on various high transmission data rates using a differential quadrature phase-shift keying (DQPSK) modulation format to double the spectrum efficiency, and a noncoherent direct-detection scheme to simplify the receiver design [18]. The availability of silicon (Si) photonics [19], hybrid photonic integration platform [20], and monolithically integrated InP transmitter that include laser source [21] increase the cost-effectiveness of the combination DQPSK modulation format and noncoherent direct-detection scheme, which is a compact solution compared to complex coherent detection techniques [22] for single span applications.

The rest of this paper is structured as follows. In Section 2, we derive the generalized Raman amplification formulas where the fiber effective core area is no longer a constant value but a function of propagation distance by modifying the procedure of the standard Raman amplification formulas [1,4,5]. In Section 3, we explain that the reduction of nonlinear phase shift and the improvements of OSNR can be achieved simultaneously by implementing three-segment hybrid fiber core structure. In Section 4, we simulate the transmission performance of the three-segment hybrid structure and compare to the conventional single-segment single fiber core structure on 80 Gb/s and various data rate of DQPSK modulated data signals over a propagation distance of 390 km. Finally, we conclude the article in Section 5.

2. Modeling of Generalized Mathematical Formulas for Multi-Segment Transmission Link

In order to provide proper gain to overcome fiber attenuation and improve the noise performance of the optical transmission system, distributed Raman amplification has many advantages compared to conventional lump amplification, such as with erbium-doped fiber amplifiers or semiconductor optical amplifiers [1]. Distributed Raman amplifications can be placed on the transmitter side to work as forward pumped configurations and on the receiver side to work as backward pumped configurations. A bidirectional pumped configuration can be constructed by combining both forward and backward pumped configurations. The Raman gain depends primarily on the material and the optical characteristics of the transmission fibers, such as the Raman gain coefficient, the size of the effective core area, and the attenuation at the signal and pump wavelengths [4,5].

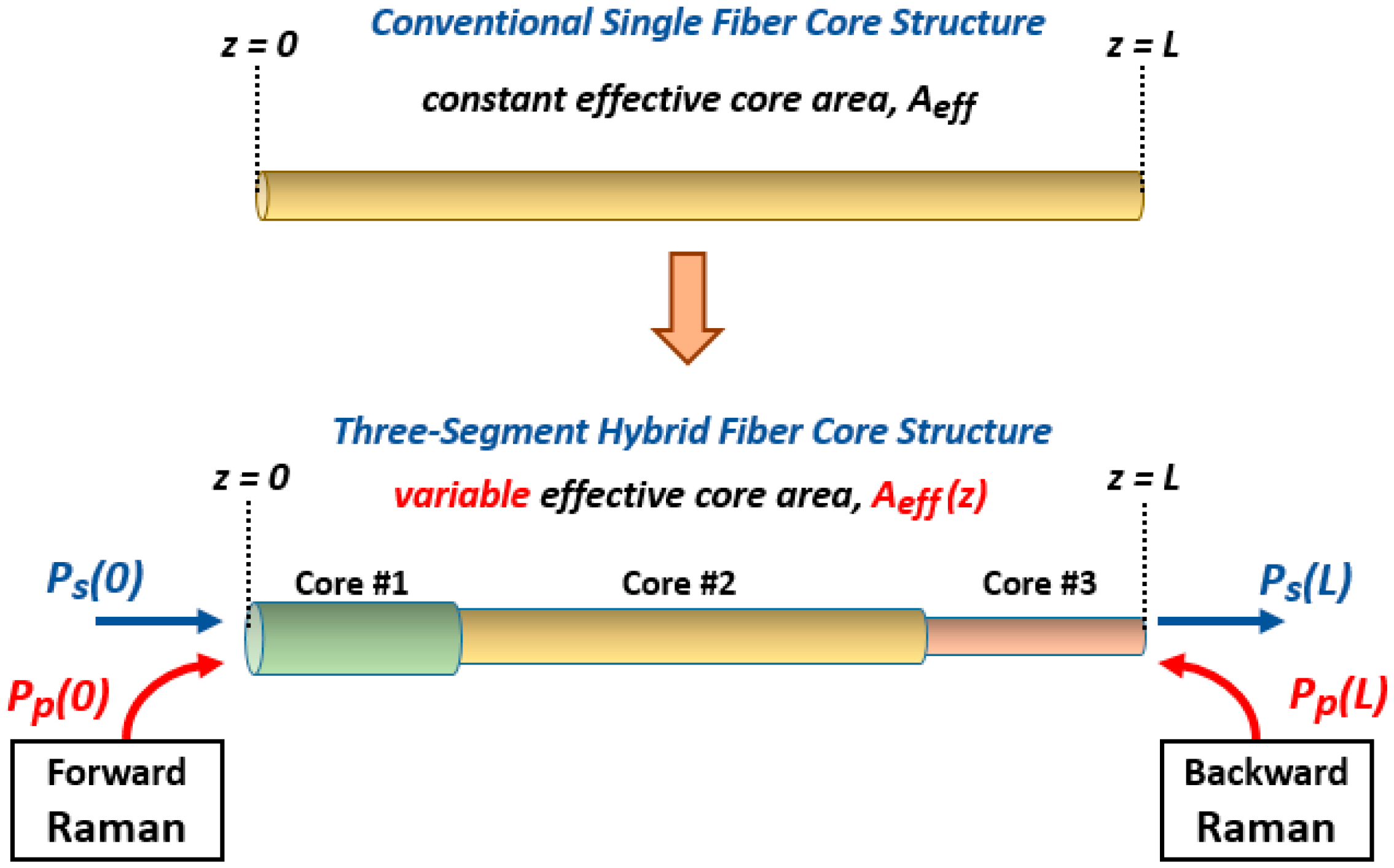
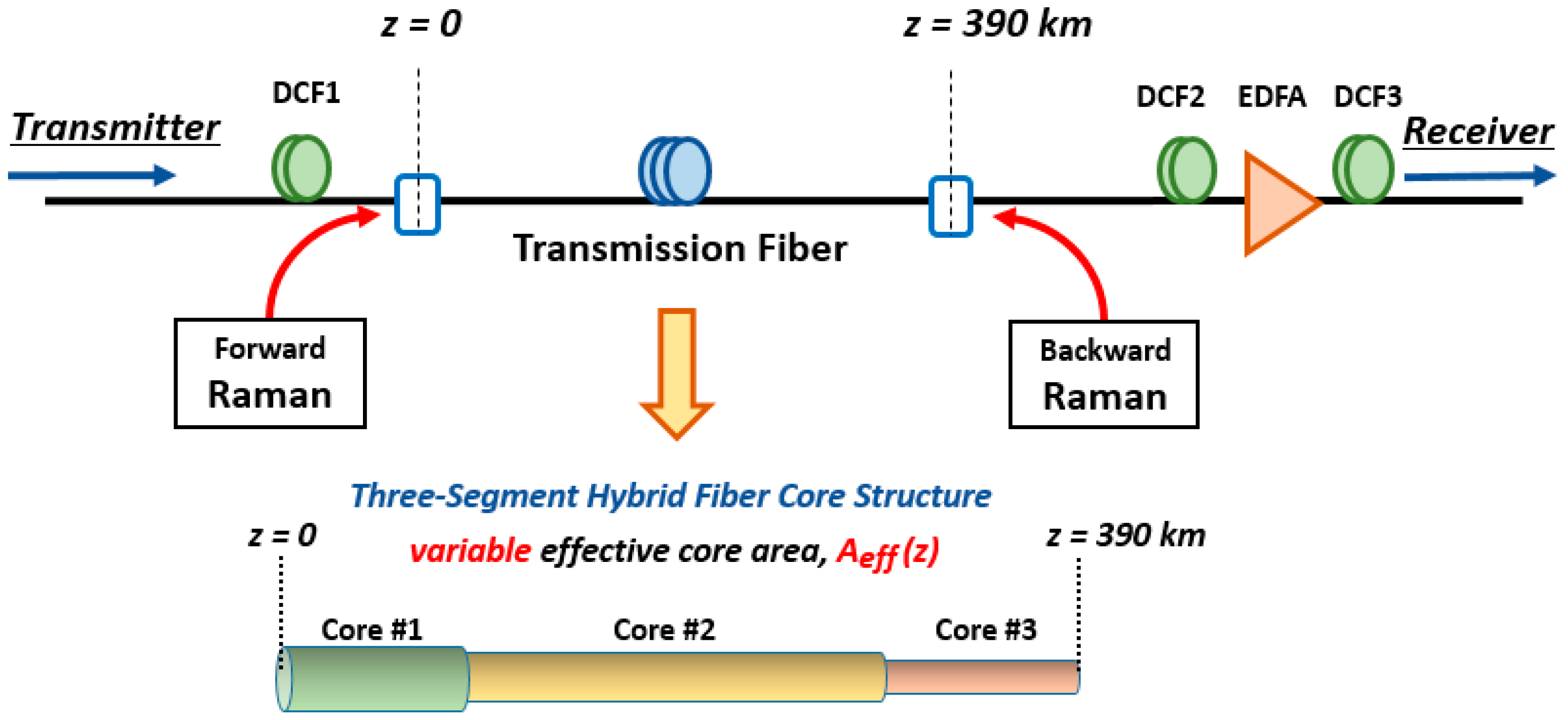
Figure 2 is a schematic diagram of unrepeatered ultra-long single span transmission using a novel hybrid fiber effective core area structure that combines three segments of optical fiber consisting of different fiber effective core area and configured as a bidirectional pumped Raman amplified transmission span. In this model, the transmission span is divided into three segments and consists of three types of fiber cores. The choice of fiber for the individual fiber segment is based on the following design objective: the first segment (core #1) uses a large-sized core to reduce the nonlinear Kerr effect; the second segment (core #2) uses a medium-sized core to function as the major transmission medium and has the longest distance compared to the other segments; and the third segment (core #3) uses a small-sized core to optimize the Raman gain when the signal power is already weak after long-distance propagation. A special splicing technique is available to minimize signal distortion at the joining point between two different fiber core sizes.

All fibers are selected from actual fibers available on the market, in this case, Vascade^® EX3000, Vascade^® EX1000 and SMF-28 ULL fibers (Corning Inc., Corning, NY, USA). The fibers follow step-index single-mode fiber (SMF) characteristics at the transmission signal wavelength where optical fiber normalized frequency (V parameter) has to value less than 2.405 and defined as [23]

$$\mathrm{V}=\frac{2\pi a}{\lambda }{\left(n_1^2-n_2^2\right)}^{1/2}<2.405,$$

(1)

where n₁ and n₂ are the refractive index of core and cladding, a is the fiber core radius, and λ is the signal wavelength. To maintain the characteristics of a single mode, the larger the size of the core, the smaller the refractive index difference between the core and cladding so that it requires more precise thickness control during fiber manufacturing.

The proposed three-segment hybrid fiber core structure is expected to increase flexibility in the Raman gain profile, reduce the negative impact of the nonlinear Kerr effect, and improve the OSNR that could be translated to the improvement on the link capacity of conventional single mode fiber. To overcome the issue of capacity limits in the optical fiber infrastructure, multicore fiber (MCF) is one of the most promising technologies for increasing the spatial efficiency within the available fiber cross-section and reducing the footprint of network equipment [24].

In general, distributed Raman amplification systems generate three types of optical noise: amplified spontaneous emission (ASE) noise, double Rayleigh backscattering (DRS) noise, and relative intensity noise (RIN). These three types of noise have distinct characteristics and different impacts on the system performance. The ASE noise has a flat spectral distribution across the operating bandwidth similar to a white noise and its impact is inherently dominant. The DRS noise creates cross-talk component that has nearly the same spectral shape as the signal itself [25] and leads to a large power penalty in multi-span long-haul transmission system [26]. RIN noise is a spectrum dependent quantity caused by power fluctuation of Raman pump laser source that will directly transfer to the signal’s power [27] and can be reduced by improving the quality of the semiconductor laser source. Since this article focuses on single-span transmission systems, the initial analysis can be limited to ASE noise and the other two noise sources could be added in a future study.

In the multi-segment hybrid fiber effective core area structure, the value of the fiber effective core area changes along the propagation distance. Therefore, the standard Raman amplification formulas should be rewritten to generalized formulas where the fiber effective core area is no longer a constant value but a function of propagation distance. To accommodate the variation in fiber core size along the propagation distance, the generalized form of Raman amplification formulas for multi-segment transmission link should be recalculated from the procedure discussed on the standard Raman amplification formulas [1,4,5]. Based on standard Raman coupled equations, we derived the generalized Raman formulas started from rewriting the fiber effective core area as a function of propagation distance A_eff(z) as

$$\frac{d{P}_s}{dz}=-{\alpha }_s{P}_s+\frac{g_R}{A_{eff}\left(z\right)}{P}_p{P}_s,$$

(2)

$$\kappa \frac{d{P}_p}{dz}=-{\alpha }_p{P}_p-\frac{{\lambda }_s}{{\lambda }_p}\frac{g_R}{A_{eff}\left(z\right)}{P}_s{P}_p,$$

(3)

where z is the propagation distance, A_eff(z) is the fiber effective core area as a function of propagation distance, P_p and P_s are pump and signal powers, α_s and α_p are signal and pump loss coefficients, and λ_s and λ_p are signal and pump operating wavelengths. The signal-pump coupling interaction of the Raman scattering process is determined by multiplying the signal and pump powers, and the intensity is determined by the fiber Raman gain coefficient g_R, whose value depends on the signal and pump wavelengths. The value of parameter κ depends on the choice of Raman pump configuration, κ = 1 for the forward pumping and κ = −1 for the backward pumping.

In the bidirectional pumped Raman amplification model for fiber length z = L, both pump lasers are located at opposite fiber ends. The contribution of pump power to the forward direction can be calculated from Equation (3) by setting κ = 1 and integrating along the span from 0 to z. Similarly, the contribution of pump power to the backward direction can be calculated from Equation (3) by setting κ = −1 and integrating along the span from z to L. Considering a practical situation in which the pump powers are far larger than the signal power and pump power depletion can be ignored, the total pump power P_p at distance z can be obtained by adding the pump power from both directions and introducing the pump power ratio parameter r as the ratio of the forward pump power over the total pump power at launch P_p0. Thus, the combined pump power can be written in the form

$$P_p\left(z\right)=P_{p0}\left\{r\exp \left(-{\alpha }_{p}z\right)+\left(1-r\right)exp(-{\alpha }_p\left(L-z\right))\right\}.$$

(4)

Signal power P_s along the propagation fiber can be calculated from Equation (2) by integrating along the z distance and can be written as

$$P_s\left(z\right)=P_{s0}exp\left({{\displaystyle \int }}_0^z\frac{g_R}{A_{eff}\left(z^{\prime }\right)}{P}_p\left(z^{\prime }\right)d{z}^{\prime }-{\alpha }_{s}z\right).$$

(5)

The profile for Raman net gain G_net along the propagation can be calculated by comparing the signal power at propagation distance P_s(z) to the signal power at initial point P_s0 using Equation (5), which then yields

$$G_{net}\left(z\right)=exp\left({{\displaystyle \int }}_0^z\frac{g_R}{A_{eff}\left(z^{\prime }\right)}{P}_p\left(z^{\prime }\right)d{z}^{\prime }-{\alpha }_{s}z\right).$$

(6)

Since the fiber effective core area varies along transmission span, the standard Raman equation with constant fiber effective core area has to be modified to a generic formula that accommodates the position z dependency of fiber effective core area A_eff(z). To better understand the hybrid fiber core system, signal power density I_s(z) can be defined as the amount of signal power P_s(z) per unit effective core area A_eff(z) and can be written from Equation (5) as

$$I_s\left(z\right)=\frac{P_{s0}}{A_{eff}\left(z\right)}exp\left({{\displaystyle \int }}_0^z\frac{g_R}{A_{eff}\left(z^{\prime }\right)}{P}_p\left(z^{\prime }\right)d{z}^{\prime }-{\alpha }_s\left(z\right)\right).$$

(7)

Based on the Raman analysis results, the Kerr nonlinear limit and Raman noise limit can be measured using the nonlinear phase shift and OSNR. In a single-channel system, the nonlinear phase shift parameter ${\Phi }_{NL}$ indicates the degree of distortion caused by the nonlinear Kerr effect induced self-phase modulation is given by [23]

$${\Phi }_{NL}\left(z\right)={{\displaystyle \int }}_0^z\gamma ·P_s\left(z\right)dz,$$

(8)

where the nonlinear parameter γ used in our model varies along propagation distance z due to the variation of A_eff(z) in the span with multi-segmented structure. Therefore, the nonlinear parameter that changes along propagation γ(z) must be used and can then be modified from [23] in the form

$$\gamma \left(z\right)=\frac{2\pi n_2}{{\lambda }_s{A}_{eff}\left(z\right)},$$

(9)

where n₂ is the nonlinear Kerr parameter and λ_s is the signal wavelength. Finally, by inserting Equation (9) into Equation (8), accumulated nonlinear phase shift becomes

$${\Phi }_{NL}\left(z\right)=\frac{2\pi n_2}{{\lambda }_s}{{\displaystyle \int }}_0^z\frac{P_s\left(z^{\prime }\right)}{A_{eff}\left(z^{\prime }\right)}d{z}^{\prime }.$$

(10)

The spontaneous Raman scattering (SRS) process generates random phases associated with all spontaneously generated photons and adds noise to the amplified signal that appears as a spontaneous Raman noise, which affects the performance of distributed Raman amplifiers and becomes the main sources of optical noise. The spectral density of amplified spontaneous emission (ASE) in Raman span S_ASE is defined as [8]

$$S_{ASE}\left(z\right)=n_{sp}\frac{hc}{{\lambda }_p}\frac{g_R}{A_{eff}\left(z\right)}{G}_{net}\left(z\right)·{{\displaystyle \int }}_0^z\frac{P_p\left(z^{\prime }\right)}{G_{net}\left(z^{\prime }\right)}d{z}^{\prime },$$

(11)

where n_sp is the spontaneous scattering factor, λ_p is the Raman pump wavelength, and hc/λ_p is the photon energy of the Raman pump. The total ASE power can be calculated by integrating ASE spectral density S_ASE within the range of the filter’s optical bandwidth B_opt after the amplifier.

The OSNR shows the signal quality after it is affected by the substantial amount of spontaneous Raman noise generated by ASE. Since the OSNR of the amplified signal is defined by input signal power P_s0 divided by total ASE power [8], the final calculation result is given by

$$OSNR\left(z\right)=\frac{P_{s0}}{B_{opt}{n}_{sp}\frac{hc}{{\lambda }_p}{{\displaystyle \int }}_0^z\frac{g_R}{A_{eff}\left(z^{\prime }\right)}\frac{P_p\left(z^{\prime }\right)}{G_{net}\left(z^{\prime }\right)}d{z}^{\prime }}.$$

(12)

All these generalized formulas where the fiber effective core area is no longer a constant value but a function of link distance will be used for performance modeling on the following sections.

3. Performance Improvement of Three-Segment Raman Amplified Link

The detail system parameters and their values used in the model analysis are listed in

Table 1. List of parameters.

Parameter	Notation	Value	Unit
Fiber span length	L	390	km
Signal wavelength	λs	1550	nm
Fiber attenuation at signal wavelength	αs	0.166	dB/km
Pump wavelength	λp	1450	nm
Fiber attenuation at pump wavelength	αp	0.21	dB/km
Raman gain coefficient	gR	4 × 10−14	m/W
Fiber effective core area	Aeff	76, 82, 150	µm2
Raman net gain	Gnet	5	dB
Filter optical bandwidth	Bop	0.1	nm
Nonlinear Kerr parameter	n2	2.7 × 10−20	m2/W
Spontaneous scattering	nsp	1.13	--

. The specific fiber parameters and their values for the three-segment hybrid fiber effective core area structure and conventional single fiber core structure are listed in

Table 2. Three-segment hybrid fiber core structure.

Parameter	Core #1	Core #2	Core #3
Fiber effective core area (µm2)	150	82	76
Segment length (km)	90	200	100
Segment attenuation (dB/km)	0.166	0.166	0.166

and

Table 3. Conventional single fiber core structure.

Parameter	Single Core
Fiber effective core area (µm2)	82
Segment length (km)	390
Segment attenuation (dB/km)	0.166

.

In order to get a lower peak power of signal power density and a sufficient reduction in the Kerr nonlinear distortion measured as a nonlinear phase shift, the length of the first segment (core #1) is set to 90 km. In parallel, to improve the Raman gain in the signal power prior to reaching the minimum point of signal power and to maintain the power level of the backward Raman pump after fiber penetration, the length of the third segment (core #3) is set to 100 km. Both segment lengths are preliminary values to prove the concept of the three-segment hybrid fiber core systems, and we believe there is still room to fine-tune these values to obtain the optimum individual length in the future study.

Figure 3 shows the distribution profile of bidirectional Raman pump power for both the conventional single-segment single fiber core structure and the three-segment hybrid fiber effective core area structure when the pump powers are adjusted to provide the equal 5 dB Raman net gain (G_net), which is the residual gain after the total Raman gain is reduced by total fiber attenuation loss. In both cases, the forward and backward pumps provide significant gain contributions in the initial 50 km and additional, but lower, contributions from 50 to 100 km. Due to continuous fiber attenuation at a rate of 0.21 dB/km for a pump wavelength of 1450 nm, the Raman pump power decreased significantly beyond 100 km. Therefore, the gain contribution at this stage can be considered negligible and the fiber span experiences a passive fiber loss. In the forward pump, the three-segment hybrid fiber core structure requires higher pump power to achieve equal Raman net gain compared to the conventional single fiber core structure due to the gain characteristic of Raman scattering, which has a lower gain on larger sized cores. In the backward pump, the pump power difference is small because the fiber core size difference is small.

Figure 4 illustrates a comparison of signal power density I_s(z) between the three-segment hybrid fiber effective core area structure and the conventional single-segment single fiber core structure along the 390-km fiber transmission span. In the span with the three-segment hybrid fiber core structure, the first segment (0–90 km), with a larger effective core area, provides a lower signal power density that helps to reduce the nonlinear Kerr effect; the third segment (290–390 km), with a smaller effective core area, provides a higher signal power density that helps to improve the OSNR. These two results strongly indicate the advantage of the span with the three-segment hybrid fiber core structure compared to the span with the conventional single fiber core structure.

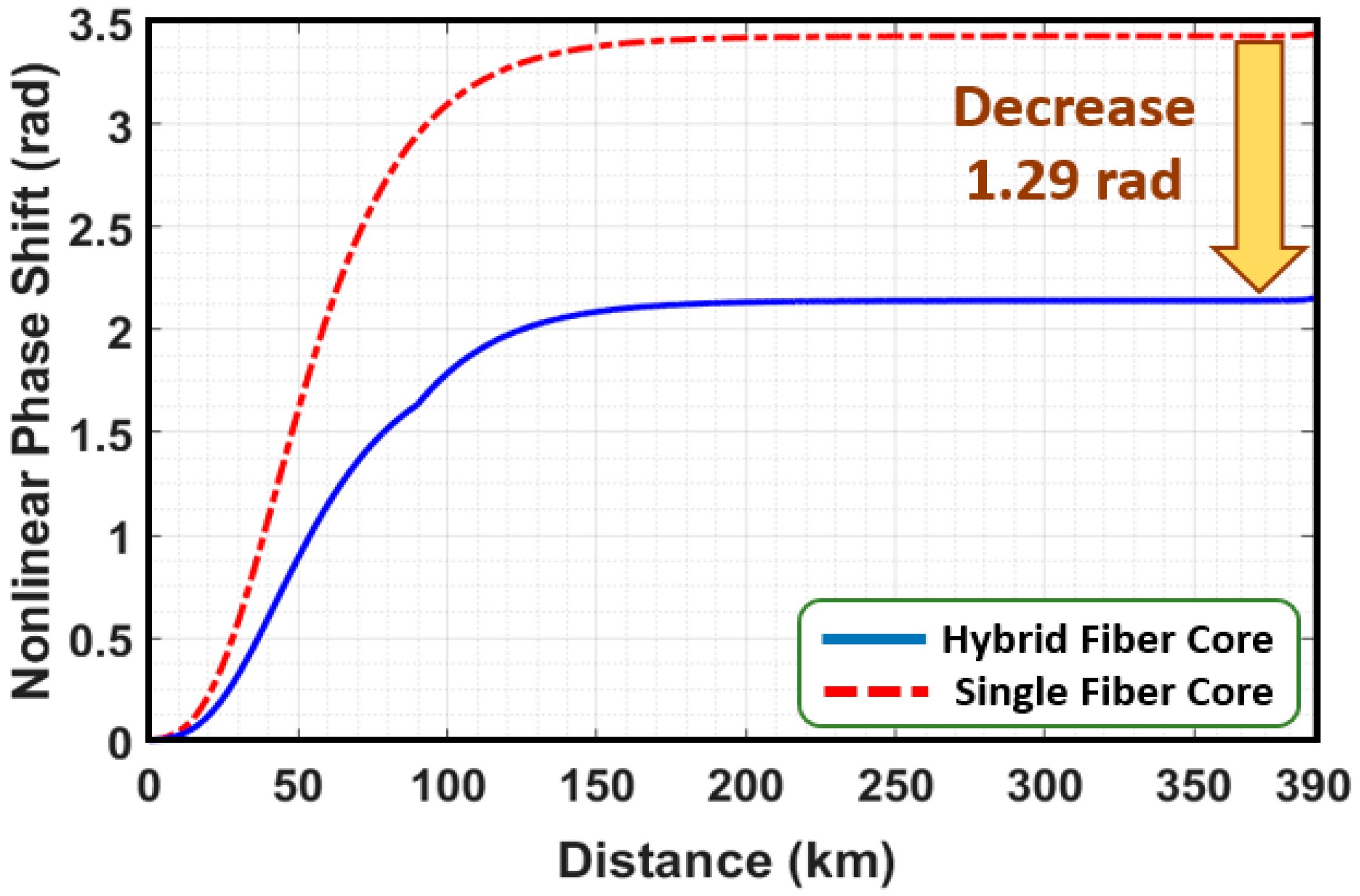
The nonlinear Kerr effect in the form of self-phase modulation (SPM) induces a nonlinear phase shift that indicates the degree of signal distortion and the reduction of quality factor [28]. In a single-channel optical transmission system, the amount of nonlinear phase shift (${\Phi }_{NL}$) is proportional to the integral of signal power density, as shown in Equation (8). Figure 5 shows a comparison of the nonlinear phase shift between the three-segment hybrid fiber effective core area structure and the conventional single-segment single fiber core structure along the 390-km fiber transmission span. The span with the three-segment hybrid fiber core structure has a lower accumulated nonlinear phase shift compared to the conventional single fiber core structure. The decrease of 1.29 radian is due to the lower signal power density of the three-segment hybrid fiber core structure at the first segment (0–90 km).

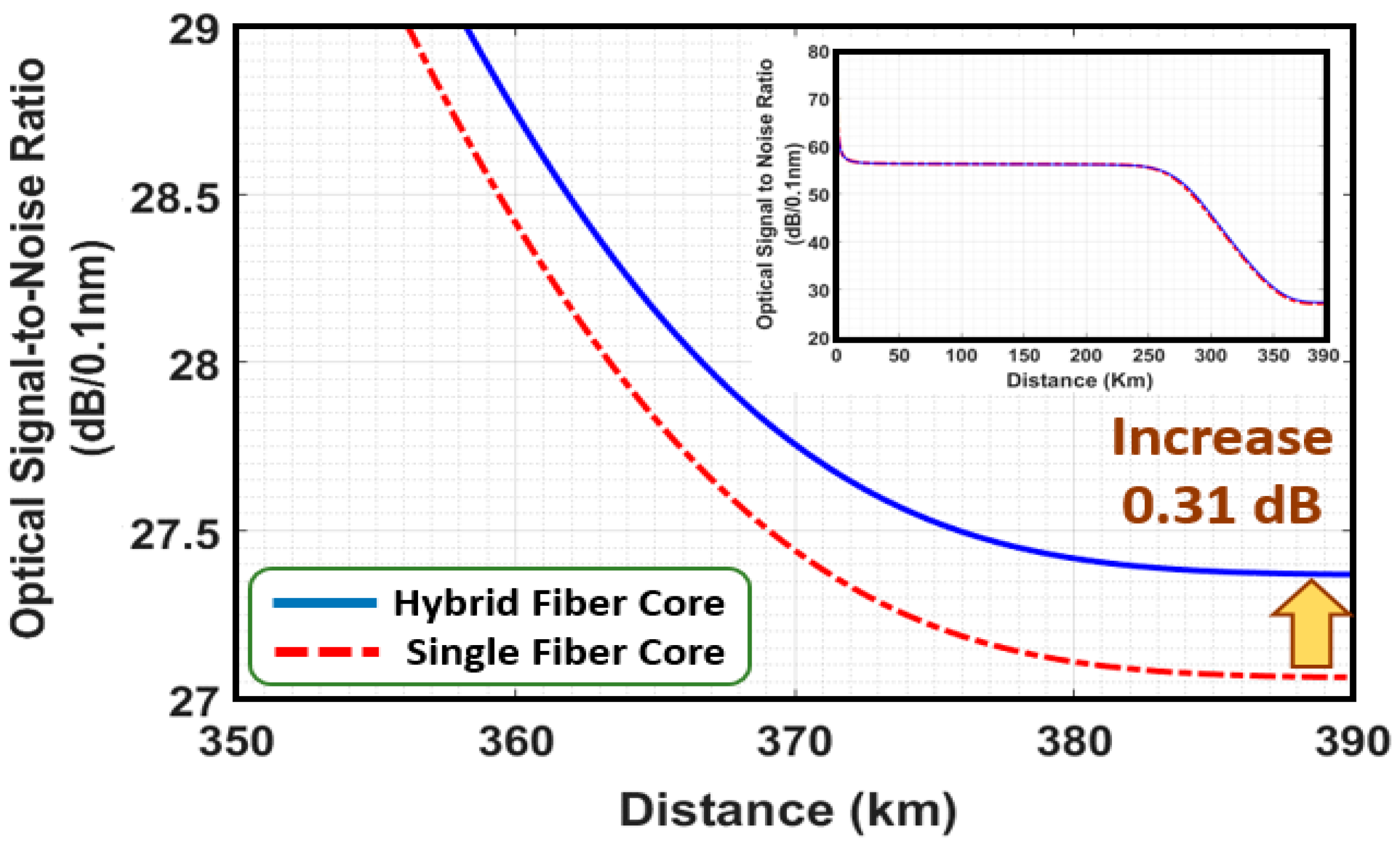
Figure 6 illustrates a comparison of the OSNR profile of a 1 mW signal between the three-segment hybrid fiber effective core area structure and the conventional single-segment single fiber core structure along a 390-km fiber transmission span. The span with the three-segment hybrid fiber core structure achieved a 0.31 dB higher OSNR compared to the conventional single fiber core structure. This improvement is due to the higher minimum value of the signal power density at the third segment (290–390 km). The OSNR calculation is based on the single-polarization of the single-sided-passband power spectrum density of the optical signal and the dual-polarization of the Raman ASE noise.

Table 4. Summary of performance improvement result.

Structure	NLPS (rad)	OSNR (dB)
Conventional single fiber core	3.44	27.06
Three-segment hybrid fiber core	2.15	27.37
Improvement	1.29	0.31

provides a summary of the numerical analysis results for the nonlinear phase shift (NLPS) and OSNR for the conventional single fiber core structure and three-segment hybrid fiber core structure, respectively. The numerical analysis results show that improvements to the NLPS and OSNR can be achieved simultaneously. This achievement would be impossible with the sole use of a conventional single fiber core structure. The realization of a modulated signal in the transmission simulation, which is expected to improve transmission performance, will be explained in the next section.

4. Simulation Model of DQPSK Modulated Data Transmission

In this study, computer simulation based on MATLAB programming was used to mathematically analyze and numerically simulate the data transmission in an unrepeatered ultra-long span system. In a single mode optical fiber, the complex field envelope of the slow-varying pico-second range optical pulse is governed by the non-linear Schrodinger equation (NLSE), a nonlinear partial differential equation that provides an analytical solution only in specific cases. The numerical method most commonly used to investigate the dispersive nonlinear effect of optical wave propagation along a transmission fiber is the split-step Fourier method (SSFM) due to its simplicity for implementation and high computational efficiency [29].

The efficiency of the SSFM depends on both the time-domain or frequency-domain resolution and on the distribution of step sizes along the fiber. In simulations of optical-fiber transmission systems, the time and frequency resolutions are determined by the bandwidth of the signal and the number of bits that are to be propagated through the system respectively. In the SSFM model, the fiber is divided into many small sections that are short enough that the effect of Kerr nonlinearity and dispersion can be calculated separately. In the first step, the NLSE is used to solve the nonlinear Kerr effect term by ignoring the dispersion term and in the next step, the NLSE is used to solve the dispersion term by ignoring the nonlinear Kerr effect term. The interplay between nonlinearity and dispersion is thus indicated for each step after the completion of each computation pair. The introduction of symmetrized-SSF model can improve the computational efficiency requirement for the simulation and optimization of fiber-optic communication systems [30].

The optical pulse field envelope U(z,t) propagating at normalized distance z in single mode optical fiber is governed by the NLSE and can be expressed as [23]

$$\frac{\partial U\left(z,t\right)}{\partial z}+i\frac{{\beta }_2}{2}\frac{{\partial }^{2}U\left(z,t\right)}{\partial t^2}-i\gamma \left(z\right){\left|U\left(z,t\right)\right|}^{2}U\left(z,t\right)=\frac{g\left(z\right)}{2}U\left(z,t\right),$$

(13)

where t represents the normalized time in the retarded frame co-moving with the group velocity of the envelope. The optical characteristics of the transmission fiber depend on the group velocity dispersion β₂, the nonlinear coefficient γ(z) of the fiber due to the Kerr self-focusing effect, and the distributed gain g(z) obtained from the distributed Raman amplification where the passive loss of the propagation fiber is already included. Even though Equation (13) does not provide a complete physical description of a system, it is the basis for modeling optical-fiber communications systems. Because a bidirectional pumped distributed Raman amplifier is used, the optical pulse propagation along the transmission fiber can be modeled by integrating the calculation of the impact of dispersion, the effect of Kerr nonlinearity, the fiber loss, and the Raman gain profile.

Each orthogonal branch of a DQPSK modulator encodes information on two sets of binary phase changes between two adjacent bits, and uses differential precoding as a simple alternative compared to more complex encoding and decoding scheme in the coherent system. DQPSK is the first step to higher spectral efficiency, which can transmit 2 bits/symbol by utilizing a pair of nested MZMs called I&Q (in-phase and quadrature) modulator. Several relative advantages of using DQPSK modulation are higher data rate, reduction in the required OSNR, increasing spectrum efficiency, resistance to the signal power fluctuation, robust to nonlinear distortion, and improving linear sensitivity that enhances the overall system performance [31,32]. Return-to-zero (RZ) pulse shape has superior performance compared to non-return-to-zero (NRZ) pulse shape because RZ is inherently more tolerant to inter-symbol interference (ISI), chromatic dispersion (CD), and polarization mode dispersion (PMD). Moreover, RZ pulse shape has an excellent nonlinear performance on high power signal, which is mandatory for ultra-long span applications with high nonlinear Kerr distortion [33].

The simulation model in this study uses RZ-DQPSK transmitter consisting of a laser diode at a wavelength of 1550 nm, which is externally modulated to form an RZ pulse train. The implementation of RZ-DQPSK transmitters most conveniently use dual stages Mach-Zehnder modulators (MZMs) as a phase modulator and pulse carver [32]. The phase modulator works as a data modulator driven by the incoming electrical data stream. The optical channel power into the fiber launch point is set to 0 dBm (1 mW) to balance between providing a sufficient OSNR and reducing the impact of the nonlinear effect to achieve optimum BER performance [34,35].

Figure 7 shows a schematic diagram of the simulation setup for the ultra-long span transmission system, which was configured without an active repeater or optical line amplifier (OLA) component along the 390-km transmission link. This unrepeatered system consists of a bidirectional pumped distributed Raman amplifier to compensate transmission fiber loss, chromatic dispersion compensation fiber (DCF), and EDFA which is mainly to compensate DCF loss at the receiver side. A pulse broadening technique is used to reduce the Kerr nonlinear distortion by broadening the initial pulse shape using a 6-km dispersion compensation fiber (DCF1) which is placed prior to launching the signal into the fiber span. Moreover, in order to maintain high OSNR and to compensate the DCF1 loss, a relatively high forward Raman pump is installed right before the launch point.

The signal power in the fiber propagation follows a profile of optical gain/loss in which the bidirectional distributed Raman amplifications provide distributed gain along the fiber link and counterbalance the passive attenuation of the fiber, resulting in acceptable signal power at the receiver point, z = 390 km. When the optical signal reaches the received side, the optical power is still strong enough due to 5 dB Raman net gain provided by the bidirectional Raman system. The following step is a dispersion compensation process to counter balance the accumulated fiber anomalous dispersion by cascading DCF2 and DCF3 with normal dispersion, which equally can be substituted using electrical dispersion compensation. Since the length of the span is very long, the amount of the dispersion to be compensated becomes very high. Compensating for the dispersion on a single DCF spool will drop the signal power to an extremely low level. Therefore, we chose to split the DCF and put the EDFA in between to compensate for the attenuation of the two DCFs, to maintain optical power at a moderate level, and finally to provide enough optical power to be detected by the receiver photodiode [10,36]. This transmission system does not have a ROPA along the propagation fiber or a forward error correction (FEC) component on signal recovery subsystem.

In order to evaluate the BER performance for variation values of the required OSNR or SNR per bit (Eb/No) with a relatively short simulation run-time (i.e., compared to the Monte Carlo simulation, which requires a very long extended run-time), we decided to use a semi-analytical BER estimation method based on the Karhunen-Loeve series expansion (KLSE) in our BER performance simulation. The term "semi-analytical" means that some portions of this method are based on analytical derivations, while others are based on numerical computation. The BER performance simulation using the KLSE method was initially proposed by Forestieri [37] to calculate the BER value in an optically pre-amplified on-off keying (OOK) modulated system.

An extension to the phase-modulated system (DBPSK) was proposed in [38] by using the Fourier transform of the input electric field. The stream of the simulated input data signal is modeled to be a periodic repetition of a binary sequence such that the input data signal electric field can be expanded in a Fourier series. Using a Karhunen-Loeve expansion, the ASE noise generated by optical amplifiers can be expanded in a Fourier series. After expressing both the data signal and the ASE noise in a Fourier series, the decision sample can be readily formulated and will comprise three terms: data signal, signal-ASE beat noise, and ASE-ASE beat noise. By writing these three terms in a matrix form and using matrix transformation techniques, both types of noises can be combined into one term. This combined noise term can be expressed as a non-central quadratic form of Gaussian random variables and has a non-central chi-square distribution. Therefore, the moment generating function (MGF) of the decision sample can be derived. The probability density function (PDF) of the photocurrent can be obtained from the MGF by using the inverse Laplace transform and saddle-point integration approximation. The calculated PDF reflects the exact statistics of the photocurrent appearing at the decision gate and shows the overall estimated error probability for different required OSNR values [31,37,38,39].

In a phase-modulated DBPSK receiver, the KLSE method is used to obtain the MGF of the combined decision sample by multiplying the MGFs of the two photocurrent branches of a balanced photodiodes [38]. The probability of an error occurring at the sample time upon the data sequence can be calculated after setting the decision threshold value. Therefore, the BER can be estimated over a range of required OSNR values. In computing the BER for a DQPSK system, we need to compute the BER for the in-phase (I) and quadrature (Q) signals separately and then average the BER values of I and Q. In conclusion, with knowledge of the exact statistics of the photocurrents appearing at the decision gates, it becomes possible to estimate the BER performance by integrating over the PDF of the photocurrents means over a different OSNR or SNR per bit (Eb/No), without needing to simulate a very large number of bits, as is necessary in Monte Carlo simulations.

The bit sequence used in the simulation is a De Bruijn bit sequence (DBBS) of length 2¹², which is equivalent to a pseudo-random binary sequence (PRBS) 2¹² − 1 with an additional “0” bit inserted into the longest chain of zeros. In the DBBS-generated bit pattern, every possible distinct bit combination occurs exactly once, thus correctly representing the average distribution of bit combinations generated by the statistically independent data generator [40]. Figure 8 illustrates an example of an eye diagram and power spectrum density (PSD) of the in-phase (real) part of an 80 Gb/s DQPSK-modulated signal after a 390-km transmission over the unrepeatered ultra-long span system using three-segment hybrid fiber effective core area structure. The eye diagram monitored at the receiving side indicates the amplitude fluctuation of the signal power and also the timing jitter fluctuation of the sampling clock. In a phase-modulated format (in this case DQPSK) with an RZ pulse shape, the pulse trails are repeated at the same pulse amplitude at any given time, leading to a minor amplitude fluctuations. The eye diagram is widely open which indicates suitable filters are set at the receiver. Since the information data are coded in the signal phase, the transmission performance will be affected mainly by the accumulated phase shift and phase fluctuation along the transmission line. The absence of a zero-intensity rail in the eye diagram is characteristic of a phase-modulated format. The spectrum shows that the signal bandwidth of the RZ pulse up to the first null is twice the clock rate. Although twice the bandwidth is required compared to the NRZ format, the RZ format has much better nonlinear performance, which is mandatory for ultra-long span application.

As an important transmission parameter, OSNR has two distinct meanings from an application point of view: delivered OSNR (OSNR_Del) and required OSNR (OSNR_Req) [41]. The delivered OSNR is a measurable parameter that shows the OSNR at the end of a transmission line and depends only on the transmission line parameters and launched signal powers but not on the modulation formats or transmission impairments. The required OSNR is a design parameter that specifies the minimum necessary OSNR that is required to achieve a certain target BER as an indication of the tolerance of a modulation format to ASE noise and any other transmission impairments. The OSNR of the Raman analysis in Section 2 and Section 3 is a delivered OSNR, while the OSNR of the BER performance analysis in this section (Section 4) is a required OSNR.

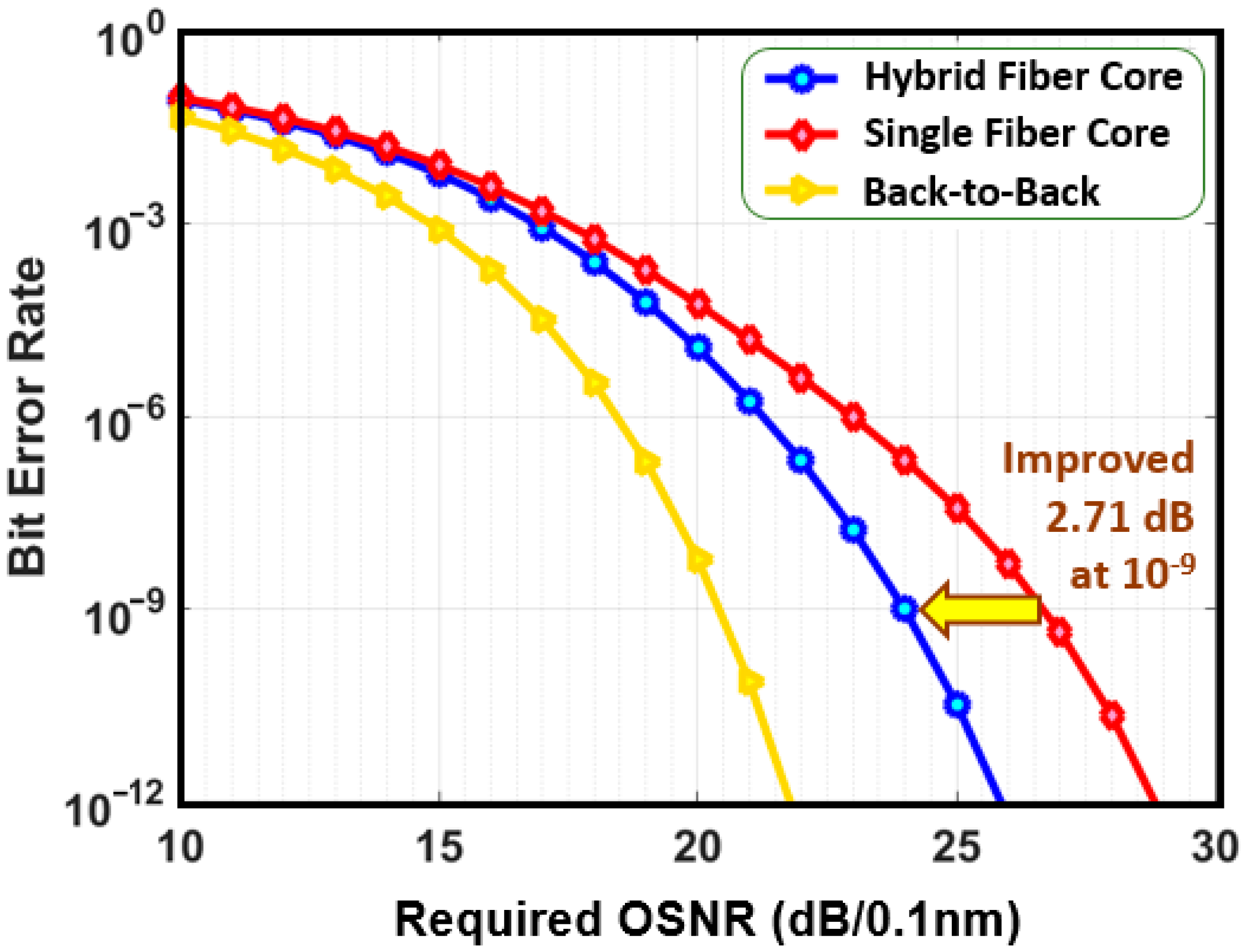
The simulated BER performance of 80 Gb/s RZ-DQPSK direct-detection system as a function of the required OSNR (OSNR_Req) after propagation over the 390-km unrepeatered transmission span is illustrated in Figure 9. A comparison of the BER performance between the three-segment hybrid fiber effective core area structure and the conventional single-segment single fiber core structure shows that the span with the three-segment hybrid fiber core structure was superior. To achieve the target BER of 10⁻⁹, the required OSNR (OSNR_Req) of the three-segment hybrid fiber core structure is reduced by 2.71 dB, indicating improvement in the transmission performance.

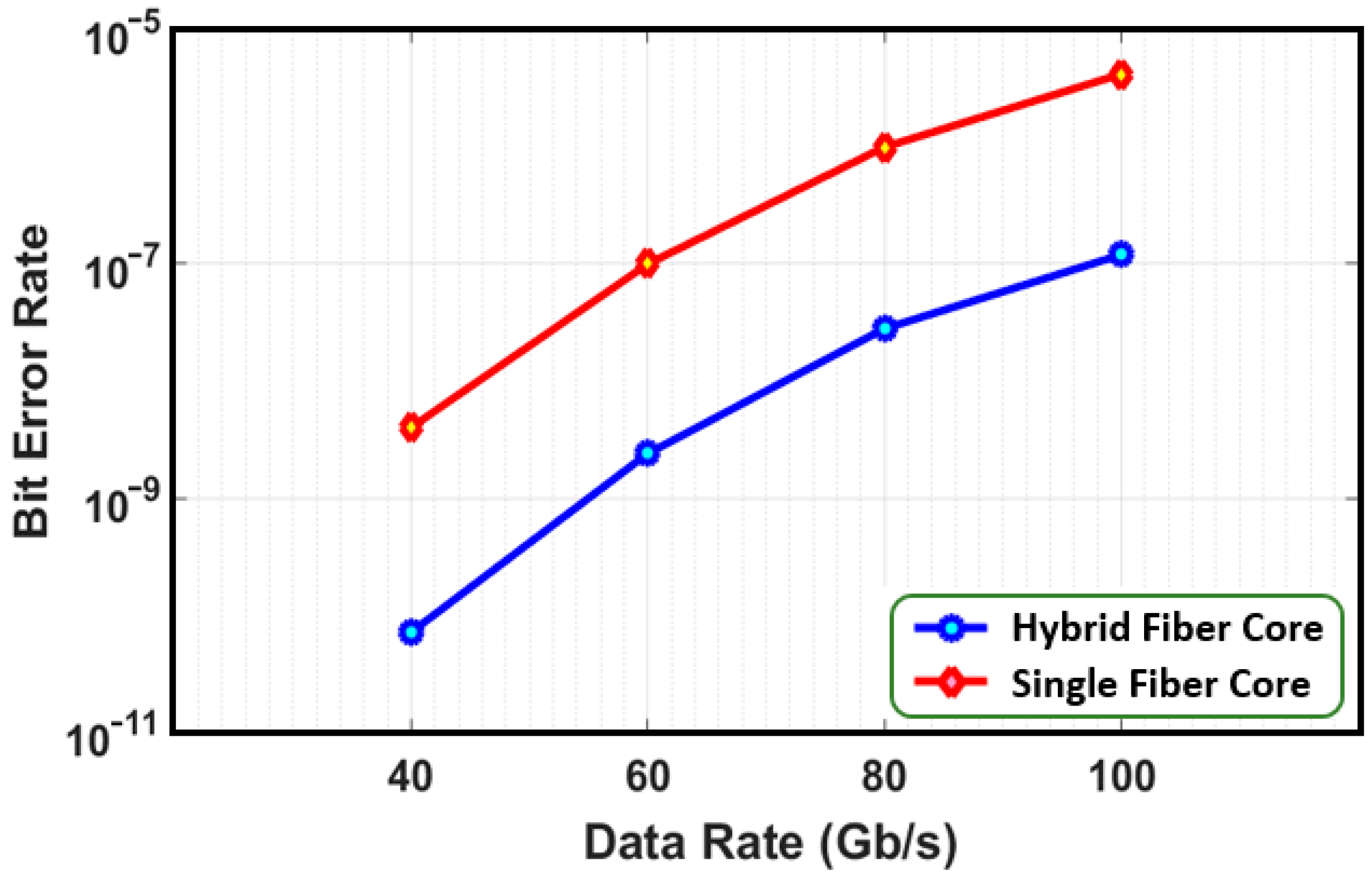
The required signal-to-noise ratio per bit (Eb/No) can be used as an alternative when measuring required optical signal-to-noise performance independent of the data bit rate and to free from the 0.1 nm noise bandwidth definition. Figure 10 shows BER performance for various data rates (40, 60, 80, and 100 Gb/s) when using the three-segment hybrid fiber effective core area structure. A high data rate has a narrow pulse width and is more sensitive to dispersions that trigger inter-symbol interference (ISI). The interaction between dispersion and the nonlinear Kerr effect (SPM in a single-channel system) enhance the pulse distortion, leading to a higher error rate. The stability and consistency of the system’s performance across different data rates indicate the ability to meet various applications’ demands.

Figure 11 shows a summary of BER performance for various data rates, comparing the BER performance results between the three-segment hybrid fiber effective core area structure and the conventional single-segment single fiber core structure when the required signal-to-noise ratio per bit (Eb/No) is set to 18 dB for both cases. The three-segment hybrid fiber core structure shows superior transmission performance across all data rates. For any given data rates, the transmission impairment of the span with the three-segment hybrid fiber core structure is smaller than the span with the conventional single fiber core structure. This excellent transmission performance is due to a higher delivered optical signal-to-noise ratio (OSNR_Del) at the receiving end and a smaller Kerr nonlinear penalty accumulated along the transmission span, as predicted by previous analysis and illustrated in Figure 5 and Figure 6. In general, excluding the impact of polarization mode dispersion and intra/inter-channel interaction on single-channel single-span transmission links with short to medium length, the bit error rate result is promising for a data rate of 40 Gb/s, but will require FEC for higher data rates to improve the BER performance sufficiently for field applications.

5. Conclusions

Kerr nonlinear distortion and Raman amplifier noise have been identified as two major limiting factors in improving the transmission performance of unrepeatered ultra-long span systems. A configuration of a hybrid fiber effective core area consisting of a three-segment structure was proposed as an alternative to conventional single-segment fiber effective core area structure. The generalized mathematical formulations and the performance analysis of a bidirectional distributed Raman amplified link using a three-segment hybrid fiber effective core area structure were presented. An improvement of the transmission performance and the possibility to extend the transmission distance of ultra-long span system were simulated.

The introduction of a hybrid fiber effective core area in a three-segment structure indicated an increase in the flexibility of the gain profile of the distributed Raman amplified link, a reduction of negative impact of the nonlinear Kerr effect due to the high signal power, and an improvement of the delivered OSNR by means of the reduction of the Raman optical pump-induced amplified spontaneous emissions. The three-segment span with the hybrid fiber effective core area reduced the accumulated nonlinear phase shift by 1.29 radian, increased the delivered OSNR by 0.31 dB, and improved the transmission performance of the DQPSK-modulated signal compared to the conventional single fiber core structure.

The simulated BER performance of the 80 Gb/s data signal showed the reduction of the required OSNR by 2.71 dB to achieve the target BER of 10⁻⁹. BER performance for various data rates (40, 60, 80, and 100 Gb/s) was examined, and the results showed the stability and consistency of the system performance across different data rates. These single-channel analytical and simulation studies on a three-segment hybrid fiber effective core area structure could be used as basic guidelines for further studies on the multi-channel broadband multi-wavelength Raman amplification scheme, which has useful applications in the dense wavelength division multiplexing (DWDM) optical transmission systems.