Design of an Ultrahigh Birefringence Photonic Crystal Fiber with Large Nonlinearity Using All Circular Air Holes for a Fiber-Optic Transmission System
Abstract
1. Introduction
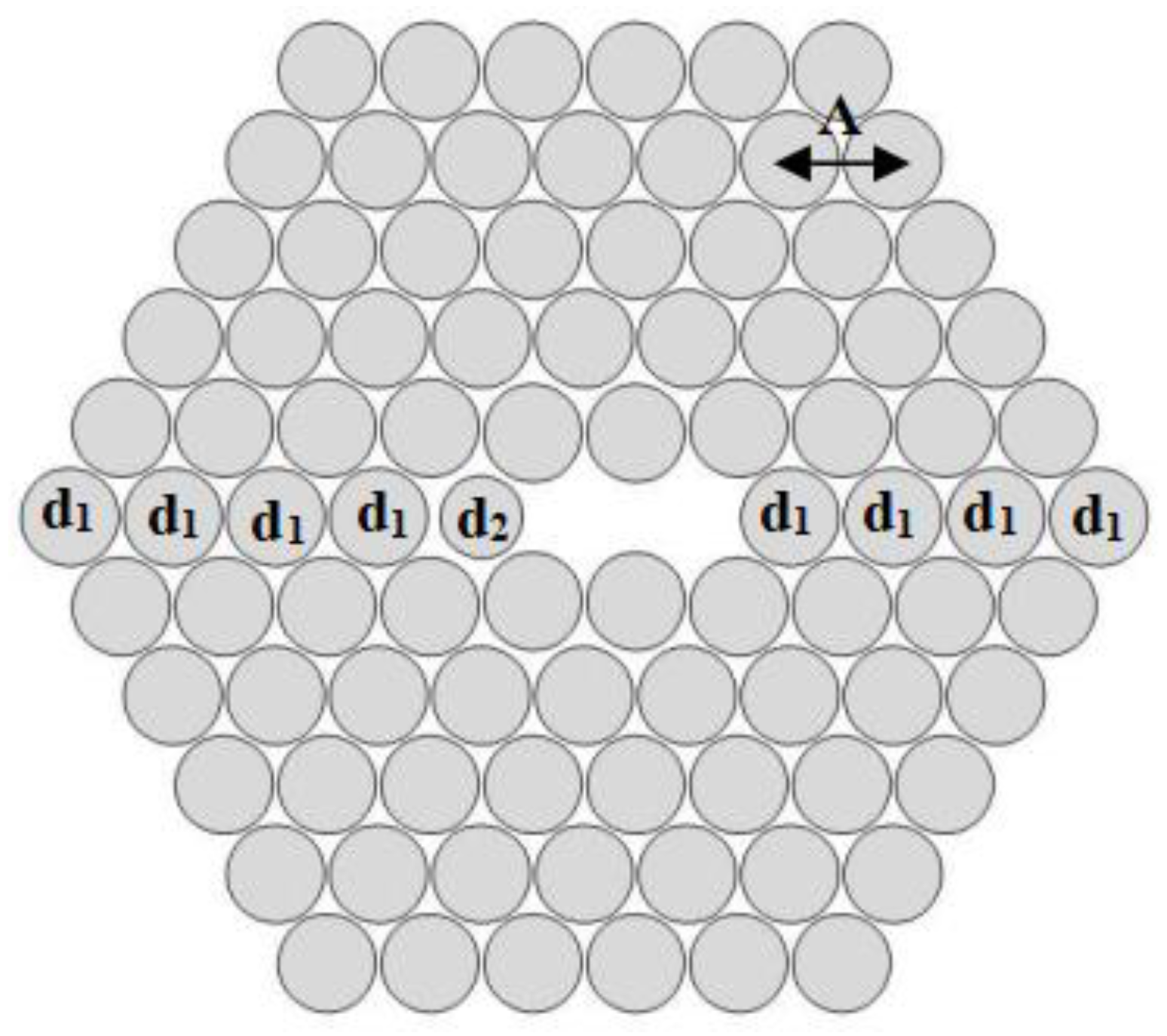
2. Design Methodology of the Proposed H-PCF
3. Numerical Method
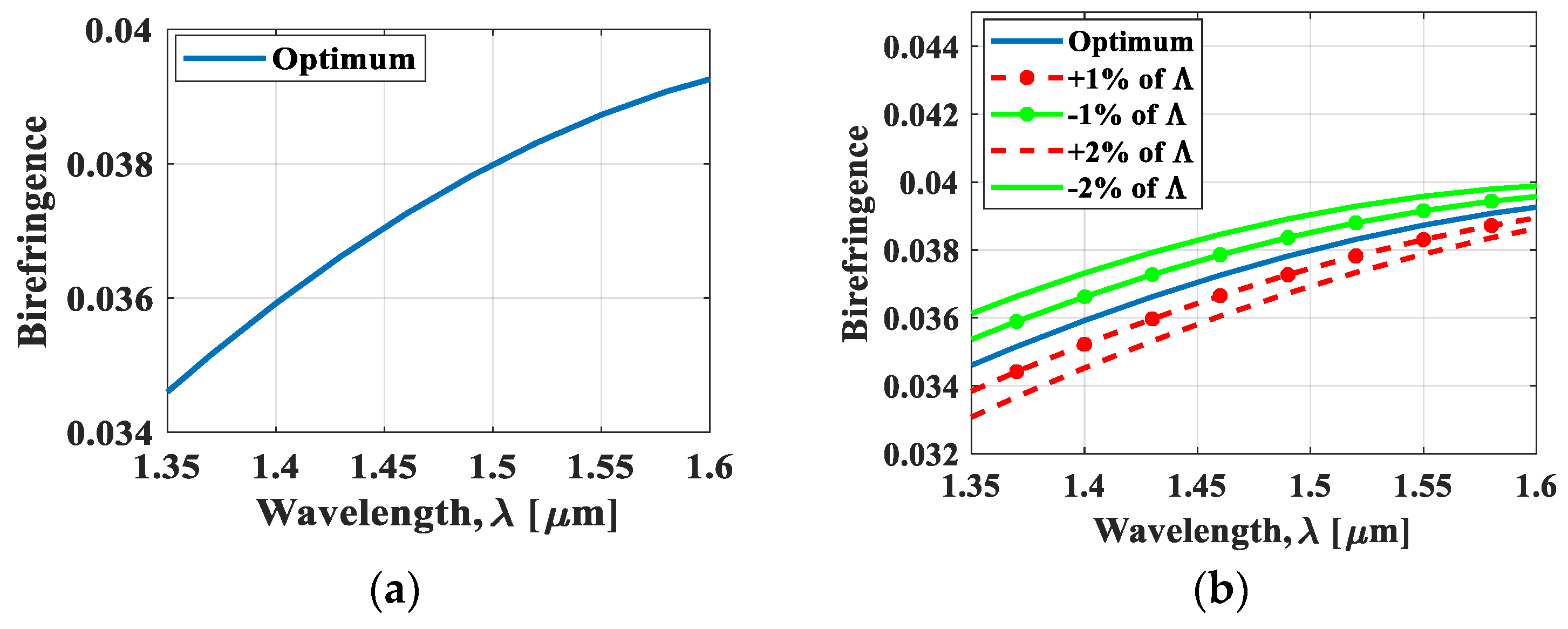
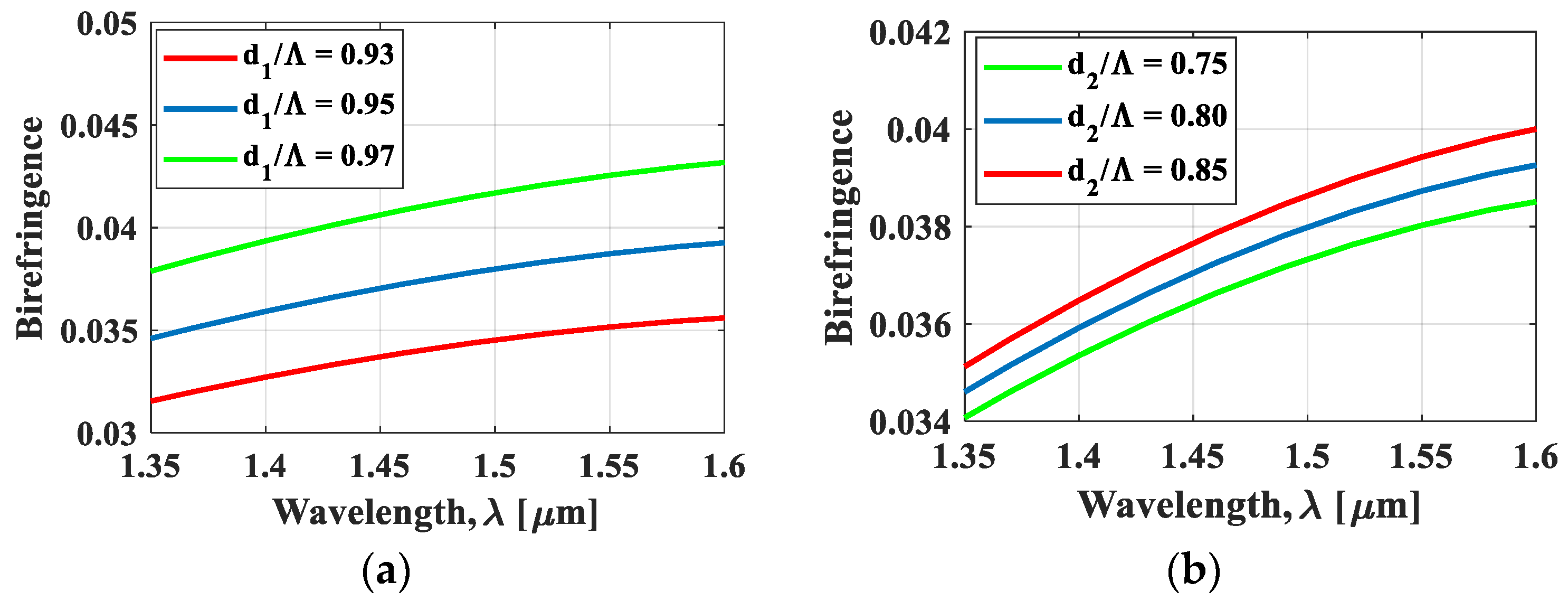
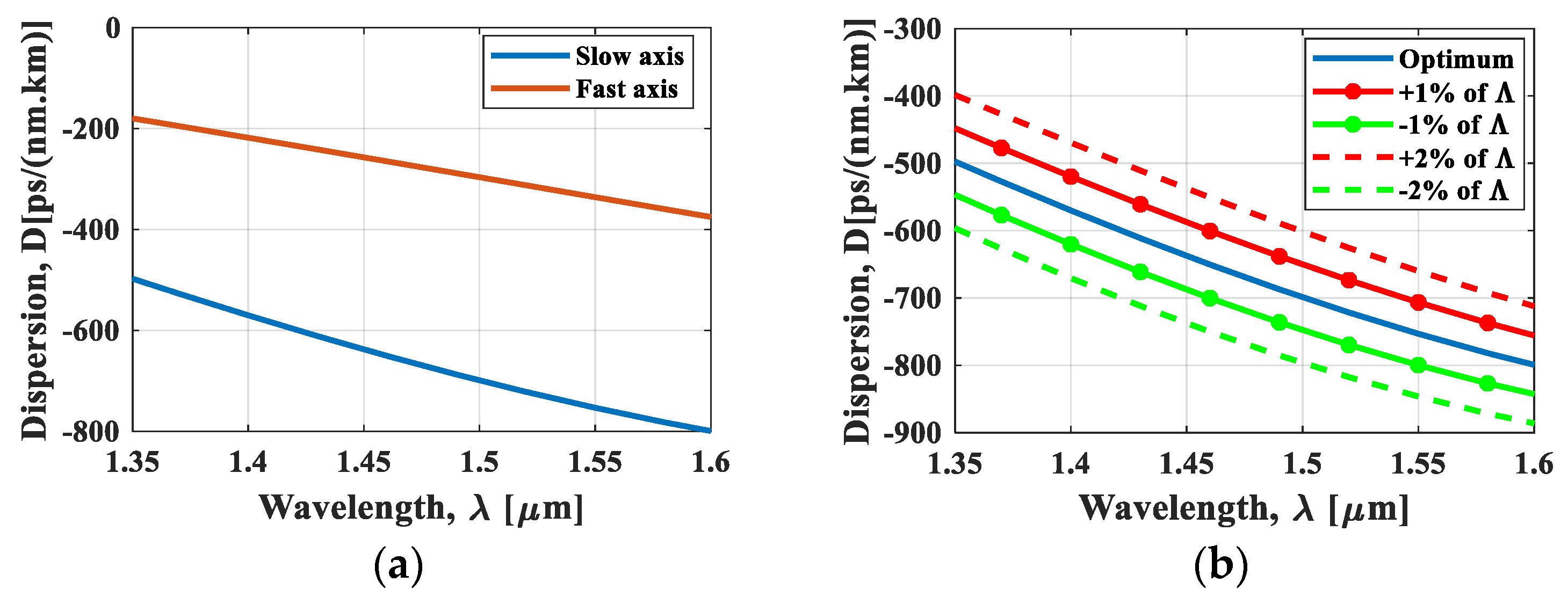
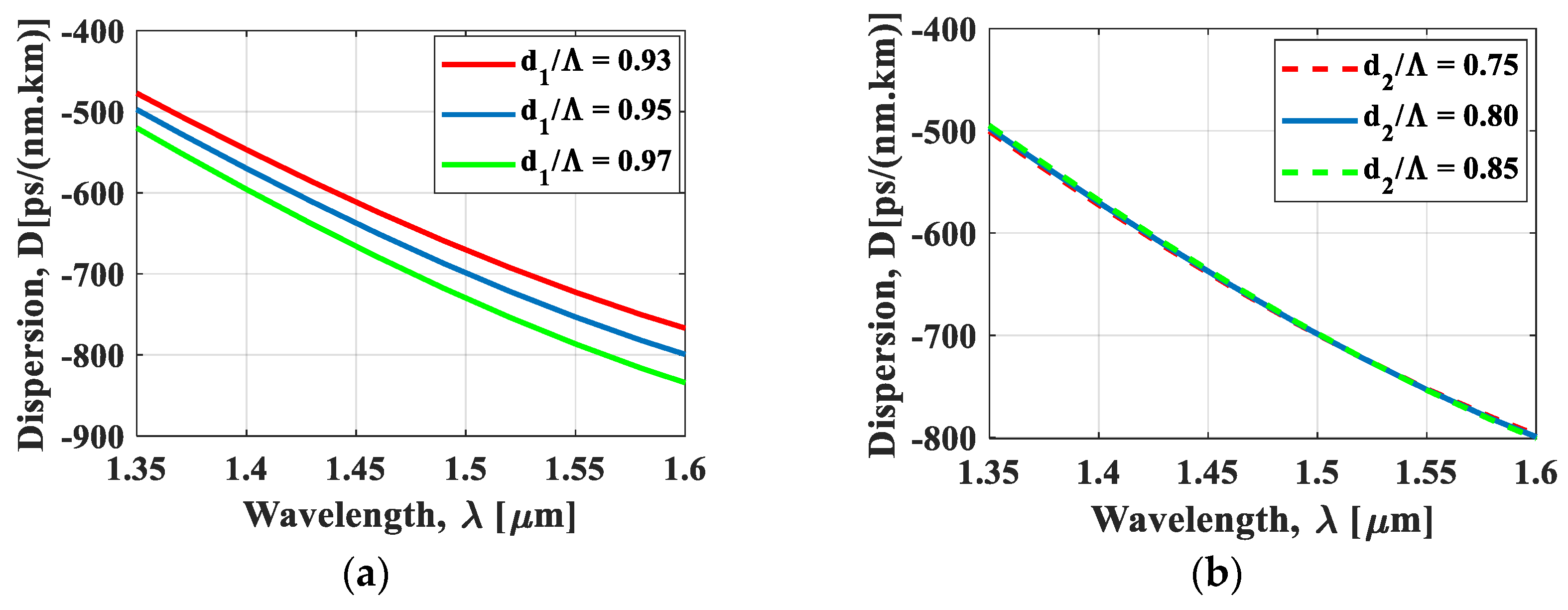
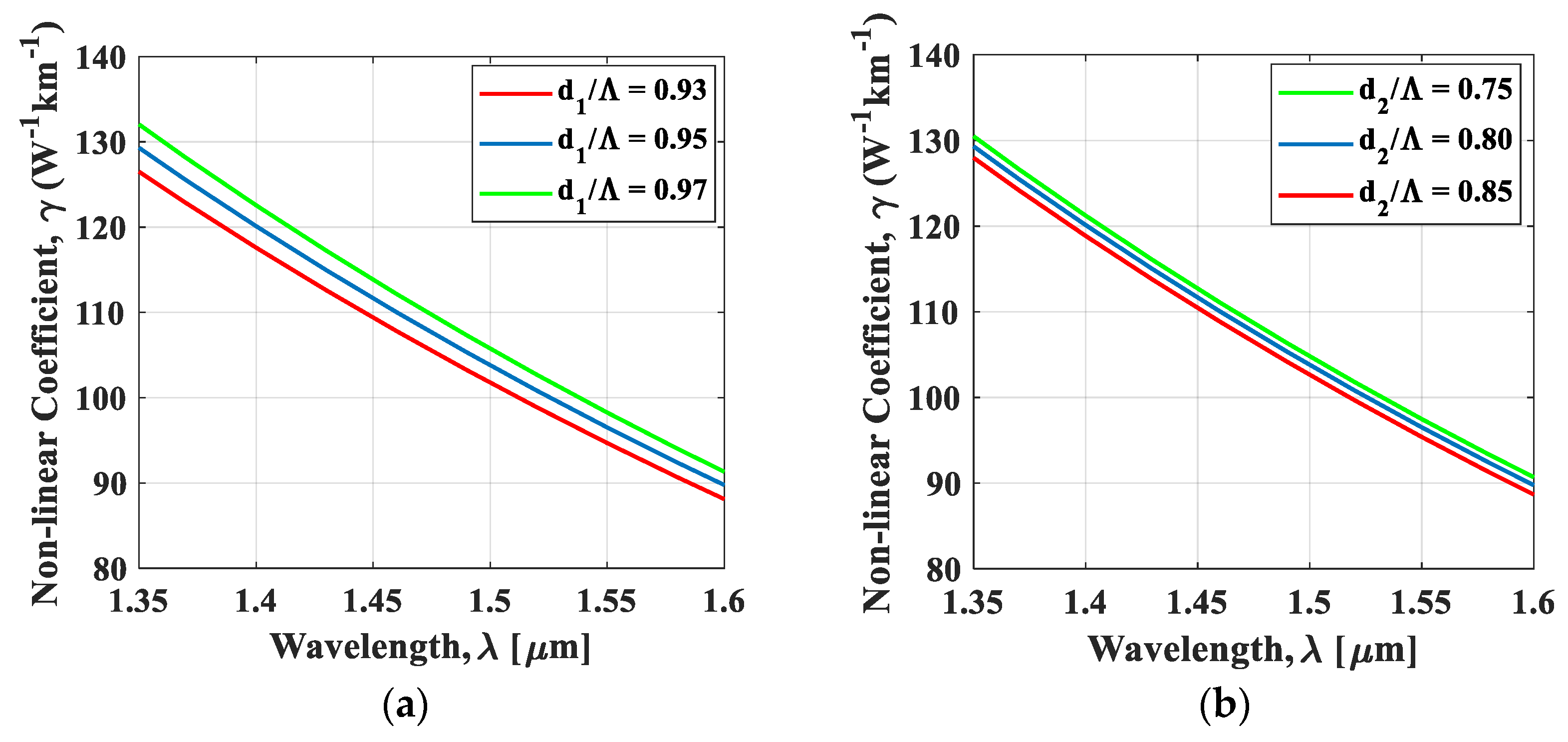
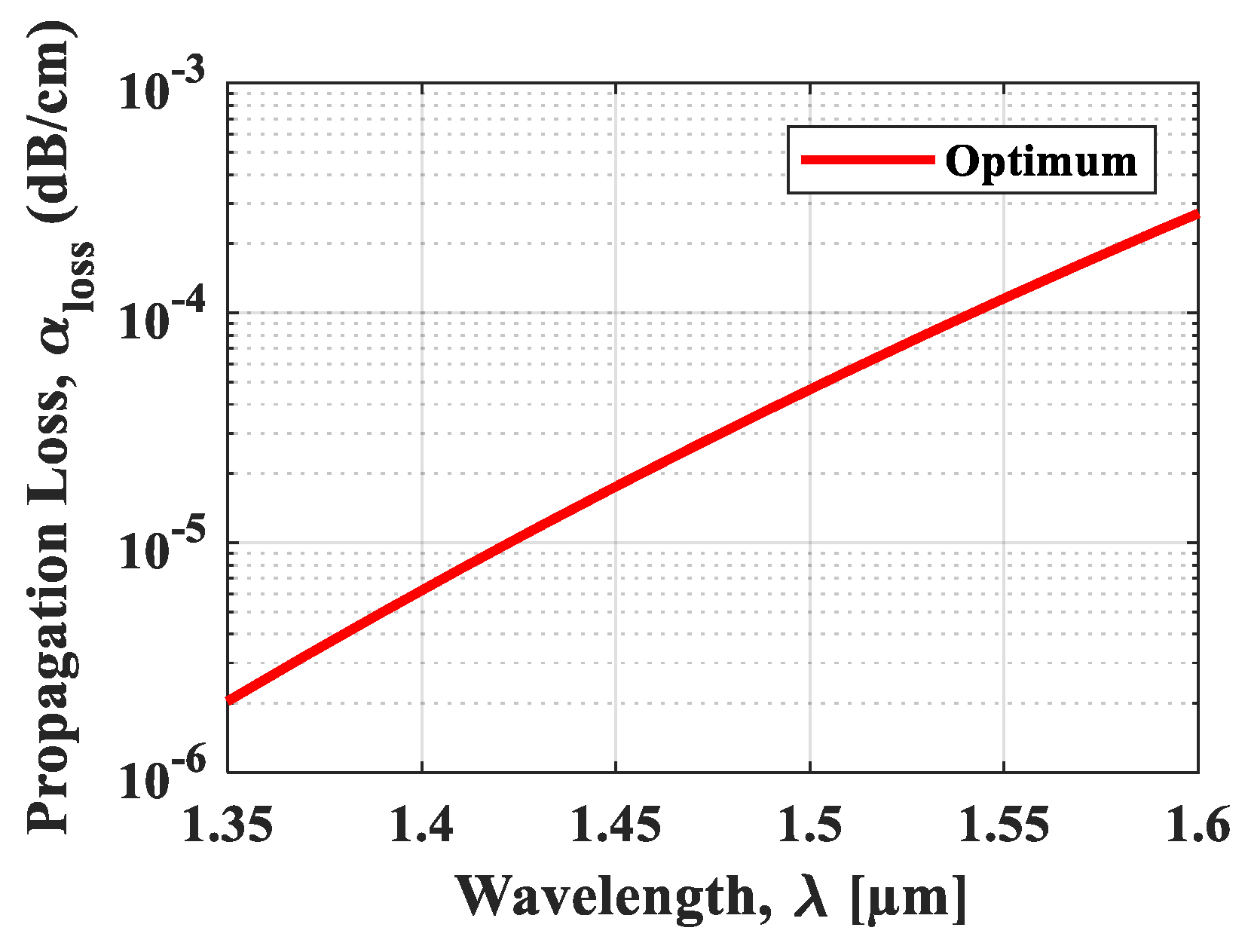
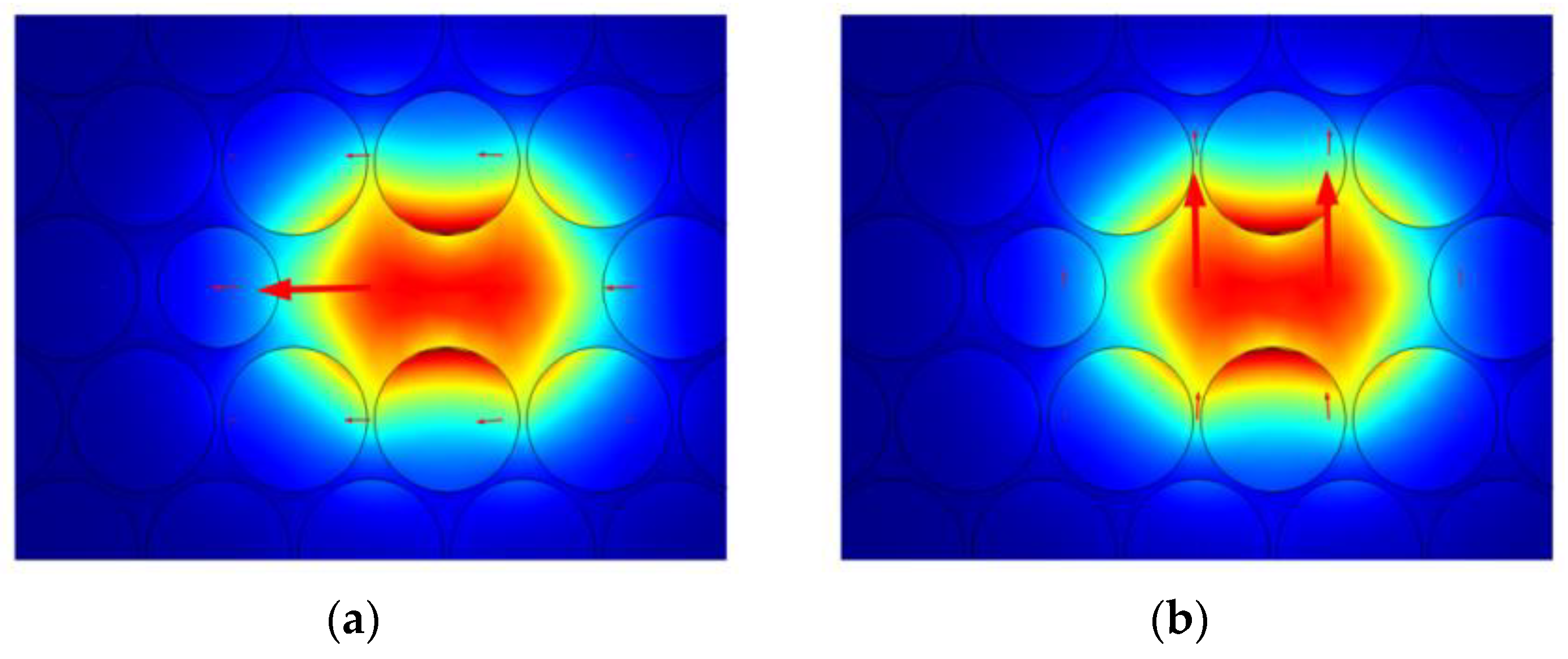
4. Simulation Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sonne, A.; Ouchar, A. Improving of high birefringence photonic crystal fiber with low confinement loss using small elliptical air holes in the core region. J. Mod. Opt. 2015, 62, 588–592. [Google Scholar] [CrossRef]
- Sonne, A.; Ouchar, A.; Sonne, K. Improving of high birefringence with negative dispersion using double octagonal lattice photonic crystal fiber. Int. J. Light Electron Opt. 2016, 127, 8–10. [Google Scholar] [CrossRef]
- Hao, R.; Li, Z.; Sun, G.; Niu, L.; Sun, Y. Analysis on photonic crystal fibers with circular air holes in elliptical configuration. Opt. Fiber Technol. 2013, 19, 363–368. [Google Scholar] [CrossRef]
- Broeng, J.; Mogilevstev, D.; Barkou, S.E.; Bjarklev, A. Photonic crystal fibers: A new class of optical waveguides. Opt. Fiber Technol. 1999, 5, 305–330. [Google Scholar] [CrossRef]
- Malka, D.; Peled, A. Power splitting of 1× 16 in multicore photonic crystal fibers. Appl. Surf. Sci. 2017, 417, 34–39. [Google Scholar] [CrossRef]
- Malka, D.; Cohen, E.; Zalevsky, Z. Design of 4× 1 power beam combiner based on multiCore photonic crystal fiber. Appl. Sci. 2017, 7, 695. [Google Scholar] [CrossRef]
- Malka, D.; Zalevsky, Z. Multicore photonic crystal fiber based 1× 8 two-dimensional intensity splitters/couplers. Electromagnetics 2013, 33, 413–420. [Google Scholar] [CrossRef]
- Malka, D.; Sintov, Y.; Zalevsky, Z. Fiber-laser monolithic coherent beam combiner based on multicore photonic crystal fiber. Opt. Eng. 2013, 54, 011007. [Google Scholar] [CrossRef]
- Sintov, Y.; Malka, D.; Zalevsky, Z. Prospects for diode-pumped alkali-atom-based hollow-core photonic-crystal fiber lasers. Opt. Lett. 2014, 39, 4655–4658. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.; Shen, L. Ultrahigh birefringent photonic crystal fiber with ultralow confinement loss. IEEE Photonics Technol. Lett. 2007, 19, 185–187. [Google Scholar] [CrossRef]
- Wang, W.; Yang, B.; Song, H.; Fan, Y. Investigation of high birefringence and negative dispersion photonic crystal fiber with hybrid crystal lattice. Int. J. Light Electron Opt. 2013, 124, 2901–2903. [Google Scholar] [CrossRef]
- Zhang, M.Y.; Li, S.G.; Yao, Y.Y.; Zhang, L.; Fu, B.; Yin, G.B. Influence of microstructured core on characteristics of photonic crystal fibers. Acta Phys. Sin. 2010, 59, 3278–3284. [Google Scholar]
- Xu, D.; Song, H.; Wang, W.; Fan, Y.; Yang, B. Numerical analysis of a novel high birefringence photonic crystal fiber. Int. J. Light Electron Opt. 2013, 124, 1290–1293. [Google Scholar] [CrossRef]
- Rashid, M.M.; Anower, M.S.; Hasan, M.R.; Tabassum, N. Hexagonal shaped core dodecagonal PCF with high birefringence and nonlinear coefficient. In Proceedings of the International Conference on Electrical, Computer and Communication Engineering (ECCE), Cox’s Bazar, Bangladesh, 16–18 February 2017; pp. 447–450. [Google Scholar]
- Agrawal, A.; Kejalakshmy, N.; Chen, J.; Rahman, B.M.A.; Grattan, K.T.V. Golden spiral photonic crystal fiber: Polarization and dispersion properties. Opt. Lett. 2008, 33, 2716–2718. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, A.; Kejalakshmy, N.; Rahman, B.M.A.; Grattan, K.T.V. Polarization and dispersion properties of elliptical hole golden spiral photonic crystal fiber. Appl. Phys. B 2010, 99, 717–726. [Google Scholar] [CrossRef]
- Revathi, S.; Inbathini, S.R.; Saifudeen, R.A. Highly nonlinear and birefringent spiral photonic crystal fiber. Adv. OptoElectron. 2014, 2014, 464391. [Google Scholar] [CrossRef]
- Revathi, S.; Inabathini, S.; Sandeep, R. Soft glass spiral photonic crystal fiber for large nonlinearity and high birefringence. Opt. Appl. 2015, 45, 15–24. [Google Scholar]
- Shawkat, M.T.B.; Razzak, S.M.A.; Kabir, S. Defected core hybrid cladding photonic crystal fiber with high birefringence & highly negative dispersion properties. In Proceedings of the 2015 IEEE International WIE Conference on Electrical and Computer Engineering (WIECON-ECE), Dhaka, Bangladesh, 19–20 December 2015; pp. 507–510. [Google Scholar]
- Chou Chau, Y.F.; Lim, C.M.; Yoong, V.N.; Syafi’ie Idris, M.N. A simple structure of all circular-air-holes photonic crystal fiber for achieving high birefringence and low confinement loss. J. Appl. Phys. 2015, 118, 243102. [Google Scholar] [CrossRef]
- Yang, T.; Wang, E.; Jiang, H.; Hu, Z.; Xie, K. High birefringence photonic crystal fiber with high nonlinearity and low confinement loss. Opt. Express 2015, 23, 8329–8337. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.T.; Moctader, M.G.; Ahmed, K.; Chowdhury, S. Benzene Shape Photonic Crystal Fiber Based Plasma Sensor: Design and Analysis. Photonic Sens. 2018, 8, 263–269. [Google Scholar] [CrossRef]
- Wang, F.; Sun, Z.; Liu, C.; Sun, T.; Chu, P.K. A highly sensitive dual-core photonic crystal fiber based on a surface plasmon resonance biosensor with silver-graphene layer. Plasmonics 2017, 12, 1847–1853. [Google Scholar] [CrossRef]
- Kumar, S.; Biswas, S.K. Impact of Kerr nonlinearity and stimulated Raman scattering on the whispering gallery modes of an optical microsphere. JOSA B 2016, 33, 1677–1687. [Google Scholar] [CrossRef]
- Hasan, M.R.; Anower, M.S.; Hasan, M.I. Polarization maintaining highly nonlinear photonic crystal fiber with closely lying two zero dispersion wavelengths. Opt. Eng. 2016, 55, 056107. [Google Scholar] [CrossRef]
- Hasan, M.R.; Islam, M.A.; Rifat, A.A.; Hasan, M.I. A single-mode highly birefringent dispersion-compensating photonic crystal fiber using hybrid cladding. J. Mod. Opt. 2017, 64, 218–225. [Google Scholar] [CrossRef]
- Lee, J.H.; Teh, P.C.; Yusoff, Z.; Ibsen, M.; Belardi, W.; Monro, T.M.; Richardson, D.J. A holey fiber-based nonlinear thresholding device for optical CDMA receiver performance enhancement. IEEE Photonics Technol. Lett. 2002, 14, 876–878. [Google Scholar] [CrossRef]
- Haque, M.M.; Rahman, M.S.; Habib, M.S.; Habib, M.S. A single mode hybrid cladding circular photonic crystal fiber dispersion compensation and sensing applications. Photonics Nanostruct. Fundam. Appl. 2015, 14, 63–70. [Google Scholar] [CrossRef]
- Islam, M.I.; Khatun, M.; Ahmed, K. Ultra-high negative dispersion compensating square lattice based single mode photonic crystal fiber with high nonlinearity. Opt. Rev. 2017, 24, 147–155. [Google Scholar] [CrossRef]
- Hasan, M.I.; Habib, M.S.; Razzak, S.M.A. An elliptical-shaped core residual dispersion compensating octagonal photonic crystal fiber. IEEE Photonics Technol. Lett. 2014, 26, 2047–2050. [Google Scholar] [CrossRef]
- Issa, N.A.; van Eijkelenborg, M.A.; Fellew, M.; Cox, F.; Henry, G.; Large, M.C. Fabrication and study of microstructured optical fibers with elliptical holes. Opt. Lett. 2004, 29, 1336–1338. [Google Scholar] [CrossRef] [PubMed]
- Bise, R.T.; Trevor, D. Solgel-derived microstructured fibers: Fabrication and characterization. In Proceedings of the Optical Fiber Communication Conference (OWL6), Anaheim, CA, USA, 6 March 2005. [Google Scholar]
- Argyros, A.; Bassett, I.M.; Van Eijkelenborg, M.A.; Large, M.C.; Zagari, J.; Nicorovici, N.A.; McPhedran, R.C.; de Sterke, C.M. Ring structures in microstructured polymer optical fibres. Opt. Express 2001, 9, 813–820. [Google Scholar] [CrossRef] [PubMed]
- Shao, J.; Kumar, S. Optical backpropagation for fiber-optic communications using optical phase conjugation at the receiver. Opt. Lett. 2012, 37, 3012–3014. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Yang, D. Optical backpropagation for fiber-optic communications using highly nonlinear fibers. Opt. Lett. 2011, 36, 1038–1040. [Google Scholar] [CrossRef] [PubMed]

| Reference | D(λ) (ps/(nm km)) | B = |nx − ny| (×10−2) | γ (W−1 km−1) | Air-Hole Nature |
|---|---|---|---|---|
| [21] | --- | 2.200 | 68.00 | Circular |
| [26] | −578.50 | 2.640 | 53.10 | Circular |
| [30] | −544.70 | 2.20 | 52.7 | Circular and elliptical |
| [28] | −650.00 | 2.10 | 45.50 | Circular |
| [29] | −1694.80 | --- | 92.83 | Circular and elliptical |
| Proposed PCF | −753.20 | 3.87 | 96.51 | Circular |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Biswas, S.K.; Islam, S.M.R.; Islam, M.R.; Mia, M.M.A.; Sayem, S.; Ahmed, F. Design of an Ultrahigh Birefringence Photonic Crystal Fiber with Large Nonlinearity Using All Circular Air Holes for a Fiber-Optic Transmission System. Photonics 2018, 5, 26. https://doi.org/10.3390/photonics5030026
Biswas SK, Islam SMR, Islam MR, Mia MMA, Sayem S, Ahmed F. Design of an Ultrahigh Birefringence Photonic Crystal Fiber with Large Nonlinearity Using All Circular Air Holes for a Fiber-Optic Transmission System. Photonics. 2018; 5(3):26. https://doi.org/10.3390/photonics5030026
Chicago/Turabian StyleBiswas, Shovasis Kumar, S. M. Rakibul Islam, Md. Rubayet Islam, Mohammad Mahmudul Alam Mia, Summit Sayem, and Feroz Ahmed. 2018. "Design of an Ultrahigh Birefringence Photonic Crystal Fiber with Large Nonlinearity Using All Circular Air Holes for a Fiber-Optic Transmission System" Photonics 5, no. 3: 26. https://doi.org/10.3390/photonics5030026
APA StyleBiswas, S. K., Islam, S. M. R., Islam, M. R., Mia, M. M. A., Sayem, S., & Ahmed, F. (2018). Design of an Ultrahigh Birefringence Photonic Crystal Fiber with Large Nonlinearity Using All Circular Air Holes for a Fiber-Optic Transmission System. Photonics, 5(3), 26. https://doi.org/10.3390/photonics5030026







