Considerations and Framework for Foveated Imaging Systems †
Abstract
1. Introduction and Motivation
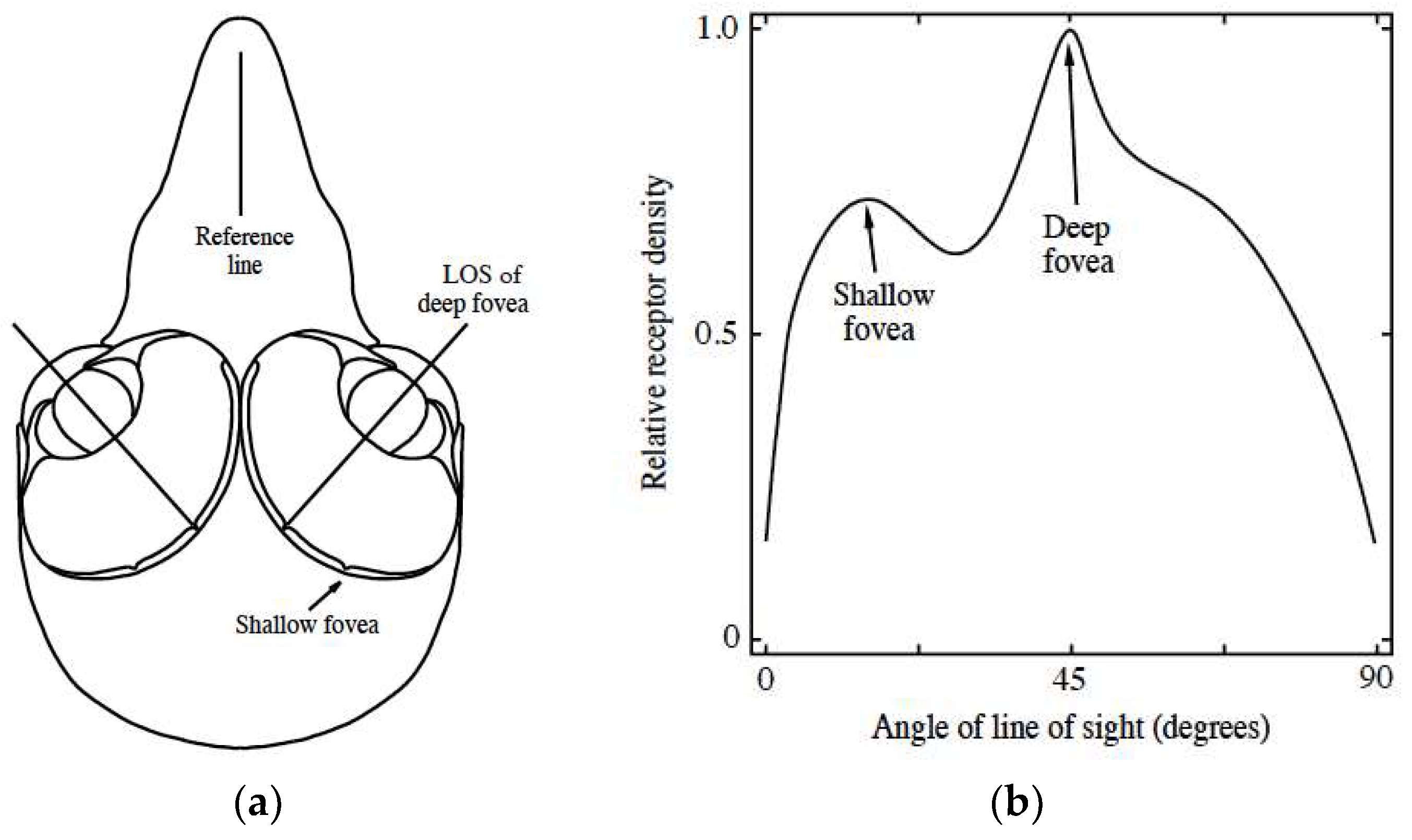
1.1. Features of Raptors’ Vision
1.2. Prior Work on Foveated Imaging
1.3. Motivation for Present Work
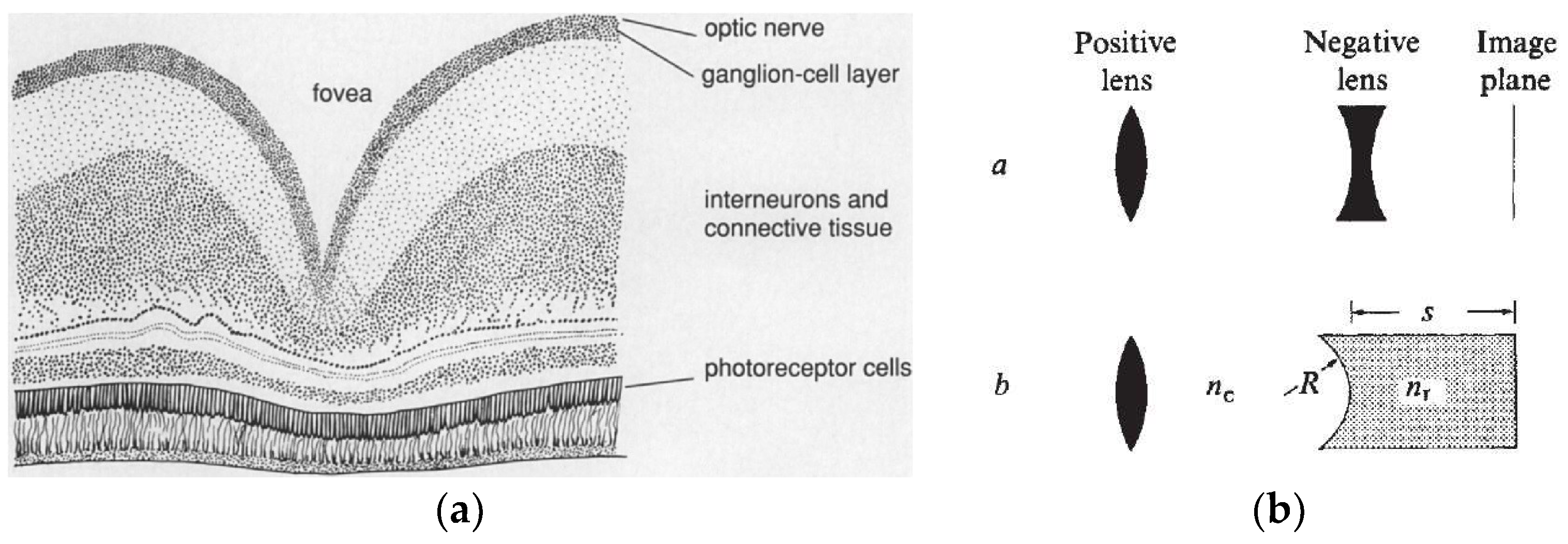
2. Raptor Eye Characteristics
3. Optical Approach to Foveated Imaging
3.1. Optical Considerations
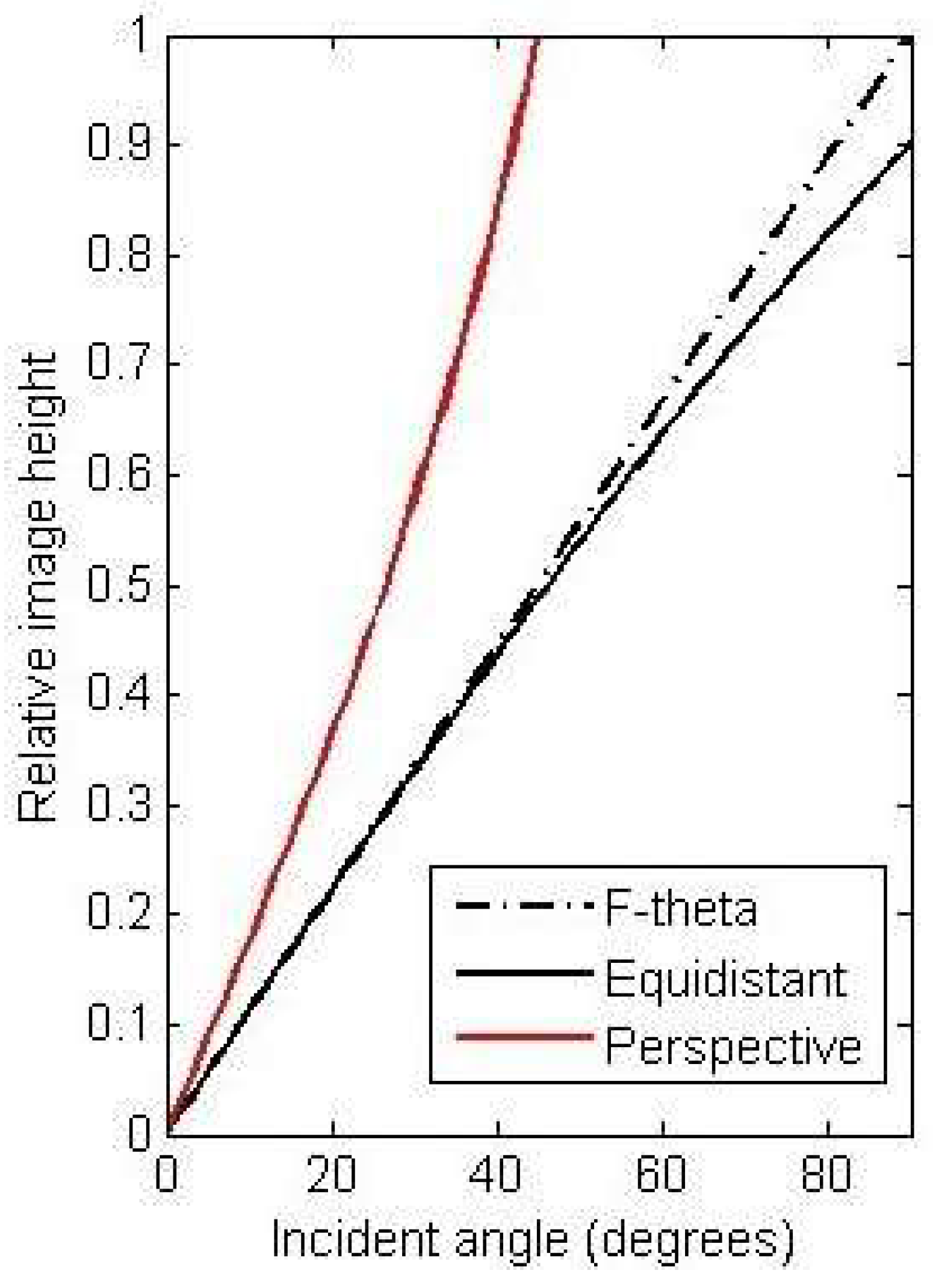
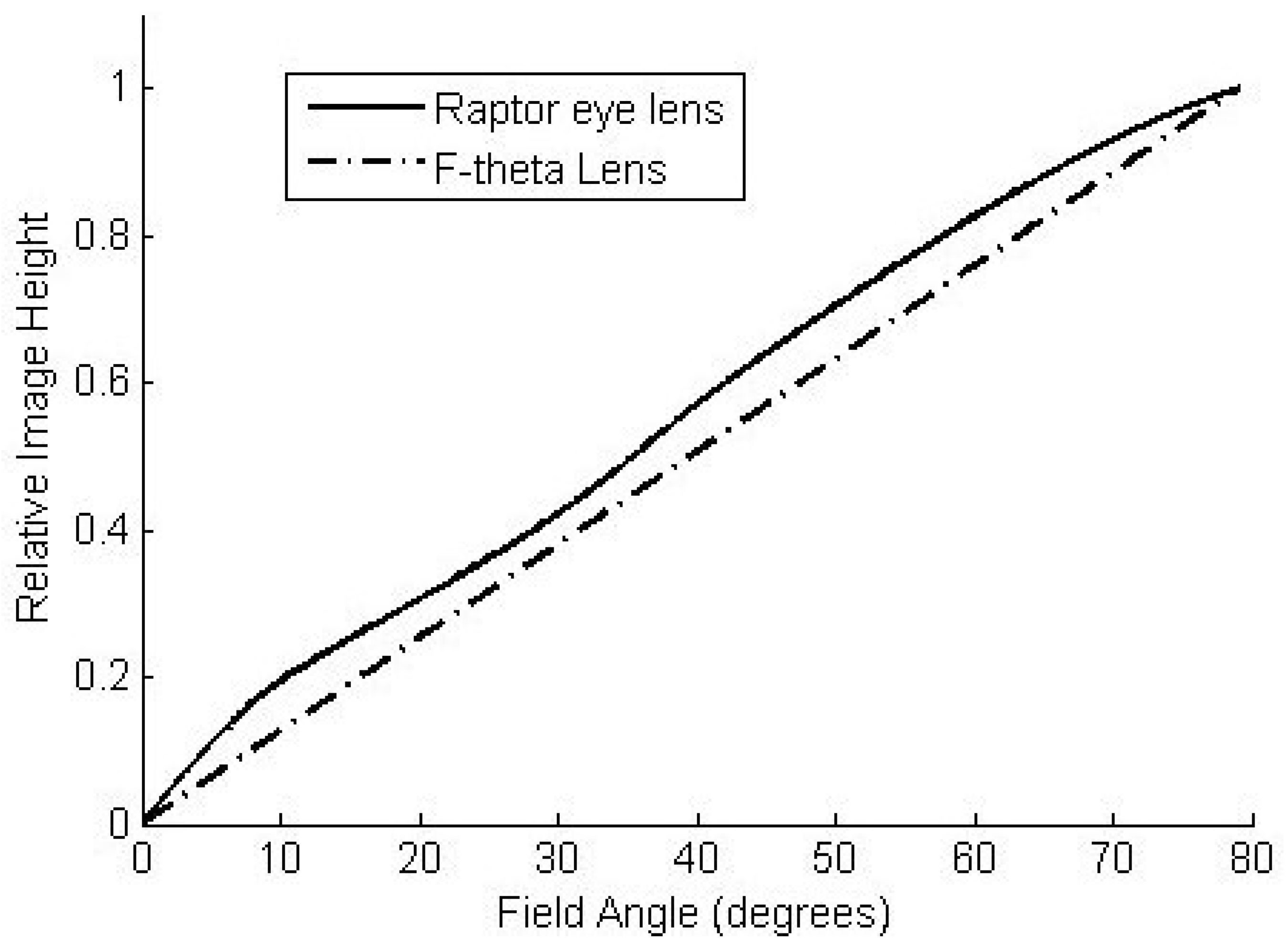
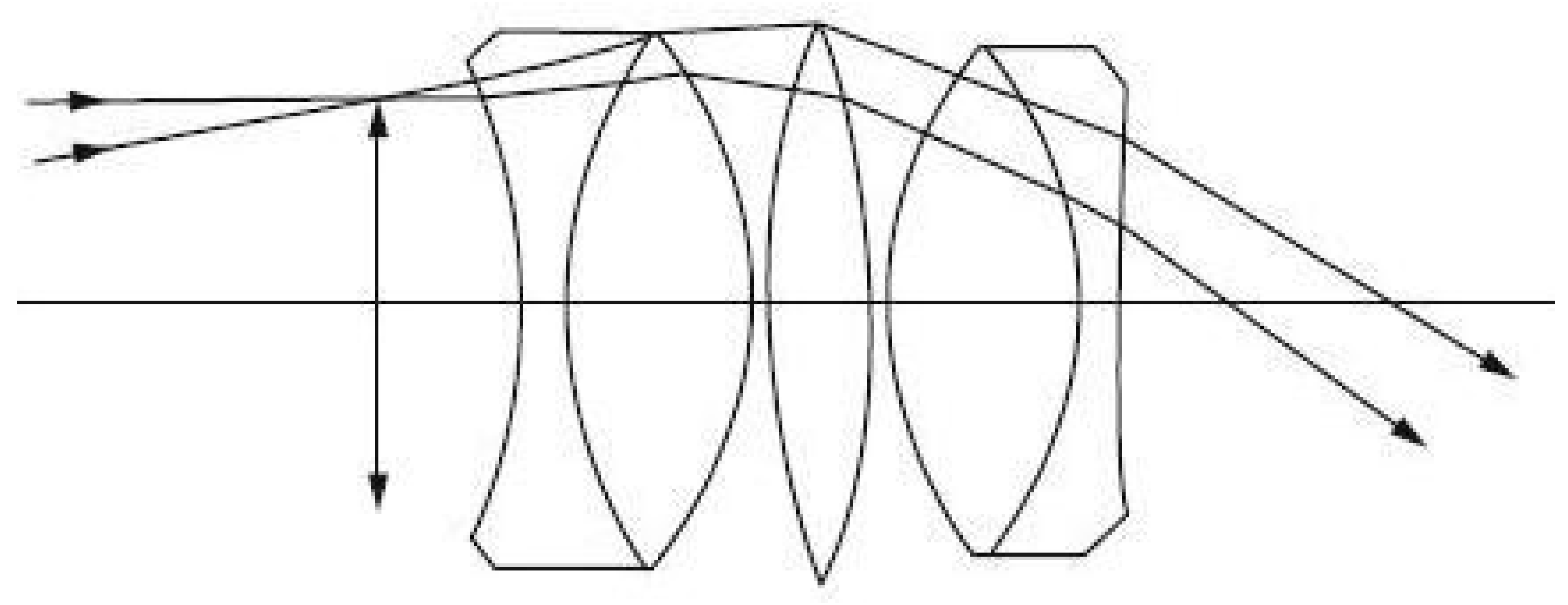
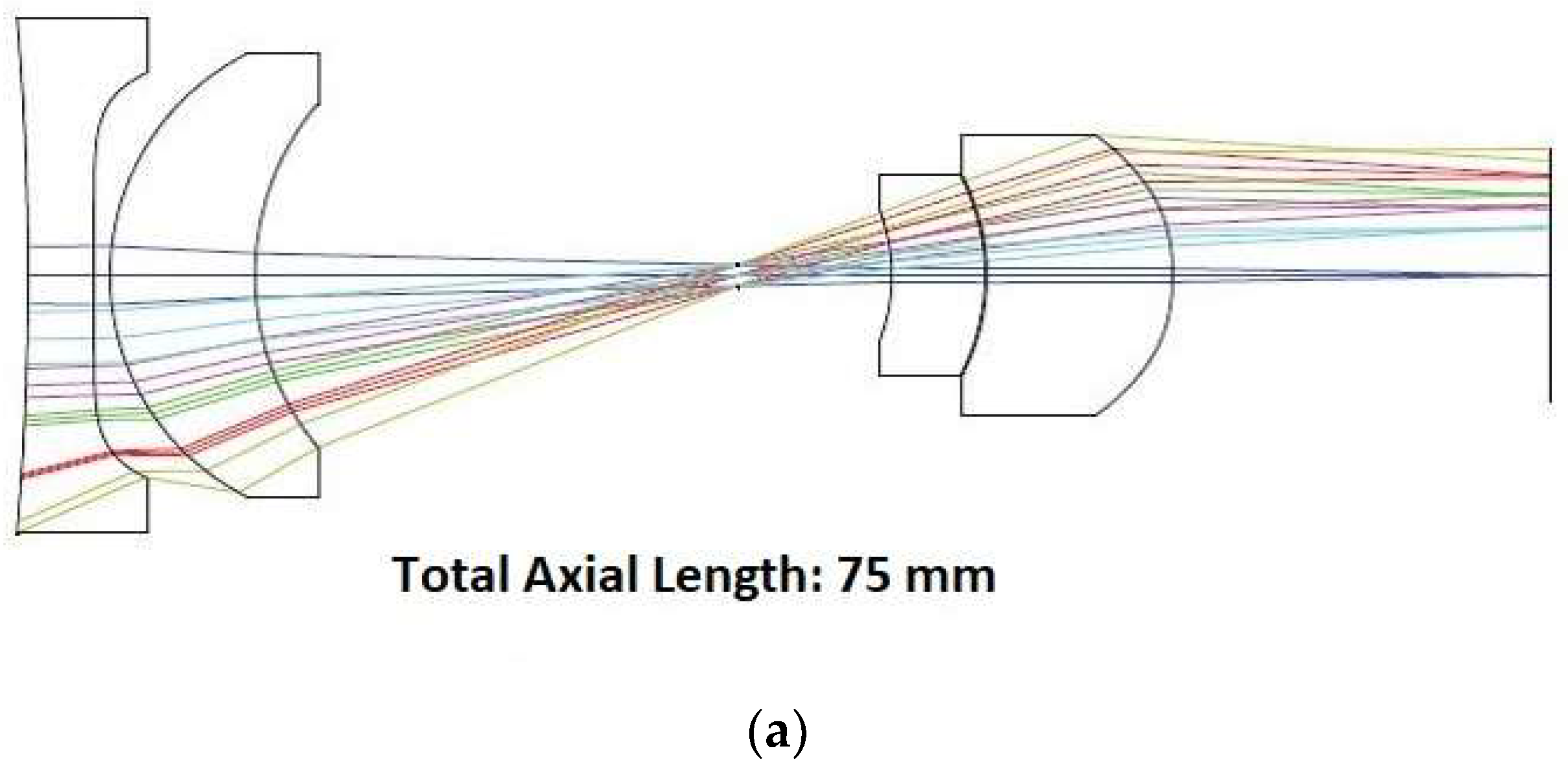
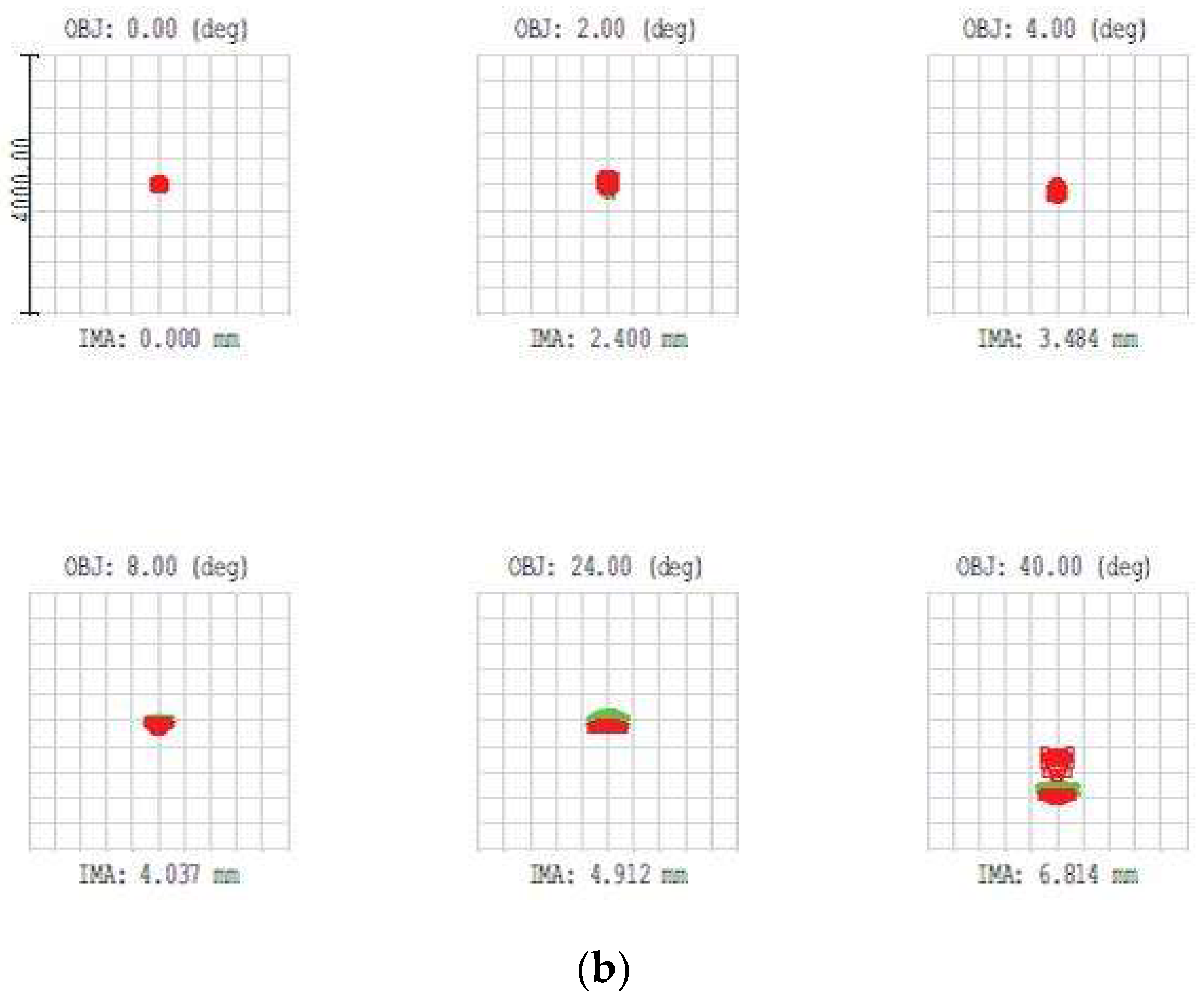
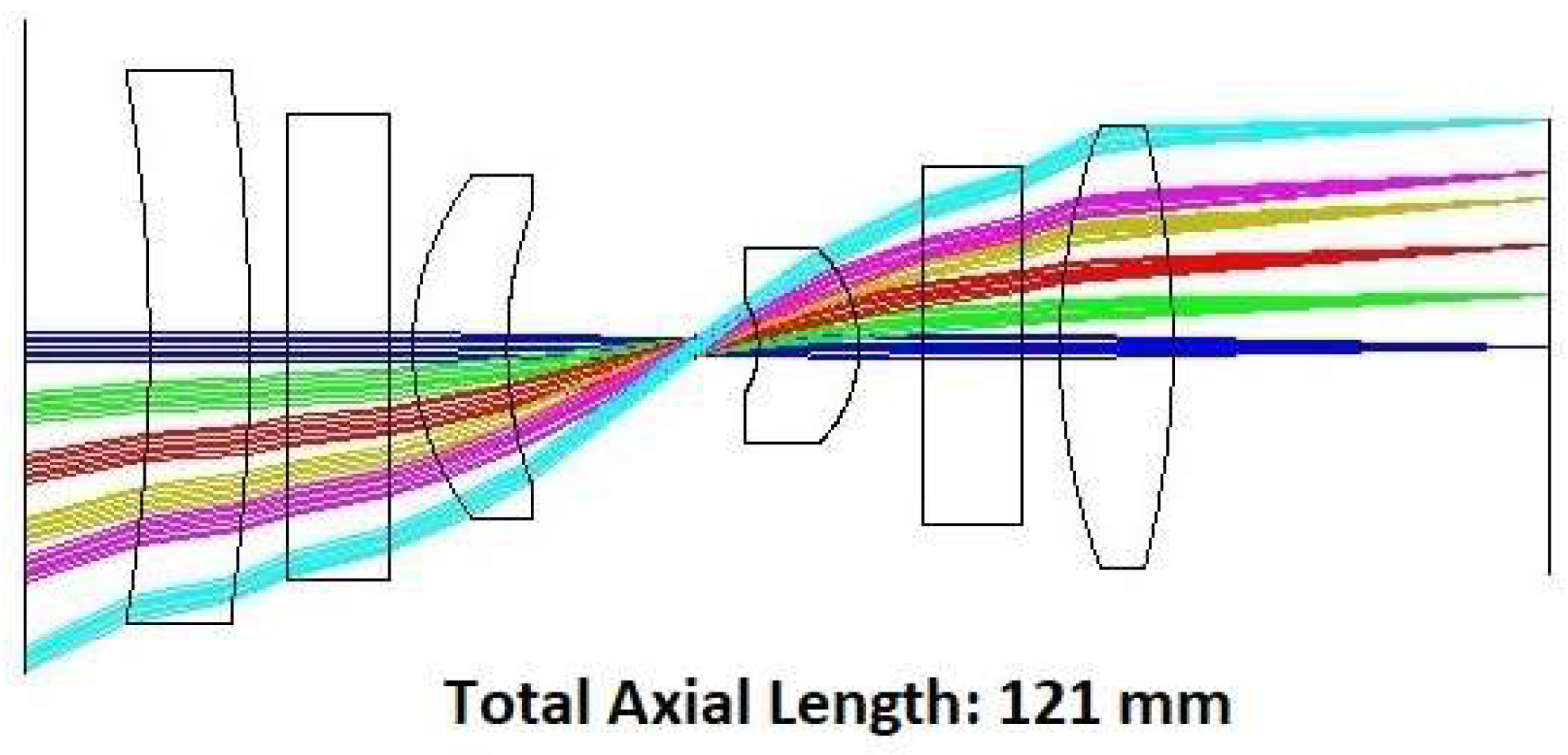
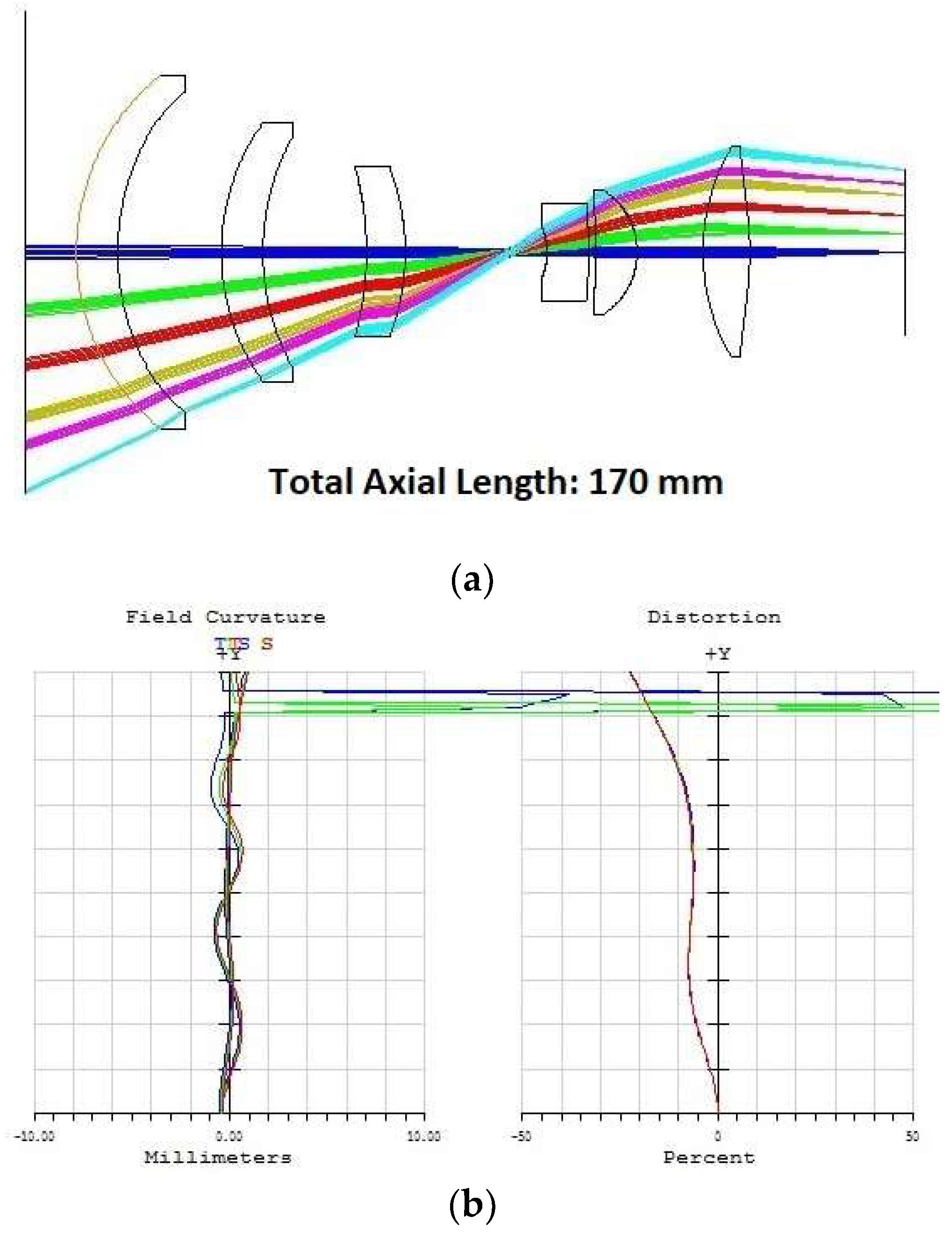
3.2. Lens Design in Sequential Mode
3.3. Issues Related to Optical Approach to Foveated Imaging
4. Electronic Approach to Foveated Imaging
4.1. Scale Issues in Foveated Image Processing
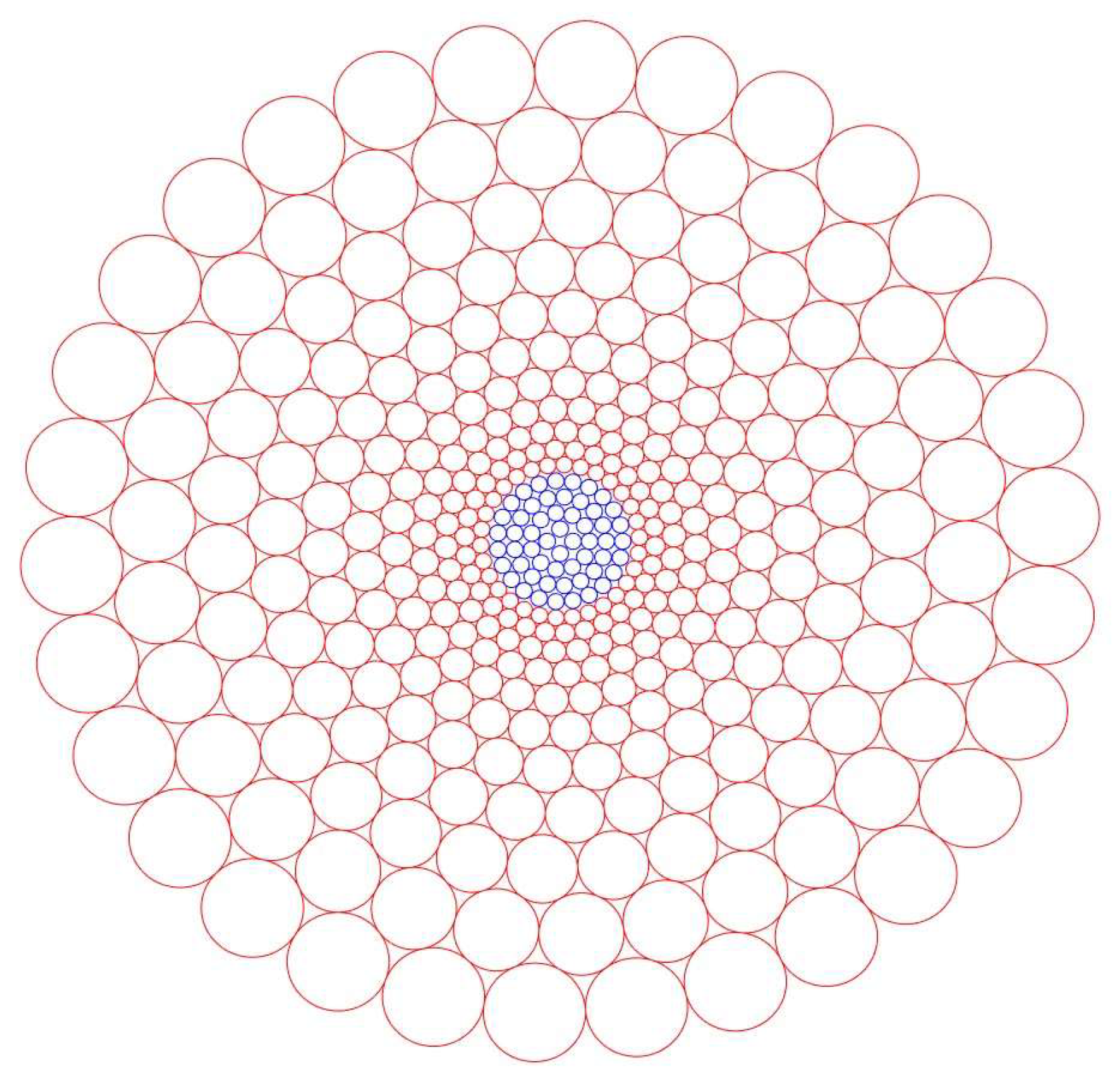
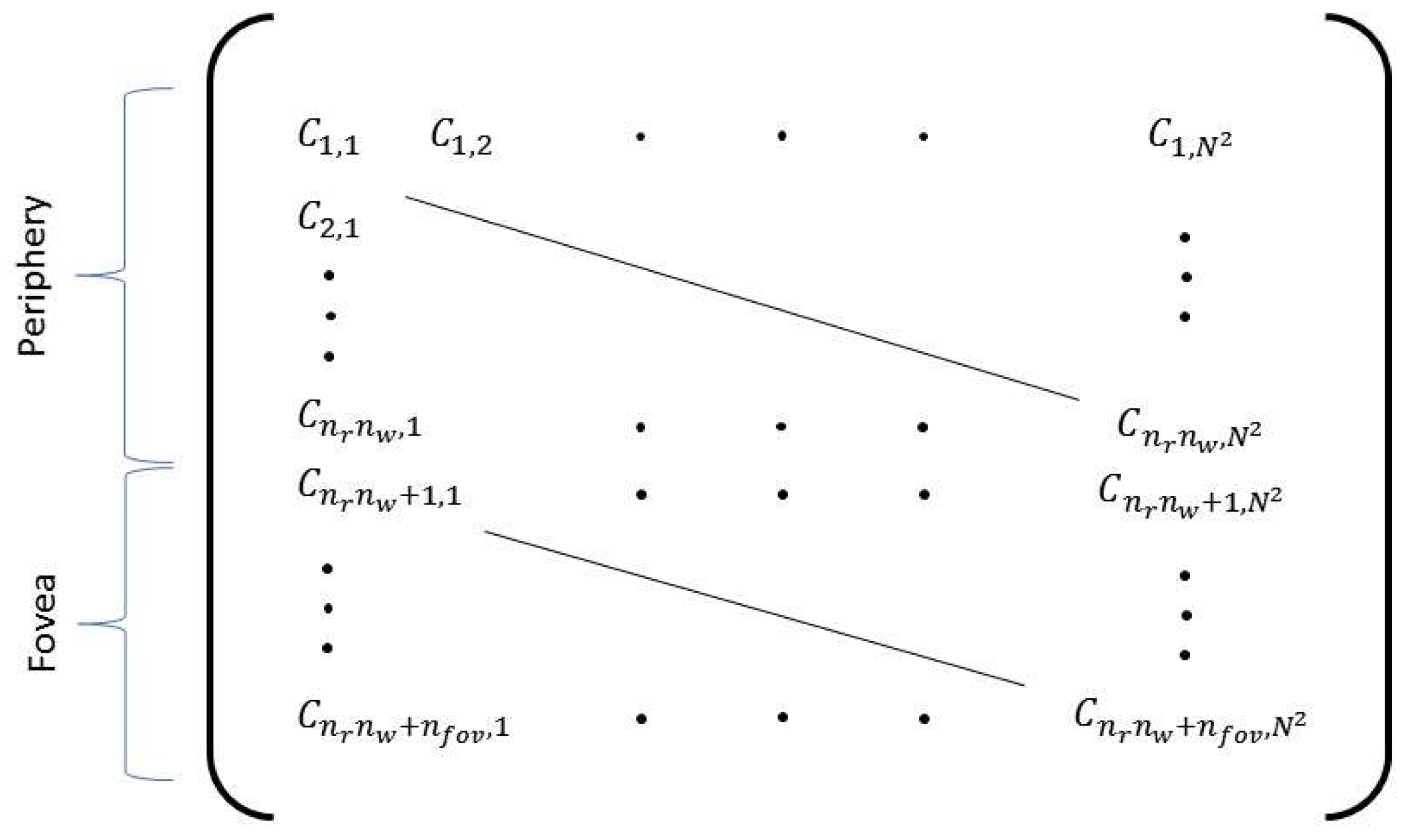
4.2. Receptive Field Layout
4.3. Foveated Downsampling
4.4. Issues Related to Electronic Approach to Foveated Imaging
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Locket, N.A. Problems of deep foveas. Aust. N. Z. J. Ophthalmol. 1992, 20, 281–295. [Google Scholar] [CrossRef] [PubMed]
- Snyder, A.W.; Miller, W.H. Telephoto lens system of falconiform eyes. Nature 1978, 275, 127–129. [Google Scholar] [CrossRef] [PubMed]
- Reymond, L. Spatial visual-acuity of the eagle Aquila-Audax: A behavioral, optical and anatomical investigation. Vis. Res. 1985, 25, 1477–1491. [Google Scholar] [CrossRef]
- Klemas, V.V. Remote sensing and navigation in the animal world: An overview. Sens. Rev. 2013, 33, 3–13. [Google Scholar] [CrossRef]
- Murphy, C.J.; Howland, H.C. Owl eyes: Accommodation, corneal curvature and refractive state. J. Comp. Physiol. 1983, 151, 277–284. [Google Scholar] [CrossRef]
- Melnyk, P.B.; Messner, R.A. Biologically motivated composite image sensor for deep-field target tracking. In Proceedings of the SPIE Conference on Vision Geometry XV, San Jose, CA, USA, 28 January–1 February 2007; pp. 649905-1–649905-8. [Google Scholar]
- Curatu, G.; Harvey, J.E. Lens design and system optimization for foveated imaging. In Proceedings of the SPIE Conference on Current Developments in Lens Design and Optical Engineering IX, San Diego, CA, USA, 10–14 August 2008; pp. 70600P-1–70600P-9. [Google Scholar]
- Du, X.; Chang, J.; Zhang, Y.; Wang, X.; Zhang, B.; Gao, L.; Xiao, L. Design of a dynamic dual-foveated imaging system. Opt. Express 2015, 23, 26032–26040. [Google Scholar] [CrossRef] [PubMed]
- McCarley, P.L.; Massie, M.A.; Curzan, J.P. Large format variable spatial acuity superpixel imaging: Visible and infrared systems applications. In Proceedings of the SPIE Conference on Infrared Technology and Applications XXX, Orlando, FL, USA, 12–16 April 2004; pp. 361–369. [Google Scholar]
- McCarley, P.L.; Massie, M.A.; Curzan, J.P. Foveating infrared image sensors. In Proceedings of the SPIE Conference on Infrared Systems and Photoelectronic Technology II, San Diego, CA, USA, 26–30 August 2007; pp. 666002-1–666002-14. [Google Scholar]
- Bryant, K.R. Foveated optics. In Proceedings of the SPIE Conference on Advanced Optics for Defense Applications: UV through LWIR, Baltimore, MD, USA, 17–19 April 2016; pp. 982216-1–982216-11. [Google Scholar]
- Thibault, S. Enhanced surveillance system based on panomorph panoramic lenses. In Proceedings of the SPIE Conference on Optics and Photonics in Global Homeland Security III, Orlando, FL, USA, 9–13 April 2007; pp. 65400E-1–65400E-8. [Google Scholar]
- Ҫöltekin, A.; Haggrén, H. Stereo foveation. Photogramm. J. Finl. 2006, 20, 45–53. [Google Scholar]
- Schindler, K. Geometry and construction of straight lines in log-polar images. Comput. Vis. Image Underst. 2006, 103, 196–207. [Google Scholar] [CrossRef]
- Tabernero, A.; Portilla, J.; Navarro, R. Duality of log-polar image representations in the space and spatial-frequency domains. IEEE Trans. Signal Process. 1999, 47, 2469–2479. [Google Scholar] [CrossRef]
- Wang, Z.; Lu, L.; Bovik, A.C. Foveation scalable video coding with automatic fixation selection. IEEE Trans. Image Process. 2003, 12, 243–254. [Google Scholar] [CrossRef] [PubMed]
- Itti, L. Automatic foveation for video compression using a neurobiological model of visual attention. IEEE Trans. Image Process. 2004, 13, 1304–1318. [Google Scholar] [CrossRef] [PubMed]
- Hua, H.; Liu, S. Dual-sensor foveated imaging system. Appl. Opt. 2008, 47, 317–327. [Google Scholar] [CrossRef] [PubMed]
- Belay, G.Y.; Ottevaere, H.; Meuret, Y.; Vervaeke, M.; Van Erps, J.; Thienpont, H. Demonstration of a multichannel, multiresolution imaging system. Appl. Opt. 2013, 52, 6081–6089. [Google Scholar] [CrossRef] [PubMed]
- Carles, G.; Muyo, G.; Bustin, N.; Wood, A.; Harvey, A.R. Compact multi-aperture imaging with high angular resolution. J. Opt. Soc. Am. A 2015, 32, 411–419. [Google Scholar] [CrossRef] [PubMed]
- Carles, G.; Chen, S.; Bustin, N.; Downing, J.; McCall, D.; Wood, A.; Harvey, A.R. Multi-aperture foveated imaging. Opt. Lett. 2016, 41, 1869–1872. [Google Scholar] [CrossRef] [PubMed]
- Carles, G.; Babington, J.; Wood, A.; Ralph, J.F.; Harvey, A.R. Superimposed multi-resolution imaging. Opt. Express 2017, 25, 33043–33055. [Google Scholar] [CrossRef]
- Long, A.D.; Narayanan, R.M.; Kane, T.J.; Rice, T.F.; Tauber, M.J. Analysis and implementation of the foveated vision of the raptor eye. In Proceedings of the SPIE Conference on Image Sensing Technologies: Materials, Devices, Systems, and Applications III, Baltimore, MD, USA, 20–21 April 2016; pp. 98540T-1–98540T-9. [Google Scholar]
- Long, A.D.; Narayanan, R.M.; Kane, T.J.; Rice, T.F.; Tauber, M.J. Foveal scale space generation with the log-polar transform. In Proceedings of the SPIE Conference on Image Sensing Technologies: Materials, Devices, Systems, and Applications IV, Anaheim, CA, USA, 12–13 April 2017; pp. 1020910-1–1020910-8. [Google Scholar]
- Walls, G.L. Significance of the foveal depression. Arch. Ophthalmol. 1937, 18, 912–919. [Google Scholar] [CrossRef]
- Waldvogel, J.A. The bird’s eye view. Am. Sci. 1990, 78, 342–353. [Google Scholar]
- Tucker, V. The deep fovea, sideways vision and spiral flight paths in raptors. J. Exp. Biol. 2000, 203, 3745–3754. [Google Scholar] [PubMed]
- Traver, V.J.; Bernardino, A. A review of log-polar imaging for visual perception in robotics. Rob. Auton. Syst. 2010, 58, 378–398. [Google Scholar] [CrossRef]
- Kingslake, R.; Johnson, R.B. Lens Design Fundamentals; Academic Press: Burlington, MA, USA, 2010; pp. 501–512. [Google Scholar]
- Samy, A.M.; Gao, Z. Fovea-stereographic: A projection function for ultra-wide-angle cameras. Opt. Eng. 2015, 54, 045104-1–045104-8. [Google Scholar] [CrossRef]
- Shimizu, S.; Hashizume, T. Development of micro wide angle fovea lens–Lens design and production of prototype. IEEJ J. Ind. Appl. 2013, 2, 55–60. [Google Scholar]
- Shimizu, S.; Tanzawa, Y.; Hashizume, T. Development of wide angle fovea telescope. IEEJ J. Ind. Appl. 2014, 3, 368–373. [Google Scholar]
- Nagy, J.G.; O’Leary, D.P. Restoring images degraded by spatially variant blur. SIAM J. Sci. Comput. 1988, 19, 1063–1082. [Google Scholar] [CrossRef]
- Šorel, M.; Šroubek, F. Space-variant deblurring using one blurred and one underexposed image. In Proceedings of the 16th IEEE International Conference on Image Processing (ICIP’09), Cairo, Egypt, 7–10 November 2009; pp. 157–160. [Google Scholar]
- Araujo, H.; Dias, J.M. An introduction to the log-polar mapping. In Proceedings of the 2nd IEEE Workshop on Cybernetic Vision, Sao Carlos, Brazil, 9–11 December 1996; pp. 139–144. [Google Scholar]
- Bolduc, M.; Levine, M.D. A review of biologically motivated space-variant data reduction models for robotic vision. Comput. Vis. Image Underst. 1998, 69, 170–184. [Google Scholar] [CrossRef]
- Griffin, G.; Holub, A.; Perona, P. Caltech-256 Object Category Dataset; California Institute of Technology Technical Report 7694; California Institute of Technology: Pasadena, CA, USA, 2007. [Google Scholar]
- Koenderink, J.J. The structure of images. Biol. Cybern. 1984, 50, 363–370. [Google Scholar] [CrossRef] [PubMed]
- Lindeberg, T. Scale-space theory: A basic tool for analyzing structures at different scales. J. Appl. Stat. 1994, 21, 225–270. [Google Scholar] [CrossRef]
- Witkin, A. Scale-space filtering: A new approach to multi-scale description. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP’84), San Diego, CA, USA, 19–21 March 1984; Volume 9, pp. 150–153. [Google Scholar]
- Lindeberg, T.; Florack, L. Foveal Scale-Space and the Linear Increase of Receptive Field Size as a Function of Eccentricity; KTH Royal Institute of Technology Technical Report ISRN KTH NA/P-94/27-SE; KTH Royal Institute of Technology: Stockholm, Sweden, 1994. [Google Scholar]
- Matungka, R.; Zheng, Y.F.; Ewing, R.L. 2D invariant object recognition using log-polar transform. In Proceedings of the 7th World Congress on Intelligent Control and Automation (WCICA 2008), Chongqing, China, 25–27 June 2008; pp. 223–228. [Google Scholar]
- Pamplona, D.; Bernardino, A. Smooth foveal vision with Gaussian receptive fields. In Proceedings of the 9th IEEE-RAS International Conference on Humanoid Robots, Paris, France, 7–10 December 2009; pp. 223–229. [Google Scholar]
- Chambers, D.R.; Flannigan, C.; Wheeler, B. High-accuracy real-time pedestrian detection system using 2D and 3D features. In Proceedings of the SPIE Conference on Three-Dimensional Imaging, Visualization, and Display 2012, Baltimore, MD, USA, 24–25 April 2012; pp. 83840G-1–83840G-11. [Google Scholar]
- Hao, Q.; Wang, Z.; Cao, J.; Zhang, F. A hybrid bionic image sensor achieving FOV extension and foveated imaging. Sensors 2018, 18, 1042. [Google Scholar] [CrossRef] [PubMed]





© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Narayanan, R.M.; Kane, T.J.; Rice, T.F.; Tauber, M.J. Considerations and Framework for Foveated Imaging Systems †. Photonics 2018, 5, 18. https://doi.org/10.3390/photonics5030018
Narayanan RM, Kane TJ, Rice TF, Tauber MJ. Considerations and Framework for Foveated Imaging Systems †. Photonics. 2018; 5(3):18. https://doi.org/10.3390/photonics5030018
Chicago/Turabian StyleNarayanan, Ram M., Timothy J. Kane, Terence F. Rice, and Michael J. Tauber. 2018. "Considerations and Framework for Foveated Imaging Systems †" Photonics 5, no. 3: 18. https://doi.org/10.3390/photonics5030018
APA StyleNarayanan, R. M., Kane, T. J., Rice, T. F., & Tauber, M. J. (2018). Considerations and Framework for Foveated Imaging Systems †. Photonics, 5(3), 18. https://doi.org/10.3390/photonics5030018





