Impedance-Matched, Double-Zero Optical Metamaterials Based on Weakly Resonant Metal Oxide Nanowires
Abstract
1. Introduction
2. Results
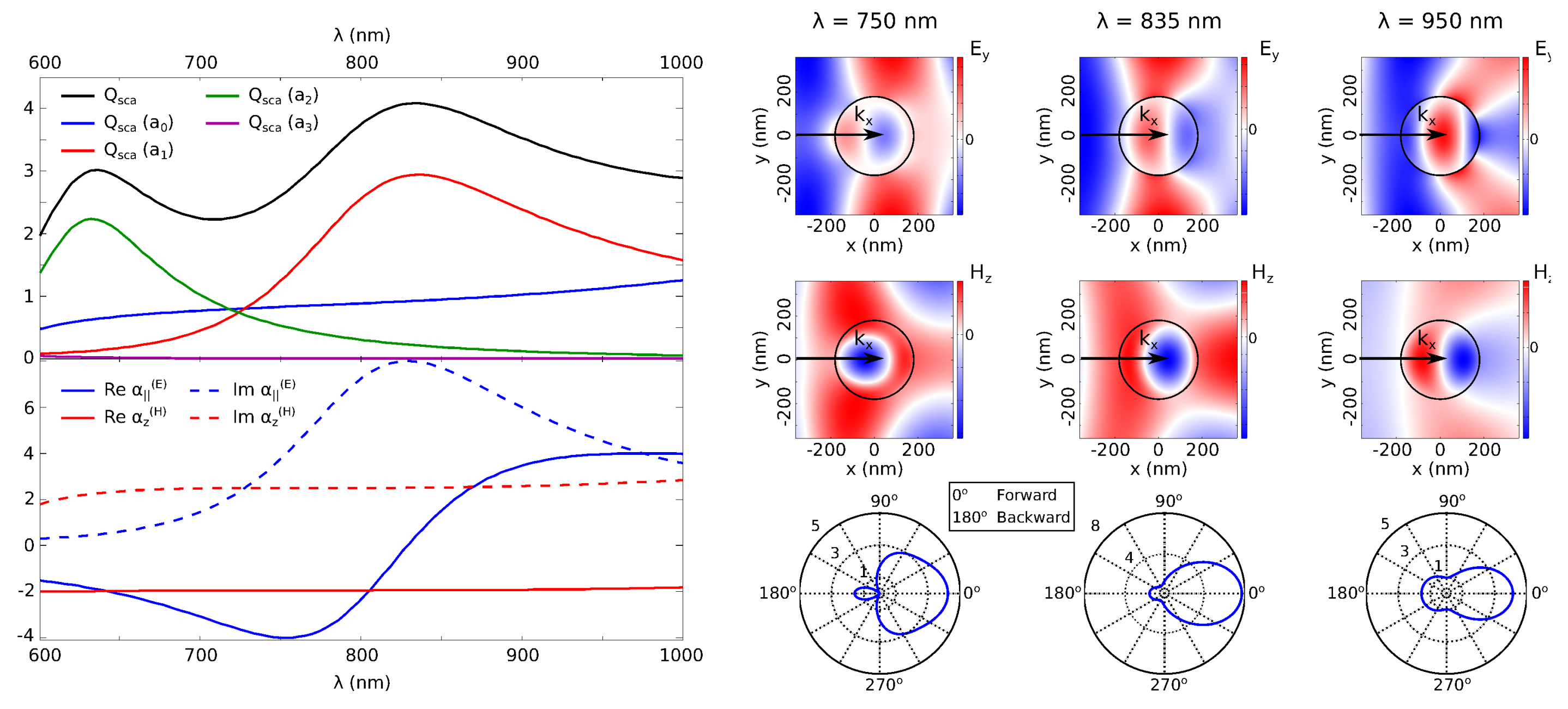
2.1. An Effective Medium Approach
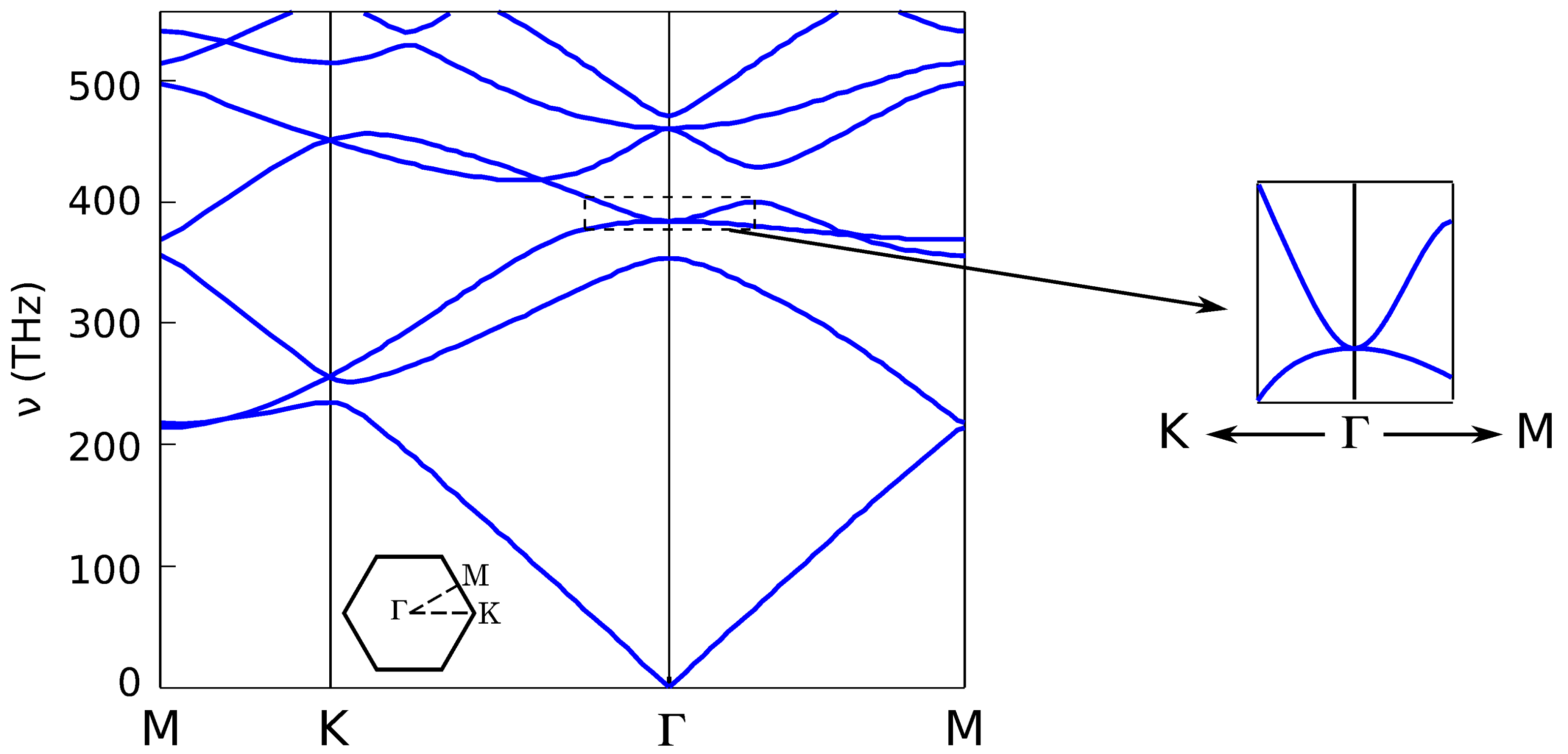
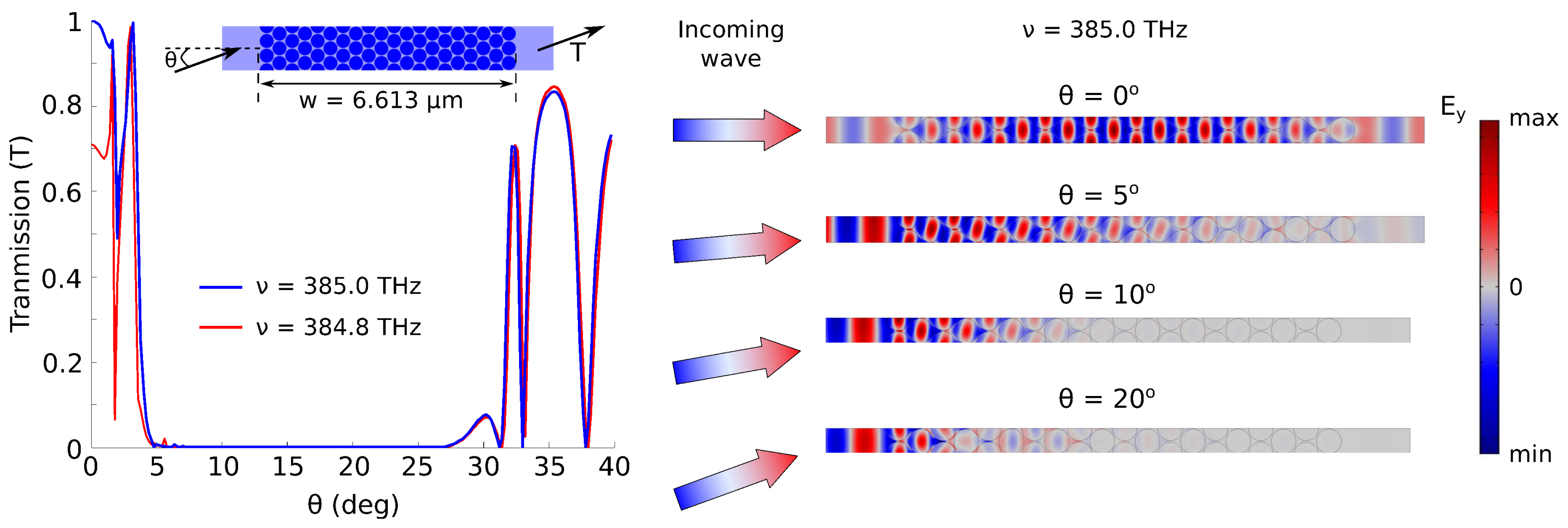
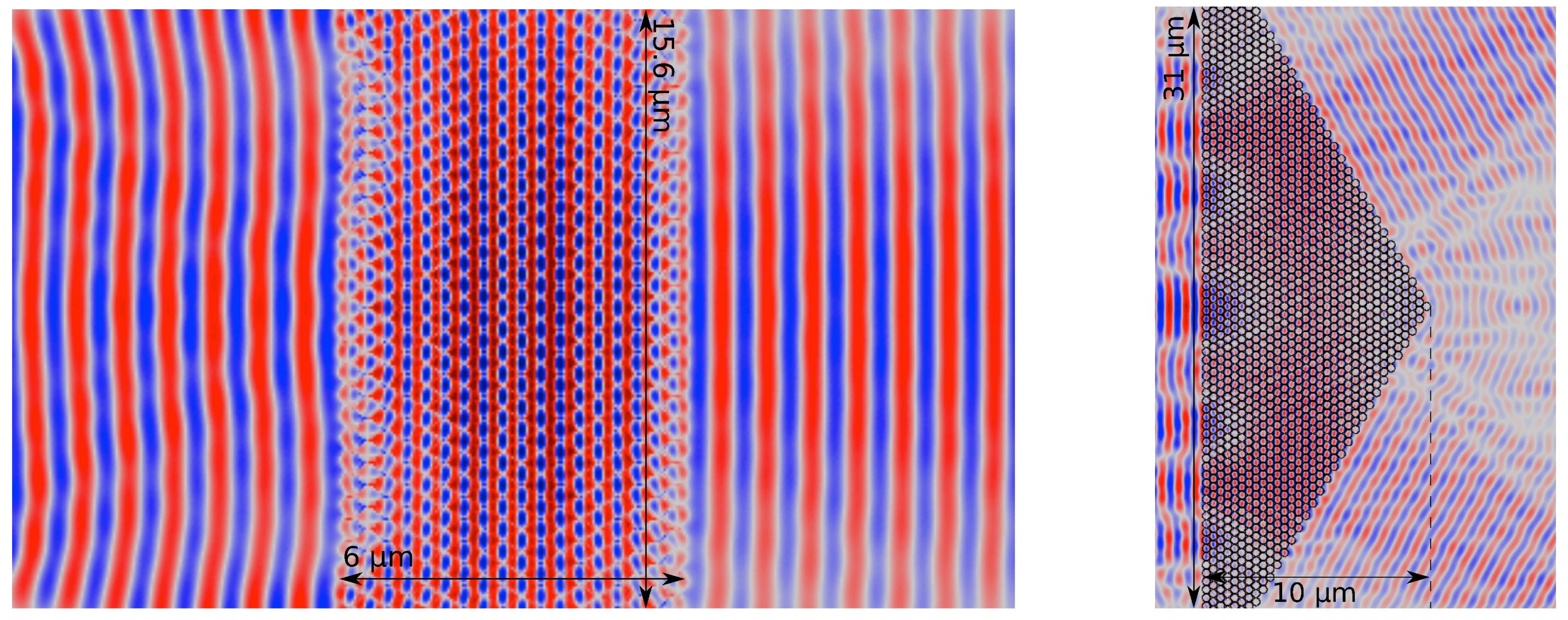
2.2. Numerical Calculations: Double-Zero Metamaterials
3. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| ENZ | -near-zero |
| DZM | Double-zero metamaterials |
| TE | Transverse electric |
| TM | Transverse magnetic |
| EM | Electromagnetic |
References
- Smith, D.; Padilla, W.; Vier, D.; Nemat-Nasser, S.; Schultz, S. Composite Medium with Simultaneously Negative Permeability and Permittivity. Phys. Rev. Lett. 2000, 84, 4184–4187. [Google Scholar] [CrossRef] [PubMed]
- Pendry, J.B. Negative refraction makes a perfect lens. Phys. Rev. Lett. 2000, 85, 3966–3969. [Google Scholar] [CrossRef] [PubMed]
- Engheta, N.; Ziolkowski, R. Metamaterials, Physics and Engineering Explorations; IEEE-Wiley: New York, NY, USA, 2006. [Google Scholar]
- Marques, R.; Martin, F.; Sorolla, M. Metamaterials with Negative Parameters: Theory, Design and Microwave Applications; Wiley: New York, NY, USA, 2007. [Google Scholar]
- Enoch, S.; Tayeb, G.; Sabouroux, P.; Guérin, N.; Vincent, P. A Metamaterial for Directive Emission. Phys. Rev. Lett. 2002, 89, 213902. [Google Scholar] [CrossRef] [PubMed]
- Ziolkowski, R. Propagation in and scattering from a matched metamaterial having a zero index of refraction. Phys. Rev. E 2004, 70, 046608. [Google Scholar] [CrossRef] [PubMed]
- Engheta, N. Pursuing Near-Zero Response. Science 2013, 340, 286–287. [Google Scholar] [CrossRef] [PubMed]
- Liberal, I.; Engheta, N. The rise of near-zero-index technologies. Science 2017, 358, 1540–1541. [Google Scholar] [CrossRef] [PubMed]
- Liberal, I.; Engheta, N. Near-zero refractive index photonics. Nat. Photonics 2017, 11, 149–158. [Google Scholar] [CrossRef]
- Silveirinha, M.; Engheta, N. Tunneling of Electromagnetic Energy through Subwavelength Channels and Bends using ϵ-Near-Zero Materials. Phys. Rev. Lett. 2006, 97, 157403. [Google Scholar] [CrossRef] [PubMed]
- Silveirinha, M.; Engheta, N. Theory of supercoupling, squeezing wave energy, and field confinement in narrow channels and tight bends using ϵ near-zero metamaterials. Phys. Rev. B 2007, 76, 245109. [Google Scholar] [CrossRef]
- Alù, A.; Silveirinha, M.; Salandrino, A.; Engheta, N. Epsilon-near-zero metamaterials and electromagnetic sources: Tailoring the radiation phase pattern. Phys. Rev. B 2007, 75, 155410. [Google Scholar] [CrossRef]
- Silveirinha, M.; Engheta, N. Design of matched zero-index metamaterials using nonmagnetic inclusions in ϵ-near-zero media. Phys. Rev. B 2007, 75, 075119. [Google Scholar] [CrossRef]
- Edwards, B.; Alù, A.; Young, M.; Silveirinha, M.; Engheta, N. Experimental Verification of Epsilon-Near-Zero Metamaterial Coupling and Energy Squeezing Using a Microwave Waveguide. Phys. Rev. Lett. 2008, 100, 033903. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Lai, Y.; Hang, Z.H.; Zheng, H.; Chan, C.T. Dirac cones induced by accidental degeneracy in photonic crystals and zero-refractive-index materials. Nat. Mater. 2011, 10, 582–586. [Google Scholar] [CrossRef] [PubMed]
- Feng, S. Loss-Induced Omnidirectional Bending to the Normal in ϵ-Near-Zero Metamaterials. Phys. Rev. Lett. 2012, 108, 193904. [Google Scholar] [CrossRef] [PubMed]
- Vesseur, E.; Coenen, T.; Caglayan, H.; Engheta, N.; Polman, A. Experimental Verification of n = 0 Structures for Visible Light. Phys. Rev. Lett. 2013, 110, 013902. [Google Scholar] [CrossRef] [PubMed]
- Alù, A.; Engheta, N. All Optical Metamaterial Circuit Board at the Nanoscale. Phys. Rev. Lett. 2009, 103, 143902. [Google Scholar] [CrossRef] [PubMed]
- Alu, A.; Engheta, N. Coaxial-to-Waveguide Matching With Epsilon-Near-Zero Ultranarrow Channels and Bends. IEEE Trans. Antennas Propag. 2010, 58, 328–339. [Google Scholar] [CrossRef]
- Yang, J.J.; Francescato, Y.; Maier, S.A.; Mao, F.; Huang, M. Mu and epsilon near zero metamaterials for perfect coherence and new antenna designs. Opt. Express 2014, 22, 9107–9114. [Google Scholar] [CrossRef] [PubMed]
- Alù, A.; Engheta, N. Boosting Molecular Fluorescence with a Plasmonic Nanolauncher. Phys. Rev. Lett. 2009, 103, 043902. [Google Scholar] [CrossRef] [PubMed]
- Suchowski, H.; O’Brien, K.; Wong, Z.J.; Salandrino, A.; Yin, X.; Zhang, X. Phase mismatch-free nonlinear propagation in optical zero-index materials. Science 2013, 342, 1223–1226. [Google Scholar] [CrossRef] [PubMed]
- Caspani, L.; Kaipurath, R.P.M.; Clerici, M.; Ferrera, M.; Roger, T.; Kim, J.; Kinsey, N.; Pietrzyk, M.; Di Falco, A.; Shalaev, V.M.; et al. Enhanced Nonlinear Refractive Index in ϵ-Near-Zero Materials. Phys. Rev. Lett. 2016, 116, 233901. [Google Scholar] [CrossRef] [PubMed]
- Liberal, I.; Mahmoud, A.M.; Li, Y.; Edwards, B.; Engheta, N. Photonic doping of epsilon-near-zero media. Science 2017, 355, 1058–1062. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Fortuño, F.J.; Vakil, A.; Engheta, N. Electric Levitation Using epsilon-Near-Zero Metamaterials. Phys. Rev. Lett. 2014, 112, 033902. [Google Scholar] [CrossRef] [PubMed]
- Jeong-Hae, L. Dual Property of Mu-near zero to Epsilon-near Zero Material. J. Korean Phys. Soc. 2010, 57, 51. [Google Scholar]
- Marcos, J.S.; Silveirinha, M.G.; Engheta, N. μ-near-zero supercoupling. Phys. Rev. B 2015, 91, 195112. [Google Scholar] [CrossRef]
- Torres, V.; Pacheco-Peña, V.; Rodríguez-Ulibarri, P.; Navarro-Cía, M.; Beruete, M.; Sorolla, M.; Engheta, N. Terahertz epsilon-near-zero graded-index lens. Opt. Express 2013, 21, 9156–9166. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Kita, S.; Muñoz, P.; Reshef, O.; Vulis, D.I.; Yin, M.; Lončar, M.; Mazur, E. On-chip zero-index metamaterials. Nat. Photonics 2015, 9, 738–742. [Google Scholar] [CrossRef]
- Moitra, P.; Yang, Y.; Anderson, Z.; Kravchenko, I.I.; Briggs, D.P.; Valentine, J. Realization of an all-dielectric zero-index optical metamaterial. Nat. Photonics 2013, 7, 791–795. [Google Scholar] [CrossRef]
- Maas, R.; Parsons, J.; Engheta, N.; Polman, A. Experimental realization of an epsilon-near-zero metamaterial at visible wavelengths. Nat. Photonics 2013, 7, 907–912. [Google Scholar] [CrossRef]
- Pollard, R.J.; Murphy, A.; Hendren, W.R.; Evans, P.R.; Atkinson, R.; Wurtz, G.A.; Zayats, A.V.; Podolskiy, V.A. Optical Nonlocalities and Additional Waves in Epsilon-Near-Zero Metamaterials. Phys. Rev. Lett. 2009, 102, 127405. [Google Scholar] [CrossRef] [PubMed]
- Soukoulis, C.M.; Wegener, M. Optical metamaterials—More bulky and less lossy. Science 2010, 330, 1633–1634. [Google Scholar] [CrossRef]
- Paniagua-Domínguez, R.; Abujetas, D.R.; Sánchez-Gil, J.A. Ultra low-loss, isotropic optical negative-index metamaterial based on hybrid metal-semiconductor nanowires. Sci. Rep. 2013, 3, 1507. [Google Scholar] [CrossRef] [PubMed]
- Abujetas, D.R.; Paniagua-Domínguez, R.; Nieto-Vesperinas, M.; Sánchez-Gil, J.A. Photonic band structure and effective medium properties of doubly-resonant core-shell metallo-dielectric nanowire arrays: Low-loss, isotropic optical negative-index behavior. J. Opt. 2015, 17, 125104. [Google Scholar] [CrossRef]
- Mahmoud, A.M.; Engheta, N. Wave-matter interactions in epsilon-and-mu-near-zero structures. Nat. Commun. 2014, 5, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Wheeler, M.; Aitchison, J.; Mojahedi, M. Three-dimensional array of dielectric spheres with an isotropic negative permeability at infrared frequencies. Phys. Rev. B 2005, 72, 193103. [Google Scholar] [CrossRef]
- Schuller, J.A.; Zia, R.; Taubner, T.; Brongersma, M.L. Dielectric Metamaterials Based on Electric and Magnetic Resonances of Silicon Carbide Particles. Phys. Rev. Lett. 2007, 99, 107401. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Q.; Kang, L.; Du, B.; Zhao, H.; Xie, Q.; Huang, X.; Li, B.; Zhou, J.; Li, L. Experimental Demonstration of Isotropic Negative Permeability in a Three-Dimensional Dielectric Composite. Phys. Rev. Lett. 2008, 101, 027402. [Google Scholar] [CrossRef] [PubMed]
- Popa, B.I.; Cummer, S. Compact Dielectric Particles as a Building Block for Low-Loss Magnetic Metamaterials. Phys. Rev. Lett. 2008, 100, 207401. [Google Scholar] [CrossRef] [PubMed]
- Vynck, K.; Felbacq, D.; Centeno, E.; Căbuz, A.; Cassagne, D.; Guizal, B. All-Dielectric Rod-Type Metamaterials at Optical Frequencies. Phys. Rev. Lett. 2009, 102, 133901. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Q.; Zhou, J.; Zhang, F.; Lippens, D. Mie resonance-based dielectric metamaterials. Mater. Today 2009, 12, 60–69. [Google Scholar] [CrossRef]
- Evlyukhin, A.B.; Reinhardt, C.; Seidel, A.; Luk’yanchuk, B.S.; Chichkov, B.N. Optical response features of Si-nanoparticle arrays. Phys. Rev. B 2010, 82, 045404. [Google Scholar] [CrossRef]
- Jelinek, L.; Marqués, R. Artificial magnetism and left-handed media from dielectric rings and rods. J. Phys. Condens. Matter 2010, 22, 025902. [Google Scholar] [CrossRef] [PubMed]
- García-Etxarri, A.; Gómez-Medina, R.; Froufe-Pérez, L.S.; López, C.; Chantada, L.; Scheffold, F.; Aizpurua, J.; Nieto-Vesperinas, M.; Sáenz, J.J. Strong magnetic response of submicron Silicon particles in the infrared. Opt. Express 2011, 19, 4815–4826. [Google Scholar] [CrossRef] [PubMed]
- Evlyukhin, A.B.; Novikov, S.M.; Zywietz, U.; Eriksen, R.L.; Reinhardt, C.; Bozhevolnyi, S.I.; Chichkov, B.N. Demonstration of Magnetic Dipole Resonances of Dielectric Nanospheres in the Visible Region. Nano Lett. 2012, 12, 3749–3755. [Google Scholar] [CrossRef] [PubMed]
- Kuznetsov, A.I.; Miroshnichenko, A.E.; Fu, Y.H.; Zhang, J.; Luk’yanchuk, B. Magnetic light. Sci. Rep. 2012, 2, 492. [Google Scholar] [CrossRef] [PubMed]
- Paniagua-Domínguez, R.; Froufe-Pérez, L.S.; Sáenz, J.J.; Sánchez-Gil, J.A. Localized magnetic plasmons in all-dielectric μ < 0 metastructures. Phys. Rev. B 2015, 91, 235120. [Google Scholar]
- Kuznetsov, A.I.; Miroshnichenko, A.E.; Brongersma, M.L.; Kivshar, Y.S.; Luk’yanchuk, B. Optically resonant dielectric nanostructures. Science 2016, 354, 846. [Google Scholar] [CrossRef] [PubMed]
- Kruk, S.S.; Camacho-Morales, R.; Xu, L.; Rahmani, M.; Smirnova, D.A.; Wang, L.; Tan, H.H.; Jagadish, C.; Neshev, D.N.; Kivshar, Y.S. Nonlinear Optical Magnetism Revealed by Second-Harmonic Generation in Nanoantennas. Nano Lett. 2017, 17, 3914–3918. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Miroshnichenko, A.E.; Kostinski, S.V.; Odit, M.; Kapitanova, P.; Qiu, M.; Kivshar, Y.S. Multimode directionality in all-dielectric metasurfaces. Phys. Rev. B 2017, 95, 165426. [Google Scholar] [CrossRef]
- Paniagua-Domínguez, R.; López-Tejeira, F.; Marqués, R.; Sánchez-Gil, J.A. Metallo-dielectric core–shell nanospheres as building blocks for optical three-dimensional isotropic negative-index metamaterials. New J. Phys. 2011, 13, 123017. [Google Scholar] [CrossRef]
- Morits, D.; Simovski, C. Isotropic negative refractive index at near infrared. J. Opt. 2012, 14, 125102. [Google Scholar] [CrossRef]
- Mirzaei, A.; Shadrivov, I.V.; Miroshnichenko, A.E.; Kivshar, Y.S. Cloaking and enhanced scattering of core-shell plasmonic nanowires. Opt. Express 2013, 21, 10454–10459. [Google Scholar] [CrossRef] [PubMed]
- Monticone, F.; Alù, A. Do Cloaked Objects Really Scatter Less? Phys. Rev. X 2013, 3, 041005. [Google Scholar] [CrossRef]
- Paniagua-Domínguez, R.; Abujetas, D.R.; Froufe-Pérez, L.S.; Sáenz, J.J.; Sánchez-Gil, J.A. Broadband telecom transparency of semiconductor-coated metal nanowires: More transparent than glass. Opt. Express 2013, 21, 22076–22089. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Liu, W.; Miroshnichenko, A.E.; Oulton, R.F.; Neshev, D.N.; Hess, O.; Kivshar, Y.S. Scattering of core-shell nanowires with the interference of electric and magnetic resonances. Opt. Lett. 2013, 38, 2621–2624. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Li, J.; Zhang, Z.Q.; Chan, C. Effective medium theory for magnetodielectric composites: Beyond the long-wavelength limit. Phys. Rev. B 2006, 74, 085111. [Google Scholar] [CrossRef]
- Palik, E.D. Handbook of Optical Constants of Solids; Academic Press: Cambridge, MA, USA, 1998; Volume 3, p. 900. [Google Scholar]
- Dai, L.; Sow, C.H.; Lim, C.T.; Tan, V.B.C. Metal Oxide Nanowires—Structural and Mechanical Properties. In Nanowires—Fundamental Research; Hashim, A., Ed.; InTech: Singapore, 2011; Chapter 9. [Google Scholar]
- Wu, J.M.; Shih, H.C.; Wu, W.T. Formation and photoluminescence of single-crystalline rutile TiO2 nanowires synthesized by thermal evaporation. Nanotechnology 2006, 17, 105–109. [Google Scholar] [CrossRef]
- Li, Y.; Wu, Y.; Chen, X.; Mei, J. Selection rule for Dirac-like points in two-dimensional dielectric photonic crystals. Opt. Express 2013, 21, 7699–7711. [Google Scholar] [CrossRef] [PubMed]
- Marini, A.; García de Abajo, F.J. Self-organization of frozen light in near-zero-index media with cubic nonlinearity. Sci. Rep. 2016, 6, 20088. [Google Scholar] [CrossRef] [PubMed]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abujetas, D.R.; Paniagua-Domínguez, R.; Sánchez-Gil, J.A. Impedance-Matched, Double-Zero Optical Metamaterials Based on Weakly Resonant Metal Oxide Nanowires. Photonics 2018, 5, 7. https://doi.org/10.3390/photonics5020007
Abujetas DR, Paniagua-Domínguez R, Sánchez-Gil JA. Impedance-Matched, Double-Zero Optical Metamaterials Based on Weakly Resonant Metal Oxide Nanowires. Photonics. 2018; 5(2):7. https://doi.org/10.3390/photonics5020007
Chicago/Turabian StyleAbujetas, Diego R., Ramón Paniagua-Domínguez, and José A. Sánchez-Gil. 2018. "Impedance-Matched, Double-Zero Optical Metamaterials Based on Weakly Resonant Metal Oxide Nanowires" Photonics 5, no. 2: 7. https://doi.org/10.3390/photonics5020007
APA StyleAbujetas, D. R., Paniagua-Domínguez, R., & Sánchez-Gil, J. A. (2018). Impedance-Matched, Double-Zero Optical Metamaterials Based on Weakly Resonant Metal Oxide Nanowires. Photonics, 5(2), 7. https://doi.org/10.3390/photonics5020007





