Efficiency Limits of Solar Energy Harvesting via Internal Photoemission in Carbon Materials
Abstract
1. Introduction
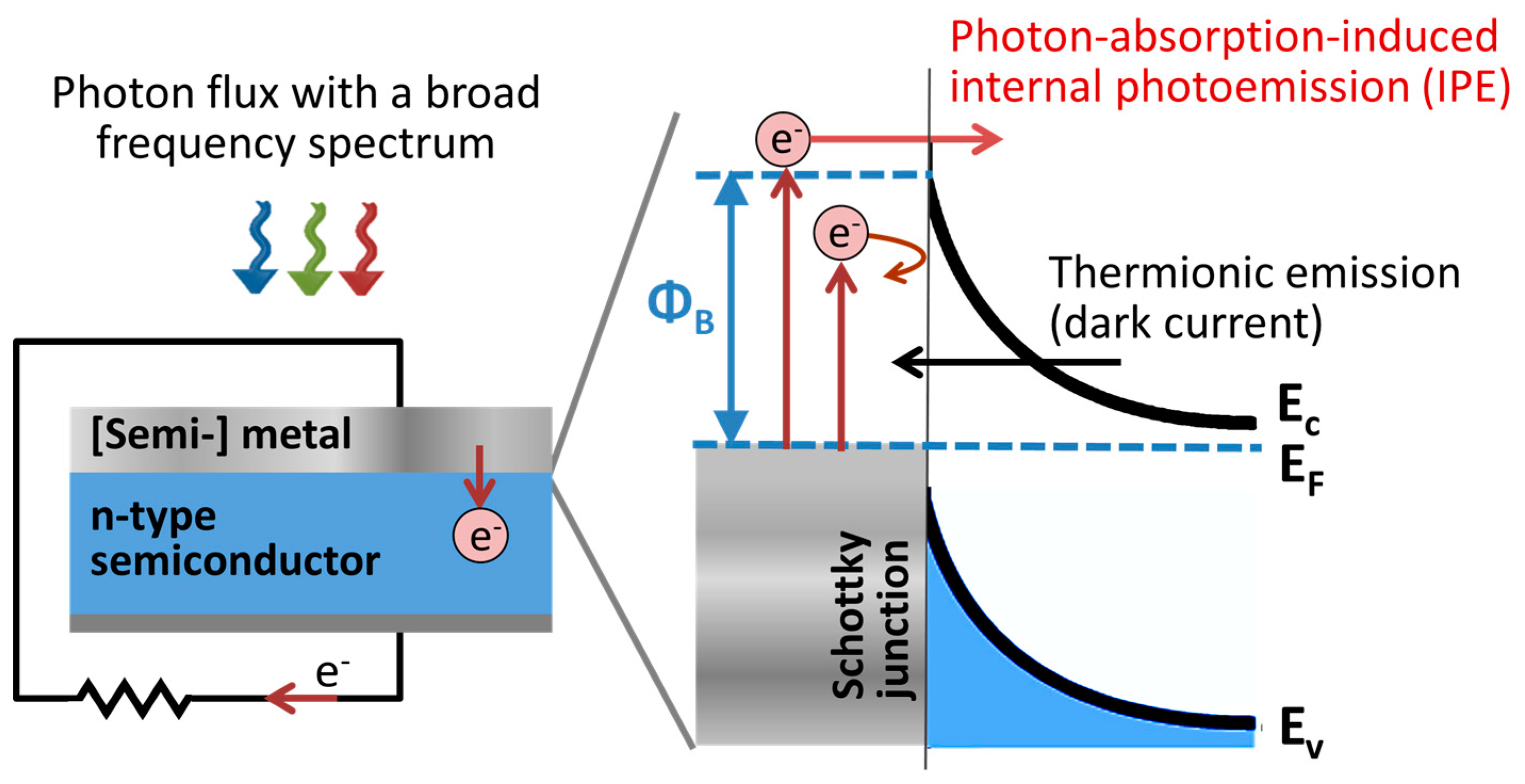
2. The Theory and Modeling of the Internal Photoemission Process
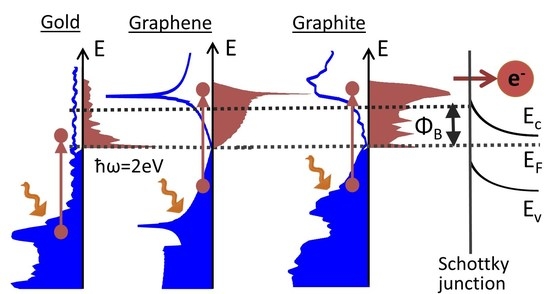
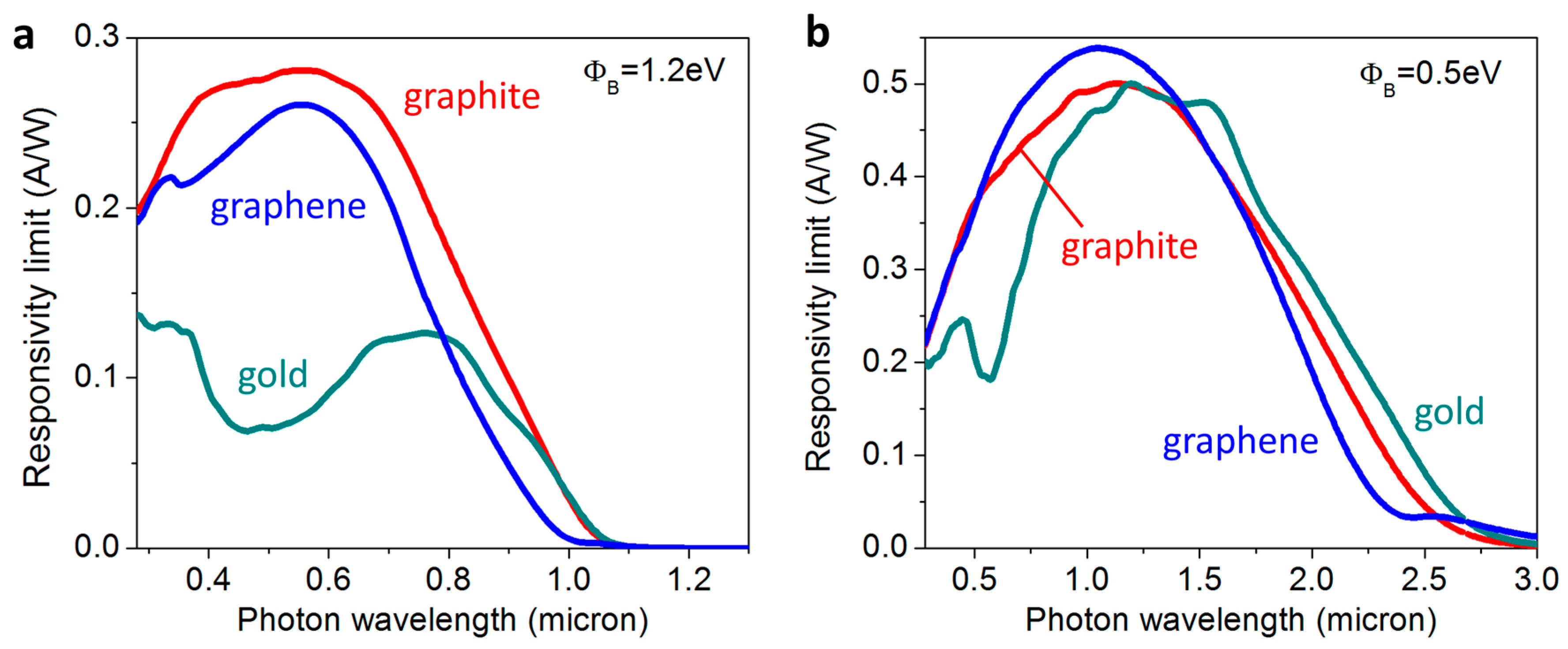
3. Band-Structure-Imposed Upper Limits of IPE Efficiency: Gold versus Carbon
4. Increasing Efficiency Levels with Solar Concentration and Spectral Splitting Strategies
5. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Boriskina, S.V.; Green, M.A.; Catchpole, K.; Yablonovitch, E.; Beard, M.C.; Okada, Y.; Lany, S.; Gershon, T.; Zakutayev, A.; Tahersima, M.H.; et al. Roadmap on Optical Energy Conversion. J. Opt. 2016, 18, 73004. [Google Scholar] [CrossRef]
- Boriskina, S.V.; Cooper, T.A.; Zeng, L.; Ni, G.; Tong, J.K.; Tsurimaki, Y.; Huang, Y.; Meroueh, L.; Mahan, G.; Chen, G. Losses in Plasmonics: From Mitigating Energy Dissipation to Embracing Loss-Enabled Functionalities. Adv. Opt. Photonics 2017, 9, 775–827. [Google Scholar] [CrossRef]
- Boriskina, S.V.; Ghasemi, H.; Chen, G. Plasmonic Materials for Energy: From Physics to Applications. Mater. Today 2013, 16, 375–386. [Google Scholar] [CrossRef]
- Brongersma, M.L.; Halas, N.J.; Nordlander, P. Plasmon-Induced Hot Carrier Science and Technology. Nat. Nanotechnol. 2015, 10, 25–34. [Google Scholar] [CrossRef] [PubMed]
- Clavero, C. Plasmon-Induced Hot-Electron Generation at Nanoparticle/metal-Oxide Interfaces for Photovoltaic and Photocatalytic Devices. Nat. Photonics 2014, 8, 95–103. [Google Scholar] [CrossRef]
- McFarland, E.W.; Tang, J. A Photovoltaic Device Structure Based on Internal Electron Emission. Nature 2003, 421, 616–618. [Google Scholar] [CrossRef] [PubMed]
- Govorov, A.O.; Zhang, H.; Gun’ko, Y.K. Theory of Photoinjection of Hot Plasmonic Carriers from Metal Nanostructures into Semiconductors and Surface Molecules. J. Phys. Chem. C 2013, 117, 16616–16631. [Google Scholar] [CrossRef]
- Li, W.; Valentine, J.G. Harvesting the Loss: Surface Plasmon-Based Hot Electron Photodetection. Nanophotonics 2017, 6, 177–191. [Google Scholar] [CrossRef]
- Sundararaman, R.; Narang, P.; Jermyn, A.S.; Goddard III, W.A.; Atwater, H.A. Theoretical Predictions for Hot-Carrier Generation from Surface Plasmon Decay. Nat. Commun. 2014, 5, 5788. [Google Scholar] [CrossRef] [PubMed]
- Zheng, B.Y.; Zhao, H.; Manjavacas, A.; McClain, M.; Nordlander, P.; Halas, N.J. Distinguishing between Plasmon-Induced and Photoexcited Carriers in a Device Geometry. Nat. Commun. 2015, 6, 7797. [Google Scholar] [CrossRef] [PubMed]
- Sobhani, A.; Knight, M.W.; Wang, Y.; Zheng, B.; King, N.S.; Brown, L.V.; Fang, Z.; Nordlander, P.; Halas, N.J. Narrowband Photodetection in the near-Infrared with a Plasmon-Induced Hot Electron Device. Nat. Commun. 2013, 4, 1643. [Google Scholar] [CrossRef] [PubMed]
- Knight, M.W.; Sobhani, H.; Nordlander, P.; Halas, N.J. Photodetection with Active Optical Antennas. Science 2011, 332, 702–704. [Google Scholar] [CrossRef] [PubMed]
- Atar, F.B.; Battal, E.; Aygun, L.E.; Daglar, B.; Bayindir, M.; Okyay, A.K. Plasmonically Enhanced Hot Electron Based Photovoltaic Device. Opt. Express 2013, 21, 7196–7201. [Google Scholar] [CrossRef] [PubMed]
- Gao, M.; Connor, P.K.N.; Ho, G.W. Plasmonic Photothermic Directed Broadband Sunlight Harnessing for Seawater Catalysis and Desalination. Energy Environ. Sci. 2016, 495, 305–307. [Google Scholar] [CrossRef]
- Mubeen, S.; Lee, J.; Singh, N.; Kramer, S.; Stucky, G.D.; Moskovits, M. An Autonomous Photosynthetic Device in Which All Charge Carriers Derive from Surface Plasmons. Nat. Natotechnol. 2013, 8, 247. [Google Scholar] [CrossRef] [PubMed]
- Mubeen, S.; Lee, J.; Lee, W.-R.; Singh, N.; Stucky, G.D.; Moskovits, M. On the Plasmonic Photovoltaic. ACS Nano 2014, 8, 6066. [Google Scholar] [CrossRef] [PubMed]
- Farrell, D.J.; Sodabanlu, H.; Wang, Y.; Sugiyama, M.; Okada, Y. A Hot-Electron Thermophotonic Solar Cell Demonstrated by Thermal up-Conversion of Sub-Bandgap Photons. Nat. Commun. 2015, 6, 8685. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Cushing, S.K.; Meng, F.; Senty, T.R.; Bristow, A.D.; Wu, N. Plasmon-Induced Resonance Energy Transfer for Solar Energy Conversion. Nat. Photonics 2015, 9, 601–607. [Google Scholar] [CrossRef]
- White, T.P.; Catchpole, K.R. Plasmon-Enhanced Internal Photoemission for Photovoltaics: Theoretical Efficiency Limits. Appl. Phys. Lett. 2012, 101, 73904–73905. [Google Scholar] [CrossRef]
- Leenheer, A.J.; Narang, P.; Lewis, N.S.; Atwater, H.A. Solar Energy Conversion via Hot Electron Internal Photoemission in Metallic Nanostructures: Efficiency Estimates. J. Appl. Phys. 2014, 115, 134301. [Google Scholar] [CrossRef]
- Boriskina, S.V.; Zhou, J.; Hsu, W.-C.; Liao, B.; Chen, G. Limiting Efficiencies of Solar Energy Conversion and Photo-Detection via Internal Emission of Hot Electrons and Hot Holes in Gold. In Proceedings of the SPIE 9608, Infrared Remote Sensing and Instrumentation XXIII, San Diego, CA, USA, 1 September 2015; SPIE: Bellingham, WA, USA, 2015; Volume 960816. [Google Scholar]
- Chang, Y.-J.; Shih, K.-H. Solar Energy Conversion via Internal Photoemission in Aluminum, Copper, and Silver: Band Structure Effects and Theoretical Efficiency Estimates. J. Appl. Phys. 2016, 119, 183101. [Google Scholar] [CrossRef]
- Gong, T.; Munday, J.N. Materials for Hot Carrier Plasmonics. Opt. Mater. Express 2015, 5, 2501. [Google Scholar] [CrossRef]
- Tongay, S.; Schumann, T.; Hebard, A.F. Graphite Based Schottky Diodes Formed on Si, GaAs, and 4H-SiC Substrates. Appl. Phys. Lett. 2009, 95, 222103. [Google Scholar] [CrossRef]
- Li, X.; Zhu, H.; Wang, K.; Cao, A.; Wei, J.; Li, C.; Jia, Y.; Li, Z.; Li, X.; Wu, D. Graphene-on-Silicon Schottky Junction Solar Cells. Adv. Mater. 2010, 22, 2743–2748. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Heo, J.; Park, S.; Song, H.J.; Seo, D.H.; Byun, K.-E.; Kim, P.; Yoo, I.; Chung, H.-J.; Kim, K. Graphene Barristor, a Triode Device with a Gate-Controlled Schottky Barrier. Science 2012, 336, 1140–1143. [Google Scholar] [CrossRef] [PubMed]
- Akama, T.; Okita, W.; Nagai, R.; Li, C.; Kaneko, T.; Kato, T. Schottky Solar Cell Using Few-Layered Transition Metal Dichalcogenides toward Large-Scale Fabrication of Semitransparent and Flexible Power Generator. Sci. Rep. 2017, 7, 11967. [Google Scholar] [CrossRef] [PubMed]
- Tongay, S.; Schumann, T.; Miao, X.; Appleton, B.R.; Hebard, A.F. Tuning Schottky Diodes at the Many-Layer-Graphene/semiconductor Interface by Doping. Carbon N. Y. 2011, 49, 2033–2038. [Google Scholar] [CrossRef]
- Braun, F. Ueber Die Stromleitung Durch Schwefelmetalle. Ann. Phys. Chem. 1875, 229, 556–563. [Google Scholar] [CrossRef]
- Pierce, G.W. Crystal Rectifiers for Electric Currents and Electric Oscillations. Part I. Carborundum. Phys. Rev. 1907, 25, 31–60. [Google Scholar] [CrossRef][Green Version]
- Tung, R.T. The Physics and Chemistry of the Schottky Barrier Height. Appl. Phys. Rev. 2014, 1, 11304. [Google Scholar]
- Shih, K.-H.; Chang, Y.-J. Internal Photoemission for Photovoltaic Using P-Type Schottky Barrier: Band Structure Dependence and Theoretical Efficiency Limits. J. Appl. Phys. 2018, 123, 23107. [Google Scholar] [CrossRef]
- Szydlo, N.; Poirier, R. I-V and C-V Characteristics of Au/TiO2 Schottky Diodes. J. Appl. Phys. 1980, 51, 3310–3312. [Google Scholar] [CrossRef]
- Li, X.-H.; Chou, J.B.; Kwan, W.L.; Elsharif, A.M.; Kim, S.-G. Effect of Anisotropic Electron Momentum Distribution of Surface Plasmon on Internal Photoemission of a Schottky Hot Carrier Device. Opt. Express 2017, 25, A264. [Google Scholar] [CrossRef] [PubMed]
- Fowler, R.H. The Analysis of Photoelectric Sensitivity Curves for Clean Metals at Various Temperatures. Phys. Rev. 1931, 38, 45–56. [Google Scholar] [CrossRef]
- Ratchford, D.C.; Dunkelberger, A.D.; Vurgaftman, I.; Owrutsky, J.C.; Pehrsson, P.E. Quantification of Efficient Plasmonic Hot-Electron Injection in Gold Nanoparticle–TiO2 Films. Nano Lett. 2017, 17, 6047–6055. [Google Scholar] [CrossRef] [PubMed]
- Vashaee, D.; Shakouri, A. Improved Thermoelectric Power Factor in Metal-Based Superlattices. Phys. Rev. Lett. 2004, 92, 106103. [Google Scholar] [CrossRef] [PubMed]
- Chen, G. Diffusion–transmission Interface Condition for Electron and Phonon Transport. Appl. Phys. Lett. 2003, 82, 991–993. [Google Scholar] [CrossRef]
- Scales, C.; Berini, P. Thin-Film Schottky Barrier Photodetector Models. IEEE J. Quantum Electron. 2010, 46, 633–643. [Google Scholar] [CrossRef]
- Dalal, V.L. Simple Model for Internal Photoemission. J. Appl. Phys. 1971, 42, 2274–2279. [Google Scholar] [CrossRef]
- ASTM International. ASTM Standard G173-03: Standard Tables for Reference Solar Spectral Irradiances: Direct Normal and Hemispherical on 37° Tilted Surface; ASTM International: West Conshohocken, PA, USA, 2008. [Google Scholar]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A Modular and Open-Source Software Project for Quantum Simulations of Materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Zunger, A. Self-Interaction Correction to Density-Functional Approximations for Many-Electron Systems. Phys. Rev. B 1981, 23, 5048–5079. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector Augmented-Wave Method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Hartwigsen, C.; Goedecker, S.; Hutter, J. Relativistic Separable Dual-Space Gaussian Pseudopotentials from H to Rn. Phys. Rev. B 1998, 58, 3641–3662. [Google Scholar] [CrossRef]
- Blöchl, P.E.; Jepsen, O.; Andersen, O.K. Improved Tetrahedron Method for Brillouin-Zone Integrations. Phys. Rev. B 1994, 49, 16223–16233. [Google Scholar] [CrossRef]
- Ni, M.; Leung, M.; Leung, D.; Sumathy, K. Theoretical Modeling of TiO2/TCO Interfacial Effect on Dye-Sensitized Solar Cell Performance. Sol. Energy Mater. Sol. Cells 2006, 90, 2000–2009. [Google Scholar] [CrossRef]
- Wurfel, P. Physics of Solar Cells: From Principles to New Concepts; WILEY-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2005. [Google Scholar]
- Boriskina, S.V.; Tong, J.K.; Ferry, V.E.; Michel, J.; Kildishev, A.V. Breaking the Limits of Optical Energy Conversion. Opt. Photonics News 2015, 26, 48–51. [Google Scholar] [CrossRef]
- Mojiri, A.; Taylor, R.; Thomsen, E.; Rosengarten, G. Spectral Beam Splitting for Efficient Conversion of Solar Energy: A Review. Renew. Sustain. Energy Rev. 2013, 28, 654–663. [Google Scholar] [CrossRef]
- Cao, F.; Huang, Y.; Tang, L.; Sun, T.; Boriskina, S.V.; Chen, G.; Ren, Z. Toward a High-Efficient Utilization of Solar Radiation by Quad-Band Solar Spectral Splitting. Adv. Mater. 2016, 28, 10659. [Google Scholar] [CrossRef] [PubMed]
- Branz, H.M.; Regan, W.; Gerst, K.J.; Borak, J.B.; Santori, E.A. Hybrid Solar Converters for Maximum Exergy and Inexpensive Dispatchable Electricity. Energy Environ. Sci. 2015, 8, 3083–3091. [Google Scholar] [CrossRef]
- Henry, C.H. Limiting Efficiencies of Ideal Single and Multiple Energy Gap Terrestrial Solar Cells. J. Appl. Phys. 1980, 51, 4494–4500. [Google Scholar] [CrossRef]
- Shockley, W.; Queisser, H.J. Detailed Balance Limit of Efficiency of p-n Junction Solar Cells. J. Appl. Phys. 1961, 32, 510–519. [Google Scholar] [CrossRef]
- Boriskina, S.V.; Chen, G. Exceeding the Solar Cell Shockley-Queisser Limit via Thermal up-Conversion of Low-Energy Photons. Opt. Commun. 2014, 314, 71–78. [Google Scholar] [CrossRef]
- Chan, E.; Card, H.; Teich, M. Internal Photoemission Mechanisms at Interfaces between Germanium and Thin Metal Films. IEEE J. Quantum Electron. 1980, 16, 373–381. [Google Scholar] [CrossRef]
- Chen, G. Nanoscale Energy Transfer and Conversion; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Narang, P.; Zhao, L.; Claybrook, S.; Sundararaman, R. Effects of Interlayer Coupling on Hot-Carrier Dynamics in Graphene-Derived van Der Waals Heterostructures. Adv. Opt. Mater. 2017, 5, 1600914. [Google Scholar] [CrossRef]
- Li, W.; Valentine, J. Metamaterial Perfect Absorber Based Hot Electron Photodetection. Nano Lett. 2014, 14, 3510–3514. [Google Scholar] [CrossRef] [PubMed]
- Sun, D.; Aivazian, G.; Jones, A.M.; Ross, J.S.; Yao, W.; Cobden, D.; Xu, X. Ultrafast Hot-Carrier-Dominated Photocurrent in Graphene. Nat. Nanotechnol. 2012, 7, 114–118. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.-H.; Chang, Y.-C.; Norris, T.B.; Zhong, Z. Graphene Photodetectors with Ultra-Broadband and High Responsivity at Room Temperature. Nat. Nanotechnol. 2014, 9, 273–278. [Google Scholar] [CrossRef] [PubMed]
- Tielrooij, K.J.; Song, J.C.W.; Jensen, S.A.; Centeno, A.; Pesquera, A.; Zurutuza Elorza, A.; Bonn, M.; Levitov, L.S.; Koppens, F.H.L. Photoexcitation Cascade and Multiple Hot-Carrier Generation in Graphene. Nat. Phys. 2013, 9, 248–252. [Google Scholar] [CrossRef]
- Jang, M.S.; Brar, V.W.; Sherrott, M.C.; Lopez, J.J.; Kim, L.; Kim, S.; Choi, M.; Atwater, H.A. Tunable Large Resonant Absorption in a Midinfrared Graphene Salisbury Screen. Phys. Rev. B 2014, 90, 165409. [Google Scholar] [CrossRef]
- Ober, J.A. Mineral Commodity Summaries 2018; U.S. Department of the Interior & U.S. Geological Survey: Reston, VA, USA, 2018.




| Material | Graphite | Graphene | Gold |
|---|---|---|---|
| Cut-off energy (Ry) | 60 | 80 | 80 |
| Gaussian broadening parameter (Ry) | 0.005 | 0.005 | 0.005 |
| k-mesh (before interpolation) | 20 × 20 × 12 | 20 × 20 × 1 | 25 × 25 × 25 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boriskina, S.V.; Zhou, J.; Ding, Z.; Chen, G. Efficiency Limits of Solar Energy Harvesting via Internal Photoemission in Carbon Materials. Photonics 2018, 5, 4. https://doi.org/10.3390/photonics5010004
Boriskina SV, Zhou J, Ding Z, Chen G. Efficiency Limits of Solar Energy Harvesting via Internal Photoemission in Carbon Materials. Photonics. 2018; 5(1):4. https://doi.org/10.3390/photonics5010004
Chicago/Turabian StyleBoriskina, Svetlana V., Jiawei Zhou, Zhiwei Ding, and Gang Chen. 2018. "Efficiency Limits of Solar Energy Harvesting via Internal Photoemission in Carbon Materials" Photonics 5, no. 1: 4. https://doi.org/10.3390/photonics5010004
APA StyleBoriskina, S. V., Zhou, J., Ding, Z., & Chen, G. (2018). Efficiency Limits of Solar Energy Harvesting via Internal Photoemission in Carbon Materials. Photonics, 5(1), 4. https://doi.org/10.3390/photonics5010004