Extraordinary Light-Trapping Enhancement in Silicon Solar Cell Patterned with Graded Photonic Super-Crystals
Abstract
:1. Introduction
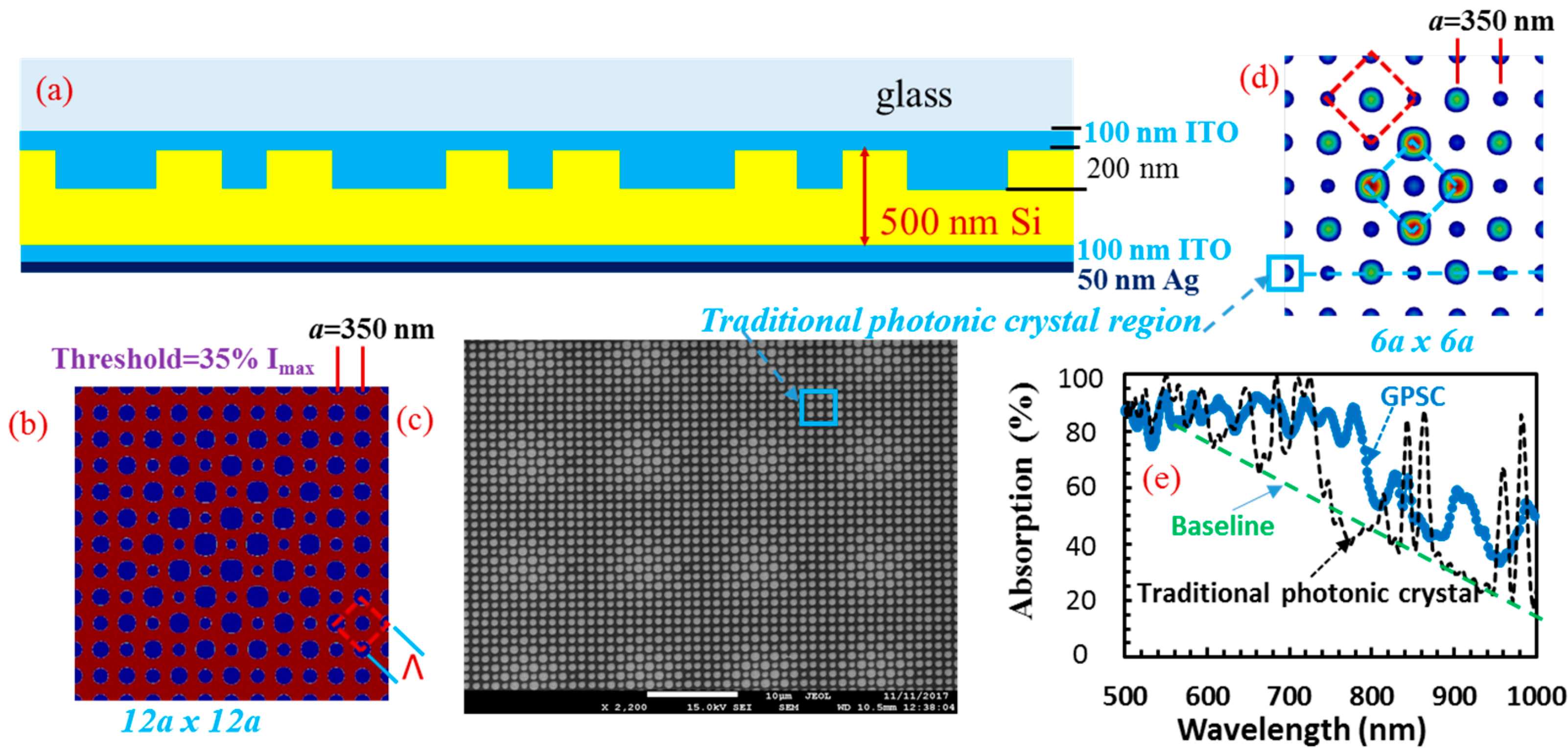
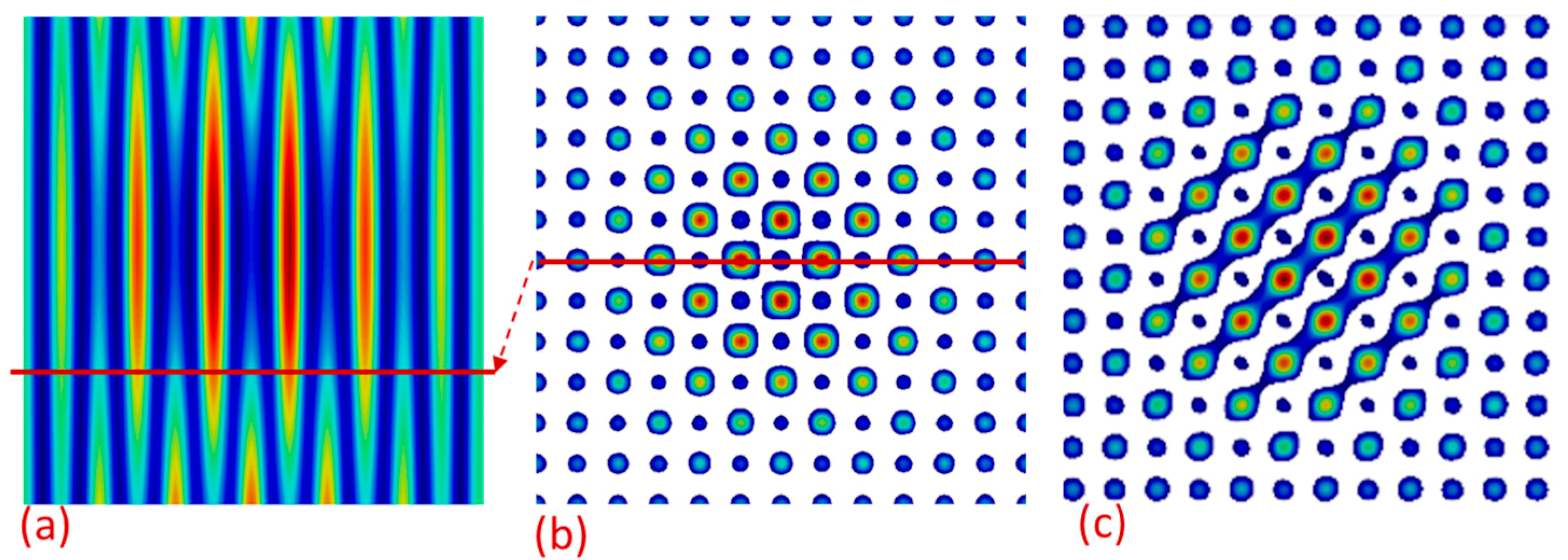
2. Description of Graded Photonic Super-Crystals and Simulation Methods
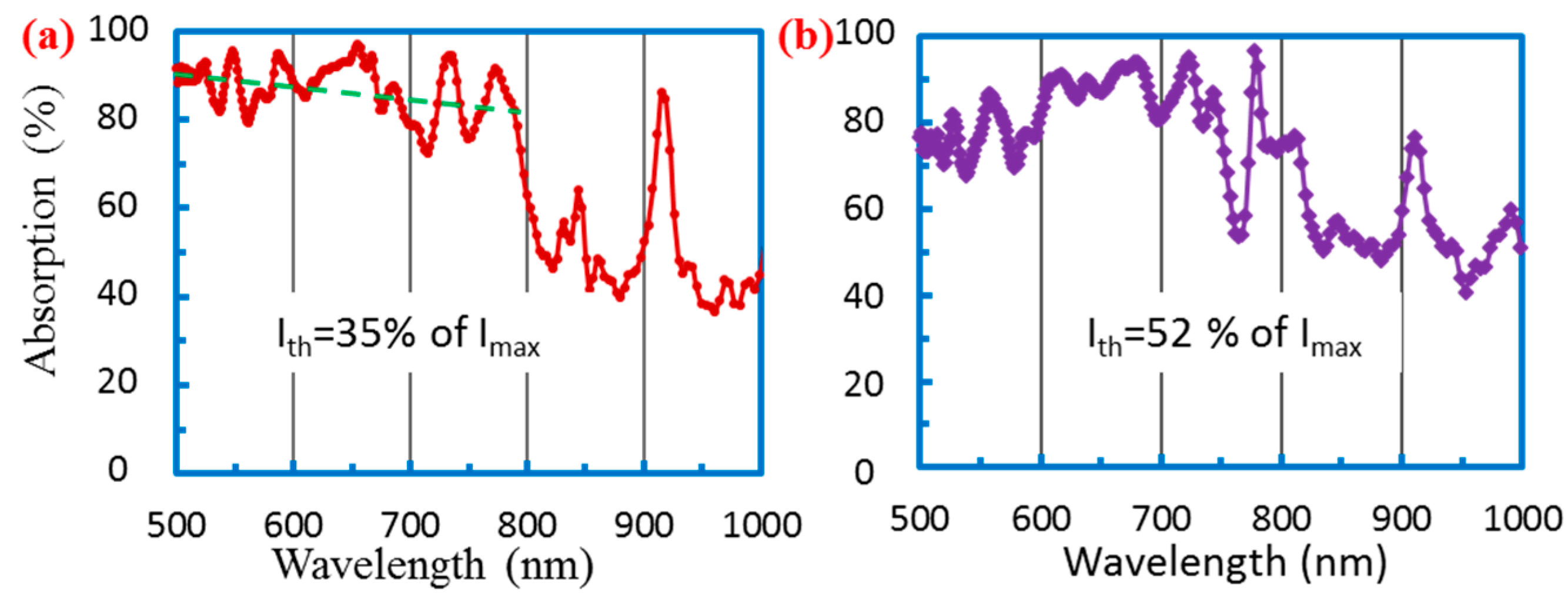
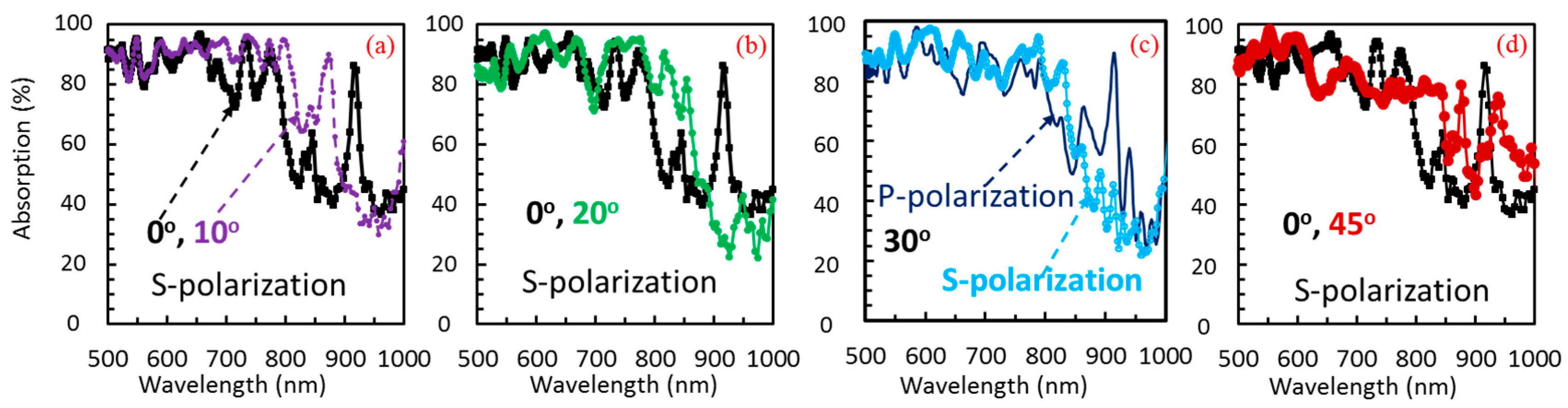
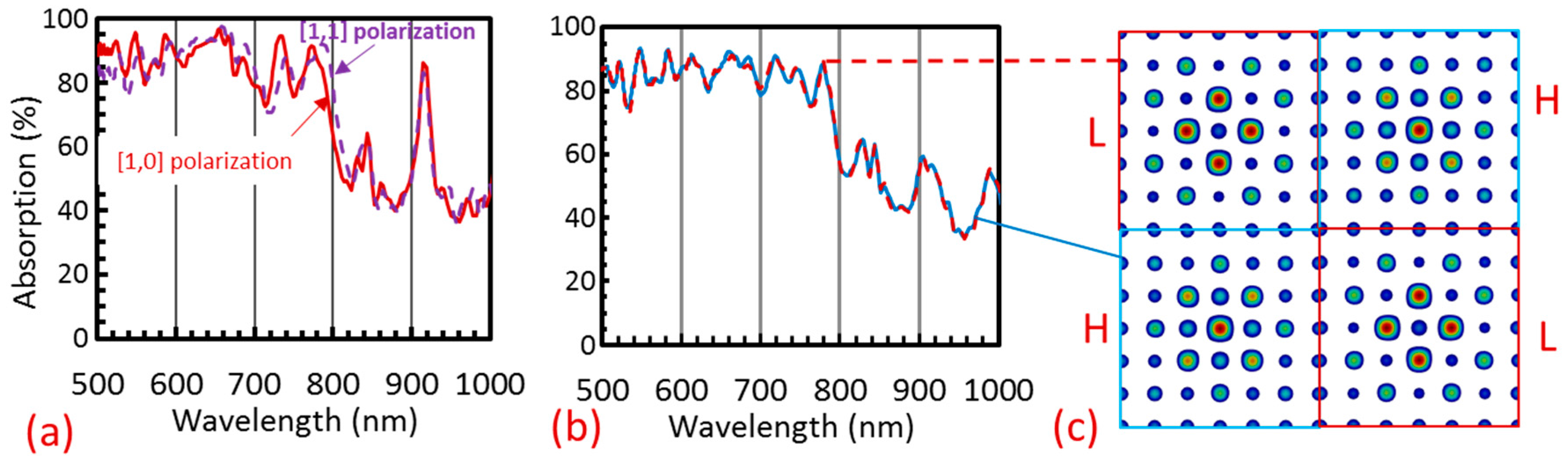
3. Results
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Atwater, H.; Polman, A. Plasmonics for improved photovoltaic devices. Nat. Mater. 2010, 9, 205–513. [Google Scholar] [CrossRef] [PubMed]
- Garnett, E.; Yang, P. Light trapping in silicon nanowire solar cells. Nano Lett. 2010, 10, 1082–1087. [Google Scholar] [CrossRef] [PubMed]
- Kelzenberg, M.D.; Boettcher, S.W.; Petykiewicz, J.A.; Turner-Evans, D.B.; Putnam, M.C.; Warren, E.L.; Spurgeon, J.M.; Briggs, R.M.; Lewis, N.S.; Atwater, H.A. Enhanced absorption and carrier collection in Si wire arrays for photovoltaic applications. Nat. Mater. 2010, 9, 239–244. [Google Scholar] [CrossRef] [PubMed]
- Brongersma, M.L.; Cui, Y.; Fan, S. Light management for photovoltaics using high-index nanostructures. Nat. Mater. 2014, 13, 451–460. [Google Scholar] [CrossRef] [PubMed]
- Bermel, P.; Luo, C.; Zeng, L.; Kimerling, L.; Joannopoulos, J. Improving thin-film crystalline silicon solar cell efficiencies with photonic crystals. Opt. Express 2007, 15, 16986–17000. [Google Scholar] [CrossRef] [PubMed]
- Hsu, C.M.; Battaglia, C.; Pahud, C.; Ruan, Z.; Haug, F.J.; Fan, S.; Ballif, C.; Cui, Y. High-efficiency amorphous silicon solar cell on a periodic nanocone back reflector. Adv. Energy. Mater. 2012, 2, 628–633. [Google Scholar] [CrossRef]
- Sai, H.; Fujiwara, H.; Kondo, M.; Kanamori, Y. Enhancement of light trapping in thin-film hydrogenated microcrystalline Si solar cells using back reflectors with self-ordered dimple pattern. Appl. Phys. Lett. 2008, 93, 143501. [Google Scholar] [CrossRef]
- Sai, H.; Saito, K.; Kondo, M. Enhanced photocurrent and conversion efficiency in thin-film microcrystalline silicon solar cells using periodically textured back reflectors with hexagonal dimple arrays. Appl. Phys. Lett. 2012, 101, 173901. [Google Scholar]
- Chutinan, A.; Kherani, N.P.; Zukotynski, S. High-efficiency photonic crystal solar cell architecture. Opt. Express 2009, 17, 8871–8878. [Google Scholar] [CrossRef] [PubMed]
- Mallick, S.; Agrawal, M.; Peumans, P. Optimal light trapping in ultra-thin photonic crystal crystalline silicon solar cells. Opt. Express 2010, 18, 5691–5706. [Google Scholar] [CrossRef] [PubMed]
- Bozzola, A.; Liscidini, M.; Andreani, L.C. Photonic light-trapping versus Lambertian limits in thin film silicon solar cells with 1D and 2D periodic patterns. Opt. Express 2012, 20, A224–A244. [Google Scholar] [CrossRef] [PubMed]
- Han, S.; Chen, G. Toward the lambertian limit of light trapping in thin nanostructured silicon solar cells. Nano Lett. 2010, 10, 4692–4696. [Google Scholar] [CrossRef] [PubMed]
- Sheng, X.; Liu, J.; Kozinsky, I.; Agrawal, A.; Michel, J.; Kimerling, L. Design and non-lithographic fabrication of light trapping structures for thin film silicon solar cells. Adv. Mater. 2011, 23, 843–847. [Google Scholar] [CrossRef] [PubMed]
- Park, Y.; Drouard, E.; El Daif, O.; Letartre, X.; Viktorovitch, P.; Fave, A.; Kaminski, A.; Lemiti, M.; Seassal, C. Absorption enhancement using photonic crystals for silicon thin film solar cells. Opt. Express 2009, 17, 14312–14321. [Google Scholar] [CrossRef] [PubMed]
- Callahan, D.M.; Horowitz, K.A.; Atwater, H.A. Light trapping in ultrathin silicon photonic crystal superlattices with randomly-textured dielectric incouplers. Opt. Express 2013, 21, 30315–30326. [Google Scholar] [CrossRef] [PubMed]
- Rinnerbauer, V.; Shen, Y.; Joannopoulos, J.D.; Soljačić, M.; Schäffler, F.; Celanovic, I. Superlattice photonic crystal as broadband solar absorber for high temperature operation. Opt. Express 2014, 22, A1895–A1906. [Google Scholar] [CrossRef] [PubMed]
- Rinnerbauer, V.; Lausecker, E.; Schäffler, F.; Reininger, P.; Strasser, G.; Geil, R.D.; Joannopoulos, J.D.; Soljačić, M.; Celanovic, I. Nanoimprinted superlattice metallic photonic crystal as ultraselective solar absorber. Optica 2015, 2, 743–746. [Google Scholar] [CrossRef]
- Hendrickson, J.; Guo, J.; Zhang, B.; Buchwald, W.; Soref, R. Wideband perfect light absorber at midwave infrared using multiplexed metal structures. Opt. Lett. 2012, 37, 371–373. [Google Scholar] [CrossRef] [PubMed]
- Oskooi, A.; Favuzzi, P.; Tanaka, Y.; Shigeta, H.; Kawakami, Y.; Noda, S. Partially-disordered photonic-crystal thin films for enhanced and robust photovoltaics. Appl. Phys. Lett. 2012, 100, 181110. [Google Scholar] [CrossRef] [Green Version]
- Oskooi, A.; De Zoysa, M.; Ishizaki, K.; Noda, S. Experimental Demonstrtion of Quasi-resonant Absorption in Silicon Thin Films for Enhanced Solar Light Trapping. ACS Photonics 2014, 1, 304–309. [Google Scholar] [CrossRef]
- Martins, E.; Li, J.; Liu, Y.; Depauw, V.; Chen, Z.; Zhou, J.; Krauss, T. Deterministic quasi-random nanostructures for photon control. Nat. Commun. 2013, 4, 2665. [Google Scholar] [CrossRef] [PubMed]
- Vynck, K.; Burresi, M.; Riboli, F.; Wiersma, D.S. Photon management in two-dimensional disordered media. Nat. Mater. 2012, 11, 1017–1022. [Google Scholar] [CrossRef] [PubMed]
- Rockstuhl, C.; Fahr, S.; Bittkau, K.; Beckers, T.; Carius, R.; Haug, F.-J.; Söderström, T.; Ballif, C.; Lederer, F. Comparison and optimization of randomly textured surfaces in thin-film solar cells. Opt. Express 2010, 18, A335–A342. [Google Scholar] [CrossRef] [PubMed]
- Ferry, V.E.; Verschuuren, M.A.; van Lare, M.C.; Schropp, R.E.I.; Atwater, H.A.; Polman, A. Optimized Spatial Correlations for Broadband Light Trapping Nanopatterns in High Efficiency Ultrathin Film a-Si:H Solar Cells. Nano Lett. 2011, 11, 4239–4245. [Google Scholar] [CrossRef] [PubMed]
- Lowell, D.; Lutkenhaus, J.; George, D.; Philipose, U.; Chen, B.; Lin, Y. Simultaneous direct holographic fabrication of photonic cavity and graded photonic lattice with dual periodicity, dual basis, and dual symmetry. Opt. Express 2017, 25, 14444–14452. [Google Scholar] [CrossRef] [PubMed]
- Nukala, P.; Sapkota, G.; Gali, P.; Philipose, U. Transport properties of Sb doped Si nanowires. J. Cryst. Growth 2012, 353, 140–144. [Google Scholar] [CrossRef]
- Lowell, D.; Hassan, S.; Adewole, M.; Philipose, U.; Chen, B.; Lin, Y. Holographic fabrication of graded photonic super-crystals using an integrated spatial light modulator and reflective optical element laser projection system. Appl. Opt. 2017, 56, 9888–9891. [Google Scholar] [CrossRef]
- Janai, M.; Allred, D.D.; Booth, D.C.; Seraphin, B.O. Optical properties and structure of amorphous silicon films prepared by CVD. Sol. Energy Mater. 1979, 1, 11–27. [Google Scholar] [CrossRef]
- Green, M. Self-consistent optical parameters of intrinsic silicon at 300 K including temperature coefficients. Sol. Energy Mater. Sol. Cells 2008, 92, 1305–1310. [Google Scholar] [CrossRef]
- Oskooi, A.F.; Roundy, D.; Ibanescu, M.; Bermel, P.; Joannopoulos, J.D.; Johnson, S. MEEP: A flexible free software package for electromagnetic simulations by the FDTD method. Comput. Phys. Commun. 2010, 181, 687–702. [Google Scholar] [CrossRef]
- Shi, J.; Pollard, M.E.; Angeles, C.A.; Chen, R.; Gates, J.C.; Charlton, M.D.B. Photonic crystal and quasi-crystals providing simultaneous light coupling and beam splitting within a low refractive-index slab waveguide. Sci. Rep. 2017, 7, 1812. [Google Scholar] [CrossRef] [PubMed]
- Hassan, S.; Lowell, D.; Yuankun, L. High light extraction efficiency in organic light-emitting diodes by patterning the cathode in graded superlattice with dual periodicity and dual basis. J. Appl. Phys. 2017, 121, 233104. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hassan, S.; Lowell, D.; Adewole, M.; George, D.; Zhang, H.; Lin, Y. Extraordinary Light-Trapping Enhancement in Silicon Solar Cell Patterned with Graded Photonic Super-Crystals. Photonics 2017, 4, 50. https://doi.org/10.3390/photonics4040050
Hassan S, Lowell D, Adewole M, George D, Zhang H, Lin Y. Extraordinary Light-Trapping Enhancement in Silicon Solar Cell Patterned with Graded Photonic Super-Crystals. Photonics. 2017; 4(4):50. https://doi.org/10.3390/photonics4040050
Chicago/Turabian StyleHassan, Safaa, David Lowell, Murthada Adewole, David George, Hualiang Zhang, and Yuankun Lin. 2017. "Extraordinary Light-Trapping Enhancement in Silicon Solar Cell Patterned with Graded Photonic Super-Crystals" Photonics 4, no. 4: 50. https://doi.org/10.3390/photonics4040050
APA StyleHassan, S., Lowell, D., Adewole, M., George, D., Zhang, H., & Lin, Y. (2017). Extraordinary Light-Trapping Enhancement in Silicon Solar Cell Patterned with Graded Photonic Super-Crystals. Photonics, 4(4), 50. https://doi.org/10.3390/photonics4040050





