Development of a Multi-Objective Evolutionary Algorithm for Strain-Enhanced Quantum Cascade Lasers
Abstract
:1. Introduction
2. Background of Evolutionary Algorithms and QCLs
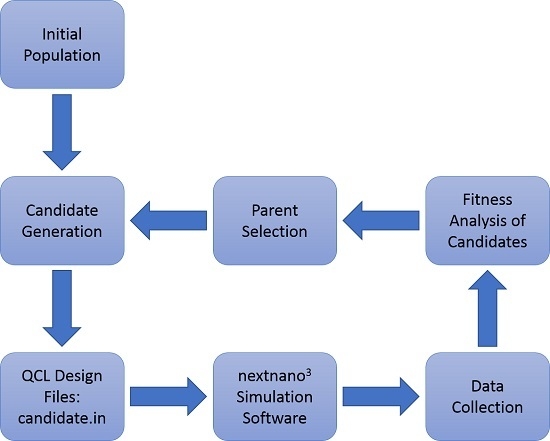
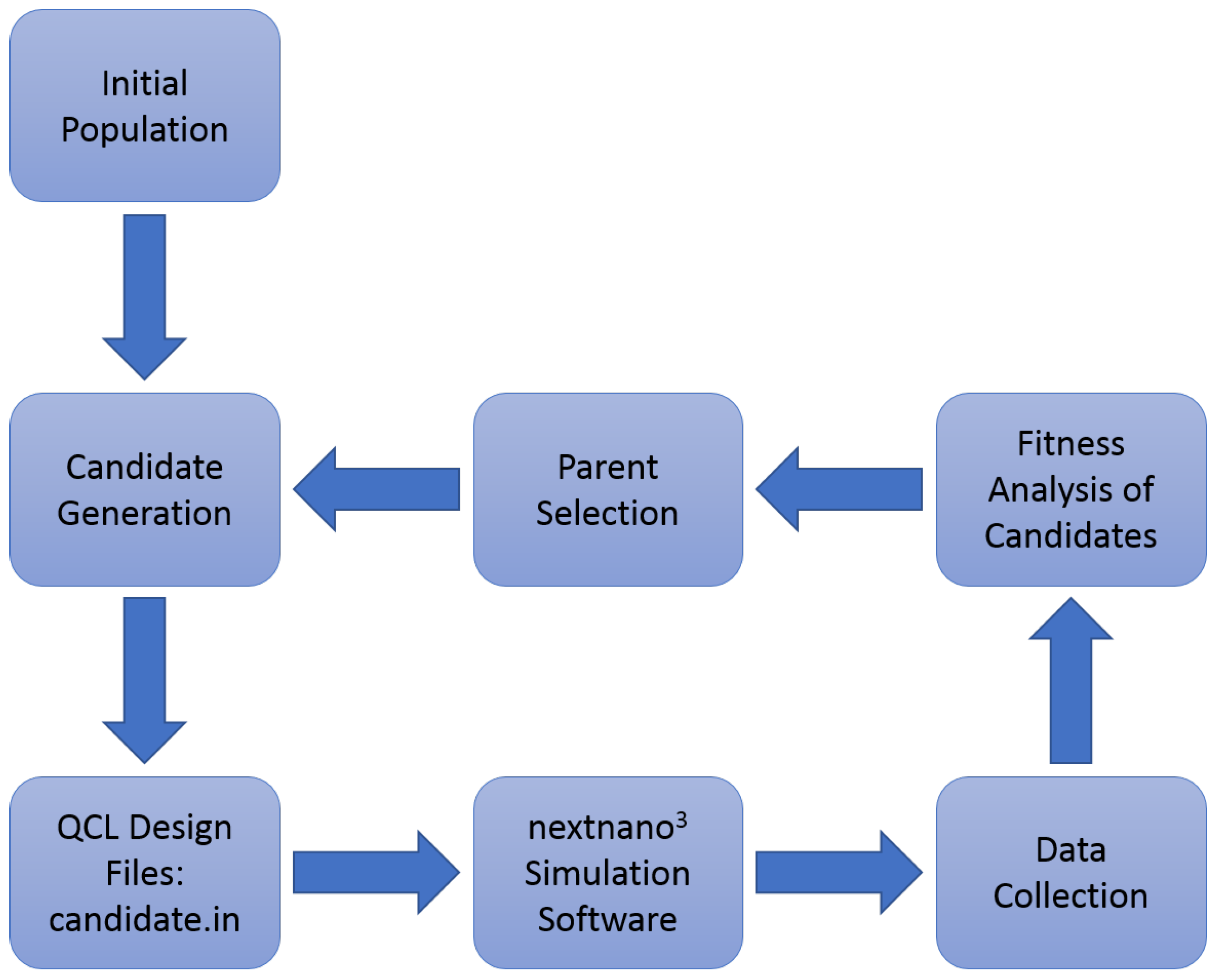
3. Algorithm Description and Design Approach
3.1. Initial Population
3.2. Simulation and Data Collection
3.3. Fitness Evaluation and Candidate Selection
3.4. Fitness Objective Calculation
4. Results and Discussion
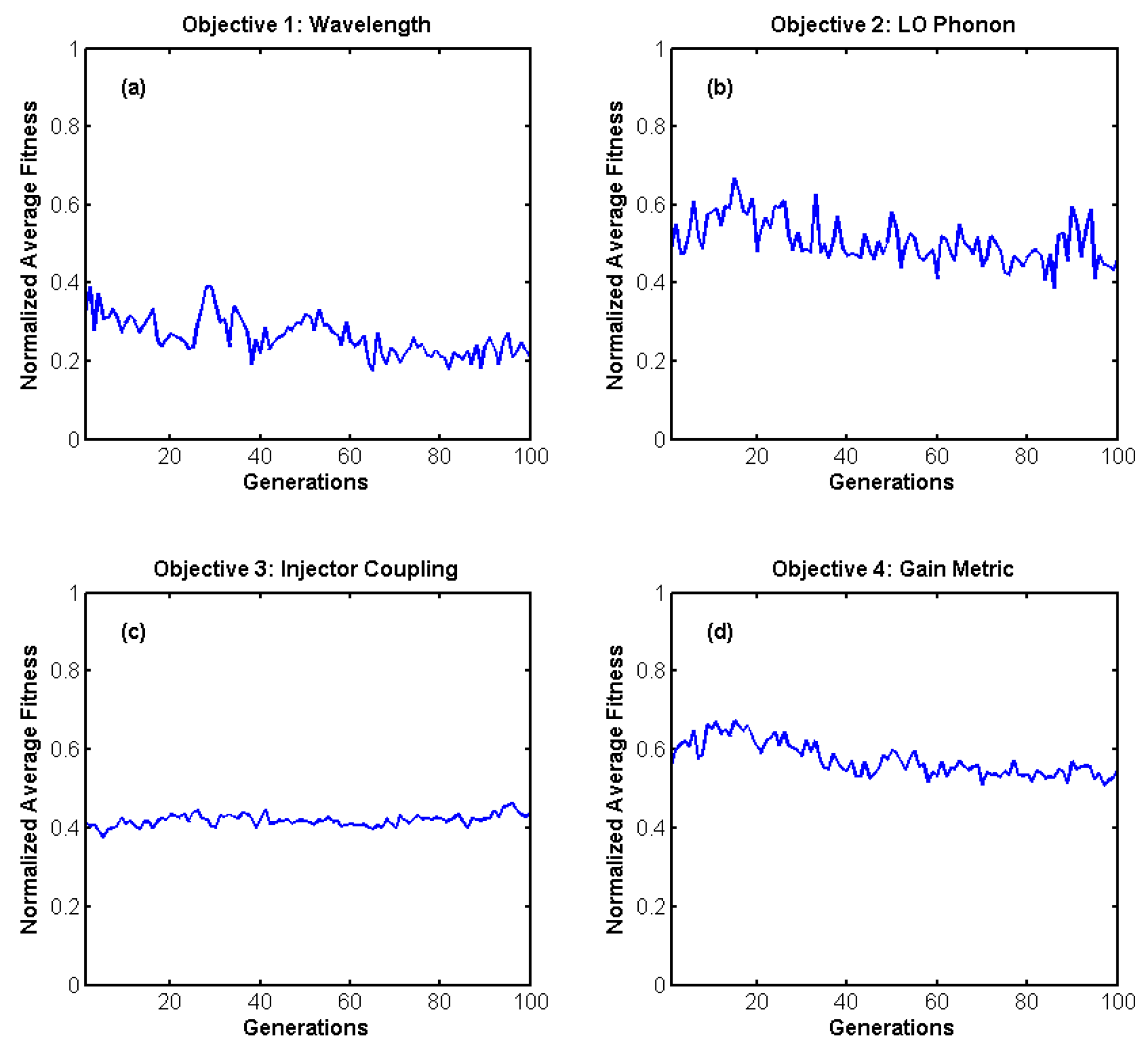
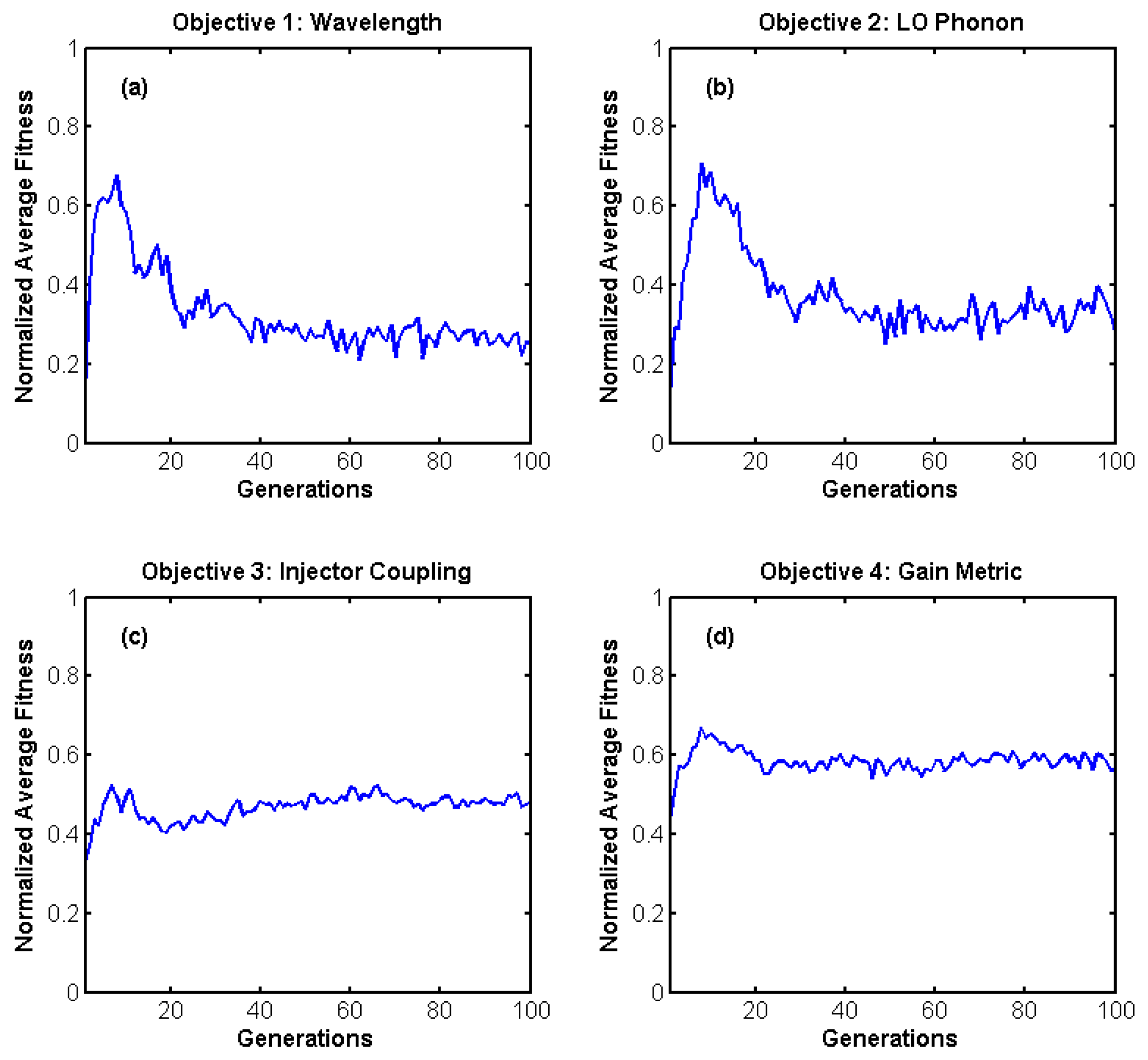
4.1. Average Fitness Values over Time
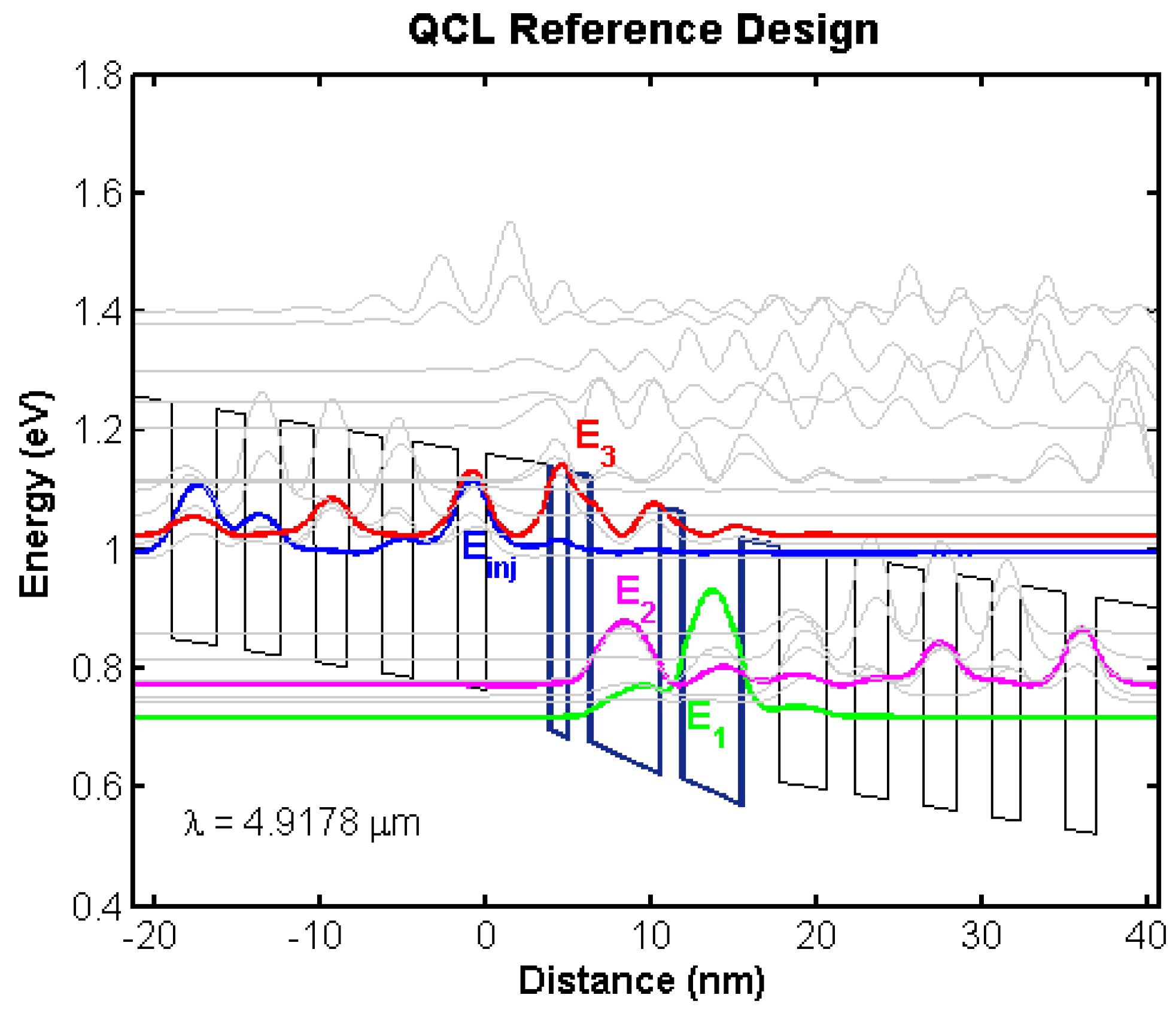
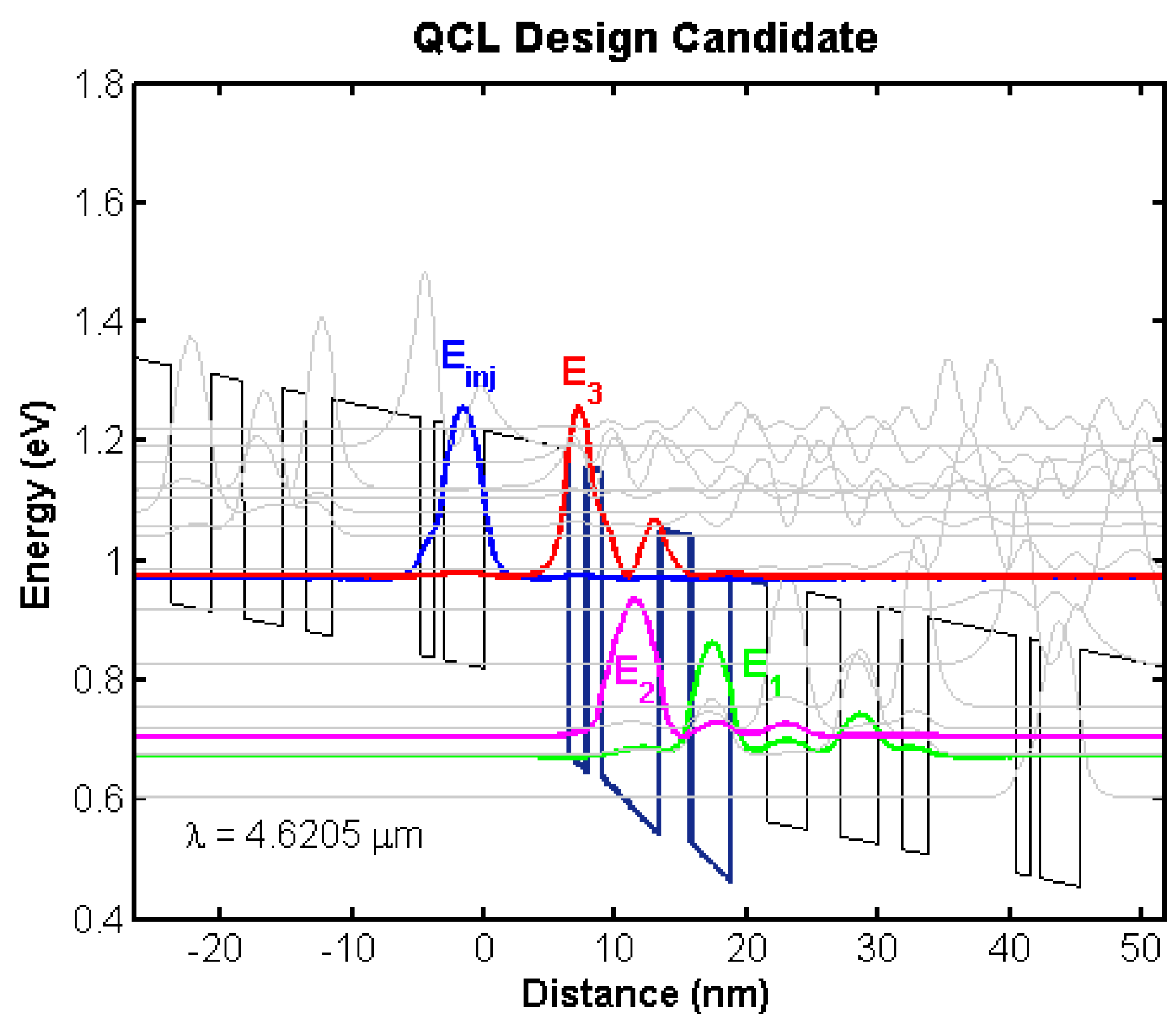
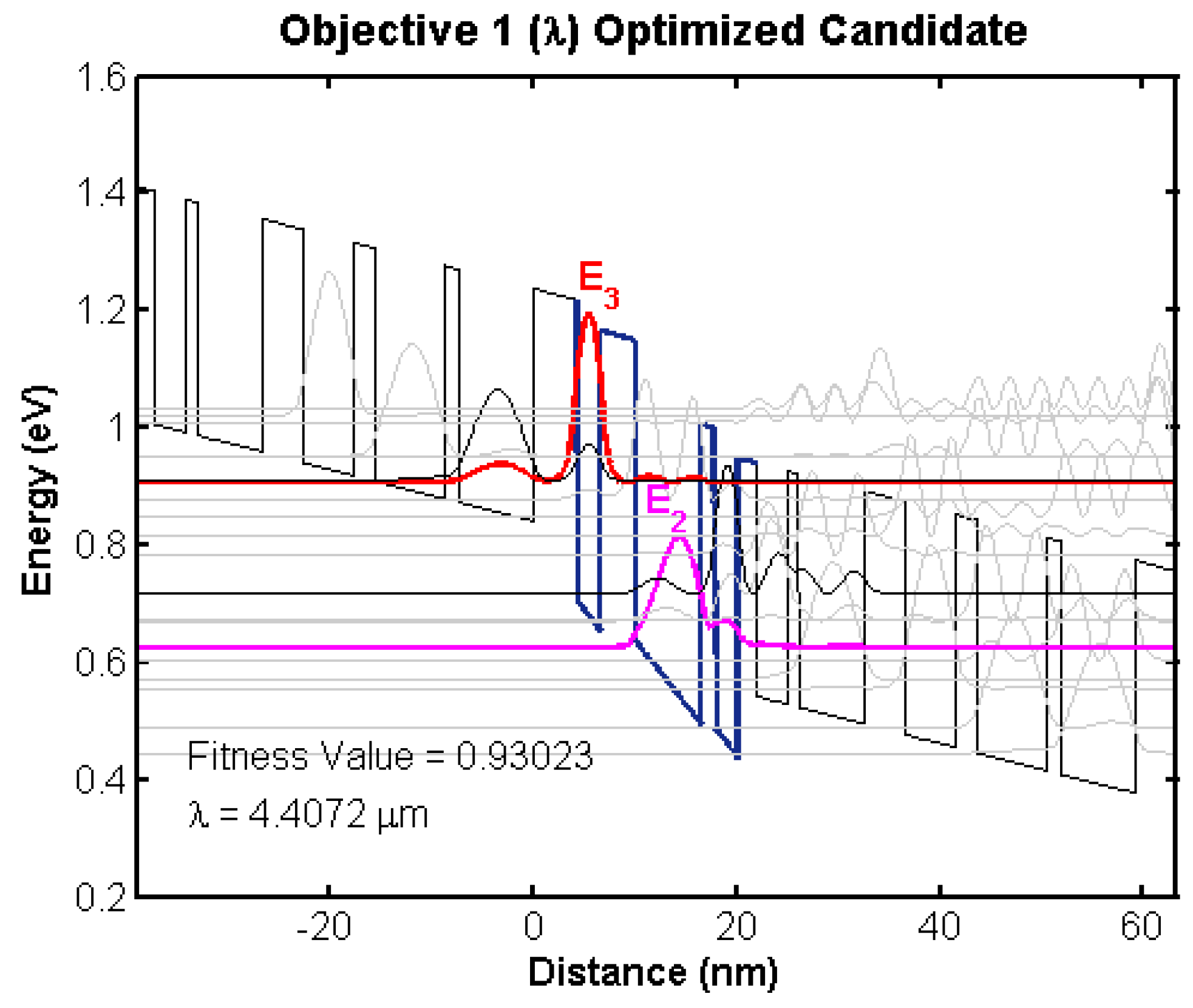
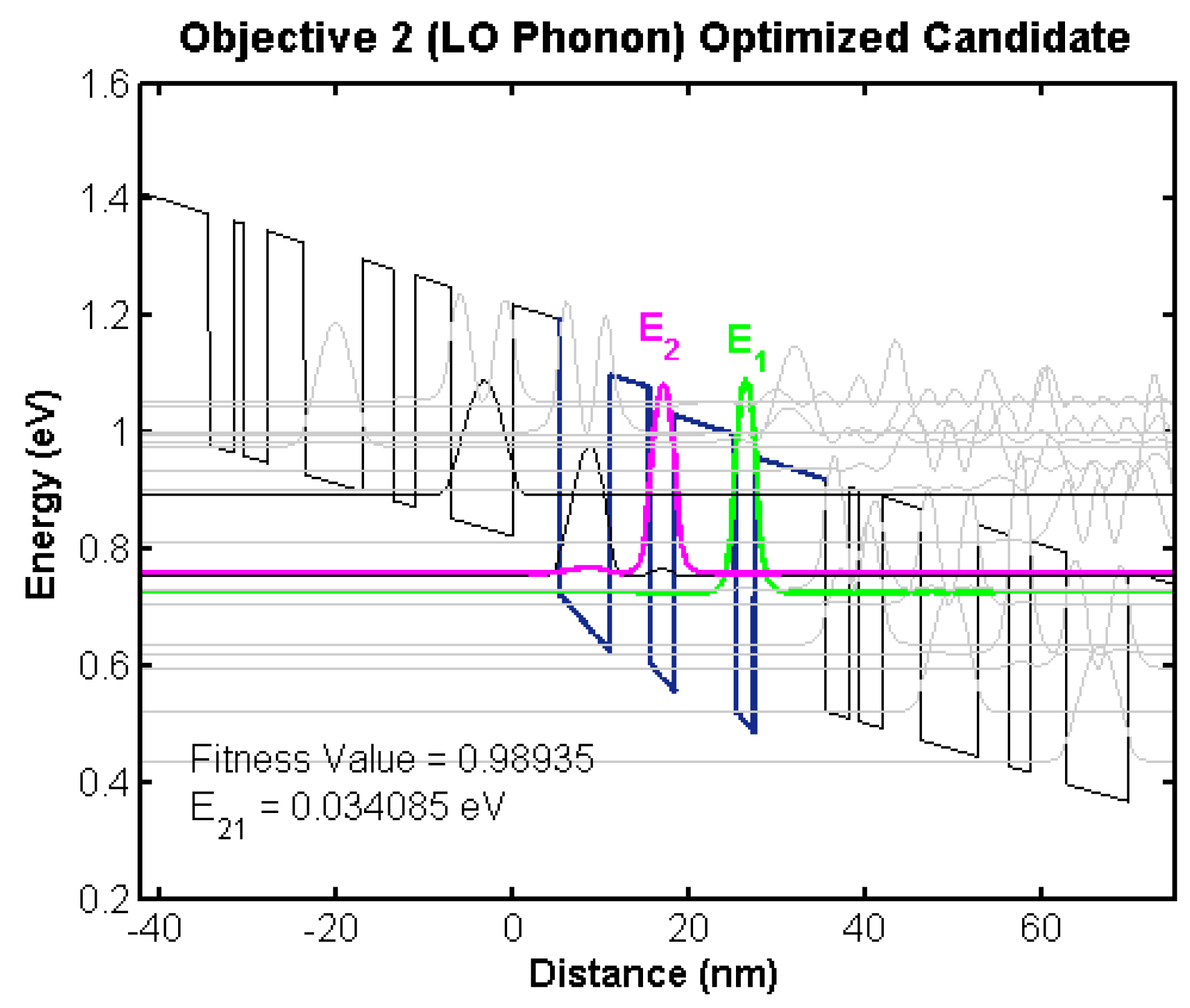
4.2. Bandstructure Diagrams of Top Candidates
4.2.1. Initial Training Population
4.2.2. Random Initial Population
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Faist, J. Quantum Cascade Lasers, 1st ed.; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Vitiello, M.S.; Scalari, G.; Williams, B.; Natale, P.D. Quantum cascade lasers: 20 years of challenges. Opt. Express 2015, 23, 5167–5182. [Google Scholar] [CrossRef] [PubMed]
- Triplett, G.; Roberts, D. Strained Active Regions in GaAs-based Quantum Cascade Lasers. IEEE J. Quantum Electron. 2010, 46, 1782–1787. [Google Scholar] [CrossRef]
- Mueller, D.W.; Roberts, D.; Triplett, G. Sensitivity of Strained and Unstrained Structure Growth on GaAs (111)B. J. Electron. Mater. 2012, 41, 959–964. [Google Scholar] [CrossRef]
- Meyer, C.; Cheng, E.; Grayer, J.; Mueller, D.; Triplett, G.; Roberts, D.; Graham, S. Pseudomorphic growth of InAs on misoriented GaAs for extending quantum cascade laser wavelength. J. Vac. Sci. Technol. A 2013, 31. [Google Scholar] [CrossRef]
- Birner, S.; Hackenbuchner, S.; Sabathil, M.; Zandler, G.; Majewski, J.; Andlauer, T.; Zibold, T.; Morschl, R.; Trellakis, A.; Vogl, P. Modeling of semiconductor nanostructures with nextnano(3). Acta Phys. Polon. A 2006, 110, 111–124. [Google Scholar] [CrossRef]
- Vurgaftman, I.; Meyer, J.R.; Ram-Mohan, L.R. Band parameters for III-V compound semiconductors and their alloys. J. Appl. Phys. 2001, 89, 5815–5875. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Ko, Y.H.; Yu, J.S. Design optimization of quantum cascade laser structures at λ ∼ 11–12 µm. Phys. Status Solidi A 2010, 207, 2190–2197. [Google Scholar] [CrossRef]
- Valavanis, A.; Dinh, T.V.; Lever, L.J.M.; Ikonić, Z.; Kelsall, R.W. Material configurations for n-type silicon-based terahertz quantum cascade lasers. Phys. Rev. B 2011, 83, 195321. [Google Scholar] [CrossRef]
- Dinh, T.V.; Valavanis, A.; Lever, L.J.M.; Ikonić, Z.; Kelsall, R.W. Extended density-matrix model applied to silicon-based terahertz quantum cascade lasers. Phys. Rev. B 2012, 85, 235427. [Google Scholar] [CrossRef]
- Smiljanić, J.; Žeželj, M.; Milanović, V.; Radovanović, J.; Stanković, I. MATLAB-based program for optimization of quantum cascade laser active region parameters and calculation of output characteristics in magnetic field. Comput. Phys. Commun. 2014, 185, 998–1006. [Google Scholar] [CrossRef]
- Mircetic, A.; Indjin, D.; Ikonic, Z.; Harrison, P.; Milanovic, V.; Kelsall, R.W. Towards automated design of quantum cascade lasers. J. Appl. Phys. 2005, 97, 084506. [Google Scholar] [CrossRef]
- Waldmueller, I.; Wanke, M.C.; Lerttamrab, M.; Allen, D.G.; Chow, W.W. Inverse-Quantum-Engineering: A New Methodology for Designing Quantum Cascade Lasers. IEEE J. Quantum Electron. 2010, 46, 1414–1420. [Google Scholar] [CrossRef]
- Danicic, A.; Radovanovic, J.; Milanovic, V.; Indjin, D.; Ikonic, Z. Optimization and magnetic-field tunability of quantum cascade laser for applications in trace gas detection and monitoring. J. Phys. D Appl. Phys. 2010, 43, 045101. [Google Scholar] [CrossRef]
- Bismuto, A.; Terazzi, R.; Hinkov, B.; Beck, M.; Faist, J. Fully automatized quantum cascade laser design by genetic optimization. Appl. Phys. Lett. 2012, 101, 021103. [Google Scholar] [CrossRef]
- Dupont, E.; Fathololoumi, S.; Wasilewski, Z.R.; Aers, G.; Laframboise, S.R.; Lindskog, M.; Razavipour, S.G.; Wacker, A.; Ban, D.; Liu, H.C. A phonon scattering assisted injection and extraction based terahertz quantum cascade laser. J. Appl. Phys. 2012, 111, 073111. [Google Scholar] [CrossRef]
- Gajic, A.; Radovanovic, J.; Milanovic, V.; Indjin, D.; Ikonic, Z. Genetic algorithm applied to the optimization of quantum cascade lasers with second harmonic generation. J. Appl. Phys. 2014, 115, 053712. [Google Scholar] [CrossRef]
- Gajic, A.; Radovanovic, J.; Milanovic, V.; Indjin, D.; Ikonic, Z. Optimizing optical nonlinearities in GaInAs/AlInAs quantum cascade lasers. Nucl. Technol. Radiat. Prot. 2014, 29, 10–16. [Google Scholar] [CrossRef]
- Radovanovic, J.; Milanovic, V.; Ikonic, Z.; Indjin, D. Application of the genetic algorithm to the optimized design of semimagnetic semiconductor-based spin-filters. J. Phys. D Appl. Phys. 2007, 40, 5066. [Google Scholar] [CrossRef]
- Matyas, A.; Chashmahcharagh, R.; Kovacs, I.; Lugli, P.; Vijayraghavan, K.; Belkin, M.A.; Jirauschek, C. Improved terahertz quantum cascade laser with variable height barriers. J. Appl. Phys. 2012, 111, 103106. [Google Scholar] [CrossRef]
- Mojibpour, A.; Pourfath, M.; Kosina, H. Optimization study of third harmonic generation in quantum cascade lasers. Opt. Express 2014, 22, 20607–20612. [Google Scholar] [CrossRef] [PubMed]
- Kleeman, M.P.; Lamont, G.B.; Cooney, A.; Nelson, T.R. A Multi-tiered Memetic Multiobjective Evolutionary Algorithm for the Design of Quantum Cascade Lasers. In Evolutionary Multi-Criterion Optimization; Obayashi, S., Deb, K., Poloni, C., Hiroyasu, T., Murata, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4403, pp. 186–200. [Google Scholar]
- Page, H.; Becker, C.; Robertson, A.; Glastre, G.; Ortiz, V.; Sirtori, C. 300 K operation of a GaAs-based quantum-cascade laser at λ ≈ 9 µm. Appl. Phys. Lett. 2001, 78, 3529–3531. [Google Scholar] [CrossRef]
- Roberts, D. Gallium Arsenide-based Quantum Cascade Lasers for Mid-Infrared Operation at 3–5 Micron Grown by Molecular Beam Epitaxy. Ph.D. Thesis, University of Missouri, Columbia, MO, USA, 2011. [Google Scholar]
- Faist, J.; Capasso, F.; Sivco, D.L.; Hutchinson, A.L.; Chu, S.N.G.; Cho, A.Y. Short wavelength (λ ∼ 3.4 µm) quantum cascade laser based on strained compensated InGaAs/AlInAs. Appl. Phys. Lett. 1998, 72, 680–682. [Google Scholar] [CrossRef]
- Evans, A.; Darvish, S.R.; Slivken, S.; Nguyen, J.; Bai, Y.; Razeghi, M. Buried heterostructure quantum cascade lasers with high continuous-wave wall plug efficiency. Appl. Phys. Lett. 2007, 91, 1011. [Google Scholar] [CrossRef]
- Evans, A.; Yu, J.S.; Slivken, S.; Razeghi, M. Continuous-wave operation of λ ∼ 4.8 µm quantum-cascade lasers at room temperature. Appl. Phys. Lett. 2004, 85, 2166–2168. [Google Scholar] [CrossRef]
- Strasser, G.; Gianordoli, S.; Schrenk, W.; Gornik, E.; Mucklich, A.; Helm, M. MBE-grown GaAs/AlGaAs and strained InGaAs/AlGaAs/GaAs quantum cascade lasers. J. Cryst. Growth 2001, 227, 197–201. [Google Scholar] [CrossRef]
- Faist, J.; Capasso, F.; Sivco, D.L.; Sirtori, C.; Hutchinson, A.L.; Cho, A.Y. Quantum Cascade Laser. Science 1994, 264, 553–556. [Google Scholar] [CrossRef] [PubMed]


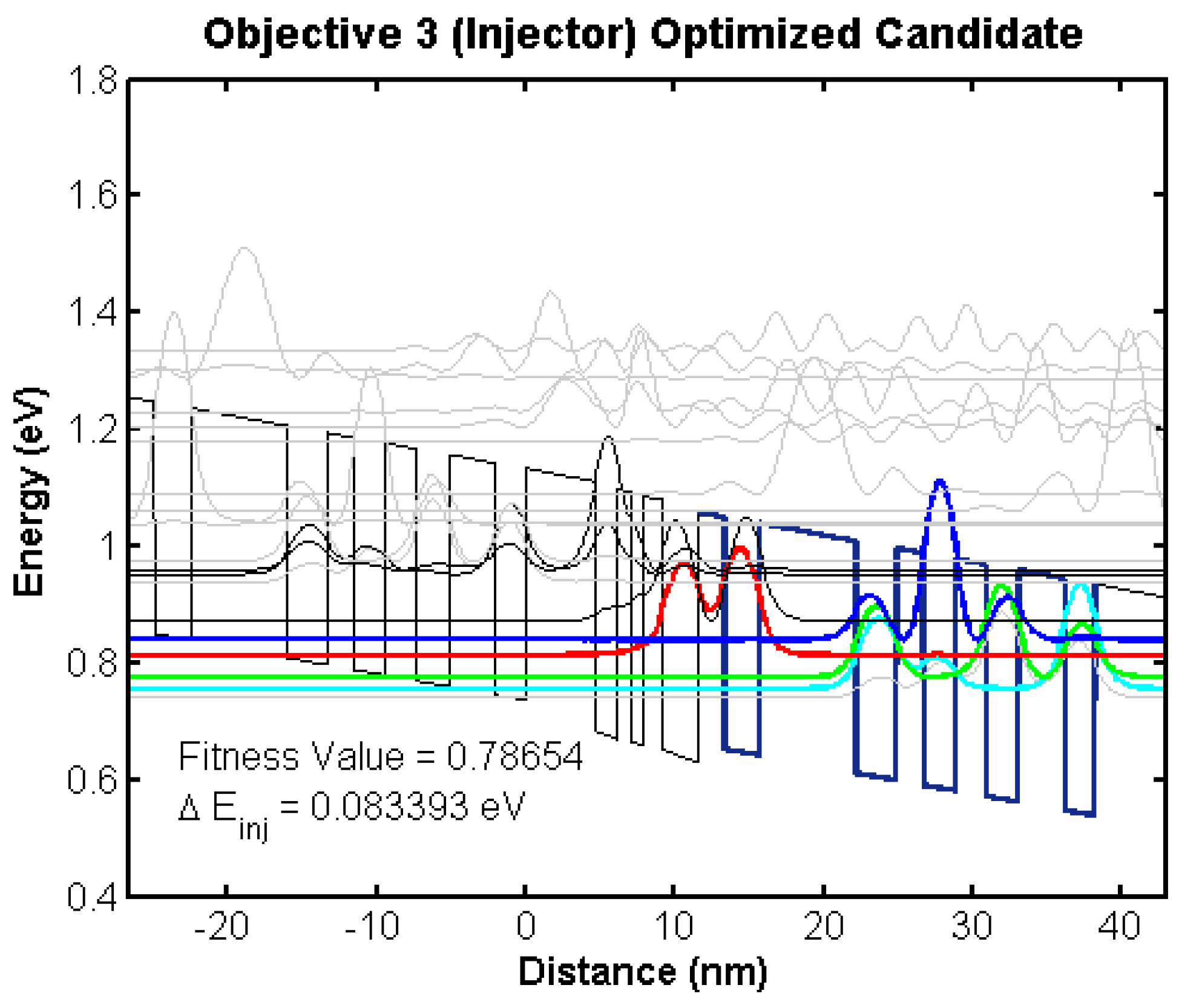
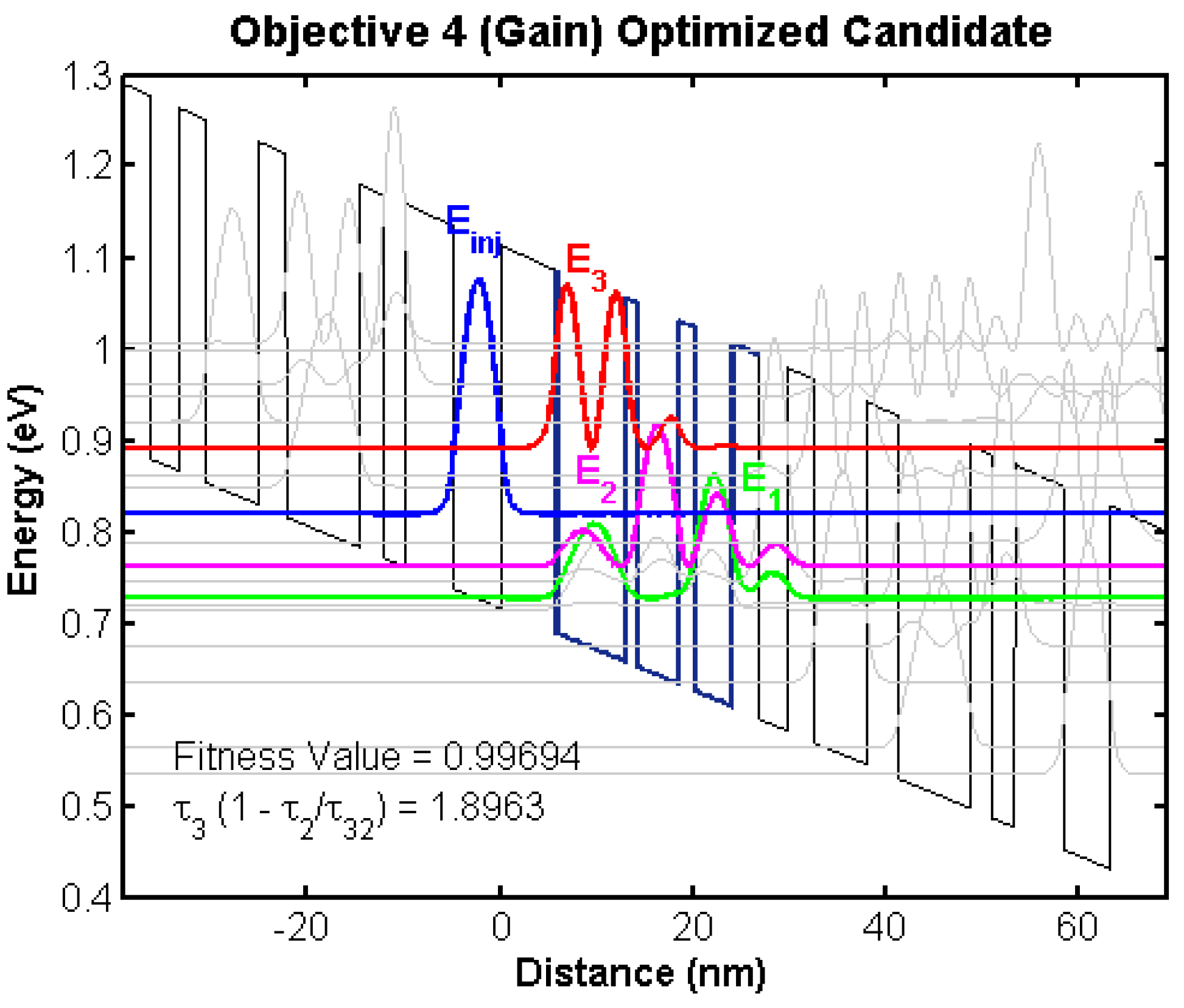
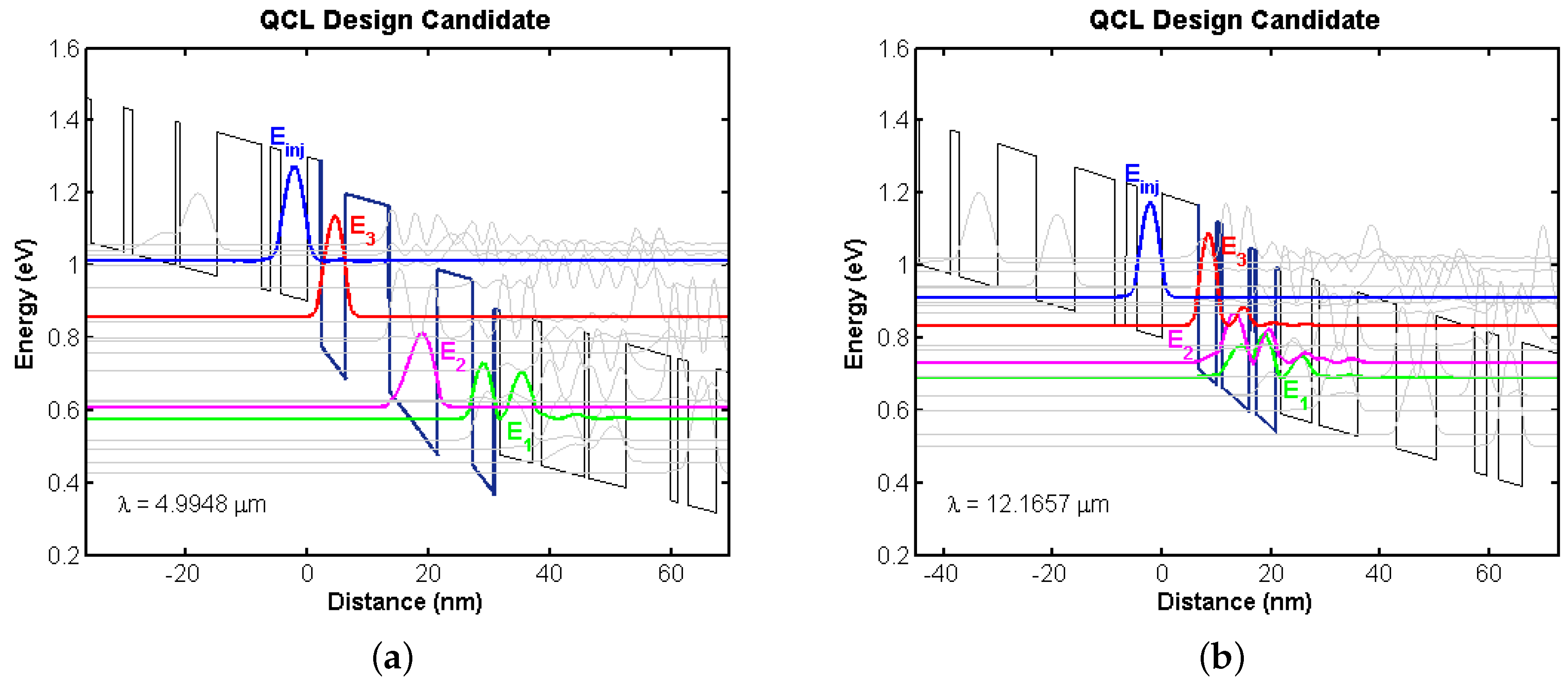
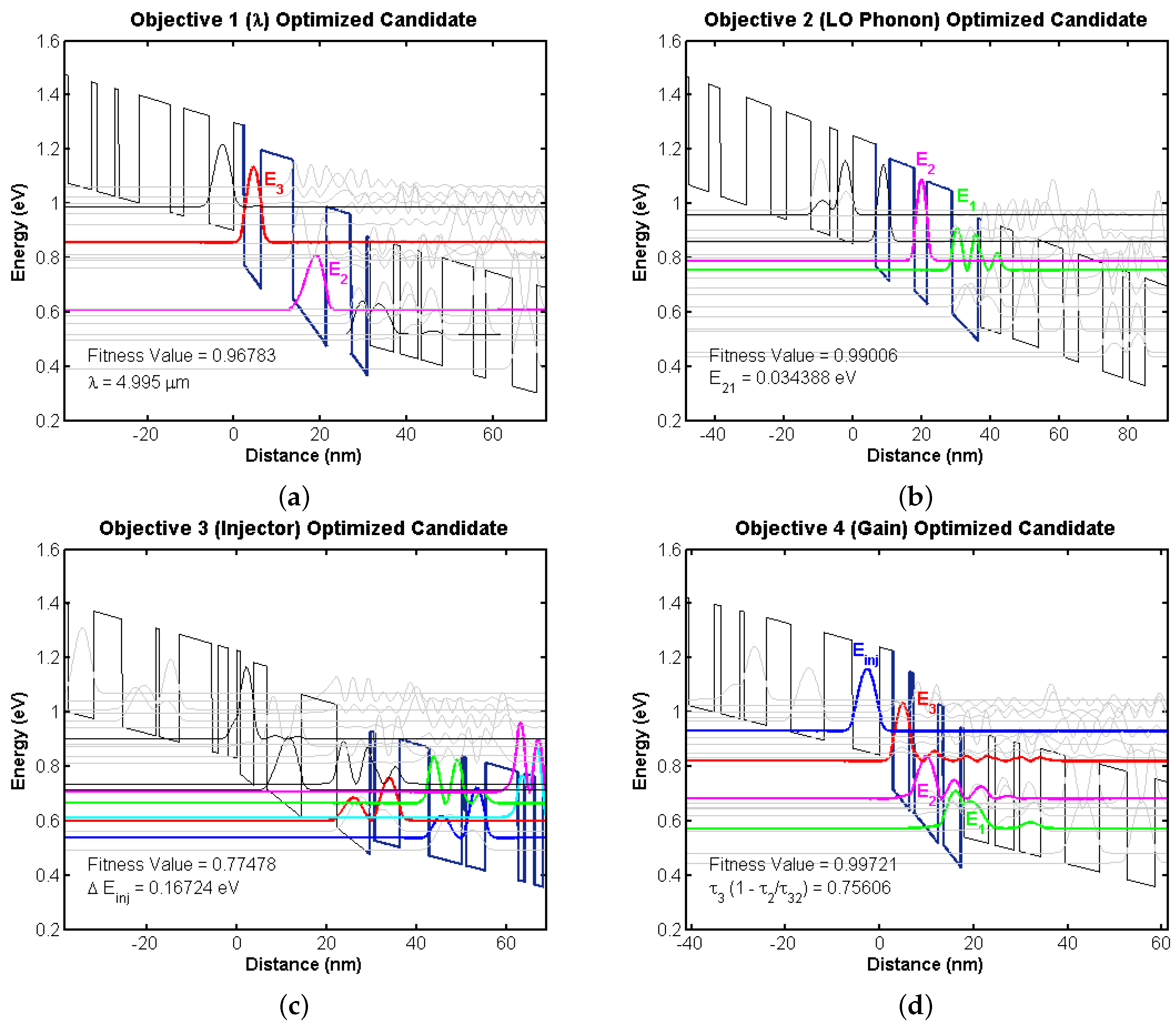
| Parameter | Value |
|---|---|
| Initial Population Size | 8 |
| Population | 64 |
| Generations | 100 |
| Variables | 18 |
| Objectives | 4 |
| Parameter | Value(s)/Range |
|---|---|
| Surface Indices | (111) |
| Electric Field (kV/cm) | 48 |
| Well Widths (ML) | 1–96 |
| Barrier Widths (ML) | 1–96 |
| Well Alloy (%) | 0–100 |
| Barrier Alloy (%) | 10–45 |
| Active Region Wells | 3 |
| Active Region Barriers | 3 |
| Injector Well | 5 |
| Injector Barriers | 5 |
| Objective | Normalized Fitness Value |
|---|---|
| Target Wavelength | 0.743 |
| LO Phonon Resonance | 0.779 |
| Injector Coupling | 0.564 |
| Gain Metric | 0.4194 |
| Objective | Normalized Fitness Value |
|---|---|
| Target Wavelength | 0.8611 |
| LO Phonon Resonance | 0.9732 |
| Injector Coupling | 0.6622 |
| Gain Metric | 0.8829 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mueller, D.; Triplett, G. Development of a Multi-Objective Evolutionary Algorithm for Strain-Enhanced Quantum Cascade Lasers. Photonics 2016, 3, 44. https://doi.org/10.3390/photonics3030044
Mueller D, Triplett G. Development of a Multi-Objective Evolutionary Algorithm for Strain-Enhanced Quantum Cascade Lasers. Photonics. 2016; 3(3):44. https://doi.org/10.3390/photonics3030044
Chicago/Turabian StyleMueller, David, and Gregory Triplett. 2016. "Development of a Multi-Objective Evolutionary Algorithm for Strain-Enhanced Quantum Cascade Lasers" Photonics 3, no. 3: 44. https://doi.org/10.3390/photonics3030044