Fractional Effective Charges and Misner-Wheeler Charge without Charge Effect in Metamaterials

Abstract

Transformation optics enables engineering of the effective topology and dimensionality of the optical space in metamaterials. Nonlinear optics of such metamaterials may mimic Kaluza-Klein theories having one or more kinds of effective charges. As a result, novel photon blockade devices may be realized. Here we demonstrate that an electromagnetic wormhole may be designed, which connects two points of such an optical space and changes its effective topological connectivity. Electromagnetic field configurations, which exhibit fractional effective charges, appear as a result of such topology change. Moreover, such effects as Misner-Wheeler “charge without charge” may be replicated.

1. Introduction

Recent development of artificial electromagnetic metamaterials enables unprecedented control over the coordinate dependencies of the dielectric permittivity and magnetic permeability tensors of an electromagnetic medium. This development gave rise to numerous novel device ideas based on the concept of “electromagnetic space”, which is different from the actual physical space [1,2,3,4], and may have non-trivial topological connectivity [5,6]. The current emphasis of research in this field is concentrated in the area of novel linear electromagnetic devices, such as superlenses and various versions of “invisibility cloaks”. On the other hand, nonlinear transformation optics of metamaterials also appears to be extremely interesting. It has a unique capability to realize tabletop models of many gravitational and field theoretical phenomena [7,8,9]. In particular, very recently, it was demonstrated that using extraordinary waves in anisotropic uniaxial metamaterials a model of four-dimensional Kaluza-Klein theory may be created [7]. Nonlinear optics of such a metamaterial space was shown to resemble interaction of effective charges. Here we demonstrate that similar to recent reports in [5,6], an electromagnetic wormhole may be designed, which connects two points of such an optical space and changes its effective topological connectivity. It also may provide an illusion of superluminal propagation. Electromagnetic field configurations, which exhibit fractional effective charges, may appear as a result of such topology engineering.

2. Methods

Let us start with a brief review of the four dimensional Kaluza-Klein model, which is based on the nonlinear electromagnetic metamaterials. The effective spatial geometry of this model may be approximated as a product R₂ × S₁ of a 2D plane R₂ and a circle S₁, as shown in Figure 1a.

The line element of such an optical space may be written as:

$$d{l}^2=d{x}^2+d{y}^2+R^{2}d{\varphi }^2$$

(1)

Using the stereographic projection z = 2Rsin$\varphi$/(1 + cos$\varphi$), this line element may be re-written as:

$$d{l}^2=d{x}^2+d{y}^2+\frac{d{z}^2}{{\left(1+\frac{z^2}{4R^2}\right)}^2}$$

(2)

which indicates that a uniaxial anisotropic metamaterial may be used to emulate such a space. Let us consider a non-magnetic uniaxial anisotropic metamaterial with dielectric permittivities ε_x = ε_y = ε₁ and ε_z = ε₂. The wave equation in such a material may be written as:

$$-\frac{{\partial }^2\overrightarrow{E}}{c^2\partial t^2}={\overleftrightarrow{\epsilon }}^{-1}\overrightarrow{\nabla }\times \overrightarrow{\nabla }\times \overrightarrow{E}$$

(3)

where ${\overleftrightarrow{\epsilon }}^{-1}=\overleftrightarrow{\xi }$ is the inverse dielectric permittivity tensor calculated at the center frequency ω of the signal bandwidth [10]. Any electromagnetic field propagating in this metamaterial may be expressed as a sum of the “ordinary” and “extraordinary” plane waves. For the ordinary field vector $\overrightarrow{E}$ of the electromagnetic wave is perpendicular to the optical axis. On the other hand, for the extraordinary field vector $\overrightarrow{E}$ is parallel to the plane defined by the k-vector of the wave and the optical axis. Let us define an extraordinary wave function as Ψ = E_z. Such a definition means that the ordinary portion of the electromagnetic field does not contribute to Ψ. Equation (3) then results in the following wave equation for the extraordinary wave function:

$$\frac{{\partial }^2\psi }{c^2\partial t^2}=\frac{{\partial }^2\psi }{{\epsilon }_1\partial z^2}+\frac{1}{{\epsilon }_2}\left(\frac{{\partial }^2\psi }{\partial x^2}+\frac{{\partial }^2\psi }{\partial y^2}\right)$$

(4)

Comparison of Equations (2) and (4) demonstrates that the extraordinary field will perceive the optical space as R₂ × S₁, if

$${\epsilon }_2=n^2 \text{and} {\epsilon }_1=\frac{n^2}{{\left(1+\frac{z^2}{4R^2}\right)}^2}$$

(5)

where n is a constant. Such an anisotropic uniaxial metamaterial may be realized using a 3D layered hyperbolic metamaterial structure shown in Figure 1b. Let us assume that the metallic layers are oriented perpendicular to the z-direction. The diagonal components of the permittivity tensor in this case have been calculated in Reference [11] using Maxwell-Garnett approximation:

$${\epsilon }_1=\alpha {\epsilon }_m+\left(1-\alpha \right){\epsilon }_d, {\epsilon }_2=\frac{{\epsilon }_m{\epsilon }_d}{\left(1-\alpha \right){\epsilon }_m+\alpha {\epsilon }_d}$$

(6)

where α is the fraction of metallic phase, and ε_m < 0 and ε_d > 0 are the dielectric permittivities of metal and dielectric layers, respectively. We would like to produce the anisotropic dielectric permittivity behavior described by Equation (5) by changing α as a function of z. Simple analysis of Equations (5) and (6) indicates that:

$$\alpha =\frac{{\epsilon }_d-n^2/{\left(1+\frac{z^2}{4R^2}\right)}^2}{{\epsilon }_d-{\epsilon }_m}$$

(7)

produces the required z dependence of ε₁, while ε₂ remains approximately constant if –ε_m >> ε_d. Such a geometry is similar to the well-established experimental geometries used in fabrication of multilayer Al/Al₂O₃ superlenses and hyperlenses [12,13].

3. Results

Let us consider nonlinear optics of the R₂ × S₁ metamaterial space, and demonstrate that it resembles the picture of effective charges interacting with each other via gauge fields. This result is natural, since the nonlinear optics of this space is modelled after the usual Kaluza-Klein theory. The eigenmodes of the extraordinary field may be chosen as:

$${\mathsf{\Psi }}_{kL}=\psi e^{iL\varphi }=e^{ik\rho }{e}^{iL\varphi }$$

(8)

where L is the quantized integer “angular momentum” number and k is the 2D momentum. The dispersion law of these eigenmodes of the extraordinary field is:

$$\frac{n^2}{c^2}{\omega }^2=k^2+\frac{L^2}{R^2}$$

(9)

It is clear that the L = 0 extraordinary photons behave as massless 2D quasiparticles. On the other hand, L ≠ 0 photons possess an effective mass m* ~ L/R. Let us demonstrate that the “angular momentum” number L behaves as a conserved quantized integer effective charge in the nonlinear optical interactions of extraordinary photons.

Indeed, the nonlinear optical effects deform the ${\overleftrightarrow{\epsilon }}^{-1}=\overleftrightarrow{\xi }$ tensor and therefore deform the line element (1). In general, the ${\overleftrightarrow{\epsilon }}^{-1}=\overleftrightarrow{\xi }$ tensor will not remain a diagonal tensor for a general field configuration. While corrections to the diagonal elements of ${\overleftrightarrow{\epsilon }}^{-1}$ are small and may be disregarded in the weak field approximation (in which the nonlinear corrections higher than the third order are disregarded), corrections to the off-diagonal terms of ${\overleftrightarrow{\epsilon }}^{-1}$ cannot be neglected. Therefore, the effective metric of the deformed optical space should be written as:

$$d{s}^2=g_{\alpha \beta }d{x}^{\alpha }d{x}^{\beta }+2g_{\alpha 3}d{x}^{\alpha }d\varphi +g_{33}d{\varphi }^2$$

(10)

where the Greek indices α = 0, 1, 2 indicate coordinates of the almost flat planar 3D Minkowski space-time: dx⁰ = cdt, dx¹ = dx, and dx² = dy. This 3D space-time is populated by extraordinary photons, which are described by the wave function Ψ. These extraordinary photons are affected by the vector field g_α3 (its components are g₀₃ = 0, g₁₃ = 2ξ₁₃dz/d$\varphi$, and g₂₃ = 2ξ₂₃dz/d$\varphi$) and the scalar field g₃₃ = R² (the dilaton). The dilaton field may be assumed constant in the weak field approximation. For a given value of L, the wave equation may be written as:

$$\widehat{D}\psi ={\mathrm{\Delta }}^{(2)}\psi -L^2\frac{1-g_{\alpha 3}{g}^{\alpha 3}}{g_{33}}\psi +2iL{g}^{\alpha 3}\frac{\partial \psi }{\partial x^{\alpha }}+iL\frac{\partial g^{\alpha 3}}{\partial x^{\alpha }}\psi =0$$

(11)

where ∆⁽²⁾ is the covariant three-dimensional d’Alembert operator [7]. Equation (11) is identical to the 3D Klein-Gordon equation for a charged particle. It describes a particle of mass:

$$m=\frac{\hslash L}{c{g}_{33}^{1/2}}$$

(12)

which interacts with a vector field g^α3 (playing the role of a vector potential) via its quantized effective charge L. Indeed, the linear portion of $\widehat{D}$ in Equation (11) describes free particles which propagate in the background metric defined by the dielectric permittivities (5) of the metamaterial.

On the other hand, if we artificially engineer the third order optical nonlinearity of the metamaterial in such a way that:

$$g^{\alpha 3}=2{\xi }^{\alpha 3}dz/d\varphi \propto S_3\propto (E_1{B}_2-E_2{B}_1)\propto L$$

(13)

where S₃ is the z component of the Poynting vector, this would lead to Coulomb-like interaction of the effective charges with each other. Indeed, in such a case the extraordinary photons having nonzero angular momentum L ≠ 0 would act as sources of the g^α3 field, which in turn acts on other “charged” (L ≠ 0) extraordinary photons. Such a nonlinear interaction may be realized using a dielectric component ε_d of the metamaterial (see Equation (6)), which exhibits recently suggested Poynting nonlinearity in the nonlinear Fabry-Perot (NLFP) resonator geometry [14]. The proposed metamaterial geometry shown in Figure 1b is indeed quite similar to the NLFP geometry, so that the Poynting nonlinearity is expected to occur.

Since g⁰³ = 0 (which corresponds to the Weil or temporal gauge), the effective “electric field” in our model equals:

$${\overrightarrow{E}}_{eff}=\left(i\omega g^{13}, i\omega g^{23}\right)=\nabla f_{eff}$$

(14)

Therefore, a natural choice of the effective “potential” f_eff is:

$$f_{eff}=(E_1{B}_2-E_2{B}_1)$$

(15)

Indeed, such a choice leads to an effective “Poisson equation”:

$${\mathrm{\Delta }}_2{f}_{eff}=-4k^2(E_1{B}_2-E_2{B}_1)\propto L$$

(16)

where ${\mathrm{\Delta }}_2={\partial }^2/\partial x^2+{\partial }^2/\partial y^2$ and k is defined by Equation (9). By its definition as the “angular momentum” number, such an effective charge L is conserved. At large enough R and small L:

$$k\approx \frac{n}{c}\omega$$

(17)

The effect of such 2D effective Coulomb interaction cannot be neglected when the kinetic energy term in Equation (11) becomes comparable with the potential energy terms.

As a second step, let us demonstrate that similar to the recent reports in [5,6], an electromagnetic wormhole may be designed, which connects two points of the R₂ × S₁ metamaterial space and changes its effective topology. Based on the spatial distribution of the dielectric permittivity tensor components given by Equation (5), it is clear that the electromagnetic field distribution in the R₂ × S₁ metamaterial space must be somewhat similar to a field distribution in a planar waveguide. This conclusion has been confirmed by numerical calculations using Comsol Multiphysics 4.2a solver (COMSOL, Inc., Burlington, MA, USA), as shown in Figure 1c. 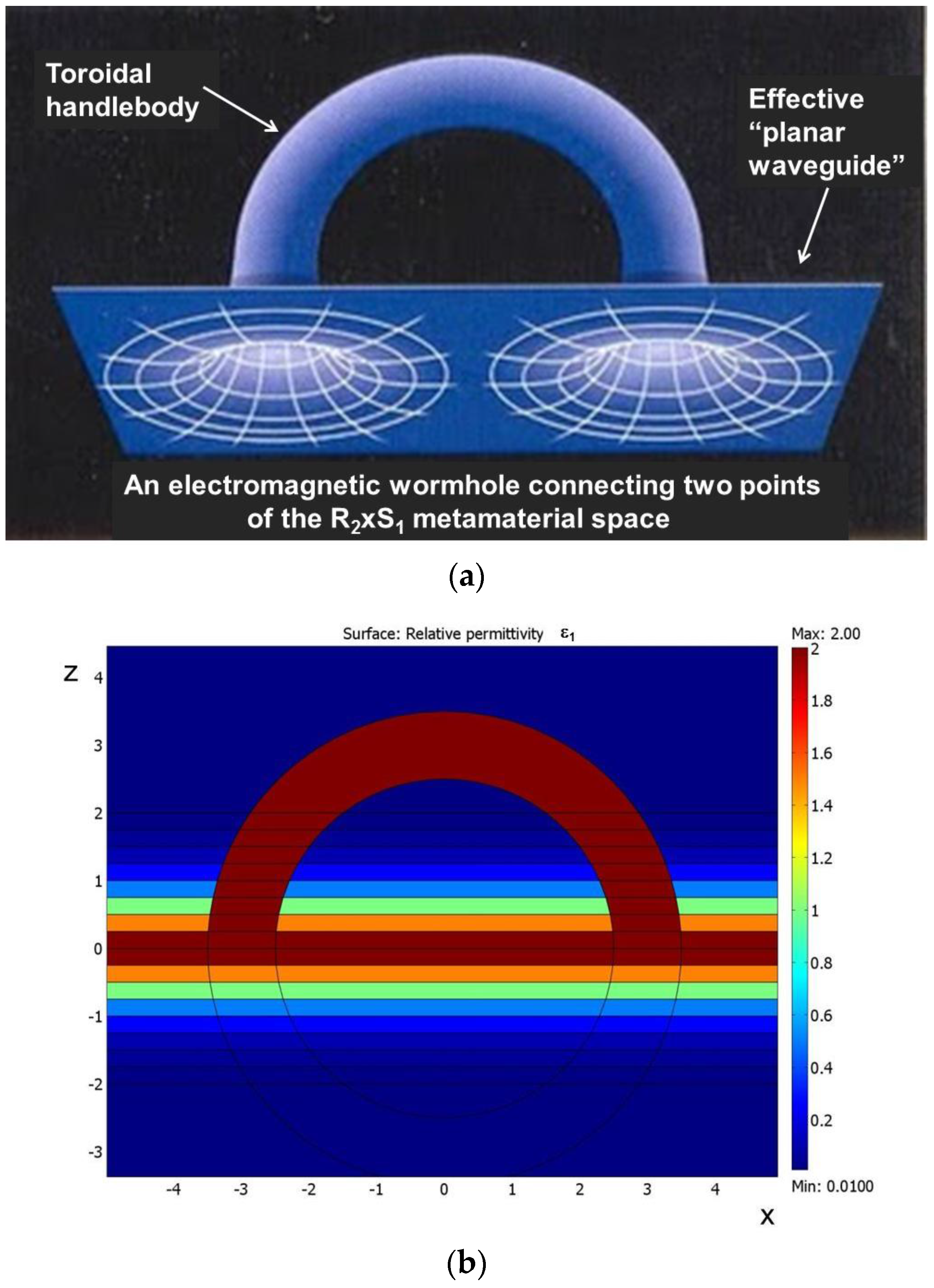Therefore, design of an electromagnetic wormhole connecting two points of the R₂ × S₁ metamaterial space appears to be similar to the design of a plasmonic analogue of an electromagnetic wormhole described in [6]. Such a wormhole may be designed as a toroidal handlebody (Figure 2a), which bridges two remote locations of the planar waveguide. We may implement the same recipe as in [6], where the metamaterial parameters for an invisible toroidal handlebody were designed as follows. Using toroidal coordinates (r,u,v), which are related to the Cartesian coordinates (x,y,z) as:

$$\begin{array}{l}x=r\cos u\\ y=(R+r\sin u)\sin v\\ z=(R+r\sin u)\cos v\end{array}$$

(18)

(where 2R is the distance between points connected by the wormhole), the metamaterial parameters of the handlebody may be obtained by coordinate transformations:

$$r^{\prime }=a+(b-a)r/b, u^{\prime }=u, v^{\prime }=v$$

(19)

where a and b are the inner and outer radii of the cloaked wormhole area, respectively. The corresponding material parameters are [6]:

$$\begin{array}{l}{\epsilon }_{rr}={\mu }_{rr}=\frac{r-a}{r}\frac{\left(b-a\right)R+b\left(r-a\right)\sin u}{\left(b-a\right)\left(R+r\sin u\right)}\\ {\epsilon }_{uu}={\mu }_{uu}=\frac{r}{r-a}\frac{\left(b-a\right)R+b\left(r-a\right)\sin u}{\left(b-a\right)\left(R+r\sin u\right)}\\ {\epsilon }_{vv}={\mu }_{vv}=\frac{b^2}{b-a}\frac{r-a}{r}\frac{R+r\sin u}{\left(b-a\right)R+b(r-a)\sin u}\end{array}$$

(20)

However, unlike the invisible “plasmonic electromagnetic wormhole” prescription in Reference [6], we do not need to make the handlebody invisible for light waves incident on the plasmonic waveguide from the outside 3D space. There are no such “outside” waves in the R₂ × S₁ metamaterial space. Moreover, as clearly demonstrated by Figure 1c, all waves which exist in the R₂ × S₁ space attenuate strongly away from the z = 0 plane. Since our goal is only to change the effective topology of the metamaterial space, the requirement of wormhole “invisibility” does not need to be strictly observed. As a result, complicated spatial material parameters distribution described by Equation (20) may be simplified without considerable effect on visibility of the toroidal handlebody, and the Soft-and-Hard (SH) boundary condition [5] imposed at the wormhole openings may be somewhat relaxed. Such a “reduced visibility” wormhole may be implemented using a toroidal handlebody having isotropic homogeneous ε. Numerical simulations of such a wormhole are shown in Figure 2b,c.

Based on the “effective Gauss theorem” expressed by Equations (14)–(16), it is clear that the wormhole-induced topology changes of the R₂ × S₁ metamaterial space must result in electromagnetic field configurations which exhibit fractional effective charges. Indeed, we may introduce an effective “electric field flux” through a closed contour C enclosing an area A of the R₂ plane as:

$${\mathsf{\Phi }}_{Eeff}={\displaystyle {\oint }_C{\overrightarrow{E}}_{eff}}d\overrightarrow{l}$$

(21)

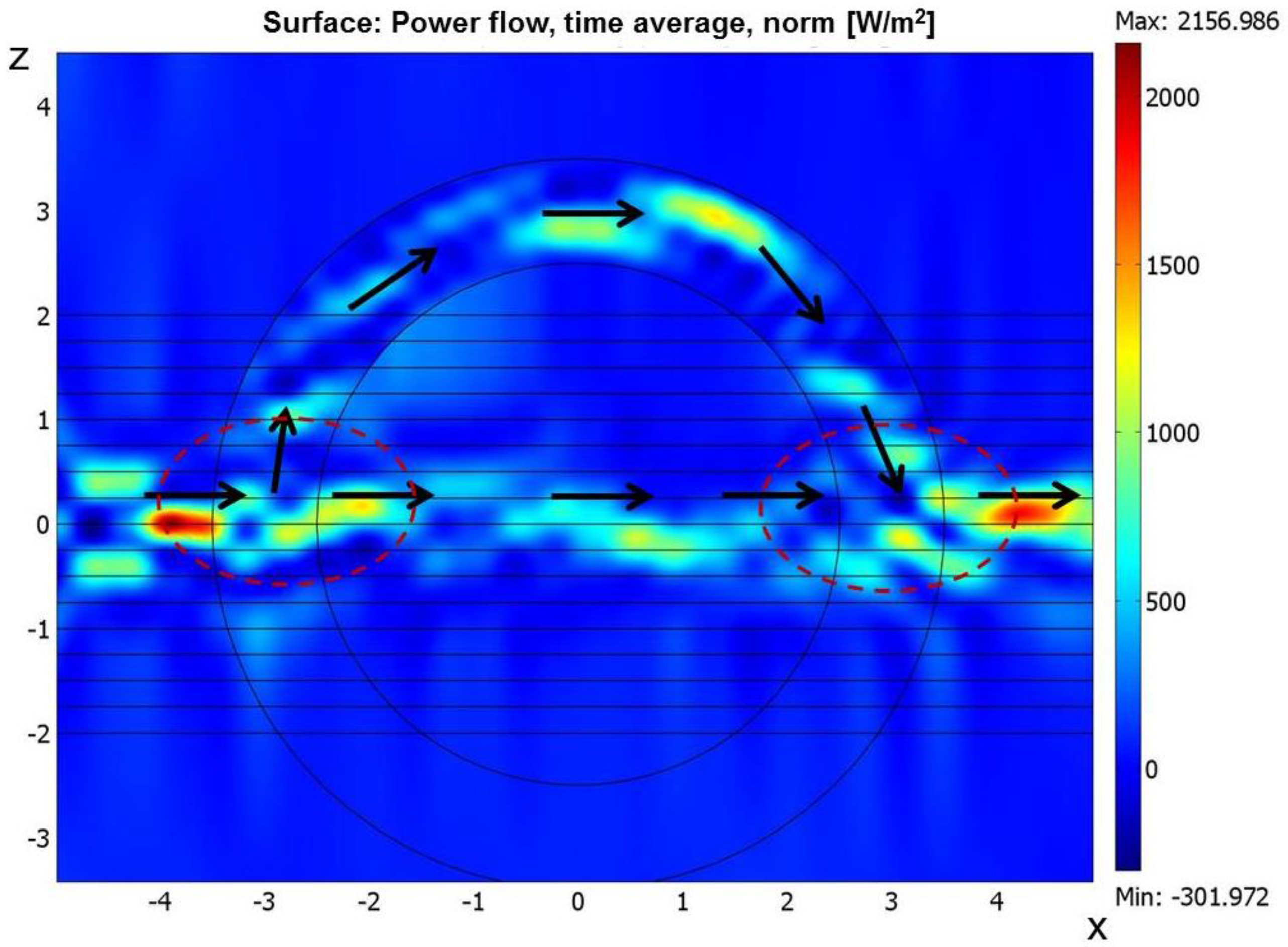
where $d\overrightarrow{l}$ is a vector representing an infinitesimal element of the contour length oriented normally to the contour. According to Equation (16), such an effective flux is quantized if the metamaterial R₂ × S₁ space is simply connected. On the other hand, if a wormhole connects an inside point of the area A to some other distant point (as shown in Figure 2a), the integral in Equation (21) may produce a non-integer fractional value. This effect may be illustrated by Figure 3, which shows numerical simulations of power flow near the electromagnetic wormhole in the same geometry as in Figure 2b,c. The average Poynting vector directions are indicated by black arrows. Near the wormhole openings the z components of the Poynting vector S₃ are nonzero and have opposite signs, which according to Equations (13)–(16) leads to appearance of opposite contributions to the effective charges of the wormhole openings.

4. Discussion

Appearance of fractional charges in our metamaterial model is interesting because such effects are extremely rare. Fractional charges are known to appear in quantum chromodynamics as fractional charges of quarks [15], and in systems, which exhibit the fractional quantum Hall effect [16]. Studying such metamaterial space configurations also appears interesting in light of recent demonstrations that two colored quasiparticles (quarks) in maximally supersymmetric Yang-Mills theory entangled in a color singlet EPR pair are connected by a wormhole [17,18], and that the physical vacuum appears to exhibit hyperbolic metamaterial properties when subjected to a very strong magnetic field [19]. In addition, such effects as Misner-Wheeler “charge without charge” [20] and the recently proposed charge-hiding effect [21] may be replicated in the metamaterial system. Indeed, as obvious from Figure 3, coupling of some of the L = 0 mode power into the wormhole leads to appearance of the opposite effective charges of the wormhole openings due to non-zero S₃ near the openings.

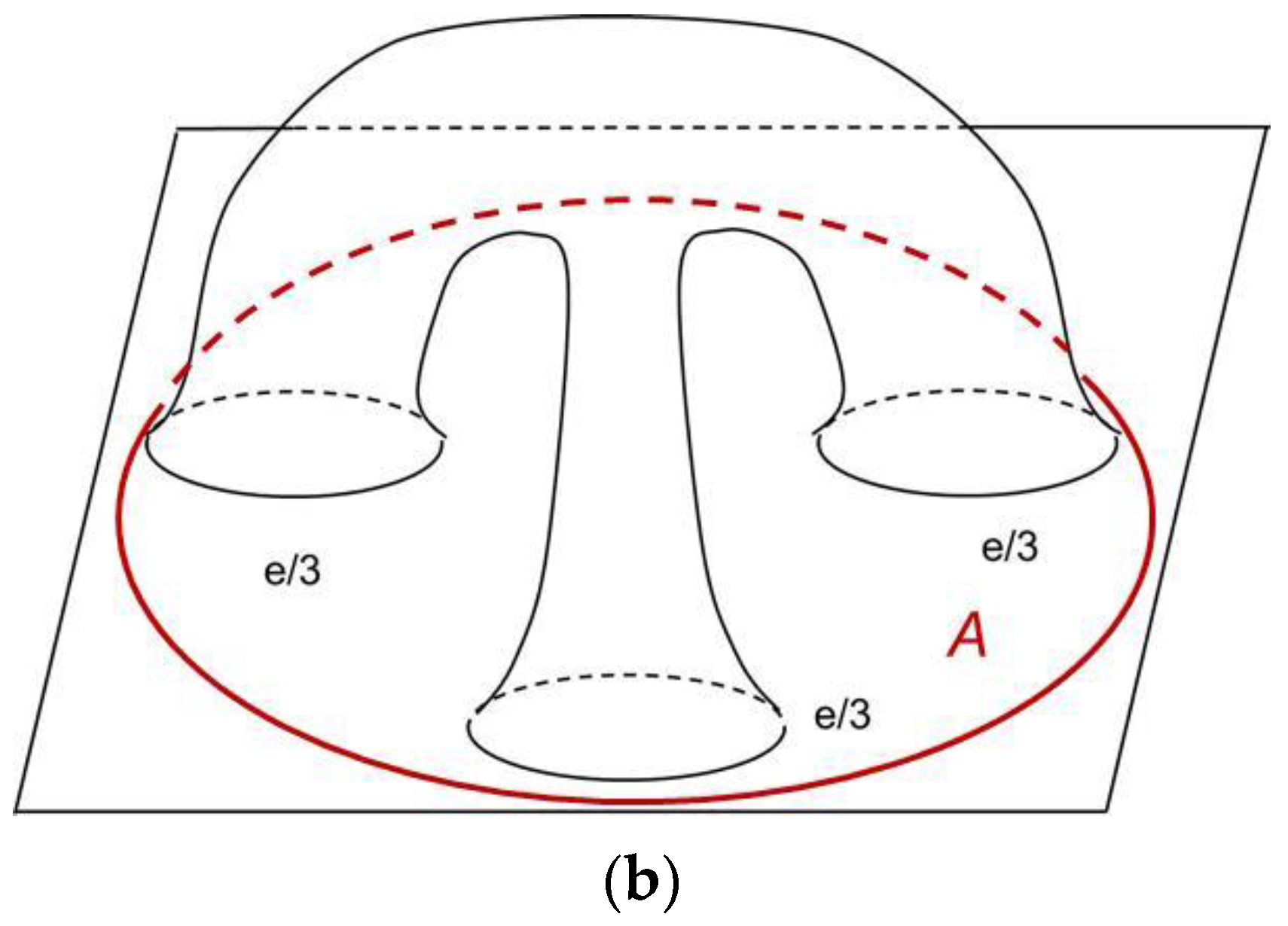
As far as the fractional charge values are concerned, any non-integer value of the effective charge may appear in our model if the wormhole geometry is arbitrary. However, if the wormhole geometry exhibits some symmetry (such as symmetry under rotation by either π or 2π/3 radian, as shown schematically in Figure 4a,b), the allowed values of effective charges may become restricted to some simple fractions. The total charge of a closed area A defined by Equation (21) must be integer if all the wormholes, which originate inside A do not lead outside of this area. If a rotational symmetry is imposed on the electromagnetic field configurations, the integer effective charge inside A must be divided equally between the wormhole openings, leading to appearance of either 1/2 or 1/3 charges in wormhole configurations shown schematically in Figure 4a,b. Because of the effective charge conservation, a photon with L = −1 traveling through one of the openings of the latter wormhole may also lead to appearance of −2/3 charge. However, the exact amount of power flow that goes through the wormhole and determines its effective charge needs to be determined from the numerical analysis, which is similar to the one presented in Figure 3. As was pointed out in Reference [22], the transmission and reflection amplitudes through a (gravitational-electromagnetic) wormhole indeed determine its effective net charge.

We should also point out that as was already indicated in Reference [5], monopolar magnetic charges may also appear at the wormhole openings.

5. Conclusions

In conclusion, we have demonstrated that the transformation optics of metamaterials presents us with new opportunities to engineer topologically non-trivial “optical spaces”. Nonlinear optics of extraordinary light in these spaces resembles Coulomb interaction of effective charges. Electromagnetic wormholes may be designed which connect two points of such an optical space and change its effective topology. Electromagnetic field configurations, which exhibit fractional charges appear as a result of such topology change. Moreover, such effects as Misner-Wheeler “charge without charge” [20] may be replicated. As far as potential applications of the effects are concerned, when individual photon behavior starts to look like behavior of charges, such systems may be used in various quantum computing and communication schemes, due to expected emergence of photon blockade behavior.