1. Introduction
One of the primary appeals of the quantum cascade laser (QCL) is its ability to access a wide portion of the infrared spectrum (3 < λ < 11 μm) in continuous operation at room temperature [
1,
2]. High output power and a small form factor are also key characteristics. This makes the QCL a very important, even enabling, technology for many applications which would benefit from portability, such as spectroscopy. While initial development concentrated on fixed frequency (or mildly tunable) applications, recent years have seen a resurgence in QCL development based on wide wavelength coverage from a single device.
The first step to achieving this is to demonstrate a laser medium with an extremely broad gain bandwidth. With a QCL, a single, homogeneously broadened emitter can exhibit several hundred inverse centimeters of bandwidth, especially at shorter wavelengths. This is one advantage of an intersubband emitter over a mid-infrared interband laser like the interband cascade laser (ICL). The second advantage of the QCL relies on the intersubband gain lineshape, which has very little absorption adjacent to the primary gain peak (when properly designed). This allows multiple wavelength emitters to be combined within the same laser waveguide (a so-called heterogeneous QCL) without significant cross-absorption. All emitters can emit simultaneously, or a single wavelength can be selected with the proper feedback.
While a single homogeneous QCL might have a gain bandwidth of 200 cm
−1 (24.8 meV), a properly designed heterogeneous QCL can exhibit significantly broader bandwidth. Our group has recently demonstrated a room temperature long wavelength infrared (LWIR) DFB laser array capable of emission wavelengths from 5.9–10.9 μm [
3]. This represents a bandwidth of 760 cm
−1 (94 meV). The waveguide core of this wafer was composed of six different emitting stages. This covers a significant portion of mid-infrared spectral region and will be part of a new generation of tunable infrared sources. Another, as yet unpublished, initial effort was made to generate an ultra-broadband gain region used eight emitting stages. This wafer showed electroluminescence that covered the entire 4–12 μm wavelength region (>1600 cm
−1), although some additional optimization is necessary to flatten the gain distribution.
The second step to achieving broadband emission from a laser is to provide a means of adjustable, wavelength-selective feedback. One of the more common methods of doing this relies on external cavity feedback via a diffraction grating. Overall, this is very successful, and it has been applied to heterogeneous QCLs in the past. However, this technique relies on multiple optical components beyond the QCL gain medium [
4]. Precise optical alignment is also required to maintain smooth operation. Finally, the tuning is traditionally mechanical in nature, which has a limited tuning speed. Some recent demonstrations, however, have significantly increased the tuning speed using MEMs or acousto-optic elements, but the other restrictions still apply [
5,
6].
The more robust alternative that many groups are now developing is tuning via the Vernier effect. In this arrangement, the laser is composed of at least two sections with comb-like reflectivity behavior. When the comb spacing of the two sections is different, the combs do not overlap perfectly, and only certain wavelength have strong feedback in both sections. When the grating reflectivity envelope is properly aligned to the gain bandwidth of the laser, the resultant coupled cavity can exhibit single mode output. Adjusting current or temperature in one of the sections causes a shift in the overlap, which can lead to a large, controllable, shifts in the output wavelength.
Though there are many geometries that can exhibit the Vernier effect, one of the most successful for the QCL at present is the sampled grating distributed feedback (SGDFB) laser. This architecture is similar to that developed for electrical tuning of telecom lasers [
7], and was demonstrated for the QCL in 2012 [
8]. Over an order of magnitude, improvement in tuning was demonstrated compared to traditional single mode DFB QCLs. Since then, multiple demonstrations of this technology have been made, leading to mid-infrared lasers with published pulsed and continuous wave tuning ranges of 243 cm
−1 and 120 cm
−1 from individual lasers, respectively [
9,
10]. Single mode power output has also been increased significantly, with over 5 W (1.25 W) tunable peak (continuous wave) output power demonstrated from single devices [
10]. Even wider tuning is possible with more advanced grating designs, like the superstructure grating (SSG), with predicted tuning limited only by the gain bandwidth of the laser itself [
11].
Other interesting configurations are also being investigated. While one SGDFB has a broad range, an array of SGDFB lasers has even a wider range. This was demonstrated in the mid-wavelength infrared (MWIR, 3 < λ < 5 μm) shortly after the first SGDFB QCL, and showed a pulsed wavelength coverage of 351 cm
−1 at room temperature in pulsed mode [
12]. Also, combining the SGDFB with an additional distributed Bragg reflector section has been used to generate a tunable dual wavelength laser. This was utilized recently as an on-chip pump source for room temperature, single mode, tunable continuous wave THz emission [
13].
2. Combining Broadband Gain and Electrical Tuning
The next evolutionary step in tunable QCL development is the combination of broadband gain media with Vernier-type feedback. The first demonstration builds on the 6-core laser design from [
3]. An 8-laser SGDFB array, each with a shifted central wavelength, was demonstrated on a similar broadband wafer that can emit at almost any wavelength within the 6–10 μm wavelength range. Additionally, an on-chip beam combiner was developed which emits all light out of a single aperture. The laser was incorporated into a system capable of rapid scanning over the whole tuning range [
14].
Though this is impressive, it has a somewhat complex control scheme. If spectral coverage is preferred over continuous tuning, another approach is under investigation. A standard sampled grating has a reflectivity envelope width (of the central lobe) that is inversely proportional to the number of gratings periods (N
g) within one sampling period. This can lead to very wide envelopes, with a full width at half maximum (FWHM) up to 500 cm
−1 for N
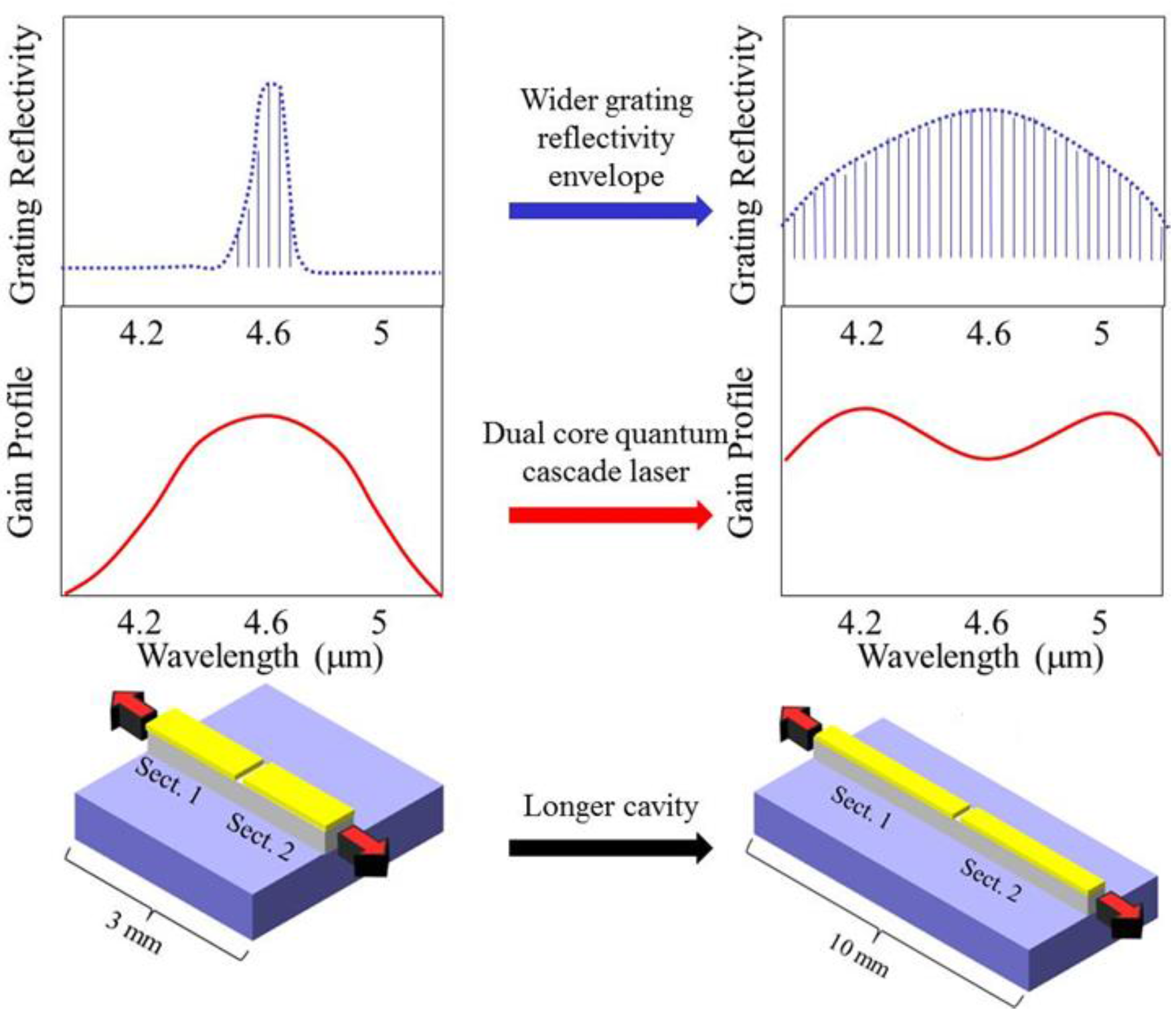
g = 4. The consequence is the need for a longer cavity (more sampling periods) in order to build up sufficient grating reflectivity for single mode operation. Also, the reflectivity is peaked, which leads to non-uniform threshold gain for a standard QCL. However, this can be efficiently compensated for by using a dual core (dual emitter) QCL, whose modal gain can be engineered to partially compensate for the varying grating reflectivity. The progression from a simple SGDFB to this dual core approach is shown in
Figure 1.
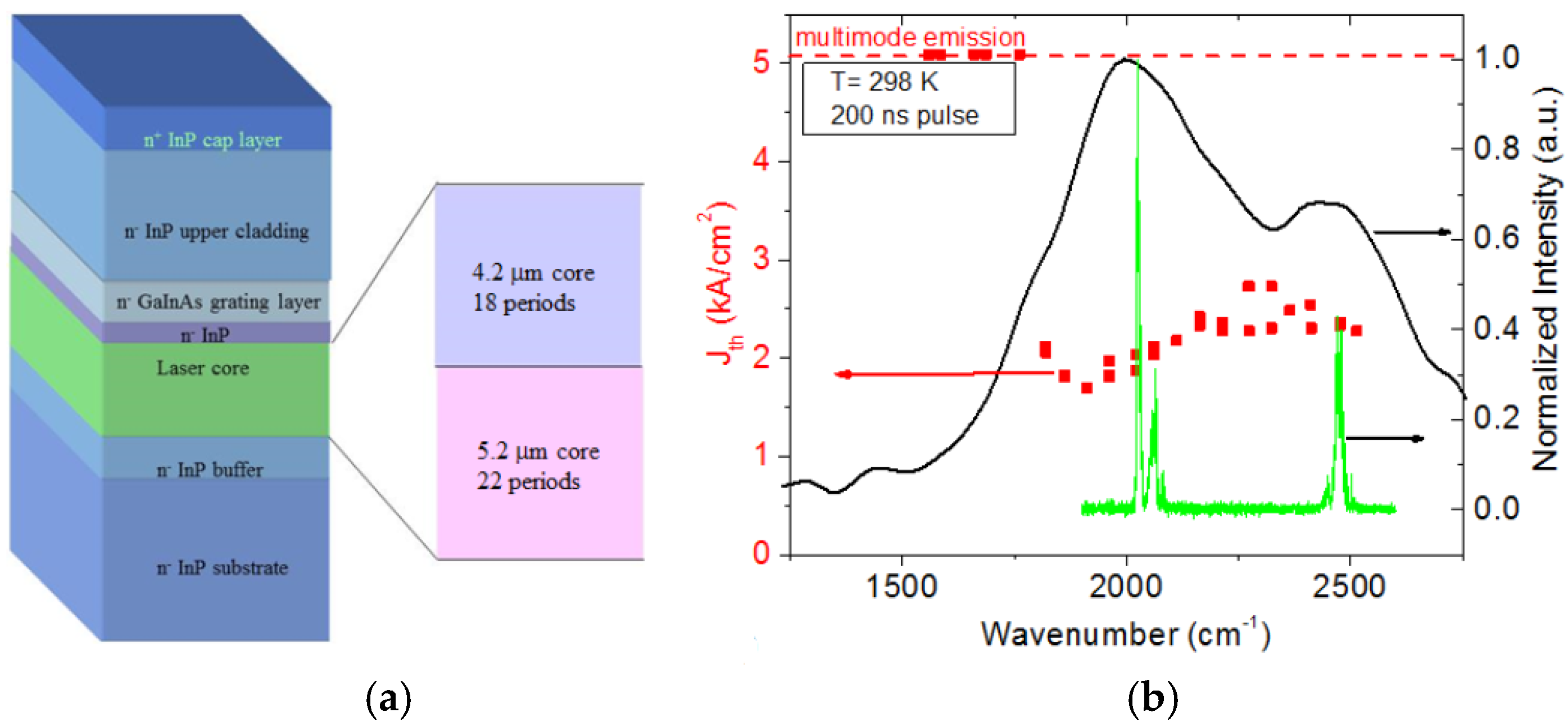
A MWIR dual core QCL has been designed to test the proposed methodology. The emitters used in the laser core are based on the high efficiency λ = 4.9 μm laser demonstrated by our group. The primary design change used to shift the wavelength is the adjustment of the 1st quantum well in the active region from 5 (λ = 5.2 μm) to 2 (λ = 4.2 μm) monolayers. These wavelengths are appropriate considering the gain FWHM of this laser design is typically 400–500 cm−1. Minor adjustments (1–2 monolayers) were also made to a few other layers just to adjust alignment of the energy levels. These altered designs have not yet been optimized for efficiency. The waveguide core starts with 22 periods of the longer wavelength emitter and 18 periods of the shorter wavelength emitter. This asymmetry is due the presence of a 450 nm thick GaInAs grating layer, which is also part of the waveguide.
The layer structure (as shown in
Figure 2) was grown on n- InP by gas-source molecular beam epitaxy without the upper cladding and cap layer. Initially, two pieces were set aside. The first piece had diffraction gratings fabricated by e-beam lithography and plasma etching. Uniform DFB gratings of varying period were defined. Both pieces then had the upper cladding and cap layers deposited by MOCVD.
The first sample was fabricated into several identical arrays of DFB lasers, with some Fabry Perot (FP) reference lasers (no DFB grating). The second piece was fabricated into circular mesas for measurement of intersubband electroluminescence (EL).
Figure 2 shows testing data for these pieces of the dual core wafer. The most noticeable feature is that the EL shows two peaks, which is matched fairly well by the dual peaked multimode emission from the FP laser. The FWHM of the EL is over 750 cm
−1. Also shown are the threshold current densities from two identical DFB arrays as a function of the targeted emission wavenumber. The DFB array showed single mode emission over the 4–5.5 μm wavelength range (700 cm
−1). While the threshold behavior is fairly flat over this range, some improvement in gain balancing is still necessary.
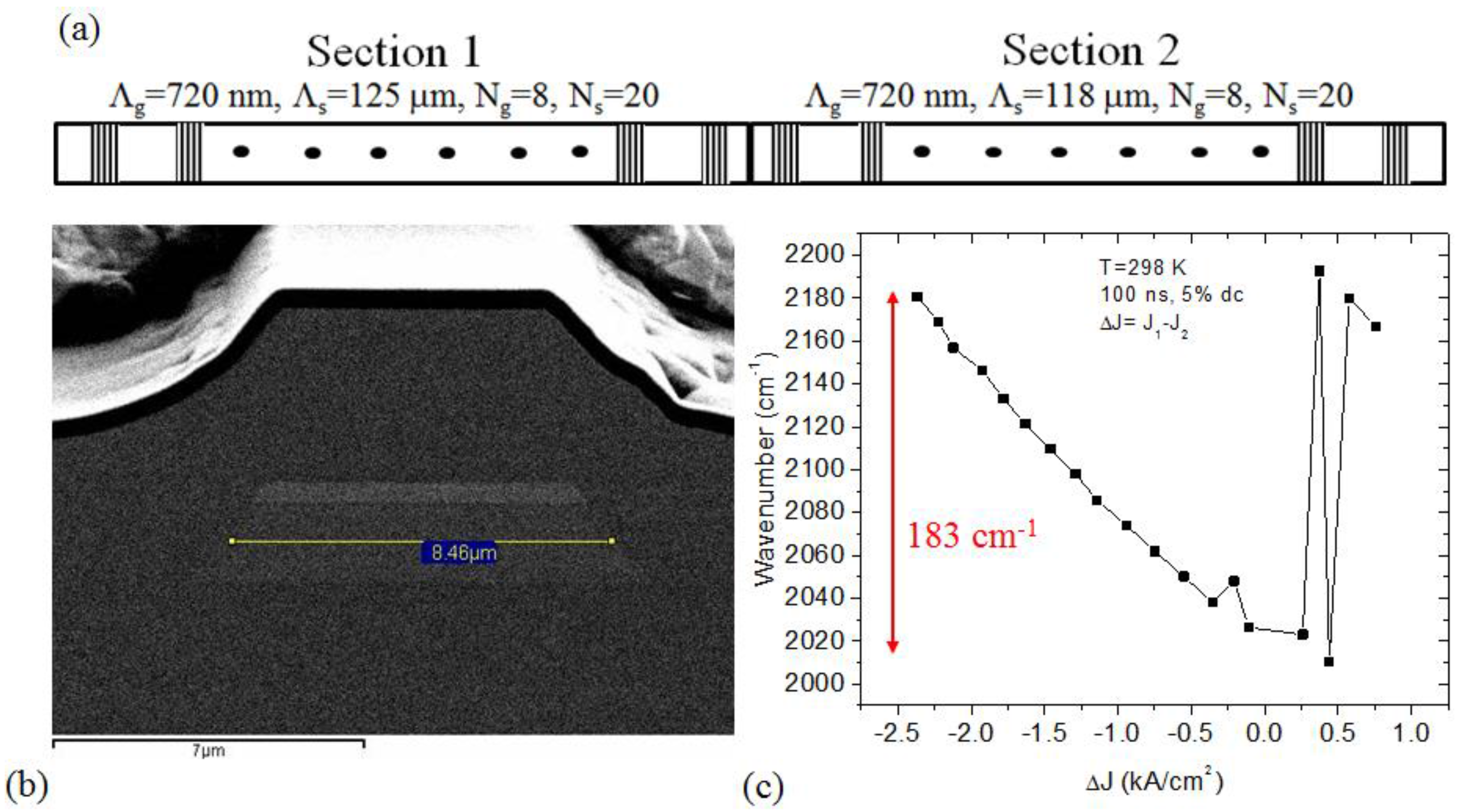
Based on this initial wafer testing, an early stage dual core SGDFB was also fabricated from the same wafer. Unlike previous SGDFB fabrication, however, a buried ridge geometry was utilized. The main purpose was to try and produce a more ideal grating reflectivity by reducing parasitic reflections from the waveguide sidewalls. A cross-section of a finished device (w = 8.48 μm), is shown in
Figure 3.
Several different grating periods and ratios of sampling periods between sections were used to explore the tuning behavior. All designs were based on 5 mm long, uncoated cavities, in order to get as much data as possible. The number of sampling periods (Ns) was varied between 7 and 20 per section, and the number of grating periods per sampling periods was varied from 8 to 12. Based on the section lengths, this translates to comb spacings between 5 and 13 cm−1, with theoretical tuning ranges from 92–180 cm−1.
Lasers were tested in pulsed mode at room temperature with a pulse width of 100 ns and a 5% duty cycle (pulse width/period). The emission wavelength is tuned by changing the current density in one section relative to the other. The tuning behavior is shown in
Figure 3b as a function of the difference in current density (ΔJ). Most of the lasers behaved as expected, with some exhibiting tuning up to 183 cm
−1 using a standard SGDFB short period grating design (N
g = 8, N
s = 20). This is the widest tuning reported for a SGDFB QCL with a single grating basis. In this case, the step tuning behavior has a spacing of ~12 cm
−1. The measuring current was not carefully optimized to minimize the side mode suppression ratio in this experiment, but the measured values range from 10–20 dB. As the grating period reduced, the spectrum gradually became multimode, however, which shows insufficient reflectivity at shorter wavelength to suppress emission from the longer wavelength peak. This indicates, as with the DFB measurement, that broadband (>250 cm
−1) tuning will benefit from a more balanced gain lineshape, which will require only minor modification of the number of emitting periods.
3. Discussion
One challenge with the dual core method presented above is maintaining alignment between the laser gain curve and the sampled grating reflectivity function. The tuning mechanism of the laser, while controlled electrically, is actually enabled by local temperature changes in the waveguide which are related to the current density. As the change in gain curve peak position is faster with temperature than the Bragg peak position, a small (<10 cm−1) misalignment is expected to occur over the full tuning range of the laser. However, this is small compared to the gain FWHM (~750 cm−1), and the error can be corrected by a small increase in the grating period and careful choice of the sampling periods in the two sections.
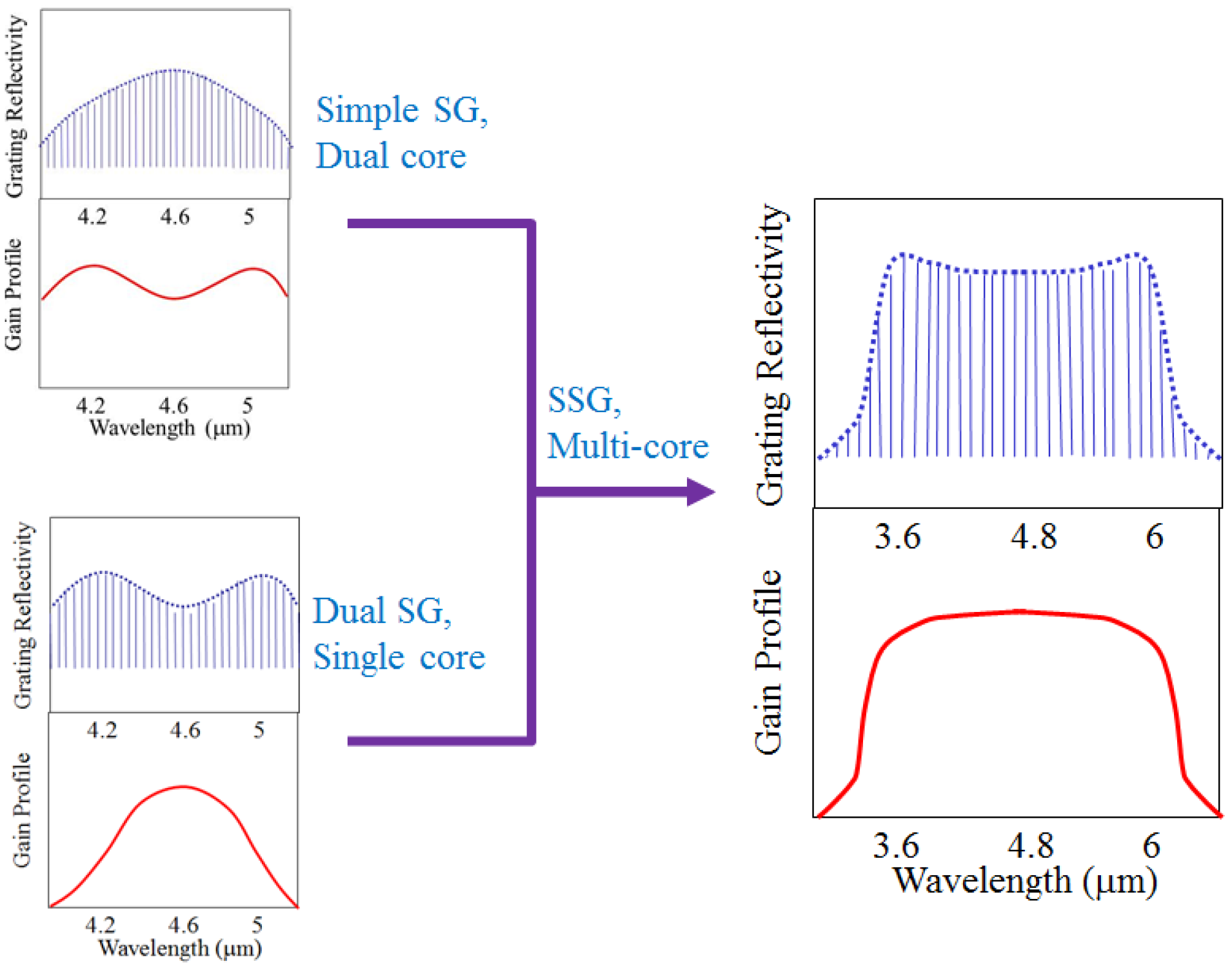
Though the initial goal described above was to a combine a dual core QCL with a simple sampled grating to produce a very wide tuning range, there is a more elegant path forward to reach this architecture’s true potential. Beyond the use of a simple grating basis, a tailored SSG can be adapted to compensate for a more general gain lineshape. In addition, the gain lineshape can be tailored to produce a nearly arbitrary gain lineshape with the use of multiple emitter designs. In combination, an extremely broad spectral range can be accessed with minimal variation in threshold or power output.
The main goal will be to achieve flat gain and reflectivity across the tuning range of interest. The general idea is sketched in
Figure 4. Besides improving power uniformity, this architecture will also make alignment of the two components (gain and reflectivity curves) less critical as there are no sharp features. The first task is to develop the SSG basis using discretized grating periods and phase shifts. This is not trivial, but the approach can be adapted from prior related efforts [
15]. Optimization of the gain curve must then be achieved which has now been investigated extensively in the LWIR for heterogeneous QCLs. Some optimization will be required to arrive at the proper shape without sacrificing device efficiency, however, which will follow the procedure developed in [
3].