Abstract
We report on the dynamic behavior of dual-wavelength distributed feedback (DFB) quantum cascade lasers (QCLs) in continuous wave and intermittent continuous wave operation. We investigate inherent etaloning effects based on spectrally resolved light-current-voltage (LIV) characterization and perform time-resolved spectral analysis of thermal chirping during long (>5 µs) current pulses. The theoretical aspects of the observed behavior are discussed using a combination of finite element method simulations and transfer matrix method calculations of dual-section DFB structures. Based on these results, we demonstrate how the internal etaloning can be minimized using anti-reflective (AR) coatings. Finally, the potential and benefits of these devices for high precision trace gas analysis are demonstrated using a laser absorption spectroscopic setup. Thereby, the atmospherically highly relevant compounds CO2 (including its major isotopologues), CO and N2O are simultaneously determined with a precision of 0.16 ppm, 0.22 ppb and 0.26 ppb, respectively, using a 1-s integration time and an optical path-length of 36 m. This creates exciting new opportunities in the development of compact, multi-species trace gas analyzers.
1. Introduction
Quantum cascade lasers are unipolar coherent light sources emitting in the mid-infrared (MIR) part of the electromagnetic spectrum. Their emission spectrum gives access to the fundamental absorption bands of many molecular species, allowing for gas concentration measurements with high precision and sensitivity by direct laser absorption spectroscopy [1,2,3,4,5,6].
However, single mode devices, such as quantum cascade lasers (QCLs) with a distributed feedback (DFB) grating, are tunable only within a narrow tuning range of about 5 cm−1 and are thus typically limited to one or two species that can be targeted with a single laser. However, the capability to simultaneously measure multiple species is highly preferred or even required, especially, but not only, in environmental monitoring. For instance, measuring concentrations of CO and 12/13CO2 simultaneously is of great interest given their linkage in combustion processes. Thus, CO can be used as a tracer for the CO2 originating from anthropogenic sources [7,8].
Although multi-species analyzers are available, they involve the addition of further laser sources along with a beam combination scheme and the necessary driving hardware. With such an approach combinations of three [9] or even four [10] QCLs were realized at the expense of increased optical complexity, complicated and sensitive alignment, bulky instrumental setups and higher overall costs.
A more attractive alternative to realize multi-species detection is to use lasers able to emit more than one wavelength. Such devices can be treated as a single point source and thus do not require any beam combination scheme. QCLs are ideal candidates for such an approach, because their atomic-like joint density of states of the intersubband lasing transitions makes the active region transparent on both sides of its resonance. This allows the combination of several active regions designed for different emission wavelengths in a single waveguide [11]. The first demonstration of simultaneous emission of two wavelength in one QCL was presented by Straub et al. [12] at cryogenic temperatures. Meanwhile, independent emission of two wavelengths close to room temperature was demonstrated in pulsed operation, together with successful spectroscopic measurements [13,14]. A more convenient use of a dual-wavelength QCL, however, is in intermittent continuous wave (iCW) operation, where relatively simple driving electronics provide laser pulses in the order of tens to hundreds of microseconds, which significantly lowers the heat dissipation and inherently allows for sequential laser operation. The thermal chirp during these pulses can then be used as frequency tuning for spectroscopy [15].
In this article we investigate the dynamic behavior of dual-section DFB QCLs operated in continuous wave (CW) and iCW mode. The devices are designed to emit at 4.3 and 4.6 µm, i.e., to optimally probe fundamental vibrations of CO, N2O and CO2. We present a phenomenological description of the etaloning, inherent to such dual-section DFB designs, and show a solution to minimize this detrimental effect by means of AR coatings. Finally, we demonstrate the performance of the device in a laser spectroscopic setup and show the results of the simultaneous measurements of the three target species. These data are then compared with published state-of-the-art values.
2. Dual-Wavelength QCLs
2.1. Materials and Methods
2.1.1. Laser Fabrication
The dual-wavelength DFB QCLs were implemented with an inverted buried hetero-structure protocol [16,17]. The active region was grown on InP and based on a heterogeneous quantum cascade stack of two bound-to-continuum single wavelength-active regions. The first consisted of 17 In0.66Ga0.34As and In0.335Al0.665As quantum cascade (QC) periods with the layer sequence 27.6/14/24.1/14.8/24.6/13.3/21.91.3/15.80.7/18.51.3/19.70.7/17.41.3/20.6/14.7/21.7/15.6/35/13.1/14.8/37.6/10.3/32.9/19.9 optimized for emission at 4.3 µm, followed by 18 QC periods with the layer sequence 27/19/26/15/23/14/211.3/220.7/191.3/200.7/191.3/19/17/24/17/35/11/13/38/10/35/18 optimized for emission at 4.6 µm. The thickness (in Å) of the InAlAs barriers are given in bold face and of the InGaAs wells in standard script, while the Si-doped layers are underlined with the doping concentration (1017 cm−3) indicated in superscript. The active region was capped with a lattice-matched InGaAs spacer layer, which was used for the definition of the gratings. Two DFB gratings with different grating periodicities and 2 or 2.5 mm length were etched into this spacer layer, which was then wet etched to form 6–8 µm wide ridges. Electrical contacts were deposited to individually provide current to either one of the gratings, effectively forming a front and rear laser section. In order to reduce cross-leakage between the two devices, the thickness of the InP cladding on top of the active waveguide was reduced to 2 µm in between the two devices by means of a shallow wet etch.
Finally, the devices were mounted junction-down on AlN submounts coated with a gold-tin solder, which was segmented by means of a plasma-focused ion beam (PFIB-SEM Fera3, Tescan a.s.), in order to separate the electrical contact for front and rear section.
2.1.2. Laser Characterization
For characterization purposes, the lasers were driven with either a pulse generator (8114A, Agilent Technologies, Inc., Santa Clara CA, USA) or a direct current source (2400, Keithley Instruments, Inc., Cleveland OH, USA). LIV characteristics were recorded with a calibrated photodiode (AN/2 OPH-09, Ophir, Optronics, Jerusalem, Israel). Spectral data was acquired with a Fourier-transform infrared spectrometer (FTIR) (Vertex 80, Bruker Corp., Billerica MA, USA), run by a commercial analysis software package (OPUS 7.2, Bruker Corp.). The signal was recorded on a pyroelectric deuterated triglycine sulphate (DTGS) detector. To investigate the tuning behavior of the devices in iCW operation, time-resolved spectra were recorded with the same interferometer. The lasers were set to operate at 18 kHz repetition frequency and 10% duty cycle. A boxcar integrator (SR250, Stanford Research Systems, Inc., Sunnyvale CA, USA) was used to filter the signal for a certain trigger delay and gate width. The gate width was set to 10 ns, while the trigger delay was stepped in intervals of 10 ns. The signal was recorded on a mercury cadmium telluride (MCT) detector (PVM-2TE-10.6-1×1, Vigo System S.A., Warsaw, Poland), averaged by the boxcar integrator, and then fed back to the spectrometer through an analog-digital-coupler.
2.1.3. Simulations
Finite element method (FEM) simulations (Comsol Multiphysics 5.2, Stockholm, Sweden) were performed to investigate the temperature distribution in the operating QCL. The simulations comprised a three-dimensional model of the laser mounted on top of the AlN submount, including the different material layers. The QC active region was approximated with averaged material parameters and an anisotropic thermal conductivity to account for in-plane confinement of phonons in the QC layer stack [5]. The boundary conditions were set to “perfect insulation” at all interfaces with air and to “fixed temperature” at the interface with the Peltier-cooled Cu heat sink. All used material parameters are listed in Table 1.

Table 1.
Physical parameters used for FEM simulations.
Transfer matrix method (TMM) calculations were performed using a custom written code to calculate the transmission of each structure for identification of potential modes.
The calculations included thickness and effective refractive index of each grating hill and trench. At lasing, the diagonal element t22 of the overall transfer matrix (tik) is zero, i.e., |t22| is minimal. To find the local minima in the frequency/gain range of interest, |t22| was calculated on a coarse grid in a first step. From the local minima on this grid, the downhill simplex method [22] was then started to refine the minima and finally deliver frequency and threshold gain of the lasing modes.
2.1.4. Anti-Reflective Coating
AR coatings were designed using a genetic optimization algorithm to minimize reflectivity for the desired wavelengths. They are three-layer stacks consisting of Al2O3 and Ge, whereas the thickness of the layers is used for the optimization. The coatings were applied to the laser facets with an e-beam evaporator (UNIVEX 500, Oerlikon Balzers AG, Balzers, Lichtenstein).
2.2. Results
2.2.1. Device Characteristics and Internal Etaloning
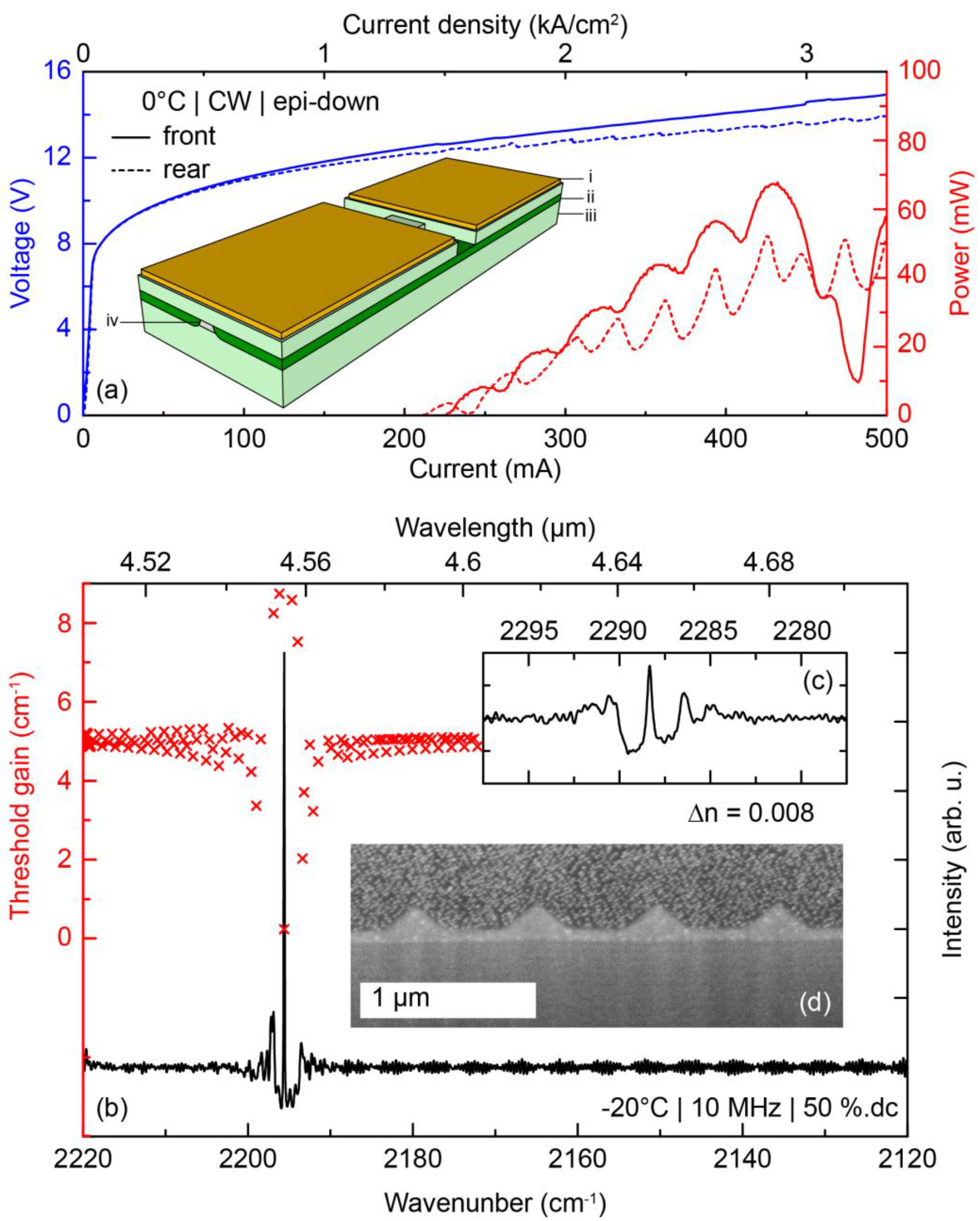
Figure 1a shows a typical LIV characteristic of a 2 × 2.5 mm long and 6 µm wide dual section DFB QCL device operated at 0 °C. A schematic drawing of the device featuring a front and a rear section is shown in the inset. A grating with quarter-wave shift (QWS) enables single mode lasing close to 4.4 µm and 4.6 µm. The high-resolution sub-threshold electroluminescence spectrum recoded at −20 °C reveals the stopbands at 2196 cm−1 and at 2288 cm−1 (Figure 1b,c) of the front and rear gratings, respectively (scanning electron microscope cross section shown in Figure 1d). A refractive index contrast Δn = 0.008 is estimated from the width of the stopband. The electroluminescence spectrum in Figure 1b is superimposed with a TMM calculation of the cavity losses for the whole dual-DFB grating, which shows that the cavity losses are lowest for the QWS defect mode.
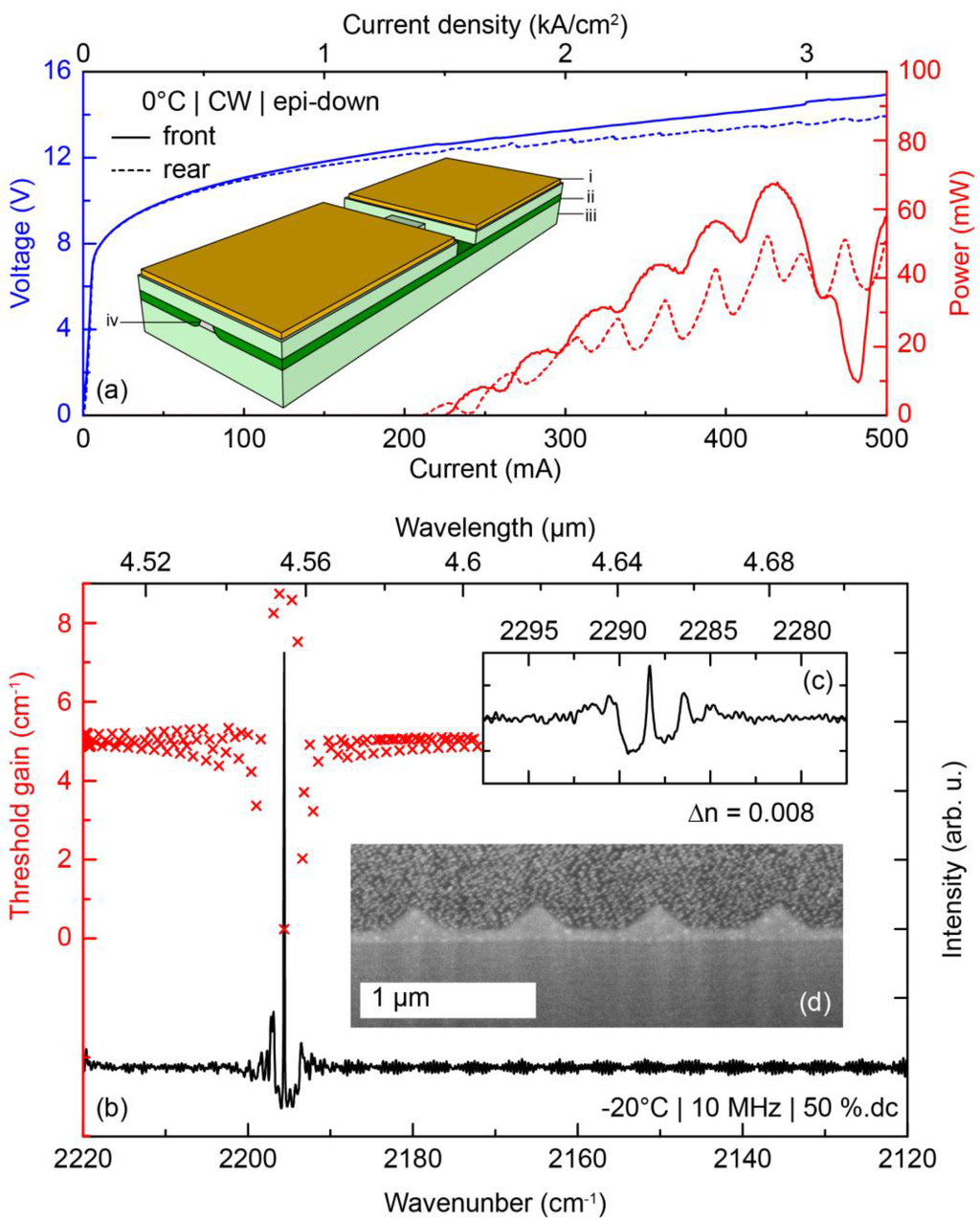
Figure 1.
Device characteristics of the investigated dual-section DFB QCL. (a) LIV characteristic of a typical device with a device schematic in the inset. The color code for the inset is as follows: (i) yellow—Au electrode; (ii) dark green—insulating InP; (iii) light green—conducting InP; (iv) gray—dual-wavelength active region); (b) Sub-threshold electroluminescence revealing the stopband of the rear (b) and front (c) section. The spectrum is superimposed with a simulation of the threshold gain of each mode, highlighting that lasing occurs on the QWS; (d) FIB-SEM cross section through a laser revealing the wet-etched grating on top of the active region. The roughness seen in the upper part of this micrograph is ion-beam damage from the FIB preparation.
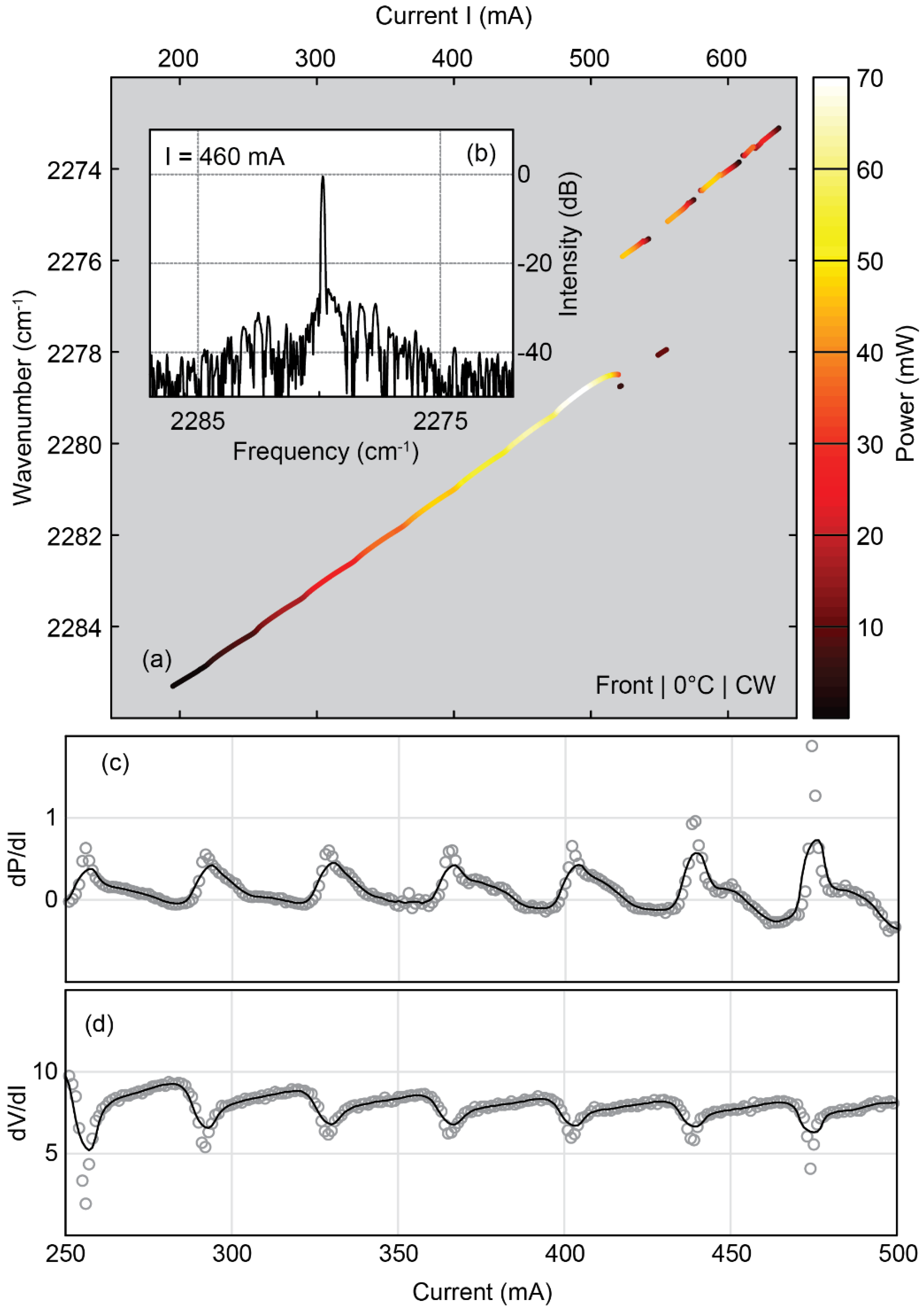
Besides comparable thresholds and operation powers for both sections, the LI curves in Figure 1a also show periodic power fluctuations. We attribute these oscillations to internal etaloning. During the operation of one laser section, the heating—and thus the temperature—is different in the active (pumped) and passive (not pumped) section. Hence the effective refractive index (neff) difference between these two sections—and thus the cavity resonance—changes, which affects both the emission frequency and power. This behavior was investigated via spectra recorded as a function of pumping current with a resolution of 1 mA (Figure 2a). For currents below 500 mA, the whole power is located in a single mode and exhibits the oscillations as indicated in Figure 1b. At currents above 500 mA, mode hops and the occurrence of lateral modes are observed, discontinuing the side mode suppression ratio (SMSR) of 25 dB recorded at lower currents (Figure 2b). The derivative of the current-voltage and the power-current curves (Figure 2c,d) show the reciprocal behavior indicative for photo-induced current [5], which supports the hypothesis of destructive interferences in the laser due to an internal etalon.
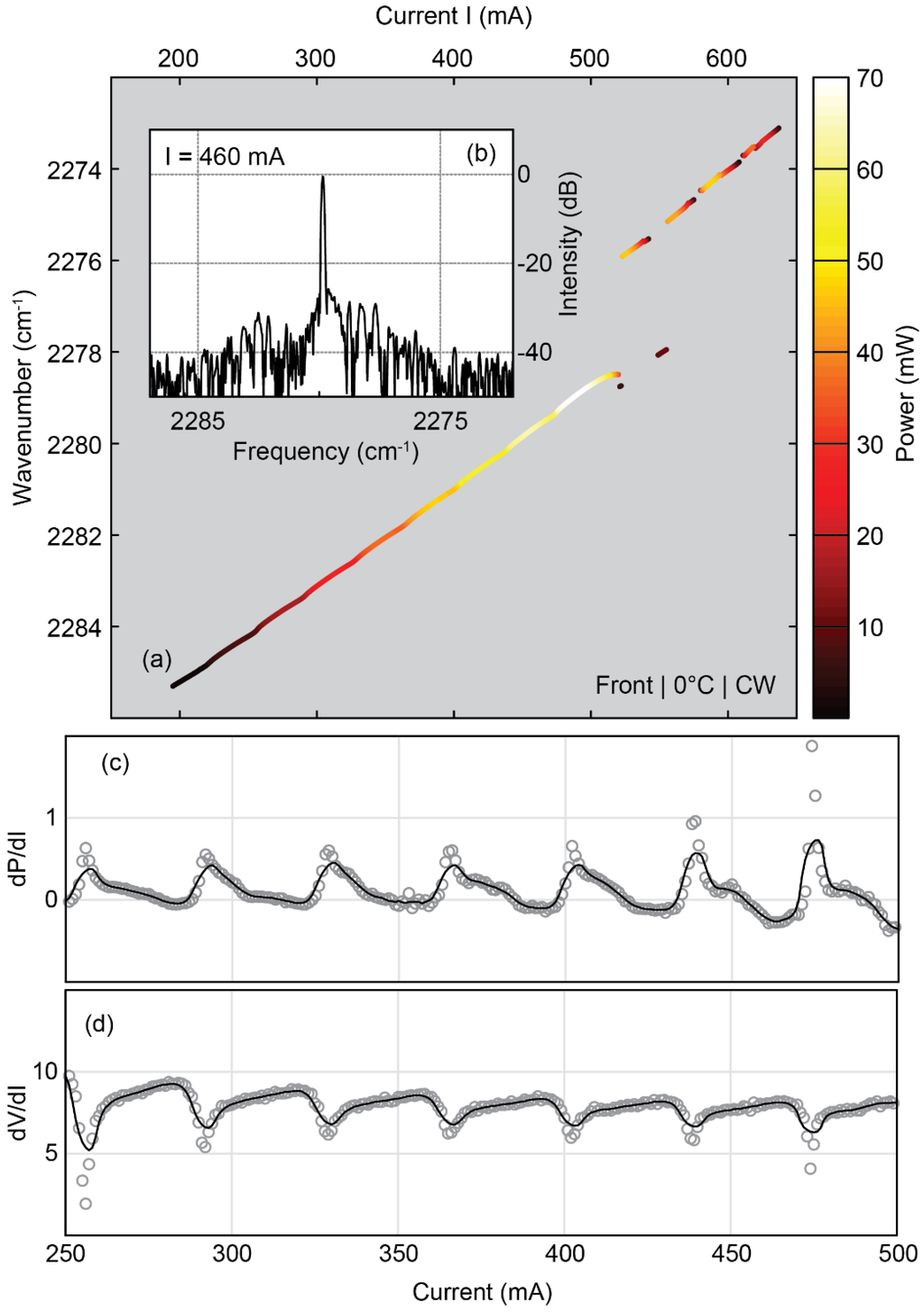
Figure 2.
Analysis of etaloning behavior observed in spectrally resolved LIV characteristics. (a) Mode map of the front section; (b) Spectra recorded at 460 mA pumping current showing a SMSR of 25 dB. The derivative of the power (c) and the voltage (d) reveal a reciprocal behavior, the typical sign of photo-induced current.
2.2.2. FEM and TMM Simulation of the Internal Etalon
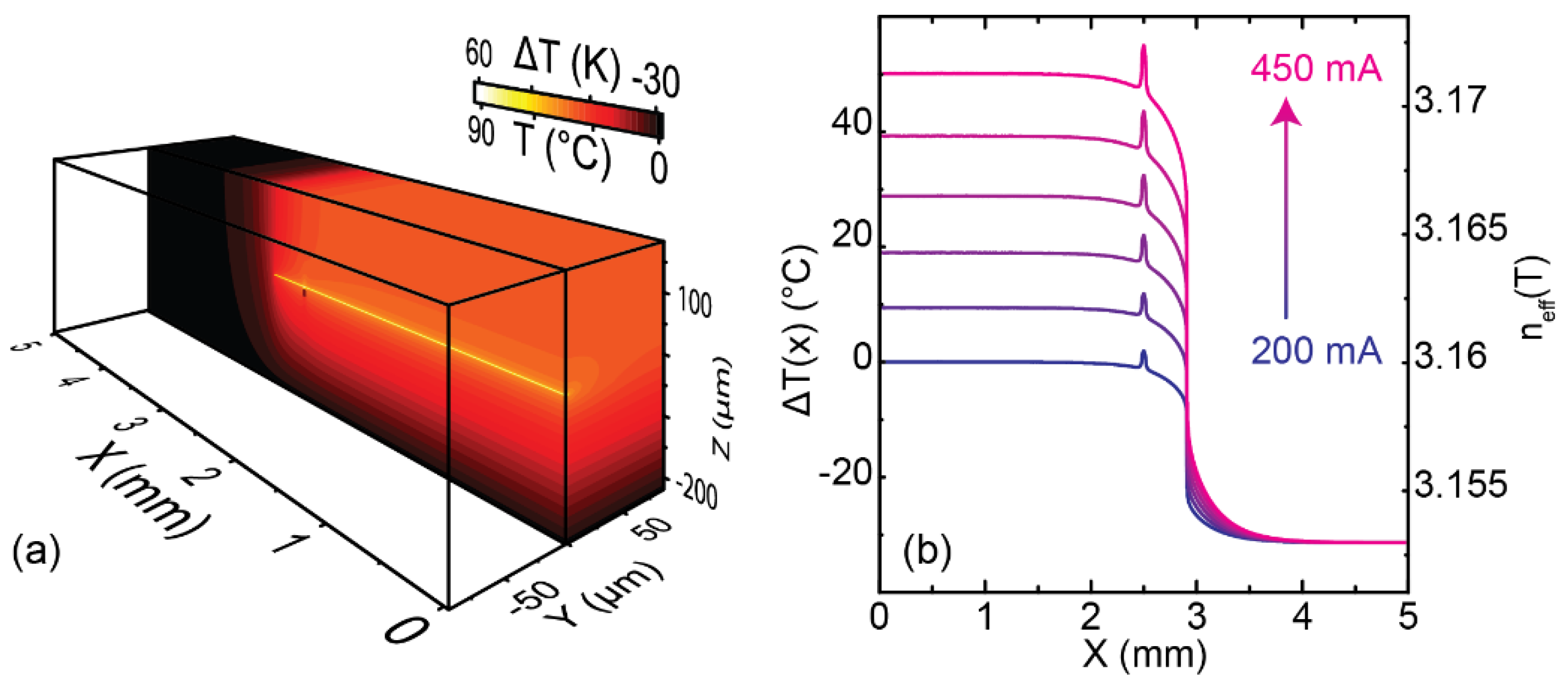
In order to better understand this effect, thermal 3D FEM simulations (Figure 3) were used to calculate temperature profiles along the active region in the laser for different pumping currents (ΔI = 1 mA). In this simulation only the front section (2.5 mm) plus a leakage segment (0.43 mm) is pumped, making the passive section (i.e., the etalon) 2.07 mm long. The length of the leakage segment was determined from the free spectral range of the oscillations in the spectrally resolved LI curve (Figure 2a). The gold electrode on the laser is separated (40 µm) between front and rear section. At this position, the InP cladding is exposed to air, whose thermal conductivity causes a local heat dissipation deficit, which reflects as a temperature spike in the temperature profiles in Figure 3. The temperature profiles T(x) are referenced to the lasing section at threshold
with the base temperature T0 = 0 °C. ΔT(x) in turn can be used to calculate a temperature and position dependent effective refractive index neff(ΔT, x) [5,23]:
with the thermal tuning coefficient β = 7.1 × 10−5 K−1 [24], and the effective refractive index at threshold neff(T0) = 3.1598, which was extracted from the laser spectrum at threshold.
ΔT(x) = T(x) − T0
neff(ΔT, x) = neff(T0) × (β × ΔT(x) + 1)
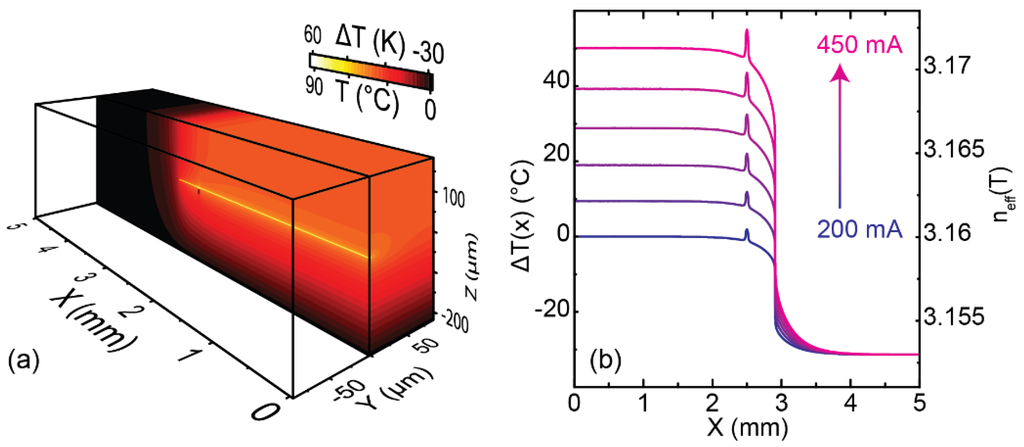
Figure 3.
(a) 3D thermal FEM simulation displaying the temperature distribution along the laser when only one section is pumped (I = 450 mA). (b) The 1D temperature profiles along the active region are extracted from a full 3D model displayed in (a) for different pumping currents. The base temperature is 0 °C, the temperature difference is referenced to the pumped section.
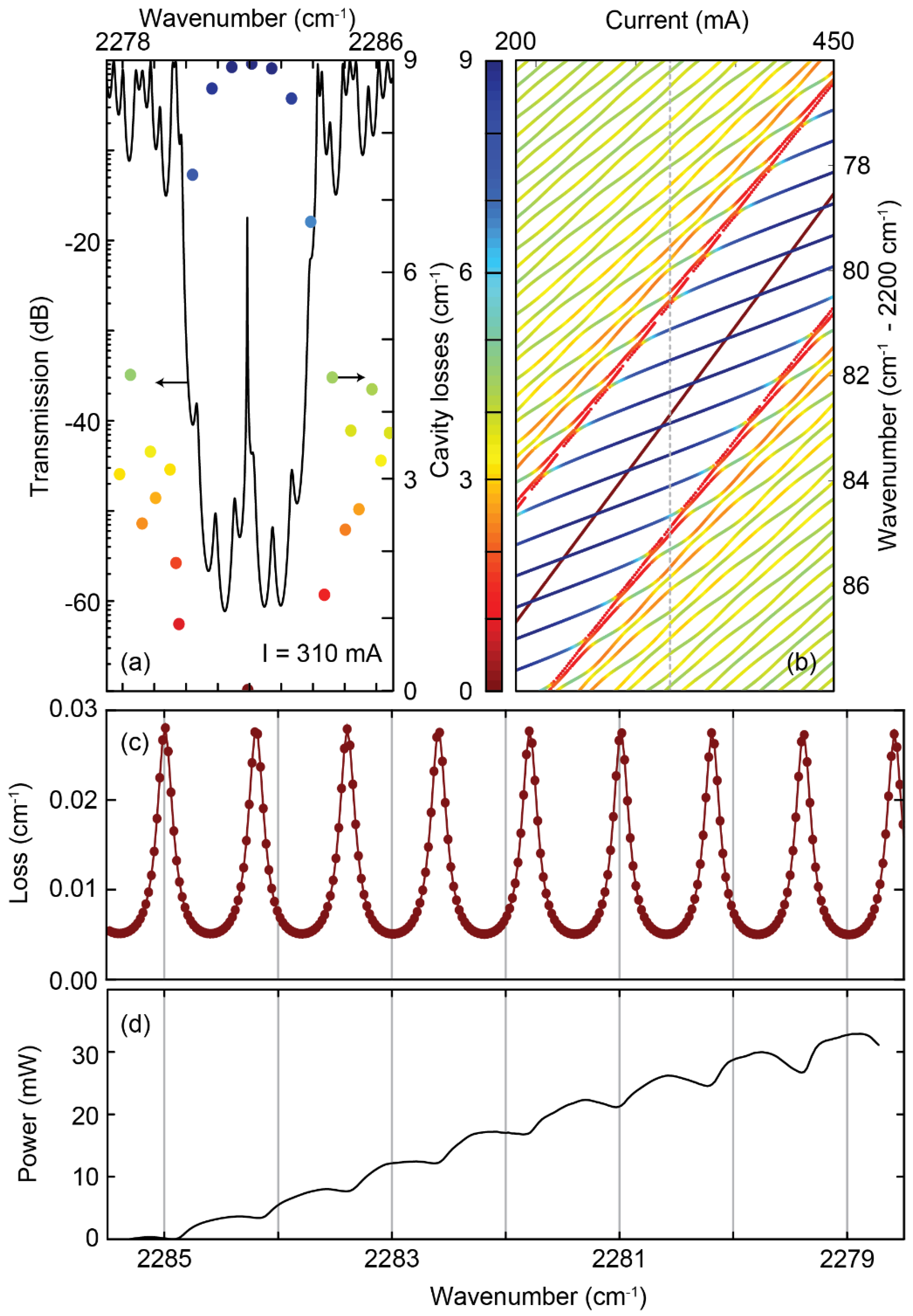
The function neff(ΔT, x) can now be used in TMM calculations to predict the transmission and waveguide losses of thermally influenced dual DFB structures (Figure 4a). Figure 4b depicts the waveguide losses as a function of pumping current for all modes around the QWS mode. As expected, with increasing current the modes tune to lower frequencies, i.e., higher wavelengths. The lowest losses are observed for the QWS mode, followed by the stopband edges. In general, two sets of modes can be observed. One set propagates with the same slope (approx. −0.033 cm−1/mA) as the QWS mode and can therefore be associated to the active section. The other set propagates at a lower slope (approx. −0.009 cm−1/mA), best observed as lossy modes in the stopband, and can be attributed to the passive section. The two sets of modes interact upon crossing and if the magnitude of losses matches, anti-crossings are observed. However, the losses of the QWS and the interfering modes are approximately three orders of magnitude apart and their crossing points do not anti-cross, but merely attract each other when they are in spectral proximity (Figure 4c). It should be noted that, although the TMM calculations neglect intersubband losses in the passive section as well as the full complexity of the device, the spectral periodicity of the intensity modulation is well reproduced in comparison to the experimental data (Figure 4d), confirming the hypothesis of an internal etalon caused by the different tuning of the two sets of modes in the thermally different laser sections.
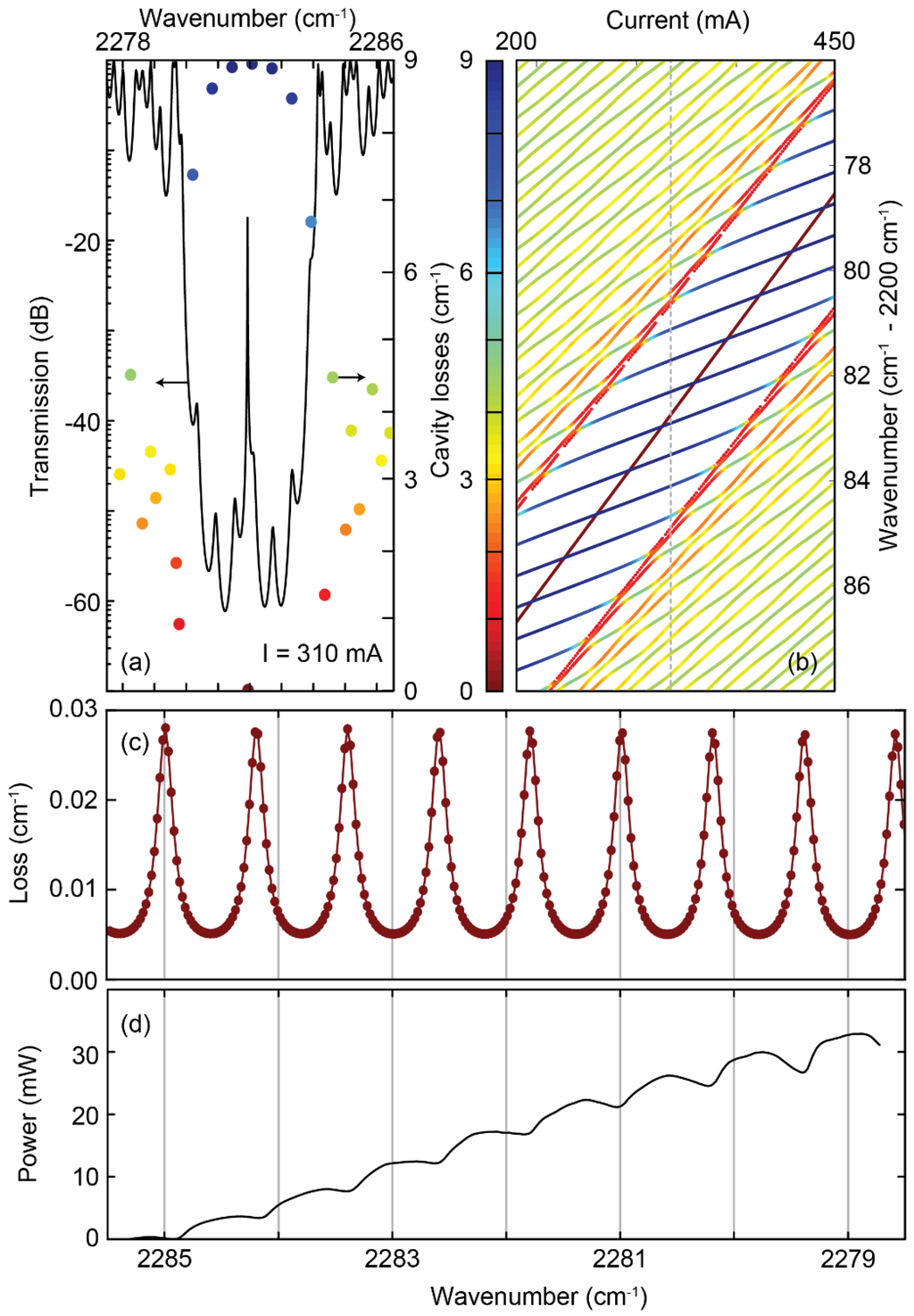
Figure 4.
Temperature dependent TMM calculations including waveguide losses of the wave propagation in dual-section DFBs. (a) The transmission and the extrapolated waveguide losses of the same structure at fixed current I = 310 mA (indicated in (b) with a grey dashed line); (b) The extrapolated waveguide losses of all cavity modes as a function of current and frequency; (c) Losses of the QWS mode extracted from (b); (d) Mode power versus spectral position, as comparison to (c).
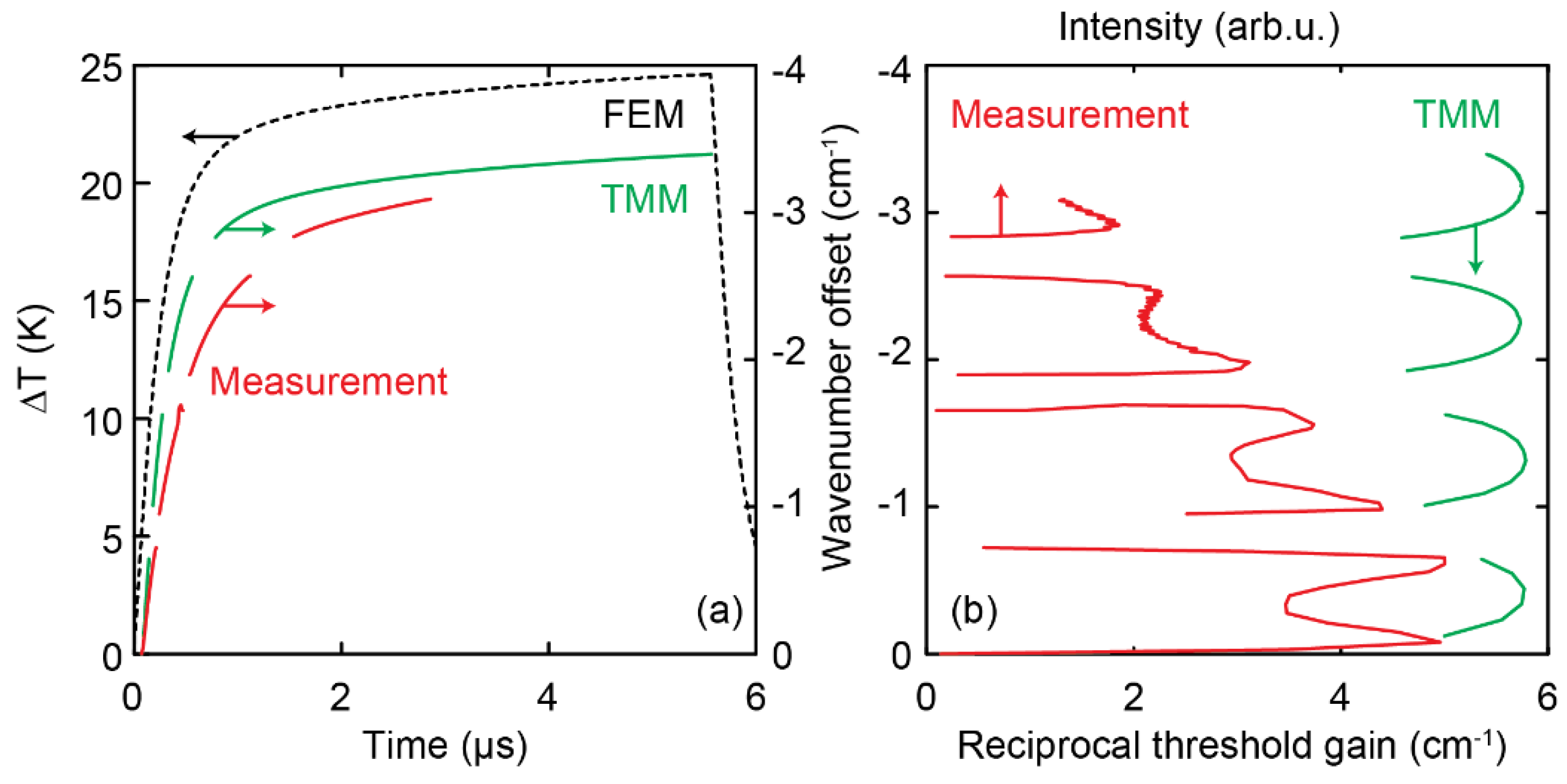
The same effect can also be observed when operating the laser in iCW mode, which is the preferred driving approach for a dual-section DFB-QCL. Here, time-dependent FEM simulations can be used to calculate the laser temperature, similar to the stationary simulations described above. The resulting average temperature in a laser section during the pulse is depicted in Figure 5a (black dashed line). The resulting temperature profiles can again be used to calculate the cavity losses via the TMM. The green curve in Figure 5a is the result of this calculation, where the spectral position of the QWS mode was extracted for each time step. It is compared to the red curve, which shows the position of the lasing mode, determined experimentally via a boxcar measurement (cf. Section 2.1.2.) on the rear section of a 2 × 2 mm long dual section DFB QCL. In contrast to the laser discussed above, the lasing action indeed stops temporarily during the pulse. The slope of the temperature evolution and the simulated mode evolution scale directly, as they are in principle only related to each other via the wavelength-independent thermal tuning coefficient. The slope of the experimentally determined mode tuning is slightly different, which can be explained by the geometrical differences between the FEM model and the actual laser, and/or an overestimation of the thermal tuning coefficient. The experimentally observed spectral spacing of the oscillations, however, is again well reproduced by the simulation (Figure 5b).
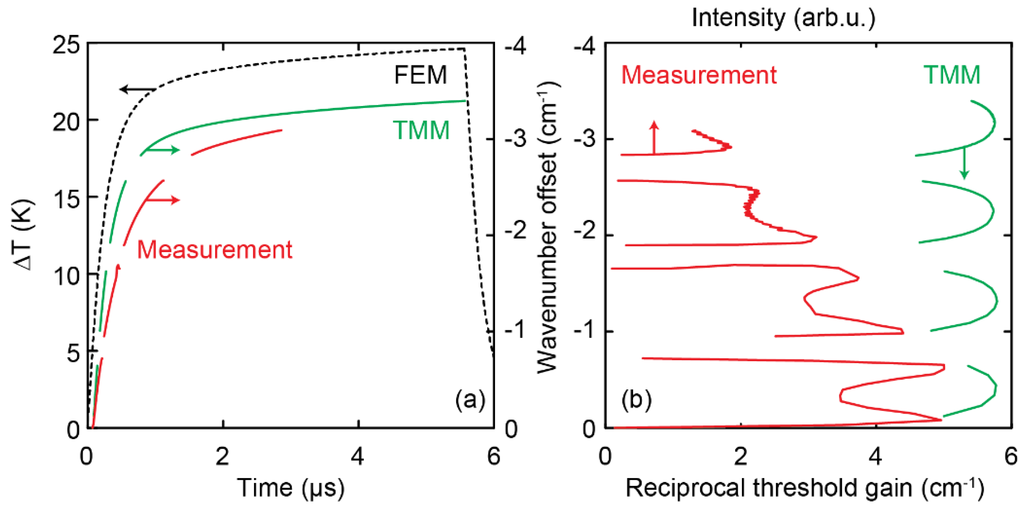
Figure 5.
Comparison between a measured and simulated iCW operation of a dual DFB section. (a) The average temperature offset extracted from thermal finite element situation (black, dashed), frequency offset extracted from TMM calculations (green) and measurement (red) as a function of iCW pulse duration. (b) Comparison of the same measurement and simulation data displayed in (a), plotted in function of intensity and reciprocal threshold gain, respectively.
2.2.3. Effects of AR Coatings
The large intensity variations caused by the internal etalon seriously impair the device performance, especially for spectroscopic applications. In order to mitigate this effect, various approaches can be used. One option is to consider other device concepts. For example, as already implemented in telecom lasers [25], an additional, individually biased section could be added to the laser, used to compensate the phase difference between the waves entering and leaving the grating section. Nevertheless, the driving scheme of such devices would become more elaborate. Yet another alternative are device concepts without strong temperature gradients in front and rear section. Such lasers were recently published by Bidaux et al. [26]. These lasers are Vernier tuners [27] with integrated heaters, allowing to shift the reflectivity of the gratings in the front and rear section. While these devices profit from extended tuning range and more uniform temperature distribution, the tuning stability of these lasers in iCW are constrained by the thermal transport properties in the device and might be limited to operation at frequencies of few hundreds Hz [28].
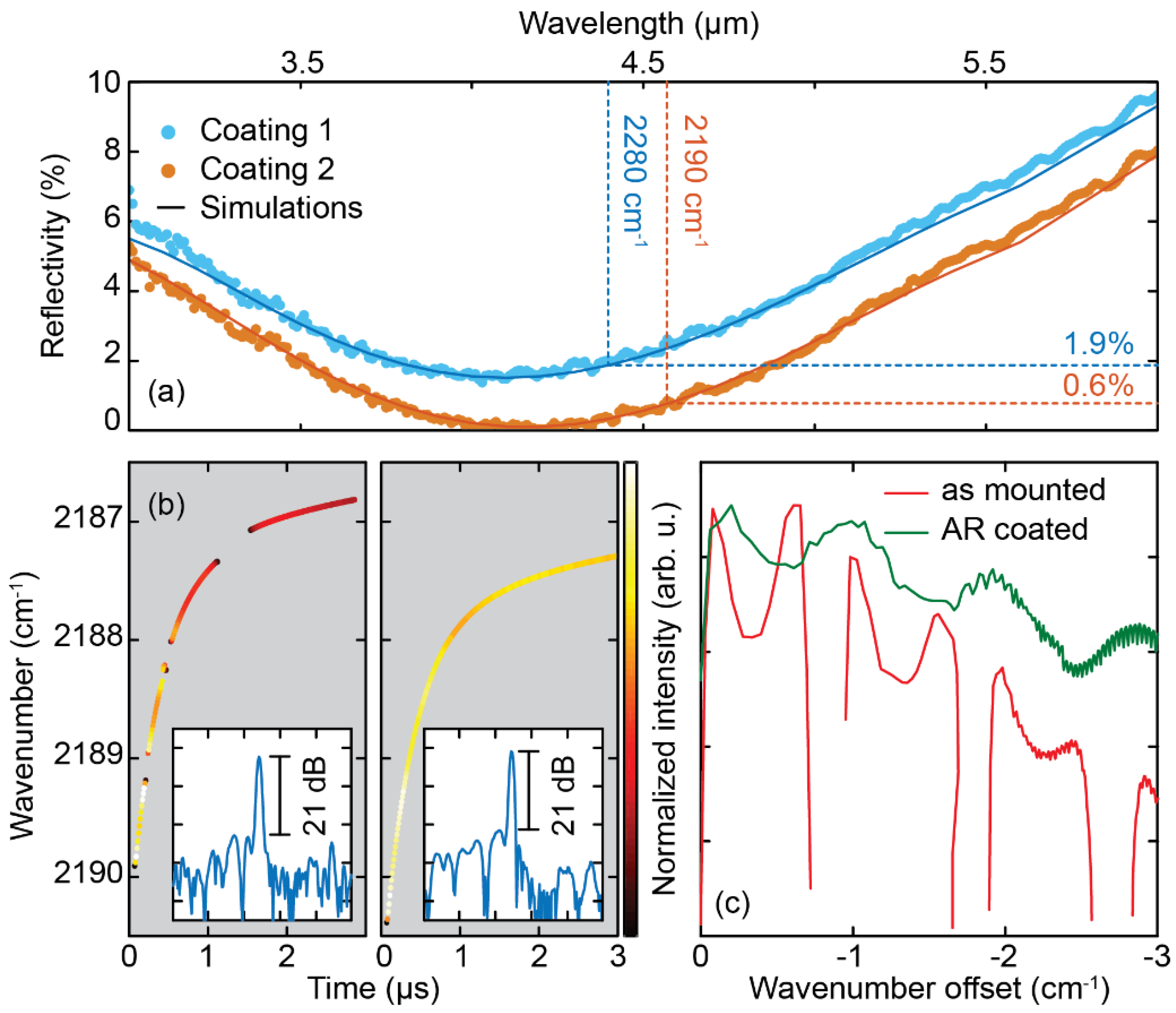
Our approach to reduce the effect of the internal etaloning, was to increase the losses of the Fabry-Perot modes of the passive section by tailoring the facet reflectivity of the laser. Therefore, two different AR coatings were applied to the laser facets. Hereby, the coating matching to the wavelength of the front section was applied to the rear facet and vice versa. The reflectivity of these coatings was measured on reference samples and matched with TMM calculations in order to determine the thickness of the layers (Figure 6a). The final composition and layer thickness of the coatings was Al2O3/Ge/Al2O3:140/48/450 nm and 100/46/560 nm for Coating 1 and Coating 2, respectively. The reflectivity of the coatings at the wavelengths of front and rear section was 1.9% and 0.6%, respectively. Boxcar measurements (cf. Section 2.1.2) were performed on the rear section of a dual section DFB QCL operated in iCW mode, before and after the application of the AR coatings (Figure 6b). The comparison of the intensity evolution during the pulse (Figure 6c) shows that the effect of the internal etalon can be reduced significantly. Whereas the laser before coating temporarily turned off during the pulse (red curve), the amplitude of the fluctuations stayed below 15% after the application of the coating (green curve), without affecting the SMSR (Figure 6b, inset, representative for both sections).
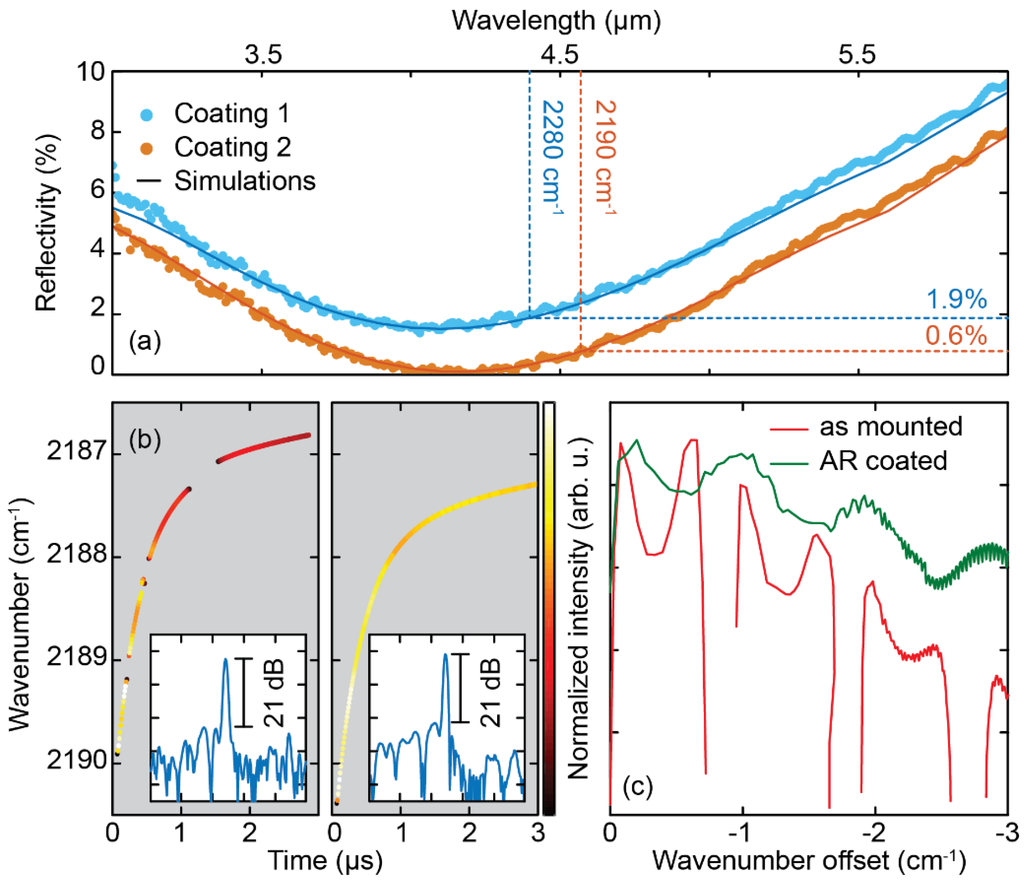
Figure 6.
Effects of AR coating on dual section DFBs. (a) Reflectivity measurements of two coatings applied either to front and rear facet, respectively. The mismatch between the target wavelength and the minimum reflectivity are due to process uncertainties; (b) Mode maps of a dual-section DFB operated in iCW before and after AR coating. The spectra in the inset show that the SMSR is maintained after coating (inset); (c) Mode intensity as a function of frequency offset extracted from the mode maps in (b), before and after coating.
3. Spectroscopy
An AR coated dual-section DFB-QCL was applied in a direct laser absorption spectroscopic setup to test its suitability for trace gas detection. The laser was designed to lase at 2190 cm−1 (front DFB) and 2281 cm−1 (rear DFB). The goal was to target the spectral regions, where N2O and CO (front DFB) as well as the CO2-isotopologues 12C16O2 and 13C16O2 (rear DFB) can be optimally measured.
A major concern of any spectroscopic measurement is the mode purity and the intensity stability of the laser source. As already mentioned, the etaloning effect observed for the dual-section DFB-QCL rises serious doubts regarding the usability of such devices for high precision trace gas measurements. Although, the AR coating on the laser facets significantly reduces the intensity variations caused by the internal etaloning, the remaining amplitude modulation still causes up to 15% changes in the optical power of the laser across the tuning range. Spectroscopic measurements were carried out to investigate the performance of AR coated dual-section DFB-QCLs.
3.1. Laser Driving
The laser was operated in iCW mode using a custom-built driver described previously [15]. The driver was modified for dual-section DFB-QCL operation. This modification mainly involved the addition of another channel and a logic-circuit for switching between the channels after each current pulse. Synchronously to the current pulse, the laser driver generates a trigger signal using an onboard microprocessor. This signal is used to synchronize the data acquisition and also to trigger a multifunction DAQ (USB-6212 OEM, National Instruments, USA), which then generates a transistor-transistor logic (TTL) signal (called “gate”) required for switching between the two DFB sections.
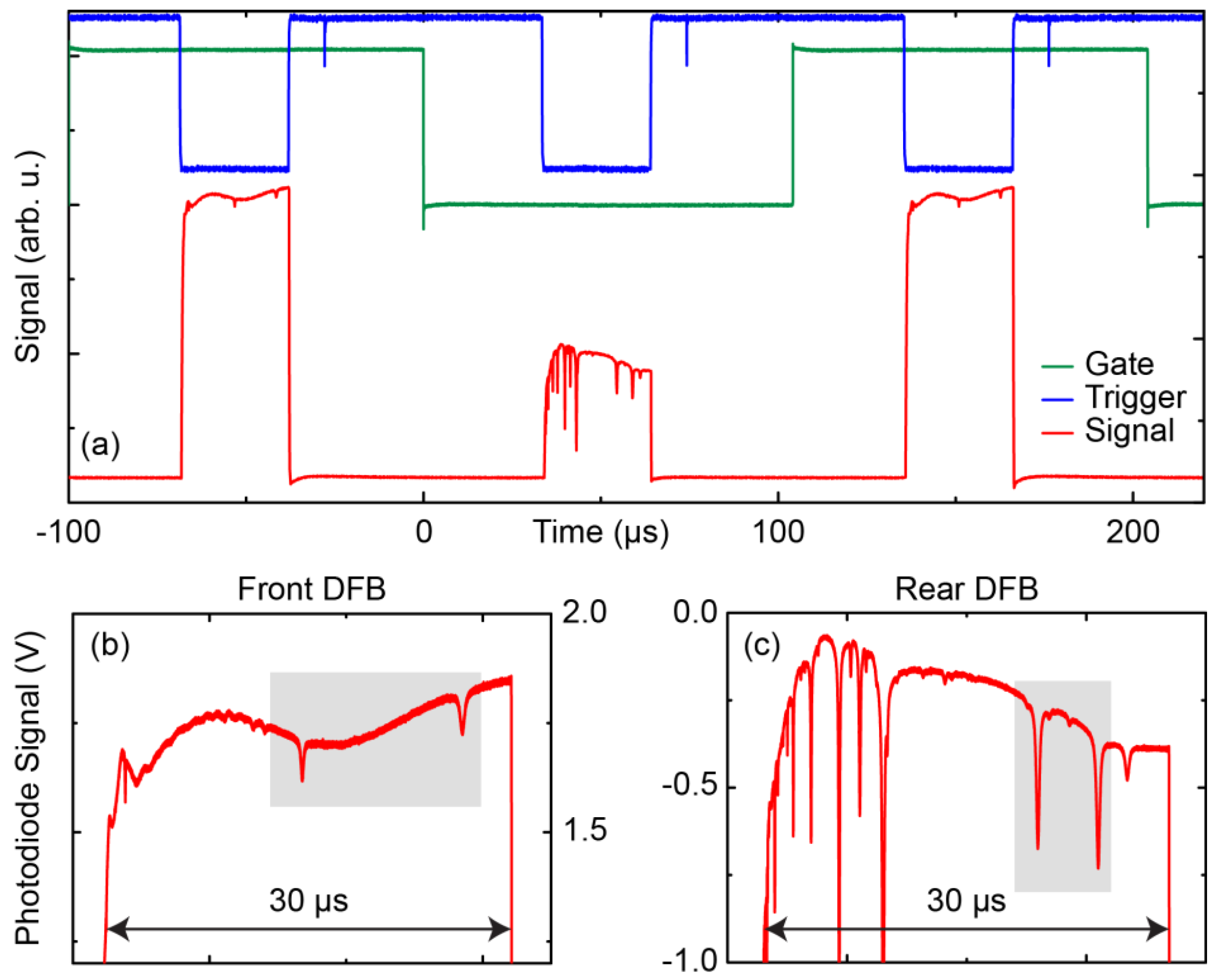
A gate-duration of 100 μs with a trigger pulse duration of 30 μs was applied, resulting in a duty cycle of 15% for each laser section (Figure 7a). Under these configurations, the laser could be operated close to room-temperature emitting at the desired spectral range (Figure 7b,c).
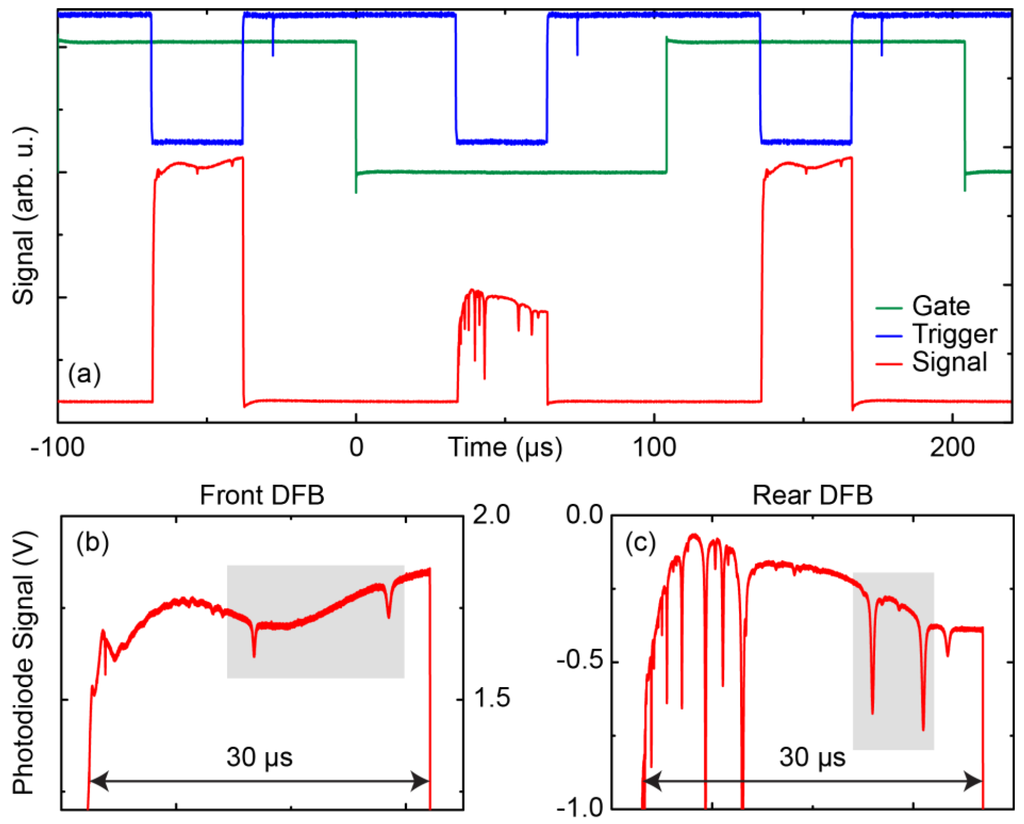
Figure 7.
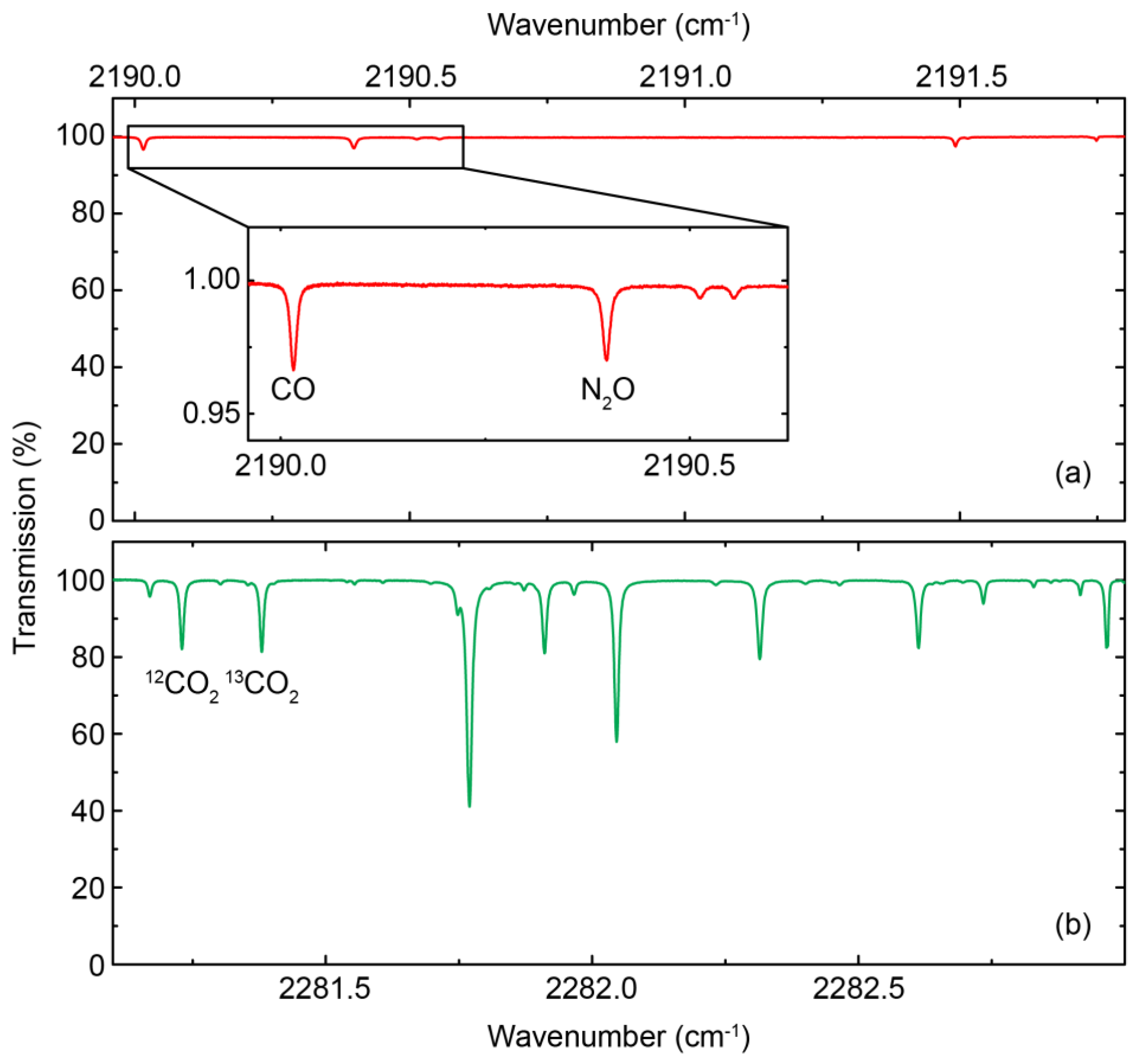
(a) Timing scheme of the dual-section DFB QC laser driving. The TTL signals (gate and trigger) are used to alternatively switch between the two sections. The detector signal is also shown (red trace). Lower panel: Close-up of the transmission signals of air sample measured at 50 hPa pressure using a multipass cell with 36 m optical path length; (b) Front DFB for N2O and CO; (c) Rear DFB (CO2) isotopologues. The regions used for the concentration measurements are highlighted in grey.
3.2. Optical Layout and Data Acquisition
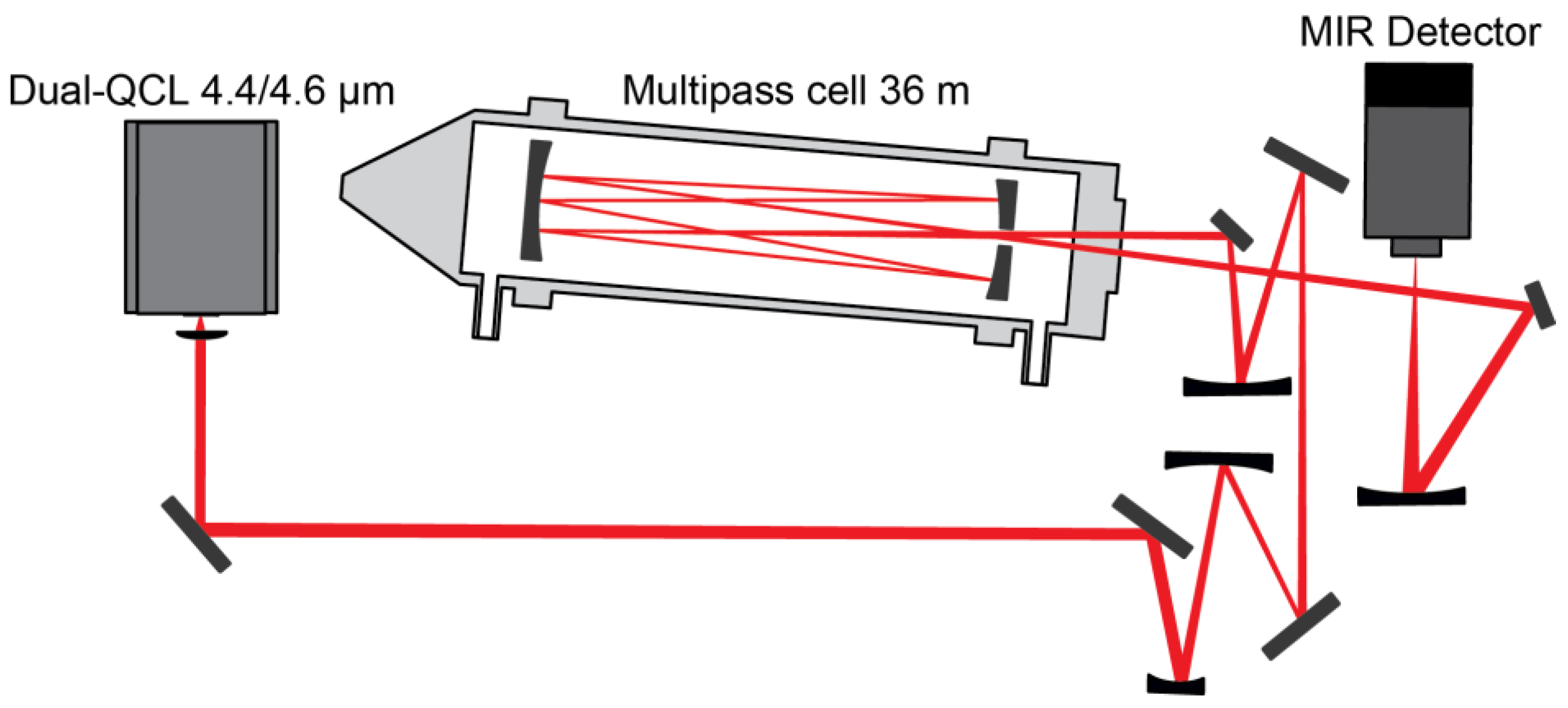
The optical layout is schematically shown in Figure 8. The divergent output beam of the dual-section DFB QCL is collimated by an AR coated (3–5 μm) aspheric lens (feff = 5.95 mm), which is mounted on an XYZ translation stage for optimal alignment. The collimated beam passes through a sequence of beam shaping and steering mirrors and is then coupled into an astigmatic multipass absorption cell (AMAC-36LW, Aerodyne Research Inc., Billerica MA, USA). The light undergoes 182 reflections creating a total absorption path length of 36 m. The back mirror of the multipass cell is dithered by a piezoelectric actuator at a frequency of 360 Hz to suppress interference fringes. After exiting the cell, the beam is focused onto a thermoelectrically cooled broadband MCT detector (PVM-4TE-8, Vigo System S.A., Warsaw, Poland). The detector has a bandwidth of 70 MHz and is coupled to a preamplifier with a high cut-off frequency of 200 MHz.
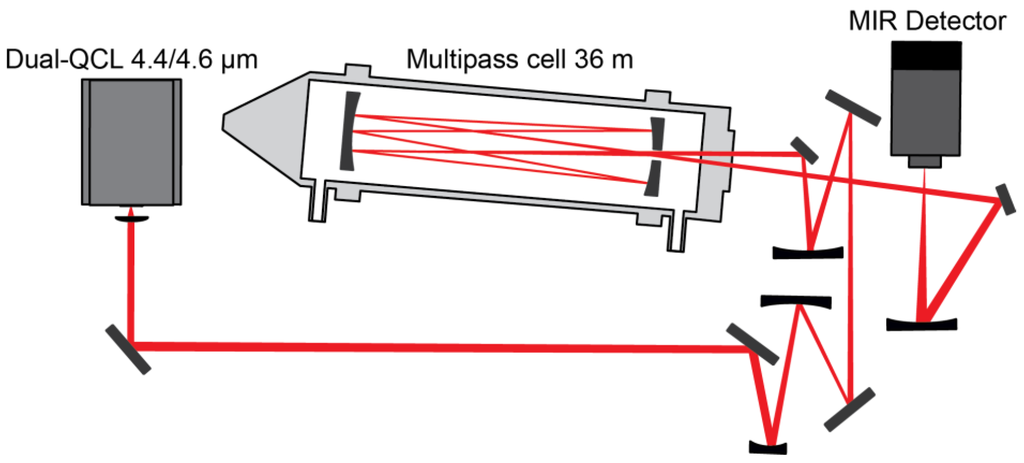
Figure 8.
Schematic of the optical layout.
The detector signal is digitized with 15-bit resolution at a rate of 125 MS/s by a digital oscilloscope (Picoscope 5000 Series, Pico Technology, St. Neots, UK). Data acquisition and analysis is performed by a custom-built LabVIEW-based software. The spectra are discerned based on the gate signal and treated separately. Real-time fitting is performed on the acquired and averaged (N = 1000) spectra using the line-parameters that are provided by the high-resolution transmission (HITRAN) database [29] to determine the concentrations of the target species.
For the spectroscopic measurements of the trace gases, dry air from a pressurized cylinder is used. The air pressure in the multipass cell is maintained at 50 hPa in a flow-through regime. The air flow is regulated to 300 mL/min by a mass-flow-controller, while a vacuum pump (N920, KNF GmbH, Freiburg, Germany) is used down-stream of the cell.
3.3. Spectroscopic Results and Discussion
Figure 9a,b show normalized transmission spectra of dry air at 50 hPa recorded using the dual-section DFB QCL operated in iCW mode. These spectra are obtained by normalizing the transmission spectrum of air with the transmission signal of the evacuated multipass cell, i.e., the background signal. Thereby, the laser intensity variations caused by the etaloning effect are efficiently removed, indicating a good stability of these fringe-like structures. The laser tuning rate during the current pulses was determined by inserting a solid 2ʺ Ge etalon (free spectral range: 0.0244 cm−1) in the beam path and using the resulting fringe-pattern to convert the time scale to wavelength. Both DFB sections were tunable over a range of more than 2 cm−1, which is in full agreement with our previous findings using an iCW-driving scheme for standard single-DFB QCLs [15].
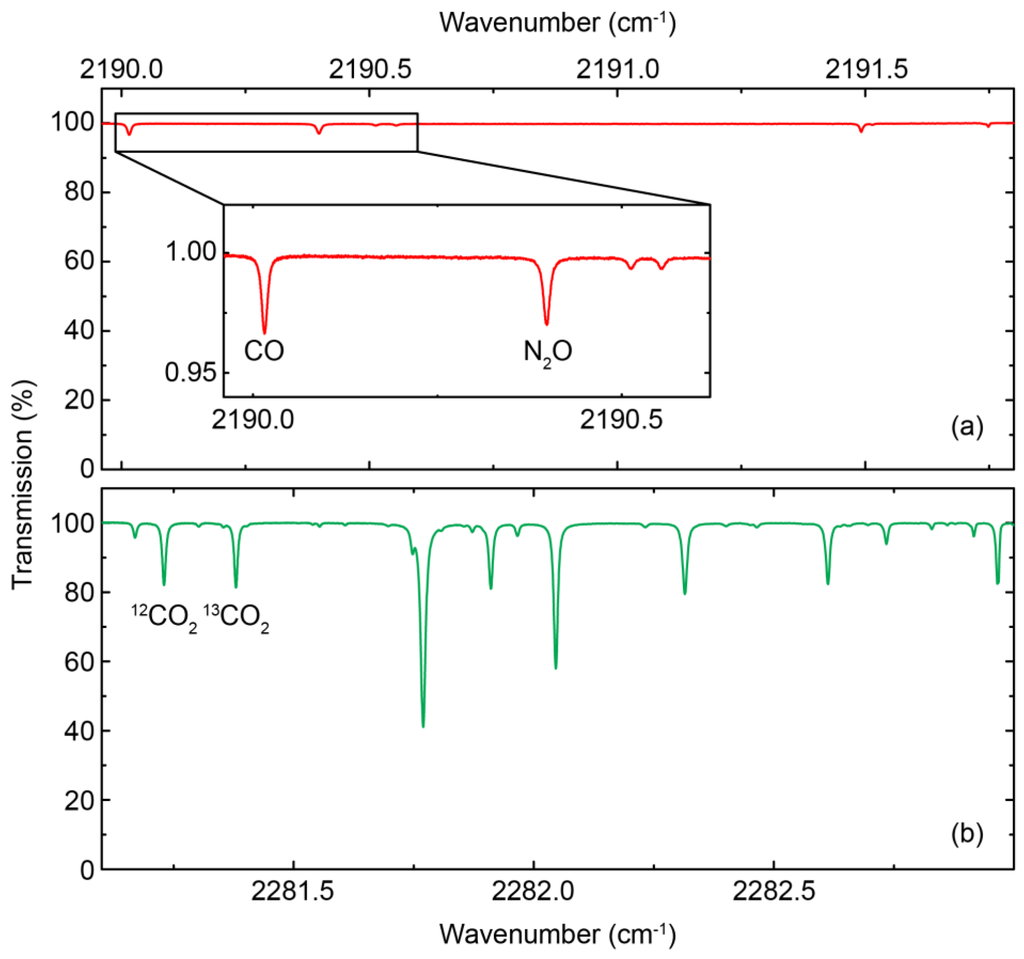
Figure 9.
Absorption spectra of dry air recorded at 50 hPa pressure using the front (a) and rear (b) section of the DFB-QCL. The absorption lines used for the concentration measurements are labeled. The inset in (a) shows a close-up of the range with the absorption lines of CO and N2O.
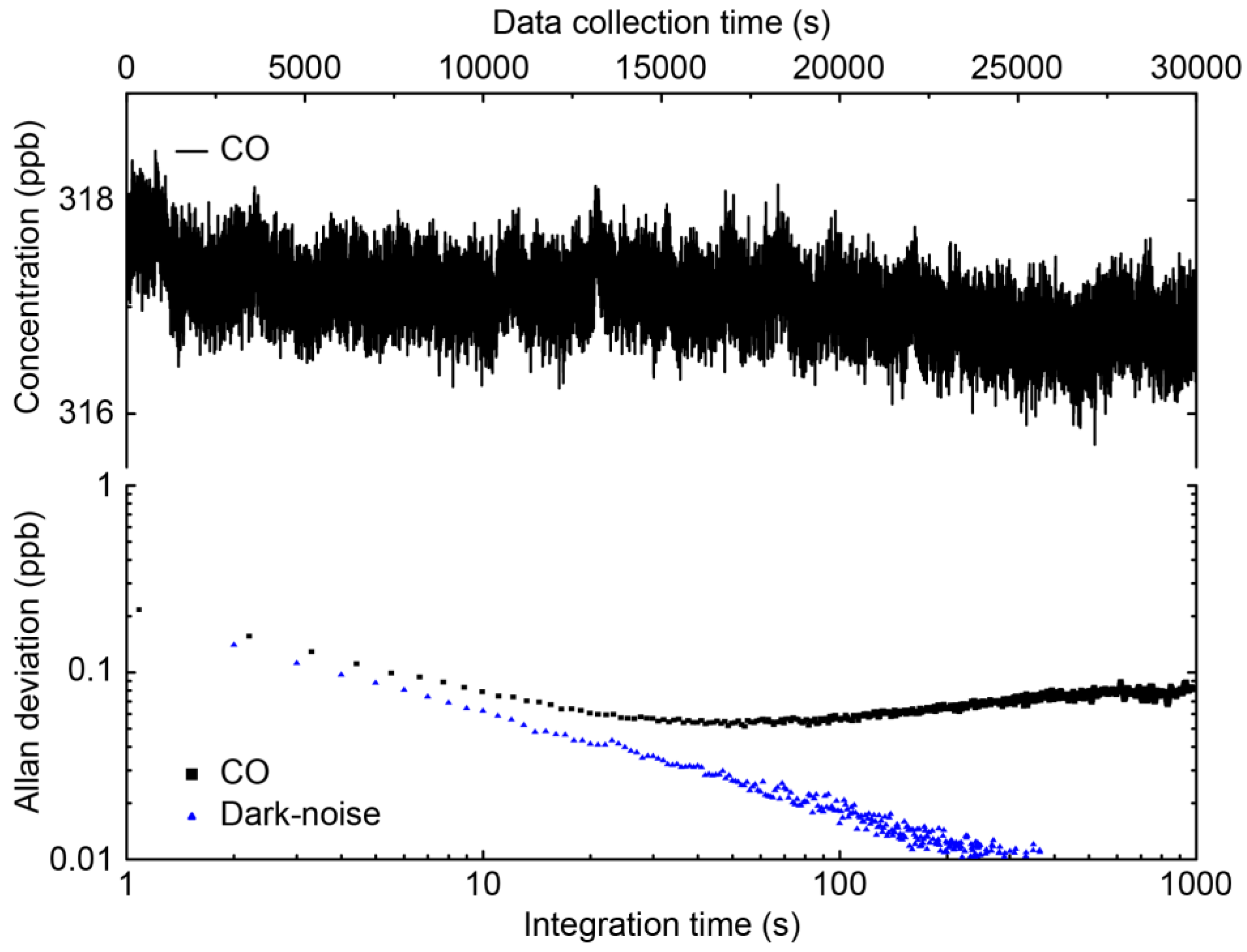
The precision of the concentration measurements was determined using the Allan-variance technique [30]. Therefore, the concentrations of the target species in air were continuously measured from a gas cylinder. Figure 10 shows such a time series and the associated Allan-deviation plot for CO. Table 2 summarizes the precision values obtained for averaging times of 1 s and 60 s, respectively.
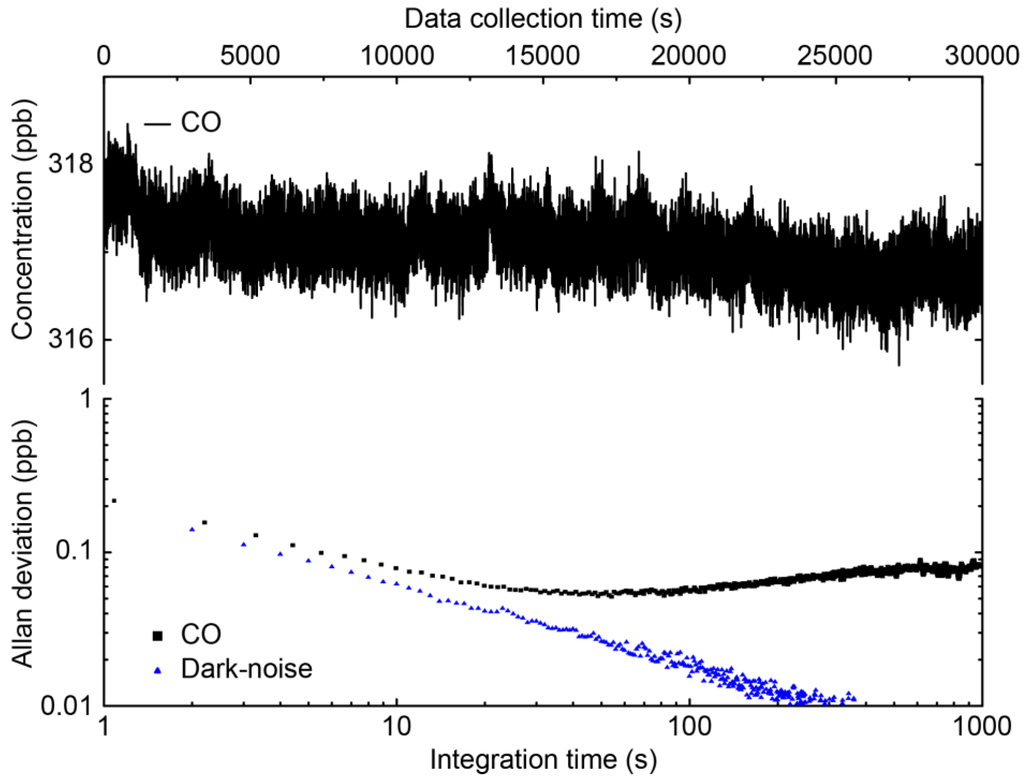
Figure 10.
Time series of the measured CO concentration and the associated Allan deviation plot. As a reference, the Allan deviation of the detector dark noise is plotted as well. A precision of 0.055 ppb is reached at 60 s integration time.

Table 2.
Precision of concentration measurements with dual-wavelength QCL.
The Allan deviation plot (Figure 10) shows that the concentration measurement is detector dark-noise limited. The one second precision that is reached by the spectrometer is about 5 (for CO) to 18 (for N2O) times lower than the precision reported recently for commercial single-laser instruments [4]. This difference, however, can be largely rationalized by considering the shorter (2x) absorption path-length of 36 m and the low duty cycle of 15% (equivalent to a factor 2.6) at which the lasers are operated (Figure 7). For N2O, an additional factor of two in precision could be gained by choosing a stronger absorption, e.g., at 2200 cm−1. Furthermore, the setup was operated without controlling the temperature or sealing the optics, which potentially resulted in increased short-term variations and drifts at timescales of minutes. Considering these factors, the performance achieved with the dual-wavelength QCL are up to the state-of-the-art with the additional benefit of using a single light source and a rather simple optical layout. Hence, the advantages of dual-wavelength QCLs are obvious: they allow the development of compact, robust and multi-species instruments at affordable costs and without performance loss.
4. Conclusions and Outlook
In this work, we have shown technological advances enabling continuous wave operation in dual-section DFB QCLs, which represents a further step towards their application in high-performance spectroscopic systems. Although, dual-section DFB-QCLs suffer from internal etaloning due to non-uniform heating in the device when only one of the sections is operated, we successfully mitigate this effect by applying AR coatings to the facets of the lasers. The resulting performance of the laser relies heavily on the design and fabrication of these coatings. We showed that a reduction from 26.9% to 0.6% in the laser facet reflectivity suppressed the intensity fluctuation amplitude due to etaloning from 100% to 15%. A refinement of the AR coating (e.g., by better layer thickness control, the use of additional layers, etc.) could further diminish the facet reflectivity, leading to even better laser intensity stability. Nevertheless, we demonstrated the suitability of the dual-section DFB QCL as a light source for high precision laser spectroscopic measurements. Thereby, three different trace gas species of great atmospheric relevance were simultaneously measured, despite their spectral separation of 90 cm−1, with a precision comparable to state-of-the-art analyzers based on single-DFB QCLs.
This constitutes a significant step towards compact, portable, and highly sensitive spectroscopic systems, which can be installed at industrial sites or even embedded in vehicles for atmosphere or exhaust monitoring.
Acknowledgments
This work was supported by the Nano-Tera funding agency (SNF) under the project name “IrSens 2”. The authors acknowledge ETHZ infrastructures FIRST and SCOPEM for the use of their facilities. We thank Philipp Scheidegger for the modification of the laser driver to drive dual-section DFB QCLs and BAFU for funding.
Author Contributions
M.J.S. designed, fabricated and characterized the lasers used in this work. J.M.W. designed the quantum cascade active region. S.R. designed and fabricated the AR coatings. M.B. grew the quantum cascade active region. M.J.S., R.P. and J.M.W. performed and interpreted the simulations. M.H. performed and analyzed the spectroscopic measurements. H.L. developed the software for hardware control, data acquisition and analysis, and the TMM simulation code. B.T., L.E. and J.F. designed and oversaw the experiments.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| CW | continuous wave |
| DFB | Distributed feedback |
| FEM | finite element methods |
| FIB | focused ion beam |
| HITRAN | high-resolution transmission |
| iCW | intermittent continuous wave |
| LIV | light-current-voltage |
| MCT | mercury cadmium telluride |
| MIR | mid-infrared |
| QCL | Quantum cascade laser |
| QWS | quarter wave shift |
| SEM | scanning electron microscope |
| SMSR | side mode suppression ratio |
| DTGS | deuterated triglycine sulphate |
| TMM | transfer matrix method |
| TTL | transistor-transistor-logic |
References
- Faist, J.; Capasso, F.; Sivco, D.L.; Sirtori, C.; Hutchinson, A.L.; Cho, A.Y. Quantum cascade laser. Science 1994, 264, 553–556. [Google Scholar] [CrossRef] [PubMed]
- Yao, Y.; Hoffman, A.J.; Gmachl, C.F. Mid-infrared quantum cascade lasers. Nat. Photon. 2012, 6, 432–439. [Google Scholar] [CrossRef]
- McManus, J.B.; Zahniser, M.S.; Nelson, D.D., Jr.; Shorter, J.H.; Herndon, S.; Wood, E.; Wehr, R. Application of quantum cascade lasers to high-precision atmospheric trace gas measurements. Opt. Eng. 2010, 49, 111124. [Google Scholar] [CrossRef]
- McManus, J.B.; Zahniser, M.S.; Nelson, D.D.; Shorter, J.H.; Herndon, S.C.; Jervis, D.; Agnese, M.; McGovern, R.; Yacovitch, T.I.; Roscioli, J.R. Recent progress in laser-based trace gas instruments: Performance and noise analysis. Appl. Phys. B 2015, 119, 203–218. [Google Scholar] [CrossRef]
- Faist, J. Quantum Cascade Lasers; OUP Oxford: Oxford, UK, 2013. [Google Scholar]
- Jouy, P.; Mangold, M.; Tuzson, B.; Emmenegger, L.; Chang, Y.-C.; Hvozdara, L.; Herzig, H.P.; Wagli, P.; Homsy, A.; de Rooij, N.F.; et al. Mid-infrared spectroscopy for gases and liquids based on quantum cascade technologies. Analyst 2014, 139, 2039–2046. [Google Scholar] [CrossRef] [PubMed]
- Vardag, S.N.; Gerbig, C.; Janssens-Maenhout, G.; Levin, I. Estimation of continuous anthropogenic CO2: Model-based evaluation of CO2, CO, δ13C(CO2) and δ14C(CO2) tracer methods. Atmos. Chem. Phys. 2015, 15, 12705–12729. [Google Scholar] [CrossRef]
- Tuzson, B.; Henne, S.; Brunner, D.; Steinbacher, M.; Mohn, J.; Buchmann, B.; Emmenegger, L. Continuous isotopic composition measurements of tropospheric CO2 at jungfraujoch (3580 m a.S.L.), Switzerland: Real-time observation of regional pollution events. Atmos. Chem. Phys. 2011, 11, 1685–1696. [Google Scholar] [CrossRef]
- Huebner, M.; Welzel, S.; Marinov, D.; Guaitella, O.; Glitsch, S.; Rousseau, A.; Roepcke, J. Triple Q: A three channel quantum cascade laser absorption spectrometer for fast multiple species concentration measurements. Rev. Sci. Instrum. 2011, 82, 093102. [Google Scholar] [CrossRef] [PubMed]
- Baren, R.E.; Parrish, M.E.; Shafer, K.H.; Harward, C.N.; Quan, S.; Nelson, D.D.; McManus, J.B.; Zahniser, M.S. Quad quantum cascade laser spectrometer with dual gas cells for the simultaneous analysis of mainstream and sidestream cigarette smoke. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2004, 60, 3437–3447. [Google Scholar] [CrossRef] [PubMed]
- Gmachl, C.; Sivco, D.L.; Colombelli, R.; Capasso, F.; Cho, A.Y. Ultra-broadband semiconductor laser. Nature 2002, 415, 883–887. [Google Scholar] [CrossRef] [PubMed]
- Straub, A.; Gmachl, C.; Sivco, D.L.; Sergent, A.M.; Capasso, F.; Cho, A.Y. Simultaneously at two wavelengths (5.0 and 7.5 um) singlemode and tunable quantum cascade distributed feedback lasers. Electron. Lett. 2002, 38, 565–567. [Google Scholar] [CrossRef]
- Jagerska, J.; Jouy, P.; Hugi, A.; Tuzson, B.; Looser, H.; Mangold, M.; Beck, M.; Emmenegger, L.; Faist, J. Dual-wavelength quantum cascade laser for trace gas spectroscopy. Appl. Phys. Lett. 2014, 105, 161109. [Google Scholar] [CrossRef]
- Jagerska, J.; Jouy, P.; Tuzson, B.; Looser, H.; Mangold, M.; Soltic, P.; Hugi, A.; Broennimann, R.; Faist, J.; Emmenegger, L. Simultaneous measurement of NO and NO2 by dual-wavelength quantum cascade laser spectroscopy. Opt. Express 2015, 23, 1512–1522. [Google Scholar] [CrossRef] [PubMed]
- Fischer, M.; Tuzson, B.; Hugi, A.; Broennimann, R.; Kunz, A.; Blaser, S.; Rochat, M.; Landry, O.; Mueller, A.; Emmenegger, L. Intermittent operation of QC-lasers for mid-IR spectroscopy with low heat dissipation: Tuning characteristics and driving electronics. Opt. Express 2014, 22, 7014–7027. [Google Scholar] [CrossRef]
- Beck, M.; Hofstetter, D.; Aellen, T.; Faist, J.; Oesterle, U.; Ilegems, M.; Gini, E.; Melchior, H. Continuous wave operation of a mid-infrared semiconductor laser at room temperature. Science 2002, 295, 301–305. [Google Scholar]
- Bismuto, A. Mid-Infrared Quantum Cacade Lasers; ETH Zürich: Zürich, Switzerland, 2011. [Google Scholar]
- Levinsthein, M.; Rumyantsev, S.; Suhr, M. Handbook Series on Semiconductor Parameters; World Scientific: London, UK, 1996. [Google Scholar]
- Tipler, P.A. Physics for Scientists and Engineers, 6th ed.; W.H. Freeman and Company: New York, NY, USA, 2008. [Google Scholar]
- Bilek, J.; Atkinson, J.K.; Wakeham, W.A. Thermal conductivity of molten lead-free solders. Int. J. Thermophys. 2006, 27, 92–102. [Google Scholar]
- Dinwiddie, R.B.; Whittaker, A.J.; Onn, D.G. Thermal conductivity, heat capacity, and thermal diffusivity of selected commercial aln substrates. Int. J. Thermophys. 1989, 10, 1075–1084. [Google Scholar]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Wittmann, A.; Bonetti, Y.; Fischer, M.; Faist, J.; Blaser, S.; Gini, E. Distributed-feedback quantum-cascade lasers at 9 um operating in continuous wave up to 423 k. IEEE Photon. Technol. Lett. 2009, 21, 814–816. [Google Scholar] [CrossRef]
- Gmachl, C.; Straub, A.; Colombelli, R.; Capasso, F.; Sivco, D.L.; Sergent, A.M.; Cho, A.Y. Single-mode, tunable distributed-feedback and multiple-wavelength quantum cascade lasers. IEEE J. Quantum Electron. 2002, 38, 569–581. [Google Scholar] [CrossRef]
- Coldren, L.A.; Corzine, S.; Masnovic, M.L. Diode Lasers and Photonic Integrated Circuits, 2nd ed.; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Bidaux, Y.; Bismuto, A.; Tardy, C.; Terazzi, R.; Gresch, T.; Blaser, S.; Muller, A.; Faist, J. Extended and quasi-continuous tuning of quantum cascade lasers using superstructure gratings and integrated heaters. Appl. Phys. Lett. 2015, 107, 221108. [Google Scholar] [CrossRef]
- Slivken, S.; Bandyopadhyay, N.; Tsao, S.; Nida, S.; Bai, Y.; Lu, Q.Y.; Razeghi, M. Sampled grating, distributed feedback quantum cascade lasers with broad tunability and continuous operation at room temperature. Appl. Phys. Lett. 2012, 100, 261112. [Google Scholar] [CrossRef]
- Bismuto, A.; Bidaux, Y.; Tardy, C.; Terazzi, R.; Gresch, T.; Wolf, J.; Blaser, S.; Muller, A.; Faist, J. Extended tuning of mid-IR quantum cascade lasers using integrated resistive heaters. Opt. Express 2015, 23, 29715–29722. [Google Scholar] [CrossRef] [PubMed]
- Rothman, L.S.; Gordon, I.E.; Babikov, Y.; Barbe, A.; Chris Benner, D.; Bernath, P.F.; Birk, M.; Bizzocchi, L.; Boudon, V.; Brown, L.R.; et al. The HITRAN 2012 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2013, 130, 4–50. [Google Scholar] [CrossRef]
- Werle, P.; Mücke, R.; Slemr, F. The limits of signal averaging in atmospheric trace-gas monitoring by tunable diode-laser absorption spectroscopy (TDLAS). Appl. Phys. B 1993, 57, 131–139. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).